An Experimental Test of the Classical Interpretation of the Kaluza Fifth Dimension

Abstract

Kaluza was the first to realize that the four-dimensional gravitational field of general relativity and the classical electromagnetic field behave as if they were components of a five-dimensional gravitational field. We present a novel experimental test of the macroscopic classical interpretation of the Kaluza fifth dimension. Our experiment design probes a key feature of Kaluza unification—that electric charge is identified with motion in the fifth dimension. Therefore, we tested for a time dilation effect on an electrically charged clock. This test can also be understood as a constraint on time dilation from a constant electric potential of any origin. This is only the second such test of time dilation under electric charge reported in the literature, and a null result was obtained here. We introduce the concept of a charged clock in the Kaluza context, and discuss some ambiguities in its interpretation. We conclude that a classical, macroscopic interpretation of the Kaluza fifth dimension may require a timelike signature in the five-dimensional metric, and the associated absence of a rest frame along the fifth coordinate.

1. Introduction

Soon after Einstein published the field equations of general relativity, Kaluza [1] realized that the four-dimensional metric and the electromagnetic four-vector potential could be understood as components of a five-dimensional metric, and that classical gravitational and electromagnetic fields could be unified in a greater five-dimensional gravitational field.

The essence of the classical five-dimensional (5D) theory is to posit a 15-component 5D metric comprising the usual 10-component 4D metric, the electromagnetic four-vector potential, and a long-range scalar field. Applying the 5D vacuum Einstein equations to the 5D metric yields the 4D Einstein equations with electromagnetic sources, plus the vacuum Maxwell equations. Applying the 5D geodesic hypothesis to the same metric yields the 4D geodesic equation with the Lorentz force term. To this framework is added the constraint of the cylinder condition, where none of the fields depend on the fifth coordinate. Perhaps the most intriguing aspect of the 5D theory is its description of electric charge in terms of motion in the fifth dimension, as the fifth component of a energy–momentum–charge five-vector.

To account for the cylinder condition, Klein [2] introduced a quantum, compact interpretation for Kaluza’s fifth dimension that has characterized “Kaluza–Klein” theory ever since. However, we suspend that assumption and allow for a macroscopic, classical fifth dimension. There is no logical necessity to a compact interpretation of the fifth dimension [3], and the assumption does not affect the form of the classical field equations treated in the literature.

The cylinder condition as a mathematical statement is akin to a boundary condition: derivatives of classical fields, with respect to the fifth coordinate, are zero. This assigns the apparent invisibility of the fifth dimension, if it exists at all, to the lack of variation of any field along that coordinate. This is quite different than Klein’s explanation for the invisibility of the fifth dimension: that it is microscopic and compact.

Our investigation here is purely classical. Electric charge is a specific quality of matter, like density, and not necessarily tied to any quantized charge carriers. Infinitesimal volumes used to construct integrals are still assumed to be macroscopic and composed of many particles. In fact, the cylinder condition implies variation in the fifth coordinate to be only on cosmological scales, not on quantum length scales. Particle accelerator experiments will not bear on the behavior of the classical systems considered here, except possibly to constrain the existence of particles mediating the long-range scalar field. The cylinder condition can be accepted as a boundary condition necessary to pursue the mathematical fact that classical electromagnetism and gravity behave as if they are aspects of five-dimensional gravity.

A series of researchers have worked over the succeeding decades to develop the classical theory of Kaluza, which is essentially a species of scalar–tensor gravity, similar to the Brans–Dicke theory. Kaluza originally set the long-range scalar field to a constant, but it is now understood that proper treatment of the scalar field is essential to the viability of the overall theory. For an overview of the various research groups who worked on the classical scalar–tensor theory in the 20th century, see [3,4]. The correct field equations and 5D curvature tensors for the Kaluza classical theory, including the long-range scalar field, were established in 2015 with the aid of tensor algebra software [5]. There are some errors in the literature, but authors in [6,7] also obtained the correct Lagrangian and field equations. The fifth dimension has historically been considered to have a spacelike signature, e.g., [3,6,8], but the Lagrangian established in [5] seems to argue for a timelike signature.

Kaluza’s concept of a fifth dimension is intriguing but so far has been immune to verification or falsification, to the extent it reproduces general relativity and electromagnetism exactly in the limit of a constant scalar field. We can only say for sure that if the Einstein equations are written in five dimensions, then the four-dimensional Einstein equations are obtained along with the Maxwell equations of electromagnetism.

Without presuming the reality of the fifth dimension, we can continue with the hypothesis, proceeding on the grounds that similarities of the laws of gravity and electromagnetism to five-dimensional gravity may lead to potentially testable predictions that would verify or falsify the 5-dimensional theory, or which may lead to other discoveries.

2. Time Dilation Implied by a Macroscopic Fifth Dimension

Kaluza’s original paper [1] included all the elements of the classical five-dimensional theory: five-dimensional Einstein equations, metric, energy-momentum tensor, and geodesic equation; the cylinder condition; and, of interest for this study, the identification of electric charge with motion in the fifth dimension. Just as momentum arises from motion in space, and energy from “motion” in time, electric charge arises from “motion” in the fifth dimension.

The equations of motion under the 5D hypothesis, and the associated identification of electric charge with motion along the fifth coordinate, have been extensively studied [3,6,7,9]. Because the length of the proper velocity 5-vector is invariant, its projections in 4D are variable. Therefore, depending on how one assigns 4D electric charge to the fifth component of the particle five-velocity, variable charges or variable masses seem to be implied [9]. The variability in charge or mass is a 5D analog to 4D time dilation or length contraction, or to the frame-dependence of 4D particle kinetic energy.

Because of this interpretation of electric charge in terms of 5D motion, we might expect a time dilation effect analogous to the standard time dilation of a moving clock. We are therefore led to the concept of an electrically charged clock. Such a clock is understood to have a finite speed along the fifth coordinate, even while it is at rest in space, and we wish to investigate whether there is a time dilation effect for charged clocks. Just as time dilation was investigated in the internal clocks of muons in motion through the atmosphere, we investigate whether macroscopic charge states of clocks show any evidence of anomalous time dilation or time contraction.

Consider Kaluza’s theory [3,5,6,7] in the field-free case of flat 5D space, but in the special-relativistic limit of the 5D theory, where the electromagnetic field vanishes and the scalar field is a constant. The 5D metric becomes a 5D Minkowski metric. Then the invariant 5D proper time $d\theta$ is given by:

$$c^{2}d{\theta }^2=\left|c^{2}d{t}^2-d{\mathbf{x}}^2\pm {\left(d{x}^5\right)}^2\right|\to c^{2}d{t}^2-{\left(d{x}^5\right)}^2,$$

(1)

where c is the speed of light, $dt$ is the time and $d\mathbf{x}$ is the 3D space coordinates, and the fifth dimension coordinate element is $d{x}^5$. We allow for either signature in the metric for ${\left(d{x}^5\right)}^2$, spacelike or timelike. The last relation is obtained by restricting our considerations to a fixed point in space.

In order for the 5D geodesic equation to reproduce the 4D Lorentz force, the speed along the fifth coordinate must be identified with the charge Q and mass m of a body as:

$$k\frac{d{x}^5}{dt}⟶\frac{Q}{m}.$$

(2)

This assignment accords with that chosen by [3,7], but is different than [9].

The value of k is fixed by correspondence of the decomposed 5D field equations with the 4D Einstein equations:

$$k^2\equiv \frac{16\pi G}{c^4{\mu }_0}\equiv \frac{16\pi G{ϵ}_0}{c^2},$$

where G is the gravitational constant, ${\mu }_0$ is the permeability of free space, and ${ϵ}_0$ is the permittivity of free space. MKS units are adopted to make the electromagnetic constants explicit. In MKS units, distance is measured in meters, mass in kilograms, and time in seconds.

We can therefore rewrite Equation (1) suggestively

$$c^{2}d{\theta }^2=c^{2}d{t}^2(1\pm {\beta }_5^2)\equiv c^{2}d{t}^2/{\gamma }_5^2,$$

(3)

where

$${\beta }_5=\frac{Q/m}{\sqrt{16\pi G{ϵ}_0}}.$$

(4)

Elementary particles have ${\beta }_5\gg 1$. For an electron, ${\beta }_5\sim {10}^{20}$. For a proton, ${\beta }_5\sim {10}^{17}$. Strictly speaking, the Kaluza theory is not applicable to elementary particles; it is purely classical, expressing the limit of the Planck constant $\hslash \to 0$. The classical gravitational and electrical constants form a charge-to-mass ratio that characterizes the strength of the coupling, and which is substantially lower than that of elementary particles. Clocks and other complex systems of many particles will have much lower charge-to-mass ratios than the elementary particles.

Consider the case of two time coordinates $t_{\mathrm{in}}$ for a charged frame inside a conducting sphere, and $t_{\mathrm{out}}$ for the lab frame outside the sphere in which the sphere carries charge. Inside the sphere, the electric field is zero, and there is no electric charge detected in this frame. In the zero-charge reference frame inside the sphere $d\theta =d{t}_{\mathrm{in}}$ by Equation (3). Equation (3) predicts that intervals of time $\Delta t_{\mathrm{in}}$ inside the sphere are related to intervals of time $\Delta t_{\mathrm{out}}$ outside the sphere by

$$\Delta t_{\mathrm{out}}={\gamma }_5\Delta t_{\mathrm{in}}.$$

(5)

Depending on the signature in the metric of the fifth coordinate, time can pass faster or slower than outside the sphere. Using the expression for potential V of a charged sphere of radius R and mass M, we can write

$${\beta }_5=\sqrt{\frac{\pi {ϵ}_0}{G}}\frac{RV}{M}.$$

(6)

For a clock inside a conducting sphere of radius 0.5 m, charged to 20,000 V, of combined mass 1 kg, ${\beta }_5=6300$. In the limit of ${\beta }_5\gg 1$, $|{\gamma }_5|\simeq 1/{\beta }_5$. Therefore, it seems that very large dilation effects are possible.

3. Comparison of the Kaluza Result to Known Effects

The Reissner–Nordström (RN) metric is an example of time dilation/contraction from electric charge. In that case, the time coordinate undergoes a contraction due to electric charge:

$$d{\tau }^2=d{t}^2\left(1-\frac{2GM}{r{c}^2}+\frac{Q^{2}G}{r^{2}4\pi {ϵ}_0{c}^4}\right),$$

(7)

where r is the radial distance from the charged body. The time dilation from the gravity of the mass M is counteracted by time contraction from the charge Q.

Of course, RN is the vacuum solution for the space embedded with electric field from a charge. The mass M can be set to zero in Equation (7) and the solution is still valid. The charge can be at a point or on a shell at some radius $r>0$. As an observer falls toward a massless charge, her clock speeds up compared to the clock of an observer at infinity.

Setting aside the sign for now (dilation or contraction), we see that the dilation effect scales differently between the RN solution and the Kaluza hypothesis. Combining Equations (3) and (4), the Kaluza time variation is

$$d{\theta }^2=d{t}^2\left(1\pm \frac{Q^2/M^2}{16\pi G{ϵ}_0}\right).$$

(8)

The RN effect in Equation (7) is proportional to $Q^{2}G$, whereas the Kaluza effect in Equation (8) is proportional to $Q^2/M^{2}G$. Since G is a small number, the Kaluza effect is dramatically larger than the RN time contraction. This is a major distinction between the Kaluza effect and RN effect.

Let us go on to consider the classical solution interior to the RN metric, that is, the solution to the combined equations of general relativity and electrodynamics inside a bounded charged medium. These interior solutions were examined first by [10,11]. They found, not surprisingly, that the charge contributes to the mass seen at infinity.

Indeed, the charge part of the RN solution in Equation (7) is due to the mass-equivalent energy of the electrostatic field. One can start with a charge Q, write the electrostatic self-energy as an equivalent mass: $M_Q=E_Q/c^2$ and $E_Q=(1/4\pi {ϵ}_0)(Q^2/2r)$, and find $2G{M}_Q/r{c}^2=(1/4\pi {ϵ}_0)Q^{2}G/r^2{c}^4$.

However, the authors in [10] also found that the non-linear effect of gravity is important to determining the total or “clothed" mass of a classical charged point particle. Earlier efforts to assign the mass of an elementary particle to its charge were confounded by the divergence of the electrostatic energy for a point particle. Gravity stablizes the divergence of the electrostatic self-energy and keeps the total mass finite [10].

The relativistically correct self-energy is expressible in simple Newtonian terms. The total mass is the sum of the rest mass, gravitational self-energy, and electrostatic self-energy. Crucially, the gravitational self-energy couples to the total mass [10]:

$$m{c}^2=m_0{c}^2+\frac{1}{4\pi {ϵ}_0}\frac{Q^2}{2\delta }-\frac{G{m}^2}{2\delta },$$

(9)

where $\delta$ is the radius of the body of charge Q and mass m.

The Equation (9) is quadratic in the total mass m, and it has finite roots in the limit that $\delta \to 0$:

$$m\to \pm Q/\sqrt{4\pi {ϵ}_{0}G}.$$

(10)

As $\delta \to 0$, the electrostatic self-energy increases, but this is coupled to the gravitational self-energy, with the net effect of balancing the electrostatic divergence in the total energy that would otherwise occur. It is remarkable that the limit does not depend on the rest mass $m_0$. Of course, Equation (10) is purely classical, and it does not describe any elementary particle.

Nonetheless, we see in Equation (10) the same functional dependence between mass, charge, and the gravitational constant as in Equation (8). It expresses the equivalency of mass and charge that is implied by identifying electric charge with a component of an energy–momentum–charge five-vector. There is obviously a connection between the Kaluza result and the ADM mass [10].

4. Experiment Configuration and Result

Time dilation in the framework of special and general relativity has been extensively tested [12], measuring effects related to the velocity or the gravitational potential. It is essential to take time dilation into account to get accurate measurements using global positioning satellite networks such as GPS or Galileo, and dedicated experiments are being carried out using atomic clocks in space to test the effects at even higher precision [13,14,15]. The influence of electrostatic potential on time dilation using the RN metric has recently been discussed by Özer [16], proposing experiments to be done with optical clocks.

Separate from the Kaluza interpretation, our measurement can be understood as a generic test for a time dilation effect for a clock in a region of constant electric potential, where the electric field is zero in the region of the clock. If such an experiment detects the Kaluza time dilation effect, it may not necessarily validate the Kaluza theory, but rather, just indicate a time dilation effect from electric potential. Let us clarify that in this case, we are referring to an effect of the electric potential above and beyond the known gravitational time dilation due to the energy of the electric field around the shielded clock, and that would be described by the RN metric.

The only test so far of time dilation for an electrically charged clock was from Ringermacher et al. [17], although they were testing a different theory than the one investigated here. They measured time dilation using nuclear magnetic resonance and a proton sample (Benzene) inside a cylinder charged up to 5 kV. They reported a null result with $\Delta t/t\le {10}^{-9}$. However, in the Ringermacher setup, the coil inside the cylinder was connected with wires to an outside power supply (with its own ground potential) and one may wonder if any time dilation effect that should be present in the proton sample also affected the protons and electrons in the cable in a way that could have distorted the measurement.

The goal of this work is to test time dilation with an atomic clock inside a charged sphere that is read through an optical fiber such that no charges can travel between the inside and outside of the sphere, to isolate the measurement as much as possible.

The experimental setup is shown in Figure 1. An atomic clock (Rubidium atomic frequency standard FE-5680A with an Allan deviation of $1.4\times {10}^{-11}/\sqrt{t}$ and drift of $5\times {10}^{-11}$/day) is placed in the middle of a hollow aluminum sphere with an outer diameter of 48.5 cm and a thickness of 1 mm. The clock is powered by a rechargeable battery, which enables operation for around 80 min. The clock has a standard frequency of 10 MHz, which is transmitted through a glass fiber cable using two radio frequency (RF) fiber transmitter modules (RFOptic RFoF-2.5 GHz). The frequency is then determined using a counter (Tektronix FCA3100 with 12-digit frequency resolution) and a 10 s gate time. The sphere can be charged up to +/−20 kV using a high-voltage power supply. Both the power supply and the frequency counter are controlled and monitored using software on a computer.

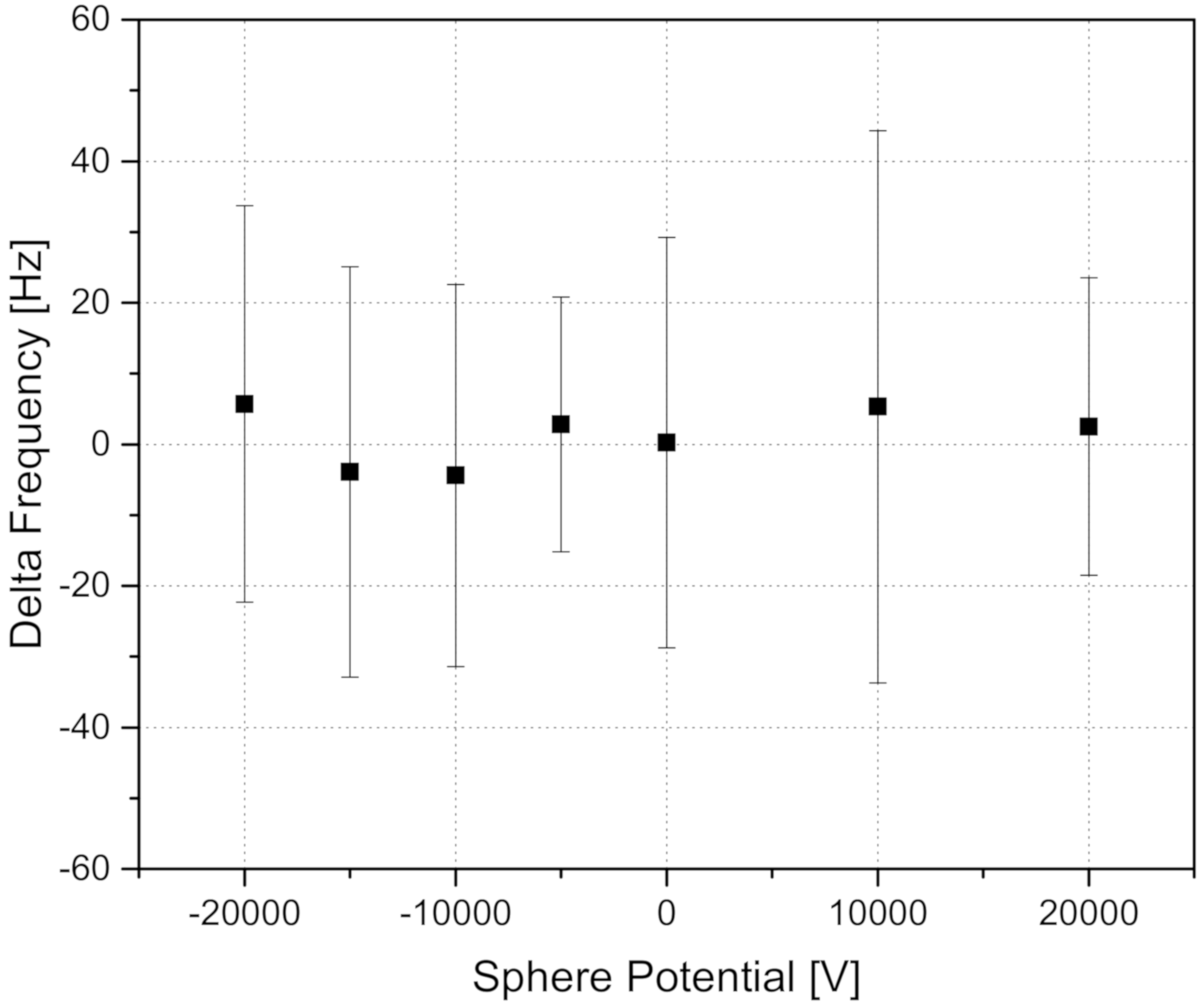
The experiment executes profiles which consist of 100 s at 0 V, then a 10 s ramp up to the designed potential, followed by a 10 s ramp down, and a 100 s again at 0 V. This allows us to determine the drift of the atomic clock before and after the sphere is charged. A linear fit along those 0 V points then subtracts the drift, and only frequency variations without drift allow us to assess the noise and any influence of the applied potential. Examples of the frequency variations along one such profile are shown in Figure 2.

Several such profiles can be signal-averaged in order to reduce the noise. Figure 3 shows frequency variations with error bars along different applied potentials between –20 to +20 kV. No influence of the potential on the clock frequency can be seen within our noise level of around 20 Hz. Using linear regression along all points, we get an error of $\Delta f<\pm 1.1\times {10}^{-4}/V$. This leads to an experimental limit at a constant potential of 20 kV of

$$\frac{\Delta t}{t}=\frac{\Delta f}{f}\le 2.2\times {10}^{-7},$$

(11)

where f is the atomic clock frequency.

This frequency noise is about one order of magnitude higher compared to the atomic clock’s drift, which is due to additional noise from the counter and the RF-optical link as well as possible temperature-related drifts. We consider this a null result with respect to any Kaluza time dilation effect from a charged reference frame. The expected effect was within our ability to measure. Our result can also be understood as a generic limit on time dilation of clocks at non-zero electrostatic potential, with a zero electric field.

5. Discussion and Conclusions

A null result in our time dilation measurement suggests several possibilities regarding the interpretation of the fifth dimension.

One is that while our treatment of time dilation might be correct, the coefficient of the fifth coordinate in the metric is much smaller than the space and time metric coefficients, so the 5D metric is not truly Minkowskian. This would imply that the Kaluza long-range scalar field is much smaller than one, or—equivalently—that the fifth dimension is microscopic. This could act to suppress any observable time dilation. However, based on the form of the field equations and Lagrangian [5], we consider it unlikely for the scalar field to be so small, even if it is constant. The proper 4D limit of the Kaluza theory is for the scalar field to go to unity.

A second possibility is a conceptual problem in our application of the Kaluza conditions. Because the interior of the sphere is neutral, only the charged shell of the sphere is actually moving in the fifth dimension. The Kaluza effect should apply strictly only to the layer of charge on the surface of the sphere. We can perhaps understand the error as analogous to looking for time dilation inside a spinning sphere, when only the moving parts of the sphere will experience time dilation from the rotational motion of the sphere. In this case, a definitive test would require a clock that is somehow uniformly smeared with electric charge.

Even so, there is an ambiguity in this case that is not present in the case of the spinning sphere. A Gaussian integral around the sphere identifies only the enclosed charge, not how it is distributed inside the sphere. From the standpoint of the Gaussian integral, the electric charge may well be smeared uniformly throughout the sphere volume. However, such a truly charged reference frame would be indistinguishable from one which is not. There should furthermore be a limit where the clock is small enough inside a shell that it is indistinguishable experimentally from being charged.

In light of this degeneracy in the measurable distribution of charge from outside a charged object, we might expect the experiment performed to be still dispositive on the question of time dilation of a charged clock, and so we hold open this possibility. However, we recommend seeking a more definitive test that somehow insures that the clock has some non-zero charge density throughout its mechanism, akin to an electric clock. We concede the strength of electrostatic forces may well make such a thing impossible to build mechanically.

Perhaps one may look in this regard to the half-lives of isotopes of nuclei. Just as muon decay was used to confirm relativistic time dilation, perhaps unstable nuclides can be identified with very similar quantum states and decay paths, differing only in the charge-to-mass ratio, and therefore in the degree of Kaluza time dilation of their half-lives.

A third possible interpretation of the null result is that there is no rest frame for electric charge. Instead of being akin to a spatial coordinate, in which there is always a frame in which momentum vanishes, the fifth dimension may instead be more akin to a time coordinate, in which there is no rest frame. The electrostatic energy of motion along the fifth coordinate does not vanish in the rest frame, just as rest mass does not vanish in the rest frame. In this regard, we are led to the concept of a rest charge in the Kaluza theory: the Kaluza theory does predict a weak variation of electric charge, violating its status as a Lorentz scalar.

This third possible interpretation of the null result comes somewhat unexpected, as there is a view in the literature that the signature of the fifth coordinate in the 5D metric must be spacelike [3,6,8]. However, an investigation of the Lagrangian for the Kaluza theory suggests that the relative sign difference in the Lagrangian results without any assumption regarding the sign of the fifth coordinate [5].

We consider this the most conservative interpretation of a Kaluza macroscopic fifth dimension, in light of our experiment and consideration of the Lagrangian—that the fifth dimension may be timelike, with no rest frame.

Due to the ambiguity in distinguishing a time coordinate reference frame that is electrically charged throughout from one that is charged only on the boundary, a definitive test of the Kaluza time dilation hypothesis may require a clock which can be constructed from purely charged matter. This could be realized with a two-dimensional clock that can be embedded on a charged surface. By purely charged matter, we mean having a net charge density everywhere. Although all matter is charged, it has a zero net charge. This effect apparently requires a non-zero net charge.

We also note that our test can be used to set a limit on the parametrization of time dilation due to a clock held at fixed electric potential. The RN time dilation is too small to be of interest, so we are searching for other effects for the experimental parameters reported here. A further extension of this line of thought is to search for time dilation effects inside a region of constant magnetostatic potential.