Simulation of Spatial Spread of the COVID-19 Pandemic on the Basis of the Kinetic-Advection Model
Abstract
:1. Introduction
2. Mathematical Model
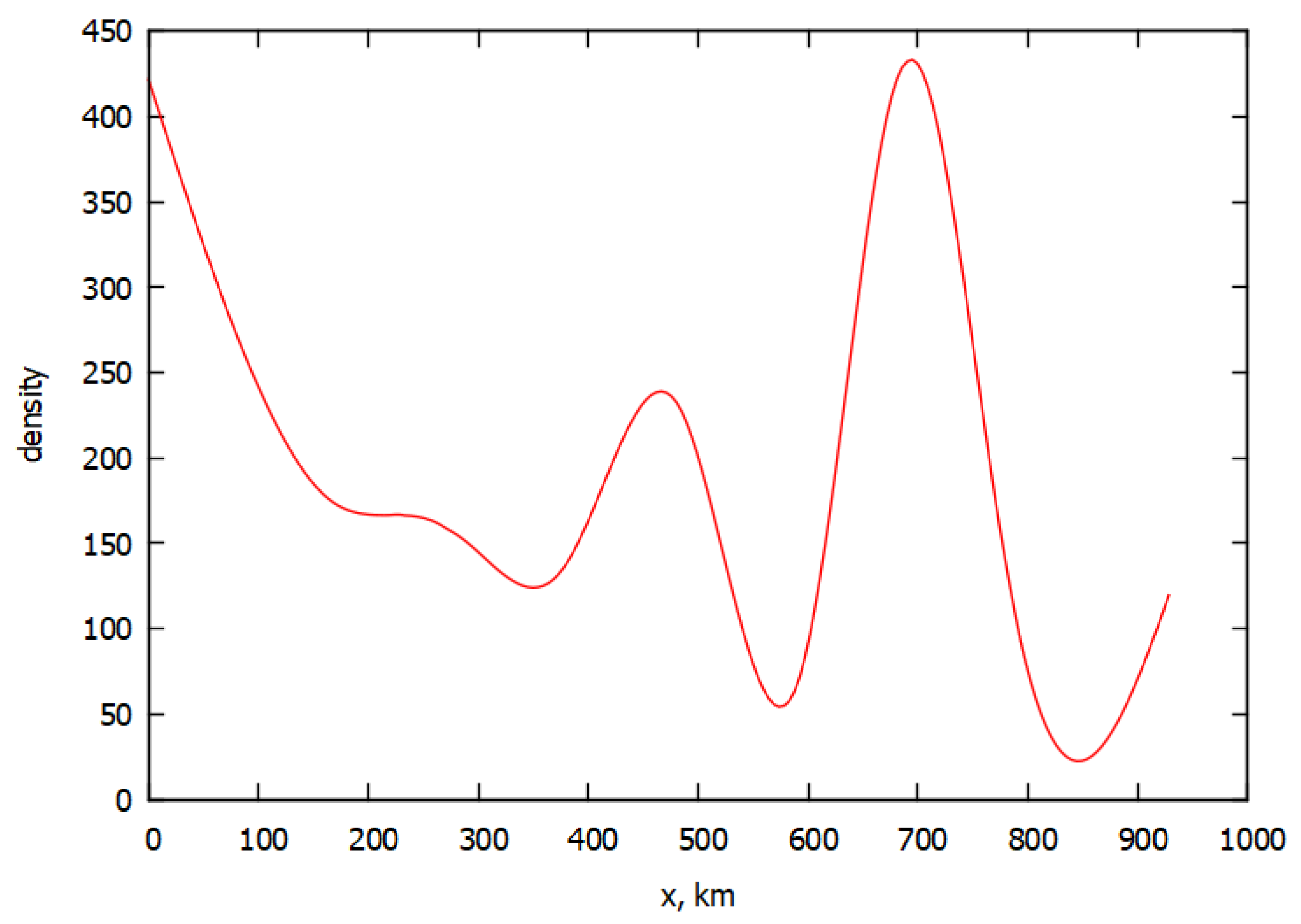
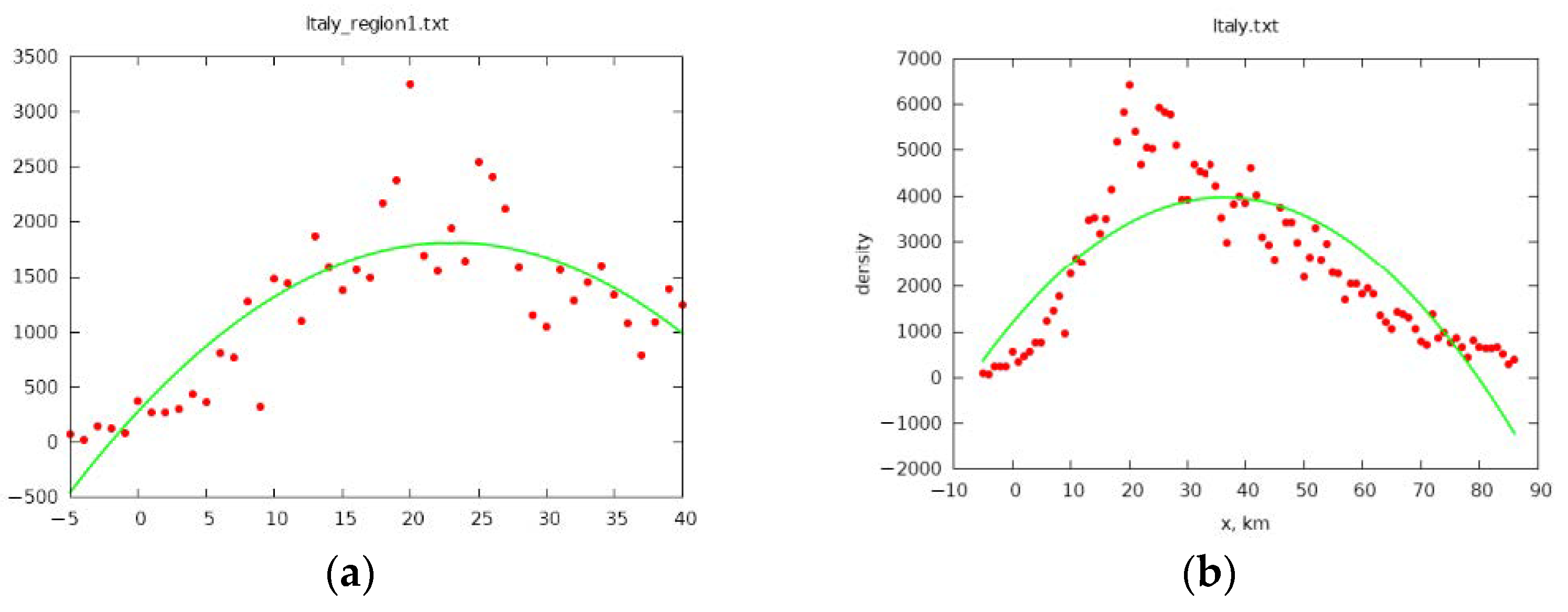
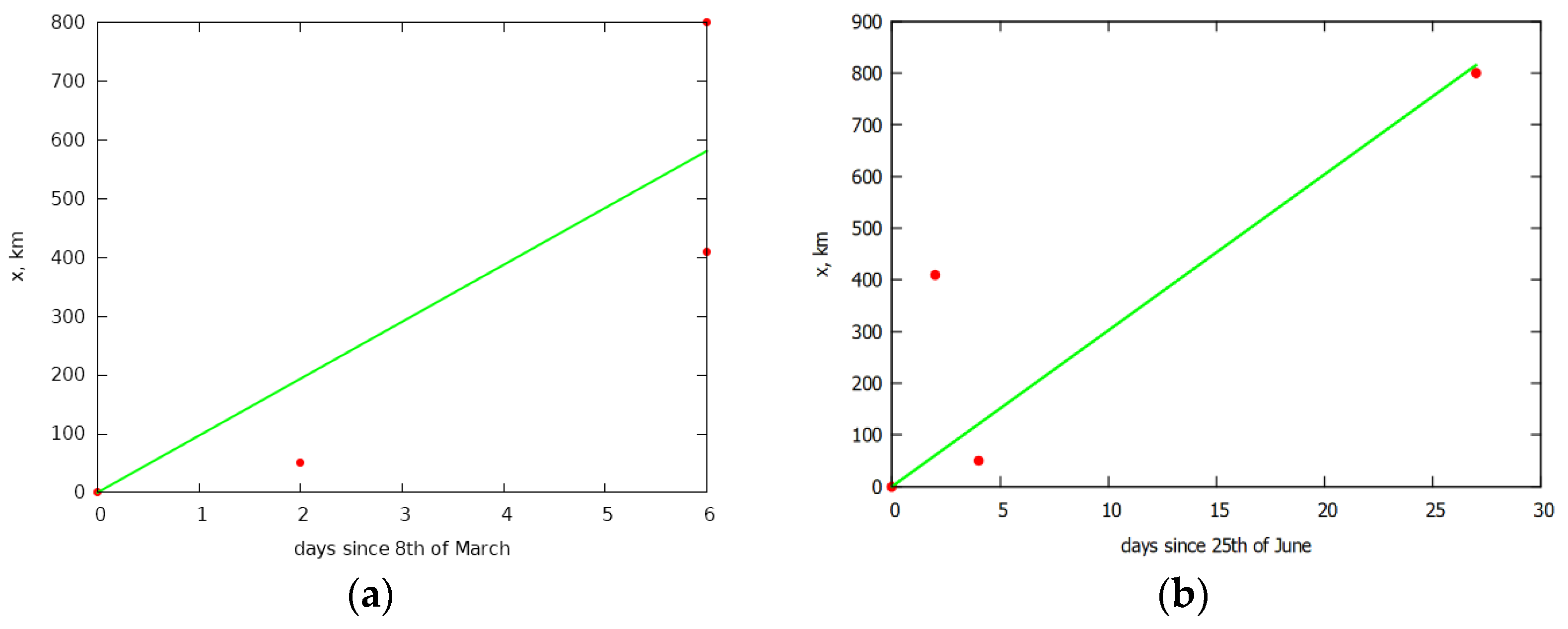
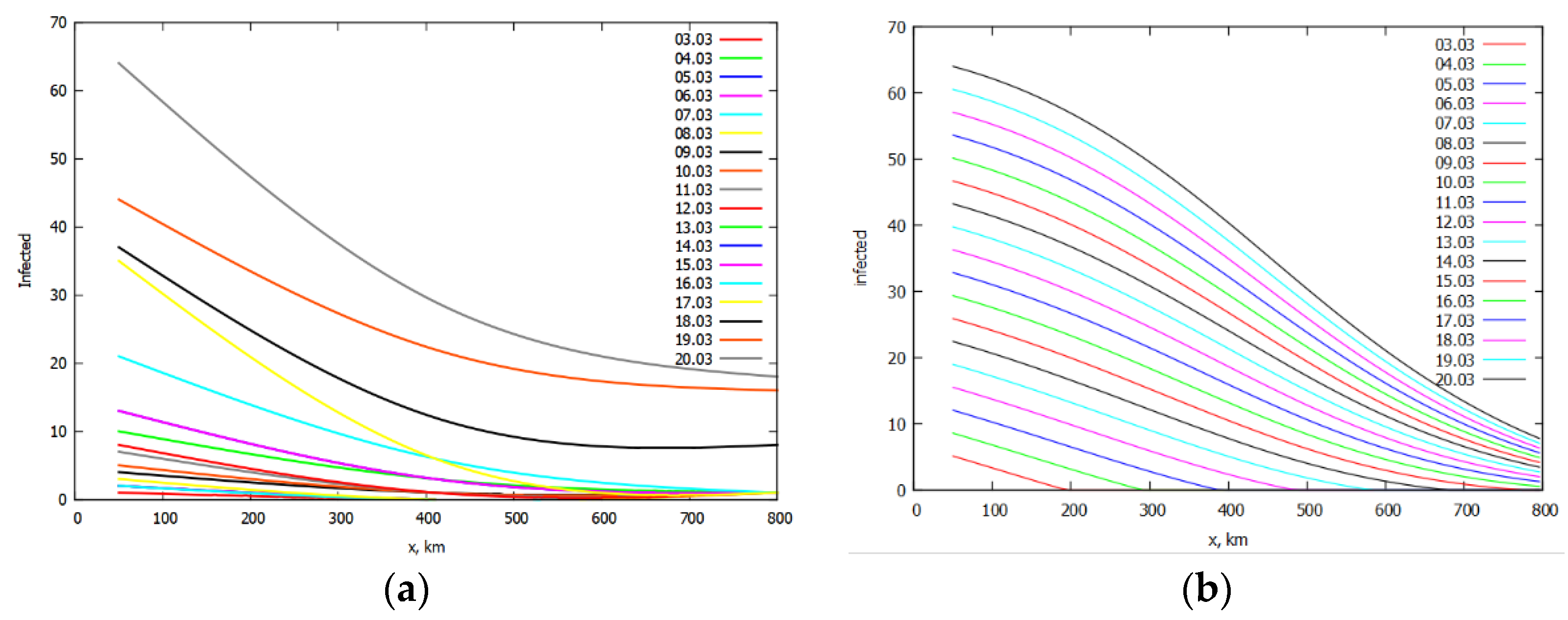
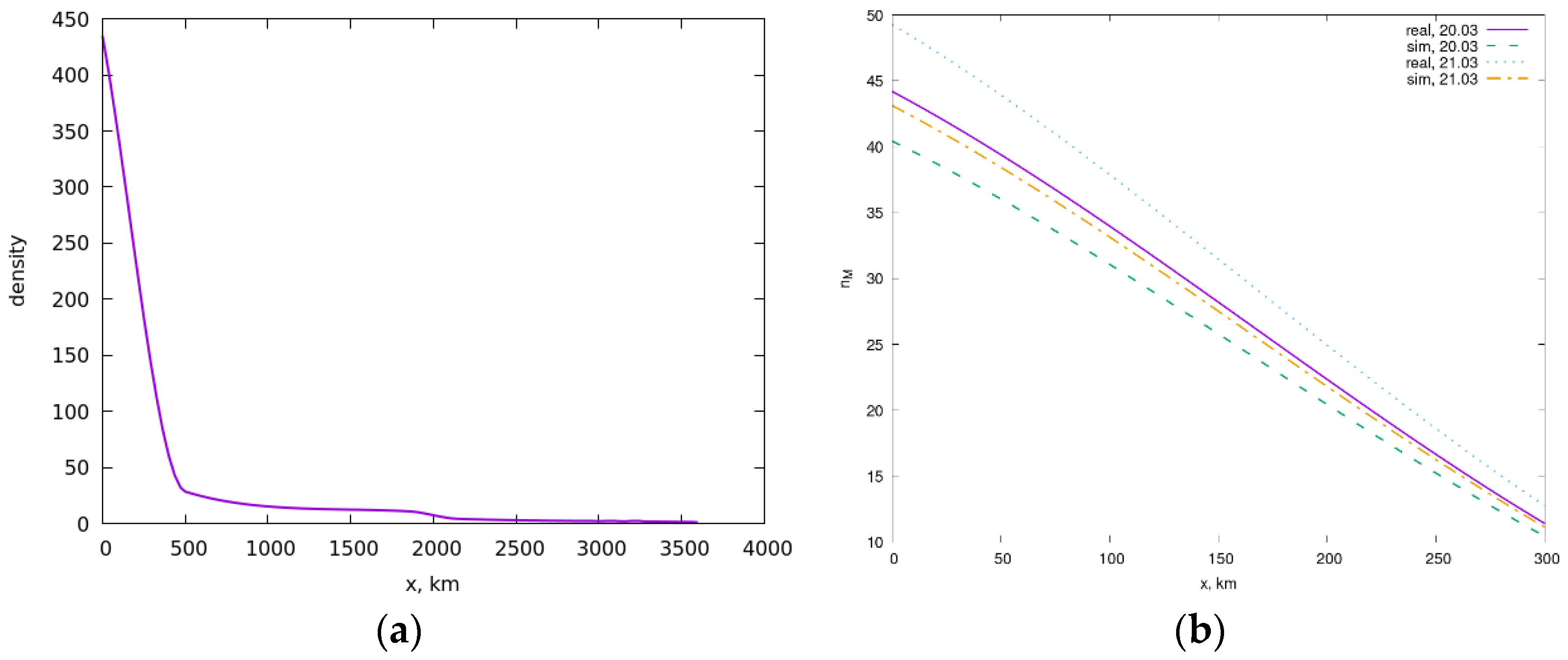
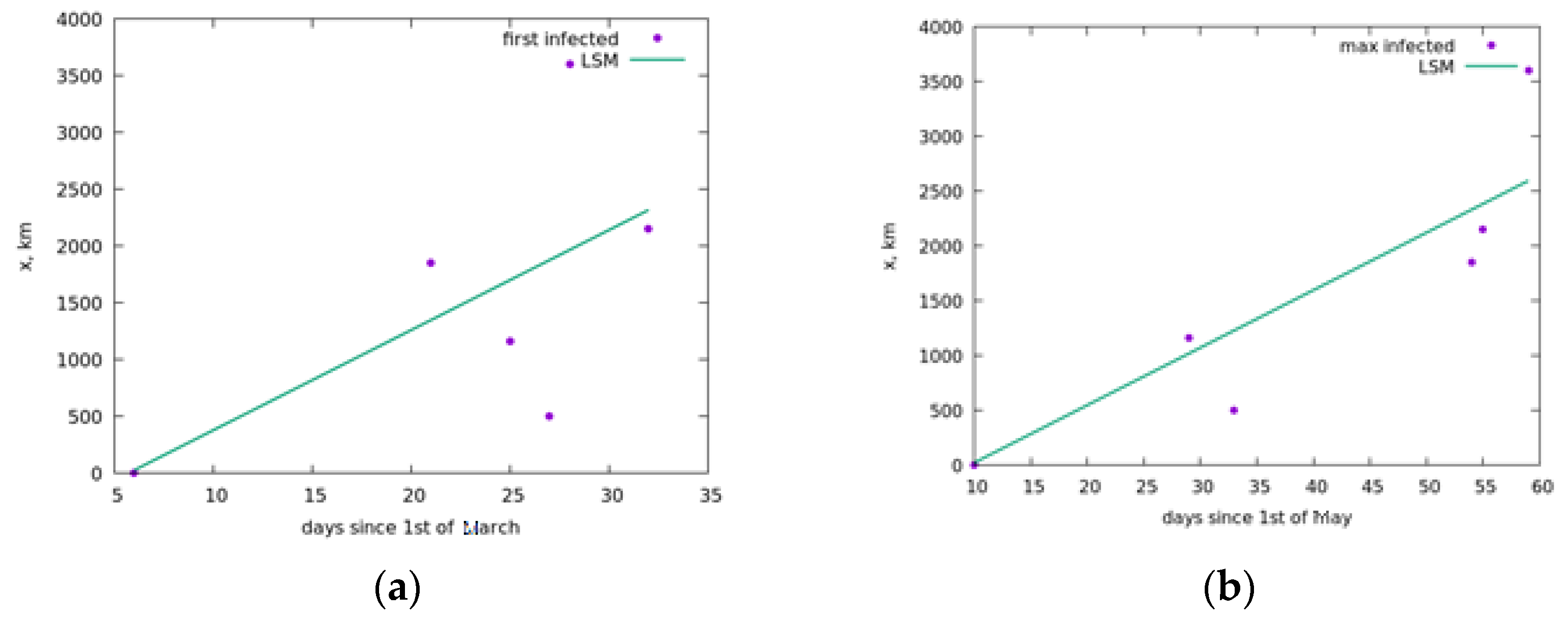
3. Simulation of the Spread of the Epidemic in Italy
4. Simulation of the Spread of the Epidemic in Chile
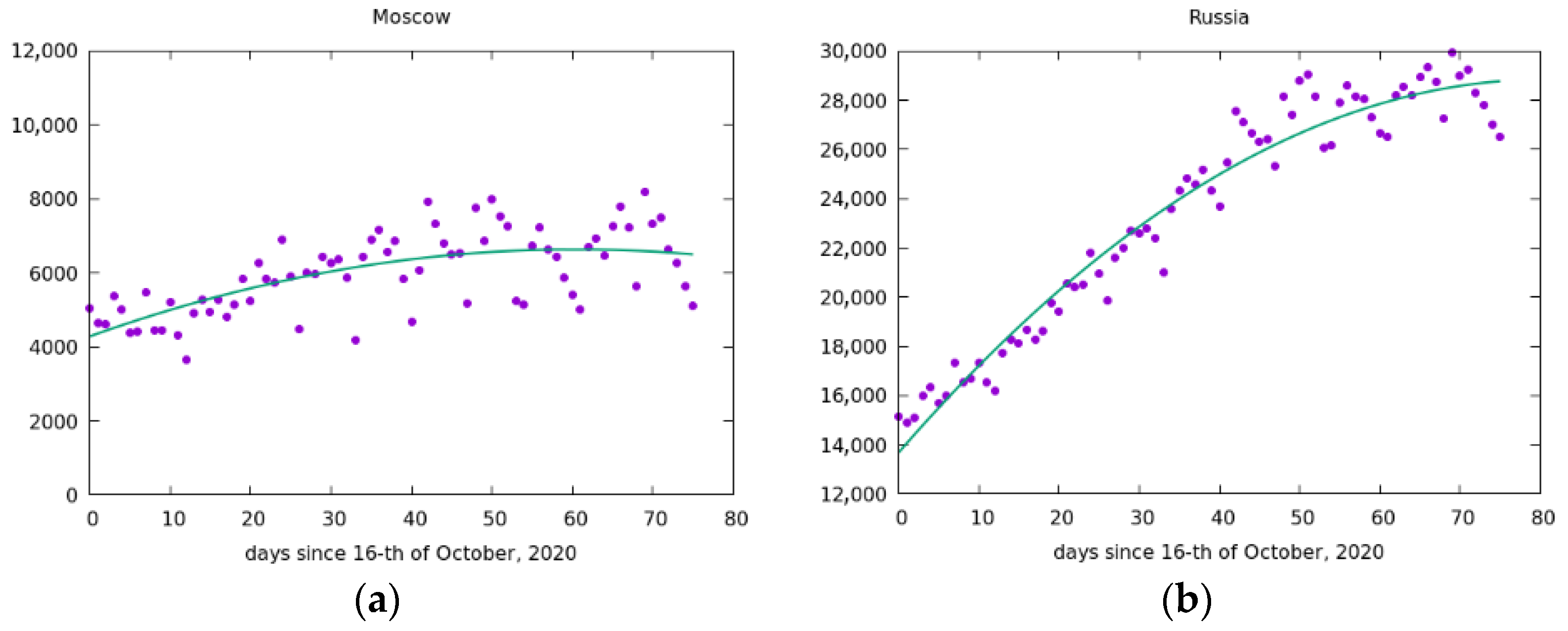
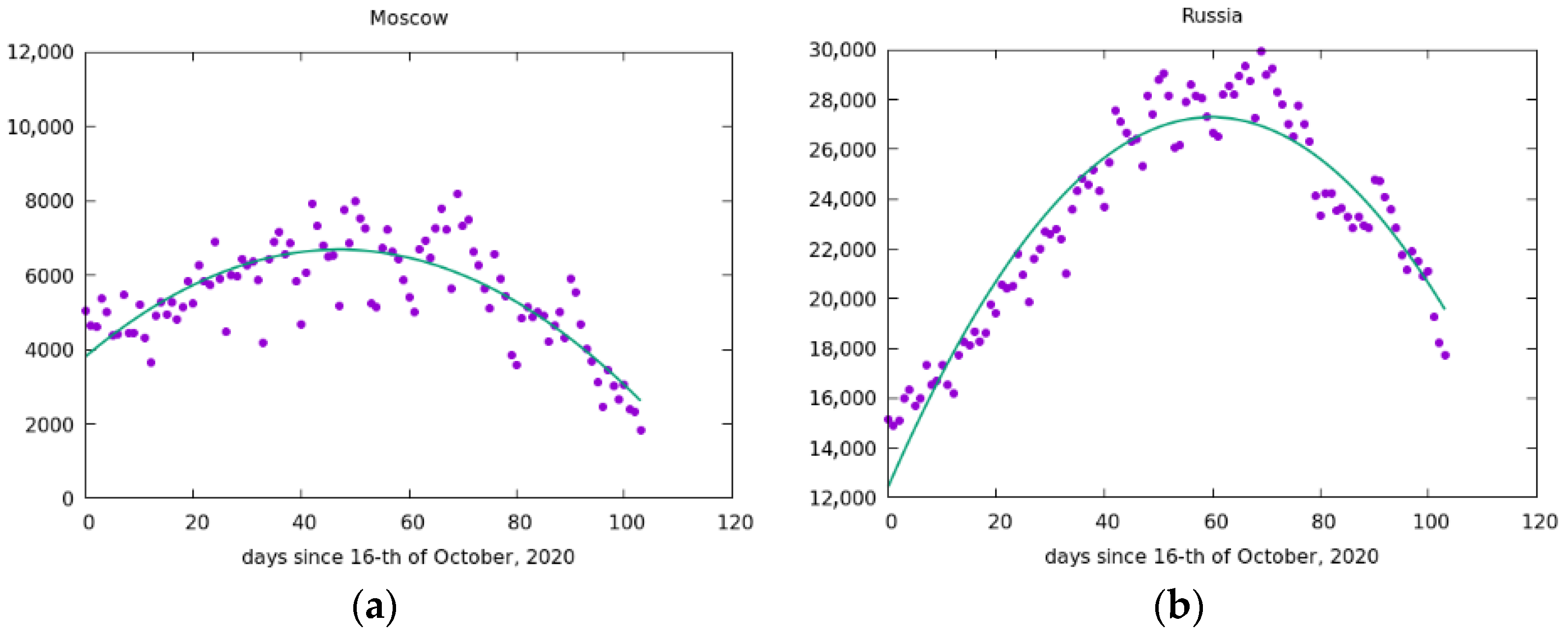
5. Simulation of the Spread of the Epidemic in Russia
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. C++ Code for Computing for Russia
References
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. A 1927, 115, 700–721. [Google Scholar] [CrossRef] [Green Version]
- Anderson, R.M.; May, R.M. Infectious Diseases in Humans; Oxford University Press: Oxford, UK, 1992. [Google Scholar] [CrossRef] [Green Version]
- Van Kampen, N.G. Stochastic Processes in Chemistry and Physics; North Holland: Amsterdam, The Neteerlands, 1981. [Google Scholar] [CrossRef]
- Pastukhova, S.E.; Evseeva, O.A. Large-time asymptotic of the solution to the diffusion equation and its application to homogenization estimates. Russ. Technol. J. 2017, 5, 60–69. [Google Scholar] [CrossRef]
- Ivorra, B.; Ferrández, M.R.; Vela-Pérez, M.; Ramos, A.M. Mathematical modeling of the spread of the coronavirus disease 2019 (COVID-19) taking into account the undetected infections. The case of China. Commun. Nonlinear Sci. Numer. Simul. 2020. [Google Scholar] [CrossRef]
- Neipel, J.; Bauermann, J.; Bo, S.; Harmon, T.; Jülicher, F. Power-law population heterogeneity governs epidemic waves. PLoS ONE 2020, 15, e0239678. [Google Scholar] [CrossRef]
- Gross, B.; Zheng, Z.; Liu, S.; Chen, X.; Sela, A.; Li, J.; Li, D.; Havlin, S. Spatio-temporal propagation of COVID-19 pandemics. EPL (Europhys. Lett.) 2020, 131, 5. [Google Scholar] [CrossRef]
- Ribeiro, H.V.; Sunahara, A.S.; Sutton, J.; Perc, M.; Hanley, Q.S. City size and the spreading of COVID-19 in Brazil. PLoS ONE 2020, 15, e0239699. [Google Scholar] [CrossRef] [PubMed]
- Ramírez-Aldana, R.; Gomez-Verjan, J.C.; Bello-Chavolla, O.Y. Spatial analysis of COVID-19 spread in Iran: Insights into geographical and structural transmission determinants at a province level. PLoS Negl. Trop. Dis. 2020, 14, e0008875. [Google Scholar] [CrossRef] [PubMed]
- Ascani, A.; Faggian, A.; Montresor, S. The geography of COVID-19 and the structure of local economies: The case of Italy. J. Reg. Sci. 2020, 1–35. [Google Scholar] [CrossRef]
- Saffary, T.; Adegboye, O.A.; Gayawan, E.; Elfaki, F.; Kuddus, M.A.; Saffary, R. Analysis of COVID-19 Cases’ Spatial Dependence in US Counties Reveals Health Inequalities. Front. Public Health 2020, 12, 579190. [Google Scholar] [CrossRef] [PubMed]
- Map of COVID-19 Spread. Available online: https://yandex.ru/web-maps/covid19 (accessed on 20 December 2020).
- Spread of COVID-19 in Italy. Available online: http://lab24.ilsole24ore.com/coronavirus (accessed on 26 May 2020).
- Rospotrebnadzor. Available online: https://www.rospotrebnadzor.ru/about/info/news/news_details.php?ELEMENT_ID=16253&sphrase_id=2989389 (accessed on 20 December 2020).
- Spread of COVID-19 in Chile. Available online: https://www.minsal.cl/nuevo-coronavirus-2019-ncov/casos-confirmados-en-chile-COVID-19/ (accessed on 15 June 2020).
- Fischer, R.A. The wave of advance of advantageous genes. Ann. Eugen. 1937, 7, 355–369. [Google Scholar] [CrossRef] [Green Version]
- Kolmogorov, A.N.; Petrovskiy, I.G.; Piskunov, N.S. Issledovanie uravneniya diffuzii, soedinennoi s vozrastaniem kolichestva veschestva, i ego primenenie k odnoy biologicheskoy probleme. Bull. MGU Ser. A Math. Meh. 1937, 1, 1–25, English translation: Selected Works of A.N. Kolmogorov, Vol. I: Mathematics and Mechanics; Tikhomirov, V.M., Ed.; Springer: Dordrecht, The Netherlands, 1991; pp. 248–270. (Originally In Russian). [Google Scholar]
- Vasilev, V.A.; Romanovskiy, Y.M.; Yahno, V.G. Avtovolnovie Processi; Nauka: Moscow, USSR, 1987. (In Russian) [Google Scholar]
- Prigogine, I.; Herman, R. Kinetic Theory of Vehicular Traffic; Elsevier: New York, NY, USA, 1971. [Google Scholar]
- Aristov, V.V.; Ilyin, O.V. Kinetic Models for Historical Processes of Fast Invasion and Aggression. Phys. Rev. E 2015, 91, 04286. [Google Scholar] [CrossRef] [PubMed]
- Aristov, V.V. Direct Methods for Solving the Boltzmann Equation and Study of Nonequilibrium Flows; Springer Science & Business Media: Berlin, Germany, 2001. [Google Scholar] [CrossRef]
- John, F. Partial Differential Equations; Springer: New York, NY, USA, 1982. [Google Scholar] [CrossRef] [Green Version]
- Courant, R.; Isaacson, E.; Rees, M. On the solutions of nonlinear hyperbolic differential equations by finite differences. Comm. Pure Appl. Math. 1952, 5, 243–255. [Google Scholar] [CrossRef]





| № | Distance, km | Regions |
|---|---|---|
| 1 | 0 | Lombardy |
| 2 | 166 | Piedmont, Veneto, Emilia-Romagna, Liguria, Aosta Valley, Trentino-South Tyrol |
| 3 | 272 | Friuli Venezia Giulia, Tuscany |
| 4 | 376 | Marche, Umbria |
| 5 | 482 | Abruzzo, Lazio |
| 6 | 592 | Molise |
| 7 | 690 | Campania |
| 8 | 781 | Apulia, Basilicata |
| 9 | 933 | Calabria |
| № | Distance, km | Regions |
|---|---|---|
| 0 | 0 | Santiago |
| 1 | 50 | Coquimbo, Valparaíso |
| 2 | 470 | Atacama |
| 3 | 850 | Antofagasta |
| 4 | 1340 | Tarapacá, Arica and Parinacota |
| № | Distance, km | Regions |
|---|---|---|
| 0 | 0 | Santiago |
| 1 | 50 | O’Higgins, Maule, Ñuble |
| 2 | 470 | Biobío, Araucanía, Los Ríos |
| 3 | 850 | Los Lagos |
| № | Distance, km | Regions |
|---|---|---|
| 0 | Moscow, Moscow region | |
| 2 | 500 | Nizhny Novgorod Region, Ivanovo Region, Republic of Mordovia, Penza Region, Tambov Region, Volgograd Region, Ulyanovsk Region, Kostroma Region, Republic of Chuvashia, Republic of Mari El, Saratov Region |
| 3 | 1160 | Perm Territory, Republic of Komi, Republic of Bashkortostan, Orenburg Region, Samara Region, Republic of Tatarstan, Kirov Region, Nenets Autonomous District |
| 4 | 1850 | Tyumen region, Khanty-Mansi Autonomous Okrug, Kurgan region, Sverdlovsk region, Chelyabinsk region |
| 5 | 2150 | Omsk Region, Tomsk Region, Yamalo-Nenets Autonomous District, Novosibirsk Region |
| 6 | 3600 | Krasnoyarsk Territory, Irkutsk Region |
| 7 | 6000 | Khabarovsk Territory, Jewish Autonomous Region, Amur Re-gion, Primorsky Territory |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aristov, V.V.; Stroganov, A.V.; Yastrebov, A.D. Simulation of Spatial Spread of the COVID-19 Pandemic on the Basis of the Kinetic-Advection Model. Physics 2021, 3, 85-102. https://0-doi-org.brum.beds.ac.uk/10.3390/physics3010008
Aristov VV, Stroganov AV, Yastrebov AD. Simulation of Spatial Spread of the COVID-19 Pandemic on the Basis of the Kinetic-Advection Model. Physics. 2021; 3(1):85-102. https://0-doi-org.brum.beds.ac.uk/10.3390/physics3010008
Chicago/Turabian StyleAristov, Vladimir V., Andrey V. Stroganov, and Andrey D. Yastrebov. 2021. "Simulation of Spatial Spread of the COVID-19 Pandemic on the Basis of the Kinetic-Advection Model" Physics 3, no. 1: 85-102. https://0-doi-org.brum.beds.ac.uk/10.3390/physics3010008




