Ascending Aorta Resection and End-to-End Anastomosis: Redistribution of Wall Shear Stress Induced by a Bioprosthetic Heart Valve
Abstract
:1. Introduction
2. Materials and Methods
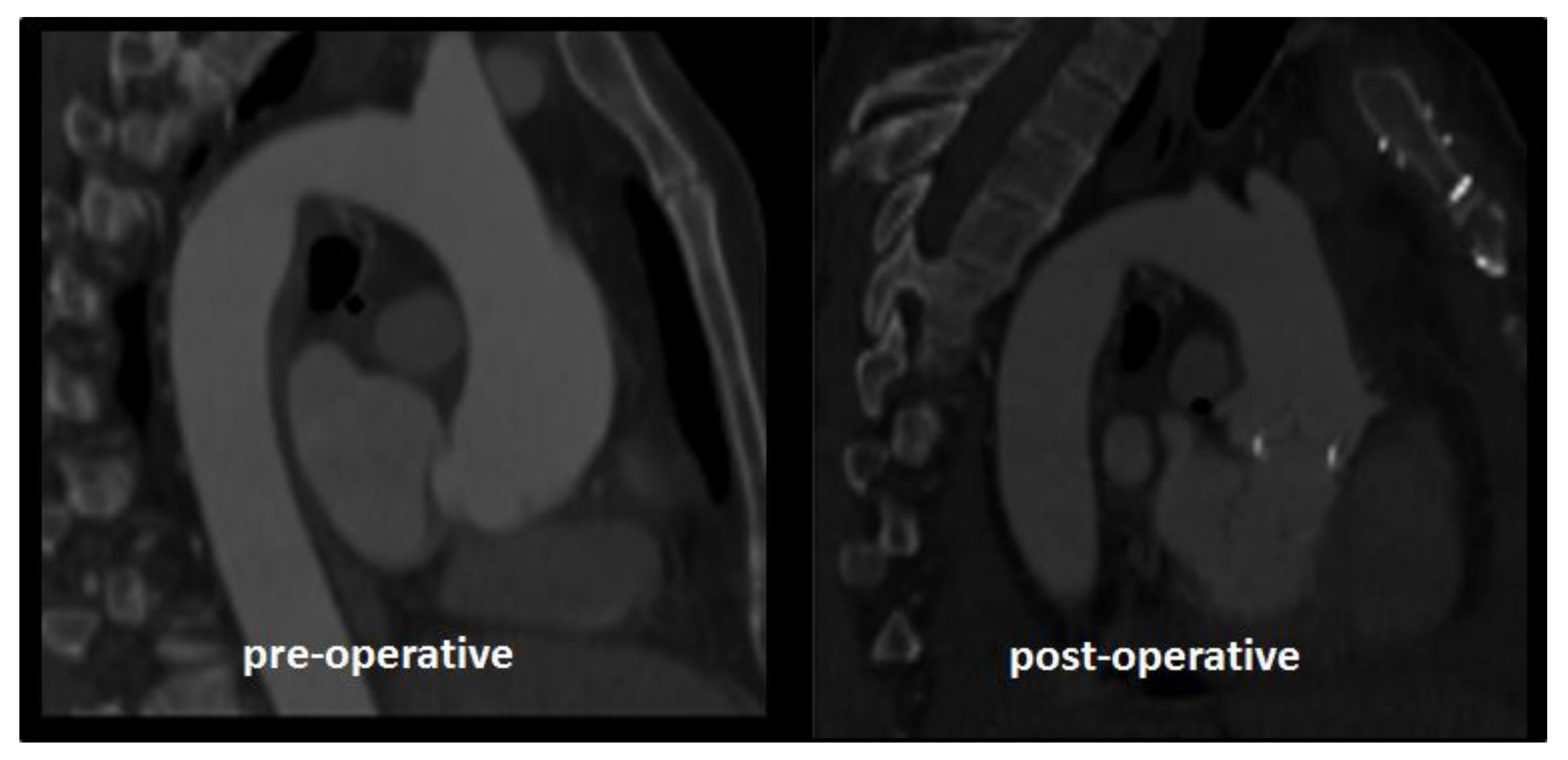
2.1. Case Study
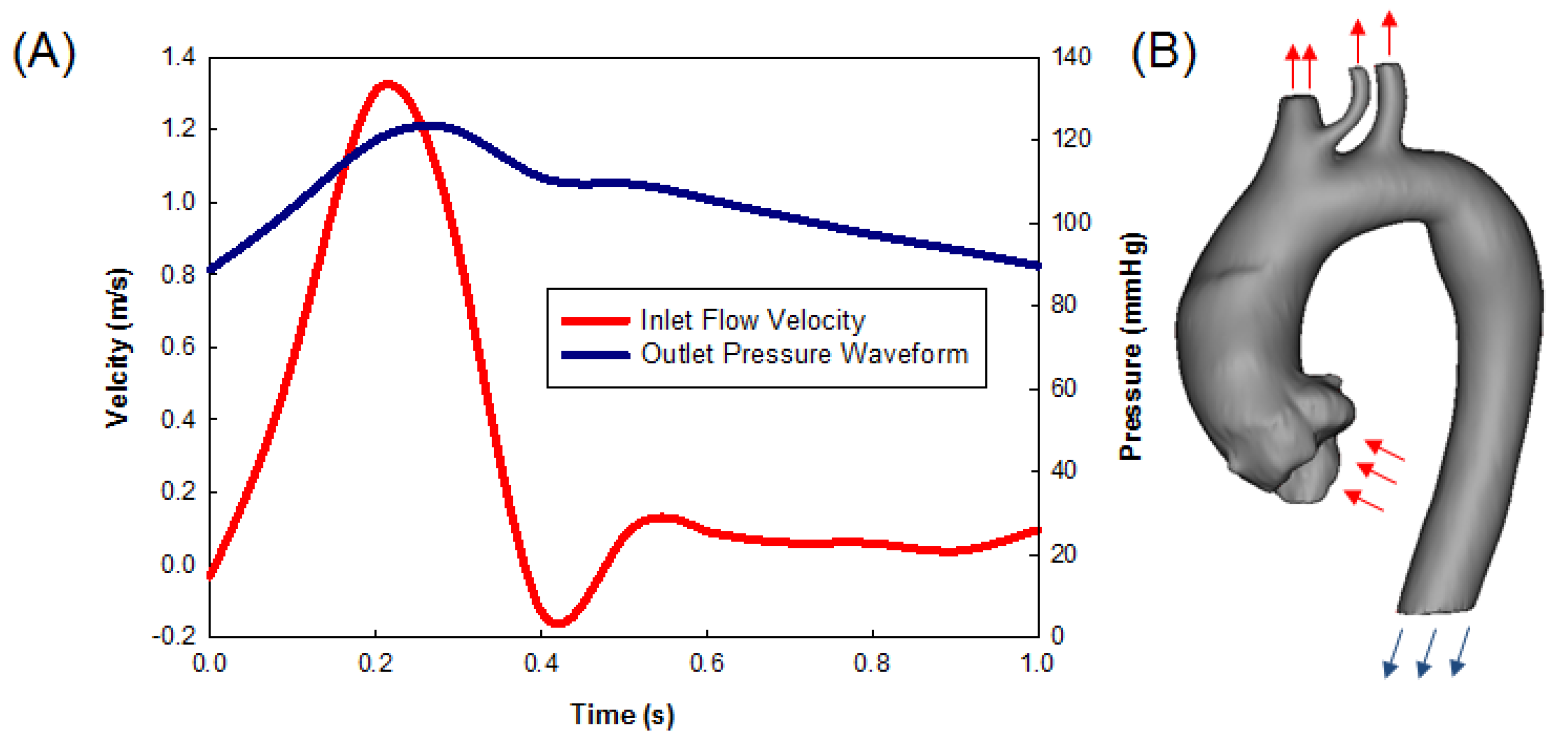
2.2. Computational Flow Analysis
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Massetti, M.; Veron, S.; Neri, E.; Coffin, O.; le Page, O.; Babatasi, G.; Buklas, D.; Maiza, D.; Gerard, J.L.; Khayat, A. Long-term durability of resection and end-to-end anastomosis for ascending aortic aneurysms. J. Thorac. Cardiovasc. Surg. 2004, 127, 1381–1387. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.J.; D’Ancona, G.; Amaducci, A.; Follis, F.; Pilato, M.; Pasta, S. Role of computational modeling in thoracic aortic pathology: A review. J. Card. Surg. 2014, 29, 653–662. [Google Scholar] [CrossRef] [PubMed]
- Cosentino, F.; Scardulla, F.; D’Acquisto, L.; Agnese, V.; Gentile, G.; Raffa, G.; Bellavia, D.; Pilato, M.; Pasta, S. Computational Modeling of Bicuspid Aortopathy: Towards Personalized Risk Strategies. J. Mol. Cell. Cardiol. 2019, 4, 122–131. [Google Scholar] [CrossRef] [PubMed]
- Rinaudo, A.; Raffa, G.M.; Scardulla, F.; Pilato, M.; Scardulla, C.; Pasta, S. Biomechanical implications of excessive endograft protrusion into the aortic arch after thoracic endovascular repair. Comput. Biol. Med. 2015, 66, 235–241. [Google Scholar] [CrossRef] [PubMed]
- Gallo, A.; Agnese, V.; Coronello, C.; Raffa, G.M.; Bellavia, D.; Conaldi, P.; Pilato, M.; Pasta, S. On the Prospect of Serum Exosomal miRNA Profiling and Protein Biomarkers for the Diagnosis of Ascending Aortic Dilatation in Patients with Bicuspid and Tricuspid aortic Valve. Int. J. Cardiol. 2018. [Google Scholar] [CrossRef] [PubMed]
- Pasta, S.; Agnese, V.; Di Giuseppe, M.; Gentile, G.; Raffa, G.M.; Bellavia, D.; Pilato, M. In-vivo Strain Analysis of Dilated Ascending Thoracic Aorta by ECG-gated CT Angiographic Imaging. Ann. Biomed. Eng. 2017, 45, 2911–2920. [Google Scholar] [CrossRef] [PubMed]
- Davies, R.R.; Goldstein, L.J.; Coady, M.A.; Tittle, S.L.; Rizzo, J.A.; Kopf, G.S.; Elefteriades, J.A. Yearly rupture or dissection rates for thoracic aortic aneurysms: Simple prediction based on size. Ann. Thorac. Surg. 2002, 73, 17–28. [Google Scholar] [CrossRef]
- Ikonomidis, J.S.; DeAnda, A.; Miller, D.C. Resection of ascending aortic aneurysm without use of an interposition aortic graft. J. Thorac. Cardiovasc. Surg. 2001, 122, 395–397. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Park, C.B.; Greason, K.L.; Suri, R.M.; Michelena, H.I.; Schaff, H.V.; Sundt, T.M., 3rd. Fate of nonreplaced sinuses of Valsalva in bicuspid aortic valve disease. J. Thorac. Cardiovasc. Surg. 2011, 142, 278–284. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mendez, V.; Di Giuseppe, M.; Pasta, S. Comparison of Hemodynamic and Structural Indices of Ascending Thoracic Aortic Aneurysm as predicted by 2-way FSI, CFD Rigid Wall Simulation and Patient-Specific Displacement-Based FEA. Comput. Biol. Med. 2018. [Google Scholar] [CrossRef] [PubMed]
- Khanafer, K.; Berguer, R. Fluid-structure interaction analysis of turbulent pulsatile flow within a layered aortic wall as related to aortic dissection. J. Biomech. 2009, 42, 2642–2648. [Google Scholar] [CrossRef] [PubMed]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raffa, G.M.; Pasta, S. Ascending Aorta Resection and End-to-End Anastomosis: Redistribution of Wall Shear Stress Induced by a Bioprosthetic Heart Valve. Prosthesis 2020, 2, 297-303. https://0-doi-org.brum.beds.ac.uk/10.3390/prosthesis2040026
Raffa GM, Pasta S. Ascending Aorta Resection and End-to-End Anastomosis: Redistribution of Wall Shear Stress Induced by a Bioprosthetic Heart Valve. Prosthesis. 2020; 2(4):297-303. https://0-doi-org.brum.beds.ac.uk/10.3390/prosthesis2040026
Chicago/Turabian StyleRaffa, Giuseppe M., and Salvatore Pasta. 2020. "Ascending Aorta Resection and End-to-End Anastomosis: Redistribution of Wall Shear Stress Induced by a Bioprosthetic Heart Valve" Prosthesis 2, no. 4: 297-303. https://0-doi-org.brum.beds.ac.uk/10.3390/prosthesis2040026





