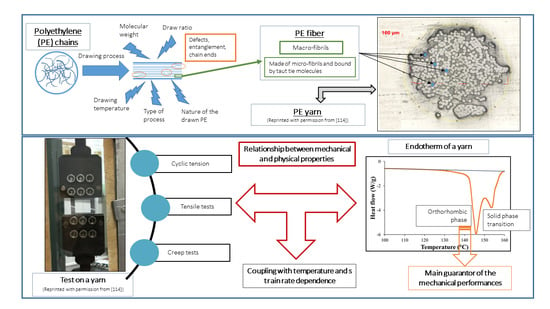
A Review of the Mechanical and Physical Properties of Polyethylene Fibers
Abstract
:1. Introduction
1.1. Context
1.2. Focus on PE Fibers
2. Basic Principles of Property Enhancement
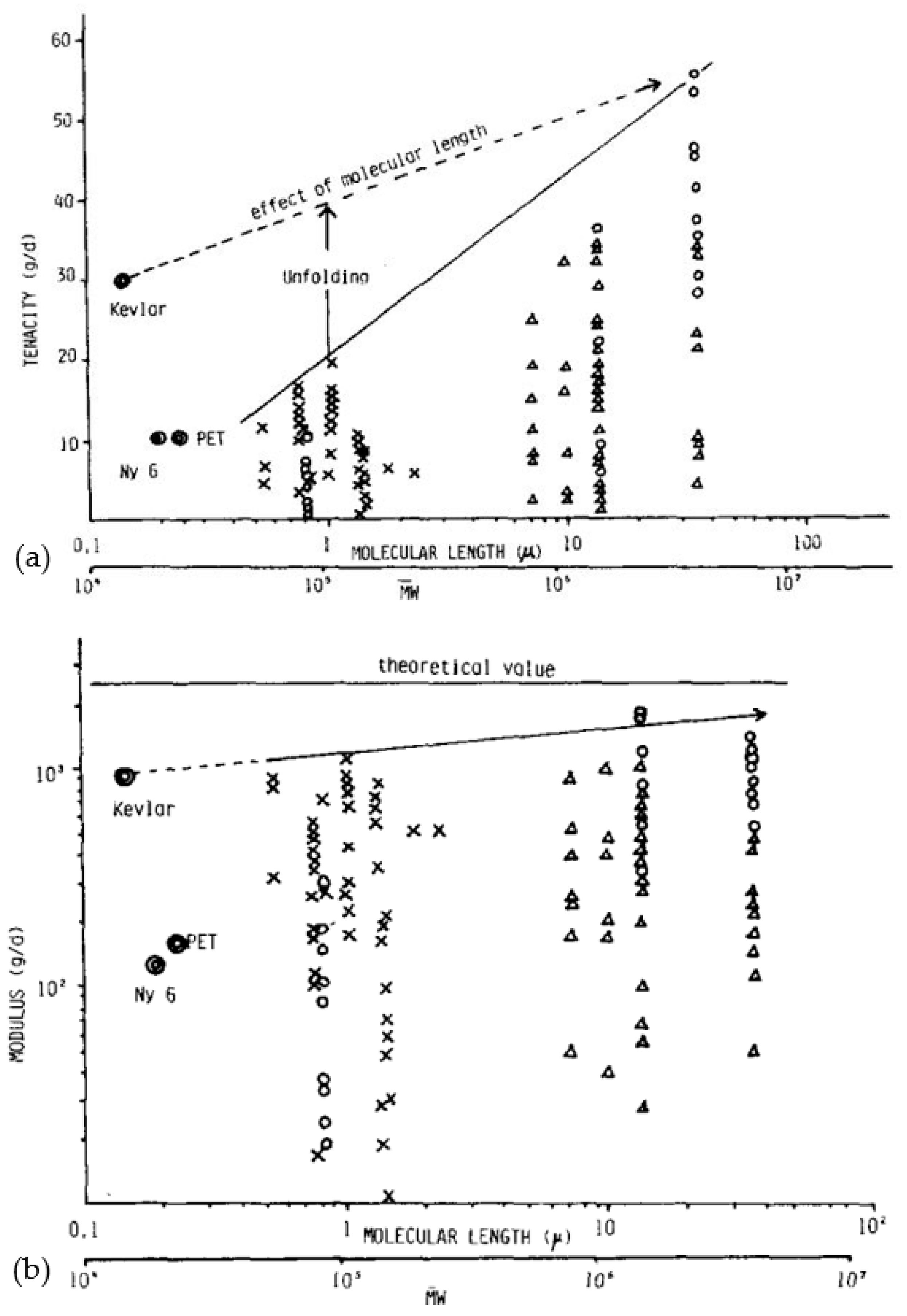
2.1. Outstanding Performance from a Basic Polymer
2.2. Processes
3. Molecular Structure
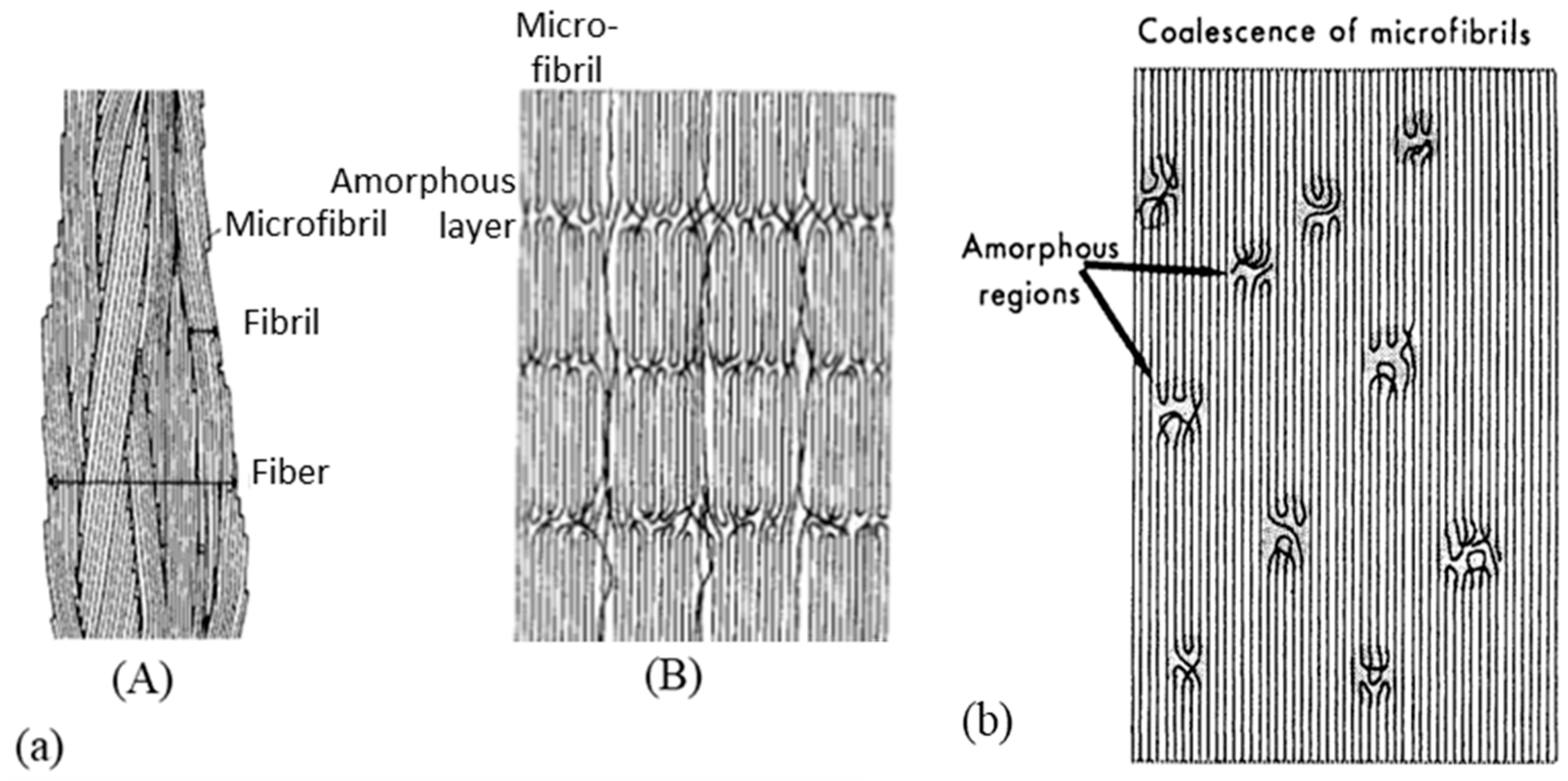
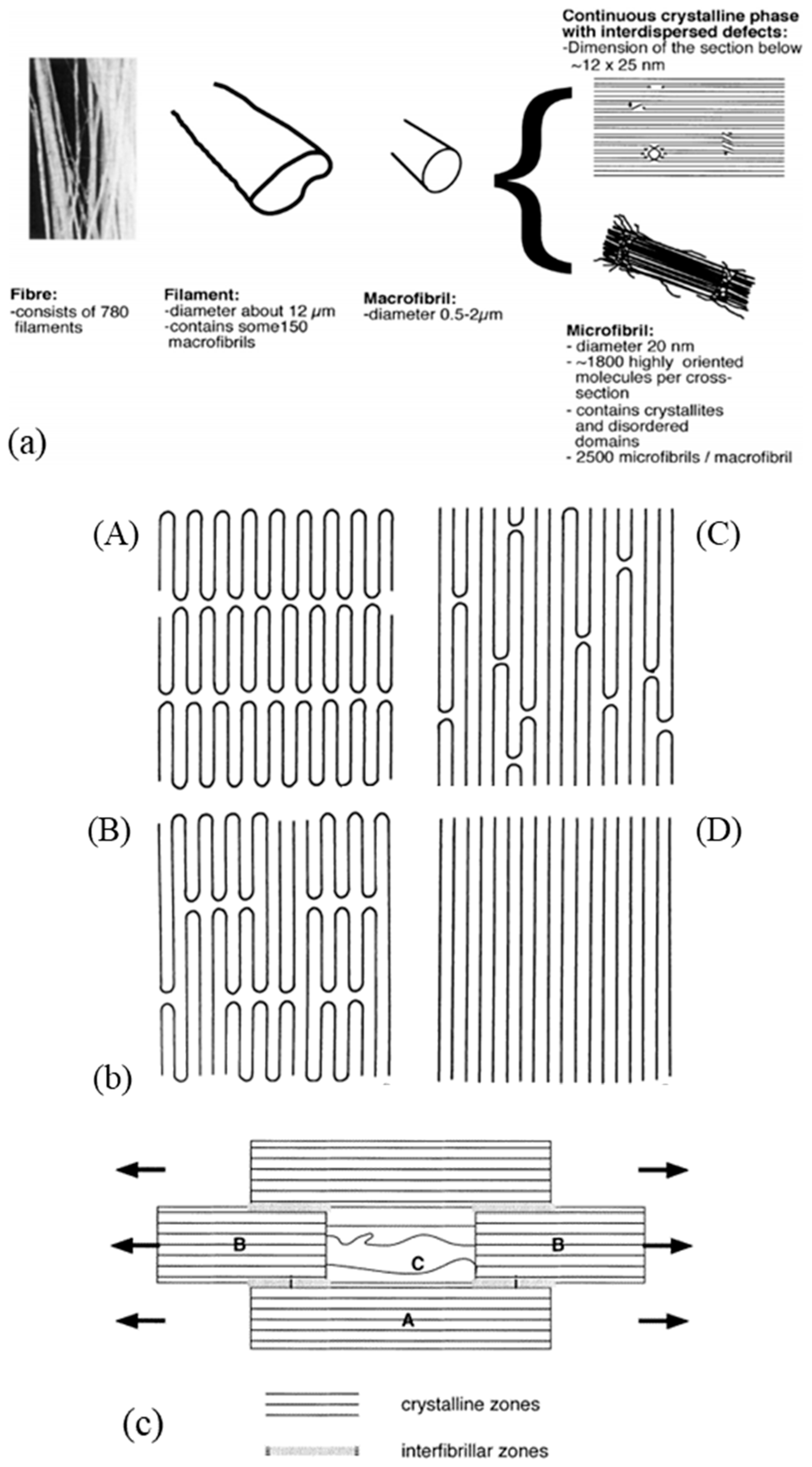
3.1. Microstructural Model
3.2. Structure Formation during the Process
- The continuous plastic deformation of the spherulites before necking, which occurs in the entire sample at approximately the same low stress;
- The transformation of the spherulites into fibrils, which he attributes to the breaking of the small crystal blocks that are present in the lamella packs, the reorientation, and rearrangement into stacks. This discontinuous transformation of the spherulitic into fiber structure is done by micro-necking. Indeed, the formation of bundles of microfibrils is encouraged by the cracking of the folded chain lamellae and by the presence of many micro-necks at the crack;
- The plastic deformation of these fibrils after the neck. The sliding of the microfibrils relative to each other stretches the taut tie molecules. The chain sections by which these molecules are attached to the crystalline blocks can then unfold. The density, crystallinity, and draw resistance then increase. The strain-hardening process then continues until breakage.
3.3. Particular Structure of Shish-Kebab
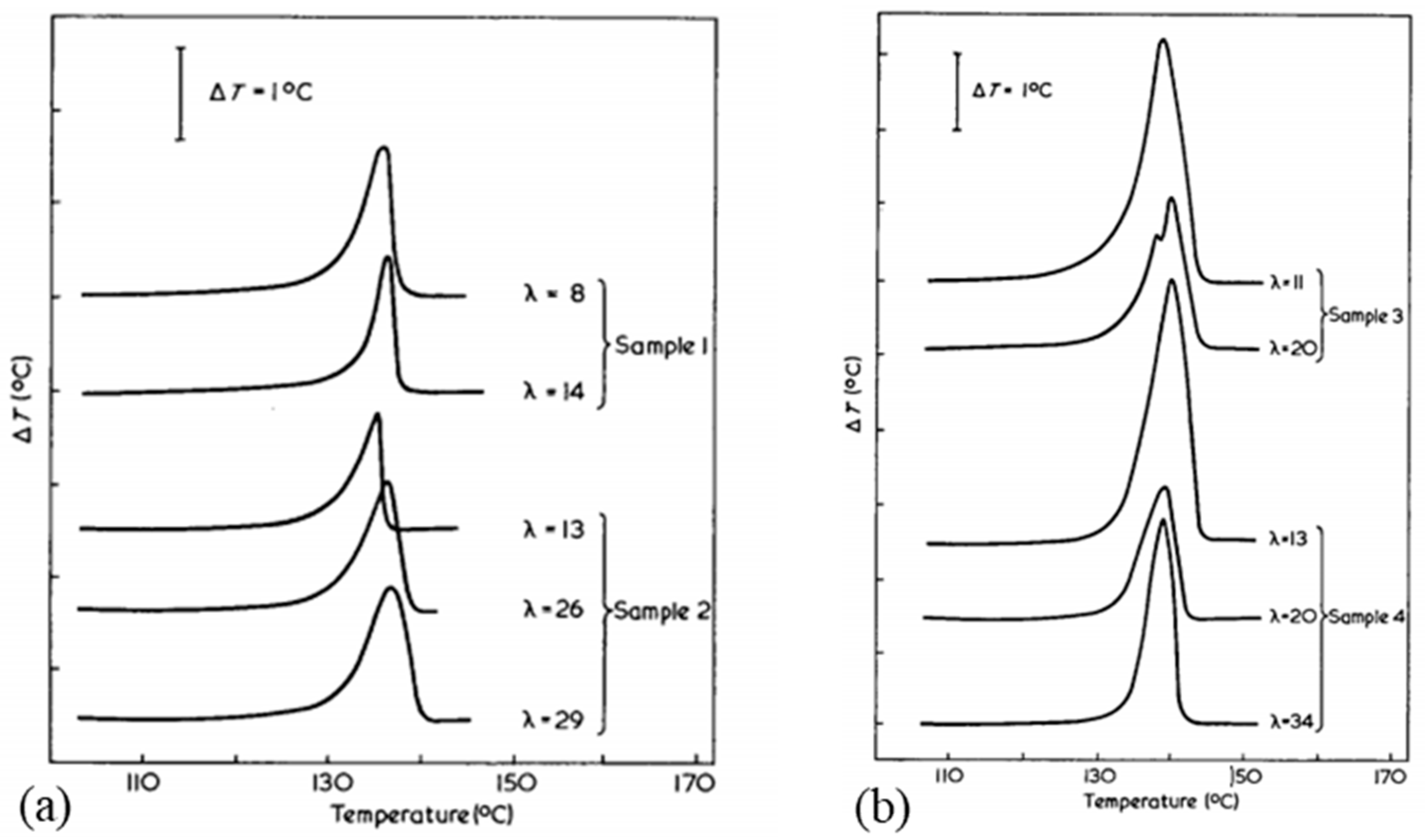
3.4. Morphology Study and Polymorphism
3.5. Consequence of a Stress on the Fiber Morphology
3.6. Effect of Sample Mass
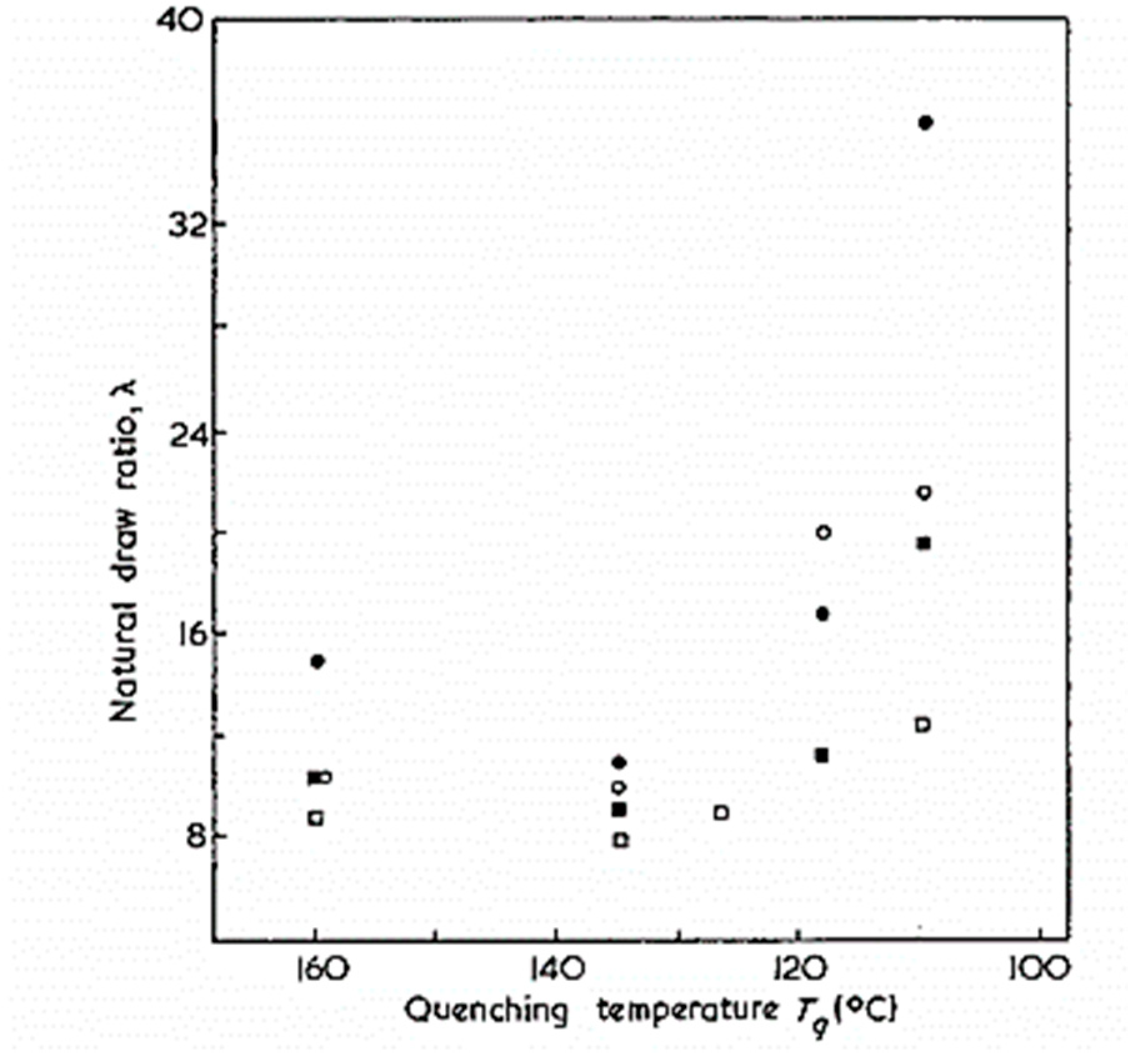
3.7. Consequence of Annealing on the Fiber Morphology
3.8. Physical Properties: An Overview
4. Mechanical Behavior
4.1. Test Protocol
4.2. Experimental Difficulties
4.3. Influence of Process Conditions and Initial Polymer Characteristics on Reinforcement Behavior
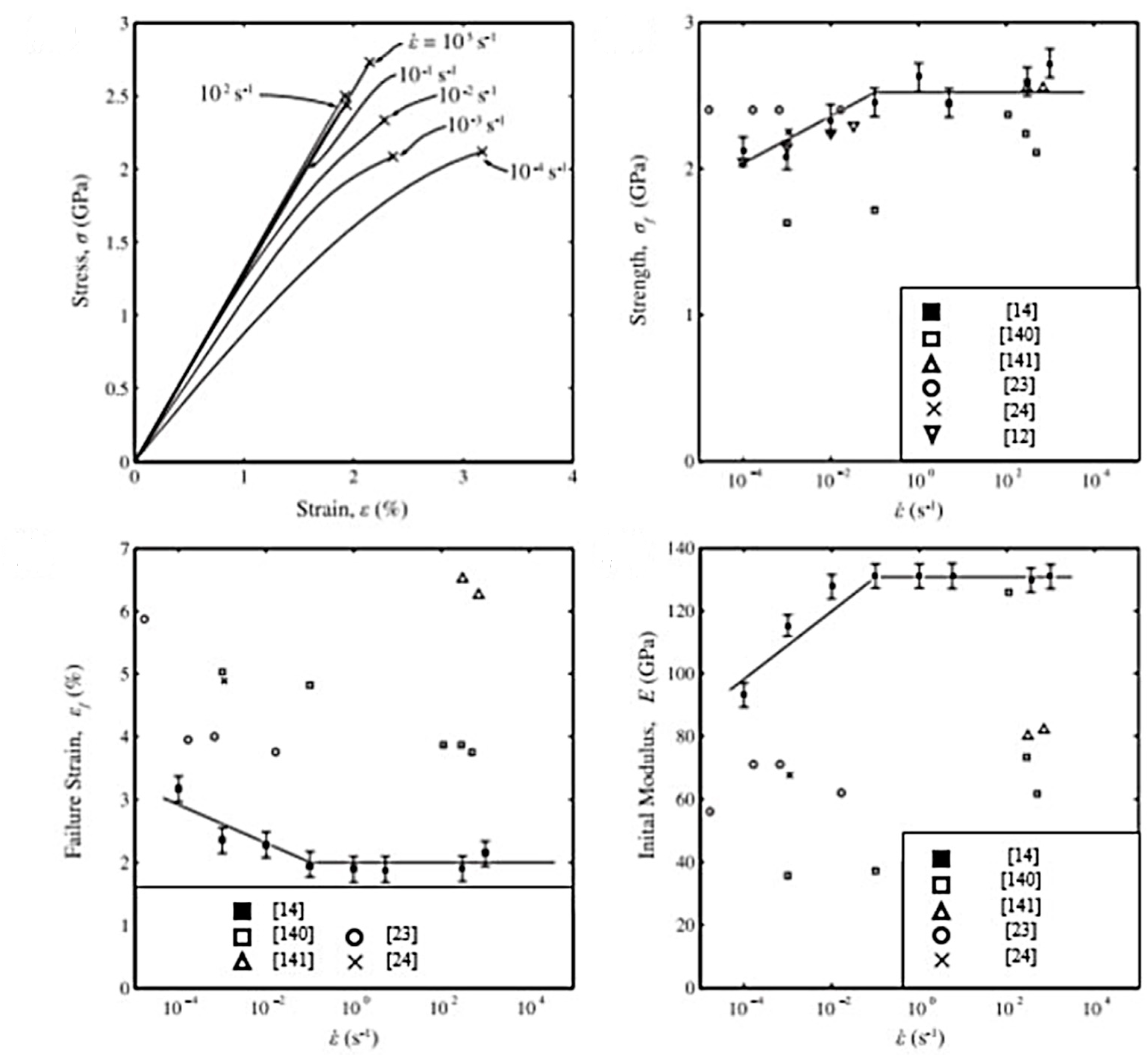
4.4. Tensile Tests
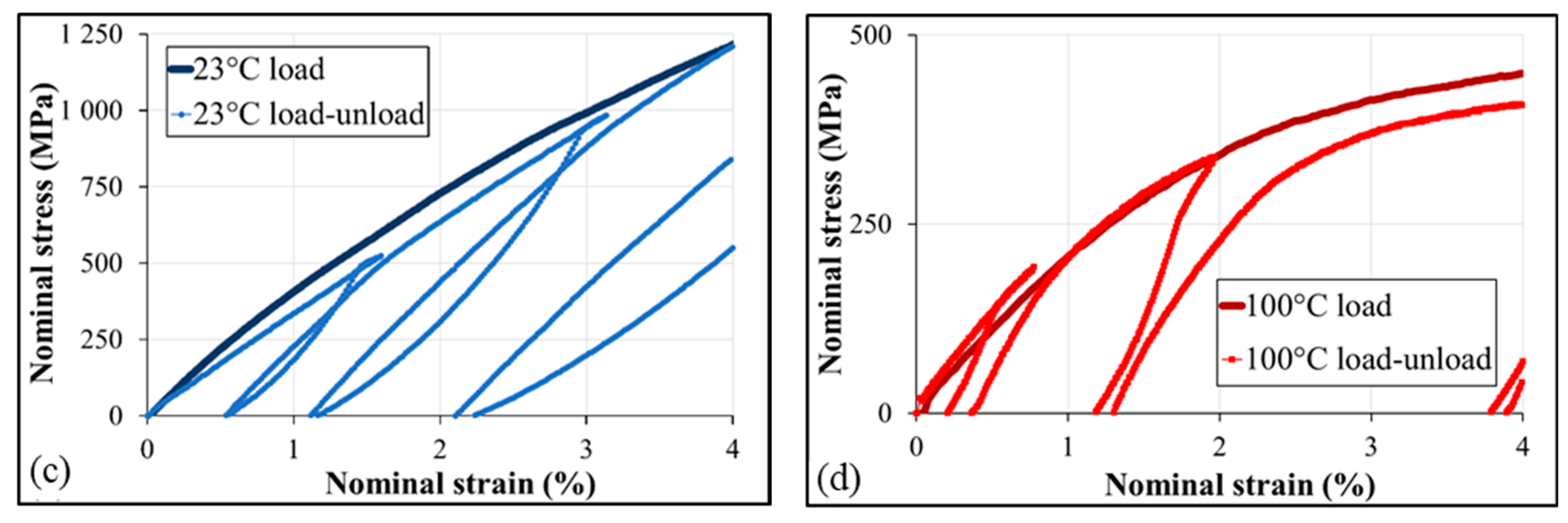
4.4.1. Cyclic Tension
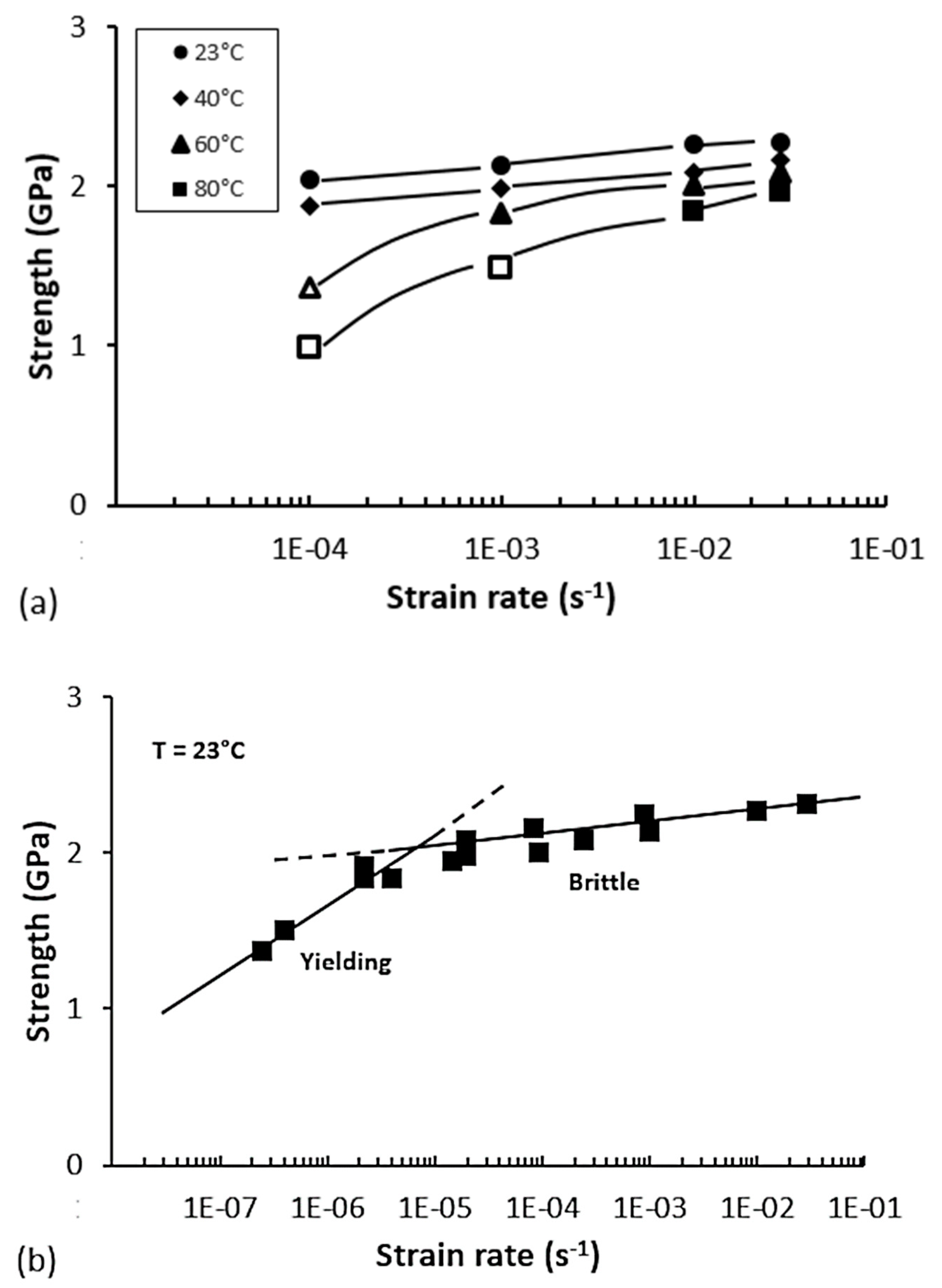
4.4.2. Time Dependence
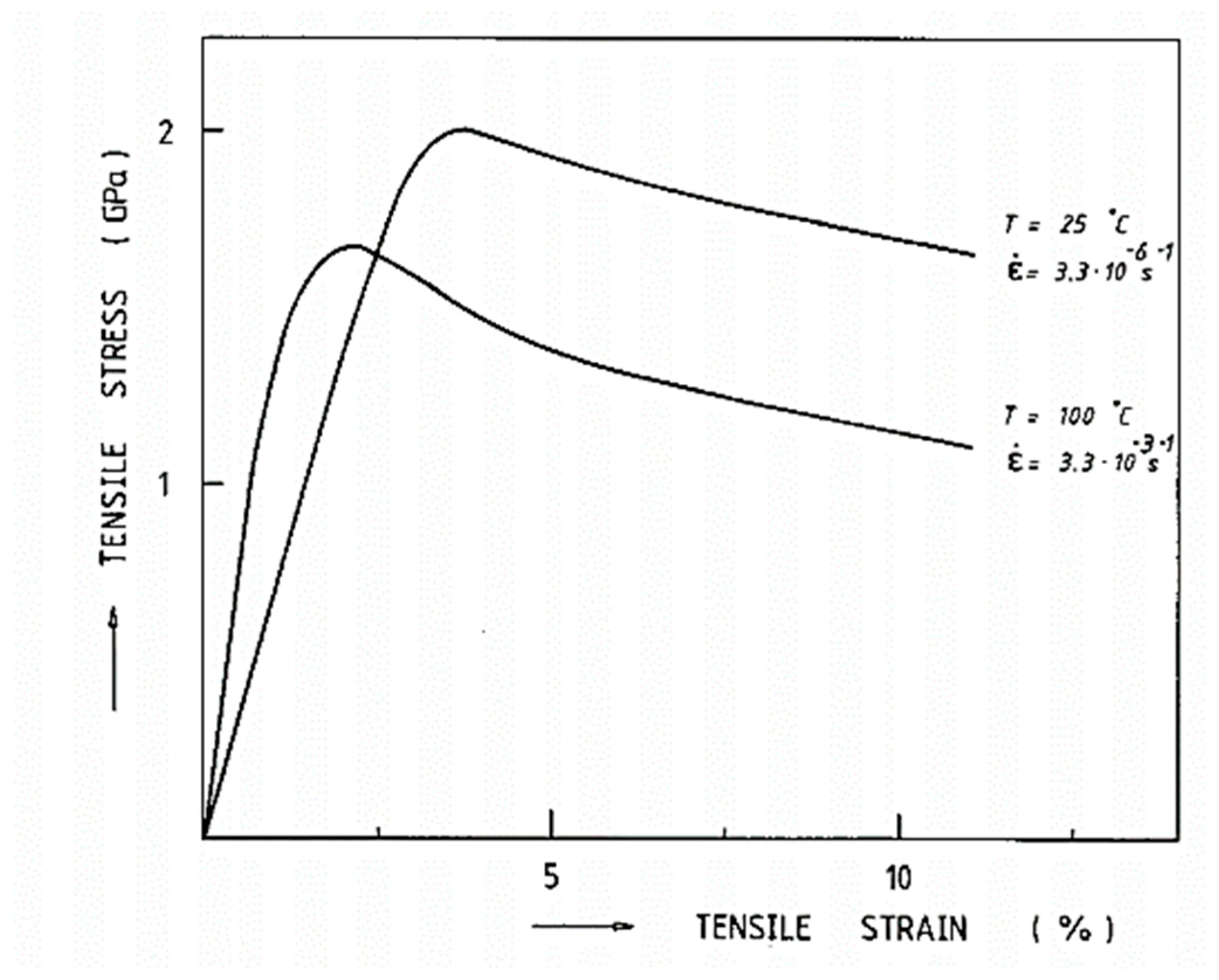
4.4.3. Temperature Dependence
4.4.4. Coupling Effect of Temperature and Time
4.4.5. Failure Mode
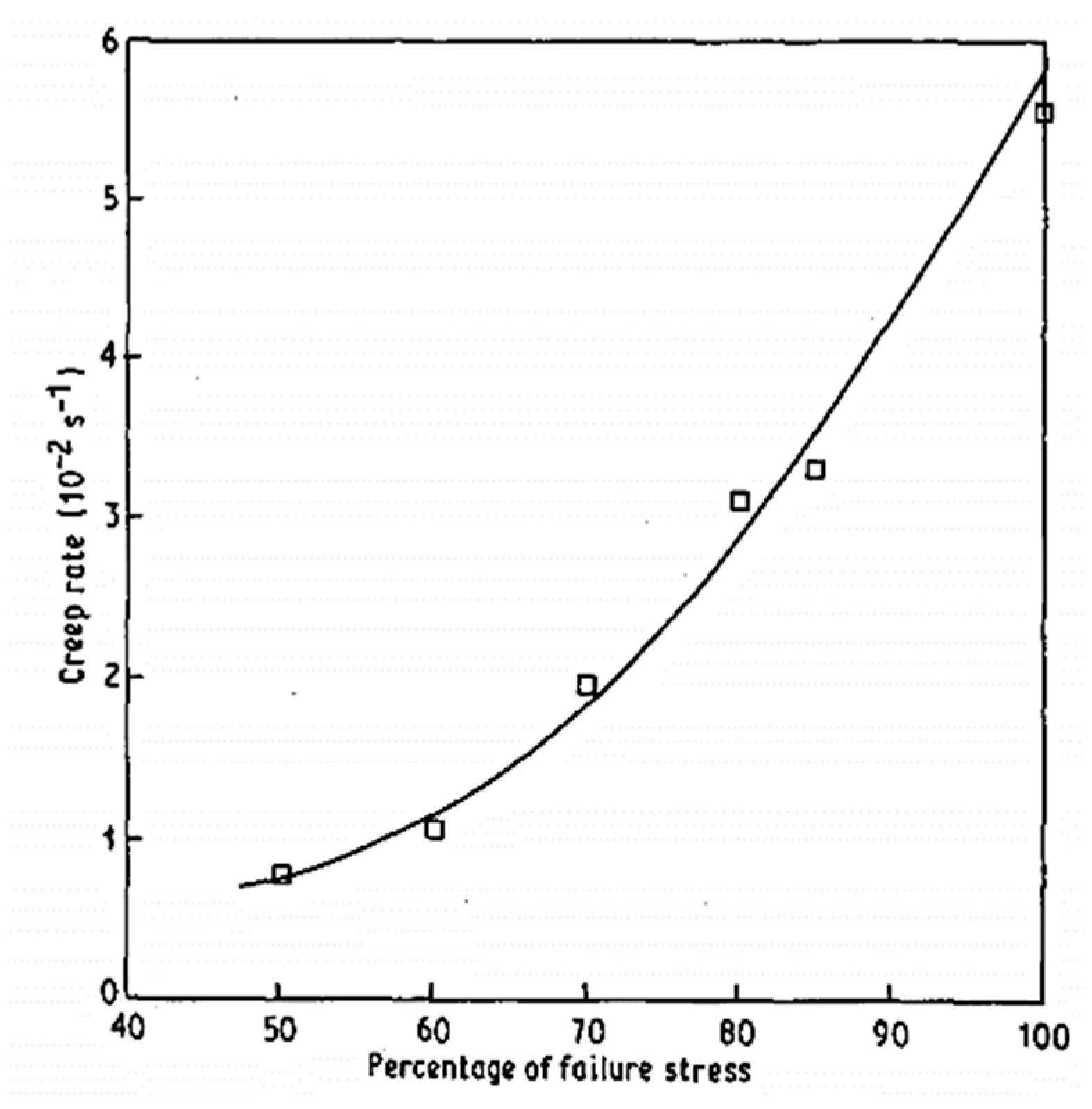
4.4.6. Creep Tests and Modeling
4.5. Relation between Mechanical and Physical Properties: An Overview
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Authors | Type of Fiber | Condition | Mass of the Sample in mg | Heating Rate | Melting Temperature in °C | |||
|---|---|---|---|---|---|---|---|---|
| Orthorhombic Phase | Orthorhombic Phase to Hexagonal Phase Transition | Hexagonal Phase | Other Phases | |||||
| [66] | Spectra® 900 | Unconstrained; Mw = 2 × 106 | 5 K/min | ≃143–144 | ||||
| Spectra® 900 | Constrained; Mw = 2 × 106 | 5 K/min | 143 | 155 | 159 | |||
| Spectra® 900 | Unconstrained; Mw = 7 × 105 | 5 K/min | 143 | 155 | ||||
| Spectra® 900 | Constrained; Mw = 7 × 105 | 5 K/min | 142 | 153 | 155 | |||
| [86] | Non-commercial | Constrained | [0.4; 0.8] | [1.25 °C/min; 20 °C/min] | [142; 147] | [152; 154] | [160; 166] | |
| Constrained | [0.4; 0.8] | 5 °C/min | 143.5 | 153 | 164 | |||
| [106] | Non-commercial | Unconstrained | 10 °C/min | 145 | ||||
| Constrained fibers with epoxy resin | 10 °C/min | 153 | 176 | |||||
| [39] | Hifax 1900 | Constrained; one winded a piece of 30 cm | 0.1 °C/min | 152 | ||||
| [13] | Dyneema® SK60 | 141 | ||||||
| [34] | Spectra® 1000 | Constrained; First heating | [3.5; 4] | 5 °C/min | 150 | 160 | ||
| Spectra® 1000 | Constrained; Second heating | [3.5; 4] | 5 °C/min | 141 | ||||
| Spectra® 1000 | Constrained; First heating | [3.5; 4] | [5 °C/min; 29.9 °C/min] | [150; 172] | [160; 188] | |||
| [28] | Spectra® 1000 | Constrained during 2 and 10 min | [3.5; 4] | 5 °C/min | 150 (superheating of the crystals) | ≃152 | ||
| Spectra® 1000 | Unconstrained | [3.5; 4] | 5 °C/min | 150 (superheating of the crystals) | ≃152 | 160 | ||
| [35] | Spectra® 900 | 0.024 | 10 K/min | ≃143 | ||||
| Spectra® 900 | [0,891; 4] | 10 K/min | ≃146–147 | [150; 155] | ||||
| [49] | Hizex powder (Mitsui Petrochemical Industries) | Mw = [89.6; 456]. 10−4 | 10 | 10 °C/min | [145; 150] | |||
| HF210 HDPE pellets (Idemitsu) | 10 | 10 °C/min | 130 | |||||
| [100] | Constrained Spectra® 900 | Cut fibers of ≃ 0.5 mm; Mw > 106 | [0.025; 1.2] | 10 K/min | [142.05; 143.65] | [150.35; 152.6] | ||
| Unconstrained Spectra® 900 | Cut fibers of ≃ 0.5 mm; Mw > 106 | [0.025; 1.2] | 10 K/min | 144 | ||||
| [44] | Non-commercial | Draw ratio = 1; Mw = 4.5 × 106 | 0.5 | 3 °C/min | 132 | |||
| Draw ratio between 20 and 150; Mw = 4.5 × 106 | 0.5 | 3 °C/min | [136; 142] | [148; 152] | 154 | |||
| [22] | Dyneema® SK75 | Fibers compacts, prepared at 145 °C | [9; 12] | 1 K/min | 145 | 151 and a shoulder at 152 | 155 | |
| Cross-linked fibers compacts, prepared at 145 °C | [9;12] | 1 K/min | ≃146–147 | 151 | 155 | |||
| Cross-linked fibers compacts, prepared at 150 °C | [9; 12] | 1 K/min | 148 | 153 | 156 | Melting of the orthorhombic folded chain at 138 | ||
| Authors | Type of Test | Type of Fiber | Condition | Test Control | Gauge Length | Study Range | Strain Calculation | Mechanical Characteristics |
|---|---|---|---|---|---|---|---|---|
| [23] | Tensile test | Dyneema® SK75 | Fibers provided are bonded with epoxy resin to a stiff frame | Machine cross head displacement at speeds [0.04; 160 mm/min] | [40; 200 mm] | Several strain rates: 0.1; 1; 4 and 100%/min | Determined through the displacement of the testing machine crosshead | 1%/min: 71 (Y), 2.4 (S), 3.95 (E) 4%/min: 71 (Y), 2.4 (S), 4 (E) 100%/min: 62 (Y), 2.4 (S), 3.76 (E) 0.1%/min: 56 (Y), 2.4 (S), 4.88 (E) |
| Tensile test | Dyneema® SK75 | Fibers provided are bonded with epoxy resin to a stiff frame | Machine cross head displacement at speeds [0.04; 160 mm/min] | Several temperatures [70; 140 °C] | Only curves but Y ≃ [5; 71] and S ≃ [0.250; 2.4] | |||
| Creep test | Dyneema® SK75 | A constant load was applied to specimens through a small metallic lever. | Constant load | Several temperatures [70; 140 °C] and constant loads 360 and 575 MPa | Only curves | |||
| [24] | Tensile test | Dyneema® SK60 | The fibers were simply gripped in the jaws between pieces of thin cardboard to prevent damage. “For tests below room temperature, the fibers were taped to a mounting board to allow them to be quickly positioned in the machine and to avoid too great a temperature rise”. | A strain gauge bridge system with appropriate amplification provides signals directly proportional to the maximum and average load on the fiber under test and actuates a servomechanism. | 150 mm and 30 mm for zero and negative temperatures | Several temperatures [−175; 100 °C], 10 mm/min | Defined from grip displacement | All values for these temperatures: −175, −160, −125, −100, −60, −30, 0, 24, 40, 70, 100 °C; Y = [114.1; 29.3], S = [0.6; 3.76] |
| Tensile test | Dyneema® SK60 | The fibers were simply gripped in the jaws between pieces of thin cardboard to prevent damage. | A strain gauge bridge system with appropriate amplification | Different gauge lengths | 24 °C, 50% relative humidity, 10 mm/min | |||
| Creep test | Dyneema® SK60 | Constant load hold by the machine | 150 mm | Constant load at 70% of the average breaking for many temperatures [25; 100 °C] | All values for 25, 40, 55, 70, 85, 100 °C; Er = [7.15; 20.16], T = [1561; 7816] | |||
| [24] | Creep test | Dyneema® SK60 | Constant load hold by the machine | 150 mm | Constant load between [50; 85%] of the average breaking at 70 and 100 °C | For 70 °C, all values for 50, 60, 70, 80 and 85%; Er = [8.5; 16.78], T = [306; 9194] For 100 °C, all values for 50, 60, 70, 80 and 85%; Er = [17.53; 21.20], T = [556, 2957] | ||
| [41] | Tensile test | Non-commercial | The sample and clamps were surrounded by a brass cylinder, which was also surrounded by a glass dewar. A flow of cold nitrogen was used to cool the brass cylinder if necessary. For temperatures above room temperature, the test was conducted in a dynamometer anda heating device, consisting of two heated brass blocks. The sample is placed in a cavity left. | Elongation rate: 3.3 × 10−3 s−1 | 50 mm | Many temperatures: [−150; 139 °C] | Only curves | |
| [39] | Tensile test | Hifax 1900 | Machine crosshead speed: 24 mm/min | 50 mm | Room temperature, annealing temperatures between [149; 152 °C] during [1; 24 h] | For initial fiber, Y = 150 and E = 3 and for annealing at 149 °C during 24 h, Y = 70 and E = 6, otherwise no precise value, only curves | ||
| [38] | Dead-load test | Hifax 1900 | Various weights are attached to the free end of the specimen | 50 cm | Room temperature | Defined from grip displacement | Only curves | |
| Tensile test | Hifax 1900 | Several crosshead speeds corresponding to [3.3 × 10−5; 3.6 × 10−2 s−1] | Room temperature | Only curves but E ≃ [3; 6.5] and S ≃ [2.3; 4] | ||||
| [37] | Dead-load test | Hifax 1900, then fibers are crosslinked | 25 cm | Various temperatures: [25; 143 °C] | Only curves for lifetime at 25, 43, 73, 98, 121, 138, and 143 °C for various nominal stresses | |||
| Tensile test | Hifax 1900, then fibers are crosslinked | Machine crosshead speed: 12 mm/min | 25 mm | At 20 °C | ||||
| [45] | Tensile test | Gel-spun yarns | Experiments carried out according to ISO 2062 | Machine crosshead speed: 250 mm/min | 25 cm | With aging temperature of 43, 65, 90, and 115 °C for weeks | Standard ISO 2062 | Only curves for various aging at 43, 65, 90, and 115 °C |
| [33] | Tensile test | Spectra® 900 | Special capstan inserts were developed to fit standard Instron pneumatic grips. | 50 mm | Several strain rates: [0.004; 1.0 min−1], at 21 °C and 65% RH | 0.004 min−1: S = 2.126 0.04 min−1: S = 2.652 0.10 min−1: S = 2.982 0.40 min−1: S = 3.040 1.0 min−1: S = 3.336 | ||
| Tensile test | Spectra® 900 | Special capstan inserts were developed to fit standard Instron pneumatic grips. | Various gauge lengths: [10; 100 mm] | At 21 °C, 65% RH, and 0.1 min−1 | 10 mm: S = 2.992 50 mm: S = 2.982 100 mm: S = 3.025 200 mm: S = 3.053 | |||
| [14] | Tensile test | Dyneema® SK76 | Yarn is wrapped around a semicircular anvil. For rate tests > 100 s−1, a projectile load the system, whereas for test < 100 s−1, the load is applied by a servo-hydraulic machine. It is connected to the device by a loading rod. | Various gauge lengths: [5; 20 mm] | Several strain rates: [10−3; 104 s−1] | DIC from the identification of two marker bands. Measurements verified with a LVDT system on the machine crosshead | Only curves but Y ≃ [92; 130], S ≃ [2; 2.6], and D ≃ [2; 3.2] | |
| [36] | Cyclic deformations | Hifax 1900 (2 different Mw) | Pneumatic action grips are used. Fibers can’t slip because the gripping force is adjusted via the air pressure. | Constant crosshead speed: 50 mm/min | 500 mm | Only curves | ||
| Stress relaxation | Hifax 1900 (2 different Mw) | Only curves | ||||||
| [36] | Tensile test | Hifax 1900 (2 different Mw) | 28 mm | Several crosshead speeds: [0.5; 512 mm/min] | Only curves but S ≃ [0.88; 1.15] | |||
| Tensile test | Hifax 1900 specimen b | Constant crosshead speed: 50 mm/min | 500 mm | Various draw ratio: 15, 30 and 70 | S = [0.85; 4.16]; Y = [22.6; 175], Elastic D = [2.38; 3.8] and Plastic D = [1.56; 21.17] | |||
| [46] | Tensile test | Dyneema® SK60 | The oven is thermostatically controlled and pneumatic clamps are used. | 250 mm | Several strain rates: [10−5; 101 s−1]; and temperatures: [−40; 80 °C] | Only curves but Y ≃ [20; 100] and S ≃ [1; 2.2] | ||
| Creep test | Dyneema® SK60 | The oven is thermostatically controlled and pneumatic clamps are used. Yarns are glued on cardboard tabs. | Different stress levels: [250; 1250 MPa]; and temperatures: [23; 90 °C] | Determined through an extensometer | Only curves | |||
| [29] | Creep test | Dyneema® SK60 | Two tensile test machines used: one commercial and an in-house-built. | Stress range 0.65–2 GPa for a period of 30 h | Measured from an optical extensometer with a video camera | Only curves | ||
| [15] | Tensile test | Made from UHMWPE sheets (GUR 410) | After pre-heat treatments, return to room temperature in an oven. | Constant crosshead speed: 3 mm/min | Before the test, pre-heat treatments of the UHMWPE specimens at 50, 80, and 100 °C for 2 and 4 h. Tests at room temperature. | Defined from an extensometer clipped on to the specimen | Virgin: 1.136 (Y), 0.025 (S) 50 °C 2 h: 1.264 (Y), 0.026 (S) 50 °C 4 h: 1.350 (Y), 0.0276 (S) 80 °C 2 h: 1.358 (Y), 0.0268 (S) 80 °C 4 h: 1.410 (Y), 0.02865 (S) 100 °C 2 h: 1.390 (Y), 0.0275 (S) 100 °C 4 h: 1.420 (Y), 0.0292 (S) | |
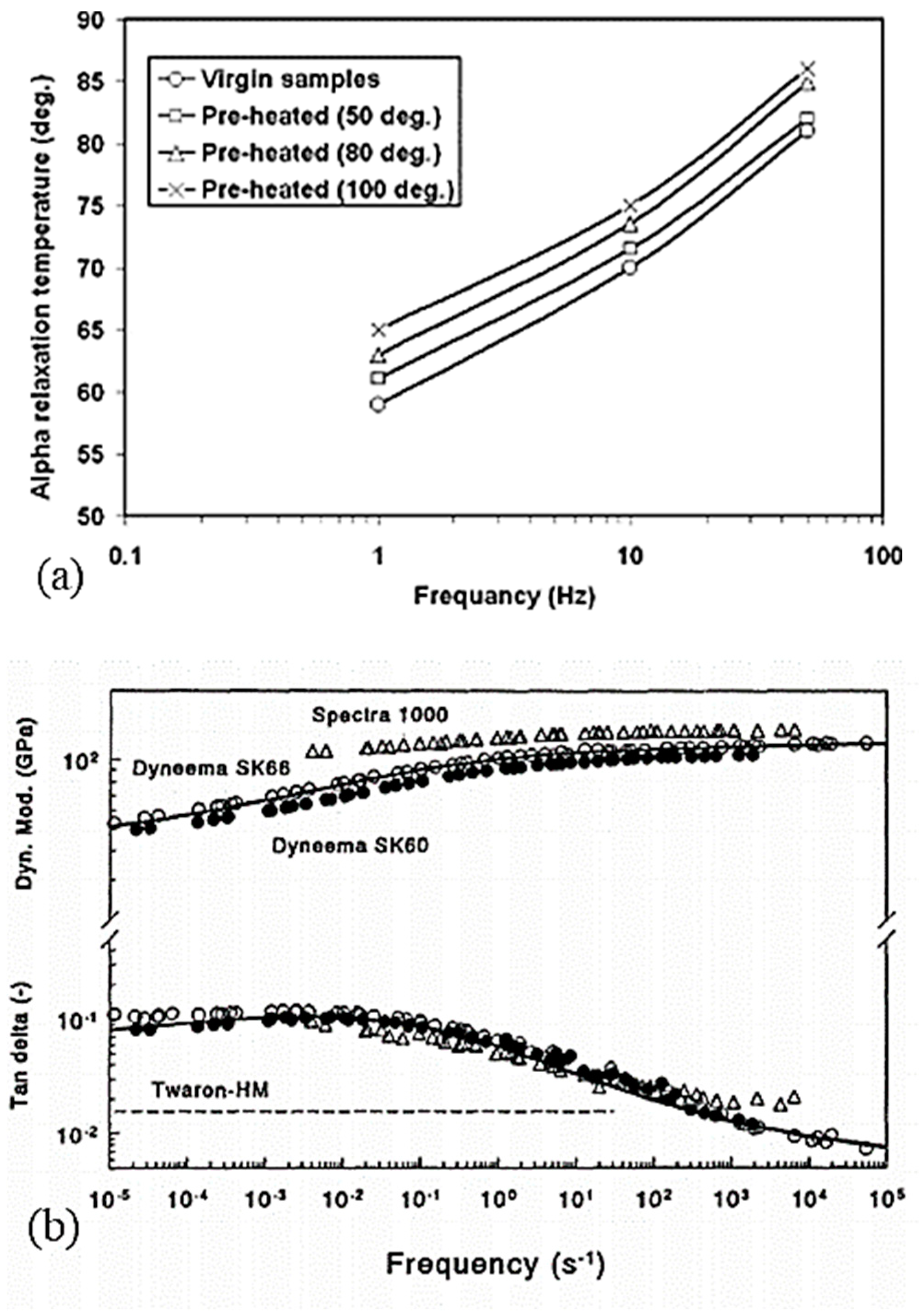
| DMA tests | Made from UHMWPE sheets (GUR 410) | Before the test, pre-heat treatments of the UHMWPE specimens at 50, 80, and 100 °C for 2 and 4 h. Frequency range from 0.01 to 100 Hz at temperatures from 30 to 100 °C, achieved using a heating rate of 1 °C/min. | Only curves | |||||
| [25] | Stress relaxation | Dyneema® SK60 | The oven is thermostatically controlled and pneumatic clamps are used. | Constant crosshead speed | Several temperatures: 13, 50 and 90 °C, and different Hencky strains: [0.2; 2%] | Only curves | ||
| Creep tests | Dyneema® SK60 | The oven is thermostatically controlled and pneumatic clamps are used. | Constant stresses | At 50 °C, and different stresses: 0.4 and 0.8 GPa | Only curves | |||
| Stress build-up under a constant Hencky strain rate | Dyneema® SK60 | Pneumatic clamps are used. | Constant Hencky strain rates | Several Hencky strain rates: [8.4 × 10−4; 4.2 × 10−7 s−1] | Only curves | |||
| [32] | DMA tests | Dyneema® SK66 | To prevent creep, a relatively low static stress level of 150 MPa was chosen. | 20 mm | Different frequencies: [0.2; 3 Hz]; and temperatures: [−20; 105 °C] | Only curves but DM ≃ [40; 120] | ||
| Stress relaxation | Dyneema® SK66 | Fiber ends were glued on cardboard tabs with an epoxy resin, to improve clamping. | 255 mm | Several strains: [0.5; 2.5%]; and temperatures [30; 70 °C], loading times < 150 h | Defined from an extensometer | Only curves | ||
| [32] | Creep test (dead-load test) | Dyneema® SK66 | Fiber ends were glued on cardboard tabs with an epoxy resin, to improve clamping. | 255 mm | Different loads: [200; 1500 MPa], and temperatures: [30; 90 °C], loading times < 50 h | Only curves | ||
| [40] | Creep test (dead-load test) | Made from commercial PE grades (Rigidex 50 and H020-54P) | Constant load | Test at 20 °C and several applied stresses: [0.05; 0.5 GPa] depending on the sample | Determined from grip displacement | Curves and values of the modulus and the viscosity of each element of the four elements mechanical model proposed | ||
| [111] | Creep test (dead-load test) | Made from commercial PE grades (Rigidex 50, H020-54P and 002-55) | Constant load | 10 cm | Loading times between 24 and 48 h, temperature [20; 70 °C], and stress levels [0.1; 0.2 GPa] | Determined from grip displacement | Only curves | |
| [112] | Creep test (dead-load test) | Made from commercial PE grades (Rigidex 50 and H020-54P) | Constant load | 10 cm | Stress levels [0.093; 0.3 GPa] | Determined from grip displacement | Curves and fitted parameters to modified model | |
| Authors | Type of test | Type of fiber | Condition | Test control | Gauge length | Study range | Strain calculation | Mechanical characteristics |
| [112] | Stress relaxation | Made from commercial PE grades (Rigidex 50) | A purpose-built device was designed. the fixed-grip was attached to a bending beam load cell, and the second one was driven, via an electro-magnetic clutch, by a variable speed gearbox. | Maximum stress applied: 0.27 GPa, stress relaxation between 0.2 and 106 s. | Only curves | |||
| [12] | Tensile test | Dyneema® SK60 | Pneumatic fiber clamps are used. | 250 mm | Several strain rates: [10−5; 10−1 s−1], and temperatures [−40; 80 °C] | Determined from grip displacement | Only curves but Y ≃ [20; 100] and S ≃ [1; 2.2] | |
| Creep tests | Dyneema® SK60 | Yarns are provided with adhesive cardboard tabs. | Constant load | Several stresses: [250; 1250 MPa], and temperatures [23; 90 °C] | Defined from an extensometer | Only curves | ||
| DMA tests | Spectra® 1000 | Uniaxial extension tests were carried out. | Different frequencies: [0.2; 3 Hz]; and temperatures: [−20; 105 °C] | Only curves | ||||
| [153] | Step stress relaxation tests | Alathon 7050 | An electric motor operating via a gearbox, controlled by an electromagnetic clutch, allows the application of a strain and the force in the specimen sensed by a strain gauge transducer. A microcomputer controls the motor and clutch with digital signals. | Fast loading at 1.2 × 10−3 s−1 | 65 mm | Lower limit stress: 205 MPa, and different steps: [13.7; 58.4 MPa] | Only curves |
References
- Cabrera, N.; Alcock, B.; Loos, J.; Peijs, T. Processing of all-polypropylene composites for ultimate recyclability. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2004, 218, 145–155. [Google Scholar] [CrossRef]
- Eurostat. End-of-Life Vehicle Statistics. 2020. Available online: https://ec.europa.eu/eurostat/statistics-explained/pdfscache/24943.pdf (accessed on 22 April 2021).
- Witten, E.; Mathes, V.; Sauer, M.; Kühnel, M. Composites Market Report 2018, Market Developments, Trends, Outlooks and Challenges. In Federation of Reinforced Plastics; Available online: https://compositesuk.co.uk/system/files/documents/2018%20European%20Market%20Report.pdf (accessed on 2 June 2021).
- Capiati, N.J.; Porter, R.S. The concept of one polymer composites modelled with high density polyethylene. J. Mater. Sci. 1975, 10, 1671–1677. [Google Scholar] [CrossRef]
- Gao, C.; Meng, L.; Yu, L.; Simon, G.P.; Liu, H.; Chen, L.; Petinakis, S. Preparation and characterization of uniaxial poly(lactic acid)-based self-reinforced composites. Compos. Sci. Technol. 2015, 117, 392–397. [Google Scholar] [CrossRef]
- Karger-Kocsis, J.; Bárány, T. Single-polymer composites (SPCs): Status and future trends. Compos. Sci. Technol. 2014, 92, 77–94. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.M.; Lin, P.C.; Murakami, R. Long-term creep behavior of self-reinforced PET composites. Express Polym. Lett. 2017, 11, 820–831. [Google Scholar] [CrossRef]
- Stellbrink, K.K.U.; Hausser, G.; Steegmuller, R. One-component composites as functionally gradient materials. J. Thermoplast. Compos. Mater. 1999, 12, 188–200. [Google Scholar] [CrossRef]
- Ward, I.M.; Hine, P.J. The science and technology of hot compaction. Polymer 2004, 45, 1413–1427. [Google Scholar] [CrossRef]
- Gao, C.; Yu, L.; Liu, H.; Chen, L. Development of self-reinforced polymer composites. Prog. Polym. Sci. 2012, 37, 767–780. [Google Scholar] [CrossRef]
- Deng, M.; Shalaby, S.W. Properties of self-reinforced ultra-high-molecular-weight polyethylene composites. Biomaterials 1997, 18, 645–655. [Google Scholar] [CrossRef]
- Peijs, T.; Smets, E.A.M.; Govaert, L.E. Strain rate and temperature effects on energy absorption of polyethylene fibres and composites. Appl. Compos. Mater. 1994, 1, 35–54. [Google Scholar] [CrossRef]
- Marais, C.; Feillard, P. Manufacturing and mechanical characterization of unidirectional polyethylene-fibre/polyethylene-matrix composites. Compos. Sci. Technol. 1992, 45, 247–255. [Google Scholar] [CrossRef]
- Russell, B.P.; Karthikeyan, K.; Deshpande, V.S.; Fleck, N.A. The high strain rate response of Ultra High Molecular-weight Polyethylene: From fibre to laminate. Int. J. Impact Eng. 2013, 60, 1–9. [Google Scholar] [CrossRef]
- Fouad, H.; Mourad, A.H.; Barton, D.C. Effect of pre-heat treatment on the static and dynamic thermo-mechanical properties of ultra-high molecular weight polyethylene. Polym. Test. 2005, 24, 549–556. [Google Scholar] [CrossRef]
- Hine, P.J.; Ward, I.M.; Jordan, N.D.; Olley, R.; Bassett, D.C. The hot compaction behaviour of woven oriented polypropylene fibres and tapes. I. Mechanical properties. Polymer 2003, 44, 1117–1131. [Google Scholar] [CrossRef]
- Vecchione, P.; Acierno, D.; Abbate, M.; Russo, P. Hot-compacted self reinforced polyamide 6 composite laminates. Compos. Part B Eng. 2017, 110, 39–45. [Google Scholar] [CrossRef]
- Schneider, C.; Kazemahvazi, S.; Åkermo, M.; Zenkert, D. Compression and tensile properties of self-reinforced poly(ethylene terephthalate)-composites. Polym. Test. 2013, 32, 221–230. [Google Scholar] [CrossRef] [Green Version]
- Rojanapitayakorn, P.; Mather, P.T.; Goldberg, A.J.; Weiss, R.A. Optically transparent self-reinforced poly(ethylene terephthalate) composites: Molecular orientation and mechanical properties. Polymer 2005, 46, 761–773. [Google Scholar] [CrossRef]
- Kazemahvazi, S.; Schneider, C.; Deshpande, V.S. A constitutive model for self-reinforced ductile polymer composites. Compos. Part A Appl. Sci. Manuf. 2015, 71, 32–39. [Google Scholar] [CrossRef]
- Li, L.; Liu, X.; Zhou, X.; Hong, J.; Zhuang, X.; Yan, X. Mechanical properties of unidirectional continuous fiber self-reinforced polyethylene graded laminates. Polym. Compos. 2015, 36, 128–137. [Google Scholar] [CrossRef]
- Ratner, S.; Weinberg, A.; Wachtel, E.; Moret, P.M.; Marom, G. Phase transitions in UHMWPE fiber compacts studied by in situ synchrotron microbeam WAXS. Macromol. Rapid Commun. 2004, 25, 1150–1154. [Google Scholar] [CrossRef]
- Kromm, F.X.; Lorriot, T.; Coutand, B.; Harry, R.; Quenisset, J.M. Tensile and creep properties of ultra high molecular weight PE fibres. Polym. Test. 2003, 22, 463–470. [Google Scholar] [CrossRef]
- Dessain, B.; Moulaert, O.; Keunings, R.; Bunsell, A.R. Solid phase change controlling the tensile and creep behaviour of gel-spun high-modulus polyethylene fibres. J. Mater. Sci. 1992, 27, 4515–4522. [Google Scholar] [CrossRef]
- Leblans, P.J.R.; Bastiaansen, C.W.M.; Govaert, L.E. Viscoelastic properties of UHMW-PE fibers in simple elongation. J. Polym. Sci. Part B Polym. Phys. 1989, 27, 1009–1016. [Google Scholar] [CrossRef] [Green Version]
- Govaert, L.E.; Lemstra, P.J. Deformation behavior of oriented UHMW-PE fibers. Colloid Polym. Sci. 1992, 270, 455–464. [Google Scholar] [CrossRef]
- McDaniel, P.B.; Deitzel, J.M.; Gillespie, J.W. Structural hierarchy and surface morphology of highly drawn ultra high molecular weight polyethylene fibers studied by atomic force microscopy and wide angle X-ray diffraction. Polymer 2015, 69, 148–158. [Google Scholar] [CrossRef]
- Hsieh, Y.-L.; Hu, X.-P. Structural transformation of ultra-high modulus and molecular weight polyethylene fibers by high-temperature wide-angle X-ray diffraction. J. Polym. Sci. Part B Polym. Phys. 1997, 35, 623–630. [Google Scholar] [CrossRef]
- Berger, L.; Kausch, H.; Plummer, C.J. Structure and deformation mechanisms in UHMWPE-fibres. Polymer 2003, 44, 5877–5884. [Google Scholar] [CrossRef]
- Tashiro, K.; Sasaki, S.; Kobayashi, M. Structural investigation of orthorhombic-to-hexagonal phase transition in polyethylene crystal: The experimental confirmation of the conformationally disordered structure by X-ray diffraction and infrared/raman spectroscopic measurements. Macromolecules 1996, 29, 7460–7469. [Google Scholar] [CrossRef]
- Rein, D.M.; Shavit, L.; Khalfin, R.L.; Cohen, Y.; Terry, A.; Rastogi, S. Phase transitions in ultraoriented polyethylene fibers under moderate pressures: A synchrotron X-ray study. J. Polym. Sci. Part B Polym. Phys. 2004, 42, 53–59. [Google Scholar] [CrossRef]
- Govaert, L.; Bastiaansen, C.; Leblans, P. Stress-strain analysis of oriented polyethylene. Polymer 1993, 34, 534–540. [Google Scholar] [CrossRef]
- Schwartz, P.; Netravali, A.; Sembach, S. Effects of strain rate and gauge length on the failure of ultra-high strength polyethylene fibers. Text. Res. J. 1986, 56, 502–508. [Google Scholar] [CrossRef]
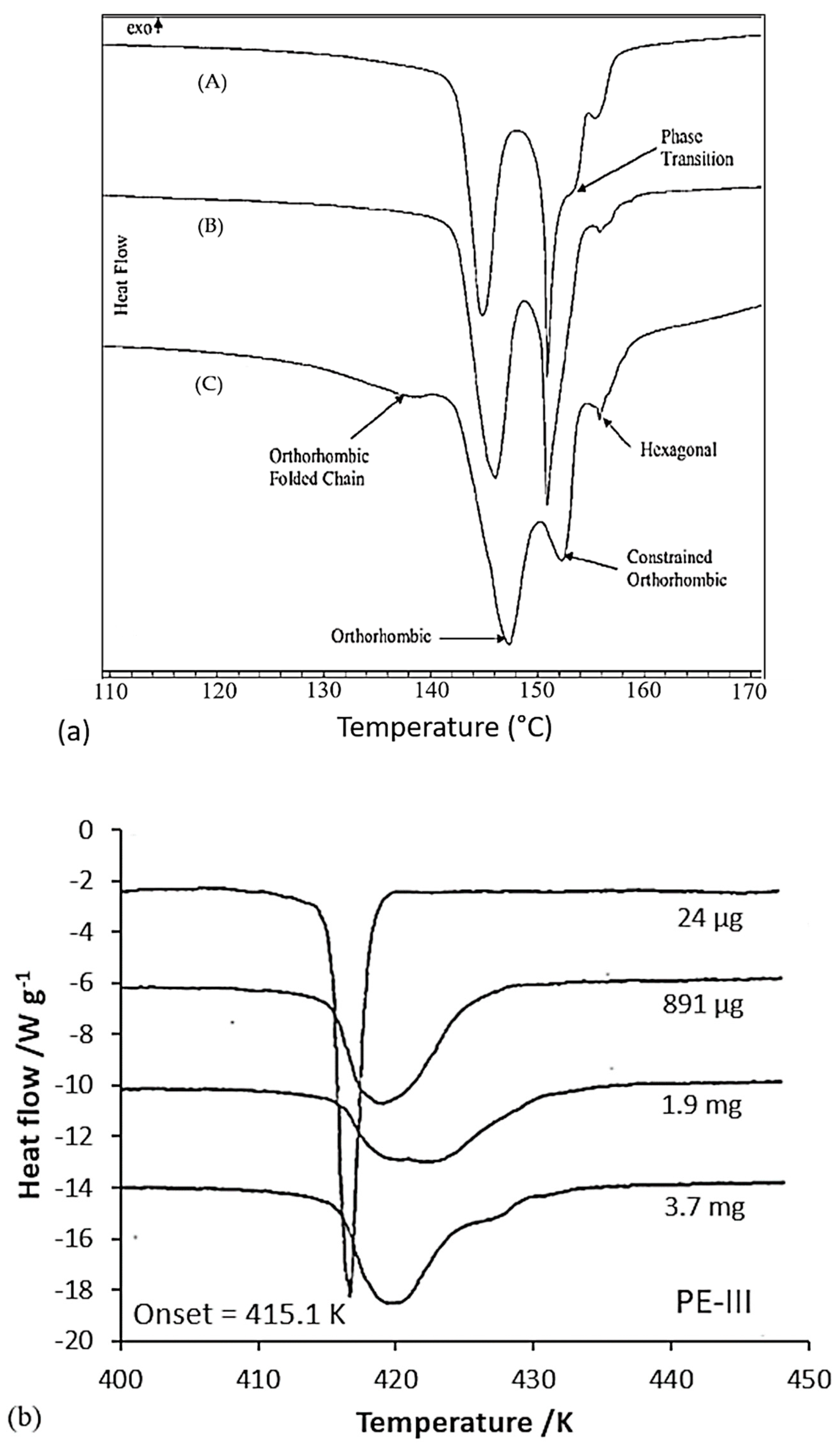
- Hsieh, Y.L.; Ju, J. Melting behavior of ultra-high modulus and molecular weight polyethylene (UHMWPE) fibers. J. Appl. Polym. Sci. 1994, 53, 347–354. [Google Scholar] [CrossRef]
- Boller, A.; Wunderlich, B. Multiple melting peak analysis with gel-spun ultra-high molar mass polyethylene. J. Therm. Anal. 1997, 49, 343–349. [Google Scholar] [CrossRef] [Green Version]
- Van der Werff, H.; Pennings, A.J. Tensile deformation of high strength and high modulus polyethylene fibers. Colloid Polym. Sci. 1991, 269, 747–763. [Google Scholar] [CrossRef]
- Smook, J.; Hamersma, W.; Pennings, A.J. The fracture process of ultra-high strength polyethylene fibres. J. Mater. Sci. 1984, 19, 1359–1373. [Google Scholar] [CrossRef]
- Dijkstra, D.J.; Pennings, A.J. The role of taut tie molecules on the mechanical properties of gel-spun UHMWPE fibres. Polym. Bull. 1988, 19. [Google Scholar] [CrossRef]
- Dijkstra, D.J.; Pennings, A.J. Annealing of gel-spun hot-drawn ultra-high molecular weight polyethylene fibres. Polym. Bull. 1988, 19, 481–486. [Google Scholar] [CrossRef]
- Wilding, M.; Ward, I. Tensile creep and recovery in ultra-high modulus linear polyethylenes. Polymer 1978, 19, 969–976. [Google Scholar] [CrossRef]
- Dijkstra, D.J.; Torfs, J.C.M.; Pennings, A.J. Temperature-dependent fracture mechanisms in ultra-high strength polyethylene fibers. Colloid Polym. Sci. 1989, 267, 866–875. [Google Scholar] [CrossRef]
- R’Mili, M.; Murat, M. Caractérisation des fibres par amélioration de l’essai sur mèche avec mesure directe de la déformation. Comptes Rendus Académie Sci. Ser. IIB Mech. Phys. Chem. Astron. 1997, 324, 355–364. [Google Scholar] [CrossRef]
- Chi, Z.; Chou, T.W.; Shen, G. Determination of single fibre strength distribution from fibre bundle testings. J. Mater. Sci. 1984, 19, 3319–3324. [Google Scholar] [CrossRef]
- Yeh, J.-T.; Lin, S.-C.; Tu, C.-W.; Hsie, K.-H.; Chang, F.-C. Investigation of the drawing mechanism of UHMWPE fibers. J. Mater. Sci. 2008, 43, 4892–4900. [Google Scholar] [CrossRef]
- Forster, A.L.; Forster, A.M.; Chin, J.W.; Peng, J.-S.; Lin, C.-C.; Petit, S.; Kang, K.-L.; Paulter, N.; Riley, M.A.; Rice, K.D.; et al. Long-term stability of UHMWPE fibers. Polym. Degrad. Stab. 2015, 114, 45–51. [Google Scholar] [CrossRef]
- Govaert, L.E.; Peijs, T. Tensile strength and work of fracture of oriented polyethylene fibre. Polymer 1995, 36, 4425–4431. [Google Scholar] [CrossRef]
- Carothers, W.H.; Hill, J.W. Studies of polymerization and ring formation. XV. Artificial fibers from synthetic linear condensation superpolymers. J. Am. Chem. Soc. 1932, 54, 1579–1587. [Google Scholar] [CrossRef]
- Ohta, T. Review on processing ultra high tenacity fibers from flexible polymer. Polym. Eng. Sci. 1983, 23, 697–703. [Google Scholar] [CrossRef]
- Rudnik, E.; Dobkowski, Z. Thermal degradation of UHMWPE. J. Therm. Anal. 1997, 49, 471–475. [Google Scholar] [CrossRef]
- Barham, P.J.; Keller, A. High-strength polyethylene fibres from solution and gel spinning. J. Mater. Sci. 1985, 20, 2281–2302. [Google Scholar] [CrossRef]
- Frank, F.C. The strength and stiffness of polymers. Proc. R. Soc. Lond. Math. Phys. Sci. 1970, 319, 127–136. [Google Scholar] [CrossRef]
- Holliday, L. The stiffness of polymers in relation to their structure. In Structure and Properties of Oriented Polymers; Ward, I.M., Ed.; Springer: Dordrecht, The Netherlands, 1975; pp. 242–263. [Google Scholar] [CrossRef]
- Yeh, J.; Chang, S. Ultradrawing behavior of gel films of ultrahigh molecular weight polyethylene and low molecular weight polyethylene blends at varying drawing conditions. Polym. Eng. Sci. 2002, 42, 1558–1567. [Google Scholar] [CrossRef]
- Song, M.S.; Hu, G.X. Study on the relationship between the mechanical properties and processing for self-reinforced polymers: A method for estimating the theoretical strength of UHMWPE fiber. Polym. Test. 1991, 10, 367–378. [Google Scholar] [CrossRef]
- Bigg, D.M. A review of techniques for processing ultra-high modulus polymers. Polym. Eng. Sci. 1976, 16, 725–734. [Google Scholar] [CrossRef]
- Chodák, I. High modulus polyethylene fibres: Preparation, properties and modification by crosslinking. Prog. Polym. Sci. 1998, 23, 1409–1442. [Google Scholar] [CrossRef]
- Smook, J.; Pennings, J. Influence of draw ratio on morphological and structural changes in hot-drawing of UHMW polyethylene fibres as revealed by DSC. Colloid Polym. Sci. 1984, 262, 712–722. [Google Scholar] [CrossRef]
- Peterlin, A. Drawing and extrusion of semi-crystalline polymers. Colloid Polym. Sci. 1987, 265, 357–382. [Google Scholar] [CrossRef]
- Capaccio, G.; Ward, I.M. Preparation of ultra-high modulus linear polyethylenes; effect of molecular weight and molecular weight distribution on drawing behaviour and mechanical properties. Polymer 1974, 15, 233–238. [Google Scholar] [CrossRef]
- Capaccio, G.; Ward, I.M. Properties of ultra-high modulus linear polyethylenes. Nat. Phys. Sci. 1973, 243, 143. [Google Scholar] [CrossRef]
- Capaccio, G.; Ward, I.M. Ultra-high-modulus linear polyethylene through controlled molecular weight and drawing. Polym. Eng. Sci. 1975, 15, 219–224. [Google Scholar] [CrossRef]
- Smith, P.; Lemstra, P.J. Ultra-high-strength polyethylene filaments by solution spinning/drawing. J. Mater. Sci. 1980, 15, 505–514. [Google Scholar] [CrossRef] [Green Version]
- Lemstra, P.J.; Kirschbaum, R.; Ohta, T.; Yasuda, H. High-strength/high-modulus structures based on flexible macromolecules: Gel-spinning and related processes. In Developments in Oriented Polymers—2; Ward, I.M., Ed.; Springer: Dordrecht, The Netherlands, 1987; pp. 39–77. [Google Scholar] [CrossRef] [Green Version]
- Smith, P.; Lemstra, P.J.; Booij, H.C. Ultradrawing of high-molecular-weight polyethylene cast from solution. II. Influence of initial polymer concentration. J. Polym. Sci. Polym. Phys. Ed. 1981, 19, 877–888. [Google Scholar] [CrossRef] [Green Version]
- Klein, P.G.; Woods, D.W.; Ward, I.M. The effect of electron irradiation on the structure and mechanical properties of highly drawn polyethylene fibers. J. Polym. Sci. Part B Polym. Phys. 1987, 25, 1359–1379. [Google Scholar] [CrossRef]
- Tsubakihara, S.; Nakamura, A.; Yasuniwa, M. Melting and crystallization of ultra-high molecular weight polyethylene with appearance of hexagonal phase I. Melting processes of fibers under constrained state. Polym. J. 1996, 28, 489–495. [Google Scholar] [CrossRef] [Green Version]
- Taylor, W.N.; Clark, E.S. Superdrawn filaments of polypropylene. Polym. Eng. Sci. 1978, 18, 518–526. [Google Scholar] [CrossRef]
- Irvine, P.A.; Smith, P. Development of the axial Young’s modulus with draw ratio of flexible-chain polymers. Macromolecules 1986, 19, 240–242. [Google Scholar] [CrossRef]
- Porter, R.S.; Wang, L.-H. Uniaxial extension and order development in flexible chain polymers. J. Macromol. Sci. Part C Polym. Rev. 1995, 35, 63–115. [Google Scholar] [CrossRef]
- Peterlin, A. Molecular model of drawing polyethylene and polypropylene. J. Mater. Sci. 1971, 6, 490–508. [Google Scholar] [CrossRef]
- Grubb, D.T.; Keller, A. Thermal contraction and extension in fibrous crystals of polyethylene. Colloid Polym. Sci. 1978, 256, 218–233. [Google Scholar] [CrossRef]
- Grubb, D.T.; Li, Z.-F. Molecular stress distribution and creep of high-modulus polyethylene fibres. Polymer 1992, 33, 2587–2597. [Google Scholar] [CrossRef]
- Hu, W.-G.; Schmidt-Rohr, K. Characterization of ultradrawn polyethylene fibers by NMR: Crystallinity, domain sizes and a highly mobile second amorphous phase. Polymer 2000, 41, 2979–2987. [Google Scholar] [CrossRef]
- Clark, E.S.; Scott, L.S. Superdrawn crystalline polymers: A new class of high-strength fiber. Polym. Eng. Sci. 1974, 14, 682–686. [Google Scholar] [CrossRef]
- Reneker, D.H. Point dislocations in crystals of high polymer molecules. J. Polym. Sci. 1962, 59, S39–S42. [Google Scholar] [CrossRef]
- Sprague, B.S. Relationship of structure and morphology to properties of “hard” elastic fibers and films. J. Macromol. Sci. Part B 1973, 8, 157–187. [Google Scholar] [CrossRef]
- Clark, E.S. Structure and Properties of Polymer Films; Springer: Boston, MA, USA, 1973. [Google Scholar] [CrossRef]
- Patell, Y.R.; Schultz, J.M. Microstructure and tensile behavior of solid-state polymerized polyoxymethylene. J. Macromol. Sci. Part B 1973, 7, 445–464. [Google Scholar] [CrossRef]
- Southern, J.H.; Porter, R.S. The properties of polyethylene crystallized under the orientation and pressure effects of a pressure capillary viscometer. J. Appl. Polym. Sci. 1970, 14, 2305–2317. [Google Scholar] [CrossRef]
- Southern, J.H.; Porter, R.S. Polyethylene crystallized under the orientation and pressure of a pressure capillary viscometer. Part I. J. Macromol. Sci. Part B 1970, 4, 541–555. [Google Scholar] [CrossRef]
- Desper, C.R.; Southern, J.H.; Ulrich, R.D.; Porter, R.S. Orientation and structure of polyethylene crystallized under the orientation and pressure effects of a pressure capillary viscometer. J. Appl. Phys. 1970, 41, 4284–4289. [Google Scholar] [CrossRef]
- Zachariades, A.; Kanamoto, T. High Modulus Polymers with Stiff and Flexible Chains; Marcel Dekker Inc.: New York, NY, USA, 1987. [Google Scholar]
- Gibson, A.G.; Davies, G.R.; Ward, I.M. Dynamic mechanical behaviour and longitudinal crystal thickness measurements on ultra-high modulus linear polyethylene: A quantitative model for the elastic modulus. Polymer 1978, 19, 683–693. [Google Scholar] [CrossRef]
- Arridge, R.G.C.; Barham, P.J. A fibre composite model of drawn crystalline polymers. Polymer 1978, 19, 654–658. [Google Scholar] [CrossRef]
- Gao, X.; Jensen, R.E.; Li, W.; Deitzel, J.; McKnight, S.H.; Gillespie, J.W. Effect of fiber surface texture created from silane blends on the strength and energy absorption of the glass fiber/epoxy interphase. J. Compos. Mater. 2008, 42, 513–534. [Google Scholar] [CrossRef]
- Pennings, A.J.; Zwijnenburg, A. Longitudinal growth of polymer crystals from flowing solutions. VI. Melting behavior of continuous fibrillar polyethylene crystals. J. Polym. Sci. Polym. Phys. Ed. 1979, 17, 1011–1032. [Google Scholar] [CrossRef]
- Li, J.; Lee, Y.-W. Evolution of morphology in high molecular weight polyethylene during die drawing. J. Mater. Sci. 1993, 28, 6496–6502. [Google Scholar] [CrossRef]
- Iguchi, M.; Tonami, H.; Kawai, T. Crystallization of polyethylene under molecular orientation. Kolloid Z. Z. Polym. 1967, 221, 28–40. [Google Scholar] [CrossRef]
- Peterlin, A. Crystalline character in polymers. J. Polym. Sci. Part C Polym. Symp. 1965, 9, 61–89. [Google Scholar] [CrossRef]
- Kobayashi, K.; Geil, P.H. Polymer Single Crystals; Interscience Publisher: New York, NY, USA, 1963. [Google Scholar]
- Judge, J.T.; Stein, R.S. Growth of crystals from molten crosslinked oriented polyethylene. J. Appl. Phys. 1961, 32, 2357–2363. [Google Scholar] [CrossRef]
- Pennings, A.J. Fractionation of polymers by crystallization from solutions. II. J. Polym. Sci. Part C Polym. Symp. 1967, 16, 1799–1812. [Google Scholar] [CrossRef]
- Mackley, M.R.; Keller, A. Flow induced polymer chain extension and its relation to fibrous crystallization. Philos. Trans. R. Soc. Lond. Ser. Math. Phys. Sci. 1975, 278, 29–66. [Google Scholar] [CrossRef]
- Wikjord, A.G.; John Manley, R.S. The morphology of fibrillar polyethylene crystals. J. Macromol. Sci. Part B 1968, 2, 501–537. [Google Scholar] [CrossRef]
- Keller, A.; Willmouth, F.M. Some macroscopic properties of stirring-induced crystals of polyethylene. J. Macromol. Sci. Part B 1972, 6, 493–537. [Google Scholar] [CrossRef]
- Pennings, A.J. Bundle-like nucleation and longitudinal growth of fibrillar polymer crystals from flowing solutions. J. Polym. Sci. Polym. Symp. 1977, 59, 55–86. [Google Scholar] [CrossRef]
- Pennings, A.J.; Lageveen, R.; de Vries, R.S. Hydrodynamically induced crystallization of polymers from solution: VII.: On the origin of persistent lamellar overgrowth of Shish-kebab fibers. Colloid Polym. Sci. 1977, 255, 532–542. [Google Scholar] [CrossRef]
- Barham, P.J. Gelation and the production of stiff polyethylene fibres. Polymer 1982, 23, 1112–1122. [Google Scholar] [CrossRef]
- Hill, M.J.; Barham, P.J.; Keller, A. On the hairdressing of shish-kebabs. Colloid Polym. Sci. 1980, 258, 1023–1037. [Google Scholar] [CrossRef]
- Kwon, Y.K.; Boller, A.; Pyda, M.; Wunderlich, B. Melting and heat capacity of gel-spun, ultra-high molar mass polyethylene fibers. Polymer 2000, 41, 6237–6249. [Google Scholar] [CrossRef]
- Tzou, D.L.; Schmidt-Rohr, K.; Spiess, H.W. Solid-state n.m.r. studies of crystalline phases in gel-spun ultrahigh molecular weight polyethylene. Polymer 1994, 35, 4728–4733. [Google Scholar] [CrossRef]
- Kaji, A.; Ohta, Y.; Yasuda, H.; Murano, M. Phase structural analysis of ultra high-molecular weight polyethylene fibers by solid state high resolution NMR. Polym. J. 1990, 22, 455–462. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, Y.; Ishida, T.; Furusaka, M. Monoclinic-to-orthorhombic transformation in polyethylene. J. Polym. Sci. Part B Polym. Phys. 1988, 26, 2267–2277. [Google Scholar] [CrossRef]
- Hellmuth, E.; Wunderlich, B. Superheating of linear high-polymer polyethylene crystals. J. Appl. Phys. 1965, 36, 3039–3044. [Google Scholar] [CrossRef]
- Clough, S.B. Melting of stress-crystallized polyethylene. J. Macromol. Sci. Part B 1970, 4, 199–214. [Google Scholar] [CrossRef]
- Van Aerle, N.A.J.M.; Lemstra, P.J. Chain-extended polyethylene in composites—Melting and relaxation behaviour—. Polym. J. 1988, 20, 131–141. [Google Scholar] [CrossRef] [Green Version]
- Tsubakihara, S.; Nakamura, A.; Yasuniwa, M. Hexagonal phase of polyethylene fibers under high pressure. Polym. J. 1991, 23, 1317–1324. [Google Scholar] [CrossRef] [Green Version]
- Clough, S.B. Melting of drawn polyethylene films. J. Appl. Polym. Sci. 1971, 15, 2141–2148. [Google Scholar] [CrossRef]
- Vaughan, A.S.; Ungar, G.; Bassett, D.C.; Keller, A. On hexagonal phases of paraffins and polyethylenes. Polymer 1985, 26, 726–732. [Google Scholar] [CrossRef]
- Ungar, G.; Keller, A. Effect of radiation on the crystals of polyethylene and paraffins: 1. Formation of the hexagonal lattice and the destruction of crystallinity in polyethylene. Polymer 1980, 21, 1273–1277. [Google Scholar] [CrossRef]
- Wilding, M.A.; Ward, I.M. Creep and recovery of ultra high modulus polyethylene. Polymer 1981, 22, 870–876. [Google Scholar] [CrossRef]
- Wilding, M.A.; Ward, I.M. Creep and stress-relaxation in ultra-high modulus linear polyethylene. J. Mater. Sci. 1984, 19, 629–636. [Google Scholar] [CrossRef]
- Govaert, L.; Brown, B.; Smith, P. Temperature dependence of the Young’s modulus of oriented polyethylene. Macromolecules 1992, 25, 3480–3483. [Google Scholar] [CrossRef]
- Roiron, C.; Lainé, E.; Grandidier, J.-C.; Olivier, D.; Garois, N.; Vix, C. Study of the thermomechanical behavior of UHMWPE yarns under different loading paths. Polym. Test. 2020, 89, 106717. [Google Scholar] [CrossRef]
- Phani, K.K. Evaluation of single-fibre strength distribution from fibre bundle strength. J. Mater. Sci. 1988, 23, 941–945. [Google Scholar] [CrossRef]
- Wang, Y.; Xia, Y.M. Experimental and theoretical study on the strain rate and temperature dependence of mechanical behaviour of Kevlar fibre. Compos. Part A Appl. Sci. Manuf. 1999, 30, 1251–1257. [Google Scholar] [CrossRef]
- Perkins, W.G.; Capiati, N.J.; Porter, R.S. The effect of molecular weight on the physical and mechanical properties of ultra-drawn high density polyethylene. Polym. Eng. Sci. 1976, 16, 200–203. [Google Scholar] [CrossRef]
- Kavesh, S.; Prevorsek, D.C. High Tenacity, High Modulus Polyethylene and Polypropylene Fibers and Intermediates Therefore. U.S. Patent No. 4,413,110, 1 November 1983. [Google Scholar]
- Williams, J.L.; Peterlin, A. A study of the sorption and permeability of gases and vapors in solvent-drawn polyethylene. Makromol. Chem. 1970, 135, 41–47. [Google Scholar] [CrossRef]
- Smith, P.; Lemstra, P.J. Ultra-high strength polyethylene filaments by solution spinning/drawing. 3. Influence of drawing temperature. Polymer 1980, 21, 1341–1343. [Google Scholar] [CrossRef] [Green Version]
- Smith, P.; Lemstra, P.J. Ultrahigh-strength polyethylene filaments by solution spinning/drawing, 2†. Influence of solvent on the drawability. Makromol. Chem. 1979, 180, 2983–2986. [Google Scholar] [CrossRef]
- Kalb, B.; Pennings, A.J. General crystallization behaviour of poly(l-lactic acid). Polymer 1980, 21, 607–612. [Google Scholar] [CrossRef]
- Wu, W.; Simpson, P.G.; Black, W.B. Morphology and tensile property relations of high-strength/high-modulus polyethylene fiber. J. Polym. Sci. Polym. Phys. Ed. 1980, 18, 751–765. [Google Scholar] [CrossRef]
- Zachariades, A.; Kanamoto, T.; Porter, R.S. Solid-state coextrusion of high-density polyethylene. II. Effect of molecular weight and molecular weight distribution. J. Polym. Sci. Polym. Phys. Ed. 1980, 18, 575–585. [Google Scholar] [CrossRef]
- Smith, P.; Lemstra, P.J.; Pijpers, J.P.L.; Kiel, A.M. Ultra-drawing of high molecular weight polyethylene cast from solution: III. Morphology and structure. Colloid Polym. Sci. 1981, 259, 1070–1080. [Google Scholar] [CrossRef] [Green Version]
- Furuhata, K.; Yokokawa, T.; Miyasaka, K. Drawing of ultrahigh-molecular-weight polyethylene single-crystal mats. J. Polym. Sci. Polym. Phys. Ed. 1984, 22, 133–138. [Google Scholar] [CrossRef]
- Kanamoto, T.; Sherman, E.S.; Porter, R.S. Extrusion of polyethylene single crystals. Polym. J. 1979, 11, 497–502. [Google Scholar] [CrossRef] [Green Version]
- Statton, W.O. Coherence and deformation of lamellar crystals after annealing. J. Appl. Phys. 1967, 38, 4149–4151. [Google Scholar] [CrossRef]
- Ishikawa, K.; Miyasaka, K.; Maeda, M. Drawing of single-crystal mats of linear polyethylene. J. Polym. Sci. Part A-2 Polym. Phys. 1969, 7, 2029–2041. [Google Scholar] [CrossRef]
- Maeda, M.; Miyasaka, K.; Ishikawa, K. Properties and structures of films drawn from polyethylene single-crystal mats. J. Polym. Sci. Part A-2 Polym. Phys. 1970, 8, 355–369. [Google Scholar] [CrossRef]
- Barham, P.J.; Keller, A. A study on the achievement of high-modulus polyethylene fibres by drawing. J. Mater. Sci. 1976, 11, 27–35. [Google Scholar] [CrossRef]
- Jarecki, L.; Meier, D.J. Ultra-high modulus polyethylene. 1 Effect of drawing temperature. Polymer 1979, 20, 1078–1082. [Google Scholar] [CrossRef]
- Bashir, Z.; Odell, J.A.; Keller, A. High modulus filaments of polyethylene with lamellar structure by melt processing; the role of the high molecular weight component. J. Mater. Sci. 1984, 19, 3713–3725. [Google Scholar] [CrossRef]
- Barham, P.J.; Keller, A. Some observations on the production of polyethylene fibres by the surface growth method. J. Mater. Sci. 1980, 15, 2229–2235. [Google Scholar] [CrossRef]
- Pennings, A.J.; Schouteten, C.J.H.; Kiel, A.M. Hydrodynamically induced crystallization of polymers from solution. V. Tensile properties of fibrillar polyethylene crystals. J. Polym. Sci. Part C Polym. Symp. 1972, 38, 167–193. [Google Scholar] [CrossRef]
- Smook, J.; Torfs, J.C.; van Hutten, P.F.; Pennings, A.J. Ultra-high strength polyethylene by hot drawing of surface growth fibers. Polym. Bull. 1980, 2, 293–300. [Google Scholar] [CrossRef]
- Capaccio, G.; Crompton, T.A.; Ward, I.M. The drawing behavior of linear polyethylene. I. Rate of drawing as a function of polymer molecular weight and initial thermal treatment. J. Polym. Sci. Polym. Phys. Ed. 1976, 14, 1641–1658. [Google Scholar] [CrossRef]
- Smith, P.; Lemstra, P.J. Ultra-drawing of high molecular weight polyethylene cast from solution. Colloid Polym. Sci. 1980, 258, 891–894. [Google Scholar] [CrossRef] [Green Version]
- Koh, A.C.P.; Shim, V.P.W.; Tan, V.B.C. Dynamic behaviour of UHMWPE yarns and addressing impedance mismatch effects of specimen clamps. Int. J. Impact Eng. 2010, 37, 324–332. [Google Scholar] [CrossRef]
- Huang, W.; Wang, Y.; Xia, Y. Statistical dynamic tensile strength of UHMWPE-fibers. Polymer 2004, 45, 3729–3734. [Google Scholar] [CrossRef]
- Matsuo, M.; Sawatari, C. Temperature dependence of the crystal lattice modulus and the Young’s modulus of polyethylene. Macromolecules 1988, 21, 1653–1658. [Google Scholar] [CrossRef]
- Lacher, R.C.; Bryant, J.L.; Howard, L.N.; Sumners, D.W. Linking phenomena in the amorphous phase of semicrystalline polymers. Macromolecules 1986, 19, 2639–2643. [Google Scholar] [CrossRef]
- Kausch, H.H.; Becht, J. Elektronenspinresonanz, eine molekulare Sonde bei der mechanischen Beanspruchung von Thermoplasten. In Aktuelle Probleme der Polymer-Physik III; Fischer, E.W., Müller, F.H., Eds.; Steinkopff: Heidelberg, Germany, 1972; pp. 56–73. [Google Scholar] [CrossRef]
- Meinel, G.; Peterlin, A. Changes in noncrystalline regions of polyethylene during annealing. J. Polym. Sci. Part B 1967, 5, 613–618. [Google Scholar] [CrossRef]
- Arridge, R.G.C.; Barham, P.J.; Keller, A. Self-hardening of highly oriented polyethylene. J. Polym. Sci. Polym. Phys. Ed. 1977, 15, 389–401. [Google Scholar] [CrossRef]
- Takayanagi, M.; Imada, K.; Kajiyama, T. Mechanical properties and fine structure of drawn polymers. J. Polym. Sci. Part C 1966, 15, 263–281. [Google Scholar] [CrossRef]
- Hosemann, R. Crystalline and paracrystalline order in high polymers. J. Appl. Phys. 1963, 34, 25–41. [Google Scholar] [CrossRef]
- Peterlin, A. Drawing and annealing of fibrous material. J. Appl. Phys. 1977, 48, 4099–4108. [Google Scholar] [CrossRef]
- Decandia, F.; Vittoria, V.; Peterlin, A. Time dependence of mechanical and transport properties of drawn and annealed linear polyethylene. J. Polym. Sci. Polym. Phys. Ed. 1985, 23, 1217–1234, juin. [Google Scholar] [CrossRef]
- De Boer, J.; Pennings, A.J. Crosslinking of ultra-high strength polyethylene fibers by means of γ-radiation. Polym. Bull. 1981, 5, 317–324. [Google Scholar] [CrossRef]
- Govaert, L.E.; D’Hooghe, E.L.J.C.J.; Peijs, A.A.J.M. A micromechanical approach to the viscoelasticity of unidirectional hybrid composites. Composites 1991, 22, 113–119. [Google Scholar] [CrossRef]
- Seitz, J.T.; Balazs, C.F. Application of time-temperature superposition principle to long term engineering properties of plastic materials. Polym. Eng. Sci. 1968, 8, 151–160. [Google Scholar] [CrossRef]
- Sweeney, J.; Ward, I.M. A unified model of stress relaxation and creep applied to oriented polyethylene. J. Mater. Sci. 1990, 25, 697–705. [Google Scholar] [CrossRef]
- Marichin, V.A.; Mjasnikova, L.P.; Zenke, D.; Hirte, R.; Weigel, P. Ultra-high strength and ultra-high modulus fibers from polyethylene. Polym. Bull. 1984, 12, 287–292. [Google Scholar] [CrossRef]
- Woods, D.W.; Busfield, W.K.; Ward, I.M. Improved mechanical behaviour in ultra high modulus polyethylenes by controlled crosslinking. Polym. Commun. 1984, 25, 298–300. [Google Scholar]
- Ohta, Y.; Yasuda, H. The influence of short branches on the α, β and γ-relaxation processes of ultra-high strength polyethylene fibers. J. Polym. Sci. Part B Polym. Phys. 1994, 32, 2241–2249. [Google Scholar] [CrossRef]

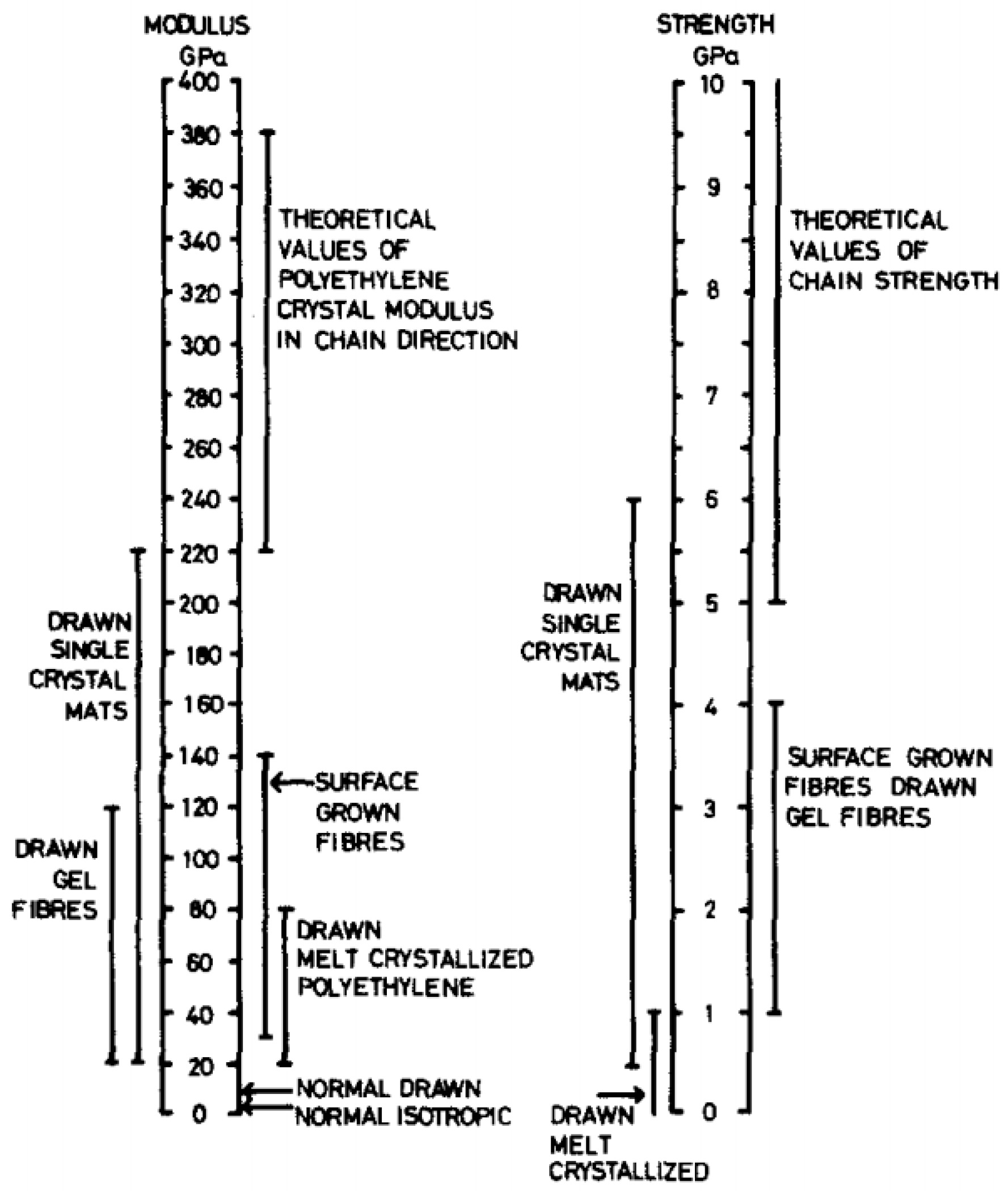









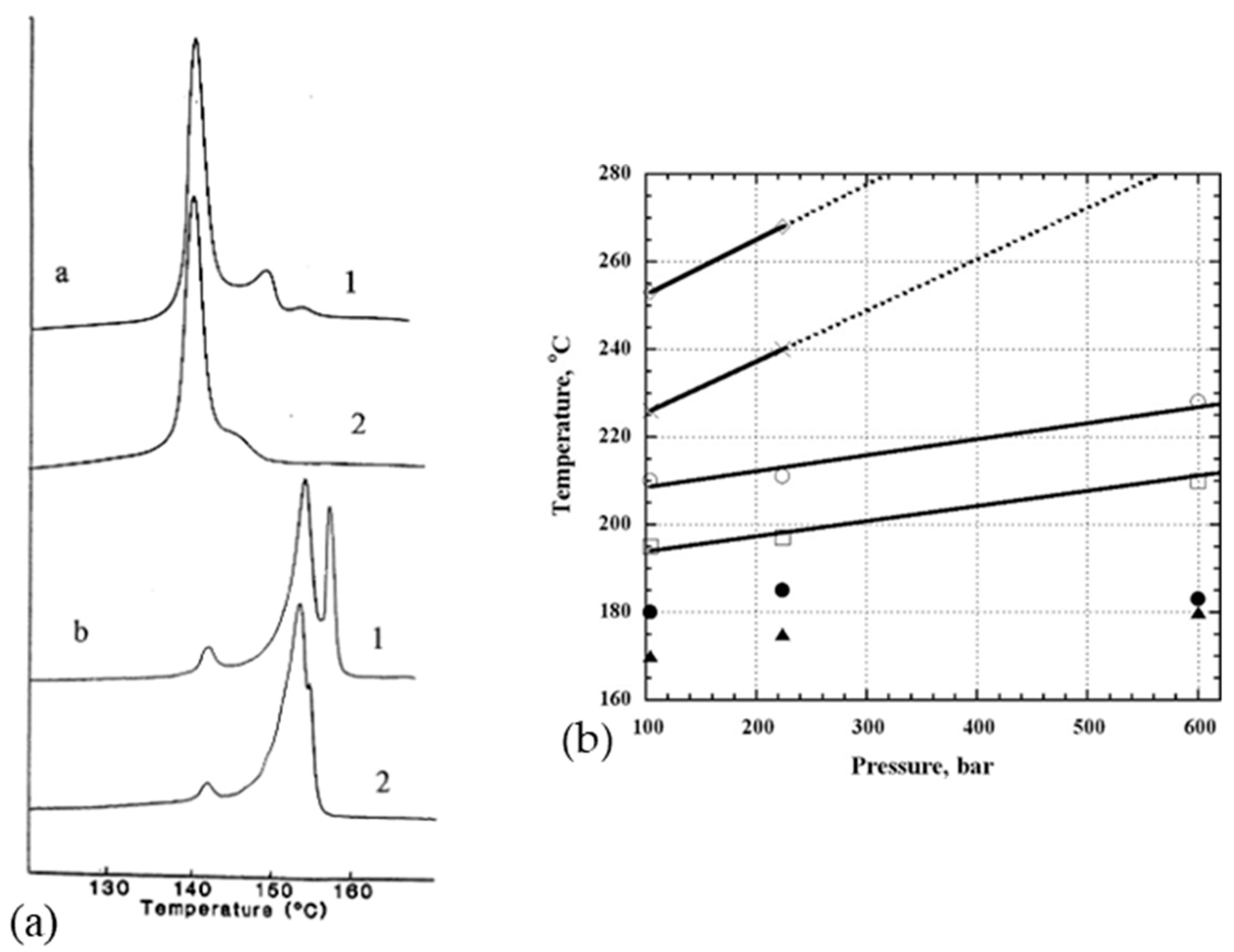


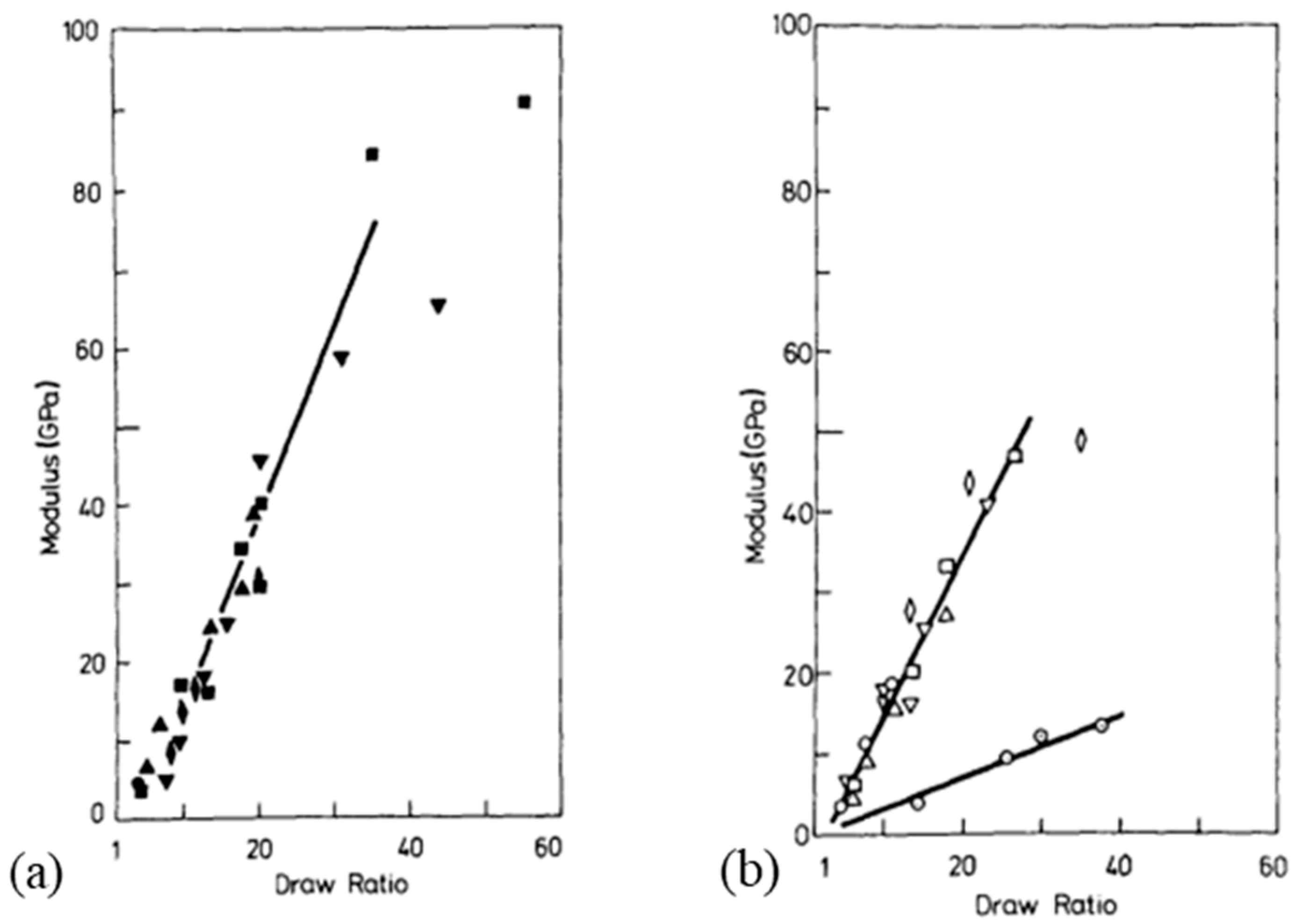
 ), Hot drawing [123] (∆), Solid-state extrusion [55,117,124] (x)) (reprinted with permission from ref. [48]. 2021 Roiron.).
), Hot drawing [123] (∆), Solid-state extrusion [55,117,124] (x)) (reprinted with permission from ref. [48]. 2021 Roiron.).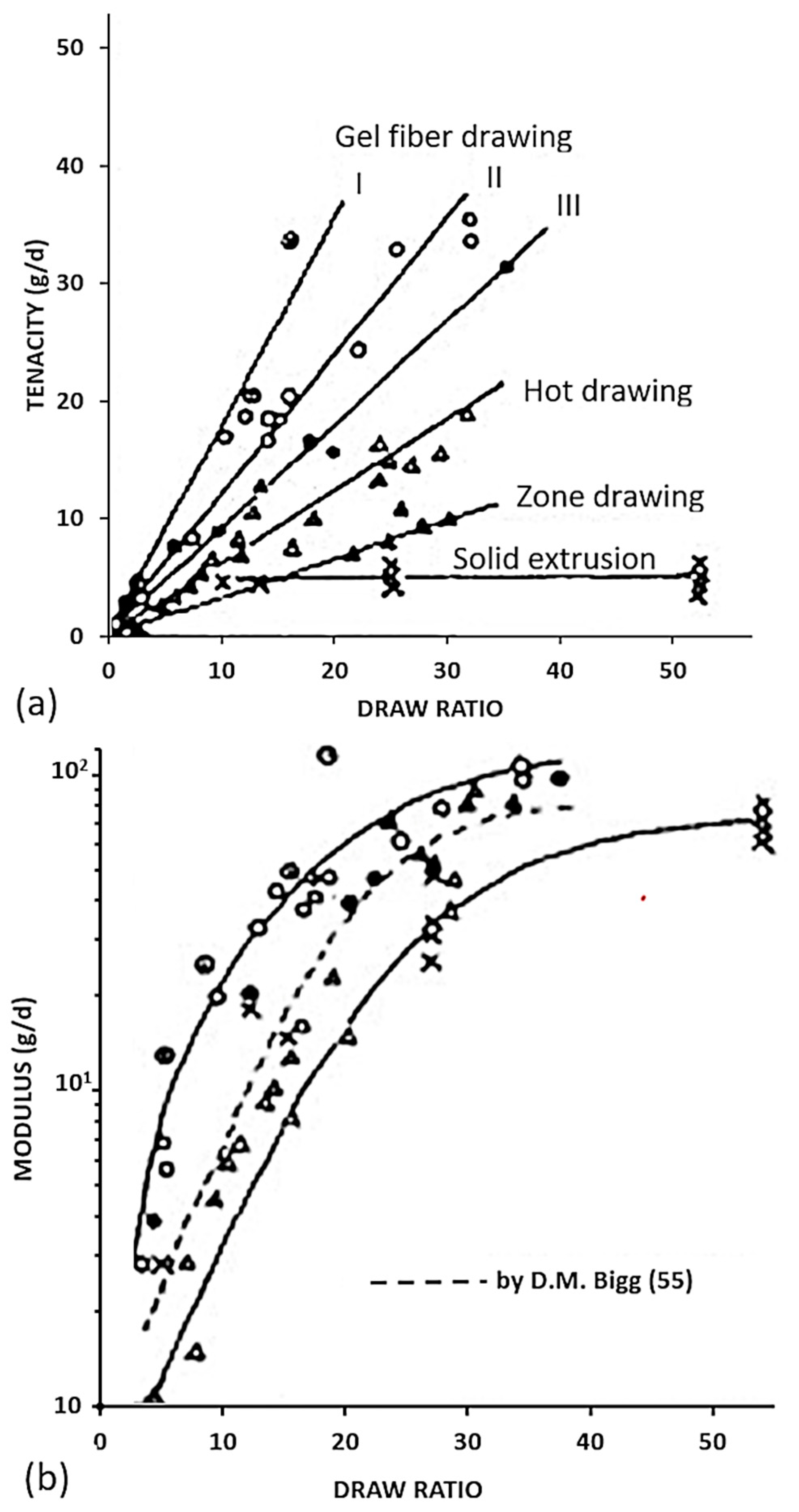








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roiron, C.; Lainé, E.; Grandidier, J.-C.; Garois, N.; Vix-Guterl, C. A Review of the Mechanical and Physical Properties of Polyethylene Fibers. Textiles 2021, 1, 86-151. https://0-doi-org.brum.beds.ac.uk/10.3390/textiles1010006
Roiron C, Lainé E, Grandidier J-C, Garois N, Vix-Guterl C. A Review of the Mechanical and Physical Properties of Polyethylene Fibers. Textiles. 2021; 1(1):86-151. https://0-doi-org.brum.beds.ac.uk/10.3390/textiles1010006
Chicago/Turabian StyleRoiron, Coline, Eric Lainé, Jean-Claude Grandidier, Nicolas Garois, and Cathie Vix-Guterl. 2021. "A Review of the Mechanical and Physical Properties of Polyethylene Fibers" Textiles 1, no. 1: 86-151. https://0-doi-org.brum.beds.ac.uk/10.3390/textiles1010006