Next Article in Journal
Manufacturing and Characterization of Customizable Flexible Carbon Nanotube Fabrics for Smart Wearable Applications
Next Article in Special Issue
Stretchable Textile Yarn Based on UHF RFID Helical Tag
Previous Article in Journal
An Alternative Method to Develop Embroidery Textile Strain Sensors
Previous Article in Special Issue
Development of a Consumer-Based Quality Scale for Artisan Textiles: A Study with Scarves/Shawls
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Textiles
Volume 1
Issue 3
10.3390/textiles1030027
textiles-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

A Review on Tough Soft Composites at Different Length Scales

by
Wei Cui
1,2,* and
Ruijie Zhu
3
1
State Key Laboratory of Polymer Materials Engineering, College of Polymer Science and Engineering, Sichuan University, Chengdu 610065, China
2
Faculty of Advanced Life Science, Hokkaido University, Sapporo 001-0021, Japan
3
Graduate School of Chemical Sciences and Engineering, Hokkaido University, Sapporo 060-8628, Japan
*
Author to whom correspondence should be addressed.
Textiles 2021, 1(3), 513-533; https://0-doi-org.brum.beds.ac.uk/10.3390/textiles1030027
Submission received: 26 October 2021 / Revised: 12 November 2021 / Accepted: 16 November 2021 / Published: 17 November 2021
(This article belongs to the Special Issue New Research Trends for Textiles)
Browse Figures
Versions Notes

Abstract

:
Soft composites are widely employed in industrial and biomedical fields, which often serve as load-bearing structural materials by virtue of a special combination of high strength, high toughness, and low flexural stiffness. Understanding the toughening mechanism of such composites is crucial for designing the next-generation soft materials. In this review, we give an overview of recent progress in soft composites, focusing on the design strategy, mechanical properties, toughening mechanisms, and relevant applications. Fundamental design strategies for soft composites that dissipate energy at different length scales are firstly described. By subsequently elucidating the synergistic effects of combining soft and hard phases, we show how a resulting composite can achieve unprecedented mechanical performance by optimizing the energy dissipation. Relevant toughening models are discussed to interpret the superior strength and fracture toughness of such soft composites. We also highlight relevant applications of these soft composites by taking advantage of their special mechanical responses.

1. Introduction

Composite materials are widely applied in industrial and biomedical fields as structural materials due to their superior comprehensive properties, such as high strength, high stiffness, low weight, corrosion resistance, etc. [1,2,3,4]. Conventional hard composites are generally composed of rigid matrices (resins, metals, ceramics, etc.) and rigid fibers or fabrics, showing isotropically high stiffness [5,6,7]. Soft composite, in contrast, is a sort of composite material with low flextural stiffness [8,9,10,11,12]. Commonly, both hard and soft composites show very high fracture stress and Young’s modulus in tension, which can reach values on the order of 100 and 101 GPa, respectively. The biggest difference between hard and soft composites is their mechanical performance upon bending. The bending stiffness of soft composites (100 MPa) is usually several orders of magnitude lower than that of hard composites (101 GPa) [5,12]. Because of a unique combination of high stiffness in tension and low hardness upon bending, soft composites are uniquely applicable to numerous applications such as soft robotics, sensors, actuators, etc. [9,11,12].
Although a variety of soft composites have been developed for specific applications, a timeless topic is how to toughen them, as mechanical properties always determine the reliability and lifespan of relevant products. The toughening of materials has a long history and the main concept is widely accepted for either soft or hard materials, i.e., simultaneously enhancing the size of energy dissipation zone and energy dissipation density [13,14,15,16]. In other words, a material with high toughness should, on one hand, dissipate energy at a large length scale, and on the other hand, dissipate as much as energy per unit volume [16,17,18]. For instance, glass is a strong, stiff, but extremely brittle material. This is because the glass plate can only dissipate energy at the atom scale, although it has a high energy dissipation density (Figure 1a) [19]. In contrast, rubber is not as strong as glass, whereas it possesses a much higher fracture toughness due to a significantly increased energy dissipation zone at the polymer chain scale (Figure 1b) [15,20]. Double network materials can show even superior fracture toughness to rubbers because their energy dissipation density is further increased due to the introduction of extra network chains (Figure 1c) [21,22,23]. That is, tough soft composites always possess high fracture toughness over 100 kJ m−2 and are highly resistant to crack growth even when they are notched.
Many biological tissues are essentially tough soft composites by exploiting the above concept [24,25,26,27]. These natural materials, generally consisting of stiff fibrous skeletons and soft extracellular matrices, are anisotropic, strong, and tough via the synergy of a large energy dissipation zone and high energy dissipation density. For example, heart valves possess fracture toughness around 1200 J m−2 while showing high resilience [28]. Tendon is a strong connective tissue that connects muscle to bone and muscle to muscle, which can sustain over 1 million cycles of loading per year and show fracture toughness as high as 20–30 kJ m−2 [28]. The efficient stress transfer between the stiff and soft phases enables these tissues to dissipate energy at a large length scale, and the energy-dissipative components both contribute to a high energy dissipation density.
Until now, immense efforts using synthetic approaches have been taken in an endeavor to fabricate tough soft composites. Generally, soft composites can be classified by their energy dissipation mechanisms at different length scales (Figure 2). At the molecular level, double network (DN) material is a typical soft composite, which dissipates energy by breaking polymer chains [29,30]. At the nanometer scale, phase-separated material is an example, dissipating energy via the rupture of nanophases [31,32,33]. At the micron scale, common soft composites are micro-fiber-reinforced polymers. The energy dissipation relies on the stress transfer between the stiff fibrils and soft matrices [34,35,36,37]. At the millimeter scale, macroscopic fiber fabrics are combined with soft polymer matrices, generating soft composites that dissipate energy by breaking both fibers and matrices [18,38,39,40].
Reviews on traditional hard composites are well documented and have provided widespread instruction for the development of next-generation industrial and biomedical products [41,42,43]. However, important reviews focusing on soft composites are still rare. Therefore, we are stimulated to propose this review. Herein, we give a summary of recently developed tough soft composites with energy dissipation mechanisms at a variety of length scales. In Section 2, we describe the common design strategies of tough soft composites and relevant structure characteristics. In Section 3, we show how these soft composites can achieve superior mechanical properties via a delicate combination of stiff and soft phases. In Section 4, we explain the toughening mechanism of different soft composites that dissipate energy from micro- to macro-scales. In Section 5, some intriguing applications enabled by the soft composite design are demonstrated. Finally, we provide a summary and outlook on the future directions of soft composites.

2. Fabrication

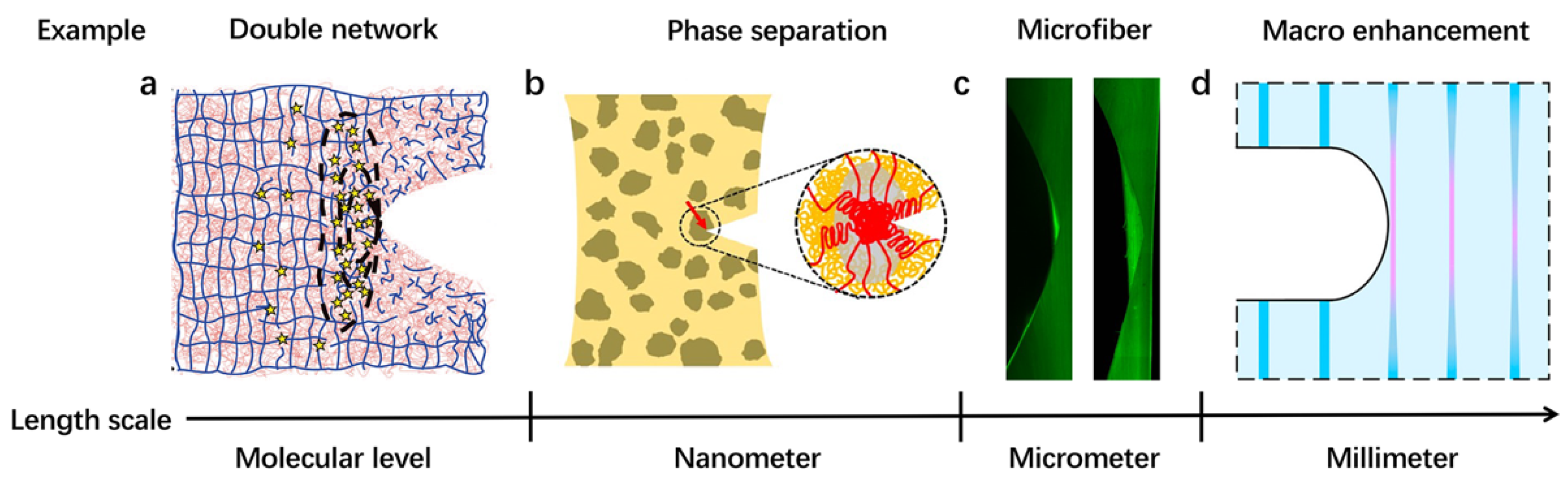
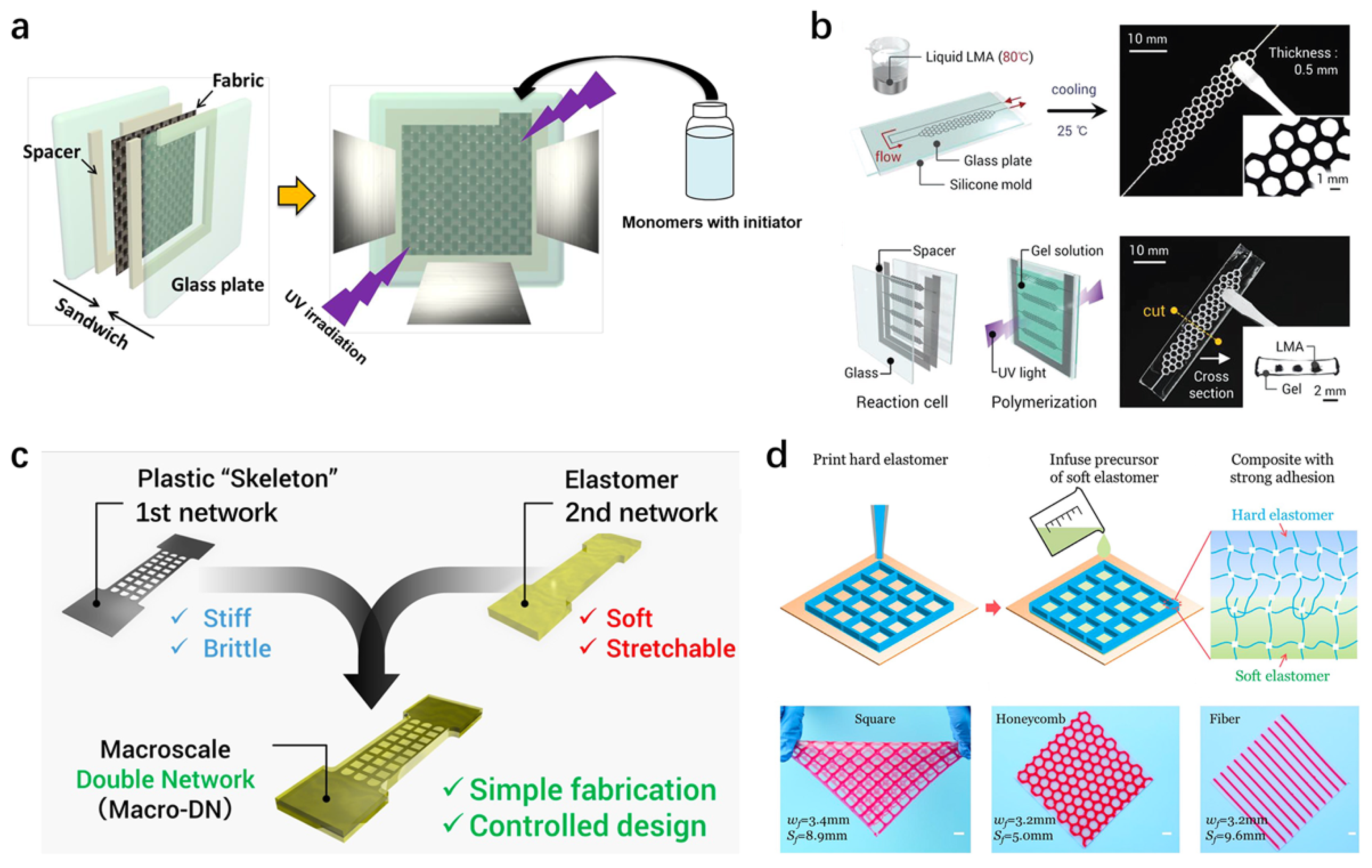
2.1. Double Network

The double network (DN) method is one of the most pioneering strategies to toughen soft materials, especially for hydrogels and elastomers. The general concept of the DN strategy is to combine two interpenetrating polymer networks with contrasting structures (Figure 3a) [44]. The first network is usually densely cross-linked, which is rigid and brittle. The second network is a sparsely cross-linked neutral polymer with a much higher concentration, which is soft and stretchable [45]. A DN gel or elastomer can be deemed as a molecular-level soft composite with high heterogeneity, although it behaves like a homogenous material.
The key factors to construct an efficient DN network instead of a simple interpenetrating network are, on one hand, to highly pre-stretch the first network, resulting in taut molecular chains with high stiffness, on the other hand, to swell the first network as much as possible in the second monomer solution with a low concentration of the cross-linking agent, enabling the high concentration ratio of the second network to the first network. In classical hydrogel systems, such a contrasting DN structure is realized by utilizing polyelectrolytes as the first network, which dramatically swell in the second neutral monomer solution due to high osmotic pressure. This effect leads to highly extended first network chains and a high concentration ratio between two networks (Figure 3b) [46]. Because both networks are chemically cross-linked, the classical DN hydrogels cannot self-recover after damage. Physical DN hydrogels are then developed to enable recoverable energy dissipation mechanisms. A typical example is the Ca2+-alginate/polyacrylamide system, which exploits the unzipping of ionic crosslinks between Ca2+ and alginate to dissipate energy and the re-zipping of the ionic bonds to heal the damage [23]. Another example is the physical DN gels based on an amphiphilic triblock copolymer that contains strong hydrophobic domains and sacrificial hydrogen bonds [47]. The reversible physical interactions of the first network enable the resulting DN gels to partially restore the mechanical properties after damage. The fabrication of physical DN gels is different from that of chemical ones. Only a one-pot method is required when preparing physical DN gels because the first network is usually a pre-polymer, which can dissolve in the second monomer solution by either stirring or heating (Figure 3c) [46]. As long as the concentration ratio between the first and second networks is carefully controlled, physical hydrogels with DN features can also be successfully fabricated. The DN method was firstly employed in the hydrogel systems and later proven to be applicable in elastomer systems [29,48,49,50]. The preparation of typical DN elastomers is slightly different from that of DN hydrogels since neutral monomers are commonly utilized to construct the first network. A multi-step swelling method was introduced to sufficiently pre-stretch the first network and form a high concentration contrast between the soft and the rigid networks. A drawback of this multi-step method is that it consumes significant time and energy. To overcome this dilemma, Matsuda et al. employed polyelectrolytes as the first network and dissolved them in organic solvents that have a similar dielectric constant to the monomer, giving rise to the formation of highly extended first network chains and enabling the dramatic swelling of the first network in second neutral monomer solutions (Figure 3d) [51]. In this way, a DN elastomer can be manufactured using the traditional method for DN hydrogels.
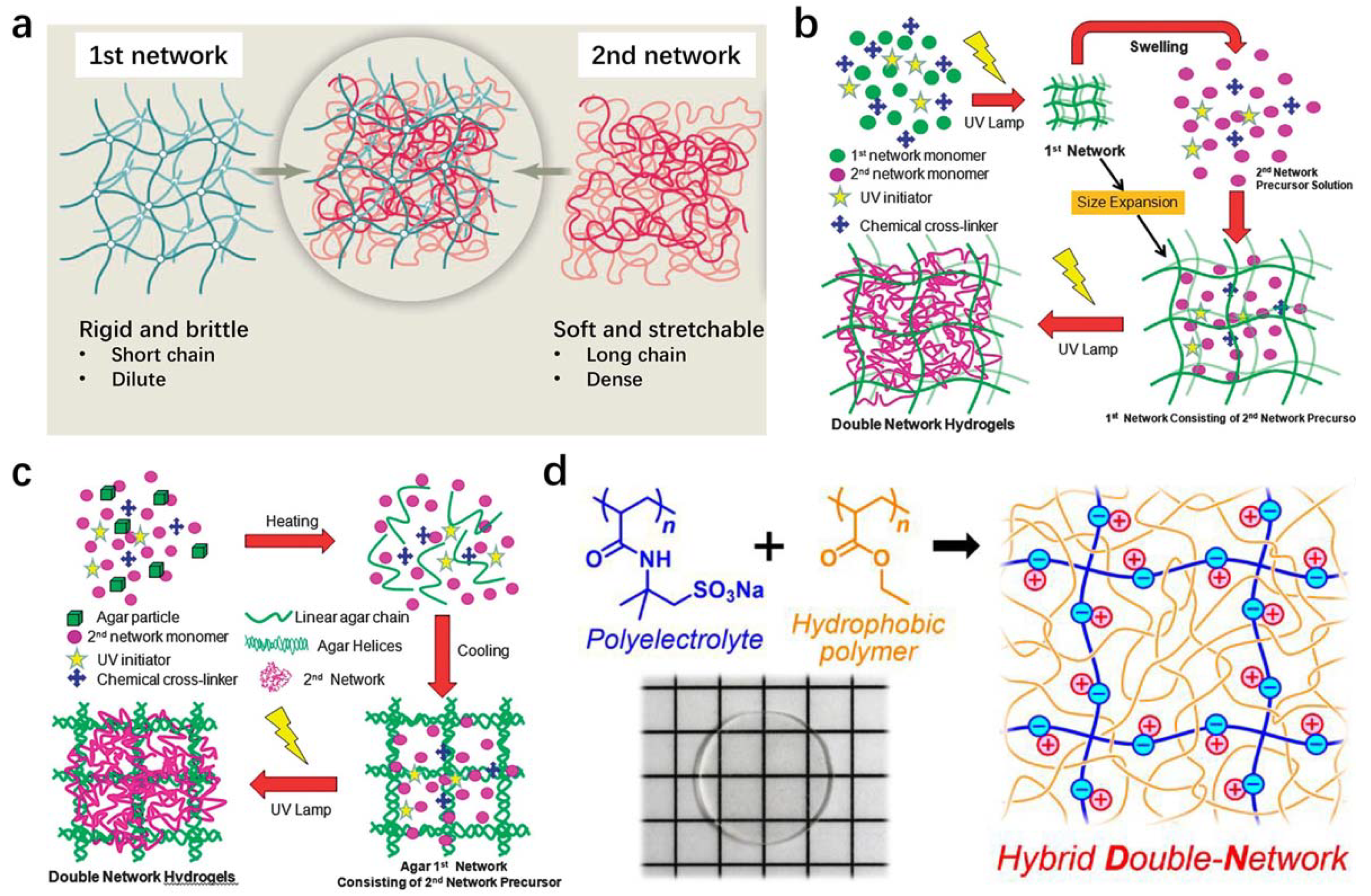
Textiles 01 00027 g003 550
Figure 3. Fabrication of double network hydrogels and elastomers. (a) The composition of conventional chemical double network hydrogels. Reproduced with permission from reference [44] Copyright 2014 The American Association for the Advancement of Science. (b) Fabrication of conventional chemical double network hydrogels. Reproduced with permission from reference [46] Copyright 2015 Royal Society of Chemistry. (c) Fabrication of physical double network hydrogels. Reproduced with permission from reference [46] Copyright 2015 Royal Society of Chemistry. (d) Fabrication of double network elastomers. Reproduced with permission from reference [51] Copyright 2019 American Chemical Society.
Figure 3. Fabrication of double network hydrogels and elastomers. (a) The composition of conventional chemical double network hydrogels. Reproduced with permission from reference [44] Copyright 2014 The American Association for the Advancement of Science. (b) Fabrication of conventional chemical double network hydrogels. Reproduced with permission from reference [46] Copyright 2015 Royal Society of Chemistry. (c) Fabrication of physical double network hydrogels. Reproduced with permission from reference [46] Copyright 2015 Royal Society of Chemistry. (d) Fabrication of double network elastomers. Reproduced with permission from reference [51] Copyright 2019 American Chemical Society.
Textiles 01 00027 g003

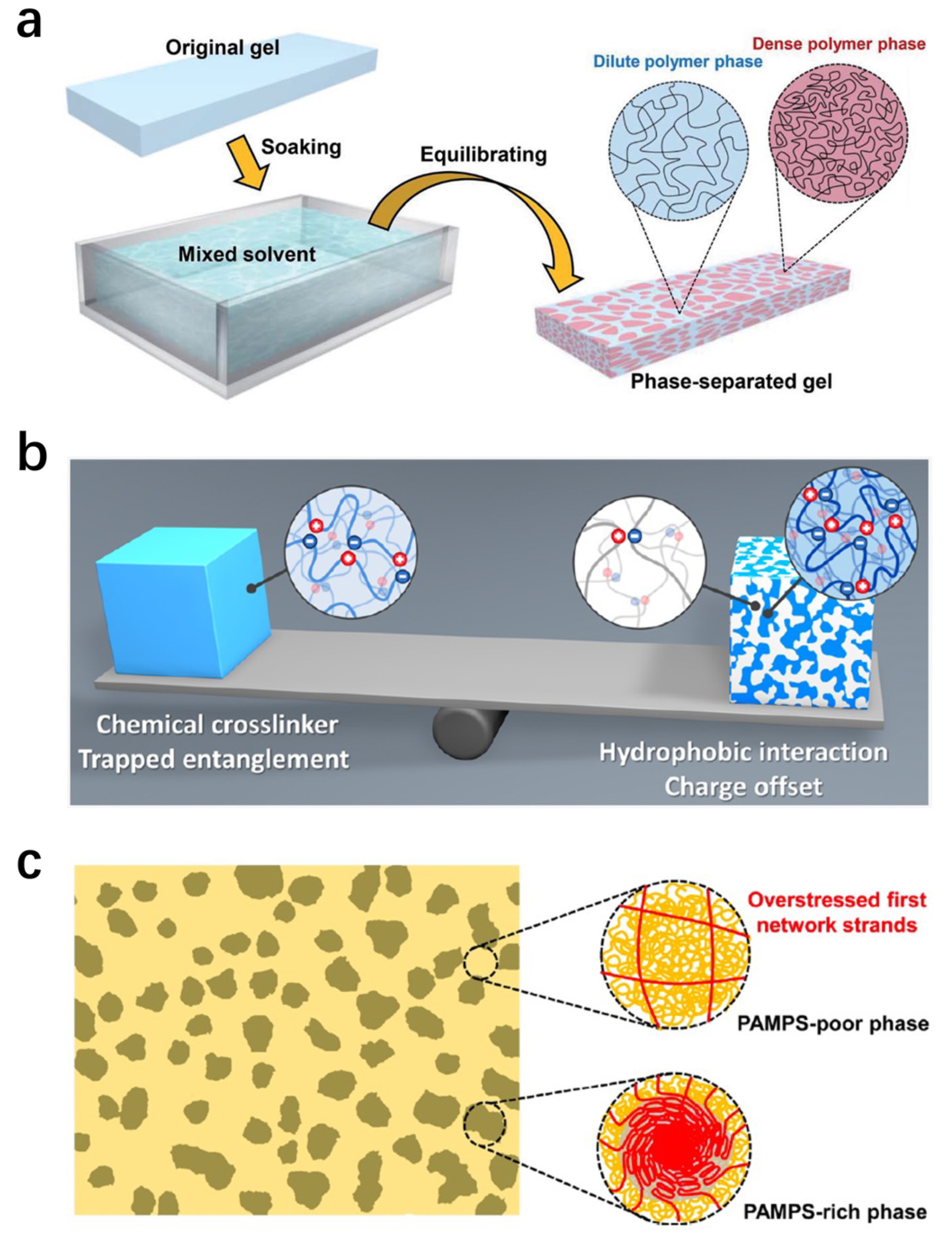
2.2. Phase Separation

Phase separation results in hydrogels or elastomers that possess dilute and dense polymer phases [52,53,54]. The dilute phase is soft, consisting of polymers with low volume fractions. On the contrary, the dense phase is relatively hard, which is composed of polymers with high volume fractions. The energy dissipation of phase-separated materials depends on the rupture of massive dense polymer phases at the nanometer scale. Therefore, phase-separated materials can be simply considered nano-scale soft composites.
There are a variety of methods to fabricate hydrogels or elastomers with phase-separated structures. One simple way is to utilize mixed-solvent-induced phase separation. Equilibrating a neutral hydrogel in a mixture of both good and poor solvents induces phase separation, resulting in an inhomogeneous network structure with bicontinuous domains (Figure 4a) [55]. Because of the low polymer-solvent affinity between the network chains and the poor solvent, a portion of polymer chains aggregate into local dense phases, which possess a considerably high polymer volume fraction to induce inter-/intra- polymer interactions. In contrast, other polymer chains in low volume fractions form the dilute polymer phases, which have relatively low modulus. Another example is the polyampholyte (PA) hydrogel system (Figure 4b) [52,56]. Unlike the solvent-initiated phase separation, the PA gels show a bicontinuous network structure due to the distribution of ionic bonds. The different density of ionic bonds leads to the local aggregation of polymer backbones via hydrophobic association, giving rise to a network structure with soft and hard phases. The phase separation method is also applicable in elastomer systems by using an ionic polymer as the first network and a nonpolar polymer as the second network (Figure 4c) [31]. Firstly, the polyelectrolyte network is polymerized and then soaked into the second monomer solution using a cosolvent of a high dielectric constant. Due to the high osmotic pressure, the first network is highly pre-stretched and brittle. Afterward, the second network is polymerized and formed within the first network, producing DN materials with a highly contrasting architecture. A DN elastomer is formed by finally removing the cosolvent.

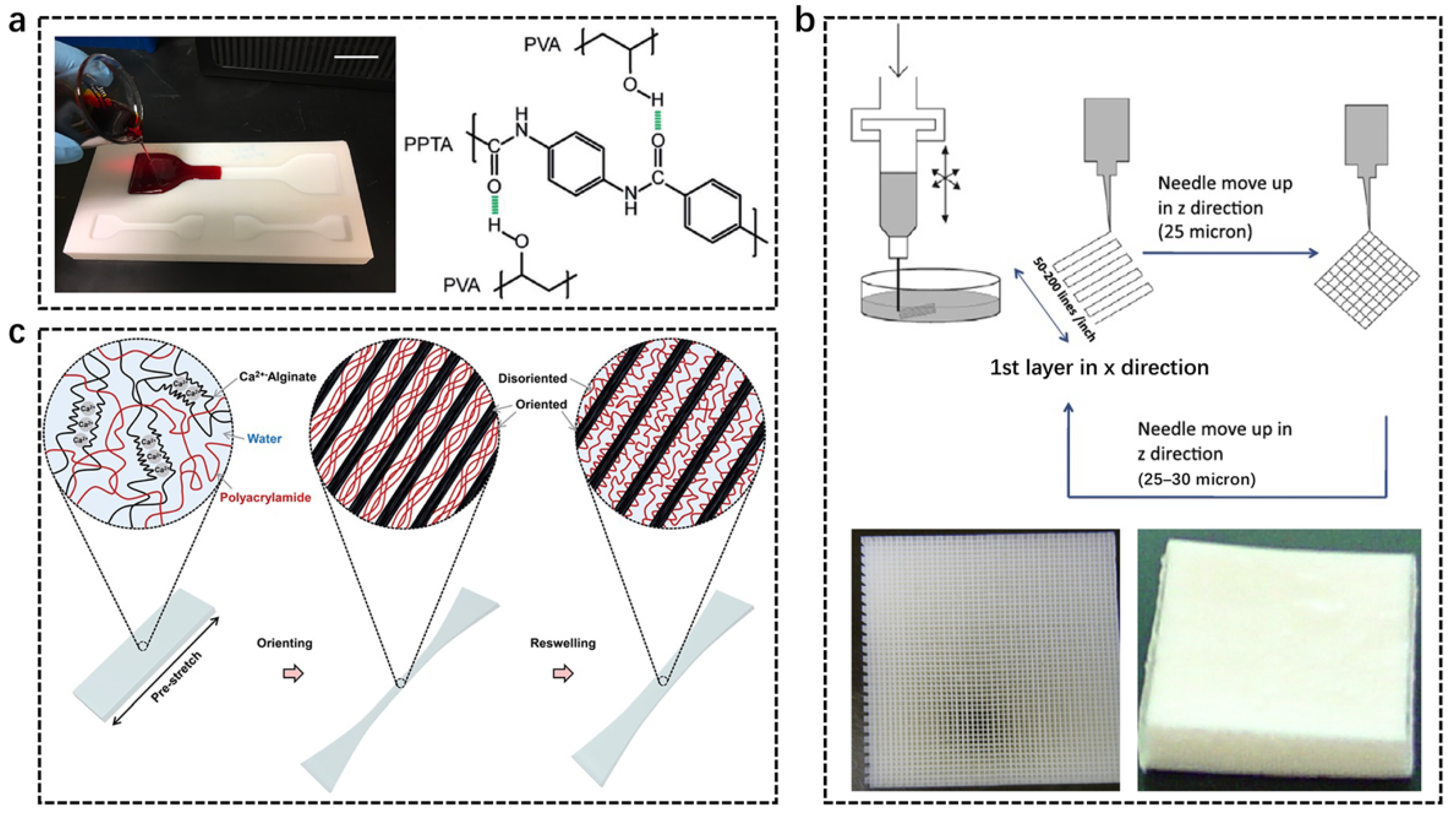
2.3. Microscopic Reinforcement

Introducing microfibers into a soft matrix is a well-established way to develop soft composites [57,58,59,60]. Usually, the added microfibers have a relatively low volume fraction, which, however, can lead to obvious mechanical enhancement of the soft composites. Interfacial interactions between the fibers and the matrix are crucial for efficient stress transmission and resulting energy dissipation. In this part, we give several common ways to fabricate tough soft composites by introducing micro-fibers as the enhancement phases.
The most common way to fabricate micro-fiber-reinforced soft composites is direct blending. A great number of examples can be listed because this method is simple and efficient. For the hydrogel system, it is worth noting that the micro-fiber should interact strongly with the hydrophilic polymer matrix to prevent interfacial delamination upon load. For instance, aramid micro-fibers can form massive hydrogen bonding with polyvinyl alcohol chains, the mixture of which gives rise to a strong and tough composite hydrogel (Figure 5a) [61]. The efficient stress transfer between the stiff fibers and the soft matrices enables the gel to show self-organization behaviors, resembling biological tissues. Apart from common fillers, 3D printed fibers can also be used to fabricate strong soft composites. By employing a 3D rapid prototyping technique, crossed log-piles of elastic fibers are fabricated (Figure 5b) [62]. Epoxy-based hydrogels are combined with the fibers to form an interpreting structure. Adjusting the construct geometry, corresponding mechanical properties of the soft composite such as strength, modulus, and toughness can be facilely regulated. The above methods mainly involve the introduction of external fiber fillers, which must carefully consider the interfacial interactions between the fillers and the matrices. An emerging method that can ignore the interface problem is to form microfibers in situ in soft composites [63]. This strategy is originally inspired by biological fibrous tissues. In bio-tissues, microfibers impregnate thoroughly with soft extracellular matrices, without the concern of interfacial problems. The key to the formation of microfibers is the utilization of rigid polymers with a large persistence length. By orienting and drying such polymers, strong microfibers can be formed, which are capable of maintaining the fibrous structure after reswelling. On the contrary, an oriented soft polymer with a small persistence length tends to restore the isotropic network structure after reswelling. Based on the contrasting reswelling behaviors, soft hydrogel composites can be fabricated by orienting and reswelling two interpreting networks with different persistence lengths (Figure 5c) [64].

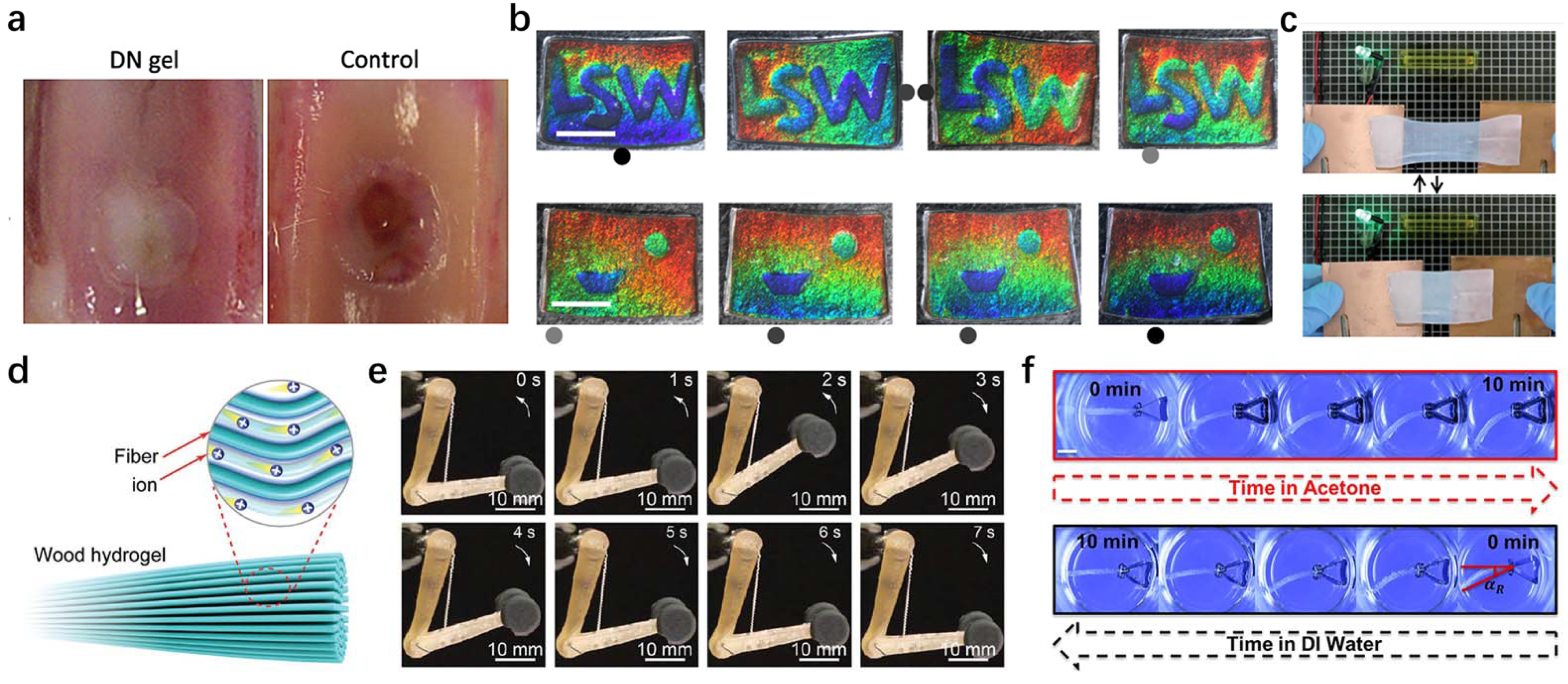
2.4. Macroscopic Reinforcement

Soft composites with satisfactory mechanical properties can also be produced by using macroscopic reinforcement, which includes, but is not limited to, fiber fabrics, metal meshes, plastic grids, etc. The preparation method of soft composites with macroscopic enhancement is similar to that of micro-filler-reinforced soft materials and the interface is still a key point that should be taken into account. Here, we give some examples for developing soft composites with macroscopic reinforcing phases.
A very familiar system with macroscopic phases is the fabric-reinforced soft composite. Unlike soft composites enhanced by microfibers, fabric-reinforced soft composites are usually fabricated by combining soft matrices with woven fiber fabrics (Figure 6a) [18]. In this case, the fiber volume fraction is relatively high, and the mechanical properties are mainly dominated by the fabric phases. Moreover, the mechanical and structural anisotropy of the soft composites can be regulated by exploiting a variety of weave patterns of the fabrics, which are different from the random distribution of fillers in micro-fiber-reinforced soft composites. Besides common fabrics, some novel rigid phases are also applicable to develop soft composites. Hydrogel composites with a series of desired properties, such as excellent mechanical performance, shape memory, and thermal healing, are created by integrating a low-melting-point alloy into a hydrogel system (Figure 6b) [65]. The alloy is able to transform from a load-bearing solid state to a free-deformable liquid state upon temperature increase, enabling the release of stress concentration between the soft and rigid phases. The resulting hydrogel composites can be uniquely applied in controlled electrochemical reactions and channel-structure templating by virtue of the special metal-hydrogel combination. The 3D printed rigid plastic grids are also proven efficient to construct tough soft composites. By simply combining silicon rubber and such rigid grids, macroscopic double network composites are fabricated (Figure 6c) [66]. The topological interlocking enables significant force transmission between the soft and rigid phases, preventing delamination. The optimal mechanical properties appear when the grid/matrix strength ratio is approaching one. Interestingly, soft composites with macroscopic reinforcement can also be fabricated from the same type of elastomers with different rigidity. By tuning the cross-linking density, a hard elastomer and a soft elastomer can be prepared, which shows contrasting Young’s modulus. The hard elastomer acts as the macroscopic reinforcing phase while the soft elastomer is the matrix (Figure 6d) [67,68]. Such a soft/hard combination allows the composite elastomers to show excellent fatigue resistance by virtue of the efficient stress de-concentration.

3. Mechanical Property

Depending on the size scale and volume fraction of the reinforcing phase, soft composites can show very different mechanical properties. In this section, we summarize the mechanical performance of typical soft composites at different length scales.

3.1. Tensile Performance

Double network (DN) hydrogel is a typical molecular-scale soft composite, consisting of a stiff but brittle first network and a soft, stretchable second network. The mechanical performance of DN hydrogels usually far exceeds its components via the synergy of significantly enlarged process zone and energy dissipation density. One of the important features of DN gels is the rate-independent hysteresis, i.e., dramatic energy dissipation during the first loading-unloading cycle, which is entirely different from traditional elastic gels or elastomers such as polyacrylamide hydrogel and natural rubber. Interestingly, during the second loading cycle, it is impossible to observe the large hysteresis again, indicating the fracture of covalent bonds in the first network. This is also well-known as the sacrificial bond effect. Another interesting characteristic during the tension of DN gels is the yielding and necking phenomenon (Figure 7a) [21]. Narrow zones appear in the sample during loading and grow up with further stretching, which again is attributed to the fracture of the fragile first network. After the neck propagation, the DN gel becomes rather soft, showing a greatly reduced stiffness compared with the original sample. Large elongation can be sustained by the second network before the entire sample is failed. By introducing physical interactions into the DN systems, self-recover in DN hydrogels can be realized. Either via ionic cross-linking or hydrophobic association, corresponding DN hydrogels can recover the initial shape after a certain amount of resting time (Figure 7b) [69]. Compared with traditional gels and biological tissues, DN hydrogels exhibit superior comprehensive properties while they still contain more than 90 wt% of water, which are ideal candidates for biomedical applications.
Nanometer-level soft composites formed by phase separation have a distinct tensile behavior in contrast to non-phase-separated ones. For instance, homogenous network structure is usually observed in non-phase-separated hydrogels, which can be soft, stretchable, but relatively weak. Phase separation leads to the formation of polymer dense phases in the hydrogels and the reduction of overall water content. These effects allow the formation of strong inter-/intra- polymer interactions and contribute to a significantly improved tensile performance (Figure 7c) [70,71]. The elongation firstly leads to the rupture of the hard phases in the gels, which play a similar sacrificial role to the first networks in DN hydrogels. Afterward, the soft phases sustain the load until the entire sample fails. Notably, owing to the dynamic nature of physical interactions in phase-separated hydrogels, damage in structures can usually be recovered. That is, the gels are able to show a large hysteresis due to massive viscous dissipation, yet they can finally restore the initial hysteresis loop after a certain amount of resting time. Moreover, the phase-separated gels are often viscoelastic and show a rate-dependent tensile behavior (Figure 7d) [32]. These special features enable phase-separated gels to be applied in many fields that require self-healing ability, viscoelasticity, etc.
Soft composites with hard phases at the micron-scale also have their unique tensile behaviors. These composites can behave very similarly to biological tissues such as ligaments, skin, and blood vessels. J-shaped non-linear stress-strain curves during elongation of biological tissues can be commonly observed, mainly attributed to wavy and crimped collagen fibers within the tissue that progressively uncoil and eventually straighten. These tissues are fairly soft at low strains, whereas they become extremely stiff at high strains. Soft composites containing wavy and crimped micro-fibers are also able to show such J-shaped stress-strain curves, demonstrating three load-bearing regions during elongation (Figure 7e) [72]. When the strain is quite low, the tensile performance is dominated by the matrix, and the wavy fibers do not contribute significantly to the energy dissipation. As the strain increases, the fibers gradually uncoil and start to sustain load, resulting in a gradually increasing stiffness and strength of the composites. Finally, when the strain is high enough, the fibers become extremely taut. In this case, rapid strain hardening occurs, and the tensile performance at this stage mainly stems from fibers.
Macroscopic soft composites dissipate energy similarly to the strain-hardening stage of the micro-level soft composites since the macroscopic reinforcing phases are usually extremely stiff compared with the matrix phases. Glass fiber fabric-reinforced polyampholyte hydrogels exhibit high fracture stress but low fracture strain, similar to the tensile performance of neat glass fiber fabric (Figure 7f) [39]. Notably, by utilizing macroscopic reinforcing phases that have relatively low fracture force compared with the soft matrix phases, the energy dissipation of the resulting soft composites can be optimized by a multi-step fracture process, which is superior to either the soft or hard phase (Figure 7g) [65]. The tensile fracture stresses of soft composites that dissipate energy at different length scales are summarized in Table 1.
Textiles 01 00027 g007 550
Figure 7. Tensile properties of soft composites at different length scales. (a) Typical tensile behaviors and properties of double network hydrogels. Reproduced with permission from reference [21] Copyright 2010 Royal Society of Chemistry. (b) The superior compressive performance of tough hydrogels. Reproduced with permission from reference [69] Copyright 2015 Royal Society of Chemistry. (c) Phase-separation results in dramatic mechanical enhancement of hydrogels. Reproduced with permission from reference [70] Copyright 2020 Elsevier. (d) Rate-dependent tensile properties of phase-separated hydrogels. Reproduced with permission from reference [32] Copyright 2013 Springer Nature. (e) The J-shaped stress-strain curve of micro-fiber-based soft composites. Reproduced with permission from reference [72] Copyright 2020 American Chemical Society. (f) Tensile performance of fabric-reinforced soft composites. Reproduced with permission from reference [39] Copyright 2015 Royal Society of Chemistry. (g) Multi-step fracture process of low-melting-point alloy reinforced soft composites. Reproduced with permission from reference [65] Copyright 2018 Wiley.
Figure 7. Tensile properties of soft composites at different length scales. (a) Typical tensile behaviors and properties of double network hydrogels. Reproduced with permission from reference [21] Copyright 2010 Royal Society of Chemistry. (b) The superior compressive performance of tough hydrogels. Reproduced with permission from reference [69] Copyright 2015 Royal Society of Chemistry. (c) Phase-separation results in dramatic mechanical enhancement of hydrogels. Reproduced with permission from reference [70] Copyright 2020 Elsevier. (d) Rate-dependent tensile properties of phase-separated hydrogels. Reproduced with permission from reference [32] Copyright 2013 Springer Nature. (e) The J-shaped stress-strain curve of micro-fiber-based soft composites. Reproduced with permission from reference [72] Copyright 2020 American Chemical Society. (f) Tensile performance of fabric-reinforced soft composites. Reproduced with permission from reference [39] Copyright 2015 Royal Society of Chemistry. (g) Multi-step fracture process of low-melting-point alloy reinforced soft composites. Reproduced with permission from reference [65] Copyright 2018 Wiley.
Textiles 01 00027 g007

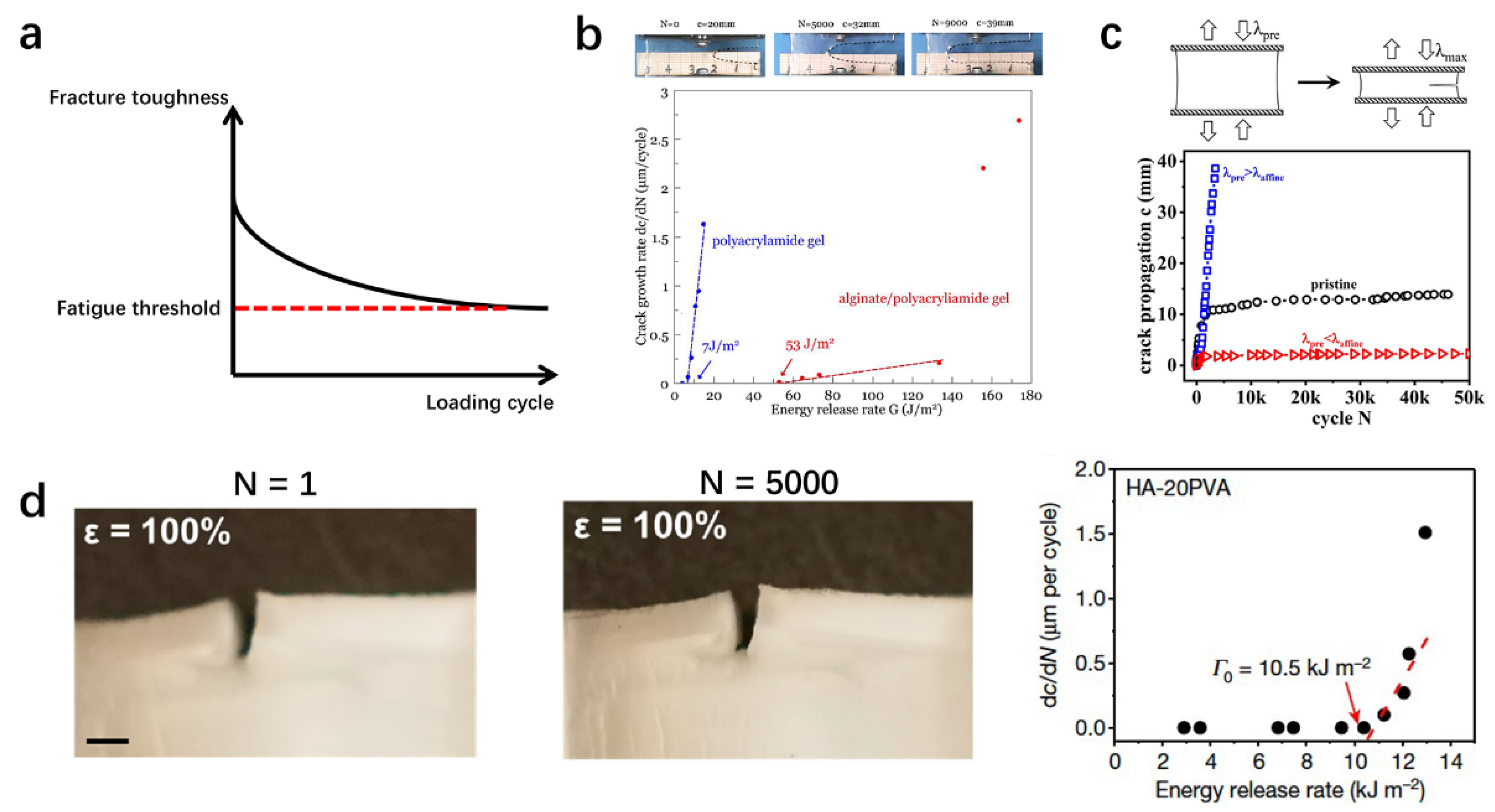
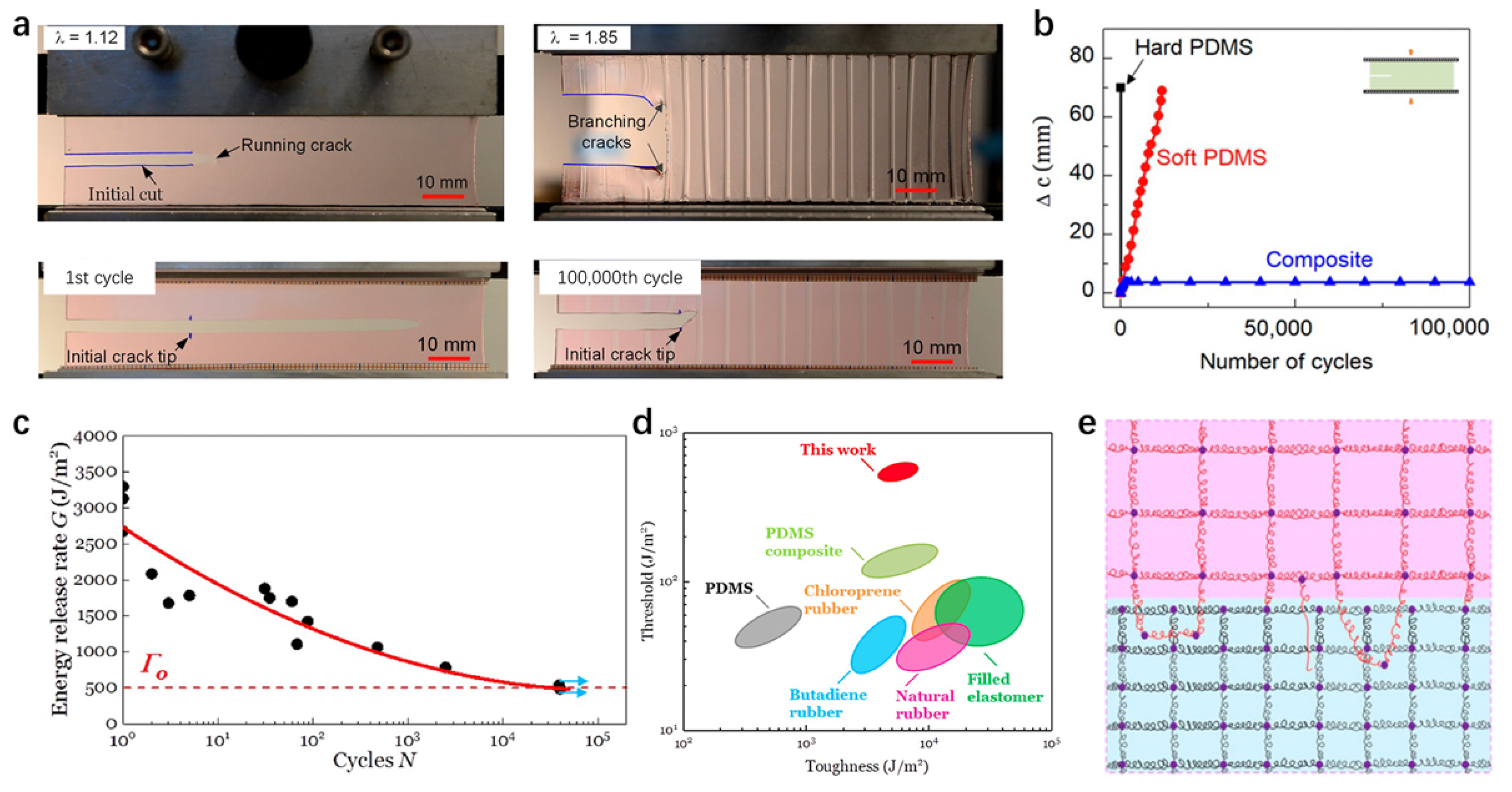
3.2. Fracture Toughness

The toughness of a material is usually characterized by fracture energy, i.e., the energy to create unit surface area for crack growth [73,74,75,76]. Soft composites at different length scales are all able to show excellent fracture toughness above 103 J m−2 [77]. For the individual network of DN hydrogels, either the stiff first one or the soft second one can hardly achieve fracture toughness on the 101 J m−2 [78,79,80]. The combination of two weak networks, in contrast, generates an extremely tough material by virtue of the sacrificial bond effect. Meanwhile, the fracture toughness of molecular-scale double network hydrogels can be adjusted by simply tuning the network concentration (Figure 8a) [23], allowing a wide window of mechanical tunability for practical applications. Phase-separated materials commonly show fracture toughness similar to that of DN materials. The way of energy dissipation is also close. Polymer dense phases in phase-separated elastomers, i.e., the hard phases, fracture preferentially upon crack growth, serving the role of sacrificial bonds (Figure 8b) [31]. Because the polymer density in the hard phases is considerably high, the energy to propagate the crack growth is greatly increased compared with non-phase-separated homogenous structures. In other words, the energy dissipation density of the bulk materials is enhanced, leading to a rise of fracture toughness even when the energy dissipation zone remains constant. For the micro-level soft composites consisting of microscopic fibers, the fracture toughness can be one or two orders of magnitude higher than molecular or nanoscale soft composites. The reason stems from efficient stress transfer between the stiff fillers and the soft matrices, which enables the bulk materials to dissipate energy in a broad area with a high energy dissipation density. Such composites are usually highly notch-insensitive and achieve fracture energy of around 101 to 102 J m−2 (Figure 8c) [34]. By introducing macroscopic reinforcing phases into soft composites, the fracture energy can be improved to an even higher level. Because the stiff phases, such as woven fabrics can possess an extremely high Young’s modulus of tens of GPa, the force transfer between the hard and soft phases is further optimized. The resultant soft composites are capable of achieving unprecedented fracture toughness, rivaling best-in-class tough materials in industrial and biomedical fields (Figure 8d) [77]. The fracture energies of soft composites that dissipate energy at different length scales are summarized in Table 1.

3.3. Fatigue Resistance

Fatigue resistance of a material is usually represented by the fatigue threshold under repeated loading-unloading cycles (Figure 9a). By tuning the input energy to a notched material, the critical energy release rate at which the notch starts to propagate can be determined by extrapolation, which is defined as the fatigue threshold, i.e., the reflect of fatigue resistance.
Molecular-level soft composites, such as DN hydrogels, have relatively limited fatigue resistance, the fatigue threshold of which is on the order of 101 J m−2. Once DN hydrogels are notched, the crack will propagate continuously as the gels are repetitively loaded and unloaded (Figure 9b) [81]. The irreversible fracture of covalent bonds in the first network is the main reason for the low fatigue resistance of DN hydrogels, which can be improved by utilizing physical cross-links to construct a recoverable first network [82,83,84,85]. Phase-separated gels show a desirable fatigue resistance due to the existence of the bicontinuous network structure. Very different fatigue behavior can be observed when the input energy is above or below the critical point to fracture the hard phases (Figure 9c) [86]. Below the critical energy, the hard phases are able to pin the crack growth and delay the fatigue fracture, resulting in a crack blunting ahead of the crack tip. Above the critical energy, the hard phases rupture and give rise to a fast crack propagation during the loading-unloading process. Micro-fiber-reinforced soft composites are extremely fatigue resistant. As shown in Figure 9d, the crack does not propagate after loading-unloading process for N = 5000 cycles [34]. The fatigue threshold (Γ0) of these composites can be several orders of magnitude higher than molecular and nanoscale soft composites, mainly attributed to the efficient stress transmission and highly energy dissipative components.
Textiles 01 00027 g009 550
Figure 9. Fatigue resistance of soft composites at different length scales. (a) Common materials show gradually decreased fracture toughness upon continuous loading-unloading cycles, which can be utilized to determine the fatigue threshold of a material. (b) Limited fatigue resistance of double network hydrogels. Reproduced with permission from reference [81] Copyright 2018 Elsevier. (c) Phase-separated hydrogels show excellent fatigue resistance via a multiscale energy dissipation mechanism. Reproduced with permission from reference [86] Copyright 2020 National Academy of Sciences. (d) Extremely high fatigue resistance of micro-fiber-based soft composites. Reproduced with permission from reference [34] Copyright 2021 Springer Nature.
Figure 9. Fatigue resistance of soft composites at different length scales. (a) Common materials show gradually decreased fracture toughness upon continuous loading-unloading cycles, which can be utilized to determine the fatigue threshold of a material. (b) Limited fatigue resistance of double network hydrogels. Reproduced with permission from reference [81] Copyright 2018 Elsevier. (c) Phase-separated hydrogels show excellent fatigue resistance via a multiscale energy dissipation mechanism. Reproduced with permission from reference [86] Copyright 2020 National Academy of Sciences. (d) Extremely high fatigue resistance of micro-fiber-based soft composites. Reproduced with permission from reference [34] Copyright 2021 Springer Nature.
Textiles 01 00027 g009
Soft composites with macroscopic fiber reinforcing phases are usually not fatigue-resistant since the mechanical properties are dominated by the rigid phases, which break at relatively low fracture strain despite having high energy dissipation density. However, by utilizing macroscopic phases that have relatively low Young’s modulus, fatigue-resistant soft composites can also be obtained. An example is a soft composite made up of two elastomer phases that have a high and low cross-linking density, respectively. Compared with a neat elastomer composed of merely a soft phase, the soft composites with a modulus contrast show superior fatigue resistance (Figure 10a) [38]. The velocity of crack growth of the soft composites is greatly reduced by crack deflection, which is attributed to the existence of stiff phases that can stop the crack propagation (Figure 10b). Even after a loading-unloading cycle of over 104 times, the composites still maintain a high energy release rate. The fatigue threshold (Γ0) is estimated to be around 500 J m−2 (Figure 10c) [67]. Through such a soft/hard design, a combination of high fatigue resistance and fracture toughness is realized, exceeding a great many of traditional elastomers (Figure 10d). It is worth noting that the interface between the soft and hard phases is extremely important for achieving high fatigue resistance, which is usually realized via topological entanglement of two polymer phases (Figure 10e). The fatigue thresholds of soft composites that dissipate energy at different length scales are summarized in Table 1.

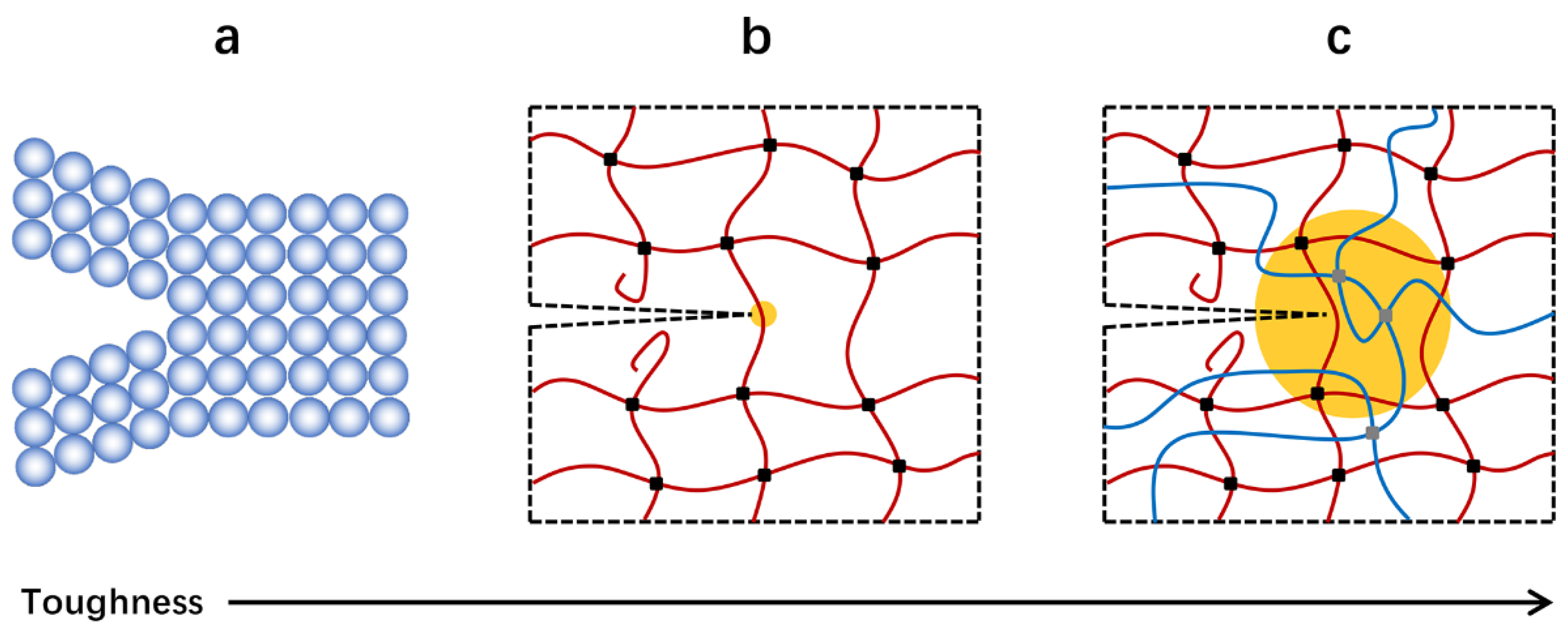
4. Toughening Mechanisms

Soft composites composed of different reinforcing phases have distinguished toughening mechanisms. In this section, we explain how soft composites from molecular- to macro-scales can achieve remarkable toughness that far exceeds what can be expected from a simple mixture of individual components.

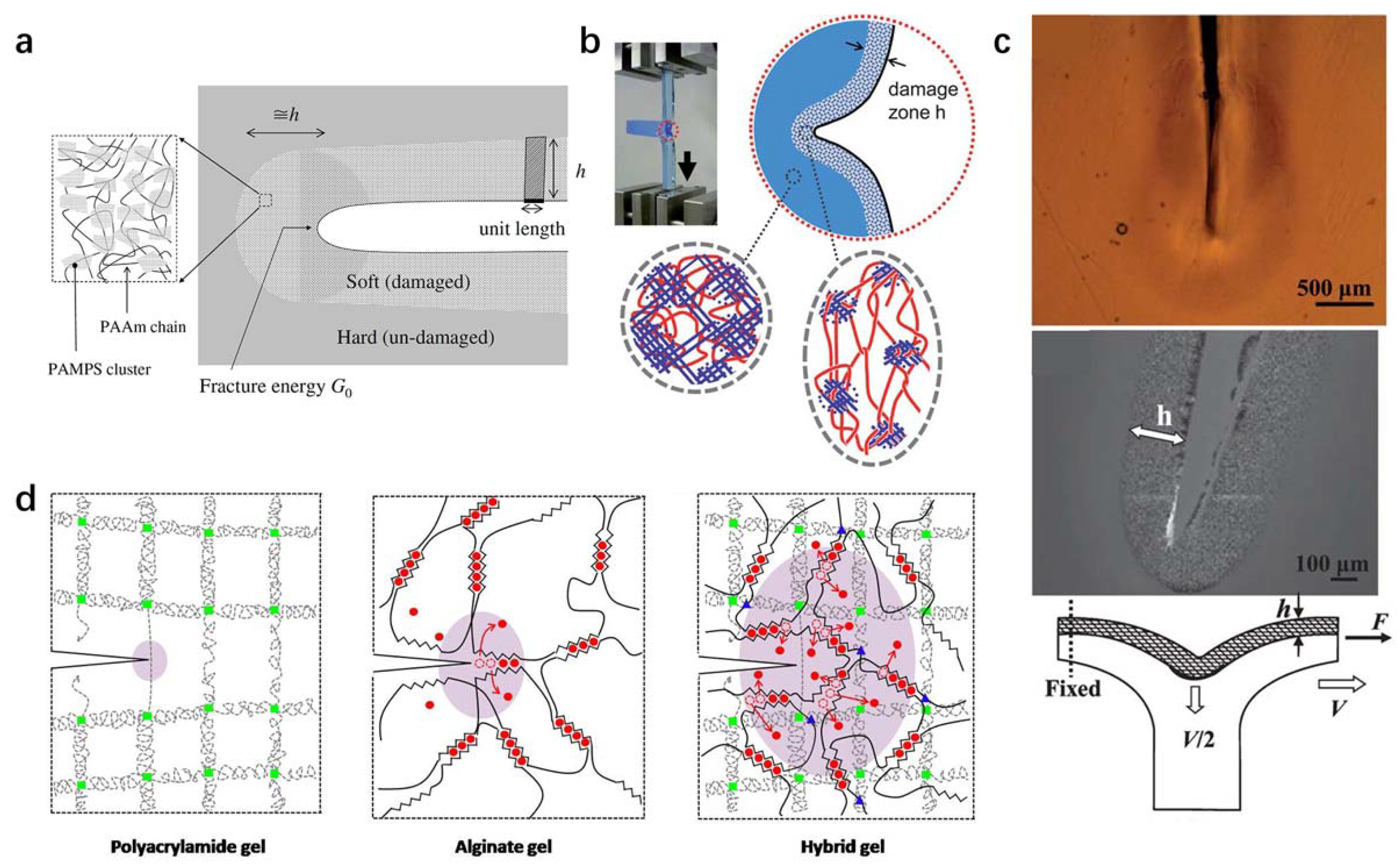
4.1. Molecular Cluster

DN hydrogel as a molecular-scale soft composite attains high fracture toughness depending on the preferential fracture of the sacrificial first network. Because the first network is highly pre-stretched and brittle, it is prone to fracture ahead of the second network rupture. A damage zone is formed once a crack tends to propagate in a DN hydrogel (Figure 11a) [87], inside which the sacrificial network breaks into molecular clusters and connects the second network as cross-linking points (Figure 11b) [21,88,89]. To further grow the crack, additional energy has to be input to fracture the second network. Thus, the double network hydrogels are endowed with high fracture toughness. The size scale of the damage zone determines the energy dissipation area of the DN gel, which is found to be hundreds of microns (Figure 11c) [90,91]. Physical DN gels dissipate energy in a similar way to conventional DN gels. The sacrificial networks are usually physically cross-linked by ionic bonds, hydrogen bonding, hydrophobic association, etc. The stress transmission between the first and second networks enables a relatively large energy dissipation zone, giving rise to a high fracture toughness (Figure 11d) [23]. Because the non-covalent bonds are self-healable, physical DN gels can partially or entirely restore the initial toughness after a certain amount of healing time.

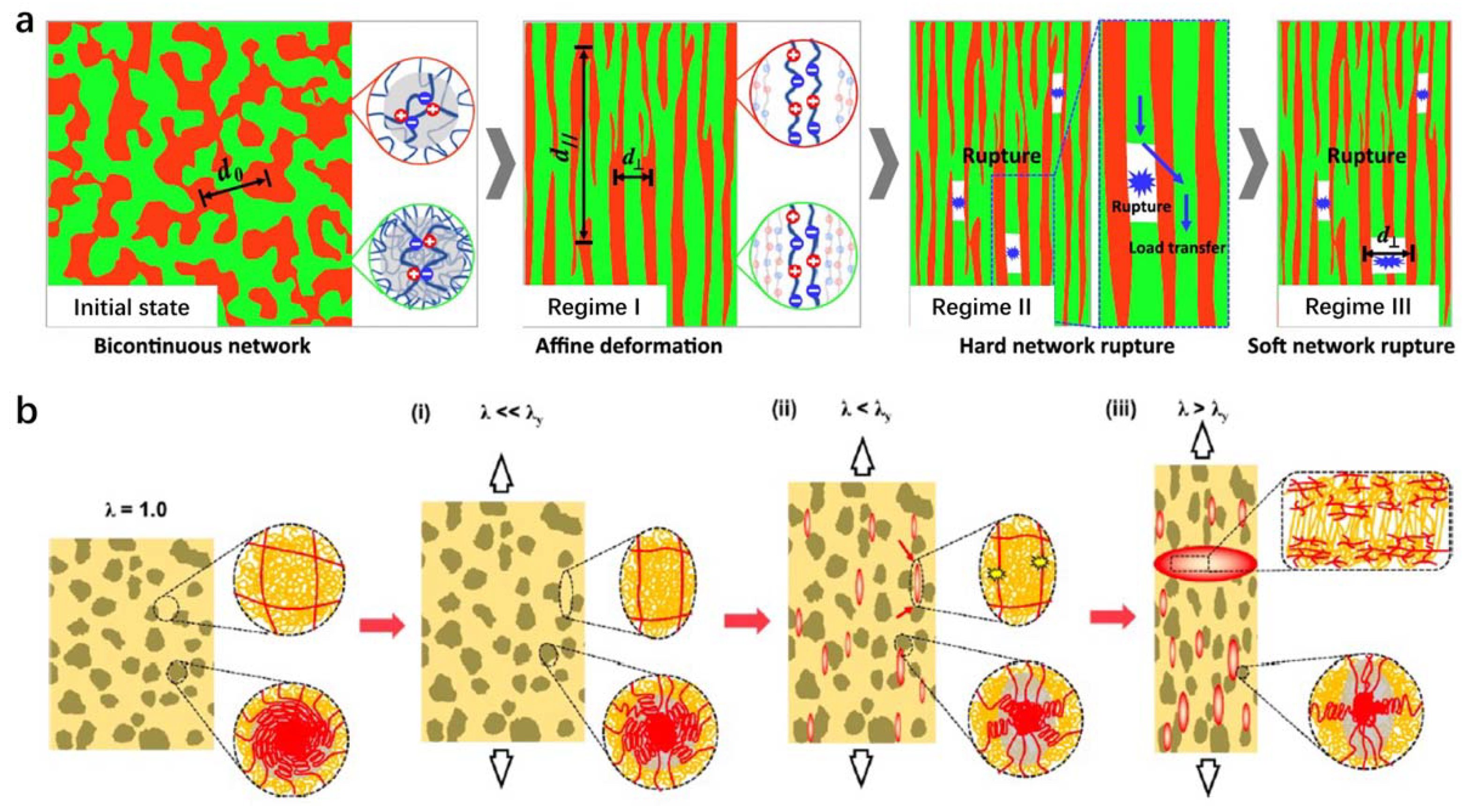
4.2. Nanophse Pinning

Soft composites with nanophase separation commonly have a multiscale toughening mechanism. The deformation of the bicontinuous network is affine to the macroscopic deformation of the bulk material. Taking polyampholyte hydrogel as an example, the fracture process can be divided into three regimes (Figure 12a) [33]. At the initial state, the bicontinuous soft and hard networks, represented by red and green areas, are isotropic, which have a length scale of hundreds of nanometers. Because of the ionic association, all polymer chains are in globule conformation. Once the bulk material starts to sustain load, the ionic association breaks, leading to the unfolding of the aggregated polymer chains. This effect allows the hydrogel network to sustain a considerably large yet reversible affine deformation. As the deformation increases, some hard phases reach the strength limit and begin to rupture. Subsequently, the load will be transferred to neighboring hard phases via soft phases. Since the soft phases are still intact and can sustain much larger deformation, the bulk gel softens yet are able to revert to the initial state when unloaded. After the fracture of most of the hard phases, the soft phases have to rupture, resulting in global failure of the bulk hydrogel. The above multiscale fracture process leads to a great amount of energy dissipation, enabling the polyampholyte hydrogel to exhibit high toughness.
Another example is the nanophase-separated elastomer, which shows a similar energy dissipation mechanism to the polyampholyte hydrogel although it does not show a bicontinuous network structure (Figure 12b) [31]. The nanophases form via the dipole-dipole interaction induced collapse of hard phases (gray island). This kind of phase-separated structure, on one side, results in overstressing of the hard phases, which show a significant increase in stiffness, on the other side, gives rise to structural changes even at small deformations to dissipate massive energy. When the deformation is below the yielding point, the collapsed hard phases are partially unfolded by the rupture of the non-covalent dipole-dipole interaction, dissipating energy. At moderate deformation, more and more hard phases start to unfold, along with the rupture of some soft phases. When the deformation is sufficiently large, both phases rupture globally, leading to the failure of the bulk sample.

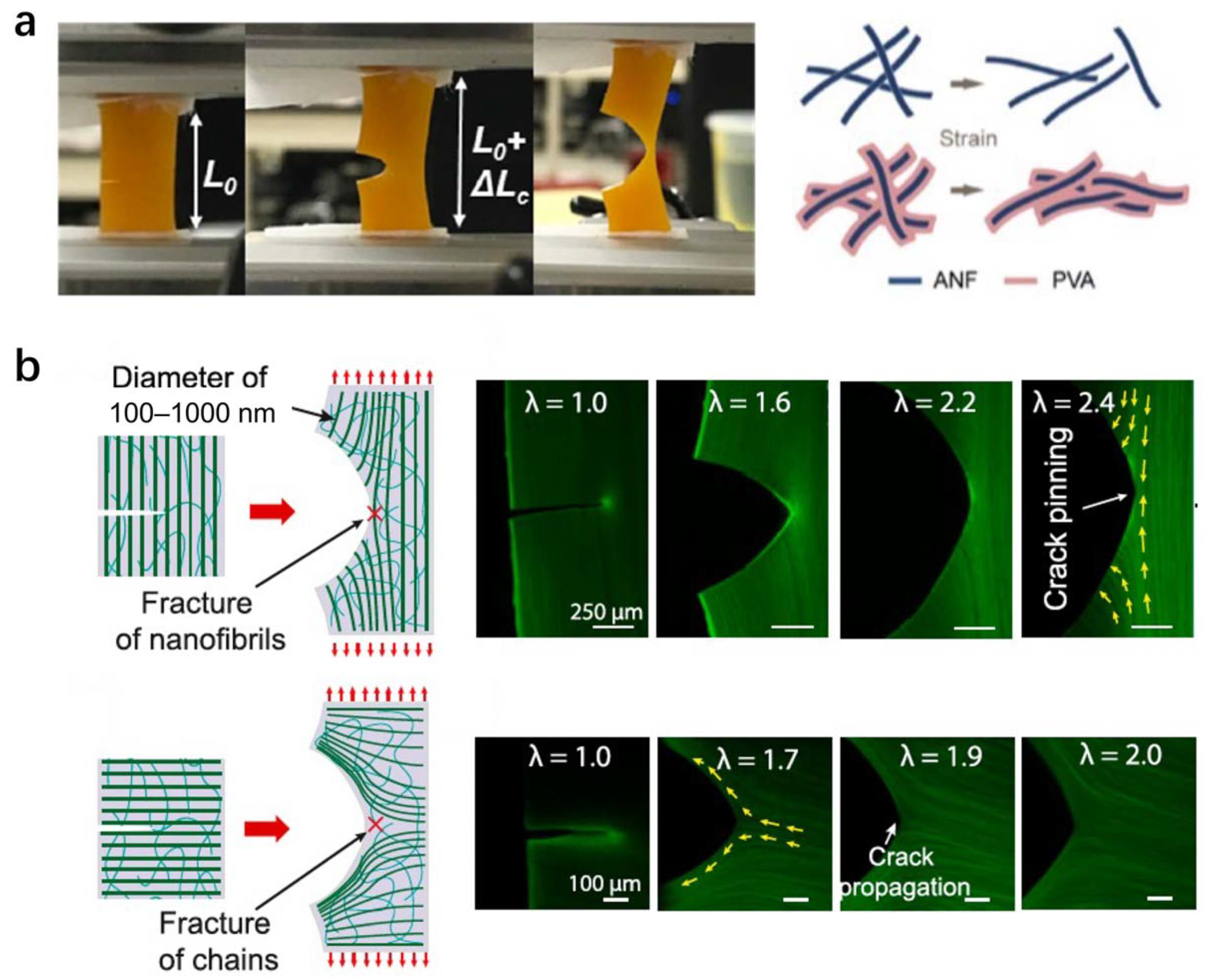
4.3. Microfiber Enhancement

The energy dissipation mechanisms of micro-fiber-reinforced soft composites need to be classified into two types. One is for the short micro-fiber-reinforced soft composites. In this case, the fracture process of the soft composites is dominated by the matrix, while the fiber phases enhance the overall performance. As a crack is initiated, its propagation must fracture a broad area of the matrix due to the efficient force transmission between the fiber and matrix phases. That is, the energy dissipation zone is relatively large compared with that of the neat matrix, which leads to high fracture toughness. Strong interfacial interactions between the fiber and matrix are important for force transmission (Figure 13a) [61]. The other type is for long micro-fiber-reinforced soft composites, inside which the fibers are continuous and exist throughout the entire sample. Such soft composites show an anisotropic fracture behavior. When the crack is made perpendicular to the fiber direction, the soft composites demonstrate superior fracture toughness due to the high difficulty of growing crack through the stiff and strong fiber phases. In contrast, if the crack is made along the fiber direction, the soft composites show a much-decreased fracture toughness because the crack can grow by fracturing the soft matrix along fibers (Figure 13b) [37].

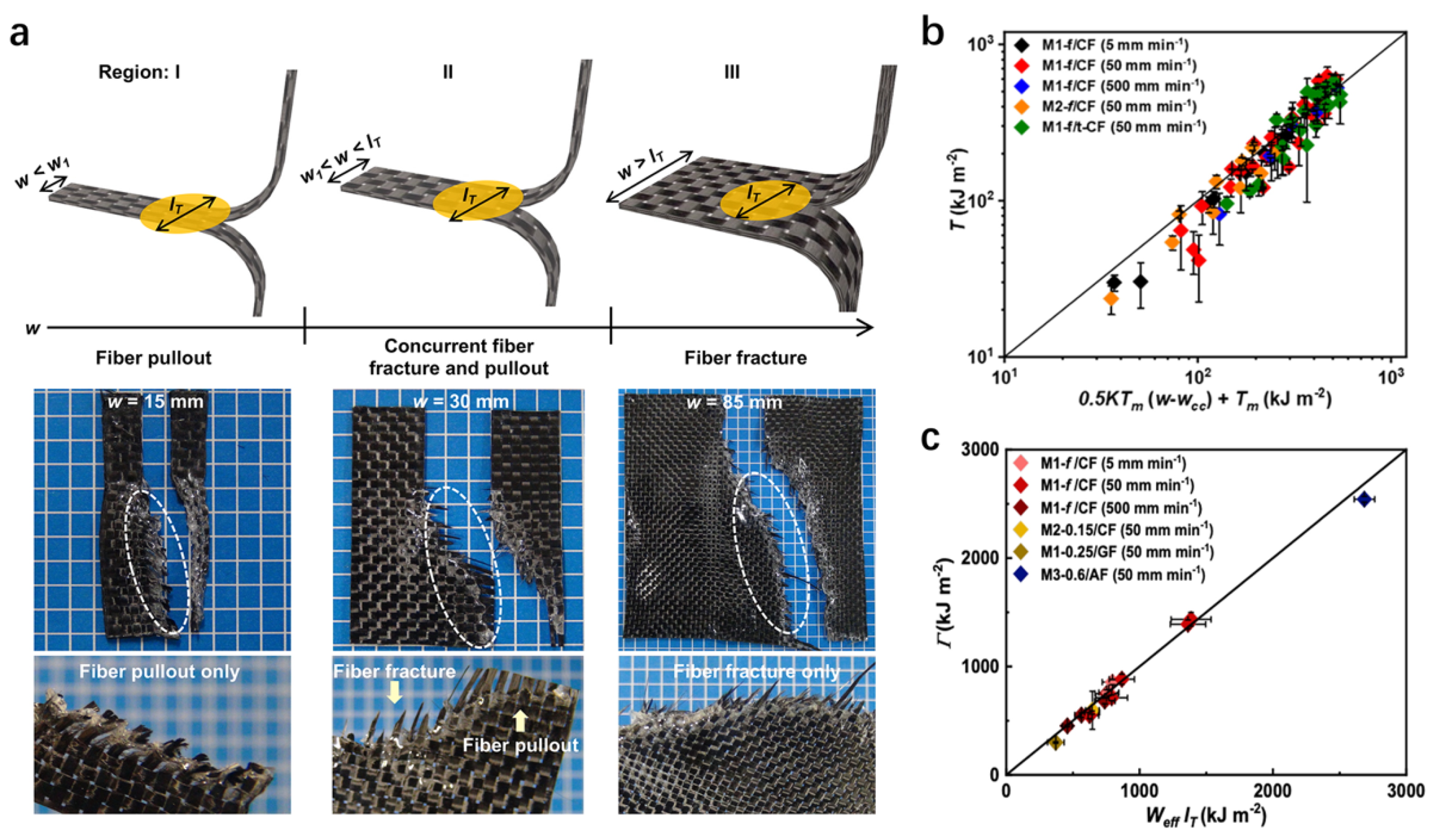
4.4. Macroscale Bulk Dissipation

Macroscopic fabric-reinforced soft composites can dissipate energy in a macro length scale, and the fracture toughness is size-dependent. Taking the fiber-reinforced viscoelastic polymer as an example, the change of sample width leads to three regions with different fracture behaviors (Figure 14a) [92]. When the sample width is below a first characteristic with, w1, the soft composite fails via fiber pullout-induced matrix rupture (region I). In this case, the fiber itself does not fracture to dissipate energy. However, the fiber bundle geometry significantly influences the load transfer between the stiff and soft phases, affecting the fracture toughness of the resulting soft composites. Under such conditions, the fracture energy of the soft composites is determined by the work to pull out transverse fiber bundles in a unit area, which is related to the matrix toughness (Tm), fiber bundle geometry (K), center-to-center distance between adjacent fiber bundles (wcc), and composite width (w) (Figure 14b). Another special region appears when the sample size is above the other characteristic width, lT, which is dominated by fiber fracture. In this region III, the fracture energy of the soft composites is decided by two factors: load transfer length (lT) and energy dissipation density (Weff) (Figure 14c) [18,93]. The load transfer length is found to be proportional to the fiber/matrix modulus ratio, while the energy dissipation density stems from the work of extension of two-component phases. By optimizing the above two factors, the fracture toughness of soft composites can achieve 103 J m−2, even exceeding metals. When the sample width is larger than w1 but smaller than lT, the fracture behavior of the soft composite is concurrent fiber fracture and pullout. The fracture mechanism in this region II is a mixed-mode of region I and region III.

5. Applications

Soft composites, due to their unique mechanical and physical properties, have found great potential for numerous applications in biomedical and industrial fields. For example, DN hydrogels, due to their biocompatibility, can be utilized in cartilage regeneration (Figure 15a) [94]. By plugging in a DN gel into the vacant space in the damaged cartilage, induction of cartilage regeneration can be realized. After four weeks of repairing, the defect treated with the DN gel is almost filled with regenerated white tissue, whereas the defects without any treatment are still insufficiently repaired. These results open the opportunity of applying DN gel as a tissue-repairing agent in biomedical applications. Interestingly, some other types of DN gels can also be employed in industrial fields such as pressure sensors. A photonic DN hydrogel consisting of self-assembled bilayer structures shows fast-response time, full-color tunable range, and fast color-switching via small compressive stress (Figure 15b) [95,96,97,98,99]. Phase-separation soft gels are found to be tough adhesives. Because of the greatly increased polymer chain density at the surface as well as the enhanced energy dissipation capability, a phase-separated hydrogel can show superior adhesion properties to a variety of solid surfaces. Soft-rigid hybrid devices such as hybrid conductors are enabled by the tough bonding between the phase-separated gels and hard substrates (Figure 15c) [55]. Soft composites with micro-fiber reinforcing phases are applicable in other fields. Taking wood hydrogels with continuous cellulose fibers, the anisotropic, low-tortuosity, and negatively charged structures facilitate ion transport, enabling the gels to show high ionic conductivity even at low ion concentrations (Figure 15d) [100,101,102]. Moreover, by utilizing thermal-responsive fibers as the main components, the soft composites are able to behave like human muscles under temperature change (Figure 15e) [103]. Soft composites with macroscopic reinforcing phases are mainly employed as load-bearing structural materials. However, functionalities can be realized by special designs of the composite structure. By using two soft matrices with different solvent responses and bonding them using a fabric phase, a soft composite actuator can be fabricated, which shows different bending behaviors under solvent change (Figure 15f) [12]. Relevant applications of soft composites that dissipate energy at different length scales are summarized in Table 1.
Table
Table 1. Summarized mechanical properties and applications of soft composites that dissipate energy at different length scales.
Table 1. Summarized mechanical properties and applications of soft composites that dissipate energy at different length scales.
Soft CompositeLength Scale
for Energy
Dissipation		Fracture Stress (MPa)Fracture
Toughness
(kJ m−2)		Fatigue
Threshold
(kJ m−2)		ApplicationReference
DN materialsMolecular level10−1–10010−1–10010−2Tissue engineering, sensors[21,23,29,44,46,51,81,94,95]
Phase-separated
materials		Nanometer10−1–100100–10110−1Adhesives[31,32,33,52,55,70,86]
Microfiber-reinforced gelsMicrometer100–101100–102100–101Conductor,
artificial muscles		[34,37,61,62,64,72,100,103]
Macrophase-reinforced compositesMillimeter100–102100–10310−1Actuators[12,18,38,39,65,66,67,77,92]

6. Conclusions

Soft composite is not a strange word in many fields. This special type of composite has been widely applied in biomedical engineering and industry. Either on the micro- or the macro-scale, the soft composites always show superior comprehensive properties to their individual components, or understanding the underlying toughening mechanisms of such materials will greatly benefit the development of next-generation soft materials. In this review, we have given an overview of the fabrication, mechanical properties, toughening mechanisms, and relevant applications of common soft composites. The energy dissipation mechanisms at different length scales give these composites distinguishing properties and behaviors. By a suitable structural and mechanical design, soft composites are able to dissipate massive energy from the molecular to the macroscopic scale. Based on their different physical and structural properties, soft composites are applicable to a wide range of practical applications, including, but not limited to, tissue engineering, sensors, adhesives, conductors, artificial muscles, and actuators.

Author Contributions

Conceptualization, W.C.; methodology, W.C. and R.Z.; software, W.C.; validation, W.C. and R.Z.; formal analysis, W.C.; investigation, W.C.; resources, W.C.; data curation, W.C.; writing—original draft preparation, W.C.; writing—review and editing, W.C. and R.Z.; visualization, W.C.; supervision, W.C.; project administration, W.C.; funding acquisition, W.C. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by start-up funding at Sichuan University.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

No new data were created or analyzed in this study. Data sharing is not applicable to this article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Coleman, J.N.; Khan, U.; Blau, W.J.; Gun’ko, Y.K. Small but strong: A review of the mechanical properties of carbon nanotube–polymer composites. Carbon 2006, 44, 1624–1652. [Google Scholar] [CrossRef]
  2. Akil, H.; Omar, M.; Mazuki, A.M.; Safiee, S.; Ishak, Z.M.; Bakar, A.A. Kenaf fiber reinforced composites: A review. Mater. Des. 2011, 32, 4107–4121. [Google Scholar] [CrossRef]
  3. Miracle, D. Metal matrix composites–from science to technological significance. Compos. Sci. Technol. 2005, 65, 2526–2540. [Google Scholar] [CrossRef]
  4. Summerscales, J.; Virk, A.; Hall, W. A review of bast fibres and their composites: Part 3–Modelling. Compos. Part A Appl. Sci. Manuf. 2013, 44, 132–139. [Google Scholar] [CrossRef] [Green Version]
  5. Ku, H.; Wang, H.; Pattarachaiyakoop, N.; Trada, M. A review on the tensile properties of natural fiber reinforced polymer composites. Compos. Part B Eng. 2011, 42, 856–873. [Google Scholar] [CrossRef] [Green Version]
  6. Thomas, W. High Strength Glass Fibre-Resin Composites. Nature 1973, 242, 455–456. [Google Scholar] [CrossRef]
  7. McLoughlin, J. New high temperature carbon fibre composite. Nature 1970, 227, 701. [Google Scholar] [CrossRef] [PubMed]
  8. Whitesides, G.M. Soft robotics. Angew. Chem. Int. Ed. 2018, 57, 4258–4273. [Google Scholar] [CrossRef] [PubMed]
  9. Liu, J.A.-C.; Gillen, J.H.; Mishra, S.R.; Evans, B.A.; Tracy, J.B. Photothermally and magnetically controlled reconfiguration of polymer composites for soft robotics. Sci. Adv. 2019, 5, eaaw2897. [Google Scholar] [CrossRef] [Green Version]
  10. Horne, J.; McLoughlin, L.; Bury, E.; Koh, A.S.; Wujcik, E.K. Interfacial phenomena of advanced composite materials toward wearable platforms for biological and environmental monitoring sensors, armor, and soft robotics. Adv. Mater. Interfaces 2020, 7, 1901851. [Google Scholar] [CrossRef]
  11. Kim, S.Y.; Choo, Y.; Bilodeau, R.A.; Yuen, M.C.; Kaufman, G.; Shah, D.S.; Osuji, C.O.; Kramer-Bottiglio, R. Sustainable manufacturing of sensors onto soft systems using self-coagulating conductive Pickering emulsions. Sci. Robot. 2020, 5, eaay3604. [Google Scholar] [CrossRef] [PubMed]
  12. Hubbard, A.M.; Cui, W.; Huang, Y.; Takahashi, R.; Dickey, M.D.; Genzer, J.; King, D.R.; Gong, J.P. Hydrogel/elastomer laminates bonded via fabric interphases for stimuli-responsive actuators. Matter 2019, 1, 674–689. [Google Scholar] [CrossRef] [Green Version]
  13. Cox, H. The elasticity and strength of paper and other fibrous materials. Br. J. Appl. Phys. 1952, 3, 72. [Google Scholar] [CrossRef]
  14. Lake, G.; Thomas, A. The strength of highly elastic materials. Proc. Math. Phys. Eng. Sci. 1967, 300, 108–119. [Google Scholar]
  15. Thomas, A.; Whittle, J. Tensile rupture of rubber. Rubber Chem. Technol. 1970, 43, 222–228. [Google Scholar] [CrossRef]
  16. Hui, C.-Y.; Liu, Z.; Phoenix, S.L.; King, D.R.; Cui, W.; Huang, Y.; Gong, J.P. Mechanical behavior of unidirectional fiber reinforced soft composites. Extrem. Mech. Lett. 2020, 35, 100642. [Google Scholar] [CrossRef]
  17. Volokh, K.; Trapper, P. Fracture toughness from the standpoint of softening hyperelasticity. J. Mech. Phys. Solids 2008, 56, 2459–2472. [Google Scholar] [CrossRef]
  18. Cui, W.; King, D.R.; Huang, Y.; Chen, L.; Sun, T.L.; Guo, Y.; Saruwatari, Y.; Hui, C.Y.; Kurokawa, T.; Gong, J.P. Fiber-reinforced viscoelastomers show extraordinary crack resistance that exceeds metals. Adv. Mater. 2020, 32, 1907180. [Google Scholar] [CrossRef]
  19. Sih, G.; Liebowitz, H. On the Griffith energy criterion for brittle fracture. Int. J. Solids Struct. 1967, 3, 1–22. [Google Scholar] [CrossRef]
  20. Greensmith, H. Rupture of rubber. XI. Tensile rupture and crack growth in a noncrystallizing rubber. J. Appl. Polym. Sci. 1964, 8, 1113–1128. [Google Scholar] [CrossRef]
  21. Gong, J.P. Why are double network hydrogels so tough? Soft Matter 2010, 6, 2583–2590. [Google Scholar] [CrossRef]
  22. Gong, J.P.; Katsuyama, Y.; Kurokawa, T.; Osada, Y. Double-network hydrogels with extremely high mechanical strength. Adv. Mater. 2003, 15, 1155–1158. [Google Scholar] [CrossRef]
  23. Sun, J.-Y.; Zhao, X.; Illeperuma, W.R.; Chaudhuri, O.; Oh, K.H.; Mooney, D.J.; Vlassak, J.J.; Suo, Z. Highly stretchable and tough hydrogels. Nature 2012, 489, 133–136. [Google Scholar] [CrossRef] [PubMed]
  24. Davey, C.L.; Gilbert, K. Tensile strength and the tenderness of beef sternomandibularis muscle. Meat Sci. 1977, 1, 49–61. [Google Scholar] [CrossRef]
  25. Kuthe, C.D.; Uddanwadiker, R.; Ramteke, A. Experimental evaluation of fiber orientation based material properties of skeletal muscle in tension. Mol. Cell. Biomech. 2014, 11, 113. [Google Scholar]
  26. Bennett1, M.; Ker1, R.; Imery, N.J.; Alexander1, R.M. Mechanical properties of various mammalian tendons. J. Zool. 1986, 209, 537–548. [Google Scholar] [CrossRef]
  27. Yang, W.; Sherman, V.R.; Gludovatz, B.; Schaible, E.; Stewart, P.; Ritchie, R.O.; Meyers, M.A. On the tear resistance of skin. Nat. Commun. 2015, 6, 1–10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  28. Zhao, X.; Chen, X.; Yuk, H.; Lin, S.; Liu, X.; Parada, G. Soft Materials by Design: Unconventional Polymer Networks Give Extreme Properties. Chem. Rev. 2021, 121, 4309–4372. [Google Scholar] [CrossRef]
  29. Ducrot, E.; Chen, Y.; Bulters, M.; Sijbesma, R.P.; Creton, C. Toughening elastomers with sacrificial bonds and watching them break. Science 2014, 344, 186–189. [Google Scholar] [CrossRef]
  30. Brown, H.R. A model of the fracture of double network gels. Macromolecules 2007, 40, 3815–3818. [Google Scholar] [CrossRef]
  31. Zheng, Y.; Kiyama, R.; Matsuda, T.; Cui, K.; Li, X.; Cui, W.; Guo, Y.; Nakajima, T.; Kurokawa, T.; Gong, J.P. Nanophase Separation in Immiscible Double Network Elastomers Induces Synergetic Strengthening, Toughening, and Fatigue Resistance. Chem. Mater. 2021, 33, 3321–3334. [Google Scholar] [CrossRef]
  32. Sun, T.L.; Kurokawa, T.; Kuroda, S.; Ihsan, A.B.; Akasaki, T.; Sato, K.; Haque, M.A.; Nakajima, T.; Gong, J.P. Physical hydrogels composed of polyampholytes demonstrate high toughness and viscoelasticity. Nat. Mater. 2013, 12, 932–937. [Google Scholar] [CrossRef] [Green Version]
  33. Cui, K.; Sun, T.L.; Liang, X.; Nakajima, K.; Ye, Y.N.; Chen, L.; Kurokawa, T.; Gong, J.P. Multiscale energy dissipation mechanism in tough and self-healing hydrogels. Phys. Rev. Lett. 2018, 121, 185501. [Google Scholar] [CrossRef]
  34. Hua, M.; Wu, S.; Ma, Y.; Zhao, Y.; Chen, Z.; Frenkel, I.; Strzalka, J.; Zhou, H.; Zhu, X.; He, X. Strong tough hydrogels via the synergy of freeze-casting and salting out. Nature 2021, 590, 594–599. [Google Scholar] [CrossRef] [PubMed]
  35. Guo, Y.Z.; Nakajima, T.; Mredha, M.T.I.; Guo, H.L.; Cui, K.; Zheng, Y.; Cui, W.; Kurokawa, T.; Gong, J.P. Facile preparation of cellulose hydrogel with Achilles tendon-like super strength through aligning hierarchical fibrous structure. Chem. Eng. J. 2022, 428, 132040. [Google Scholar] [CrossRef]
  36. Liu, R.; Xu, X.; Zhuang, X.; Cheng, B. Solution blowing of chitosan/PVA hydrogel nanofiber mats. Carbohydr. Polym. 2014, 101, 1116–1121. [Google Scholar] [CrossRef]
  37. Lin, S.; Liu, J.; Liu, X.; Zhao, X. Muscle-like fatigue-resistant hydrogels by mechanical training. Proc. Natl. Acad. Sci. USA 2019, 116, 10244–10249. [Google Scholar] [CrossRef] [Green Version]
  38. Wang, Z.; Xiang, C.; Yao, X.; Le Floch, P.; Mendez, J.; Suo, Z. Stretchable materials of high toughness and low hysteresis. Proc. Natl. Acad. Sci. USA 2019, 116, 5967–5972. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  39. King, D.R.; Sun, T.L.; Huang, Y.; Kurokawa, T.; Nonoyama, T.; Crosby, A.J.; Gong, J.P. Extremely tough composites from fabric reinforced polyampholyte hydrogels. Mater. Horiz. 2015, 2, 584–591. [Google Scholar] [CrossRef] [Green Version]
  40. Huang, Y.; King, D.R.; Sun, T.L.; Nonoyama, T.; Kurokawa, T.; Nakajima, T.; Gong, J.P. Energy-dissipative matrices enable synergistic toughening in fiber reinforced soft composites. Adv. Funct. Mater. 2017, 27, 1605350. [Google Scholar] [CrossRef] [Green Version]
  41. Cantwell, W.J.; Morton, J. The impact resistance of composite materials—a review. Composites 1991, 22, 347–362. [Google Scholar] [CrossRef]
  42. De Zanet, A.; Casalegno, V.; Salvo, M. Laser surface texturing of ceramics and ceramic composite materials–A review. Ceram. Int. 2021, 47, 7307–7320. [Google Scholar] [CrossRef]
  43. Yu, X.; Manthiram, A. A review of composite polymer-ceramic electrolytes for lithium batteries. Energy Stor. Mater. 2021, 34, 282–300. [Google Scholar] [CrossRef]
  44. Gong, J.P. Materials both tough and soft. Science 2014, 344, 161–162. [Google Scholar] [CrossRef]
  45. Chen, Q.; Chen, H.; Zhu, L.; Zheng, J. Engineering of tough double network hydrogels. Macromol. Chem. Phys. 2016, 217, 1022–1036. [Google Scholar] [CrossRef]
  46. Chen, Q.; Chen, H.; Zhu, L.; Zheng, J. Fundamentals of double network hydrogels. J. Mater. Chem. B 2015, 3, 3654–3676. [Google Scholar] [CrossRef]
  47. Zhang, H.J.; Sun, T.L.; Zhang, A.K.; Ikura, Y.; Nakajima, T.; Nonoyama, T.; Kurokawa, T.; Ito, O.; Ishitobi, H.; Gong, J.P. Tough physical double-network hydrogels based on amphiphilic triblock copolymers. Adv. Mater. 2016, 28, 4884–4890. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  48. Murai, J.; Nakajima, T.; Matsuda, T.; Tsunoda, K.; Nonoyama, T.; Kurokawa, T.; Gong, J.P. Tough double network elastomers reinforced by the amorphous cellulose network. Polymer 2019, 178, 121686. [Google Scholar] [CrossRef]
  49. Nakajima, T.; Ozaki, Y.; Namba, R.; Ota, K.; Maida, Y.; Matsuda, T.; Kurokawa, T.; Gong, J.P. Tough double-network gels and elastomers from the nonprestretched first network. ACS Macro Lett. 2019, 8, 1407–1412. [Google Scholar] [CrossRef]
  50. Wang, W.; Zhang, Z.; Davris, T.; Liu, J.; Gao, Y.; Zhang, L.; Lyulin, A.V. Simulational insights into the mechanical response of prestretched double network filled elastomers. Soft Matter 2017, 13, 8597–8608. [Google Scholar] [CrossRef] [Green Version]
  51. Matsuda, T.; Nakajima, T.; Gong, J.P. Fabrication of tough and stretchable hybrid double-network elastomers using ionic dissociation of polyelectrolyte in nonaqueous media. Chem. Mater. 2019, 31, 3766–3776. [Google Scholar] [CrossRef]
  52. Cui, K.; Ye, Y.N.; Sun, T.L.; Yu, C.; Li, X.; Kurokawa, T.; Gong, J.P. Phase separation behavior in tough and self-healing polyampholyte hydrogels. Macromolecules 2020, 53, 5116–5126. [Google Scholar] [CrossRef]
  53. Durmaz, S.; Okay, O. Phase separation during the formation of poly (acrylamide) hydrogels. Polymer 2000, 41, 5729–5735. [Google Scholar] [CrossRef]
  54. Broguiere, N.; Husch, A.; Palazzolo, G.; Bradke, F.; Madduri, S.; Zenobi-Wong, M. Macroporous hydrogels derived from aqueous dynamic phase separation. Biomaterials 2019, 200, 56–65. [Google Scholar] [CrossRef]
  55. Cui, W.; Zhu, R.; Zheng, Y.; Mu, Q.; Pi, M.; Chen, Q.; Ran, R. Transforming non-adhesive hydrogels to reversible tough adhesives via mixed-solvent-induced phase separation. J. Mater. Chem. A 2021, 9, 9706–9718. [Google Scholar] [CrossRef]
  56. Ihsan, A.B.; Sun, T.L.; Kuroda, S.; Haque, M.A.; Kurokawa, T.; Nakajima, T.; Gong, J.P. A phase diagram of neutral polyampholyte–from solution to tough hydrogel. J. Mater. Chem. B 2013, 1, 4555–4562. [Google Scholar] [CrossRef] [PubMed]
  57. Yodmuang, S.; McNamara, S.L.; Nover, A.B.; Mandal, B.B.; Agarwal, M.; Kelly, T.-A.N.; Chao, P.-h.G.; Hung, C.; Kaplan, D.L.; Vunjak-Novakovic, G. Silk microfiber-reinforced silk hydrogel composites for functional cartilage tissue repair. Acta Biomater. 2015, 11, 27–36. [Google Scholar] [CrossRef] [Green Version]
  58. Caves, J.M.; Cui, W.; Wen, J.; Kumar, V.A.; Haller, C.A.; Chaikof, E.L. Elastin-like protein matrix reinforced with collagen microfibers for soft tissue repair. Biomaterials 2011, 32, 5371–5379. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  59. Surajarusarn, B.; Hajjar-Garreau, S.; Schrodj, G.; Mougin, K.; Amornsakchai, T. Comparative study of pineapple leaf microfiber and aramid fiber reinforced natural rubbers using dynamic mechanical analysis. Polym. Test. 2020, 82, 106289. [Google Scholar] [CrossRef]
  60. Caves, J.M.; Kumar, V.A.; Martinez, A.W.; Kim, J.; Ripberger, C.M.; Haller, C.A.; Chaikof, E.L. The use of microfiber composites of elastin-like protein matrix reinforced with synthetic collagen in the design of vascular grafts. Biomaterials 2010, 31, 7175–7182. [Google Scholar] [CrossRef] [Green Version]
  61. Xu, L.; Zhao, X.; Xu, C.; Kotov, N.A. Water-rich biomimetic composites with abiotic self-organizing nanofiber network. Adv. Mater. 2018, 30, 1703343. [Google Scholar] [CrossRef] [PubMed]
  62. Agrawal, A.; Rahbar, N.; Calvert, P.D. Strong fiber-reinforced hydrogel. Acta Biomater. 2013, 9, 5313–5318. [Google Scholar] [CrossRef]
  63. Mredha, M.T.I.; Guo, Y.Z.; Nonoyama, T.; Nakajima, T.; Kurokawa, T.; Gong, J.P. A facile method to fabricate anisotropic hydrogels with perfectly aligned hierarchical fibrous structures. Adv. Mater. 2018, 30, 1704937. [Google Scholar] [CrossRef]
  64. Cui, W.; Pi, M.; Zhu, R.; Xiong, Z.; Ran, R. Strong anisotropic hydrogels with ion transport capability via reswelling contrast of two oriented polymer networks. J. Mater. Chem. A 2021, 9, 20362–20370. [Google Scholar] [CrossRef]
  65. Takahashi, R.; Sun, T.L.; Saruwatari, Y.; Kurokawa, T.; King, D.R.; Gong, J.P. Creating Stiff, Tough, and Functional Hydrogel Composites with Low-Melting-Point Alloys. Adv. Mater. 2018, 30, 1706885. [Google Scholar] [CrossRef] [PubMed]
  66. King, D.R.; Okumura, T.; Takahashi, R.; Kurokawa, T.; Gong, J.P. Macroscale double networks: Design criteria for optimizing strength and toughness. ACS Appl. Mater. Interfaces 2019, 11, 35343–35353. [Google Scholar] [CrossRef]
  67. Li, C.; Yang, H.; Suo, Z.; Tang, J. Fatigue-resistant elastomers. J. Mech. Phys. Solids 2020, 134, 103751. [Google Scholar] [CrossRef]
  68. Zhang, G.; Yin, T.; Nian, G.; Suo, Z. Fatigue-resistant polyurethane elastomer composites. Extrem. Mech. Lett. 2021, 48, 101434. [Google Scholar] [CrossRef]
  69. Cui, W.; Ji, J.; Cai, Y.; Li, H.; Ran, R. Robust, anti-fatigue, and self-healing graphene oxide/hydrophobically associated composite hydrogels and their use as recyclable adsorbents for dye waste water treatment. J. Mater. Chem. A 2015, 3, 17445–17458. [Google Scholar] [CrossRef]
  70. Cui, W.; Cai, Y.; Zheng, Y.; Ran, R. Mechanical enhancement of hydrophobically associating hydrogels by solvent-regulated phase separation. Polymer 2020, 210, 123042. [Google Scholar] [CrossRef]
  71. Sato, K.; Nakajima, T.; Hisamatsu, T.; Nonoyama, T.; Kurokawa, T.; Gong, J.P. Phase-separation-induced anomalous stiffening, toughening, and self-healing of polyacrylamide gels. Adv. Mater. 2015, 27, 6990–6998. [Google Scholar] [CrossRef] [Green Version]
  72. Zhalmuratova, D.; Chung, H.-J. Reinforced gels and elastomers for biomedical and soft robotics applications. ACS Appl. Polym. Mater. 2020, 2, 1073–1091. [Google Scholar] [CrossRef]
  73. Long, R.; Hui, C.-Y. Fracture toughness of hydrogels: Measurement and interpretation. Soft Matter 2016, 12, 8069–8086. [Google Scholar] [CrossRef] [PubMed]
  74. Long, R.; Hui, C.-Y.; Gong, J.P.; Bouchbinder, E. The fracture of highly deformable soft materials: A tale of two length scales. Annu. Rev. Condens. Matter Phys. 2021, 12, 71–94. [Google Scholar] [CrossRef]
  75. Creton, C.; Ciccotti, M. Fracture and adhesion of soft materials: A review. Rep. Prog. Phys. 2016, 79, 046601. [Google Scholar] [CrossRef]
  76. Zhang, T.; Lin, S.; Yuk, H.; Zhao, X. Predicting fracture energies and crack-tip fields of soft tough materials. Extrem. Mech. Lett. 2015, 4, 1–8. [Google Scholar] [CrossRef] [Green Version]
  77. Huang, Y.; King, D.R.; Cui, W.; Sun, T.L.; Guo, H.; Kurokawa, T.; Brown, H.R.; Hui, C.-Y.; Gong, J.P. Superior fracture resistance of fiber reinforced polyampholyte hydrogels achieved by extraordinarily large energy-dissipative process zones. J. Mater. Chem. A 2019, 7, 13431–13440. [Google Scholar] [CrossRef]
  78. Li, Z.; Liu, Z.; Ng, T.Y.; Sharma, P. The effect of water content on the elastic modulus and fracture energy of hydrogel. Extrem. Mech. Lett. 2020, 35, 100617. [Google Scholar] [CrossRef]
  79. Yang, C.; Yin, T.; Suo, Z. Polyacrylamide hydrogels. I. Network imperfection. J. Mech. Phys. Solids 2019, 131, 43–55. [Google Scholar] [CrossRef]
  80. Liu, J.; Yang, C.; Yin, T.; Wang, Z.; Qu, S.; Suo, Z. Polyacrylamide hydrogels. II. Elastic dissipater. J. Mech. Phys. Solids 2019, 133, 103737. [Google Scholar] [CrossRef]
  81. Zhang, W.; Liu, X.; Wang, J.; Tang, J.; Hu, J.; Lu, T.; Suo, Z. Fatigue of double-network hydrogels. Eng. Fract. Mech. 2018, 187, 74–93. [Google Scholar] [CrossRef] [Green Version]
  82. Hou, J.; Ren, X.; Guan, S.; Duan, L.; Gao, G.H.; Kuai, Y.; Zhang, H. Rapidly recoverable, anti-fatigue, super-tough double-network hydrogels reinforced by macromolecular microspheres. Soft Matter 2017, 13, 1357–1363. [Google Scholar] [CrossRef]
  83. Chen, Q.; Yan, X.; Zhu, L.; Chen, H.; Jiang, B.; Wei, D.; Huang, L.; Yang, J.; Liu, B.; Zheng, J. Improvement of mechanical strength and fatigue resistance of double network hydrogels by ionic coordination interactions. Chem. Mater. 2016, 28, 5710–5720. [Google Scholar] [CrossRef]
  84. Chen, Q.; Zhu, L.; Chen, H.; Yan, H.; Huang, L.; Yang, J.; Zheng, J. A novel design strategy for fully physically linked double network hydrogels with tough, fatigue resistant, and self-healing properties. Adv. Funct. Mater. 2015, 25, 1598–1607. [Google Scholar] [CrossRef]
  85. Chen, Q.; Zhu, L.; Zhao, C.; Wang, Q.; Zheng, J. A robust, one-pot synthesis of highly mechanical and recoverable double network hydrogels using thermoreversible sol-gel polysaccharide. Adv. Mater. 2013, 25, 4171–4176. [Google Scholar] [CrossRef]
  86. Li, X.; Cui, K.; Sun, T.L.; Meng, L.; Yu, C.; Li, L.; Creton, C.; Kurokawa, T.; Gong, J.P. Mesoscale bicontinuous networks in self-healing hydrogels delay fatigue fracture. Proc. Natl. Acad. Sci. USA 2020, 117, 7606–7612. [Google Scholar] [CrossRef] [PubMed]
  87. Tanaka, Y. A local damage model for anomalous high toughness of double-network gels. Europhys. Lett. 2007, 78, 56005. [Google Scholar] [CrossRef]
  88. Tominaga, T.; Tirumala, V.R.; Lee, S.; Lin, E.K.; Gong, J.P.; Wu, W.-l. Thermodynamic interactions in double-network hydrogels. J. Phys. Chem. B 2008, 112, 3903–3909. [Google Scholar] [CrossRef] [PubMed]
  89. Tominaga, T.; Tirumala, V.R.; Lin, E.K.; Gong, J.P.; Furukawa, H.; Osada, Y.; Wu, W.-l. The molecular origin of enhanced toughness in double-network hydrogels: A neutron scattering study. Polymer 2007, 48, 7449–7454. [Google Scholar] [CrossRef]
  90. Yu, Q.M.; Tanaka, Y.; Furukawa, H.; Kurokawa, T.; Gong, J.P. Direct observation of damage zone around crack tips in double-network gels. Macromolecules 2009, 42, 3852–3855. [Google Scholar] [CrossRef]
  91. Liang, S.; Wu, Z.L.; Hu, J.; Kurokawa, T.; Yu, Q.M.; Gong, J.P. Direct observation on the surface fracture of ultrathin film double-network hydrogels. Macromolecules 2011, 44, 3016–3020. [Google Scholar] [CrossRef]
  92. Cui, W.; Huang, Y.; Chen, L.; Zheng, Y.; Saruwatari, Y.; Hui, C.-Y.; Kurokawa, T.; King, D.R.; Gong, J.P. Tiny yet tough: Maximizing the toughness of fiber-reinforced soft composites in the absence of a fiber-fracture mechanism. Matter 2021, 4, 3646–3661. [Google Scholar] [CrossRef]
  93. Hui, C.-Y.; Liu, Z.; Phoenix, S.L. Size effect on elastic stress concentrations in unidirectional fiber reinforced soft composites. Extrem. Mech. Lett. 2019, 33, 100573. [Google Scholar] [CrossRef]
  94. Haque, M.A.; Kurokawa, T.; Gong, J.P. Super tough double network hydrogels and their application as biomaterials. Polymer 2012, 53, 1805–1822. [Google Scholar] [CrossRef]
  95. Yue, Y.; Kurokawa, T.; Haque, M.A.; Nakajima, T.; Nonoyama, T.; Li, X.; Kajiwara, I.; Gong, J.P. Mechano-actuated ultrafast full-colour switching in layered photonic hydrogels. Nat. Commun. 2014, 5, 1–8. [Google Scholar] [CrossRef] [Green Version]
  96. Yue, Y.F.; Haque, M.A.; Kurokawa, T.; Nakajima, T.; Gong, J.P. Lamellar Hydrogels with High Toughness and Ternary Tunable Photonic Stop-Band. Adv. Mater. 2013, 25, 3106–3110. [Google Scholar] [CrossRef] [PubMed]
  97. Ye, Y.N.; Haque, M.A.; Inoue, A.; Katsuyama, Y.; Kurokawa, T.; Gong, J.P. Flower-like Photonic Hydrogel with Superstructure Induced via Modulated Shear Field. ACS Macro Lett. 2021, 10, 708–713. [Google Scholar] [CrossRef]
  98. Haque, M.A.; Kurokawa, T.; Kamita, G.; Yue, Y.; Gong, J.P. Rapid and reversible tuning of structural color of a hydrogel over the entire visible spectrum by mechanical stimulation. Chem. Mater. 2011, 23, 5200–5207. [Google Scholar] [CrossRef]
  99. Haque, M.A.; Kurokawa, T.; Gong, J.P. Anisotropic hydrogel based on bilayers: Color, strength, toughness, and fatigue resistance. Soft Matter 2012, 8, 8008–8016. [Google Scholar] [CrossRef] [Green Version]
  100. Kong, W.; Wang, C.; Jia, C.; Kuang, Y.; Pastel, G.; Chen, C.; Chen, G.; He, S.; Huang, H.; Zhang, J. Muscle-Inspired Highly Anisotropic, Strong, Ion-Conductive Hydrogels. Adv. Mater. 2018, 30, 1801934. [Google Scholar] [CrossRef]
  101. Zhou, Y.; Wan, C.; Yang, Y.; Yang, H.; Wang, S.; Dai, Z.; Ji, K.; Jiang, H.; Chen, X.; Long, Y. Highly stretchable, elastic, and ionic conductive hydrogel for artificial soft electronics. Adv. Funct. Mater. 2019, 29, 1806220. [Google Scholar] [CrossRef]
  102. Park, H.; Lee, K.; Kim, Y.; Ambade, S.; Noh, S.; Eom, W.; Hwang, J.; Lee, W.; Huang, J.; Han, T. Dynamic assembly of liquid crystalline graphene oxide gel fibers for ion transport. Sci. Adv. 2018, 4, eaau2104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  103. Kanik, M.; Orguc, S.; Varnavides, G.; Kim, J.; Benavides, T.; Gonzalez, D.; Akintilo, T.; Tasan, C.C.; Chandrakasan, A.P.; Fink, Y. Strain-programmable fiber-based artificial muscle. Science 2019, 365, 145–150. [Google Scholar] [CrossRef] [PubMed]
Textiles 01 00027 g001 550
Figure 1. Different energy dissipation mechanisms give distinct toughness. (a) Breaking a layer of bonds. (b) Snapping a layer of chains. (c) Dissipating energy in the bulk.
Figure 1. Different energy dissipation mechanisms give distinct toughness. (a) Breaking a layer of bonds. (b) Snapping a layer of chains. (c) Dissipating energy in the bulk.
Textiles 01 00027 g001
Textiles 01 00027 g002 550
Figure 2. Energy dissipation mechanisms at different length scales of soft composites. (a) Double network materials with sacrificial bonds at the molecular scale. Reproduced with permission from reference [29] Copyright 2014 The American Association for the Advancement of Science. (b) Phase-separated materials with hard phases at the nanoscale. Reproduced with permission from reference [31] Copyright 2021 American Chemical Society. (c) Micro-fiber-reinforced soft composites dissipate energy at the micrometer scale. Reproduced with permission from reference [37] Copyright 2019 National Academy of Sciences. (d) Soft composites with macroscopic reinforcing phases dissipate energy at the millimeter scale. Reproduced with permission from reference [38] Copyright 2019 National Academy of Sciences.
Figure 2. Energy dissipation mechanisms at different length scales of soft composites. (a) Double network materials with sacrificial bonds at the molecular scale. Reproduced with permission from reference [29] Copyright 2014 The American Association for the Advancement of Science. (b) Phase-separated materials with hard phases at the nanoscale. Reproduced with permission from reference [31] Copyright 2021 American Chemical Society. (c) Micro-fiber-reinforced soft composites dissipate energy at the micrometer scale. Reproduced with permission from reference [37] Copyright 2019 National Academy of Sciences. (d) Soft composites with macroscopic reinforcing phases dissipate energy at the millimeter scale. Reproduced with permission from reference [38] Copyright 2019 National Academy of Sciences.
Textiles 01 00027 g002
Textiles 01 00027 g004 550
Figure 4. Fabrication of phase-separated hydrogels and elastomers. (a) Fabrication via mixed-solvent-induced phase separation. Reproduced with permission from reference [55] Copyright 2021 Royal Society of Chemistry. (b) The bicontinuous phase-separated structure of polyampholyte hydrogels. Reproduced with permission from reference [52] Copyright 2020 American Chemical Society. (c) Elastomers fabricated via nanophase separation. Reproduced with permission from reference [31] Copyright 2021 American Chemical Society.
Figure 4. Fabrication of phase-separated hydrogels and elastomers. (a) Fabrication via mixed-solvent-induced phase separation. Reproduced with permission from reference [55] Copyright 2021 Royal Society of Chemistry. (b) The bicontinuous phase-separated structure of polyampholyte hydrogels. Reproduced with permission from reference [52] Copyright 2020 American Chemical Society. (c) Elastomers fabricated via nanophase separation. Reproduced with permission from reference [31] Copyright 2021 American Chemical Society.
Textiles 01 00027 g004
Textiles 01 00027 g005 550
Figure 5. Fabrication of micro-fiber-reinforced soft composites. (a) Micro aramid fiber-reinforced hydrogels. Reproduced with permission from reference [61] Copyright 2017 Wiley. (b) Hydrogel composites reinforced by 3D printed skeletons. Reproduced with permission from reference [62] Copyright 2012 Elsevier. (c) Hydrogel composites fabricated via reswelling disparity of two oriented polymers with contrasting persistence lengths. Reproduced with permission from reference [64] Copyright 2021 Royal Society of Chemistry.
Figure 5. Fabrication of micro-fiber-reinforced soft composites. (a) Micro aramid fiber-reinforced hydrogels. Reproduced with permission from reference [61] Copyright 2017 Wiley. (b) Hydrogel composites reinforced by 3D printed skeletons. Reproduced with permission from reference [62] Copyright 2012 Elsevier. (c) Hydrogel composites fabricated via reswelling disparity of two oriented polymers with contrasting persistence lengths. Reproduced with permission from reference [64] Copyright 2021 Royal Society of Chemistry.
Textiles 01 00027 g005
Textiles 01 00027 g006 550
Figure 6. Fabrication of soft composites with macroscopic reinforcing phases. (a) Fabrication of traditional woven fabric-reinforced soft composites. Reproduced with permission from reference [18] Copyright 2020 Wiley. (b) Soft composites made up of low-melting-point alloy reinforced hydrogels. Reproduced with permission from reference [65] Copyright 2018 Wiley. (c) Elastomer composites with 3D printed plastic skeletons as the reinforcing phases. Reproduced with permission from reference [66] Copyright 2019 American Chemical Society. (d) Combining two elastomers with different stiffness into a tough soft composite. Reproduced with permission from reference [67] Copyright 2020 Elsevier.
Figure 6. Fabrication of soft composites with macroscopic reinforcing phases. (a) Fabrication of traditional woven fabric-reinforced soft composites. Reproduced with permission from reference [18] Copyright 2020 Wiley. (b) Soft composites made up of low-melting-point alloy reinforced hydrogels. Reproduced with permission from reference [65] Copyright 2018 Wiley. (c) Elastomer composites with 3D printed plastic skeletons as the reinforcing phases. Reproduced with permission from reference [66] Copyright 2019 American Chemical Society. (d) Combining two elastomers with different stiffness into a tough soft composite. Reproduced with permission from reference [67] Copyright 2020 Elsevier.
Textiles 01 00027 g006
Textiles 01 00027 g008 550
Figure 8. Fracture toughness of soft composites at different length scales. (a) Superior crack resistance of physical double network hydrogels. Reproduced with permission from reference [23] Copyright 2012 Springer Nature. (b) Nanophase-separated elastomers prevent crack growth via nanophase pinning. Reproduced with permission from reference [31] Copyright 2021 American Chemical Society. (c) Crack deflection in micro-fiber-based soft composites. Reproduced with permission from reference [34] Copyright 2021 Springer Nature. (d) Extremely high fracture energy of fabric-reinforced soft composites compared with common tough materials. Reproduced with permission from reference [77] Copyright 2019 Royal Society of Chemistry.
Figure 8. Fracture toughness of soft composites at different length scales. (a) Superior crack resistance of physical double network hydrogels. Reproduced with permission from reference [23] Copyright 2012 Springer Nature. (b) Nanophase-separated elastomers prevent crack growth via nanophase pinning. Reproduced with permission from reference [31] Copyright 2021 American Chemical Society. (c) Crack deflection in micro-fiber-based soft composites. Reproduced with permission from reference [34] Copyright 2021 Springer Nature. (d) Extremely high fracture energy of fabric-reinforced soft composites compared with common tough materials. Reproduced with permission from reference [77] Copyright 2019 Royal Society of Chemistry.
Textiles 01 00027 g008
Textiles 01 00027 g010 550
Figure 10. Fatigue resistance of macroscopic soft composites consisting of two elastomers with different stiffness. (a) Distinct crack growth behavior in a neat elastomer and composite elastomer. Reproduced with permission from reference [38] Copyright 2019 National Academy of Sciences. (b) Superior fatigue resistance of the composite elastomer to its individual components. Reproduced with permission from reference [38] Copyright 2019 National Academy of Sciences. (c) The critical energy release rate of the composite elastomer. Reproduced with permission from reference [67] Copyright 2020 Elsevier. (d) Fatigue threshold versus fracture toughness of the composite elastomer compared with other elastomers. Reproduced with permission from reference [38] Copyright 2019 National Academy of Sciences. (e) The topological adhesion between the soft and hard components. Reproduced with permission from reference [38] Copyright 2019 National Academy of Sciences.
Figure 10. Fatigue resistance of macroscopic soft composites consisting of two elastomers with different stiffness. (a) Distinct crack growth behavior in a neat elastomer and composite elastomer. Reproduced with permission from reference [38] Copyright 2019 National Academy of Sciences. (b) Superior fatigue resistance of the composite elastomer to its individual components. Reproduced with permission from reference [38] Copyright 2019 National Academy of Sciences. (c) The critical energy release rate of the composite elastomer. Reproduced with permission from reference [67] Copyright 2020 Elsevier. (d) Fatigue threshold versus fracture toughness of the composite elastomer compared with other elastomers. Reproduced with permission from reference [38] Copyright 2019 National Academy of Sciences. (e) The topological adhesion between the soft and hard components. Reproduced with permission from reference [38] Copyright 2019 National Academy of Sciences.
Textiles 01 00027 g010
Textiles 01 00027 g011 550
Figure 11. Energy dissipation mechanism of double network hydrogel. (a) A damage zone is formed when a crack tends to propagate in a double network hydrogel. Reproduced with permission from reference [87] Copyright 2007 IOP Publishing. (b) Inside the damage zone, the first network breaks into molecular clusters, which work as cross-linking points to connect the second network. Reproduced with permission from reference [21] Copyright 2010 Royal Society of Chemistry. (c) Direct observation of the damage zone in the double network hydrogels. Reproduced with permission from reference [90] Copyright 2009 American Chemical Society. (d) Double network structure gives rise to a significantly increased process zone for energy dissipation. Reproduced with permission from reference [23] Copyright 2012 Springer Nature.
Figure 11. Energy dissipation mechanism of double network hydrogel. (a) A damage zone is formed when a crack tends to propagate in a double network hydrogel. Reproduced with permission from reference [87] Copyright 2007 IOP Publishing. (b) Inside the damage zone, the first network breaks into molecular clusters, which work as cross-linking points to connect the second network. Reproduced with permission from reference [21] Copyright 2010 Royal Society of Chemistry. (c) Direct observation of the damage zone in the double network hydrogels. Reproduced with permission from reference [90] Copyright 2009 American Chemical Society. (d) Double network structure gives rise to a significantly increased process zone for energy dissipation. Reproduced with permission from reference [23] Copyright 2012 Springer Nature.
Textiles 01 00027 g011
Textiles 01 00027 g012 550
Figure 12. Energy dissipation mechanisms of different phase-separated soft composites. (a) Polyampholyte hydrogels obtain high toughness via a multiscale energy dissipation mechanism. Reproduced with permission from reference [33] Copyright 2018 American Physical Society. (b) Nanophases acting as sacrificial bonds in nanophase-separated elastomers at different strains. (i) The strain is small and far below the yielding point; (ii) The strain is moderate but still below the yielding point. (iii) The strain is large and above the yielding point. Reproduced with permission from reference [31] Copyright 2021 American Chemical Society.
Figure 12. Energy dissipation mechanisms of different phase-separated soft composites. (a) Polyampholyte hydrogels obtain high toughness via a multiscale energy dissipation mechanism. Reproduced with permission from reference [33] Copyright 2018 American Physical Society. (b) Nanophases acting as sacrificial bonds in nanophase-separated elastomers at different strains. (i) The strain is small and far below the yielding point; (ii) The strain is moderate but still below the yielding point. (iii) The strain is large and above the yielding point. Reproduced with permission from reference [31] Copyright 2021 American Chemical Society.
Textiles 01 00027 g012
Textiles 01 00027 g013 550
Figure 13. Energy dissipation mechanisms of micro-fiber-based soft composites with discontinuous or continuous microfibers. (a) Micro aramid fiber-reinforced hydrogels dissipate energy via stress transmission between the soft and stiff phases. Reproduced with permission from reference [61] Copyright 2018 Wiley. (b) Polyvinyl alcohol fiber-based hydrogels show anisotropic fracture toughness. The fracture toughness along the fiber direction is orders of magnitude higher than that perpendicular to the fiber direction. Reproduced from reference [37] Copyright 2019 National Academy of Sciences.
Figure 13. Energy dissipation mechanisms of micro-fiber-based soft composites with discontinuous or continuous microfibers. (a) Micro aramid fiber-reinforced hydrogels dissipate energy via stress transmission between the soft and stiff phases. Reproduced with permission from reference [61] Copyright 2018 Wiley. (b) Polyvinyl alcohol fiber-based hydrogels show anisotropic fracture toughness. The fracture toughness along the fiber direction is orders of magnitude higher than that perpendicular to the fiber direction. Reproduced from reference [37] Copyright 2019 National Academy of Sciences.
Textiles 01 00027 g013
Textiles 01 00027 g014 550
Figure 14. Energy dissipation mechanisms of macroscopic woven fabric-reinforced soft composites. (a) Size-dependent fracture behavior of the soft composites. Reproduced with permission from reference [92] Copyright 2021 Elsevier. (b) Fracture toughness of the soft composites in the fiber-pullout region is related to fiber bundle geometry (K), center-to-center distance between adjacent fiber bundles (wcc), matrix toughness (Tm), and composite width. Reproduced with permission from reference [92] Copyright 2021 Elsevier. (c) The fracture toughness of the soft composites in the fiber-fracture region is related to load transfer length (lT) and energy dissipation density (Weff). Reproduced with permission from reference [18] Copyright 2020 Wiley.
Figure 14. Energy dissipation mechanisms of macroscopic woven fabric-reinforced soft composites. (a) Size-dependent fracture behavior of the soft composites. Reproduced with permission from reference [92] Copyright 2021 Elsevier. (b) Fracture toughness of the soft composites in the fiber-pullout region is related to fiber bundle geometry (K), center-to-center distance between adjacent fiber bundles (wcc), matrix toughness (Tm), and composite width. Reproduced with permission from reference [92] Copyright 2021 Elsevier. (c) The fracture toughness of the soft composites in the fiber-fracture region is related to load transfer length (lT) and energy dissipation density (Weff). Reproduced with permission from reference [18] Copyright 2020 Wiley.
Textiles 01 00027 g014
Textiles 01 00027 g015 550
Figure 15. Various applications of soft composites at different length scales. (a) Double network hydrogels as cartilage repairing agents. Reproduced with permission from reference [94] Copyright 2010 Elsevier. (b) Photonic double network hydrogels as pressure sensors. Reproduced with permission from reference [95] Copyright 2014 Springer Nature. (c) Phase-separated hydrogels as tough adhesives. Reproduced with permission from reference [55] Copyright 2021 Royal Society of Chemistry. (d) Micro-fiber-based hydrogels used for ion transport. Reproduced with permission from reference [100] Copyright 2018 Wiley. (e) Artificial muscle based on thermal micro-fiber-based soft composites. Reproduced with permission from reference [103] Copyright 2019 The American Association for the Advancement of Science. (f) Solvent-responsive actuators based on woven fabric-reinforced soft composites. Reproduced with permission from reference [12] Copyright 2019 Elsevier.
Figure 15. Various applications of soft composites at different length scales. (a) Double network hydrogels as cartilage repairing agents. Reproduced with permission from reference [94] Copyright 2010 Elsevier. (b) Photonic double network hydrogels as pressure sensors. Reproduced with permission from reference [95] Copyright 2014 Springer Nature. (c) Phase-separated hydrogels as tough adhesives. Reproduced with permission from reference [55] Copyright 2021 Royal Society of Chemistry. (d) Micro-fiber-based hydrogels used for ion transport. Reproduced with permission from reference [100] Copyright 2018 Wiley. (e) Artificial muscle based on thermal micro-fiber-based soft composites. Reproduced with permission from reference [103] Copyright 2019 The American Association for the Advancement of Science. (f) Solvent-responsive actuators based on woven fabric-reinforced soft composites. Reproduced with permission from reference [12] Copyright 2019 Elsevier.
Textiles 01 00027 g015
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Cui, W.; Zhu, R. A Review on Tough Soft Composites at Different Length Scales. Textiles 2021, 1, 513-533. https://0-doi-org.brum.beds.ac.uk/10.3390/textiles1030027

AMA Style

Cui W, Zhu R. A Review on Tough Soft Composites at Different Length Scales. Textiles. 2021; 1(3):513-533. https://0-doi-org.brum.beds.ac.uk/10.3390/textiles1030027

Chicago/Turabian Style

Cui, Wei, and Ruijie Zhu. 2021. "A Review on Tough Soft Composites at Different Length Scales" Textiles 1, no. 3: 513-533. https://0-doi-org.brum.beds.ac.uk/10.3390/textiles1030027

Article Metrics

Back to TopTop