Information Entropy of Regular Dendrimer Aggregates and Irregular Intermediate Structures
Abstract
:1. Introduction
2. Description of the Mathematical Model
2.1. Basic Definitions
2.2. Information Entropy of Dendrimer
3. Results and Discussion
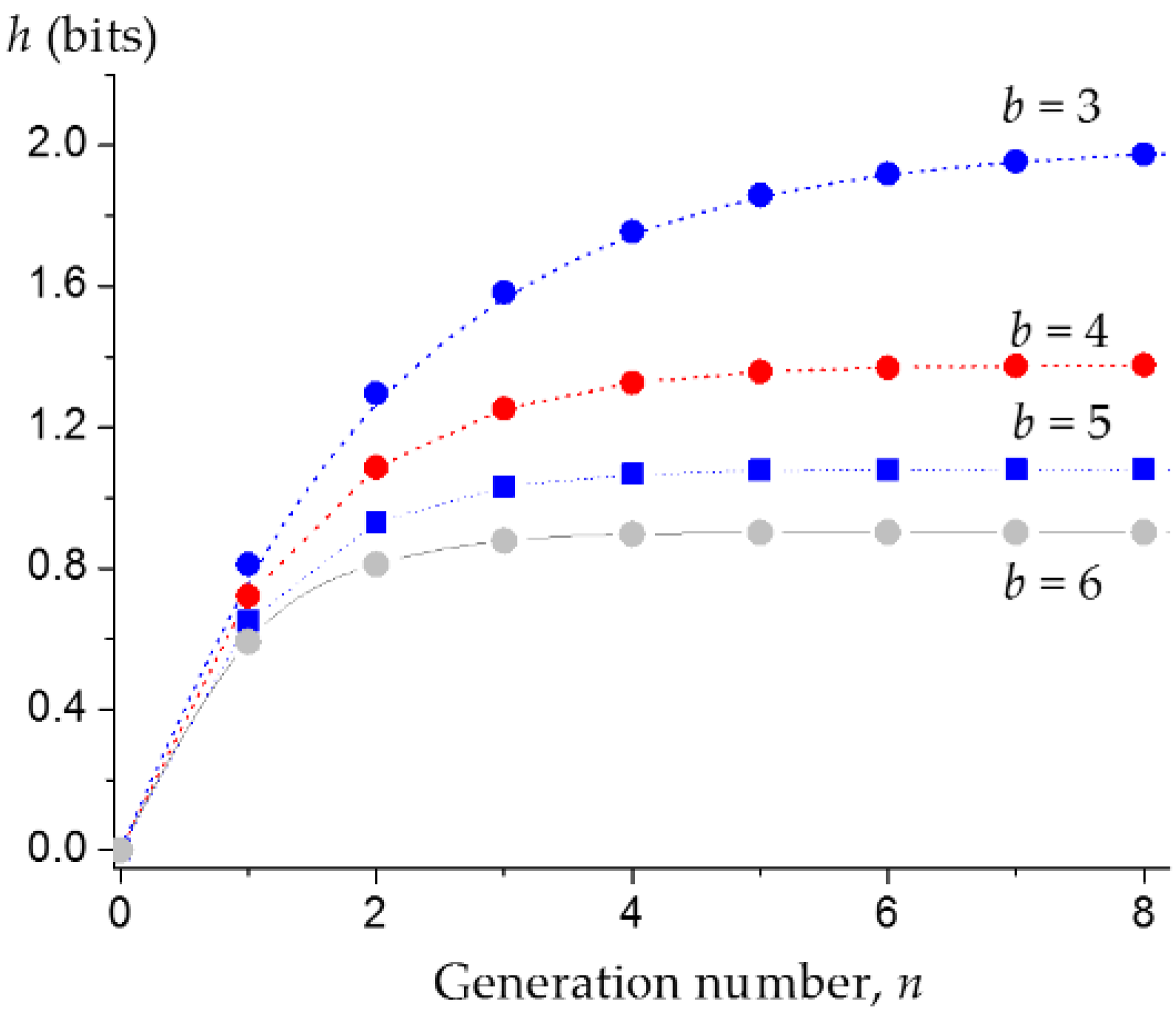
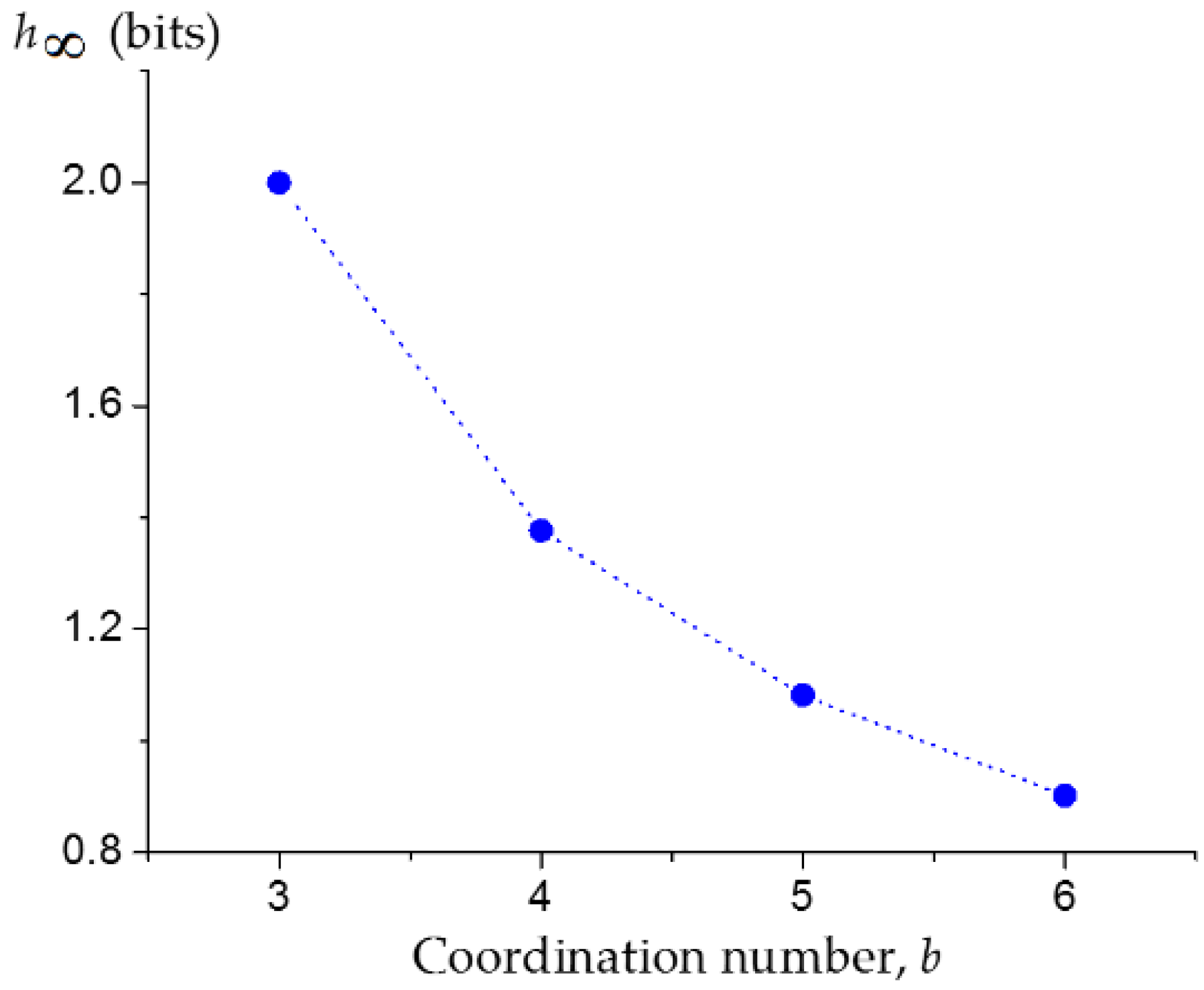
3.1. Upper Bound of the Information Entropy of Dendrimer at the Infinite Generation Number
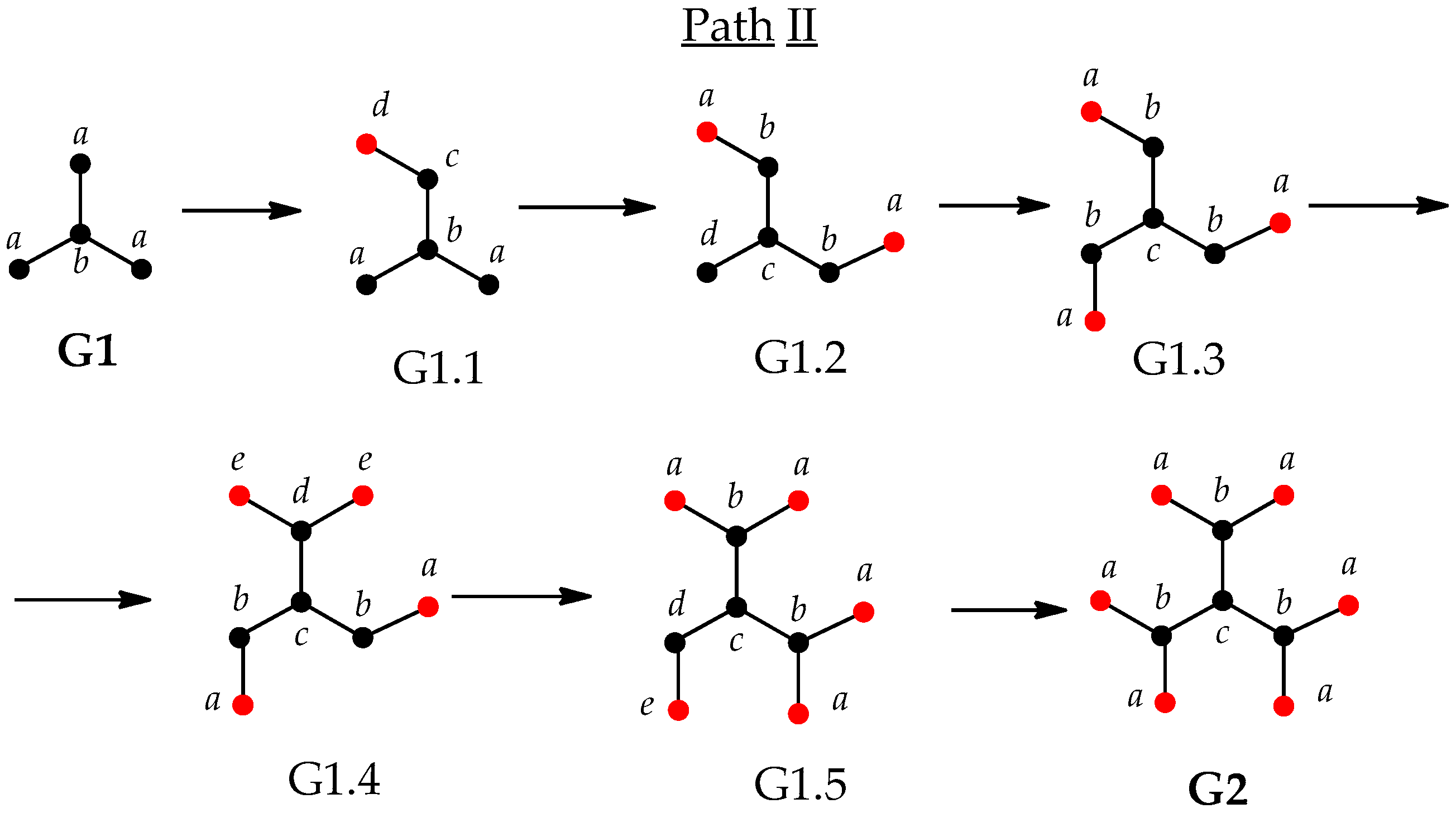
3.2. Imperfect Dendrimers and Infromation Entropy of Intermediate States
4. Prospective
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References and Note
- Mandelbrot, B. The Fractal Geometry of Nature; W. H. Freeman and Company: New York, NY, USA, 1982; pp. 1–468. [Google Scholar]
- Lazzari, S.; Nicoud, L.; Jaquet, B.; Lattuada, M.; Morbidelli, M. Fractal-like structures in colloid science. Adv. Colloid Interface Sci. 2016, 235, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Cheng, W.; Dong, S.; Wang, E. Spontaneous fractal aggregation of gold nanoparticles and controlled generation of aggregate-based fractal networks at air/water interface. J. Phys. Chem. B 2005, 109, 19213–19218. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.; Khatun, S.; Gupta, A.N. Anisotropy versus fluctuations in the fractal self-assembly of gold nanoparticles. Soft Matter 2020, 16, 7778–7788. [Google Scholar] [CrossRef]
- Eletskii, A.V.; Okun, M.V.; Smirnov, B.M. Growth of fractal structures in fullerene solutions. Phys. Scr. 1997, 55, 363–366. [Google Scholar] [CrossRef]
- Peidys, D.A.; Mosunov, A.A.; Mykhina, Y.V.; Prylutskyy, Y.I.; Evstigneev, M.P. Fractal C60 fullerene aggregation: Equilibrium thermodynamics approach. Chem. Phys. Lett. 2020, 742, 137161. [Google Scholar] [CrossRef]
- Klochkovskii, S.P. (private demonstration of the ammonia amalgam growth via the cathodic polarization of a mercury drop in solutions of ammonium salts. When voltage applied, the drop is covered with rapidly growing amalgam branches. The formation of amalgam is accompanied with a pronounced volume increase, which can be 100 times larger than the volume of the initial drop. When voltage switched off, the mercury amalgam is decomposed releasing ammonia and dihydrogen).
- Nemcsics, Á.; Nagy, S.; Mojzes, I.; Schwedhelm, R.; Woedtke, S.; Adelung, R.; Kipp, L. Investigation of the surface morphology on epitaxially grown fullerene structures. Vacuum 2009, 84, 152–154. [Google Scholar] [CrossRef]
- Miyashita, S.; Saito, Y.; Uwaha, M. Fractal aggregation growth and the surrounding diffusion field. J. Cryst. Growth. 2005, 283, 533–539. [Google Scholar] [CrossRef]
- Lenoble, J.; Campidelli, S.; Maringa, N.; Donnio, B.; Guillon, D.; Yevlampieva, N.; Deschenaux, R. Liquid−crystalline Janus-type fullerodendrimers displaying tunable smectic−columnar mesomorphism. J. Amer. Chem. Soc. 2007, 129, 9941–9952. [Google Scholar] [CrossRef]
- Scanu, D.; Yevlampieva, N.P.; Deschenaux, R. Polar and electrooptical properties of [60]fullerene-containing poly(benzyl ether) dendrimers in solution. Macromolecules 2007, 40, 1133–1139. [Google Scholar] [CrossRef]
- Yin, H.; Wang, M.; Tan, L.-S.; Chiang, L.Y. Synthesis and intramolecular energy- and electron-transfer of 3D-conformeric tris(fluorenyl-[60]fullerenylfluorene) derivatives. Molecules 2019, 24, 3337. [Google Scholar] [CrossRef] [Green Version]
- Takaguchi, Y.; Hosokawa, M.; Mayahara, M.; Tajima, T.; Sasamori, T.; Tokitoh, N. Formation of zwitterionic fullerodendron using a new DBN-focal dendron. Sensors 2010, 10, 613–624. [Google Scholar] [CrossRef] [Green Version]
- Yevlampieva, N.P.; Khurchak, A.P.; Borshchev, O.V.; Luponosov, Y.N.; Kleimyuk, E.A.; Ponomarenko, S.A.; Ryumtsev, E.I. Mechanisms of molecular polarization of bithiophenesilane dendrimers in solutions. Polymer Sci. Ser. A 2011, 53, 569–577. [Google Scholar] [CrossRef]
- Pavlov, G.M.; Korneeva, E.V.; Meijer, E.W. Translational friction of molecules of dendrimers based on poly(propylenimine). Russ. J. Appl. Chem. 2000, 73, 1784–1788. [Google Scholar]
- Zhilitskaya, L.V.; Yarosh, N.O.; Voronkov, M.G. New polyunsaturated organosilicon dendrimers. Russ. J. Gen. Chem. 2010, 80, 1929–1932. [Google Scholar] [CrossRef]
- Zhilitskaya, L.V.; Istomina, E.E.; Yarosh, N.O.; Voronkov, M.G.; Albanov, A.I.; Yarosh, O.G. Spherical polyunsaturated organosilicon and organogermanium first generation dendrimers of regular structure. Russ. J. Gen. Chem. 2006, 72, 1864–1869. [Google Scholar] [CrossRef]
- Caminade, A.-M. Inorganic dendrimers: Recent advances for catalysis, nanomaterials, and nanomedicine. Chem. Soc. Rev. 2016, 45, 5174–5186. [Google Scholar] [CrossRef] [PubMed]
- Majoral, J.-P.; Caminade, A.-M. Dendrimers containing heteroatoms (Si, P, B, Ge, or Bi). Chem. Rev. 1999, 99, 845–880. [Google Scholar] [CrossRef]
- Astruc, D.; Boisselier, E.; Ornelas, C. Dendrimers designed for functions: From physical, photophysical, and supramolecular properties to applications in sensing, catalysis, molecular electronics, photonics, and nanomedicine. Chem. Rev. 2010, 110, 1857–1959. [Google Scholar] [CrossRef]
- Rosen, B.M.; Wilson, C.J.; Wilson, D.A.; Peterca, M.; Imam, M.R.; Percec, V. Dendron-mediated self-assembly, disassembly, and self-organization of complex systems. Chem. Rev. 2009, 109, 6275–6540. [Google Scholar] [CrossRef]
- Pirozhnikov, P.B.; Korolev, I.V.; Kuzina, N.G.; Mashlyakovskii, L.N. Hyperbranched polymers and their use in the technology of paint-and-varnish materials and coatings. Russ. J. Appl. Chem. 2013, 86, 1549–1562. [Google Scholar] [CrossRef]
- Chen, Z.; Dehmer, M.; Emmert-Streib, F.; Shi, Y. Entropy bounds for dendrimers. Appl. Math. Comput. 2014, 242, 462–472. [Google Scholar] [CrossRef]
- Ghorbani, M.; Dehmer, M.; Zangi, S.; Mowshowitz, A.; Emmert-Streib, F. A note on distance-based entropy of dendrimers. Axioms 2019, 8, 98. [Google Scholar] [CrossRef] [Green Version]
- Jiménez-Ángeles, F.; Odriozola, G.; Lozada-Cassou, M. Entropy effects in self-assembling mechanisms: Also a view from the information theory. J. Mol. Liquids 2011, 164, 87–100. [Google Scholar] [CrossRef]
- Mitrokhin, Y. Two faces of entropy and information in biological systems. J. Theor. Biol. 2014, 359, 192–198. [Google Scholar] [CrossRef]
- Liu, J.-B.; Zhao, J.; Min, J.; Cao, J. On the Hosoya index of graphs formed by a fractal graph. Fractals 2019, 27, 1950135. [Google Scholar] [CrossRef]
- Andriantiana, E.O.D. Energy, Hosoya index and Merrifield–Simmons index of trees with prescribed degree sequence. Discret. Appl. Math. 2013, 161, 724–741. [Google Scholar] [CrossRef]
- Vesel, A. Linear algorithms for the Hosoya index and Hosoya matrix of a tree. Mathematics 2021, 9, 142. [Google Scholar] [CrossRef]
- Barigye, S.J.; Marrero-Ponce, Y.; Pérez-Giménez, F.; Bonchev, D. Trends in information theory-based chemical structure codification. Mol. Divers. 2014, 18, 673–686. [Google Scholar] [CrossRef]
- Basak, S.C.; Niemi, G.J.; Veith, G.D. Predicting properties of molecules using graph invariants. J. Math. Chem. 1991, 7, 243–272. [Google Scholar] [CrossRef]
- Ghorbani, M.; Dehmer, M.; Emmert-Streib, F. Properties of entropy-based topological measures of fullerenes. Mathematics 2020, 8, 740. [Google Scholar] [CrossRef]
- Ghorbani, M.; Dehmer, M.; Rajabi-Parsa, M.; Mowshowitz, A.; Emmert-Streib, F. On properties of distance-based entropies on fullerene graphs. Entropy 2019, 21, 482. [Google Scholar] [CrossRef] [Green Version]
- Ghorbani, M.; Rajabi-Parsa, M.; Mirzaie, R.A. Novel results on entropy-based measures of fullerenes. Fuller. Nanotub. Carbon Nanostruct. 2021. [Google Scholar] [CrossRef]
- Kobozev, N.I. Physicochemical modelling of information and thinking processes. I. Thermodynamics of the information processes. Russ. J. Phys. Chem. A 1966, 40, 281–284. (In Russian) [Google Scholar]
- Zhdanov, Y.A. Information Entropy in Organic Chemistry; Rostov University: Rostov-on-Don, Russia, 1979; pp. 1–55. [Google Scholar]
- Aleskovskii, V.B. Information as a factor of self-organization and organization of matter. Russ. J. Gen. Chem. 2002, 72, 569–574. [Google Scholar] [CrossRef]
- Talanov, V.M.; Ivanov, V.V. Structure as the source of information on the chemical organization of substance. Russ. J. Gen. Chem. 2013, 83, 2225–2236. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Shepelevich, I.S. Information entropy of oxygen allotropes. A still open discussion about the closed form of ozone. Comput. Theor. Chem. 2015, 1073, 61–66. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Terentyev, A.O.; Sokolov, V.I. Activation energies and information entropies of helium penetration through fullerene walls. Insights into the formation of endofullerenes nX@C60/70 (n = 1 and 2) from the information entropy approach. RSC Adv. 2016, 6, 72230–72237. [Google Scholar] [CrossRef] [Green Version]
- Sabirov, D.S. Information entropy change in [2+2]-oligomerization of the C60 fullerene. Int. J. Chem. Model. 2017, 9, 203–213. [Google Scholar]
- Sabirov, D.S. Information entropy changes in chemical reactions. Comput. Theor. Chem. 2018, 1123, 169–179. [Google Scholar] [CrossRef]
- Sabirov, D.S. Information entropy of mixing molecules and its application to molecular ensembles and chemical reactions. Comput. Theor. Chem. 2020, 1187, 112933. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Koledina, K.F. Classification of isentropic molecules in terms of Shannon entropy. In EPJ Web of Conferences; EDP Sciences: Les Ulis, France, 2020; Volume 244, p. 01016. [Google Scholar] [CrossRef]
- Chawla, M.; Kaushik, R.D.; Singh, J.; Manila. Optimization and computational studies evaluating molecular dynamics of EDA cored polymeric dendrimer. Sci. Rep. 2020, 10, 21977. [Google Scholar] [CrossRef]
- Lee, H.; Larson, R.G. Molecular dynamics simulations of PAMAM dendrimer-induced pore formation in DPPC bilayers with a coarse-grained model. J. Phys. Chem. B 2006, 110, 18204–18211. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: London, UK, 2001; pp. 1–822. [Google Scholar]
- Bar-Haim, A.; Klafter, J.; Kopelman, R. Dendrimers as controlled artificial energy antennae. J. Amer. Chem. Soc. 1997, 119, 6197–6198. [Google Scholar] [CrossRef]
- Feng, B.; Zhuang, X. Carbon-enriched meso-entropy materials: From theory to cases. Acta Chim. Sin. 2020, 78, 833–847. [Google Scholar] [CrossRef]
- Bonchev, D.; Trinajstić, N. On topological characterization of molecular branching. Int. J. Quant. Chem. 1978, 14, 293–303. [Google Scholar] [CrossRef]
- Graf, M.M.H.; Bren, U.; Haltrich, D.; Oostenbrink, C. Molecular dynamics simulations give insight into D-glucose dioxidation at C2 and C3 by Agaricus meleagris pyranose dehydrogenase. J. Comput. Aided Mol. Des. 2013, 27, 295–304. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Putz, M.V.; Lacrama, A.-M.; Ostafe, V. Full analytic progress curves of enzymic reactions in vitro. Int. J. Mol. Sci. 2006, 7, 469–484. [Google Scholar] [CrossRef]
- Champion, Y.; Thurieau, N. The sample size effect in metallic glass deformation. Sci. Rep. 2020, 10, 10801. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabirov, D.; Tukhbatullina, A.; Shepelevich, I. Information Entropy of Regular Dendrimer Aggregates and Irregular Intermediate Structures. Liquids 2021, 1, 25-35. https://0-doi-org.brum.beds.ac.uk/10.3390/liquids1010002
Sabirov D, Tukhbatullina A, Shepelevich I. Information Entropy of Regular Dendrimer Aggregates and Irregular Intermediate Structures. Liquids. 2021; 1(1):25-35. https://0-doi-org.brum.beds.ac.uk/10.3390/liquids1010002
Chicago/Turabian StyleSabirov, Denis, Alina Tukhbatullina, and Igor Shepelevich. 2021. "Information Entropy of Regular Dendrimer Aggregates and Irregular Intermediate Structures" Liquids 1, no. 1: 25-35. https://0-doi-org.brum.beds.ac.uk/10.3390/liquids1010002





