Are COVID-19 Data Reliable? A Quantitative Analysis of Pandemic Data from 182 Countries
Abstract
:1. Introduction
2. Method
2.1. Benford’s Law and Goodness-of-Fit Tests
2.2. COVID-19 Data Sampling
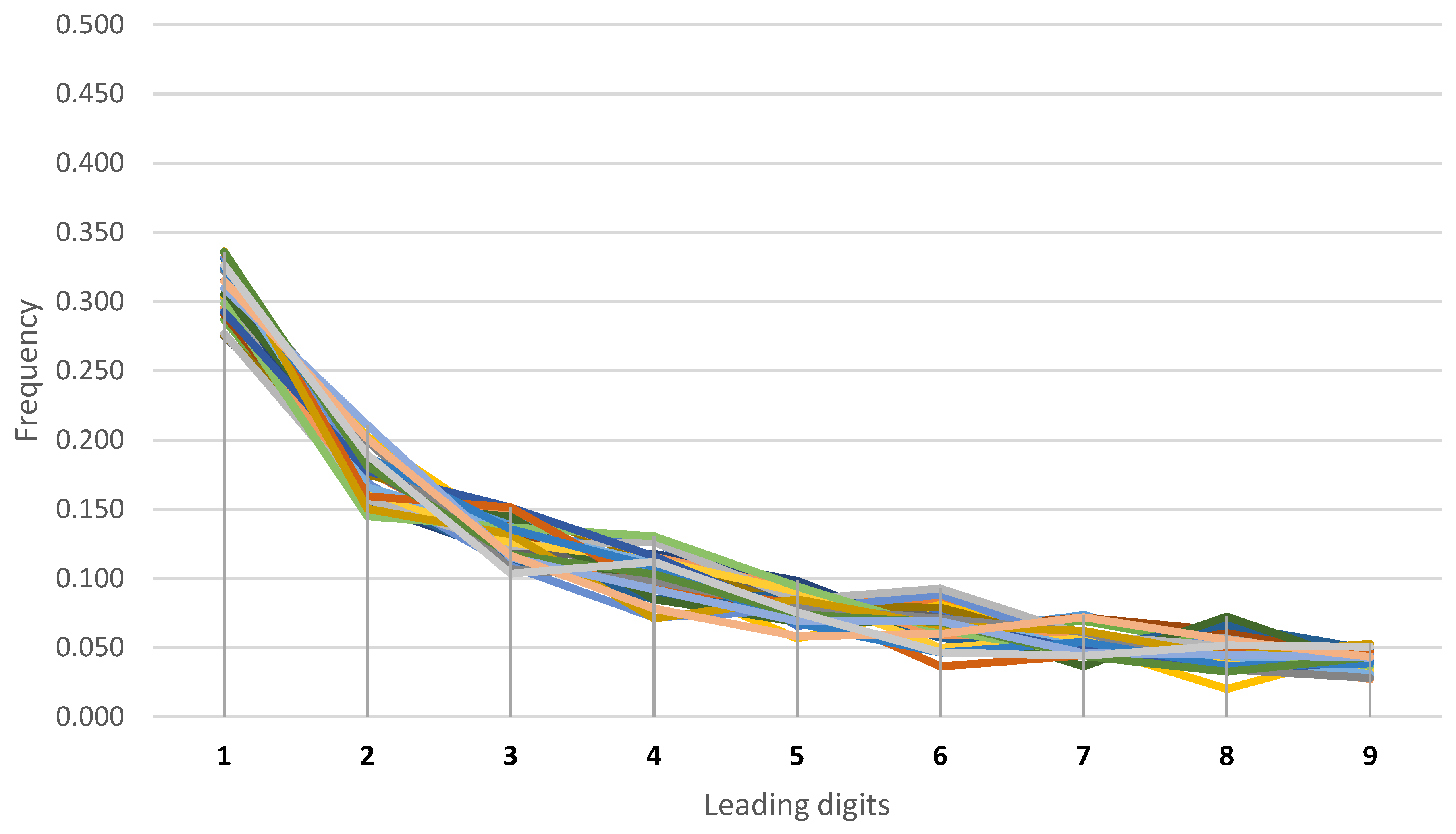
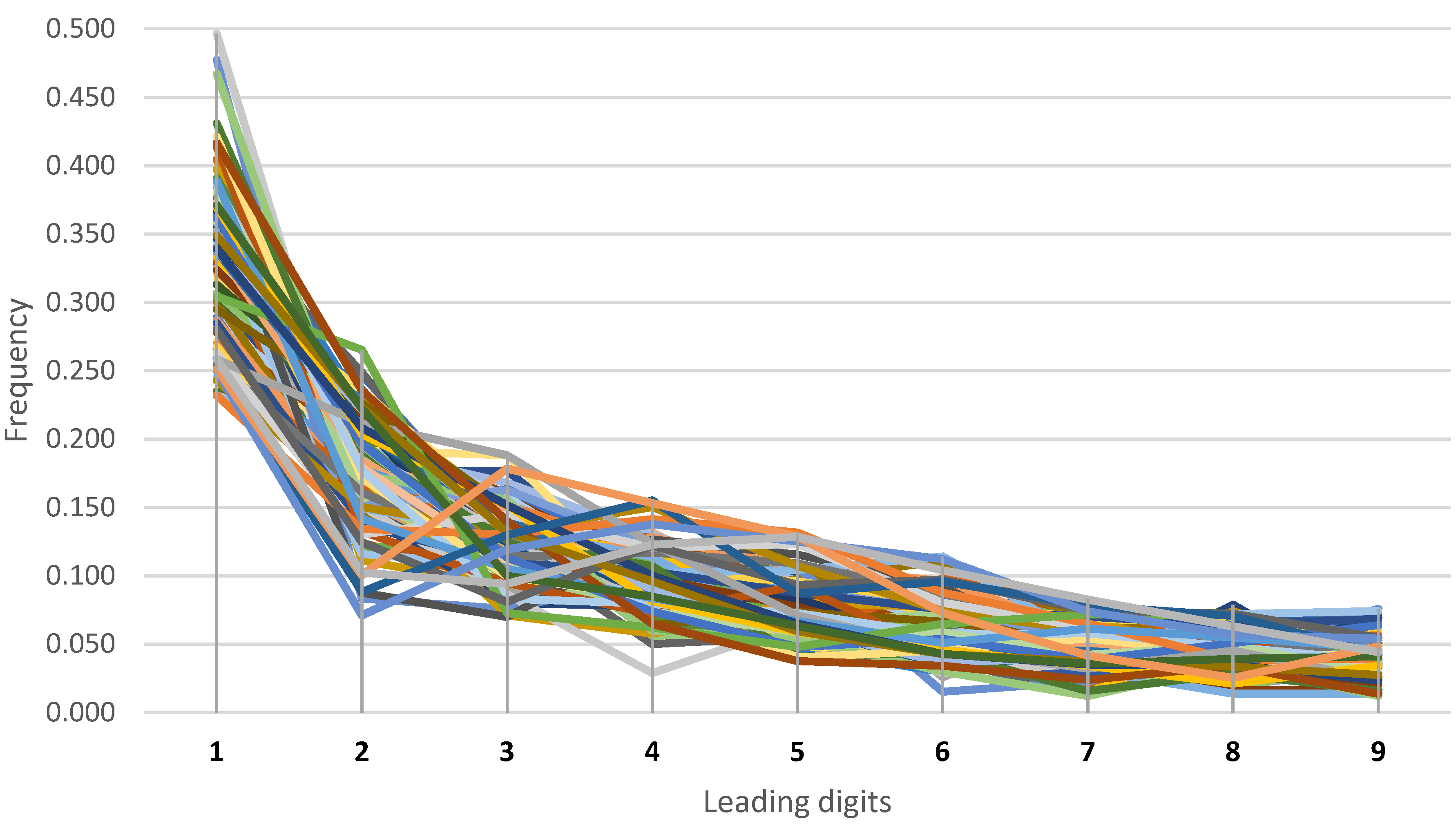
3. Results
4. Conclusions
5. Future Research
6. Limitation
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Health Organization. Coronavirus Disease (COVID-19) Outbreak; WHO: Geneva, Switzerland, 2020; Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019 (accessed on 13 June 2021).
- Farhadi, N. Can we rely on Covid-19 data? An assessment of data from over 200 countries. Sci. Prog. 2021, 104, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Castorina, P.; Iorio, A.; Lanteri, D. Data Analysis on Coronavirus Spreading by Macroscopic Growth Laws. Cornell University, 2020. Available online: https://arxiv.org/abs/2003.00507v3 (accessed on 13 June 2021).
- Koch, C.; Okamura, K. Benford’s Law and COVID-19 Reporting. 2020. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3586413 (accessed on 13 June 2021).
- Idrovo, A.J.; Manrique-Hernandez, E.F. Data Quality of Chinese Surveillance of 270 COVID-19: Objective Analysis Based on WHO’s Situation Reports. Asia Pac. J. Public Health 2020, 32, 165–167. [Google Scholar] [CrossRef] [PubMed]
- Sambridge, M.; Jackson, A. National COVID Numbers—Benford’s Law Looks for Errors. Nature 2020. Available online: https://0-www-nature-com.brum.beds.ac.uk/articles/d41586-020-01565-5 (accessed on 13 June 2021).
- Wie, A.; Vellwock, A.E. Is COVID-19 Data Reliable? A Statistical Analysis with Benford’s Law. 2020. Available online: https://www.researchgate.net/publication/344164702_Is_COVID-19_data_reliable_A_statistical_analysis_with_Benford%27s_Law (accessed on 13 June 2021).
- Lee, K.-B.; Han, S.; Jeong, Y. COVID-19 flattening the curve, and Benford’s law. Phys. A 2020. [Google Scholar] [CrossRef]
- Isea, R. How valid are the Reported Cases of People Infected with Covid-19 in the World? Int. J. Coronaviruses 2020, 1, 53–56. [Google Scholar] [CrossRef]
- Newcomb, S. Note on the Frequency of Use of the Different Digits in Natural 242 Numbers. Am. J. Math. 1881, 4, 39–40. [Google Scholar] [CrossRef] [Green Version]
- Benford, F. The Law of Anomalous Numbers. Proc. Am. Philos. Soc. 1938, 78, 551–572. [Google Scholar]
- Durtschi, C.; Hillison, W.; Pacini, C. The Effective Use of Benford’s law to assist in Detecting Fraud in Accounting Data. JFAR 2004, 5, 17–34. [Google Scholar]
- Grammatikos, T.; Papanikolaou, N.I. Applying Benford’s law to Detect Accounting 250 Data Manipulation in the Banking Industry. J. Financ. Serv. Res. 2021, 59, 115–142. [Google Scholar] [CrossRef]
- Cho, T.W.; Gaines, B.J. Breaking the (Benford) Law: Statistical Fraud Detection in Campaign Finance. Am. Stat. 2007, 61, 218–223. [Google Scholar]
- Roukema, B.F. A first-digit anomaly in the 2009 Iranian presidential election. J. Appl. Stat. 2014, 41, 164–199. [Google Scholar] [CrossRef] [Green Version]
- Furlan, L.V. Das Harmoniegesetz der Statistik: Eine Untersuchung uber die Metrische Interdependenz der Sozialen Erscheinungen. Verlag fur Recht und Gesellschaft; Verlag fur Recht und Gesellschaft: Basel, Switzerland, 1948. [Google Scholar]
- Simard, R.; L’Ecuyer, P. Computing the Two-Sided Kolmogorov–Smirnov Distribution. J. Stat. Softw. 2011, 39, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Bushee, B. Benford’s Law. Wharton University, 2018. Available online: https://www.coursera.org/lecture/accounting-analytics/benfords-Law-3-6-oPSSY (accessed on 13 June 2021).
- Goodman, Q. The promises and pitfalls of Benford’s law. Significance 2016, 13, 38–41. [Google Scholar] [CrossRef]
- Nigrini, M.J. Benford’s Law Applications for Forensic Accounting, Auditing and Fraud Detection; Wiley Corporate, F&A: Hoboken, NJ, USA, 2012. [Google Scholar]
- Slepkov, A.D.; Ironside, K.B.; DiBattista, D. Benford’s Law: Textbook Exercises and Multiple-Choice Testbanks. PLoS ONE 2019, 10, e0117972. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kossovsky, A.E. Benford’s Law: Theory, the General Law of Relative Quantities, and Forensic Fraud Detection Applications; World Scientific: Singapore, 2014. [Google Scholar]
- Dong, E.; Du, H.; Gardner, L. An interactive web-based dashboard to track COVID-19 in real time. Lancet 2020, 20, 533–534. Available online: https://www.thelancet.com/journals/laninf/article/PIIS1473-3099(20)30120-1/fulltext (accessed on 12 July 2021). [CrossRef]
- Johns Hopkins University. Global Health Security Index. 2019. Available online: https://www.ghsindex.org/ (accessed on 13 June 2021).
- Putz, C. If Only It Were That Easy: Tajikistan Declares Itself COVID-19 Free. The Diplomat. 2021. Available online: https://thediplomat.com/2021/01/if-only-it-were-that-easy-tajikistan-declares-itself-covid-19-free (accessed on 13 June 2021).
- Vector, D. What’s Happening in Belarus? Here Are the Basics. New York Times. 2021. Available online: https://www.nytimes.com/2021/05/26/world/europe/whats-happening-in-belarus.html (accessed on 13 June 2021).
- Cuddy, A. Myanmar Coup: What Is Happening and Why? BBC News. 2021. Available online: https://www.bbc.com/news/world-asia-55902070 (accessed on 13 June 2021).
- Deutsche Welle. Why Bangladeshis No Longer Fear the Coronavirus. 2021. Available online: https://www.dw.com/en/bangladesh-coronavirus-no-fear/a-55091050 (accessed on 13 June 2021).
- Yackley, A.J. Dollar Blow for Turkey as Tourism Season Runs into the Sand. Financial Times. 2021. Available online: https://www.ft.com/content/f7f4f65f-400d-437d-9ffa-e50fec485942 (accessed on 13 June 2021).
- Associate Press. El Salvador’s President Wants Bitcoin as Legal Tender. 2021. Available online: https://apnews.com/article/donald-trump-el-salvador-health-coronavirus-pandemic-technology-b1c08cae170aede89ea5cb41d97048cd (accessed on 13 June 2021).
- Farge, E. WHO to Start Coronavirus Testing in Rebel Syria; Iran Raises Efforts, Official Says. Available online: https://web.archive.org/web/20200316212446if_/https://www.reuters.com/article/us-health-coronavirus-mideast/who-to-start-coronavirus-testing-in-rebel-syria-iran-raises-efforts-official-says-idUSKBN2133PK (accessed on 13 June 2021).
- Alberti, T.; Faranda, D. On the uncertainty of real-time predictions of epidemic growths: A COVID-19 case study for China and Italy. Commun. Nonlinear Sci. Numer. Simul. 2020, 90, 105372. [Google Scholar] [CrossRef] [PubMed]
- Balsari, S.; Buckee, C.; Khanna, T. Which COVID-19 Data Can You Trust? Harvard Business Review. 2020. Available online: https://hbr.org/2020/05/which-COVID-19-data-can-you-trust (accessed on 13 June 2021).



| Researcher | Variables | Deadline | Number of Countries |
|---|---|---|---|
| Idrovo and Manrique-Hernández | Confirmed cases, suspected cases, and deaths, cumulated confirmed cases and deaths | 21 January 2020–15 March 2020 | 1 |
| Koch and Okamura | Confirmed cases, deaths, and recoveries | 20 January 2020–10 April 2020 | 3 |
| Lee, Han, and Jeong | Number of deaths | 22 January 2020–6 April 2020 | 10 |
| Jackson and Sambridge | Cumulated confirmed cases and deaths | 16 January 2020–9 April 2020 | 51 |
| Isea | Daily cases and deaths | 29 December 2019–30 April 2020 | 23 |
| Wei and Vellwock | Total confirmed cases, daily cases and deaths | not stated–1 September 2020 | 20 |
| Farhadi | Daily cases, deaths, tests | 31 December 2019–24 September 2020 | 154 |
| First Digit | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Benford’s frequency | 0.301 | 0.176 | 0.125 | 0.097 | 0.079 | 0.067 | 0.058 | 0.051 | 0.046 |
| Location | Improve | Flag | N | GHSI Score | GHSI Rank | d* | Chi Square | p-Value | K-S | Cut-Off | SSD | MAD | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Comoros | + | G | 243 | 27 | 160 | 0.041 | 0.671 | 0.715 | 0.029 | 0.087 | 17.693 | 0.012 | 0.292 | 0.181 | 0.128 | 0.128 | 0.066 | 0.074 | 0.045 | 0.058 | 0.029 |
| United Kingdom | + | G | 1358 | 78 | 2 | 0.022 | 0.269 | 0.874 | 0.015 | 0.037 | 5.308 | 0.006 | 0.295 | 0.178 | 0.122 | 0.094 | 0.088 | 0.082 | 0.059 | 0.039 | 0.043 |
| Australia | + | G | 878 | 76 | 4 | 0.025 | 0.143 | 0.931 | 0.021 | 0.046 | 6.566 | 0.006 | 0.302 | 0.154 | 0.129 | 0.101 | 0.088 | 0.069 | 0.055 | 0.057 | 0.046 |
| Cameroon | + | G | 247 | 34 | 115 | 0.048 | 0.580 | 0.748 | 0.042 | 0.087 | 24.721 | 0.013 | 0.304 | 0.202 | 0.134 | 0.101 | 0.057 | 0.081 | 0.053 | 0.020 | 0.049 |
| Cape Verde | + | G | 883 | 75 | 5 | 0.035 | 1.062 | 0.588 | 0.024 | 0.046 | 12.976 | 0.011 | 0.294 | 0.159 | 0.143 | 0.106 | 0.086 | 0.061 | 0.074 | 0.044 | 0.033 |
| Spain | + | G | 690 | 66 | 15 | 0.026 | 0.676 | 0.713 | 0.028 | 0.052 | 7.074 | 0.007 | 0.287 | 0.162 | 0.130 | 0.101 | 0.090 | 0.062 | 0.070 | 0.051 | 0.046 |
| Slovenia | + | G | 1231 | 67 | 12 | 0.040 | 4.459 | 0.108 | 0.025 | 0.039 | 17.484 | 0.012 | 0.315 | 0.154 | 0.118 | 0.118 | 0.098 | 0.058 | 0.055 | 0.041 | 0.042 |
| Israel | + | G | 1335 | 47 | 54 | 0.028 | 3.830 | 0.147 | 0.026 | 0.037 | 8.642 | 0.008 | 0.291 | 0.160 | 0.137 | 0.092 | 0.076 | 0.064 | 0.072 | 0.062 | 0.046 |
| Ecuador | - | G | 1284 | 50 | 45 | 0.032 | 4.380 | 0.112 | 0.027 | 0.038 | 11.222 | 0.008 | 0.275 | 0.179 | 0.121 | 0.113 | 0.087 | 0.072 | 0.055 | 0.046 | 0.052 |
| Portugal | + | G | 1343 | 60 | 20 | 0.042 | 8.880 | 0.012 | 0.027 | 0.037 | 19.040 | 0.012 | 0.276 | 0.175 | 0.149 | 0.114 | 0.080 | 0.079 | 0.051 | 0.042 | 0.035 |
| Lithuania | + | G | 1190 | 55 | 33 | 0.042 | 5.817 | 0.055 | 0.030 | 0.039 | 19.319 | 0.013 | 0.331 | 0.160 | 0.114 | 0.085 | 0.088 | 0.057 | 0.050 | 0.066 | 0.049 |
| Albania | + | G | 1281 | 53 | 39 | 0.040 | 0.495 | 0.781 | 0.030 | 0.038 | 16.956 | 0.012 | 0.305 | 0.183 | 0.144 | 0.085 | 0.069 | 0.068 | 0.037 | 0.073 | 0.037 |
| Bolivia | - | G | 1267 | 36 | 102 | 0.048 | 12.762 | 0.002 | 0.031 | 0.038 | 24.243 | 0.012 | 0.332 | 0.169 | 0.109 | 0.072 | 0.077 | 0.088 | 0.052 | 0.054 | 0.047 |
| Thailand | + | G | 1028 | 73 | 6 | 0.043 | 9.379 | 0.009 | 0.035 | 0.042 | 20.066 | 0.013 | 0.296 | 0.159 | 0.151 | 0.116 | 0.092 | 0.059 | 0.057 | 0.043 | 0.027 |
| Madagascar | - | G | 625 | 40 | 86 | 0.051 | 1.762 | 0.414 | 0.045 | 0.054 | 28.185 | 0.014 | 0.277 | 0.157 | 0.123 | 0.126 | 0.085 | 0.093 | 0.059 | 0.051 | 0.029 |
| Malawi | - | G | 739 | 28 | 154 | 0.041 | 7.871 | 0.020 | 0.042 | 0.050 | 17.702 | 0.012 | 0.326 | 0.164 | 0.126 | 0.114 | 0.091 | 0.050 | 0.057 | 0.039 | 0.034 |
| Kenya | - | G | 999 | 47 | 55 | 0.036 | 4.676 | 0.097 | 0.037 | 0.043 | 13.686 | 0.011 | 0.323 | 0.166 | 0.135 | 0.111 | 0.068 | 0.071 | 0.050 | 0.044 | 0.031 |
| Indonesia | - | G | 1242 | 57 | 30 | 0.050 | 6.403 | 0.041 | 0.033 | 0.039 | 27.089 | 0.013 | 0.299 | 0.145 | 0.137 | 0.130 | 0.094 | 0.063 | 0.046 | 0.049 | 0.037 |
| Democratic Rep. of Congo | - | G | 992 | 52 | 42 | 0.039 | 8.025 | 0.018 | 0.038 | 0.043 | 16.050 | 0.011 | 0.292 | 0.177 | 0.151 | 0.116 | 0.073 | 0.069 | 0.048 | 0.033 | 0.040 |
| Georgia | - | G | 740 | 52 | 42 | 0.055 | 9.347 | 0.009 | 0.044 | 0.050 | 32.725 | 0.014 | 0.335 | 0.159 | 0.151 | 0.093 | 0.082 | 0.036 | 0.045 | 0.050 | 0.047 |
| Afghanistan | - | G | 814 | 32 | 130 | 0.042 | 3.843 | 0.146 | 0.044 | 0.048 | 19.157 | 0.012 | 0.322 | 0.199 | 0.107 | 0.098 | 0.079 | 0.071 | 0.061 | 0.034 | 0.028 |
| Serbia | + | G | 1318 | 52 | 41 | 0.051 | 9.552 | 0.008 | 0.035 | 0.037 | 27.600 | 0.013 | 0.336 | 0.150 | 0.132 | 0.071 | 0.085 | 0.066 | 0.062 | 0.044 | 0.053 |
| Singapore | - | G | 516 | 59 | 24 | 0.040 | 6.294 | 0.043 | 0.057 | 0.060 | 17.148 | 0.013 | 0.324 | 0.188 | 0.136 | 0.109 | 0.068 | 0.047 | 0.054 | 0.037 | 0.039 |
| Norway | + | G | 1066 | 65 | 16 | 0.042 | 9.673 | 0.008 | 0.040 | 0.042 | 18.949 | 0.011 | 0.336 | 0.181 | 0.117 | 0.103 | 0.074 | 0.068 | 0.044 | 0.033 | 0.043 |
| Germany | - | G | 911 | 66 | 14 | 0.040 | 1.897 | 0.387 | 0.043 | 0.045 | 16.883 | 0.010 | 0.310 | 0.211 | 0.115 | 0.092 | 0.069 | 0.069 | 0.046 | 0.045 | 0.043 |
| Slovakia | + | G | 1150 | 48 | 52 | 0.043 | 2.459 | 0.292 | 0.039 | 0.040 | 19.395 | 0.013 | 0.315 | 0.201 | 0.117 | 0.078 | 0.058 | 0.060 | 0.072 | 0.056 | 0.043 |
| Ukraine | + | G | 1178 | 38 | 94 | 0.045 | 6.767 | 0.034 | 0.038 | 0.040 | 21.283 | 0.013 | 0.326 | 0.189 | 0.104 | 0.112 | 0.076 | 0.047 | 0.044 | 0.052 | 0.051 |
| Luxembourg | - | R | 1027 | 44 | 67 | 0.115 | 100.876 | 0.000 | 0.083 | 0.042 | 142.875 | 0.034 | 0.373 | 0.119 | 0.071 | 0.069 | 0.063 | 0.094 | 0.067 | 0.072 | 0.071 |
| Sao Tome and Principe | - | R | 279 | 31 | 139 | 0.170 | 47.748 | 0.000 | 0.175 | 0.081 | 308.597 | 0.039 | 0.459 | 0.194 | 0.118 | 0.093 | 0.054 | 0.029 | 0.025 | 0.011 | 0.018 |
| Pakistan | - | R | 1286 | 36 | 105 | 0.107 | 86.303 | 0.000 | 0.083 | 0.038 | 122.535 | 0.029 | 0.218 | 0.200 | 0.167 | 0.140 | 0.099 | 0.067 | 0.048 | 0.035 | 0.026 |
| Qatar | + | R | 1114 | 41 | 82 | 0.145 | 140.096 | 0.000 | 0.091 | 0.041 | 226.746 | 0.039 | 0.210 | 0.208 | 0.131 | 0.195 | 0.119 | 0.060 | 0.031 | 0.022 | 0.023 |
| Maldives | - | R | 936 | 34 | 121 | 0.112 | 49.834 | 0.000 | 0.101 | 0.044 | 135.825 | 0.027 | 0.402 | 0.136 | 0.144 | 0.096 | 0.060 | 0.046 | 0.041 | 0.033 | 0.043 |
| Russia | - | R | 1297 | 44 | 63 | 0.115 | 73.142 | 0.000 | 0.087 | 0.038 | 140.934 | 0.031 | 0.214 | 0.184 | 0.180 | 0.111 | 0.118 | 0.045 | 0.029 | 0.073 | 0.046 |
| Iraq | - | R | 1231 | 26 | 167 | 0.123 | 66.979 | 0.000 | 0.089 | 0.039 | 161.702 | 0.029 | 0.212 | 0.180 | 0.188 | 0.158 | 0.062 | 0.062 | 0.056 | 0.050 | 0.032 |
| Latvia | + | R | 1154 | 63 | 17 | 0.102 | 50.915 | 0.000 | 0.092 | 0.040 | 110.782 | 0.022 | 0.393 | 0.134 | 0.106 | 0.084 | 0.067 | 0.074 | 0.056 | 0.045 | 0.041 |
| Burkina Faso | - | R | 464 | 30 | 145 | 0.150 | 55.086 | 0.000 | 0.157 | 0.063 | 242.833 | 0.035 | 0.442 | 0.190 | 0.127 | 0.067 | 0.058 | 0.034 | 0.041 | 0.024 | 0.017 |
| Chad | - | R | 468 | 29 | 150 | 0.152 | 50.635 | 0.000 | 0.162 | 0.063 | 248.236 | 0.036 | 0.444 | 0.194 | 0.105 | 0.073 | 0.047 | 0.051 | 0.038 | 0.026 | 0.021 |
| Namibia | - | R | 951 | 36 | 104 | 0.123 | 60.390 | 0.000 | 0.118 | 0.044 | 161.190 | 0.027 | 0.416 | 0.179 | 0.091 | 0.069 | 0.064 | 0.055 | 0.044 | 0.033 | 0.048 |
| Liechtenstein | - | R | 686 | 44 | 71 | 0.117 | 41.237 | 0.000 | 0.140 | 0.052 | 145.983 | 0.031 | 0.398 | 0.219 | 0.117 | 0.082 | 0.042 | 0.041 | 0.035 | 0.031 | 0.036 |
| Sweden | - | R | 919 | 72 | 7 | 0.144 | 55.668 | 0.000 | 0.122 | 0.045 | 224.055 | 0.036 | 0.194 | 0.161 | 0.193 | 0.169 | 0.058 | 0.058 | 0.077 | 0.052 | 0.039 |
| Netherlands | - | R | 889 | 76 | 3 | 0.100 | 45.611 | 0.000 | 0.130 | 0.046 | 107.664 | 0.030 | 0.244 | 0.130 | 0.098 | 0.112 | 0.101 | 0.109 | 0.067 | 0.097 | 0.040 |
| Mozambique | - | R | 1046 | 28 | 153 | 0.134 | 83.369 | 0.000 | 0.121 | 0.042 | 192.475 | 0.029 | 0.422 | 0.161 | 0.073 | 0.061 | 0.060 | 0.060 | 0.057 | 0.054 | 0.052 |
| Tajikistan | - | R | 301 | 32 | 130 | 0.306 | 54.806 | 0.000 | 0.228 | 0.078 | 1007.938 | 0.082 | 0.203 | 0.047 | 0.282 | 0.309 | 0.050 | 0.050 | 0.013 | 0.037 | 0.010 |
| Uganda | - | R | 819 | 44 | 63 | 0.115 | 41.974 | 0.000 | 0.140 | 0.048 | 142.794 | 0.031 | 0.330 | 0.275 | 0.138 | 0.083 | 0.046 | 0.039 | 0.031 | 0.029 | 0.029 |
| Costa Rica | - | R | 1081 | 45 | 62 | 0.101 | 40.234 | 0.000 | 0.126 | 0.041 | 109.721 | 0.028 | 0.378 | 0.225 | 0.105 | 0.080 | 0.051 | 0.040 | 0.045 | 0.041 | 0.035 |
| Turkey | - | R | 1325 | 52 | 40 | 0.122 | 76.199 | 0.000 | 0.118 | 0.037 | 159.610 | 0.030 | 0.411 | 0.185 | 0.091 | 0.068 | 0.050 | 0.053 | 0.052 | 0.028 | 0.063 |
| El Salvador | - | R | 1155 | 44 | 65 | 0.226 | 72.338 | 0.000 | 0.132 | 0.040 | 546.613 | 0.047 | 0.223 | 0.385 | 0.072 | 0.093 | 0.052 | 0.037 | 0.039 | 0.049 | 0.049 |
| Belarus | - | R | 916 | 35 | 108 | 0.205 | 179.177 | 0.000 | 0.152 | 0.045 | 449.259 | 0.053 | 0.378 | 0.035 | 0.052 | 0.082 | 0.096 | 0.070 | 0.047 | 0.084 | 0.156 |
| Senegal | - | R | 1219 | 38 | 95 | 0.153 | 128.220 | 0.000 | 0.138 | 0.039 | 252.393 | 0.037 | 0.439 | 0.156 | 0.078 | 0.060 | 0.042 | 0.053 | 0.048 | 0.057 | 0.068 |
| Malta | - | R | 1081 | 37 | 98 | 0.122 | 54.984 | 0.000 | 0.161 | 0.041 | 159.349 | 0.036 | 0.345 | 0.268 | 0.150 | 0.062 | 0.046 | 0.039 | 0.025 | 0.026 | 0.039 |
| Kuwait | - | R | 1236 | 46 | 59 | 0.126 | 102.810 | 0.000 | 0.164 | 0.039 | 169.644 | 0.037 | 0.207 | 0.120 | 0.111 | 0.131 | 0.100 | 0.090 | 0.091 | 0.087 | 0.064 |
| Myanmar | - | R | 897 | 43 | 72 | 0.193 | 141.797 | 0.000 | 0.212 | 0.045 | 399.077 | 0.047 | 0.478 | 0.211 | 0.089 | 0.055 | 0.038 | 0.028 | 0.039 | 0.030 | 0.032 |
| Bangladesh | - | R | 1332 | 35 | 113 | 0.160 | 177.155 | 0.000 | 0.177 | 0.037 | 274.090 | 0.039 | 0.446 | 0.175 | 0.158 | 0.065 | 0.052 | 0.030 | 0.029 | 0.022 | 0.025 |
| Burundi | + | Y | 255 | 23 | 177 | 0.084 | 5.900 | 0.052 | 0.042 | 0.085 | 75.552 | 0.020 | 0.259 | 0.247 | 0.129 | 0.102 | 0.075 | 0.075 | 0.039 | 0.039 | 0.035 |
| Tunisia | + | Y | 741 | 34 | 122 | 0.049 | 1.681 | 0.432 | 0.028 | 0.050 | 25.807 | 0.016 | 0.321 | 0.150 | 0.108 | 0.101 | 0.097 | 0.084 | 0.070 | 0.040 | 0.028 |
| Equatorial Guinea | + | Y | 155 | 16 | 195 | 0.081 | 5.403 | 0.067 | 0.074 | 0.109 | 71.277 | 0.023 | 0.355 | 0.161 | 0.129 | 0.097 | 0.110 | 0.026 | 0.071 | 0.019 | 0.032 |
| Benin | - | Y | 168 | 29 | 150 | 0.061 | 3.663 | 0.160 | 0.075 | 0.105 | 39.345 | 0.019 | 0.321 | 0.190 | 0.149 | 0.113 | 0.065 | 0.077 | 0.018 | 0.042 | 0.024 |
| Ghana | - | Y | 793 | 36 | 105 | 0.055 | 10.155 | 0.006 | 0.035 | 0.048 | 32.314 | 0.015 | 0.266 | 0.208 | 0.142 | 0.116 | 0.067 | 0.055 | 0.055 | 0.048 | 0.042 |
| Somalia | - | Y | 331 | 17 | 194 | 0.062 | 3.019 | 0.221 | 0.055 | 0.075 | 40.701 | 0.018 | 0.341 | 0.190 | 0.097 | 0.073 | 0.076 | 0.054 | 0.054 | 0.076 | 0.039 |
| Lesotho | - | Y | 241 | 30 | 144 | 0.088 | 5.570 | 0.062 | 0.066 | 0.088 | 83.903 | 0.026 | 0.365 | 0.158 | 0.145 | 0.071 | 0.083 | 0.058 | 0.025 | 0.079 | 0.017 |
| Malaysia | + | Y | 1195 | 62 | 18 | 0.052 | 8.787 | 0.012 | 0.030 | 0.039 | 29.398 | 0.015 | 0.328 | 0.142 | 0.107 | 0.091 | 0.094 | 0.081 | 0.057 | 0.064 | 0.035 |
| Botswana | + | Y | 180 | 31 | 139 | 0.080 | 3.316 | 0.191 | 0.079 | 0.101 | 68.924 | 0.019 | 0.361 | 0.194 | 0.122 | 0.050 | 0.056 | 0.067 | 0.061 | 0.039 | 0.050 |
| Oman | - | Y | 695 | 43 | 73 | 0.063 | 8.769 | 0.012 | 0.044 | 0.052 | 43.012 | 0.018 | 0.345 | 0.153 | 0.135 | 0.065 | 0.072 | 0.059 | 0.047 | 0.059 | 0.065 |
| Papua New Guinea | - | Y | 212 | 28 | 155 | 0.093 | 7.982 | 0.018 | 0.081 | 0.093 | 92.590 | 0.024 | 0.382 | 0.156 | 0.118 | 0.085 | 0.094 | 0.033 | 0.038 | 0.061 | 0.033 |
| Kosovo | + | Y | 613 | 19 | 189 | 0.073 | 15.973 | 0.000 | 0.048 | 0.055 | 57.386 | 0.020 | 0.349 | 0.148 | 0.085 | 0.075 | 0.088 | 0.070 | 0.069 | 0.070 | 0.046 |
| Greece | + | Y | 1233 | 54 | 37 | 0.059 | 18.225 | 0.000 | 0.036 | 0.039 | 37.519 | 0.016 | 0.265 | 0.211 | 0.142 | 0.084 | 0.101 | 0.066 | 0.058 | 0.042 | 0.032 |
| Belize | + | Y | 395 | 32 | 135 | 0.065 | 6.175 | 0.046 | 0.064 | 0.068 | 45.385 | 0.016 | 0.354 | 0.182 | 0.129 | 0.068 | 0.078 | 0.056 | 0.068 | 0.035 | 0.028 |
| Central African Republic | - | Y | 211 | 27 | 159 | 0.104 | 7.976 | 0.019 | 0.088 | 0.094 | 117.203 | 0.027 | 0.389 | 0.152 | 0.085 | 0.128 | 0.066 | 0.071 | 0.047 | 0.033 | 0.028 |
| Nigeria | + | Y | 922 | 38 | 96 | 0.056 | 10.820 | 0.004 | 0.045 | 0.045 | 33.339 | 0.014 | 0.346 | 0.151 | 0.129 | 0.103 | 0.081 | 0.073 | 0.042 | 0.047 | 0.028 |
| Bulgaria | - | Y | 1194 | 46 | 61 | 0.048 | 9.217 | 0.010 | 0.040 | 0.039 | 24.370 | 0.012 | 0.341 | 0.153 | 0.121 | 0.108 | 0.072 | 0.059 | 0.049 | 0.052 | 0.044 |
| Bahamas | - | Y | 368 | 31 | 142 | 0.081 | 9.860 | 0.007 | 0.072 | 0.071 | 70.910 | 0.017 | 0.372 | 0.177 | 0.098 | 0.101 | 0.073 | 0.065 | 0.054 | 0.016 | 0.043 |
| Algeria | + | Y | 897 | 24 | 173 | 0.062 | 17.434 | 0.000 | 0.047 | 0.045 | 41.616 | 0.017 | 0.329 | 0.156 | 0.082 | 0.099 | 0.071 | 0.060 | 0.059 | 0.070 | 0.072 |
| Mauritius | - | Y | 188 | 35 | 114 | 0.116 | 9.613 | 0.008 | 0.103 | 0.099 | 145.528 | 0.029 | 0.404 | 0.154 | 0.133 | 0.069 | 0.059 | 0.043 | 0.021 | 0.059 | 0.059 |
| Eritrea | + | Y | 180 | 22 | 178 | 0.089 | 2.842 | 0.241 | 0.106 | 0.101 | 85.701 | 0.026 | 0.356 | 0.228 | 0.106 | 0.083 | 0.039 | 0.050 | 0.067 | 0.044 | 0.028 |
| St. Vincent & the Grenadines | - | Y | 162 | 34 | 117 | 0.135 | 11.659 | 0.003 | 0.113 | 0.107 | 194.677 | 0.033 | 0.414 | 0.111 | 0.093 | 0.080 | 0.074 | 0.080 | 0.037 | 0.074 | 0.037 |
| Jordan | - | Y | 904 | 42 | 80 | 0.069 | 2.339 | 0.311 | 0.048 | 0.045 | 50.371 | 0.016 | 0.289 | 0.237 | 0.100 | 0.104 | 0.062 | 0.071 | 0.044 | 0.051 | 0.043 |
| Kyrgyzstan | - | Y | 677 | 49 | 47 | 0.078 | 25.854 | 0.000 | 0.057 | 0.052 | 64.878 | 0.022 | 0.244 | 0.208 | 0.151 | 0.121 | 0.095 | 0.062 | 0.058 | 0.038 | 0.024 |
| Seychelles | + | Y | 173 | 32 | 133 | 0.096 | 8.408 | 0.015 | 0.115 | 0.103 | 99.877 | 0.026 | 0.382 | 0.208 | 0.127 | 0.087 | 0.052 | 0.046 | 0.046 | 0.023 | 0.029 |
| Andorra | + | Y | 394 | 31 | 143 | 0.057 | 12.815 | 0.002 | 0.078 | 0.069 | 34.776 | 0.017 | 0.325 | 0.185 | 0.135 | 0.132 | 0.076 | 0.056 | 0.033 | 0.033 | 0.025 |
| Yemen | + | Y | 548 | 19 | 190 | 0.057 | 6.733 | 0.035 | 0.066 | 0.058 | 35.325 | 0.015 | 0.349 | 0.193 | 0.126 | 0.086 | 0.055 | 0.058 | 0.049 | 0.047 | 0.036 |
| South Sudan | - | Y | 384 | 22 | 180 | 0.092 | 11.672 | 0.003 | 0.079 | 0.069 | 91.440 | 0.023 | 0.380 | 0.138 | 0.107 | 0.091 | 0.096 | 0.049 | 0.049 | 0.060 | 0.029 |
| Poland | + | Y | 1296 | 55 | 32 | 0.060 | 25.505 | 0.000 | 0.043 | 0.038 | 38.032 | 0.019 | 0.261 | 0.200 | 0.140 | 0.110 | 0.097 | 0.080 | 0.047 | 0.029 | 0.036 |
| Nepal | - | Y | 1170 | 35 | 111 | 0.056 | 11.773 | 0.003 | 0.046 | 0.040 | 33.148 | 0.014 | 0.347 | 0.148 | 0.118 | 0.103 | 0.078 | 0.055 | 0.051 | 0.061 | 0.040 |
| Zambia | + | Y | 1010 | 29 | 152 | 0.054 | 0.012 | 0.994 | 0.050 | 0.043 | 31.699 | 0.014 | 0.302 | 0.137 | 0.114 | 0.125 | 0.100 | 0.080 | 0.057 | 0.050 | 0.036 |
| Cambodia | + | Y | 300 | 39 | 89 | 0.075 | 13.945 | 0.001 | 0.092 | 0.079 | 60.309 | 0.025 | 0.280 | 0.200 | 0.160 | 0.117 | 0.097 | 0.083 | 0.030 | 0.017 | 0.017 |
| Ireland | - | Y | 1208 | 59 | 23 | 0.062 | 12.574 | 0.002 | 0.046 | 0.039 | 41.844 | 0.015 | 0.347 | 0.137 | 0.132 | 0.109 | 0.076 | 0.059 | 0.043 | 0.047 | 0.050 |
| Vietnam | + | Y | 452 | 49 | 50 | 0.081 | 12.304 | 0.002 | 0.075 | 0.064 | 70.418 | 0.019 | 0.376 | 0.155 | 0.131 | 0.086 | 0.062 | 0.058 | 0.049 | 0.033 | 0.051 |
| Brazil | - | Y | 888 | 60 | 22 | 0.051 | 8.189 | 0.017 | 0.055 | 0.046 | 28.303 | 0.014 | 0.262 | 0.160 | 0.127 | 0.098 | 0.100 | 0.083 | 0.075 | 0.054 | 0.039 |
| Djibouti | - | Y | 432 | 23 | 175 | 0.068 | 7.371 | 0.025 | 0.079 | 0.065 | 49.710 | 0.017 | 0.356 | 0.199 | 0.111 | 0.095 | 0.053 | 0.049 | 0.046 | 0.049 | 0.042 |
| Morocco | + | Y | 1308 | 44 | 68 | 0.049 | 6.044 | 0.049 | 0.045 | 0.038 | 26.028 | 0.011 | 0.300 | 0.222 | 0.116 | 0.096 | 0.070 | 0.050 | 0.060 | 0.046 | 0.041 |
| Congo | + | Y | 1145 | 27 | 160 | 0.038 | 12.849 | 0.002 | 0.049 | 0.040 | 15.226 | 0.011 | 0.304 | 0.182 | 0.152 | 0.110 | 0.072 | 0.063 | 0.045 | 0.034 | 0.038 |
| South Korea | + | Y | 1299 | 70 | 9 | 0.061 | 1.826 | 0.401 | 0.046 | 0.038 | 40.559 | 0.017 | 0.298 | 0.133 | 0.129 | 0.126 | 0.105 | 0.085 | 0.049 | 0.042 | 0.033 |
| Lebanon | - | Y | 807 | 43 | 73 | 0.057 | 14.883 | 0.001 | 0.058 | 0.048 | 34.396 | 0.014 | 0.346 | 0.188 | 0.125 | 0.090 | 0.079 | 0.074 | 0.045 | 0.029 | 0.024 |
| Sudan | - | Y | 847 | 26 | 163 | 0.061 | 13.935 | 0.001 | 0.058 | 0.047 | 40.087 | 0.014 | 0.359 | 0.165 | 0.115 | 0.084 | 0.083 | 0.058 | 0.048 | 0.051 | 0.038 |
| Paraguay | + | Y | 1228 | 36 | 103 | 0.058 | 3.315 | 0.191 | 0.049 | 0.039 | 36.169 | 0.017 | 0.314 | 0.196 | 0.140 | 0.056 | 0.059 | 0.092 | 0.052 | 0.052 | 0.038 |
| Azerbaijan | - | Y | 888 | 34 | 117 | 0.057 | 13.634 | 0.001 | 0.058 | 0.046 | 34.794 | 0.013 | 0.306 | 0.177 | 0.177 | 0.092 | 0.075 | 0.046 | 0.051 | 0.043 | 0.033 |
| Iceland | - | Y | 797 | 46 | 58 | 0.071 | 20.778 | 0.000 | 0.062 | 0.048 | 54.824 | 0.020 | 0.331 | 0.124 | 0.094 | 0.088 | 0.093 | 0.077 | 0.078 | 0.061 | 0.054 |
| Cuba | - | Y | 1117 | 35 | 110 | 0.061 | 11.846 | 0.003 | 0.052 | 0.041 | 40.132 | 0.018 | 0.346 | 0.184 | 0.098 | 0.089 | 0.063 | 0.045 | 0.073 | 0.064 | 0.039 |
| Angola | - | Y | 677 | 25 | 170 | 0.061 | 16.569 | 0.000 | 0.067 | 0.052 | 40.082 | 0.015 | 0.301 | 0.227 | 0.140 | 0.095 | 0.075 | 0.047 | 0.044 | 0.046 | 0.024 |
| Niger | - | Y | 423 | 32 | 132 | 0.078 | 13.168 | 0.001 | 0.086 | 0.066 | 65.329 | 0.019 | 0.371 | 0.191 | 0.106 | 0.092 | 0.073 | 0.057 | 0.040 | 0.028 | 0.040 |
| New Zealand | - | Y | 711 | 54 | 35 | 0.079 | 16.060 | 0.000 | 0.066 | 0.051 | 66.206 | 0.019 | 0.235 | 0.205 | 0.120 | 0.105 | 0.108 | 0.084 | 0.060 | 0.044 | 0.038 |
| Uzbekistan | - | Y | 655 | 34 | 116 | 0.095 | 31.531 | 0.000 | 0.069 | 0.053 | 96.707 | 0.027 | 0.232 | 0.192 | 0.168 | 0.130 | 0.096 | 0.078 | 0.058 | 0.027 | 0.018 |
| Monaco | - | Y | 335 | 33 | 125 | 0.084 | 13.777 | 0.001 | 0.097 | 0.074 | 75.835 | 0.021 | 0.373 | 0.197 | 0.128 | 0.084 | 0.069 | 0.039 | 0.033 | 0.045 | 0.033 |
| Peru | - | Y | 1216 | 49 | 49 | 0.062 | 19.499 | 0.000 | 0.051 | 0.039 | 40.612 | 0.014 | 0.352 | 0.142 | 0.112 | 0.095 | 0.070 | 0.068 | 0.061 | 0.058 | 0.043 |
| Philippines | - | Y | 1329 | 48 | 53 | 0.074 | 28.708 | 0.000 | 0.050 | 0.037 | 58.785 | 0.019 | 0.272 | 0.192 | 0.188 | 0.082 | 0.087 | 0.053 | 0.044 | 0.046 | 0.037 |
| Italy | - | Y | 1401 | 56 | 31 | 0.053 | 28.798 | 0.000 | 0.049 | 0.036 | 30.554 | 0.016 | 0.284 | 0.205 | 0.158 | 0.091 | 0.089 | 0.065 | 0.044 | 0.032 | 0.032 |
| Mali | + | Y | 641 | 29 | 147 | 0.069 | 17.817 | 0.000 | 0.072 | 0.054 | 50.585 | 0.016 | 0.360 | 0.189 | 0.125 | 0.094 | 0.070 | 0.039 | 0.058 | 0.034 | 0.031 |
| Colombia | + | Y | 1247 | 44 | 65 | 0.057 | 0.907 | 0.636 | 0.052 | 0.039 | 35.473 | 0.014 | 0.289 | 0.136 | 0.164 | 0.111 | 0.074 | 0.062 | 0.065 | 0.057 | 0.043 |
| Chile | + | Y | 1310 | 58 | 27 | 0.055 | 8.617 | 0.013 | 0.052 | 0.038 | 32.810 | 0.017 | 0.269 | 0.156 | 0.152 | 0.116 | 0.092 | 0.082 | 0.063 | 0.035 | 0.035 |
| United States | - | Y | 1389 | 84 | 1 | 0.070 | 38.599 | 0.000 | 0.050 | 0.036 | 52.595 | 0.019 | 0.351 | 0.150 | 0.088 | 0.084 | 0.071 | 0.082 | 0.065 | 0.048 | 0.060 |
| Rwanda | - | Y | 917 | 34 | 117 | 0.048 | 14.015 | 0.001 | 0.062 | 0.045 | 25.234 | 0.014 | 0.334 | 0.178 | 0.133 | 0.117 | 0.067 | 0.051 | 0.058 | 0.031 | 0.033 |
| Croatia | - | Y | 1216 | 53 | 38 | 0.049 | 15.050 | 0.001 | 0.054 | 0.039 | 26.076 | 0.013 | 0.260 | 0.182 | 0.121 | 0.082 | 0.095 | 0.076 | 0.064 | 0.065 | 0.055 |
| Canada | - | Y | 1373 | 75 | 5 | 0.062 | 24.887 | 0.000 | 0.052 | 0.037 | 41.817 | 0.015 | 0.307 | 0.121 | 0.122 | 0.111 | 0.067 | 0.090 | 0.066 | 0.059 | 0.058 |
| Togo | - | Y | 951 | 33 | 129 | 0.086 | 37.973 | 0.000 | 0.063 | 0.044 | 79.918 | 0.023 | 0.364 | 0.146 | 0.080 | 0.078 | 0.074 | 0.064 | 0.070 | 0.055 | 0.069 |
| Belgium | + | Y | 1341 | 61 | 19 | 0.052 | 35.970 | 0.000 | 0.053 | 0.037 | 29.543 | 0.017 | 0.278 | 0.195 | 0.139 | 0.128 | 0.092 | 0.059 | 0.042 | 0.040 | 0.028 |
| Guinea-Bissau | - | Y | 209 | 20 | 186 | 0.113 | 18.146 | 0.000 | 0.135 | 0.094 | 135.866 | 0.032 | 0.364 | 0.249 | 0.120 | 0.081 | 0.086 | 0.038 | 0.014 | 0.033 | 0.014 |
| Uruguay | - | Y | 1013 | 41 | 81 | 0.062 | 12.697 | 0.002 | 0.062 | 0.043 | 41.453 | 0.017 | 0.301 | 0.146 | 0.115 | 0.075 | 0.098 | 0.111 | 0.068 | 0.057 | 0.030 |
| Hong Kong | - | Y | 574 | 28 | 156 | 0.092 | 21.168 | 0.000 | 0.084 | 0.057 | 89.973 | 0.022 | 0.385 | 0.153 | 0.108 | 0.078 | 0.057 | 0.066 | 0.051 | 0.064 | 0.037 |
| Bosnia and Herzegovina | - | Y | 1030 | 43 | 79 | 0.050 | 21.187 | 0.000 | 0.063 | 0.042 | 26.605 | 0.014 | 0.305 | 0.208 | 0.152 | 0.089 | 0.081 | 0.051 | 0.042 | 0.038 | 0.034 |
| Nicaragua | - | Y | 132 | 43 | 73 | 0.211 | 19.536 | 0.000 | 0.176 | 0.118 | 476.672 | 0.052 | 0.477 | 0.083 | 0.076 | 0.098 | 0.106 | 0.015 | 0.023 | 0.045 | 0.076 |
| Mexico | + | Y | 1412 | 58 | 28 | 0.063 | 2.001 | 0.368 | 0.055 | 0.036 | 43.110 | 0.020 | 0.287 | 0.156 | 0.105 | 0.128 | 0.106 | 0.096 | 0.059 | 0.042 | 0.021 |
| Argentina | - | Y | 1369 | 59 | 25 | 0.046 | 13.457 | 0.001 | 0.056 | 0.037 | 23.115 | 0.013 | 0.307 | 0.213 | 0.137 | 0.099 | 0.063 | 0.047 | 0.053 | 0.046 | 0.036 |
| Bahrain | + | Y | 1115 | 39 | 88 | 0.070 | 22.249 | 0.000 | 0.063 | 0.041 | 53.038 | 0.017 | 0.364 | 0.157 | 0.120 | 0.078 | 0.066 | 0.062 | 0.055 | 0.038 | 0.060 |
| San Marino | + | Y | 290 | 31 | 139 | 0.100 | 19.638 | 0.000 | 0.125 | 0.080 | 106.677 | 0.028 | 0.379 | 0.197 | 0.134 | 0.114 | 0.055 | 0.062 | 0.031 | 0.014 | 0.014 |
| Romania | + | Y | 1251 | 46 | 60 | 0.054 | 5.123 | 0.077 | 0.061 | 0.038 | 31.636 | 0.014 | 0.306 | 0.220 | 0.137 | 0.089 | 0.053 | 0.070 | 0.043 | 0.044 | 0.039 |
| Liberia | - | Y | 281 | 35 | 111 | 0.135 | 26.918 | 0.000 | 0.130 | 0.081 | 195.629 | 0.029 | 0.431 | 0.171 | 0.125 | 0.078 | 0.064 | 0.043 | 0.028 | 0.028 | 0.032 |
| Guatemala | - | Y | 1295 | 33 | 125 | 0.061 | 29.478 | 0.000 | 0.061 | 0.038 | 40.320 | 0.017 | 0.261 | 0.165 | 0.141 | 0.097 | 0.053 | 0.098 | 0.076 | 0.052 | 0.056 |
| Guinea | - | Y | 1044 | 33 | 125 | 0.072 | 30.669 | 0.000 | 0.068 | 0.042 | 55.286 | 0.016 | 0.369 | 0.171 | 0.117 | 0.093 | 0.083 | 0.051 | 0.042 | 0.043 | 0.031 |
| Suriname | - | Y | 521 | 37 | 100 | 0.115 | 25.926 | 0.000 | 0.096 | 0.060 | 142.452 | 0.026 | 0.397 | 0.173 | 0.071 | 0.058 | 0.081 | 0.077 | 0.069 | 0.036 | 0.038 |
| Saint Lucia | - | Y | 236 | 34 | 117 | 0.115 | 13.386 | 0.001 | 0.144 | 0.089 | 143.057 | 0.032 | 0.390 | 0.225 | 0.131 | 0.068 | 0.047 | 0.030 | 0.047 | 0.038 | 0.025 |
| Sierra Leone | + | Y | 399 | 38 | 92 | 0.101 | 15.642 | 0.000 | 0.112 | 0.068 | 109.284 | 0.025 | 0.391 | 0.198 | 0.110 | 0.070 | 0.048 | 0.060 | 0.045 | 0.038 | 0.040 |
| Haiti | - | Y | 440 | 32 | 138 | 0.077 | 14.272 | 0.001 | 0.109 | 0.065 | 63.501 | 0.024 | 0.350 | 0.207 | 0.155 | 0.080 | 0.059 | 0.057 | 0.039 | 0.025 | 0.030 |
| South Africa | - | Y | 1307 | 55 | 34 | 0.051 | 9.914 | 0.007 | 0.064 | 0.038 | 27.618 | 0.014 | 0.323 | 0.208 | 0.135 | 0.094 | 0.054 | 0.047 | 0.049 | 0.050 | 0.040 |
| Timor | - | Y | 139 | 73 | 6 | 0.210 | 25.374 | 0.000 | 0.195 | 0.115 | 472.994 | 0.046 | 0.496 | 0.151 | 0.086 | 0.029 | 0.065 | 0.029 | 0.036 | 0.065 | 0.043 |
| Guyana | - | Y | 577 | 32 | 137 | 0.077 | 14.948 | 0.001 | 0.096 | 0.057 | 63.211 | 0.021 | 0.315 | 0.236 | 0.144 | 0.101 | 0.049 | 0.042 | 0.050 | 0.036 | 0.028 |
| India | + | Y | 1320 | 47 | 57 | 0.085 | 52.542 | 0.000 | 0.064 | 0.037 | 77.131 | 0.024 | 0.345 | 0.116 | 0.108 | 0.092 | 0.064 | 0.057 | 0.073 | 0.072 | 0.074 |
| Moldova | - | Y | 884 | 43 | 78 | 0.085 | 29.256 | 0.000 | 0.079 | 0.046 | 78.338 | 0.019 | 0.380 | 0.160 | 0.102 | 0.075 | 0.064 | 0.072 | 0.053 | 0.049 | 0.045 |
| Trinidad and Tobago | - | Y | 853 | 37 | 99 | 0.066 | 15.502 | 0.000 | 0.081 | 0.047 | 47.259 | 0.019 | 0.347 | 0.211 | 0.101 | 0.086 | 0.083 | 0.050 | 0.047 | 0.042 | 0.033 |
| Armenia | - | Y | 1063 | 50 | 44 | 0.059 | 32.450 | 0.000 | 0.074 | 0.042 | 37.683 | 0.017 | 0.324 | 0.217 | 0.134 | 0.099 | 0.077 | 0.049 | 0.050 | 0.030 | 0.021 |
| Egypt | + | Y | 901 | 40 | 87 | 0.139 | 30.916 | 0.000 | 0.081 | 0.045 | 206.061 | 0.038 | 0.382 | 0.088 | 0.070 | 0.127 | 0.115 | 0.092 | 0.039 | 0.048 | 0.040 |
| Austria | - | Y | 1265 | 59 | 26 | 0.066 | 8.700 | 0.013 | 0.068 | 0.038 | 47.003 | 0.017 | 0.295 | 0.226 | 0.149 | 0.064 | 0.074 | 0.066 | 0.053 | 0.047 | 0.026 |
| Bhutan | - | Y | 636 | 40 | 85 | 0.082 | 23.532 | 0.000 | 0.097 | 0.054 | 71.710 | 0.022 | 0.366 | 0.208 | 0.124 | 0.088 | 0.063 | 0.035 | 0.042 | 0.038 | 0.036 |
| Kazakhstan | + | Y | 1160 | 41 | 83 | 0.061 | 18.710 | 0.000 | 0.072 | 0.040 | 40.319 | 0.017 | 0.313 | 0.222 | 0.139 | 0.095 | 0.061 | 0.043 | 0.040 | 0.034 | 0.053 |
| Dominican Republic | - | Y | 1205 | 38 | 91 | 0.069 | 14.702 | 0.001 | 0.071 | 0.039 | 51.746 | 0.019 | 0.255 | 0.151 | 0.163 | 0.122 | 0.090 | 0.078 | 0.051 | 0.052 | 0.037 |
| Macedonia | - | Y | 1273 | 44 | 67 | 0.055 | 13.658 | 0.001 | 0.070 | 0.038 | 32.322 | 0.015 | 0.339 | 0.184 | 0.149 | 0.087 | 0.056 | 0.046 | 0.049 | 0.047 | 0.043 |
| Mauritania | - | Y | 621 | 28 | 157 | 0.089 | 26.356 | 0.000 | 0.100 | 0.055 | 85.478 | 0.022 | 0.382 | 0.192 | 0.129 | 0.077 | 0.066 | 0.052 | 0.034 | 0.040 | 0.029 |
| Libya | - | Y | 1032 | 26 | 168 | 0.061 | 13.766 | 0.001 | 0.078 | 0.042 | 40.384 | 0.017 | 0.267 | 0.132 | 0.135 | 0.103 | 0.096 | 0.080 | 0.069 | 0.065 | 0.053 |
| Jamaica | - | Y | 911 | 29 | 147 | 0.081 | 18.392 | 0.000 | 0.083 | 0.045 | 70.719 | 0.022 | 0.245 | 0.149 | 0.132 | 0.102 | 0.104 | 0.114 | 0.053 | 0.064 | 0.037 |
| Antigua and Barbuda | - | Y | 167 | 29 | 147 | 0.182 | 28.846 | 0.000 | 0.194 | 0.105 | 354.099 | 0.044 | 0.467 | 0.174 | 0.156 | 0.060 | 0.054 | 0.030 | 0.012 | 0.036 | 0.012 |
| Panama | - | Y | 1327 | 44 | 68 | 0.053 | 24.376 | 0.000 | 0.071 | 0.037 | 30.231 | 0.016 | 0.285 | 0.137 | 0.109 | 0.103 | 0.087 | 0.075 | 0.070 | 0.064 | 0.069 |
| Mongolia | - | Y | 528 | 50 | 46 | 0.127 | 32.670 | 0.000 | 0.114 | 0.059 | 172.786 | 0.030 | 0.415 | 0.133 | 0.095 | 0.072 | 0.093 | 0.044 | 0.061 | 0.055 | 0.034 |
| Japan | - | Y | 1403 | 60 | 21 | 0.062 | 13.994 | 0.001 | 0.071 | 0.036 | 40.952 | 0.017 | 0.256 | 0.161 | 0.114 | 0.117 | 0.109 | 0.086 | 0.063 | 0.045 | 0.050 |
| Palestine | - | Y | 1025 | 22 | 179 | 0.086 | 20.281 | 0.000 | 0.084 | 0.042 | 78.862 | 0.022 | 0.243 | 0.150 | 0.133 | 0.150 | 0.107 | 0.074 | 0.060 | 0.043 | 0.040 |
| Switzerland | - | Y | 1132 | 67 | 13 | 0.058 | 23.038 | 0.000 | 0.082 | 0.040 | 36.236 | 0.018 | 0.337 | 0.205 | 0.141 | 0.085 | 0.067 | 0.046 | 0.045 | 0.037 | 0.036 |
| Barbados | + | Y | 318 | 32 | 133 | 0.144 | 37.916 | 0.000 | 0.156 | 0.076 | 224.021 | 0.035 | 0.431 | 0.192 | 0.126 | 0.107 | 0.041 | 0.044 | 0.016 | 0.028 | 0.016 |
| Cote d’Ivoire | - | Y | 985 | 45 | 62 | 0.070 | 25.310 | 0.000 | 0.089 | 0.043 | 52.255 | 0.020 | 0.338 | 0.221 | 0.132 | 0.090 | 0.062 | 0.037 | 0.041 | 0.039 | 0.041 |
| Zimbabwe | - | Y | 1004 | 38 | 92 | 0.089 | 38.520 | 0.000 | 0.089 | 0.043 | 85.562 | 0.020 | 0.386 | 0.179 | 0.111 | 0.080 | 0.073 | 0.057 | 0.041 | 0.036 | 0.038 |
| Estonia | - | Y | 1145 | 57 | 29 | 0.080 | 9.786 | 0.007 | 0.084 | 0.040 | 69.405 | 0.023 | 0.263 | 0.130 | 0.145 | 0.121 | 0.123 | 0.080 | 0.062 | 0.046 | 0.030 |
| China | - | Y | 572 | 48 | 51 | 0.127 | 39.363 | 0.000 | 0.120 | 0.057 | 173.961 | 0.027 | 0.421 | 0.171 | 0.100 | 0.084 | 0.040 | 0.045 | 0.054 | 0.042 | 0.042 |
| Sri Lanka | + | Y | 1105 | 34 | 120 | 0.094 | 38.592 | 0.000 | 0.087 | 0.041 | 95.596 | 0.019 | 0.386 | 0.177 | 0.083 | 0.080 | 0.072 | 0.057 | 0.058 | 0.048 | 0.038 |
| Taiwan | + | Y | 853 | 20 | 188 | 0.089 | 27.857 | 0.000 | 0.100 | 0.047 | 85.408 | 0.022 | 0.381 | 0.196 | 0.113 | 0.074 | 0.059 | 0.059 | 0.042 | 0.049 | 0.028 |
| Hungary | - | Y | 1299 | 54 | 35 | 0.079 | 23.001 | 0.000 | 0.081 | 0.038 | 66.352 | 0.022 | 0.362 | 0.196 | 0.113 | 0.074 | 0.048 | 0.054 | 0.038 | 0.051 | 0.064 |
| Montenegro | - | Y | 707 | 44 | 68 | 0.105 | 16.849 | 0.000 | 0.111 | 0.051 | 119.439 | 0.029 | 0.232 | 0.134 | 0.130 | 0.141 | 0.132 | 0.088 | 0.065 | 0.038 | 0.040 |
| France | - | Y | 1281 | 68 | 11 | 0.094 | 76.522 | 0.000 | 0.082 | 0.038 | 94.449 | 0.028 | 0.258 | 0.212 | 0.188 | 0.123 | 0.071 | 0.046 | 0.032 | 0.045 | 0.024 |
| Gambia | - | Y | 614 | 34 | 117 | 0.091 | 30.900 | 0.000 | 0.123 | 0.055 | 88.921 | 0.027 | 0.370 | 0.204 | 0.151 | 0.081 | 0.059 | 0.046 | 0.034 | 0.021 | 0.034 |
| Denmark | - | Y | 1256 | 70 | 8 | 0.096 | 49.049 | 0.000 | 0.088 | 0.038 | 98.450 | 0.021 | 0.389 | 0.142 | 0.105 | 0.084 | 0.067 | 0.051 | 0.061 | 0.055 | 0.047 |
| Iran | + | Y | 1127 | 38 | 97 | 0.112 | 5.333 | 0.069 | 0.093 | 0.041 | 135.330 | 0.028 | 0.304 | 0.265 | 0.073 | 0.062 | 0.048 | 0.065 | 0.072 | 0.071 | 0.040 |
| Cyprus | - | Y | 1029 | 43 | 77 | 0.070 | 44.142 | 0.000 | 0.100 | 0.042 | 52.767 | 0.022 | 0.339 | 0.208 | 0.152 | 0.100 | 0.065 | 0.043 | 0.035 | 0.035 | 0.023 |
| Gabon | - | Y | 293 | 20 | 186 | 0.148 | 30.780 | 0.000 | 0.190 | 0.079 | 234.031 | 0.042 | 0.416 | 0.235 | 0.140 | 0.065 | 0.038 | 0.034 | 0.024 | 0.034 | 0.014 |
| Honduras | - | Y | 803 | 28 | 156 | 0.084 | 27.827 | 0.000 | 0.116 | 0.048 | 75.724 | 0.026 | 0.280 | 0.125 | 0.081 | 0.122 | 0.093 | 0.097 | 0.075 | 0.072 | 0.055 |
| United Arab Emirates | - | Y | 1313 | 47 | 56 | 0.078 | 51.925 | 0.000 | 0.102 | 0.038 | 66.126 | 0.023 | 0.349 | 0.223 | 0.132 | 0.096 | 0.059 | 0.043 | 0.037 | 0.034 | 0.027 |
| Venezuela | - | Y | 793 | 23 | 176 | 0.119 | 22.070 | 0.000 | 0.137 | 0.048 | 151.751 | 0.031 | 0.252 | 0.088 | 0.130 | 0.155 | 0.087 | 0.096 | 0.078 | 0.071 | 0.043 |
| Finland | - | Y | 1121 | 69 | 10 | 0.093 | 38.588 | 0.000 | 0.116 | 0.041 | 93.114 | 0.026 | 0.371 | 0.222 | 0.100 | 0.085 | 0.063 | 0.043 | 0.036 | 0.039 | 0.041 |
| Syria | - | Y | 704 | 20 | 188 | 0.136 | 24.703 | 0.000 | 0.162 | 0.051 | 198.265 | 0.036 | 0.250 | 0.071 | 0.119 | 0.138 | 0.125 | 0.112 | 0.074 | 0.057 | 0.054 |
| Saudi Arabia | - | Y | 1345 | 49 | 47 | 0.128 | 37.702 | 0.000 | 0.125 | 0.037 | 176.310 | 0.037 | 0.251 | 0.100 | 0.178 | 0.153 | 0.129 | 0.073 | 0.042 | 0.025 | 0.048 |
| Ethiopia | - | Y | 1222 | 41 | 84 | 0.112 | 37.873 | 0.000 | 0.147 | 0.039 | 134.157 | 0.033 | 0.259 | 0.102 | 0.094 | 0.123 | 0.128 | 0.104 | 0.083 | 0.063 | 0.044 |
| ABBREVIATION | DESCRIPTION |
|---|---|
| Location | Country or territory |
| Improve | Development of Benford’s Law in reporting, including positive and negative development |
| Flag | Red, Green, and Yellow |
| N | Number of sample |
| d* | d-factor |
| Chi square | The Chi square goodness of fit test |
| p-value | p-value of the Chi square |
| K-S | Kolmogorov-Smirnov statistic |
| Cut-Off | Kolmogorov-Smirnov cut off |
| SSD | Sum of Squares Difference |
| MAD | Mean Absolute Deviation |
| 1 | Leading digit frequency with 1 |
| 2 | Leading digit frequency with 2 |
| 3 | Leading digit frequency with 3 |
| 4 | Leading digit frequency with 4 |
| 5 | Leading digit frequency with 5 |
| 6 | Leading digit frequency with 6 |
| 7 | Leading digit frequency with 7 |
| 8 | Leading digit frequency with 8 |
| 9 | Leading digit frequency with 9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farhadi, N.; Lahooti, H. Are COVID-19 Data Reliable? A Quantitative Analysis of Pandemic Data from 182 Countries. COVID 2021, 1, 137-152. https://0-doi-org.brum.beds.ac.uk/10.3390/covid1010013
Farhadi N, Lahooti H. Are COVID-19 Data Reliable? A Quantitative Analysis of Pandemic Data from 182 Countries. COVID. 2021; 1(1):137-152. https://0-doi-org.brum.beds.ac.uk/10.3390/covid1010013
Chicago/Turabian StyleFarhadi, Noah, and Hooshang Lahooti. 2021. "Are COVID-19 Data Reliable? A Quantitative Analysis of Pandemic Data from 182 Countries" COVID 1, no. 1: 137-152. https://0-doi-org.brum.beds.ac.uk/10.3390/covid1010013






