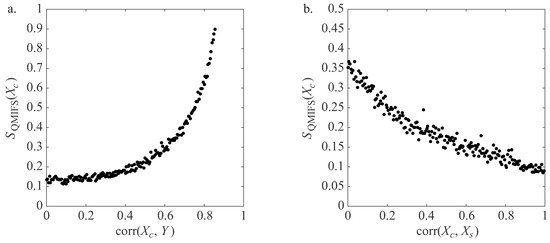
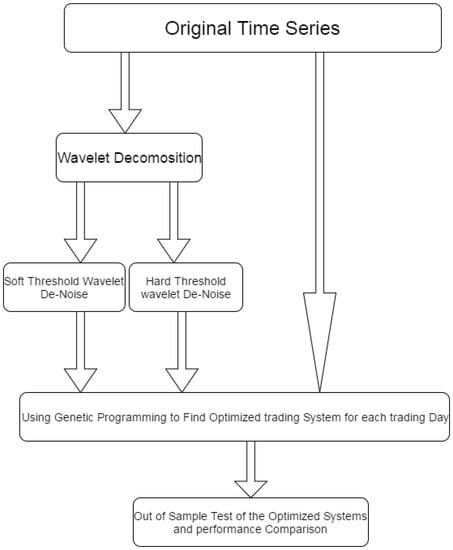
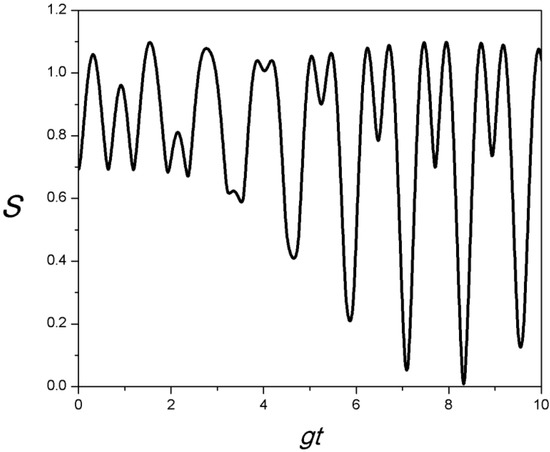
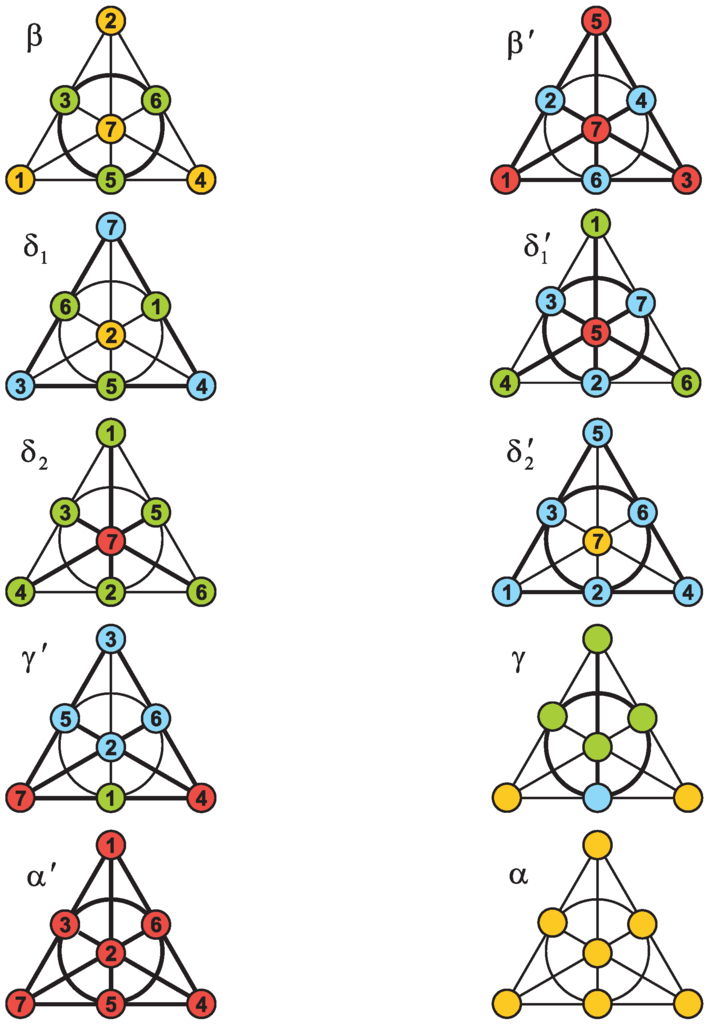
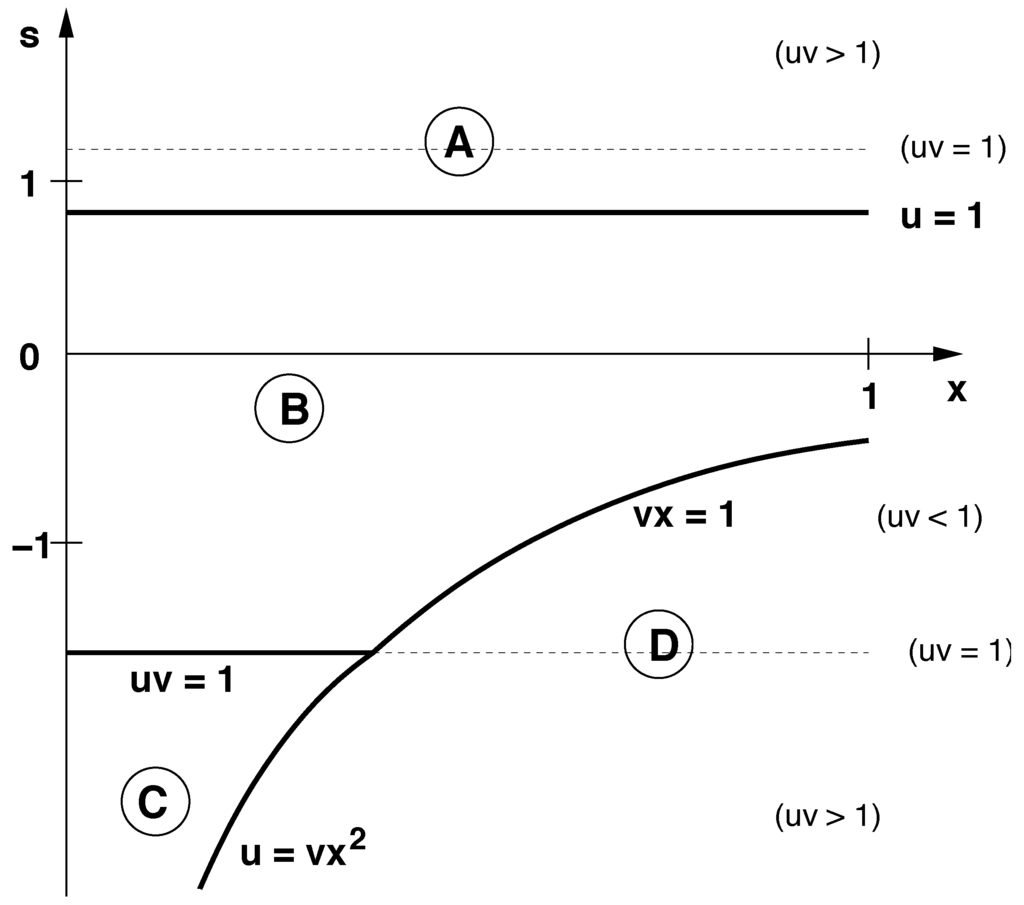
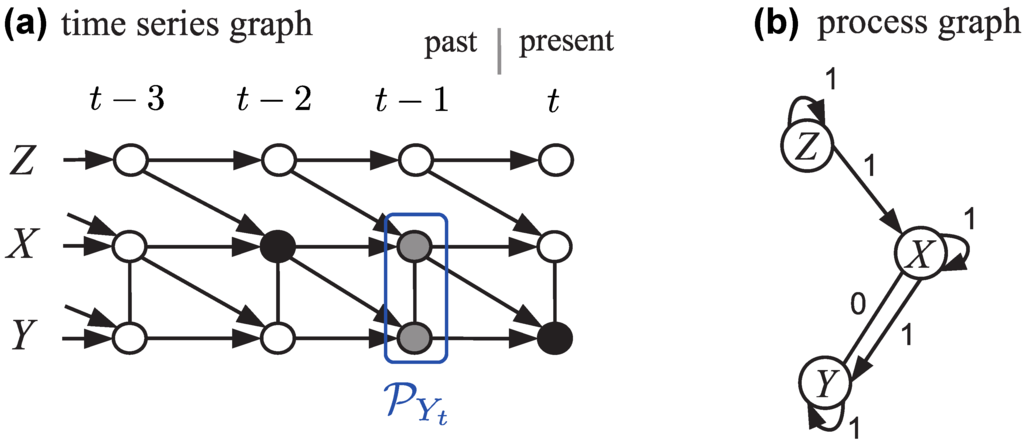
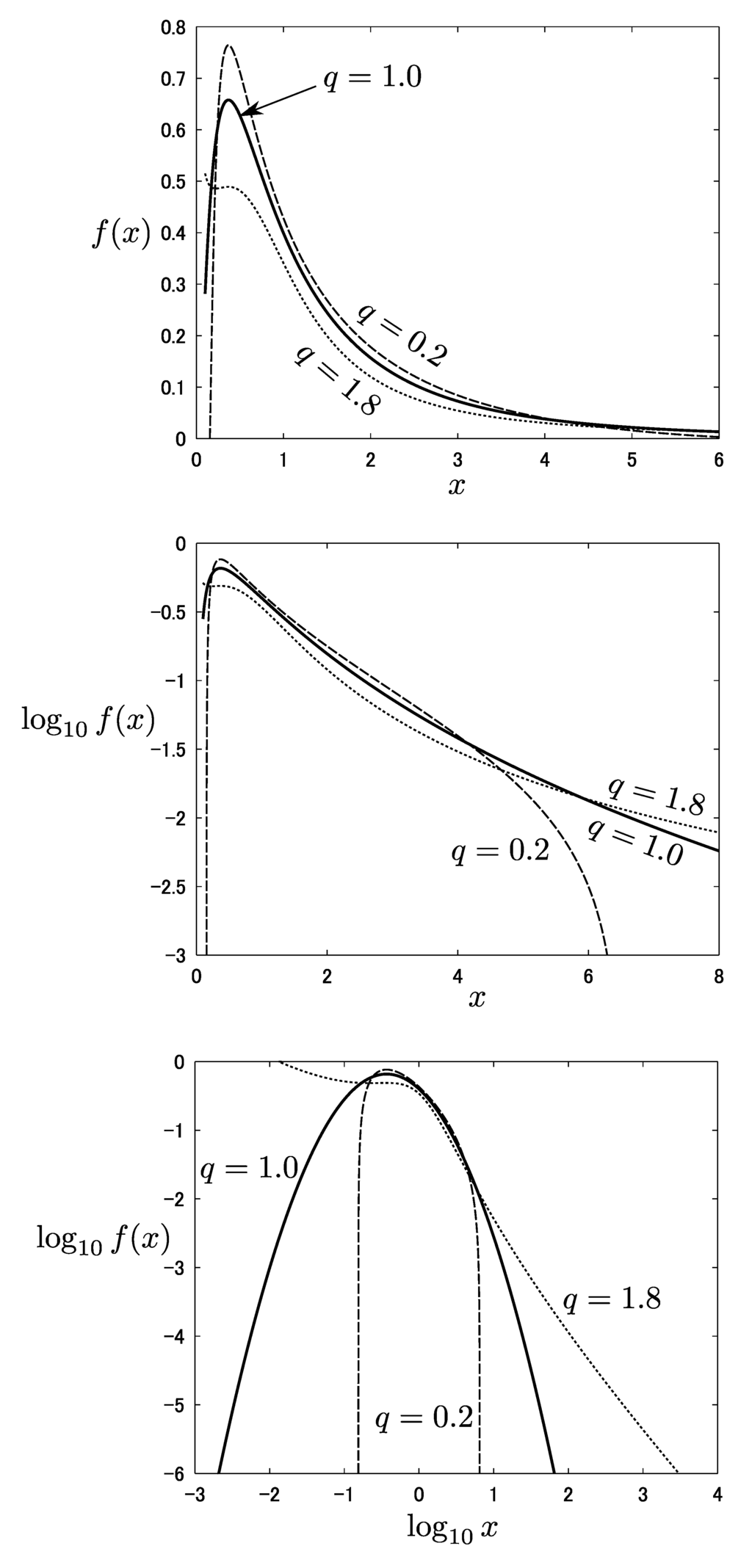
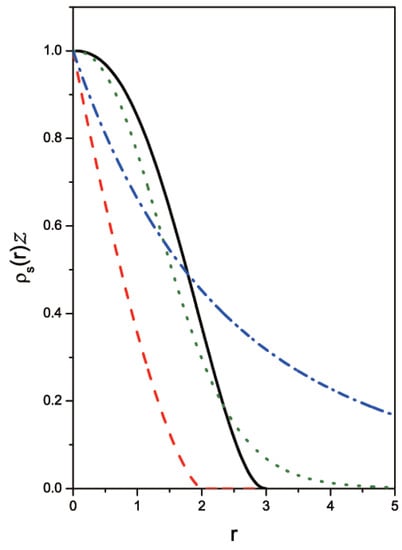
Advances in Applied Statistical Mechanics
A topical collection in Entropy (ISSN 1099-4300). This collection belongs to the section "Statistical Physics".
Viewed by 232881Editor
Interests: nonextensive statistical mechanics; nonlinear Fokker–Planck equations; geometry information; nonlinear Schroedinger equation; quantum groups and quantum algebras; complex systems
Special Issues, Collections and Topics in MDPI journals
Topical Collection Information
Dear Colleagues,
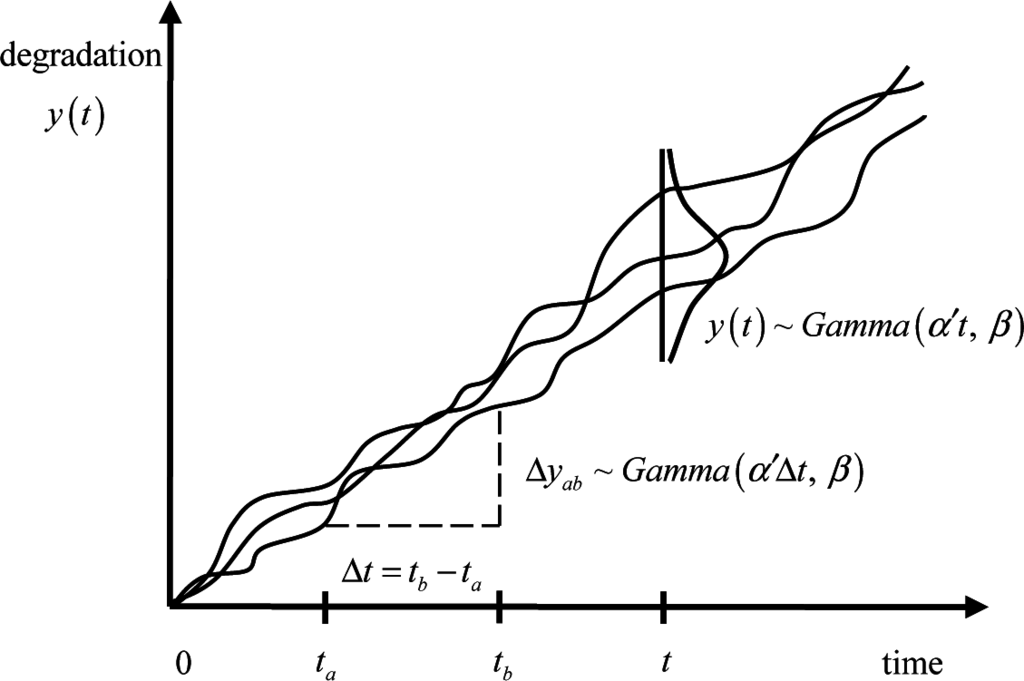
There is a diffuse belief that statistical properties of physical systems are well described by Boltzmann-Gibbs statistical mechanics. However, a constantly increasing amount of situations are known to violate the predictions of orthodox statistical mechanics. Systems where these emerging features are observed seem do not fulfill the standard ergodic and mixing properties on which the Boltzmann-Gibbs formalism are founded. In general, these systems are governed by nonlinear dynamics which establishes a deep relation among the parts. As a consequence, they reach a dynamical equilibrium in which the equilibrium probability distribution can differ deeply from the exponential shape typical of the Gibbs distribution.
In the last decades, we assisted to an intense research activity that has modified our understanding of statistical physics, extending and renewing its applicability considerably. Important developments, relating equilibrium and nonequilibrium statistical physics, kinetic theory, information theory and others, have produced a new understanding of the properties of complex systems that requires, in many cases, the extension of the theory beyond the Boltzmann-Gibbs formalism.
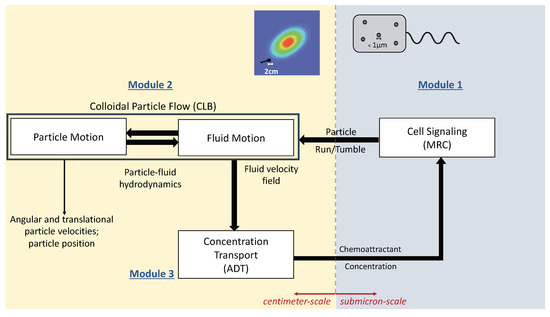
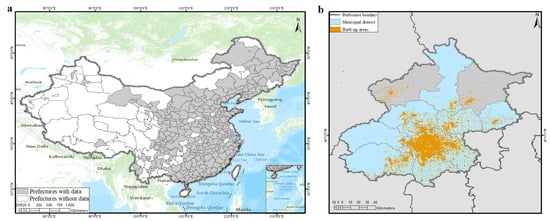
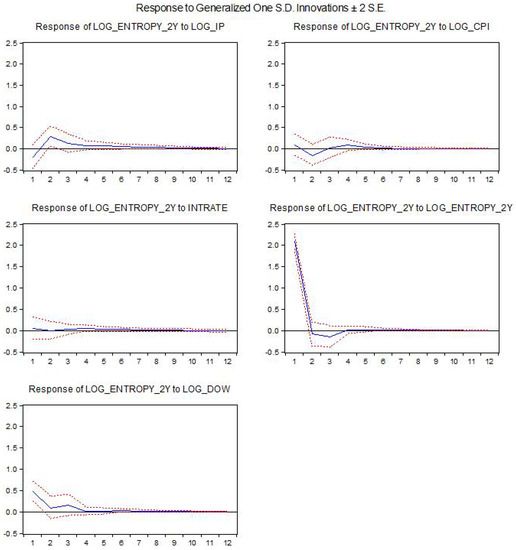
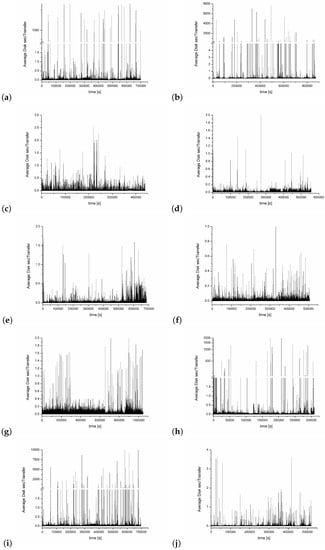
The aim of this collection, is to collect papers in both the foundations and the applications of Statistical Mechanics going outside its traditional application. In particular, foundations regard classical and quantum aspects of statistical physics including generalized entropies, free-scale distributions, information theory, geometry information, nonextensive statistical mechanics, kinetic theory, long-range interactions and small systems. Applications are different and may include biophysics, seismology, econophysics, social systems, physics of networks, physics of risk, traffic flow, complex systems, fractal systems and others.
Specific topics of interest include (but are not limited to): * Generalized entropies * Boltzmann entropy * Renyi entropy * Non linear kinetic * Fokker-Planck equations * Quantum information * Geometry information * Fractal systems * Complex systems * Networks * Econophysics * Sociophysics * Biophysics
Dr. Antonio Maria Scarfone
Collection Editor
Manuscript Submission Information
Manuscripts for the topical collection can be submitted online at www.mdpi.com by registering and logging in to this website. Once you are registered, click here to go to the submission form. All papers will be peer-reviewed. Accepted papers will be published continuously in the journal (as soon as accepted) and will be listed together on this website. The topical collection considers regular research articles, short communications and review articles. A guide for authors and other relevant information for submission of manuscripts is available on the Instructions for Authors page.
Please visit the Instructions for Authors page before submitting a manuscript. The article processing charge (APC) for publication in this open access journal is 2600 CHF (Swiss Francs).
Keywords
- non extensive systems
- generalized entropies
- boltzmann entropy
- renyi entropy
- non linear kinetic
- fokker-planck equations
- quantum information
- geometry information
- fractal systems
- complex systems
- networks
- econophysics
- sociophysics
- biophysics
Planned Papers
The below list represents only planned manuscripts. Some of these manuscripts have not been received by the Editorial Office yet. Papers submitted to MDPI journals are subject to peer-review.
Tentative Title: Entropy dynamics in the statistical dynamics of large systems of active particles
Authors: A. Elaiw, M. A. Alghamdi, and N. Bellomo