Journal Description
Fractal and Fractional
Fractal and Fractional
is an international, scientific, peer-reviewed, open access journal of fractals and fractional calculus and their applications in different fields of science and engineering published monthly online by MDPI.
- Open Access— free for readers, with article processing charges (APC) paid by authors or their institutions.
- High Visibility: indexed within Scopus, SCIE (Web of Science), Inspec, and other databases.
- Journal Rank: JCR - Q1 (Mathematics, Interdisciplinary Applications) / CiteScore - Q1 (Analysis)
- Rapid Publication: manuscripts are peer-reviewed and a first decision is provided to authors approximately 18.9 days after submission; acceptance to publication is undertaken in 3.5 days (median values for papers published in this journal in the second half of 2023).
- Recognition of Reviewers: reviewers who provide timely, thorough peer-review reports receive vouchers entitling them to a discount on the APC of their next publication in any MDPI journal, in appreciation of the work done.
Impact Factor:
5.4 (2022);
5-Year Impact Factor:
4.7 (2022)
Latest Articles
Leader-Following Formation Control for Discrete-Time Fractional Stochastic Multi-Agent Systems by Event-Triggered Strategy
Fractal Fract. 2024, 8(5), 246; https://0-doi-org.brum.beds.ac.uk/10.3390/fractalfract8050246 - 23 Apr 2024
Abstract
Fractional differential equations, which are non-local and can better describe memory and genetic properties, are widely used to describe various physical, chemical, and biological phenomena. Therefore, the multi-agent systems based on discrete-time fractional stochastic models are established. First, some followers are selected for
[...] Read more.
Fractional differential equations, which are non-local and can better describe memory and genetic properties, are widely used to describe various physical, chemical, and biological phenomena. Therefore, the multi-agent systems based on discrete-time fractional stochastic models are established. First, some followers are selected for pinning control. In order to save resources and energy, an event-triggered based control mechanism is proposed. Second, under this control mechanism, sufficient conditions on the interaction graph and the fractional derivative order such that formation control can be achieved are given. Additionally, influenced by noise, the multi-agent system completes formation control in the mean square. In addition to that, these results are equally applicable to the discrete-time fractional formation problem without noise. Finally, the example of numerical simulation is given to prove the correctness of the results.
Full article
(This article belongs to the Special Issue Synchronization and Adaptive Control for Fractional-Order Network Systems)
►
Show Figures
Open AccessArticle
Heterogeneity of Micro- and Nanopore Structure of Lacustrine Shales with Complex Lamina Structure
by
Shuning Liu, Juncheng Qiao, Jianhui Zeng, Chuanming Li, Yazhou Liu, Zheng Kong and Xinlong Liu
Fractal Fract. 2024, 8(4), 245; https://0-doi-org.brum.beds.ac.uk/10.3390/fractalfract8040245 - 22 Apr 2024
Abstract
►▼
Show Figures
Thin sections, AIM-SEM, MICP, and nitrogen adsorption were performed on laminated and layered shales to characterize their complex pore and fracture structure. Combining the MICP model with the FHH model, this work proposes a new fractal method for lacustrine shales with complex lamina
[...] Read more.
Thin sections, AIM-SEM, MICP, and nitrogen adsorption were performed on laminated and layered shales to characterize their complex pore and fracture structure. Combining the MICP model with the FHH model, this work proposes a new fractal method for lacustrine shales with complex lamina structure. The fractal characteristics presented four zones, representing the heterogeneity of fractures, macropores, mesopores, and micropores. The pores and fractures of shale have strong heterogeneity. Laminated shale has strong heterogeneity in mesopores and moderate heterogeneity in micropores. Layered shale has strong heterogeneity in fractures and moderate heterogeneity in micropores. The lamina structure and content of organic and mineral composition has a great influence on heterogeneity. The mineral laminae in laminated shale change frequently; lamellation fractures are mainly developed, and the structures are similar. Layered shales develop fractures between layers and structural fractures; the structural differences are significant. Macropores are mostly interparticle pores between quarts with similar structures. The wider lamina thickness of layered shale provides sufficient crystallization space for minerals, so the mesopores of layered shale are more homogeneous. Micropores are less developed, mainly consisting of intraparticle pores between clay minerals, which are complex but similar in structure in the two types of shale. The heterogeneity of mesopores and micropores is not conducive to hydrocarbon migration. Fractures and macropores need to be connected with meso–micropores to form a transport system. So, mesopores and micropores play decisive roles in hydrocarbon migration. Based on the above understanding, this paper points out that hydrocarbon in laminated shale with more carbonate minerals and a high thermal evolution degree has better availability.
Full article
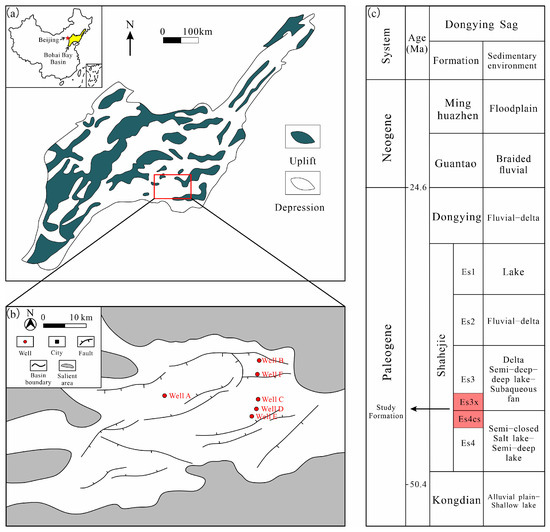
Figure 1
Open AccessArticle
Robust Fractional-Order PI/PD Controllers for a Cascade Control Structure of Servo Systems
by
Vo Lam Chuong, Ngo Hong Nam, Le Hieu Giang and Truong Nguyen Luan Vu
Fractal Fract. 2024, 8(4), 244; https://0-doi-org.brum.beds.ac.uk/10.3390/fractalfract8040244 - 22 Apr 2024
Abstract
In this paper, a cascade control structure is suggested to control servo systems that normally include a servo motor in coupling with two kinds of mechanism elements, a translational or rotational movement. These kinds of systems have high demands for performance in terms
[...] Read more.
In this paper, a cascade control structure is suggested to control servo systems that normally include a servo motor in coupling with two kinds of mechanism elements, a translational or rotational movement. These kinds of systems have high demands for performance in terms of fastest response and no overshoot/oscillation to a ramp function input. The fractional-order proportional integral (FOPI) and proportional derivative (FOPD) controllers are addressed to deal with those control problems due to their flexibility in tuning rules and robustness. The tuning rules are designed in the frequency domain based on the concept of the direct synthesis method and also ensure the robust stability of controlled systems by using the maximum sensitivity function. The M-Δ structure, using multiplicative output uncertainties for both control loops simultaneously, is addressed to justify the robustness of the controlled systems. Simulation studies are considered for two kinds of plants that prove the effectiveness of the proposed method, with good tracking of the ramp function input under the effects of the disturbances. In addition, the robustness of the controlled system is illustrated by a structured singular value (µ) plot in which its value is less than 1 over the frequency range.
Full article
(This article belongs to the Special Issue Applications of Fractional-Order Systems to Automatic Control)
►▼
Show Figures
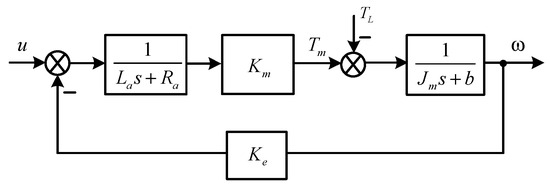
Figure 1
Open AccessArticle
Fixed Point Theorems: Exploring Applications in Fractional Differential Equations for Economic Growth
by
Afrah Ahmad Noman Abdou
Fractal Fract. 2024, 8(4), 243; https://0-doi-org.brum.beds.ac.uk/10.3390/fractalfract8040243 - 22 Apr 2024
Abstract
The aim of this research is to introduce two new notions,
The aim of this research is to introduce two new notions,
(This article belongs to the Special Issue Advances in Nonlinear Functional Analysis on Fractional Differential Equations)
Open AccessArticle
Using Fractal Theory to Study the Influence of Movable Oil on the Pore Structure of Different Types of Shale: A Case Study of the Fengcheng Formation Shale in Well X of Mahu Sag, Junggar Basin, China
by
Hong Zhang, Zhengchen Zhang, Zhenlin Wang, Yamin Wang, Rui Yang, Tao Zhu, Feifei Luo and Kouqi Liu
Fractal Fract. 2024, 8(4), 242; https://0-doi-org.brum.beds.ac.uk/10.3390/fractalfract8040242 - 20 Apr 2024
Abstract
This study investigated the influence of movable oil on the pore structure of various shale types, analyzing 19 shale samples from Well X in the Mahu Sag of the Junggar Basin. Initially, X-ray diffraction (XRD) analysis classified the shale samples. Subsequently, the geochemical
[...] Read more.
This study investigated the influence of movable oil on the pore structure of various shale types, analyzing 19 shale samples from Well X in the Mahu Sag of the Junggar Basin. Initially, X-ray diffraction (XRD) analysis classified the shale samples. Subsequently, the geochemical properties and pore structures of the samples, both pre and post oil Soxhlet extraction, were comparatively analyzed through Total Organic Carbon (TOC) content measurement, Rock-Eval pyrolysis, and nitrogen adsorption experiments. Additionally, fractal theory quantitatively described the impact of movable oil on the pore structure of different shale types. Results indicated higher movable oil content in siliceous shale compared to calcareous shale. Oil extraction led to a significant increase in specific surface area and pore volume in all samples, particularly in siliceous shale. Calcareous shale predominantly displays H2–H3 type hysteresis loops, indicating a uniform pore structure with ink-bottle-shaped pores. Conversely, siliceous shale exhibited diverse hysteresis loops, reflecting its complex pore structure. The fractal dimension in calcareous shale correlated primarily with pore structure, exhibiting no significant correlation with TOC content before or after oil extraction. Conversely, the fractal dimension changes in siliceous shale samples do not have a clear correlation with either TOC content or pore structure, suggesting variations may result from both TOC and pore structure.
Full article
(This article belongs to the Special Issue Flow and Transport in Fractal Models of Rock Mechanics)
►▼
Show Figures

Figure 1
Open AccessArticle
Unravelling the Fractal Complexity of Temperature Datasets across Indian Mainland
by
Adarsh Sankaran, Thomas Plocoste, Arathy Nair Geetha Raveendran Nair and Meera Geetha Mohan
Fractal Fract. 2024, 8(4), 241; https://0-doi-org.brum.beds.ac.uk/10.3390/fractalfract8040241 - 20 Apr 2024
Abstract
Studying atmospheric temperature characteristics is crucial under climate change, as it helps us to understand the changing patterns in temperature that have significant implications for the environment, ecosystems, and human well-being. This study presents the comprehensive analysis of the spatiotemporal variability of scaling
[...] Read more.
Studying atmospheric temperature characteristics is crucial under climate change, as it helps us to understand the changing patterns in temperature that have significant implications for the environment, ecosystems, and human well-being. This study presents the comprehensive analysis of the spatiotemporal variability of scaling behavior of daily temperature series across the whole Indian mainland, using a Multifractal Detrended Fluctuation Analysis (MFDFA). The analysis considered 1° × 1° datasets of maximum temperature (Tmax), minimum temperature (Tmin), mean temperature (Tmean), and diurnal temperature range (DTR) (TDTR = Tmax − Tmin) from 1951 to 2016 to compare their scaling behavior for the first time. Our results indicate that the Tmin series exhibits the highest persistence (with the Hurst exponent ranging from 0.849 to unity, and a mean of 0.971), and all four-temperature series display long-term persistence and multifractal characteristics. The variability of the multifractal characteristics is less significant in North–Central India, while it is highest along the western coast of India. Moreover, the assessment of multifractal characteristics of different temperature series during the pre- and post-1976–1977 period of the Pacific climate shift reveals a notable decrease in multifractal strength and persistence in the post-1976–1977 series across all regions. Moreover, for the detection of climate change and its dominant driver, we propose a new rolling window multifractal (RWM) framework by evaluating the temporal evolution of the spectral exponents and the Hurst exponent. This study successfully captured the regime shifts during the periods of 1976–1977 and 1997–1998. Interestingly, the earlier climatic shift primarily mitigated the persistence of the Tmax series, whereas the latter shift significantly influenced the persistence of the Tmean series in the majority of temperature-homogeneous regions in India.
Full article
(This article belongs to the Special Issue Fractal Analysis and Its Applications in Geophysical Science)
►▼
Show Figures
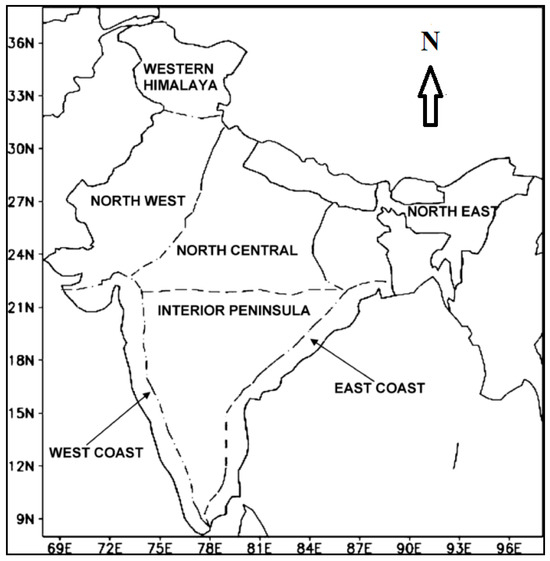
Figure 1
Open AccessArticle
Compressive Failure Characteristics of a Coal–Rock Combination at Different Angles: Experimental Study and Fractal Analysis
by
Long Tang, Shihao Tu, Hongsheng Tu, Kaijun Miao, Wenlong Li, Hongbin Zhao, Jieyang Ma and Lei Zhang
Fractal Fract. 2024, 8(4), 240; https://0-doi-org.brum.beds.ac.uk/10.3390/fractalfract8040240 - 20 Apr 2024
Abstract
In order to explore the influence of dip angles on the deformation and failure of a coal–rock combination, uniaxial compression experiments were carried out on a coal–rock combination with different dip angles, and the acoustic emissions (hereinafter referred to as AE) responses during
[...] Read more.
In order to explore the influence of dip angles on the deformation and failure of a coal–rock combination, uniaxial compression experiments were carried out on a coal–rock combination with different dip angles, and the acoustic emissions (hereinafter referred to as AE) responses during loading were collected. Based on the damage mechanics theory and fractal theory, the fractal dimensions of different damage degrees were calculated. The results show that, with the increase in the inclination angle, the compressive strength and elastic modulus of the coal–rock combination gradually decreased, while the AE ringing count gradually increased first and then decreased. At the initial loading stage of the specimen, the greater the damage degree of the coal–rock combination under the same strain condition, the larger the value of its overall fractal dimension. The AE fractal dimension of the coal–rock combination increases gradually between 10% and 20% of the damage degree. It suddenly decreased between 50% and 60%, then increased slightly before gradually decreasing to the minimum between 80% and 100%. The sudden decrease in fractal dimension, a slight increase, and then a continuous decrease can be used as the precursor information for the instability and failure of the coal–rock combination.
Full article
(This article belongs to the Special Issue Fractal Analysis and Its Applications in Rock Engineering)
►▼
Show Figures
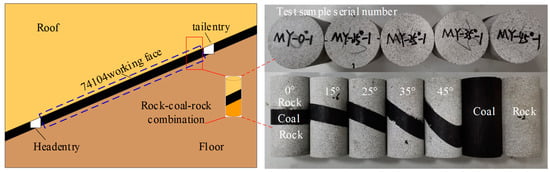
Figure 1
Open AccessArticle
Auto- and Cross-Correlation Multifractal Analysis of Sea Surface Temperature Variability
by
Gyuchang Lim and Jong-Jin Park
Fractal Fract. 2024, 8(4), 239; https://0-doi-org.brum.beds.ac.uk/10.3390/fractalfract8040239 - 19 Apr 2024
Abstract
In this study, we investigate multiscale auto- and cross-correlation structural characteristics of sea surface temperature (SST) variability using our new methodology, called the multifractal asymmetric cross-correlation analysis (MF-ACCA), incorporating signs of a segment’s detrended covariance and linear trend. SST is greatly affected by
[...] Read more.
In this study, we investigate multiscale auto- and cross-correlation structural characteristics of sea surface temperature (SST) variability using our new methodology, called the multifractal asymmetric cross-correlation analysis (MF-ACCA), incorporating signs of a segment’s detrended covariance and linear trend. SST is greatly affected by air–sea interactions and the advection of water masses with a wide range of spatiotemporal scales. Since these force factors are imprinted on SST variability, their features can be revealed in terms of long-range auto- and cross-correlation structures of SST variability via a multifractal analysis. By applying the MF-ACCA methodology to SST variability in the East/Japan Sea, we have found the following features: (1) the auto- and cross-correlation multifractal features are dependent on several parameters, such as the location, linear trends (rising or falling), level of fluctuations, and temporal scales; (2) there are crossover behaviors that are discrete for small scales (less than 1000 days) but continuous for large scales (more than 1000 days); (3) long-range persistence of auto- and cross-correlations is random for large scales during the falling phase; (4) long-range persistence is stronger during the rising phase than during the falling phase; (5) the degree of asymmetry is greater for large scales than for small scales.
Full article
(This article belongs to the Section Complexity)
►▼
Show Figures
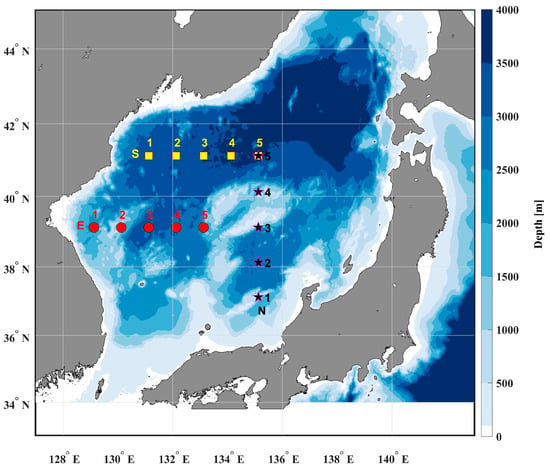
Figure 1
Open AccessArticle
Spectral and Oscillation Theory for an Unconventional Fractional Sturm–Liouville Problem
by
Mohammad Dehghan and Angelo B. Mingarelli
Fractal Fract. 2024, 8(4), 238; https://0-doi-org.brum.beds.ac.uk/10.3390/fractalfract8040238 - 19 Apr 2024
Abstract
Here, we investigate the spectral and oscillation theory for a class of fractional differential equations subject to specific boundary conditions. By transforming the problem into a modified version with a classical structure, we establish the orthogonality properties of eigenfunctions and some major comparison
[...] Read more.
Here, we investigate the spectral and oscillation theory for a class of fractional differential equations subject to specific boundary conditions. By transforming the problem into a modified version with a classical structure, we establish the orthogonality properties of eigenfunctions and some major comparison theorems for solutions. We also derive a new type of integration by using parts of formulas for modified fractional integrals and derivatives. Furthermore, we analyze the variational characterization of the first eigenvalue, revealing its non-zero first eigenfunction within the interior. Our findings demonstrate the potential for novel definitions of fractional derivatives to mirror the classical Sturm–Liouville theory through simple isospectral transformations.
Full article
(This article belongs to the Section Numerical and Computational Methods)
►▼
Show Figures
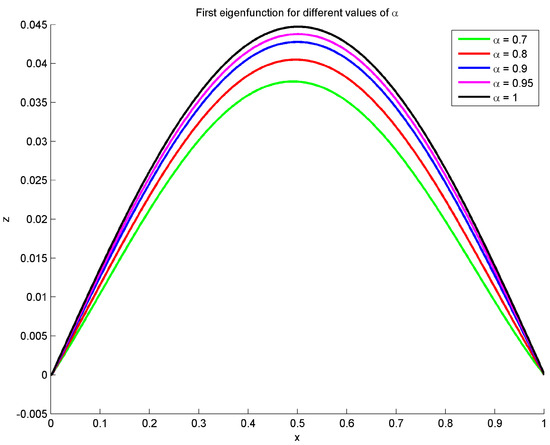
Figure 1
Open AccessArticle
COVID-19 Diagnosis by Extracting New Features from Lung CT Images Using Fractional Fourier Transform
by
Ali Nokhostin and Saeid Rashidi
Fractal Fract. 2024, 8(4), 237; https://0-doi-org.brum.beds.ac.uk/10.3390/fractalfract8040237 - 18 Apr 2024
Abstract
COVID-19 is a lung disease caused by a coronavirus family virus. Due to its extraordinary prevalence and associated death rates, it has spread quickly to every country in the world. Thus, achieving peaks and outlines and curing different types of relapses is extremely
[...] Read more.
COVID-19 is a lung disease caused by a coronavirus family virus. Due to its extraordinary prevalence and associated death rates, it has spread quickly to every country in the world. Thus, achieving peaks and outlines and curing different types of relapses is extremely important. Given the worldwide prevalence of coronavirus and the participation of physicians in all countries, information has been gathered regarding the properties of the virus, its diverse types, and the means of analyzing it. Numerous approaches have been used to identify this evolving virus. It is generally considered the most accurate and acceptable method of examining the patient’s lungs and chest through a CT scan. As part of the feature extraction process, a method known as fractional Fourier transform (FrFT) has been applied as one of the time-frequency domain transformations. The proposed method was applied to a database consisting of 2481 CT images. Following the transformation of all images into equal sizes and the removal of non-lung areas, multiple combination windows are used to reduce the number of features extracted from the images. In this paper, the results obtained for KNN and SVM classification have been obtained with accuracy values of 99.84% and 99.90%, respectively.
Full article
(This article belongs to the Special Issue Fractional Calculus in Signal, Imaging Processing and Machine Learning)
►▼
Show Figures
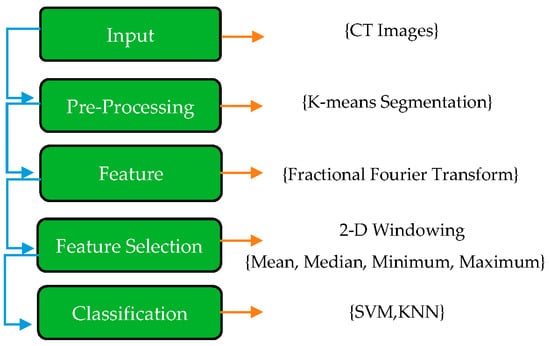
Figure 1
Open AccessArticle
On Solutions of Two Post-Quantum Fractional Generalized Sequential Navier Problems: An Application on the Elastic Beam
by
Sina Etemad, Sotiris K. Ntouyas, Ivanka Stamova and Jessada Tariboon
Fractal Fract. 2024, 8(4), 236; https://0-doi-org.brum.beds.ac.uk/10.3390/fractalfract8040236 - 17 Apr 2024
Abstract
Fractional calculus provides some fractional operators for us to model different real-world phenomena mathematically. One of these important study fields is the mathematical model of the elastic beam changes. More precisely, in this paper, based on the behavior patterns of an elastic beam,
[...] Read more.
Fractional calculus provides some fractional operators for us to model different real-world phenomena mathematically. One of these important study fields is the mathematical model of the elastic beam changes. More precisely, in this paper, based on the behavior patterns of an elastic beam, we consider the generalized sequential boundary value problems of the Navier difference equations by using the post-quantum fractional derivatives of the Caputo-like type. We discuss on the existence theory for solutions of the mentioned
(This article belongs to the Special Issue Advances in Boundary Value Problems for Fractional Differential Equations, 2nd Edition)
Open AccessArticle
Controllability of Mild Solution to Hilfer Fuzzy Fractional Differential Inclusion with Infinite Continuous Delay
by
Aeshah Abdullah Muhammad Al-Dosari
Fractal Fract. 2024, 8(4), 235; https://0-doi-org.brum.beds.ac.uk/10.3390/fractalfract8040235 - 17 Apr 2024
Abstract
This work investigates the solvability of the generalized Hilfer fractional inclusion associated with the solution set of a controlled system of minty type–fuzzy mixed quasi-hemivariational inequality (FMQHI). We explore the assumed inclusion via the infinite delay and the semi-group arguments in the area
[...] Read more.
This work investigates the solvability of the generalized Hilfer fractional inclusion associated with the solution set of a controlled system of minty type–fuzzy mixed quasi-hemivariational inequality (FMQHI). We explore the assumed inclusion via the infinite delay and the semi-group arguments in the area of solid continuity that sculpts the compactness area. The conformable Hilfer fractional time derivative, the theory of fuzzy sets, and the infinite delay arguments support the solution set’s controllability. We explain the existence due to the convergence properties of Mittage–Leffler functions (
(This article belongs to the Special Issue Fractional Mathematical Modelling: Theory, Methods and Applications)
Open AccessArticle
A Low Power Analog Integrated Fractional Order Type-2 Fuzzy PID Controller
by
Vassilis Alimisis, Nikolaos P. Eleftheriou, Evangelos Georgakilas, Christos Dimas, Nikolaos Uzunoglu and Paul P. Sotiriadis
Fractal Fract. 2024, 8(4), 234; https://0-doi-org.brum.beds.ac.uk/10.3390/fractalfract8040234 - 16 Apr 2024
Abstract
This paper introduces an analog integrated fractional order type-2 fuzzy PID control system. Current approaches frequently depend on energy-intensive embedded digital systems, consuming substantial energy levels ranging from a few μW to mW. To address this limitation we propose a fully analog design
[...] Read more.
This paper introduces an analog integrated fractional order type-2 fuzzy PID control system. Current approaches frequently depend on energy-intensive embedded digital systems, consuming substantial energy levels ranging from a few μW to mW. To address this limitation we propose a fully analog design offering insights into the potential of analog circuits for powerefficient robust control in complex and uncertain environments. It consists of Gaussian function, min/max, Operational transcoductance amplifier circuits and Resistor-Capacitor networks for the implementation of the fractional-order components. Crafted for operation under a reduced voltage supply (0.6 V), the controller attains minimal power usage (861.8 nW), facilitating uninterrupted, extended-term functioning. Post-layout simulation results confirm the proper operation of the proposed design. The proposed system is designed and simulated using the Cadence IC Suite in a TSMC 90 nm CMOS process.
Full article
(This article belongs to the Special Issue Advance on the Fractal and Fractional Calculus in Electrical and Electronic Engineering)
►▼
Show Figures

Figure 1
Open AccessEditorial
Fractional Calculus and Hypergeometric Functions in Complex Analysis
by
Gheorghe Oros and Georgia Irina Oros
Fractal Fract. 2024, 8(4), 233; https://0-doi-org.brum.beds.ac.uk/10.3390/fractalfract8040233 - 16 Apr 2024
Abstract
Fractional calculus has had a powerful impact on recent research, with many applications in different branches of science and engineering [...]
Full article
(This article belongs to the Special Issue Fractional Calculus and Hypergeometric Functions in Complex Analysis)
Open AccessArticle
Stability and Bifurcation Control for a Generalized Delayed Fractional Food Chain Model
by
Qing Li, Hongxia Liu, Wencai Zhao and Xinzhu Meng
Fractal Fract. 2024, 8(4), 232; https://0-doi-org.brum.beds.ac.uk/10.3390/fractalfract8040232 - 16 Apr 2024
Abstract
►▼
Show Figures
In this paper, a generalized fractional three-species food chain model with delay is investigated. First, the existence of a positive equilibrium is discussed, and the sufficient conditions for global asymptotic stability are given. Second, through selecting the delay as the bifurcation parameter, we
[...] Read more.
In this paper, a generalized fractional three-species food chain model with delay is investigated. First, the existence of a positive equilibrium is discussed, and the sufficient conditions for global asymptotic stability are given. Second, through selecting the delay as the bifurcation parameter, we obtain the sufficient condition for this non-control system to generate Hopf bifurcation. Then, a nonlinear delayed feedback controller is skillfully applied to govern the system’s Hopf bifurcation. The results indicate that adjusting the control intensity or the control target’s age can effectively govern the bifurcation dynamics behavior of this system. Last, through application examples and numerical simulations, we confirm the validity and feasibility of the theoretical results, and find that the control strategy is also applicable to eco-epidemiological systems.
Full article
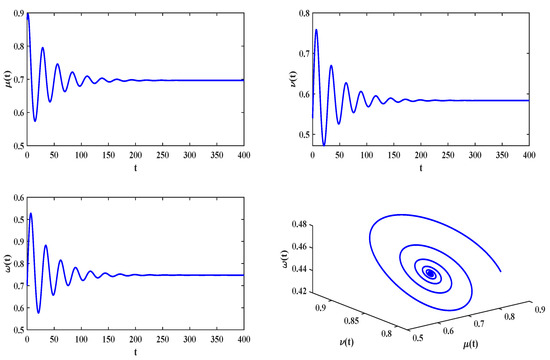
Figure 1
Open AccessArticle
Liquid Vortex Formation in a Swirling Container Considering Fractional Time Derivative of Caputo
by
Mustafa Turkyilmazoglu and A. S. Alofi
Fractal Fract. 2024, 8(4), 231; https://0-doi-org.brum.beds.ac.uk/10.3390/fractalfract8040231 - 16 Apr 2024
Abstract
This paper applies fractional calculus to a practical example in fluid mechanics, illustrating its impact beyond traditional integer order calculus. We focus on the classic problem of a rigid body rotating within a uniformly rotating container, which generates a liquid vortex from an
[...] Read more.
This paper applies fractional calculus to a practical example in fluid mechanics, illustrating its impact beyond traditional integer order calculus. We focus on the classic problem of a rigid body rotating within a uniformly rotating container, which generates a liquid vortex from an undisturbed initial state. Our aim is to compare the time evolutions of the physical system in fractional and integer order models by examining the torque transmission from the rotating body to the surrounding liquid. This is achieved through closed-form, time-developing solutions expressed in terms of Mittag–Leffler and Bessel functions. Analysis reveals that the rotational velocity and, consequently, the vortex structure of the liquid are influenced by three distinct time zones that differ between integer and noninteger models. Anomalous diffusion, favoring noninteger fractions, dominates at early times but gradually gives way to the integer derivative model behavior as time progresses through a transitional regime. Our derived vortex formula clearly demonstrates how the liquid vortex is regulated in time for each considered fractional model.
Full article
(This article belongs to the Section Engineering)
►▼
Show Figures
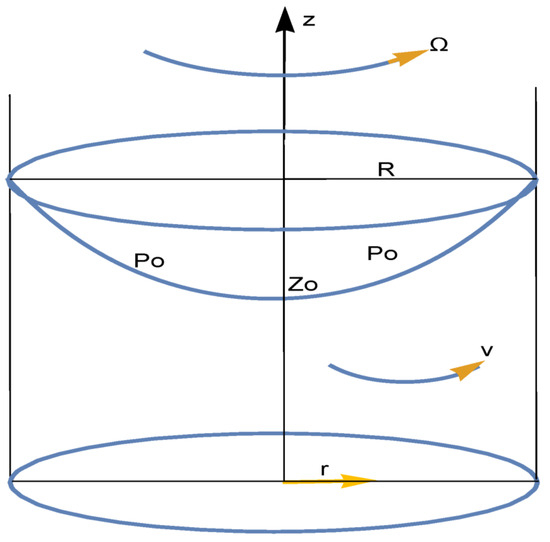
Figure 1
Open AccessArticle
Further Fractional Hadamard Integral Inequalities Utilizing Extended Convex Functions
by
Areej A. Almoneef, Mohamed A. Barakat and Abd-Allah Hyder
Fractal Fract. 2024, 8(4), 230; https://0-doi-org.brum.beds.ac.uk/10.3390/fractalfract8040230 - 16 Apr 2024
Abstract
This work investigates novel fractional Hadamard integral inequalities by utilizing extended convex functions and generalized Riemann-Liouville operators. By carefully using extended integral formulations, we not only find novel inequalities but also improve the accuracy of error bounds related to fractional Hadamard integrals. Our
[...] Read more.
This work investigates novel fractional Hadamard integral inequalities by utilizing extended convex functions and generalized Riemann-Liouville operators. By carefully using extended integral formulations, we not only find novel inequalities but also improve the accuracy of error bounds related to fractional Hadamard integrals. Our study broadens the applicability of these inequalities and shows that they are useful for a variety of convexity cases. Our results contribute to the advancement of mathematical analysis and provide useful information for theoretical comprehension as well as practical applications across several scientific directions.
Full article
(This article belongs to the Special Issue Women’s Special Issue Series: Fractal and Fractional, 2nd Edition)
Open AccessArticle
Novel Hopf Bifurcation Exploration and Control Strategies in the Fractional-Order FitzHugh–Nagumo Neural Model Incorporating Delay
by
Yunzhang Zhang and Changjin Xu
Fractal Fract. 2024, 8(4), 229; https://0-doi-org.brum.beds.ac.uk/10.3390/fractalfract8040229 - 15 Apr 2024
Abstract
In this article, we propose a new fractional-order delay-coupled FitzHugh–Nagumo neural model. Taking advantage of delay as a bifurcation parameter, we explore the stability and bifurcation of the formulated fractional-order delay-coupled FitzHugh–Nagumo neural model. A delay-independent stability and bifurcation conditions for the fractional-order
[...] Read more.
In this article, we propose a new fractional-order delay-coupled FitzHugh–Nagumo neural model. Taking advantage of delay as a bifurcation parameter, we explore the stability and bifurcation of the formulated fractional-order delay-coupled FitzHugh–Nagumo neural model. A delay-independent stability and bifurcation conditions for the fractional-order delay-coupled FitzHugh–Nagumo neural model is acquired. By designing a proper
(This article belongs to the Special Issue Analysis and Control of Fractional-Order Delay Coupling Networks)
►▼
Show Figures

Figure 1
Open AccessArticle
Fractal Characteristics and Microstructure of Coal with Impact of Starch-Polymerized Aluminum Sulfate Fracturing Fluids
by
Feng Cai, Qian Zhang and Lingling Yang
Fractal Fract. 2024, 8(4), 228; https://0-doi-org.brum.beds.ac.uk/10.3390/fractalfract8040228 - 15 Apr 2024
Abstract
The degree of irregularity and complexity of the pore structure are comprehensively reflected in the fractal dimension. The porosity of coal was determined by its fractal dimension, where a larger dimension indicates a lower porosity. Fractal theory and the Frenkel–Halsey–Hill (FHH) model were
[...] Read more.
The degree of irregularity and complexity of the pore structure are comprehensively reflected in the fractal dimension. The porosity of coal was determined by its fractal dimension, where a larger dimension indicates a lower porosity. Fractal theory and the Frenkel–Halsey–Hill (FHH) model were applied to explore the variation rules of concentration on functional groups and pore structure in this study. Combined with infrared spectroscopy (FTIR) and low-temperature nitrogen adsorption, a starch-polymerized aluminum sulfate composite fracturing fluid was prepared, which plays an important role in methane adsorption and permeability of coal samples. The test results showed that, compared with the original coal, the pore volume and specific surface area of each group of coal samples were reduced, the average pore diameter was initially enlarged and then declined, and fractal dimension D1 dropped by 5.4% to 15.4%, while fractal dimension D2 gained 1.2% to 7.9%. Moreover, the nitrogen adsorption of each group of coal samples was obviously lower than the original coal, and the concentration of starch-polymerized aluminum sulfate solution existed at a critical optimal concentration for the modification of the coal samples, and the nitrogen adsorption reached a minimum value of 0.6814 cm3/g at a concentration of 10%. The novel composite solution prepared by the combination of starch and flocculant in this paper enhanced the permeability of the coal seam, which is of great significance in improving the efficiency of coalbed methane mining.
Full article
(This article belongs to the Special Issue Fractional-Order Chaotic System: Control and Synchronization, 2nd Edition)
►▼
Show Figures

Figure 1
Open AccessArticle
The Four-Dimensional Natural Transform Adomian Decomposition Method and (3+1)-Dimensional Fractional Coupled Burgers’ Equation
by
Huda Alsaud and Hassan Eltayeb
Fractal Fract. 2024, 8(4), 227; https://0-doi-org.brum.beds.ac.uk/10.3390/fractalfract8040227 - 15 Apr 2024
Abstract
This research article introduces the four-dimensional natural transform Adomian decomposition method (FNADM) for solving the (3+1)-dimensional time-singular fractional coupled Burgers’ equation, along with its associated initial conditions. The FNADM approach represents a fusion of four-dimensional natural transform techniques and Adomian decomposition methodologies. In
[...] Read more.
This research article introduces the four-dimensional natural transform Adomian decomposition method (FNADM) for solving the (3+1)-dimensional time-singular fractional coupled Burgers’ equation, along with its associated initial conditions. The FNADM approach represents a fusion of four-dimensional natural transform techniques and Adomian decomposition methodologies. In order to observe the influence of time-Caputo fractional derivatives on the outcomes of the aforementioned models, two examples are illustrated along with their three-dimensional figures. The effectiveness and reliability of this approach are validated through the analysis of these examples related to the (3+1)-dimensional time-singular fractional coupled Burgers’ equations. This study underscores the method’s applicability and effectiveness in addressing the complex mathematical models encountered in various scientific and engineering domains.
Full article
(This article belongs to the Special Issue Advances in Fractional Order Derivatives and Their Applications, 2nd Edition)
►▼
Show Figures
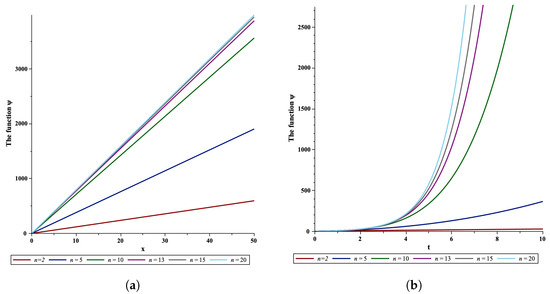
Figure 1

Journal Menu
► ▼ Journal Menu-
- Fractal Fract Home
- Aims & Scope
- Editorial Board
- Reviewer Board
- Topical Advisory Panel
- Instructions for Authors
- Special Issues
- Topics
- Sections
- Article Processing Charge
- Indexing & Archiving
- Editor’s Choice Articles
- Most Cited & Viewed
- Journal Statistics
- Journal History
- Journal Awards
- Conferences
- Editorial Office
Journal Browser
► ▼ Journal BrowserHighly Accessed Articles
Latest Books
E-Mail Alert
News
Topics
Topic in
Algorithms, Computation, Entropy, Fractal Fract, MCA
Analytical and Numerical Methods for Stochastic Biological Systems
Topic Editors: Mehmet Yavuz, Necati Ozdemir, Mouhcine Tilioua, Yassine SabbarDeadline: 10 May 2024
Topic in
Energies, Environments, Fractal Fract, Materials, Remote Sensing
Geomechanics for Energy and the Environment
Topic Editors: Gan Feng, Ang Liu, Reza Taherdangkoo, Qiao LyuDeadline: 31 May 2024
Topic in
Algorithms, Axioms, Fractal Fract, Mathematics, Symmetry
Fractal and Design of Multipoint Iterative Methods for Nonlinear Problems
Topic Editors: Xiaofeng Wang, Fazlollah SoleymaniDeadline: 30 June 2024
Topic in
Applied Sciences, Energies, Fractal Fract, Polymers, Resources
Petroleum and Gas Engineering
Topic Editors: Xiaochun Wang, Yulong ZhaoDeadline: 31 August 2024

Conferences
Special Issues
Special Issue in
Fractal Fract
Fractal Mechanics of Engineering Materials
Guest Editors: Mohd Nasir Tamin, Seyed R. KoloorDeadline: 30 April 2024
Special Issue in
Fractal Fract
New Trends on Generalized Fractional Calculus
Guest Editors: Milton Ferreira, Maria Manuela Fernandes Rodrigues, Nelson Felipe Loureiro VieiraDeadline: 15 May 2024
Special Issue in
Fractal Fract
Fractional Gravity/Cosmology in Classical and Quantum Regimes
Guest Editors: Seyed Meraj Mousavi Rasouli, Shahram JalalzadehDeadline: 31 May 2024
Special Issue in
Fractal Fract
Applications of Fractional-Order Calculus in Robotics
Guest Editors: Abhaya Pal Singh, Kishore BingiDeadline: 15 June 2024









