On Setting Day-Ahead Equity Trading Risk Limits: VaR Prediction at Market Close or Open?
Abstract
:1. Introduction
2. Overnight Information for Modeling Daily Prices
2.1. Overnight and Daytime Integrated Variance Processes
2.2. Bivariate Modeling Approach
2.3. Univariate Ex Post Overnight Modeling Approach
3. Risk Management Framework
3.1. VaR Forecasts
3.2. Predictive Ability Tests
3.3. Backtesting
4. Empirical Application
4.1. Data and Descriptive Statistics
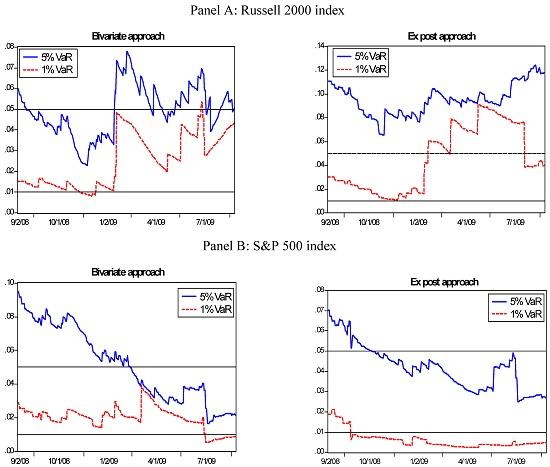
4.2. VaR Predictions and Evaluation
5. Conclusions
Author Contributions
Conflicts of Interest
References
- George, T.J.; Hwang, C.-Y. Information flow and pricing errors: A unified approach to estimation and testing. Rev. Financ. Stud. 2001, 14, 979–1020. [Google Scholar] [CrossRef]
- Jones, C.; Kaul, G.; Lipson, M. Information, trading and volatility. J. Financ. Econ. 1994, 36, 127–154. [Google Scholar] [CrossRef]
- French, K.R.; Roll, R. Stock return variances: The arrival of information and the reaction of traders. J. Financ. Econ. 1986, 17, 5–26. [Google Scholar] [CrossRef]
- De Gooijer, J.G.; Diks, C.G.H.; Gatarek, L.T. Information Flows around the Globe: Predicting Opening Gaps from Overnight Foreign Stock Price Patterns; Tinbergen Institute Discussion Papers 09-107/4; Tinbergen Institute: Rotterdam, The Netherlands, 2009. [Google Scholar]
- Ahoniemi, K.; Fuertes, A.M.; Olmo, J. Overnight news and daily equity trading risk limits. J. Financ. Econ. 2015, 13, 1–27. [Google Scholar]
- Stoll, H.R.; Whaley, R.E. Stock market structure and volatility. Rev. Financ. Stud. 1990, 3, 37–71. [Google Scholar] [CrossRef]
- Ahoniemi, K.; Lanne, M. Overnight Returns and Realized Volatility. SSRN Working Paper. Available online: http://ssrn.com/abstract=1945687 (accessed on 5 September 2012).
- Chan, K.; Chan, K.C.; Karolyi, G.A. Intraday volatility in the stock index and stock index futures market. Rev. Financ. Stud. 1991, 4, 657–684. [Google Scholar] [CrossRef]
- Masulis, R.W.; Shivakumar, L. Does market structure affect the immediacy of stock price responses to news? J. Financ. Quant. Anal. 2002, 37, 617–648. [Google Scholar] [CrossRef]
- Lin, W.-L.; Engle, R.F.; Ito, T. Do bulls and bears move across borders? International transmission of stock returns and volatility. Rev. Financ. Stud. 1994, 7, 507–538. [Google Scholar] [CrossRef]
- Giacomini, R.; White, H. Tests of conditional predictive ability. Econometrica 2006, 74, 1545–1578. [Google Scholar] [CrossRef]
- Engle, R.F.; Manganelli, S. CAViaR conditional autoregressive Value-at-Risk by regression quantiles. J. Bus. Econ. Stat. 2004, 22, 367–381. [Google Scholar] [CrossRef]
- Barclay, M.J.; Hendershott, T. A comparison of trading and non-trading mechanisms for price discovery. J. Empir. Financ. 2008, 15, 839–849. [Google Scholar] [CrossRef]
- Hasbrouck, J. High frequency quoting: Measurement, detection and interpretation. In Proceedings of the 5th EMG-ESRC Workshop on the Microstructure of Financial Markets, London, UK, 3–4 May 2012.
- Andersen, T.G.; Bollerslev, T.; Huang, X. A reduced form framework for modeling volatility of speculative prices based on realized variation measures. J. Econ. 2011, 160, 176–189. [Google Scholar] [CrossRef]
- Corsi, F.; Mittnik, S.; Pigorsch, C.; Pigorsch, U. The volatility of realized volatility. Econ. Rev. 2008, 27, 46–78. [Google Scholar] [CrossRef]
- Thomakos, D.D.; Wang, T. Realized volatility in the futures markets. J. Empir. Financ. 2003, 10, 321–353. [Google Scholar] [CrossRef]
- Andersen, T.G.; Bollerslev, T.; Diebold, F.X.; Ebens, H. The distribution of realized stock return volatility. J. Financ. Econ. 2001, 61, 43–76. [Google Scholar] [CrossRef]
- Taylor, N. A note on the importance of overnight information in risk management models. J. Bank. Financ. 2007, 31, 161–180. [Google Scholar] [CrossRef]
- Martens, M. Measuring and forecasting S & P 500 index-futures volatility using high-frequency data. J. Futures Mark. 2002, 22, 497–518. [Google Scholar]
- Giot, P.; Laurent, S. Modeling daily Value-at-Risk using realized volatility and ARCH type models. J. Empir. Financ. 2004, 11, 379–398. [Google Scholar] [CrossRef]
- Žikĕs, F. Semiparametric Conditional Quantile Models for Financial Returns and Realized Volatility; Mimeo Imperial College London, Business School: London, UK, 2009. [Google Scholar]
- Fuertes, A.-M.; Olmo, J. Optimally harnessing inter-day and intra-day information for daily value-at-risk prediction. Int. J. Forecast. 2013, 29, 28–42. [Google Scholar] [CrossRef]
- Hansen, P.R.; Lunde, A. A realized variance for the whole day based on intermittent high-frequency data. J. Financ. Econom. 2005, 3, 525–554. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E.; Shephard, N. Econometric analysis of realised volatility and its use in estimating stochastic volatility models. J. R. Stat. Soc. Ser. B 2002, 64, 253–280. [Google Scholar] [CrossRef]
- Corsi, F. A Simple Long Memory Model of Realized Volatility; University of Southern Switzerland: Lugano, Switzerland, 2004; mimeo. [Google Scholar]
- Ghysels, E.; Santa-Clara, P.; Valkanov, R. The MIDAS Touch: Mixed Data Sampling Regression Models; University of North Carolina: Chapel Hill, NC, USA, 2004; mimeo. [Google Scholar]
- Glosten, L.; Jagannathan, R.; Runkle, D. On the relation between the expected value and the volatility of the nominal excess return on stocks. J. Financ. 1993, 48, 1779–1801. [Google Scholar] [CrossRef]
- Engle, R.F. Dynamic conditional correlation—A simple class of multivariate GARCH models. J. Bus. Econ. Stat. 2002, 20, 339–350. [Google Scholar] [CrossRef]
- Aielli, G.P. Dynamic conditional correlation: On properties and estimation. J. Bus. Econ. Stat. 2013, 31, 282–299. [Google Scholar] [CrossRef]
- Wu, L. Variance dynamics: Joint evidence from options and high-frequency returns. J. Econ. 2011, 160, 280–287. [Google Scholar] [CrossRef]
- Liu, C.; Maheu, J. Forecasting realized volatility: A bayesian model-averaging approach. J. Appl. Econ. 2009, 24, 709–733. [Google Scholar] [CrossRef]
- Fuertes, A.-M.; Izzeldin, M.; Kalotychou, E. On forecasting daily stock volatility: The role of intraday information and market conditions. Int. J. Forecast. 2009, 25, 259–281. [Google Scholar] [CrossRef]
- Basel Committee on Banking Supervision. Supervisory Framework for the Use of “Backtesting” in Conjunction with the Internal Models Approach to Market Risk Capital Requirements; Bank for International Settlements: Basel, Switzerland, 1996. [Google Scholar]
- Kuester, K.; Mittnik, S.; Paolella, M.S. Value-at-Risk prediction: A comparison of alternative strategies. J. Financ. Econ. 2006, 4, 53–89. [Google Scholar] [CrossRef]
- Angelidis, T.; Degiannakis, S. Econometric modeling of Value-at-Risk. In New Econometric Modeling Research; Toggins, W.N., Ed.; Nova Science Publishers Inc.: New York, NY, USA, 2008. [Google Scholar]
- Giacomini, R.; Komunjer, I. Evaluation and combination of conditional quantile forecasts. J. Bus. Econ. Stat. 2005, 23, 416–431. [Google Scholar] [CrossRef]
- Clements, M.P.; Galvão, A.B.; Kim, J.H. Quantile forecasts of daily exchange returns from forecasts of realized volatility. J. Empir. Financ. 2008, 15, 729–750. [Google Scholar] [CrossRef]
- Brownlees, C.T.; Gallo, G.M. Comparison of volatility measures: A risk management perspective. J. Financ. Econ. 2010, 8, 29–56. [Google Scholar] [CrossRef]
- Diebold, F.X.; Mariano, R.S. Comparing predictive accuracy. J. Bus. Econ. Stat. 1995, 13, 253–263. [Google Scholar]
- West, K.D. Asymptotic inference about predictive ability. Econometrica 1996, 64, 1067–1084. [Google Scholar] [CrossRef]
- West, K.D.; McCracken, M.W. Regression-based tests of predictive ability. Int. Econ. Rev. 1998, 39, 817–840. [Google Scholar] [CrossRef]
- Newey, W.K.; West, K.D. Hypothesis testing with efficient methods of moment estimation. Int. Econ. Rev. 1987, 28, 777–787. [Google Scholar] [CrossRef]
- Christoffersen, P.; Hahn, J.; Inoue, A. Testing and comparing Value-at-Risk measures. J. Empir. Financ. 2001, 8, 325–352. [Google Scholar] [CrossRef]
- Koenker, R.; Xiao, Z. Quantile autoregression. J. Am. Stat. Assoc. 2006, 101, 980–990. [Google Scholar] [CrossRef]
- Candelon, B.; Hurlin, C.; Colletaz, G.; Tokpavi, S. Backtesting Value-at-Risk: A GMM duration-based test. J. Financ. Econ. 2011, 9, 314–343. [Google Scholar] [CrossRef]
- Berkowitz, J.; Christoffersen, P.; Pelletier, D. Evaluating Value-at-Risk models with desk-level data. Manag. Sci. 2011, 57, 2213–2227. [Google Scholar] [CrossRef]
- Dumitrescu, E.I.; Hurlin, C.; Pham, V. Backtesting Value-at-Risk: From dynamic quantile to dynamic binary tests. Finance 2012, 33, 112. [Google Scholar]
- Bandi, F.M.; Russell, J.R. Microstructure noise, realized variance and optimal sampling. Rev. Econ. Stud. 2008, 75, 339–369. [Google Scholar] [CrossRef]
- Greene, J.T.; Watts, S.G. Price discovery on the NYSE and the Nasdaq: The case of overnight and daytime news releases. Financ. Manag. 1996, 25, 19–42. [Google Scholar] [CrossRef]
- 2.De Goojier et al. [4] exploit full information in the intra-day stock price patterns in foreign markets during non-trading hours in a home market to predict the opening of an index in the home market.
- 3.Stoll and Whaley [6] document empirically that it took around five to six minutes in the 1980s for large stocks to open for trading on the NYSE. Of course, with the advent of electronic trading platforms, the average time to open in today’s markets is much shorter, but large cap stocks are still expected to open for trade faster than small cap stocks. Various empirical studies implicitly acknowledge this “delay”in price discovery. Ahoniemi and Lanne [7] and Chan et al. [8] both wait until 5 min of trading has elapsed before calculating an overnight return. Masulis and Shivakumar [9] waits 15 min, and Lin et al. [10] wait for a full 30 min.
- 4.Barndorff-Nielsen and Shephard [25] show that converges to as at rate where M denotes the intraday sampling frequency. As a byproduct of this, these authors show that the realized variance is a consistent estimator of the sum of the integrated daily variance process and the sum of the daytime jumps.
- 5.Other specifications that have been used in the empirical finance literature to approximate the long memory properties of the realized volatility are Corsi’s [26] heterogeneous autoregressive (HAR) model and Ghysels et al.’s [27] Mixed Data Sampling (MIDAS) model both of which combine information sampled at different frequencies.
- 6.Aielli [30] proves that the standard DCC method can yield inconsistent estimates of the model parameters for large systems that invalidate the traditional interpretation of the DCC correlation parameters. This author also proposes a cDCC procedure based on reformulating the DCC correlation driving process as a linear multivariate generalized autoregressive conditional heteroscedasticity (MGARCH) process. For consistency with the univariate specifications of the conditional volatility of the daytime and overnight return processes presented in this paper, we use, instead, the version of the DCC model proposed in Ahoniemi et al. [5].
- 8.Our interest is in long trading positions. For short trading positions one would analyze instead the right tail, i.e., . Commercial banks are required to report VaR at confidence level 99% to regulators but most banks adopt the 95% level for internal backtesting. We consider both coverage levels .
- 9.Other conditional coverage tests have been developed based on the duration between consecutive violations; see e.g., Candelon et al. [46] The test is based on OLS estimation of the linear probability model

| In-Sample November 1997–August 2008 | Out-of-Sample September 2008–September 2011 | |||||||
|---|---|---|---|---|---|---|---|---|
| Russell 2000 | S & P 500 | Russell 2000 | S & P 500 | |||||
| ro,t | rd,t | ro,t | rd,t | ro,t | rd,t | ro,t | rd,t | |
| night | day | night | day | night | day | night | day | |
| Panel A: returns | ||||||||
| Mean | 0.020 | 0.000 | 0.007 | 0.005 | −0.004 | −0.014 | −0.012 | −0.004 |
| Median | 0.005 | 0.040 | 0.003 | 0.047 | 0.007 | 0.138 | 0.000 | 0.095 |
| StDev | 0.234 | 1.271 | 0.190 | 1.092 | 0.572 | 2.136 | 0.249 | 1.780 |
| Skewness | −0.525 | −0.074 | −0.249 | −0.031 | −0.283 | −0.358 | −0.254 | −0.362 |
| Kurtosis | 19.80 | 4.026 | 14.99 | 5.600 | 6.930 | 6.015 | 7.774 | 8.586 |
| Correlation structure: | ||||||||
| −0.089 *** | −0.028 | −0.092 *** | 0.001 | −0.149 *** | −0.064 * | −0.118 *** | −0.026 | |
| 0.162 *** | 0.202 *** | 0.273 *** | 0.390 *** | |||||
| 0.041 ** | 0.015 | −0.011 | −0.038 ** | −0.040 | −0.085 ** | −0.048 | −0.122 | |
| (ACF) | 60.6 | 38.64 | 60.78 | 35.21 | 36.62 | 28.07 | 37.12 | 52.53 |
| Mean (hourly) | 0.003 | 0.248 | 0.002 | 0.183 | 0.019 | 0.701 | 0.004 | 0.487 |
| Median | 0.006 | 0.597 | 0.004 | 0.361 | 0.096 | 1.120 | 0.011 | 0.457 |
| StDev | 0.237 | 2.810 | 0.135 | 2.556 | 0.797 | 10.22 | 0.162 | 8.724 |
| Skewness | 14.16 | 4.661 | 11.58 | 7.089 | 8.880 | 5.307 | 6.353 | 5.905 |
| Kurtosis | 254.6 | 39.42 | 196.5 | 89.15 | 117.3 | 43.48 | 57.41 | 46.17 |
| (ACF) | 156.4 | 1697 | 247.9 | 1058 | 186.8 | 1151 | 441.3 | 1107 |
| Panel A: Bivariate Approach | Panel B: Ex Post Overnight Approach | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Russell 2000 | S & P 500 | Russell 2000 | S & P 500 | ||||||
| AR-GJR-GARCH model (overnight) | AR-ARFIMA model (daytime) | ||||||||
| 0.0181 | (0.0028) | 0.0044 | (0.0021) | −0.0291 | (0.0207) | −0.0040 | (0.0154) | ||
| −0.0031 | (0.0021) | −0.0074 | (0.0018) | 0.0440 | (0.0184) | −0.0315 | (0.0162) | ||
| −0.0659 | (0.0144) | −0.0692 | (0.0140) | −0.0032 | (0.0925) | 0.2307 | (0.0991) | ||
| −0.0001 | (0.0000) | 0.0002 | (0.0001) | 1.0553 | (0.0893) | 1.6801 | (0.1113) | ||
| 0.0900 | (0.0171) | 0.0720 | (0.0127) | −0.8061 | (0.0247) | −0.8067 | (0.0228) | ||
| 0.8620 | (0.0169) | 0.9080 | (0.0124) | 0.2313 | (0.0186) | 0.3115 | (0.0196) | ||
| 0.0020 | (0.0006) | 0.0011 | (0.0004) | −0.6453 | (0.0300) | −0.8424 | (0.0310) | ||
| −0.0274 | (0.0144) | −0.0340 | (0.0156) | 1.0250 | (0.0797) | 1.7658 | (0.1212) | ||
| 2.9625 | (0.1212) | 2.9017 | (0.1679) | −2.4760 | (0.1214) | −3.9167 | (0.1868) | ||
| AR-ARFIMA model (daytime) | θ | −0.5250 | (0.0230) | −0.5204 | (0.0147) | ||||
| −0.0074 | (0.0208) | 0.0039 | (0.0159) | d | 0.4829 | (0.0186) | 0.4949 | (0.0070) | |
| 0.0425 | (0.0189) | −0.0407 | (0.0167) | 0.9752 | (0.0692) | 0.9255 | (0.0558) | ||
| −0.0988 | (0.0917) | 0.0790 | (0.1081) | −0.1008 | (0.0242) | −0.1273 | (0.0211) | ||
| −0.5360 | (0.3810) | −0.5360 | (0.7020) | 12.1365 | (2.2368) | 6.6662 | (0.7253) | ||
| 0.3059 | (0.0194) | 0.3576 | (0.0207) | ||||||
| −0.8021 | (0.0308) | −0.9397 | (0.0325) | ||||||
| θ | −0.5482 | (0.0149) | −0.5386 | (0.0127) | |||||
| d | 0.4933 | (0.0088) | 0.4966 | (0.0046) | |||||
| 1.1431 | (0.0736) | 1.0666 | (0.0620) | ||||||
| −0.1310 | (0.0240) | −0.1138 | (0.0196) | ||||||
| 14.1627 | (3.0623) | 6.5079 | (0.7316) | ||||||
| DCC model (overnight-daytime) | |||||||||
| α | 0.0146 | (0.0105) | 0.0049 | (0.0085) | |||||
| β | 0.6828 | (0.2402) | 0.7716 | (0.1480) | |||||
| Bivariate w/o Covariance | Ex Post Overnight | ||
|---|---|---|---|
| Panel A: Russell 2000 | |||
| 5% VaR | 0.000 | 0.419 | |
| 1% VaR | 0.000 | 0.061 | |
| Panel B: S & P 500 | |||
| 5% VaR | 0.000 | 1.000 | |
| 1% VaR | 0.000 | 1.000 | |
| Bivariate | Ex Post Overnight | Bivariate | Ex Post Overnight | ||
|---|---|---|---|---|---|
| Russell 2000 | S & P 500 | ||||
| Panel A1: Equally-weighted J backtesting windows (J = 279) | |||||
| DQ test (5% VaR) | 0.222 | 0.480 | 0.237 | 0.032 | |
| DQ test (1% VaR) | 0.291 | 0.097 | 0.251 | 0.237 | |
| Probit test (5% VaR) | 0.151 | 0.741 | 0.566 | 0.097 | |
| Probit test (1% VaR) | 0.068 | 0.097 | 0.835 | 0.194 | |
| Panel A2: Equally-weighted 1/3J backtesting windows | |||||
| DQ test (5% VaR) | 0.667 | 0.957 | 0.301 | 0.097 | |
| DQ test (1% VaR) | 0.570 | 0.269 | 0.333 | 0.290 | |
| Probit test (5% VaR) | 0.452 | 1.000 | 1.000 | 0.290 | |
| Probit test (1% VaR) | 0.204 | 0.290 | 0.677 | 0.312 | |
| Panel A3: Equally-weighted 2/3J backtesting windows | |||||
| DQ test (5% VaR) | 0.000 | 0.238 | 0.200 | 0.000 | |
| DQ test (1% VaR) | 0.151 | 0.011 | 0.205 | 0.205 | |
| Probit test (5% VaR) | 0.000 | 0.611 | 0.346 | 0.000 | |
| Probit test (1% VaR) | 0.000 | 0.000 | 0.914 | 0.135 | |
| Panel B: Weighted by Absolute Coverage Error | |||||
| DQ test (5%> VaR) | 0.191 | 0.514 | 0.381 | 0.047 | |
| DQ test (1% VaR) | 0.242 | 0.054 | 0.171 | 0.281 | |
| Probit test (5% VaR) | 0.085 | 0.750 | 0.726 | 0.113 | |
| Probit test (1% VaR) | 0.021 | 0.048 | 0.813 | 0.236 | |
| Panel C1: Weighted Asymmetrically Underprediction > Overprediction | |||||
| DQ test (5% VaR) | 0.050 | 0.514 | 0.329 | 0.280 | |
| DQ test (1% VaR) | 0.243 | 0.054 | 0.143 | 0.924 | |
| Probit test (5% VaR) | 0.045 | 0.750 | 0.939 | 0.672 | |
| Probit test (1% VaR) | 0.021 | 0.048 | 0.807 | 0.919 | |
| Panel C2: Weighted Asymmetrically Overprediction > Underprediction | |||||
| DQ test (5% VaR) | 0.318 | 0.567 | 0.447 | 0.001 | |
| DQ test (1% VaR) | 0.184 | 0.019 | 0.749 | 0.174 | |
| Probit test (5% VaR) | 0.120 | 0.775 | 0.482 | 0.002 | |
| Probit test (1% VaR) | 0.003 | 0.016 | 0.949 | 0.122 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuertes, A.-M.; Olmo, J. On Setting Day-Ahead Equity Trading Risk Limits: VaR Prediction at Market Close or Open? J. Risk Financial Manag. 2016, 9, 10. https://0-doi-org.brum.beds.ac.uk/10.3390/jrfm9030010
Fuertes A-M, Olmo J. On Setting Day-Ahead Equity Trading Risk Limits: VaR Prediction at Market Close or Open? Journal of Risk and Financial Management. 2016; 9(3):10. https://0-doi-org.brum.beds.ac.uk/10.3390/jrfm9030010
Chicago/Turabian StyleFuertes, Ana-Maria, and Jose Olmo. 2016. "On Setting Day-Ahead Equity Trading Risk Limits: VaR Prediction at Market Close or Open?" Journal of Risk and Financial Management 9, no. 3: 10. https://0-doi-org.brum.beds.ac.uk/10.3390/jrfm9030010