1. Introduction
Mycotoxin contamination in cereals has been recognised as a global threat for human and animal health, especially under the pressure of climate change [
1,
2]. Deoxynivalenol (DON) produced by
Fusarium spp. (mainly
Fusarium graminearum and
Fusarium culmorum) is one of the most studied and frequently occurring mycotoxin in winter wheat globally. Contamination of wheat with
Fusarium spp. and DON is influenced by the wheat variety, agronomic practices (e.g., tillage), and local weather, especially around wheat flowering. Monitoring and predictive modelling have become some of the solutions for farmers, collectors, and food safety authorities to manage mycotoxin contamination during cereal cultivation and beyond. Some predictive models for mycotoxins have been developed and implemented in agricultural sectors in Europe as decision support systems for farmers [
2,
3,
4,
5,
6,
7,
8]. These models have been developed by either an empirical or mechanistic modelling approach. In the past five years, models have been updated with recent monitoring data, and modelling techniques have been improved. For example, machine learning algorithms have recently been introduced in food safety areas [
9,
10]. Machine learning explores the study of pattern recognition and computational learning theory in artificial intelligence. Such algorithms can learn from sample inputs and make data-driven predictions or decisions [
11]. Bayesian network (BN) modelling is one of many machine learning algorithms, and can possibly also be used to predict mycotoxin contamination in cereals.
Logistic regression is a classic method to estimate the parameters of a logistic model, in which the log-odds of the probability of a binary event (e.g., presence or absence of mycotoxins) is a linear combination of independent variables [
12]. Logistic regression is used in various areas, such as in medicines, social sciences, and life sciences. Mixed effects models contain both fixed effects (variables in the regression model) and random effects. With a hierarchical structure in the data (e.g., with repeated sampling in the same year/at the same farm), such a mixed model with random effects can improve the prediction accuracy.
A BN model is a probabilistic model that is based on Bayesian statistics and decision theory in combination with graph theory [
13,
14]. It is a directed graphical model that represents conditional probabilities among a set of variables, based on the application of the Bayes’ theorem. Compared to linear regression models, BN models can more easily analyze dependencies between variables, manage non-linear interaction, and combine different sorts of information, such as measurement data, expert knowledge, and end-user feedback [
15].
Mechanistic models simulate the fundamental mechanisms of plant and fungus development stages and their interactions. Such models require well-developed knowledge of each biological process, as well as extensive experimental research under a wide range of conditions to collect the required knowledge and input data.
This study aimed to compare and cross-validate three different modelling approaches, i.e., the empirical, BN, and mechanistic approach, for predicting DON contamination in winter wheat using data from the Netherlands as a case study. These models aim to support decision-making by farmers regarding limiting mycotoxin contamination by optimizing their agricultural management practices, such as fungicide sprays and harvest time. Grain collectors can also use the model predictions to buy wheat from low-risk areas in advance, or to optimize sampling plans for mycotoxin analysis. Food safety authorities can use the model predictions to locate high-risk areas for a more targeted and cost-efficient mycotoxin monitoring. Cross-validation of the three modelling techniques was done to further understand the pros and cons of each technique, and contribute to future research and progress in the prediction of mycotoxin contamination in food and feed.
3. Discussion and Conclusions
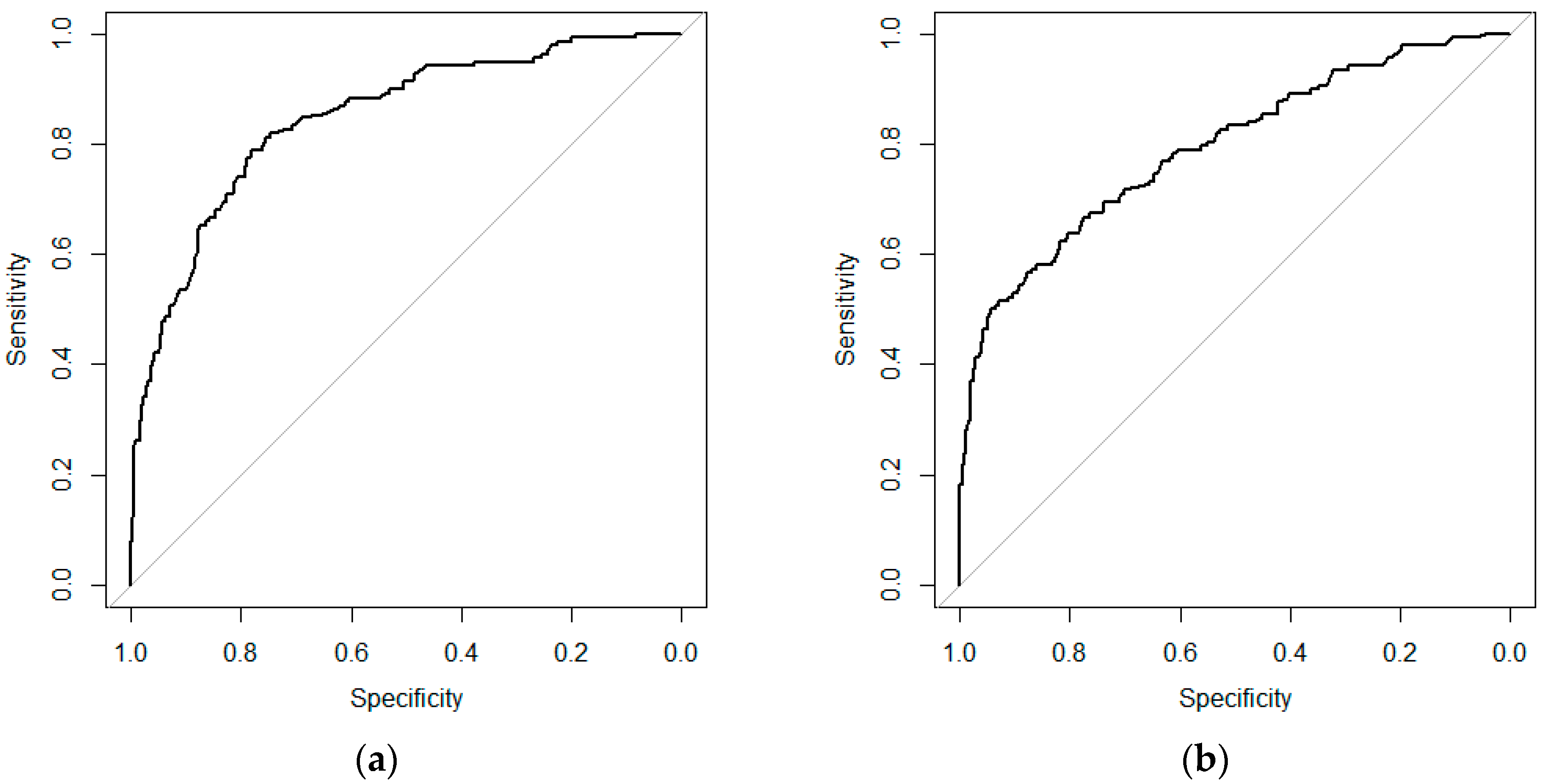
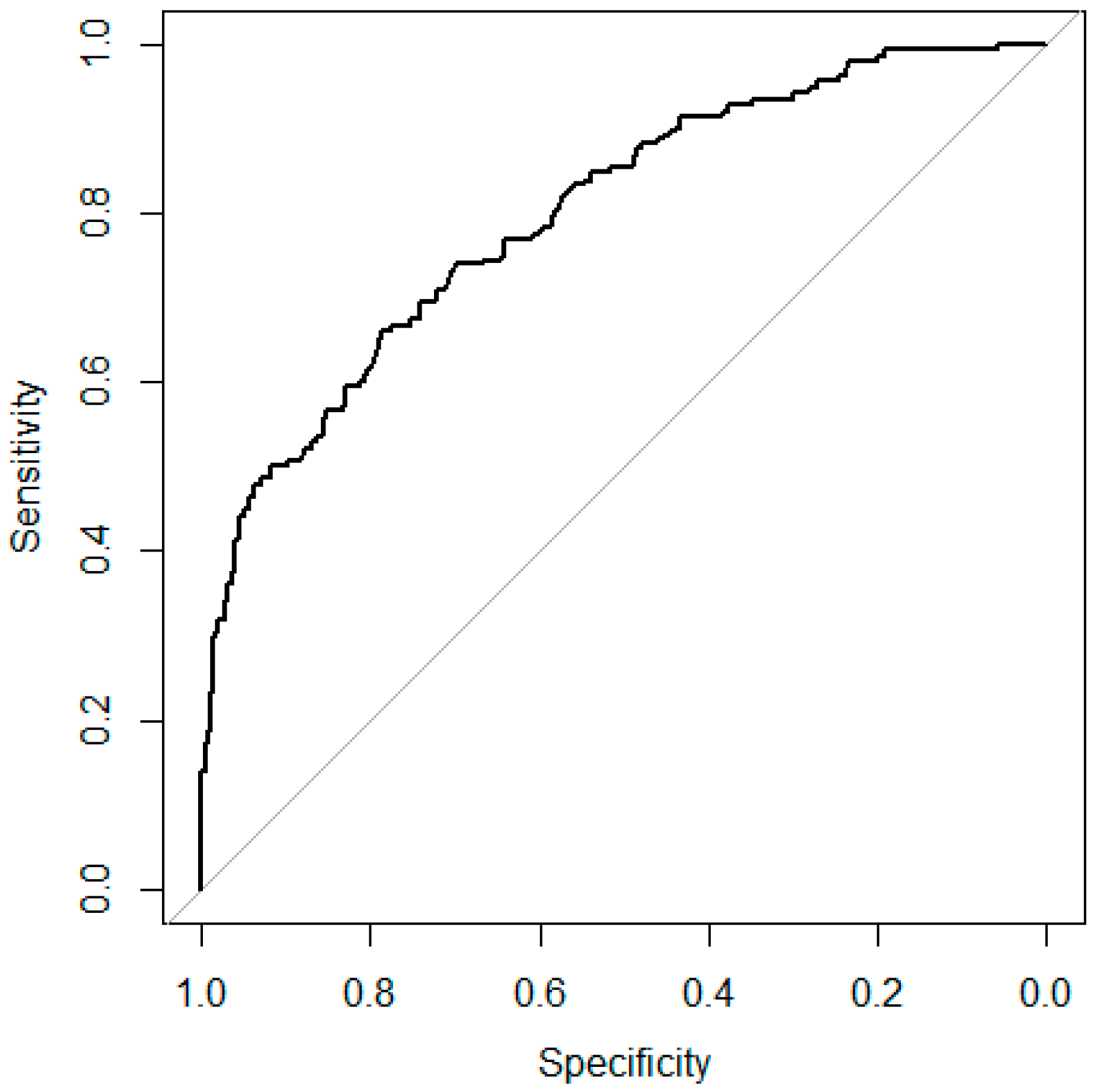
This study compared the performances of three modelling approaches for predicting DON contamination in winter wheat by using Dutch data as a case study. Two of these models (the regression-based and the BN models) are new, while the third model (the mechanistic model) was adapted (included in a DFA) for being used with Dutch data. These models have been calibrated with the same dataset collected between 2001–2013 in the Netherlands, and cross-validated with another dataset collected in 2015 and 2016 in the Netherlands. From this exercise, the pro and cons of three modelling approaches are summarized, and results are discussed (
Table 9).
Logistic regression is a classic and well-studied modelling approach that is applied in many research fields, including the food safety area. In this study, an evolution of a previously published empirical model [
3] is presented. The updated model uses mixed effect logistic regression with recent field data, and predicts DON contamination classes instead of concentrations. Out of the three considered modelling approaches, mixed effect logistic regression models had the highest accuracy for low DON contamination, but not for medium and high contaminations. This method shows the statistical relationship between independent variables and the response variable collected in a specific agricultural context, which is the Dutch wheat-growing areas, in this case. Therefore, this method is highly data-dependent (
Table 9), which implies that the regression parameter estimates cannot be used for other agricultural conditions than represented with the data used in model development, before proper validation. In addition, the model cannot be run in cases where data on one of the input variables (e.g., the resistance level of the variety) is missing. This implies that with the current models, predictions can only start from one week before FD (with using 10 days of weather forecast data).
In this study, a new Bayesian network model to predict DON contamination at harvest in winter wheat has been developed. The BN model predicted all of the cases in the low DON contamination class, and had an accuracy of 94.3%. Similar to the regression models, the BN model was not able to correctly predict any of the DON contamination cases in the medium or high class from the validation dataset. The structure of the BN enables the model developer to easily add new information and/or expert knowledge in the model. BN models can use a combination of statistical relationships and expert knowledge (
Table 9). The BN model is flexible, and can predict DON contamination even when only one variable is available. For instance, the BN model can calculate a base risk using GArea and ResisL at the beginning of the growing season. With these two variables, the BN model correctly predicted 81.6% of the cases (70 cases in the low class and one case in the high class) (data not shown). This largely extends the prediction possibilities to the start of the growing season. In this study, the BN model included all of the variables used in the regression models, in order to compare the two modelling approaches based on the same variables. In future studies, the best set of variables will be selected for the BN only.
The mechanistic model of Rossi et al. [
16,
17] was included in the DFA in order to classify DON contamination of winter wheat in the Netherlands. Similar to the other models, the mechanistic model and DFA were not able to correctly predict any DON contamination cases in the medium class, but the model predicted correctly one of the two cases in the high DON class.
In summary, all three modelling approaches have good prediction accuracy in forecasting low DON contamination in winter wheat in the Netherlands, and are suitable for providing decision support to farmers and collectors. In the present work, the three modelling approaches were developed and tested using data mostly composed by cases in the ‘low’ class of DON contamination. Further validation is needed to confirm the accuracy of the model predictions in cases in which DON contamination is higher and close to the European Union (EU) legal limit.
Implementing a mycotoxin forecasting model that has been developed for certain conditions, such as for one wheat-growing area or country, to other conditions as represented in the data used for model development, should always be done with utmost care and proper model testing and validation. From the experiences gained in our study, it was shown that the three modelling approaches each have their own advantages and disadvantages (
Table 9).
Regression-based models and BN models are empirical. Being developed and parameterised based on a specific dataset, they represent the mathematical relationships among that data or similar conditions only. Therefore, empirical models should only be used for those conditions, such as the area/country, as represented by the observational data used for model development. Thus, these models are unsuitable to predict situations that did not occur in the model development dataset (
Table 9), such as extreme weather events due to climate change or new agricultural practices (e.g., increase of conservation tillage or diffusion of new crop rotation types, which both affect the Fusarium head blight, or FHB, inoculum availability). BN models can include expert’s knowledge, and are very flexible regarding add new information to the forecasting system. In addition, BN models can produce output with incomplete information on the model’s input variables, even though this may lead to a reduction in the accuracy of their outputs.
The mechanistic model, by definition, simulates the biological processes, which are in this case fungal infection, growth, and mycotoxin production. Such process-based models are not highly location-dependent, and are thus much easier to implement in other countries (
Table 9). However, the mechanistic model has rather high requirements for data availability, and runs with specific types of data, such as heading date and leaf wetness duration, which are not always available. Furthermore, spatial differences on fungal species still need to be considered when implementing a mechanistic model in different wheat-growing areas. For instance, the frequency of
Fusarium spp. and mycotoxigenic strains within species differs between North/Central Europe and South Europe [
18]. Due to the low presence of
F. culmorum in winter wheat grown in the Netherlands [
19], only
F. graminearum was considered in the current mechanistic model for the Netherlands, whereas both
F. graminearum and
F. culmorum were considered in the Italian model.
Since all of the different modelling approaches have both pro and cons, a modelling ensemble in which different model types are combined could be interesting solution. Constructing such a modelling ensemble is part of the EC-funded MyToolBox project [
20]. It will integrate the models in a unique framework and strengthen their advantages to provide more timely and accurate advice, in order to limit mycotoxin contamination and improve the safety of cereals and derived feed and food commodities.
4. Materials and Methods
4.1. Data
In the years 2001–2013 (except for 2012), mature winter wheat samples were collected from 632 fields (records) in the Netherlands (
Figure 4). Agronomic information of these fields was also collected and included postal code, wheat variety, ResisL, Spray_freq, ploughing (yes/no), tillage method, pre-crop, observed FD, and observed harvesting date (HD). ResisL was divided into four groups with decreasing proneness to DON contamination: susceptible (5 and 5.5), medium susceptible (6, 6.5), medium resistant (7, 7.5), and resistant (8, 8.5). All of the agronomic information was collected by means of a farmer questionnaire. Unfortunately, not all of the agronomic information was available for all of the wheat fields.
Weather inputs included hourly temperature, precipitation, and relative humidity from 25 automatic weather stations in the Netherlands. These data are freely available from the Royal Netherlands Meteorological Institute (KNMI) website (
http://www.knmi.nl/nederland-nu/klimatologie/daggegevens). Then, each field was assigned to the nearest weather station based on postal codes. The average distance between a field and assigned weather station was 12 km, ranging from a minimum distance of <2 km to a maximum distance of 37 km.
Samples of wheat kernels were collected at harvest from the combiner machine. Each sample contained 1 kg of mature winter wheat kernels. The samples were transported to the laboratory of RIKILT Wageningen University & Research. At RIKILT, DON was extracted and quantified using a liquid-chromatography with double in-line mass spectrometry (LC-MS/MS) [
21]. The limit of quantification (LOQ) varied over the years from 5 µg/kg to 100 µg/kg. The highest LOQ was therefore used in further data analysis, and samples with DON concentrations below this LOQ were assigned the value of 100 µg/kg.
Observed FD and observed HD of the wheat field was not always recorded by the farmer. Therefore, the FD and HD of all of the winter wheat fields were calculated based on the sum of the daily average temperatures above 0 °C, using the method described in Van der Fels-Klerx et al. [
3].
The variable GArea was used in the models to test the influence of the farm’s geographical location on the DON concentrations. GArea was calculated using geostatistical spatial analysis Kriging in ArcMap version 10.4.1 (Environmental Systems Research Institute, Redlands, CA, USA) [
22]. Standardized DON concentrations ((DON value − average)/standard deviation) were used in the calculation [
5]. Using kriging interpolation, seven standardized DON classes were calculated from low to high. GArea was then defined as seven cultivation areas in the Netherlands with a proneness or potential probability of DON contamination in wheat, which were further grouped into three classes (standardized DON values ≤0.08, 0.08–2, >2) as in Rossi et al. (2007) for model comparison. With this calculation, the GArea class at any unknown location was obtained as a weighted average of the standardized DON contamination in the neighborhood of the location.
The wheat-growing season was divided into seven time windows that were each one week in length, by using FD as day 0. Day 0 was defined as 1 pm on the previous day to 12 am on the current day. The weekly time windows started from 24 days prior to FD to four days after FD and one week around HD, and were defined as follows:
W0: FD − 24 1 pm to FD − 17 12 am,
W1: FD − 17 1 pm to FD − 10 12 am,
W2: FD − 10 1 pm to FD − 3 12 am,
W3: FD − 3 1 pm to FD + 4 12 am,
W4: FD + 4 1 pm to FD + 11 12 am,
W5: FD + 11 1 pm to HD − 3 12 am,
W6: HD − 3 1 pm to HD + 4 12 am
Note that FD and HD were positioned in the middle of the time windows W3 and W6 to limit the influence of estimating FD and HD using growing degree days. All of the time windows consisted of seven days except for W5. The length of W5 (in days) varied between the wheat fields, because the time between FD and HD differed per location due to the differences in local weather. For each time window, the following weather variables were calculated:
Tavg: Average hourly temperature in the time window (°C)
Tmin: Minimum hourly temperature in the time window (°C)
Tmax: Maximum hourly temperature in the time window (°C)
P: Sum of the precipitation in the time window (mm)
RHh80: Number of hours that relative humidity was higher than 80% (hour)
Th25: Number of hours that temperature was higher than 25 °C (hour)
The regression model and the Bayesian network (BN) model were developed using R (version 3.3.2). The mechanistic model was developed using SPSS (version 24; IBM Corp., Armonk, NY, USA). All of the models predicted the probability of DON concentrations at harvest in three classes (DONclass): low (≤500 µg/kg), medium (500 µg/kg to 1250 µg/kg), and high (>1250 µg/kg).
4.2. Mixed Effect Logistic Regression Model
The stepwise selection was performed combining significant (p-value < 0.25) weather and agronomic variables to predict DON concentrations in winter wheat. Year was added as a random effect to the model to test whether it improved model performance, as assessed by the Akaike information criterion (AIC). The farmers’ model (Model C) and the collectors’ model (Model D) were developed using weather variables till around the flowering period (W1–W4) and the entire cultivation period (W1–W6), respectively.
Mixed effect linear regression models were developed in three steps: univariate analysis, stepwise logistic regression, and adding random effects. All of the statistical tests were assessed for significance at the 95% confidence level (
p < 0.05), except for the univariate analysis (
p < 0.25). Univariate analysis was performed following the method detailed in Van der Fels-Klerx [
3]. The resulting agronomic and weather variables were considered in the stepwise logistic regression analyses. Then, year was added as a random effect to the model, in order to explain yearly variation in DON concentrations without using year as a prediction variable. The AIC was used to compare and select the best-fitting model. FD and HD were centred and scaled (dividing the centred data by their standard deviations) in the mixed effect model to limit the large differences in the scales of parameters, especially with calculating standard deviations of fixed effects. The pre-crop and tillage variables were not included in the model, because more than two-thirds of the records had no information about pre-crop or tillage.
The final models calculated the probabilities of DON concentrations above 500 µg/kg as P1 and above 1250 µg/kg as P2. The probabilities of three DON classes were then calculated as: Low Class = 1 − P1, Mid Class = P2 − P1, and High Class = P2. The predicted class of each sample was finally defined as the class with the highest probability.
To assess the model performance, a 10-fold internal cross-validation was conducted. Data for model development (2001 to 2013) were randomly divided into 10 subsets of equal size, and nine subsets were used for training the model, while the 10th subset was used to test the model’s performance. This process was repeated 10 times, every time with a different test subset. So, all of the records were used for both training and testing, and each record was used for validation once. The mean area under the curve (AUC) was calculated.
4.3. Bayesian Network Model
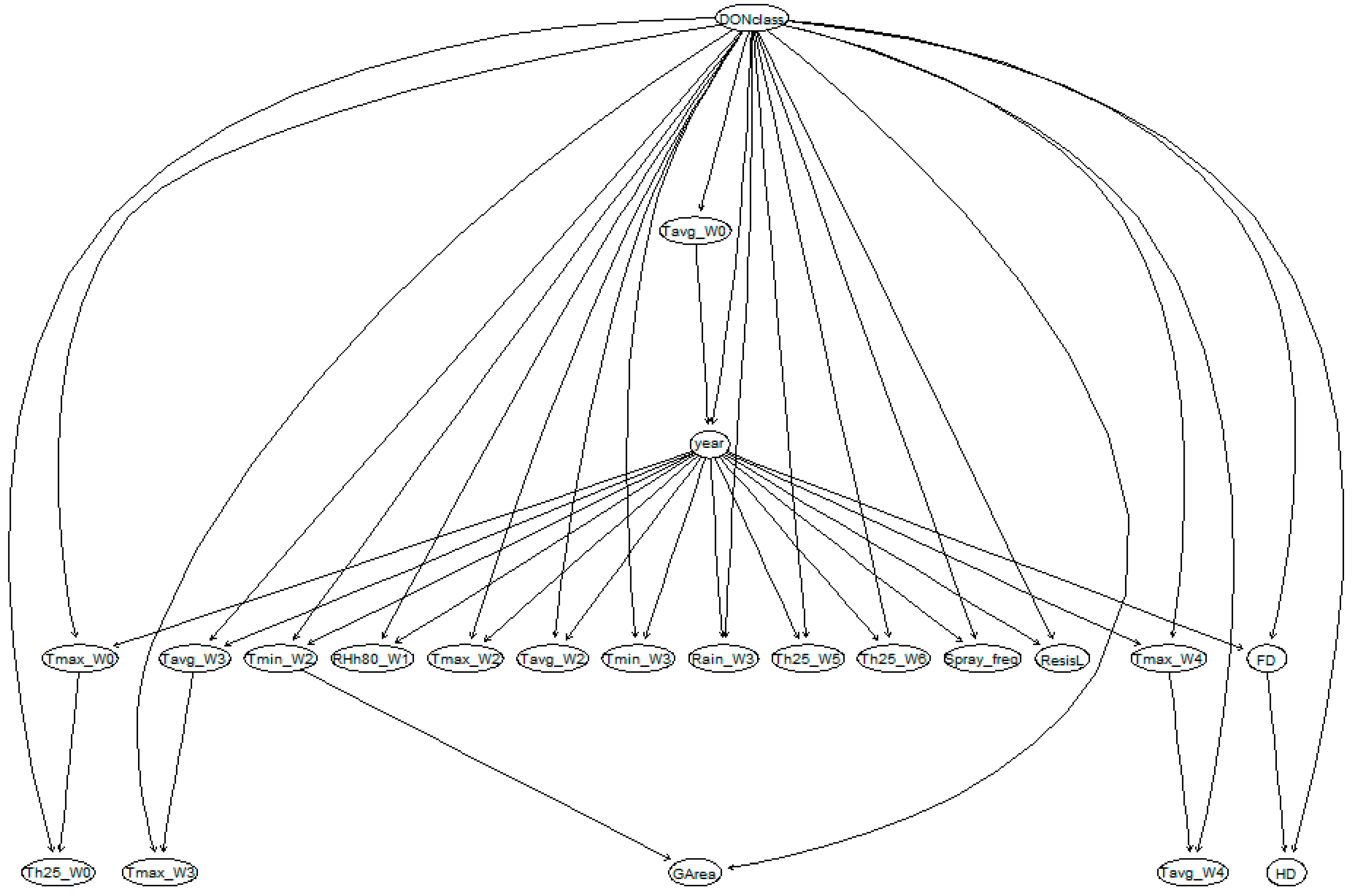
BN model development consists of four steps: (1) define variables of interests (also called notes), (2) structure learning, (3) parameter learning to calculate conditional probability tables (CPTs) for each parameter, and (4) BN validation. In order to compare different modelling approaches, a BN model was developed using the same variables as in the mixed effect linear regression models. The machine learning technique ‘Tree-Augmented Naive (TAN) Bayes’ learning algorithms was used to learn the BN model structure and compute the CPTs [
23]. The structure and parameter learning steps were performed using the R package ‘bnlearn’ [
24]. Continuous weather variables were discretised into discrete variables with eight clusters (same number of levels for variable year) by equal interval width, in order to ease and optimise the computation in the ‘bnlearn’ package. The validation step is detailed in
Section 4.5.
In this setting, the relationships among all of the variables were constructed and indicated as directed edges. Note that these directed edges do not present the causal relationships, but rather only the statistical relationships among variables.
4.4. Mechanistic Model
A mechanistic model for Fusarium head blight (FHB) and mycotoxin contamination, taking into account the effect of weather, was developed by Rossi et al. [
16,
17] using the system analysis approach [
25,
26]. Equations of the model were developed using data obtained from basic research on the biology and epidemiology of the main
Fusarium species involved in FHB in Italy (i.e.,
F. graminearum,
F. culmorum,
F. avenaceum, and
M. nivale). These studies were carried out under both controlled-environment and field conditions. As
F. graminearum is the main species present in the Netherlands [
19], the mechanistic model was adapted to consider this fungal species only.
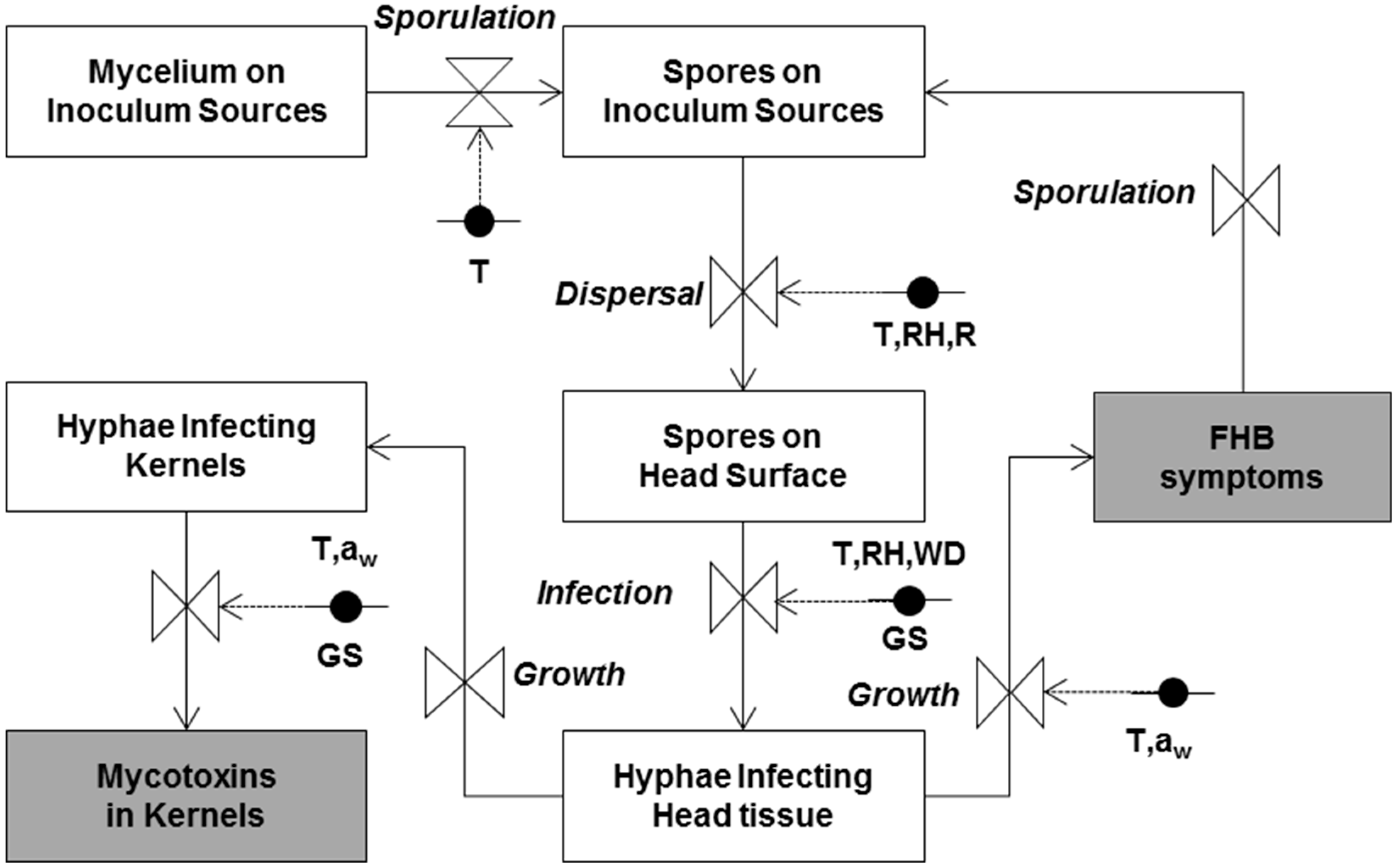
The simplified relational diagram of the model is shown in
Figure 5. State variables (in rectangular boxes) represent the status of the pathogen at a given moment. The flow (arrows) from one state variable to another is regulated by rate variables (drawn as valves), and defined as the rate of change of the state variables in time as a function of driving variables, which are constants or parameters influencing these rate variables. Rates are regulated by mathematical equations describing the relationships between the rate and the (external) influencing weather and plant variables. Circles indicate variables influencing each rate, and are linked to valves by dotted arrows. The modelling steps are detailed in the original papers by Rossi et al. [
16,
17,
26].
In a previous work [
5,
19], data for cropping practices collected in Italy in multi-annual surveys have been subjected to a cluster analysis based on the standardized DON concentration in the wheat sampled collected from the monitored fields. The categorical variables for wheat variety resistance and growing area have been combined with the model output (FHB-tox) by discriminant function analysis (DFA). Briefly, the procedure automatically selected a function (F1) that is able to separate the three classes of DON contamination as much as possible [
27].
In this study, a new DFA was carried out on the (model development) data of the 625 fields collected in years between 2001–2013. DFA was used to determine the probability that each case belonged to each of the three DON contamination groups, determine group membership based on these probabilities, and obtain information on the effect of the discriminant variables on group membership. To determine group membership, the prior probability of group membership was set as proportional to the number of observations in each group (i.e., 0.78 for low, 0.13 for medium, and 0.09 for high DON contamination). For the effect of discriminant variables on group membership, the canonical coefficients (CCs) and standardised canonical coefficients (SCCs) were calculated. The magnitude of CCs and SCCs is an indicator of the weight of each variable in each of the discriminant functions.
4.5. Validation of Three Models
The three models were validated using field data collected in 2015 and 2016 in the Netherlands from 87 fields. These data were collected similarly as the data for model development from 2001 to 2013, as described in
Section 4.1. These validation data have not been used previously for any model development or testing. Samples were classified for their DON contamination as previously described. For each of the three model types, the predicted probabilities of each sample in the DON classes of low, medium, or high were compared with the observed DON classes of low, medium, or high.
For validation of the logistic regression models (Model C and Model D), the parameter coefficients of Model C and Model D (
Section 2.1) were used to solve the logistic functions. The same method as described in
Section 4.2 was used to calculate the probabilities of each of the three contamination classes.
The BN model used the structure and conditional probabilities learned from the model development dataset for the prediction. Predictions of DONclass were tested given all of the information on agronomic factors. The parent note DONclass gave the probabilities of the three DON classes.
DFA enables prediction of new cases based on the previously established structure. DFA was evaluated for the prediction of the DON contamination class (i.e., low, medium, or high) by using the FHB-tox index calculated at wheat harvest, and the values of the other discriminant variables for the 87 validation records. These data were used to solve the canonical discriminant function by using the non-standardised canonical coefficients calculated in
Section 4.4. A non-linear regression was calculated between the value of the discriminant function for each sample (F1) and the corresponding probability (P(x)) to belong to the low or high class of DON contamination according to the following equation:
where a and b are equation parameters.
The probability for a field to belong to the medium class was calculated as the difference between one and the sum of the probabilities of the low and high classes.
Results of the fitting of Equation (1) were used to calculate the probabilities to assign new samples to the classes low, medium or high.