Next Article in Journal / Special Issue
Evolution of Cooperation with Peer Punishment under Prospect Theory
Previous Article in Journal
Measuring and Disentangling Ambiguity and Confidence in the Lab
Previous Article in Special Issue
Categorization and Cooperation across Games
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Games
Volume 10
Issue 1
10.3390/g10010010
games-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Linkage Based on the Kandori Norm Successfully Sustains Cooperation in Social Dilemmas

by
Misato Inaba
1,2,* and
Nobuyuki Takahashi
3,4
1
Japan Society for the Promotion of Science, 5-3-1 Kojimachi, Chiyoda-ku, Tokyo 102-0083, Japan
2
Department of Sociology, Kansai University, 3-3-35 Yamate-cho, Suita-shi, Osaka 564-8680, Japan
3
Department of Behavioral Science, Graduate School of Letters, Hokkaido University, N.10, W.7, Kita-ku, Sapporo, Hokkaido 060-0810, Japan
4
Center for Experimental Research in Social Sciences, Hokkaido University, N.10, W.7, Kita-ku, Sapporo, Hokkaido 060-0810, Japan
*
Author to whom correspondence should be addressed.
Games 2019, 10(1), 10; https://0-doi-org.brum.beds.ac.uk/10.3390/g10010010
Submission received: 29 November 2018 / Revised: 25 January 2019 / Accepted: 10 February 2019 / Published: 21 February 2019
(This article belongs to the Special Issue The Evolution of Cooperation in Game Theory and Social Simulation)
Browse Figure
Versions Notes

Abstract

:
Since social dilemmas among n-persons are often embedded in other types of social exchanges, the exclusion of defectors in social dilemmas from other exchanges functions as a costless selective incentive. Recently, such “linkage” has been considered as a promising solution to resolve the social dilemma problem. However, previous research showed that cooperation sustained by linkage is fragile when subjective perception errors exist. The purpose of this study is to find linkage strategies that are robust against subjective perception errors. Based on the strategies presented in previous studies on indirect reciprocity, we devised several linkage strategies and examined their evolutionary stability by agent-based simulation. The simulation results showed that the linkage strategy based on kandori was evolutionarily stable even when perception errors existed. Our study provides substantial support for the argument that linkage is a plausible solution to the social dilemma problem.

1. Introduction

Cooperation is essential for the progression of human societies. This is especially true for large-scale cooperation, which is one of the most notable characteristics of human society, because large-scale cooperation benefits are shared amongst all members of a group. However, such cooperation should be vulnerable to the force of natural selection because individuals can free ride to receive the fruits of others’ efforts. In these settings, individuals cannot prohibit defectors from enjoying the benefits produced by other members. In the social sciences, this problem is referred to as a social dilemma (SD), a public goods problem or an n-person prisoner’s dilemma problem and it has been studied extensively in many disciplines, including economics, psychology, anthropology, biology and physiology [1,2,3,4,5].
Other than kin selection [6,7,8,9], network reciprocity [10,11,12,13,14,15,16,17,18,19] and direct reciprocity [20,21,22,23,24,25,26,27], introducing a punishment is one of the most thoroughly investigated solutions to SDs [28,29,30,31,32]. Punishments transform the payoff structure of the SD so that free-riders cannot receive a higher payoff. With a punishment, the penalty imposed on a defector either can cancel out the benefit of free riding or can even make free-riders worse off than cooperators. However, the imposition of punishments generates another problem, which is called the second-order free-rider problem [29,32,33]. Since punishment inflicts a personal cost onto the punisher and given that it is impossible to prohibit nonpunishers from enjoying the benefit of punishments (i.e., a higher level of cooperation), the provision of punishment also creates another SD problem. Several answers to this problem have been proposed, such as meta-punishment (i.e., punishment toward second- or higher-order free-riders) [34,35,36,37], signaling (i.e., cooperators receive relational benefits later because cooperation signals one’s quality as a worthy individual) [38,39,40,41], coevolution of punishment and other traits [42,43] and spatial structures [44].
In the current study, we focus on the “linkage” between SDs and indirect social exchanges (ISEs) as a solution to the SD problem that does not include the second-order free-rider problem [45,46,47,48]. The SD problem does not exist in isolation. It is embedded in various kinds of social interactions, such as when members within a society try to supply public goods while simultaneously trying to conduct ISEs with another type of good based on unilateral giving between individuals. Cooperation in an ISE can be sustained by indirect reciprocity [49,50,51,52,53,54,55,56,57,58,59,60,61]. In a situation where an SD game and an ISE coexist, it is possible to design new strategies that cannot have been realized when each game is considered separately. One such strategy is the linkage strategy, which excludes people who defected in the SD game from the ISE. Past studies have shown that the linkage strategy does not inflict additional costs when compared to strategies that do not link two games, indicating that the second-order free-rider problem will not occur when using this strategy [46,47,48]. However, its evolutionary stability is not robust in situations where perception errors exist [48]. Therefore, in this current study, we devise several variations of linkage strategies in order to find a linkage strategy that is evolutionarily stable even in the presence of perception errors.
Panchanathan and Boyd [46] showed that a linkage strategy called Shunner, which does not offer help to an SD defector in ISEs, could be an evolutionarily stable strategy (ESS). In their model, players engaged in two social interaction stages. In the first stage, players engaged in a one-shot SD game in which each player decided whether or not to cooperate with members in the group. There was a cooperation cost C to the player and a benefit B that was shared equally amongst the n − 1 other group members (C < B). The second stage was an ISE in which players engaged in one form of an ISE called a multi-period mutual aid game. In each period, one player was randomly selected from a group and denoted as “needy” while each other member decided whether to help the needy player or not. There was a helping cost c incurred by the helper, which then yielded a benefit b to the needy player (0 < c < b). In this model, there was a possibility of implementation errors occurring in the ISE. For instance, such an error could occur when a player intended to help the needy but failed to do so. Everyone in the population knew the behavioral history of all group members in both stages.
The strategies in Panchanathan and Boyd’s model consisted of how to behave in the SD and in the ISE. There were two SD strategies, which were to defect or to cooperate. There were four possible strategies in the ISE, which were the following—All-D (never helps needy players), All-C (always helps needy players) and the final two strategies instruct that players should use others’ behavioral histories to assign reputation in the ISE. These two strategies using reputation based on the standing (explained below) [55,56,62], which is one of the norms for assigning reputation scores that makes mutual cooperation possible in an ISE (Table 1). From the viewpoint of standing, all players have a good score at the beginning of the game. Players lose their good scores if they fail to help a needy player who has a good score during the ISE. Those whose scores are bad can restore their good scores by helping a needy player in the future. The standing strategy only helps a needy player who has a good score. In Panchanathan & Boyd [46], the original discriminator strategy required that players ignore other players’ behaviors in the SD when they assign reputations. This original discriminator strategy stated that only the players’ ISE behaviors matter. In contrast, the linkage discriminator strategy regarded SD defectors as being permanently bad even if the defectors helped a needy player. The linkage discriminator applied their norm only to SD cooperators and this strategy therefore never helped SD defectors in the ISE. Their study includes eight possible strategies (see Table 2), four of which were investigated by Panchanathan and Boyd [46]. 1. Defectors defected in both games; 2. Cooperators cooperated in both games; 3. Reciprocators defected in the SD and played as original discriminators in the ISE; 4. Shunners (who applied the linkage strategy) cooperated in the SD and played as linkage discriminators in the ISE. Their results showed that the Shunners resisted being invaded by the other three strategies.
Inaba, Takahashi, and Ohtsuki [48] investigated the evolutionary stability of a Shunner against a new strategy called the Cooperating-Reciprocator (Table 2) using the same game structure as Panchanathan & Boyd [46]. They showed that, in the model in which the possibility of an implementation error could only occur in the ISE, Shunners were not evolutionarily stable against Cooperating-Reciprocators. Because both Cooperating-Reciprocators and Shunners cooperated in the SD, there was no chance that Shunners took action against players who defected in the SD. Consequently, these two strategies took the exact same action and were evolutionarily neutral. 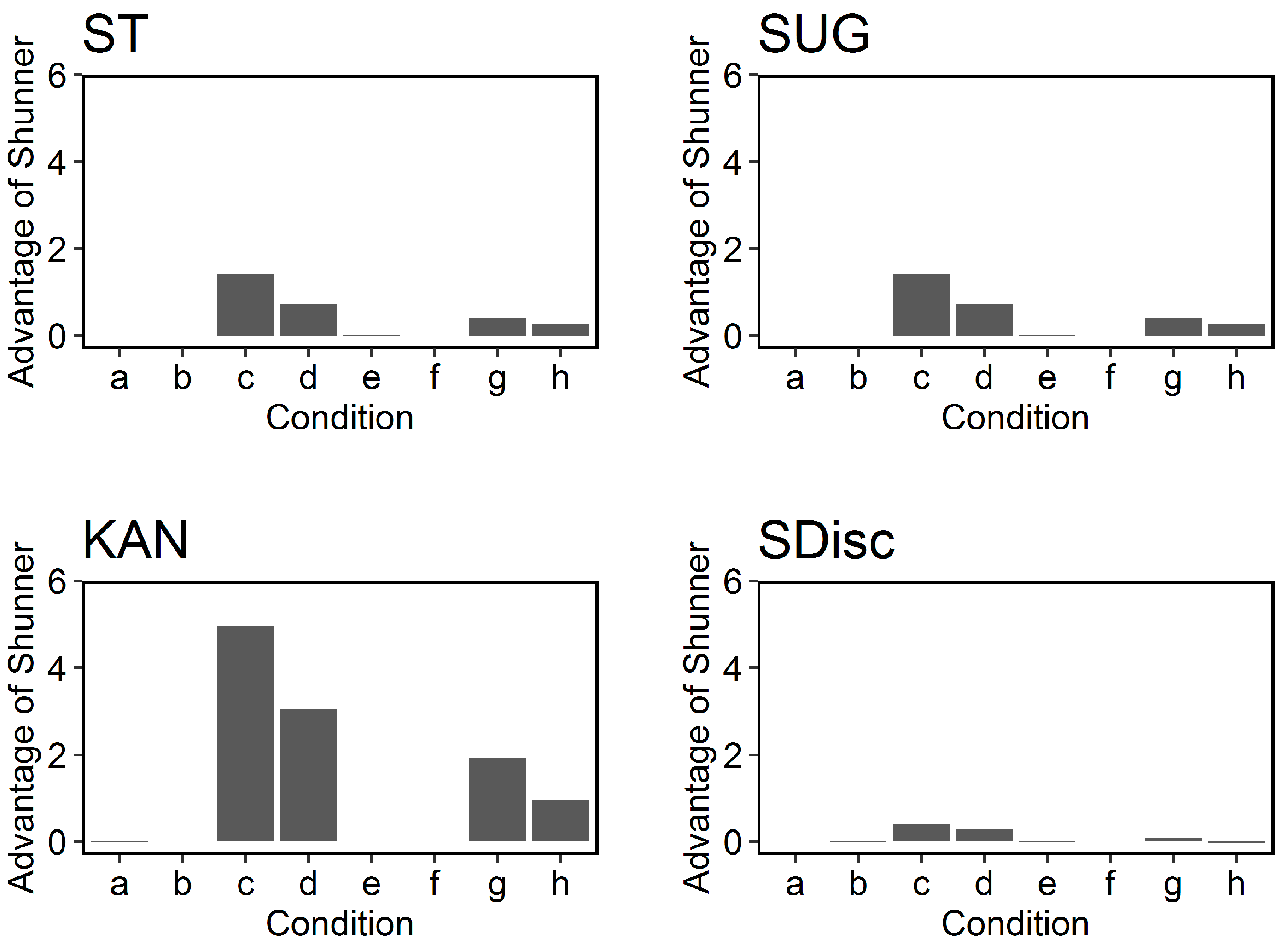In addition, Inaba, Takahashi, and Ohtsuki [48] conducted a series of computer simulations under the assumption that various error types could occur. They derived eight types of errors based on three dimensions—whether errors occurred only in the ISE or both in the ISE and the SD, whether perception errors could occur and whether errors could occur one way or two ways (Table 3). Each player might misperceive an action performed by another player, which was called a perception error based on a direct observation model [56]. Players who were willing to cooperate might mistakenly defect because of an error, which was called a one-way error. Players might cooperate or defect randomly ignoring the action that was prescribed by their employing strategy. It was called a two-way error. As a result, the existence of errors significantly affected the evolutionary stability of the Shunner. Their results showed that the linkage strategy was an ESS only when there were implementation errors in both the SD and the ISE (conditions c and d in Table 3). However, the linkage strategy was less unstable when perception errors existed (conditions g and h). In terms of the direction of the error, they found that the linkage strategy was more stable under one-way implementation error conditions than under two-way implementation error conditions. On the other hand, the linkage strategy was more stable under two-way perception error conditions than under one-way perception errors conditions.
When subjective perception errors are small, a linkage strategy in an ISE can be used as a solution for a group to achieve cooperation. However, people are hardly free from perception errors in their social lives. Does this mean that the linkage strategy can be evolutionarily stable under implausible situations only? We expect that there are some linkage strategies that are evolutionarily stable even in conditions when perception errors do exist. In previous studies, Shunners assigned a reputation to others based on standing. However, several other strategies with a different norm have been proposed in the indirect reciprocity literature [49,51,52,56,58,63,64,65,66]. Moreover, several of these strategies are known to be robust against subjective perception errors [63].
Ohtsuki and Iwasa [51,52] investigated the evolutionary stability of 4,096 strategies in ISEs. Each strategy included a norm and an action rule. A norm told a player how to judge the reputations of others and an action rule told a player which behavior to take depending on the recipient’s score and the player’s own score. Of the investigated 4,096 strategies, the researchers identified the most effective set of ESS strategies, which they called the leading eight. The common features of these strategies’ norms specified that (1) cooperation toward a good recipient is good while defection toward a good recipient is bad and (2) defection toward a bad recipient is good. Standing is included in the leading eight.
Ohtsuki and Iwasa’s model [51,52] was based on the indirect observation model, which specifies that everyone in the population has the same opinion of a focal player and therefore players did not suffer from subjective perception errors. Takahashi and Mashima [63] explored the effect of subjective perception errors on the evolutionary dynamism of indirect reciprocity. They investigated the evolutionary stability of 16 norms with the assumption that all individuals employ one kind of action rule in which the donor helps when they assess the recipient as good and refuse to help otherwise. They found that two norms, the strict discriminator (i.e., shunning [49,53]) and kandori (i.e., extra standing [63] or stern-judging [64]), were not invaded by either an All-C or an All-D strategy (see Table 1 for the norms). Under the strict discriminator, helping a good individual is the only action that can lead to a player developing a good reputation. Since strict discriminators assign bad reputations to players who defected toward bad recipients, it does not satisfy the criterion of the leading eight. On the other hand, kandori is a member of the leading eight. Under this rule, helping a good individual or refusing help to a bad individual leads to a good score, whereas refusing help to a good individual or helping a bad one leads to a bad score. Moreover, Takahashi and Mashima [36] showed that the sugden strategy was invaded by an All-D strategy when the cost-benefit ratio was low. Sugden is sometimes called simple-standing [53] because it is slightly different from standing in d4b (Table 1). Sugden is also a member of the leading eight. Ohtsuki and Iwasa [53] also investigated the evolutionary stability of norms under perception errors in which a player makes a mistake in interpreting the reputations of others where one-way implementation errors existed. They showed that the sugden, kandori, and strict discriminator strategies were evolutionarily stable when perception errors did not exist, but they found that these strategies were all unstable when perception errors did exist.1 We summarized the results of previous studies in Table 4. These results suggest that the evolutionary stabilities of strategies that adopt promising norms are affected by perception errors.
In this research, we examined the robustness of several types of linkage strategies that adopt different norms in order to examine which type of linkage strategies can firmly attain cooperation in SD games. We investigated standing, sugden, strict discriminator and kandori. Considering that multiple action rules make the model more complex, we only examined one type of action rule in which the donor helps if he/she assesses the recipient as good and refuses to help otherwise. The details of our evolutionary simulation were based on Inaba, Takahashi, and Ohtsuki [48].

2. Methods

2.1. Simulation Settings

We conducted a series of agent-based computer simulations. The settings of the computer simulations were basically the same as the ones used in Inaba, Takahashi, and Ohtsuki [48]. The only difference was the game structure of ISE, which will be explained later. We designed a group that was composed of n = 100 players, and the players engaged in two social interaction stages. In the first stage, players engaged in a one-shot SD game. Players could incur a cooperation cost C = 5, and we created a benefit B = 10 that was shared equally amongst the 100 − 1 = 99 other group members. The second stage was an ISE stage. The players participated in a multi-period “giving game,” which has a one-way, two-player relationship. Many studies have used this game to model ISEs. In each period, all players became donors. A donor was paired with a recipient who was randomly selected from the group. A donor decided whether or not to help his or her recipient. When a donor decided to help, there was a helping cost c = 1 to the donor, which yielded a benefit b = 2 to the recipient. Although previous research on linkages [46,48] used the mutual aid game as an ISE, the giving game was more commonly used as a model of ISE [51,52,58,63].2 In order to confirm that the evolutionary stability of the linkage strategy was not affected by the structure of the game, we used the giving game and compared the results to Inaba, Takahashi, and Ohtsuki’s results [48]. In our game, all group members knew the behavioral history of all players in both stages. The giving game continued for exactly 20 periods.
After the ISE stage was complete, the reproduction process occurred. Each player’s payoff was determined by the sum of their payoffs in both stages and by the baseline payoff W0 = 100. Replicator dynamics were derived based on the following rule—the more successful a player was in the previous generation, the more offspring he reproduced for the subsequent generation in a manner that was proportional to his payoff [68]. Following Grefenstette [69], we used stochastic universal sampling developed by Baker [70] in order to reduce the effects that were associated with the random fluctuation of genes. This sampling method was very simple; for each strategy, we calculated its net payoff in the population and we sampled n players in the daughter generations proportionally to the net payoffs. Mutations occurred between the generations with probability m = 0.0001 per player. If a mutation occurred, the mutated player randomly employed one of the strategies under consideration. After a mutation occurred, a single generation ended. The simulation continued for g = 10,000 generations.
We introduced eight types of errors following Inaba, Takahashi, and Ohtsuki [48] (Table 3). There was a probability δ of each player performing an action that was different from the one prescribed by the strategy. In our simulation, we had two values for δ: δ = 0.05 or 0. δsd denotes the probability of implementation errors occurring in the SD and δise denotes the probability of implementation errors occurring in the ISE. There was also a probability ε for each player to misperceive an action performed by another player. We had two values for ε: ε = 0.05 or 0. εsd denotes the probability of perception errors occurring in the SD and εise denotes the probability of perception errors occurring in the ISE. Under one-way error conditions, players who were willing to cooperate mistakenly defected with probability δ, and each player mistakenly perceived the act of cooperation by players as defection with probability ε. Under two-way error conditions, each player took an action that was not prescribed by the given strategy, but instead was randomly chosen with probability δ, and each player randomly perceived other players’ actions incorrectly with probability ε.

2.2. Strategies

Our strategies were classified into five categories: Defector, Cooperator, Cooperating-Reciprocator, Defecting-Reciprocator and Shunner (see Table 2). A Defector defects in both the SD and the ISE, while a Cooperator cooperates in both the SD and the ISE. Cooperating-Reciprocator, Defecting-Reciprocator and Shunner adopt one of the norms. Cooperating-Reciprocators and Defecting-Reciprocators only care about their recipient’s behaviors in the ISE (i.e., Original Discriminator). In contrast, Shunners regard SD defectors as being permanently bad even if the SD defectors take actions that should be assigned a good score according to the norm (i.e., Linkage Discriminator). Linkage Discriminator applies the norm only to SD cooperators and therefore never helps SD defectors in the ISE.
We investigated four norms: standing (ST), which has been used in previous research [46,48]; sugden (SUG); kandori (KAN); and strict discriminator (SDisc). We described our strategies as a combination of a categorized strategy and a norm, such as the C-R (ST), which cooperates in the SD and helps good recipients in the ISE under the standing criterion.
We investigated two or three strategies in each simulation. One of the strategies we referred to as a wild-type strategy and the other(s) as mutant strategies. At the beginning of each replication, all agents employed what we call a wild-type strategy. During each replication, a mutant was born by mutation. In each simulation, the strategy that the mutant employed was determined randomly with equal probability given to all possible strategies. We judged that invasion occurred based on how many times 10 or more players adopted mutant strategies in the last generation. Within a specific replication, we only considered the combinations of strategies that adopted the same norm [e.g., S(ST) vs. C-R(ST)]. In other words, we did not consider the combinations of strategies that adopted different norms [e.g., S(ST) vs. C-R(SDisc)]. We conducted 20 replications per each combination of strategies for each condition.
The evolutionary dynamics between S and C-R contribute additional worthy information to the evolutionary stability of the linkage strategy [48]. Therefore, in addition to examining whether mutant strategies can invade, we conducted additional simulations in the population composed of S and C-R for 100,000 generations without any selections or mutations. We calculated the average payoff for each strategy.

3. Results

3.1. Replication

In this study, we used the giving game in the ISE stage instead of the mutual aid game that had been used in previous linkage studies [46,48]. First, we confirmed that our simulation results were consistent with past studies. Table 5 shows the results of the simulations when the strategies had a standing. As shown in Table 5, Shunners [i.e., S(ST)] were not invaded by Defectors, Cooperators or Defecting-Reciprocator under any of the error conditions. However, Shunners were invaded by Cooperating-Reciprocators in the simulations in which players do not make perception errors or errors in the SD game (conditions a and b), and in the simulations with perception errors (conditions e–h). Once the Cooperating-Reciprocator strategy spread in the population, the Defecting-Reciprocators, who defect in the SD game, were able to invade (simulation 5 in Table 5). Therefore, the key to the success of cooperation sustained by linkage was based on whether or not Shunners were invaded by Cooperating-Reciprocators. These results are completely consistent with the results in Inaba, Takahashi, and Ohtsuki [48].
In order to observe the details of the evolutionary dynamics between Shunners and Cooperating-Reciprocators, we calculated the average payoff of each strategy in a population that consisted of 96 Shunners and four Cooperating-Reciprocators without any selections or mutations. Figure 1 shows the payoff advantage of Shunners against Cooperating-Reciprocators for each condition. A comparison of conditions c and d with conditions g and h shows that the advantage of Shunners was decreased by the presence of perception errors. Thus, the pattern of the payoff advantage of Shunners that decreased due to perception errors was replicated. Therefore, the ISE game type barely affected the robustness of the linkage strategy.

3.2. Other Norms

Our main interest is to find linkage strategies that are robust against perception errors. We examined the evolutionary stability of the linkage strategies when allowing for other norms. Table 6, Table 7 and Table 8 show the results of the simulations using each norm.
Shunners were not invaded by Defectors under sugden or kandori for any of the conditions (simulation 1 in Table 6 and Table 7). Under the strict discriminator, however, Shunners were invaded by Defectors when perception errors were present (simulation 1 in Table 8, conditions e, g, and h). For all conditions, Shunners were not invaded by Cooperators under the strict discriminator or kandori (simulation 2 in Table 7 and Table 8). Under sugden, Shunners were invaded by Defectors once in condition b (simulation 2 in Table 6). Shunners were not invaded by Defecting-Reciprocators for any of the condition under all of the norms (simulation 3 in Table 6, Table 7 and Table 8).
This study is particularly focused on the evolutionary dynamics of Shunners and Cooperating-Reciprocators. The results for these strategies were complicated. First of all, given that it is necessary to have errors in the SD in order to make a difference between the earnings of Shunners and Cooperating-Reciprocators, these two strategies were neutral in the conditions where SD errors were not present (conditions a–d) under all of the norms. Thus, Cooperating-Reciprocators randomly increased by genetic drift and Defecting-Reciprocators were eventually able to invade the population (simulation 7 in Table 6, Table 7 and Table 8). Next, when errors occurred in the SD (conditions e–h), Shunners and Cooperating-Reciprocators were not neutral. The Shunners, based on standing, were not invaded by Cooperating-Reciprocators when no perception errors existed; however, they were invaded when perception errors were present. Shunners, based on sugden or kandori, were not invaded by Cooperating-Reciprocators for any of the conditions with errors in the SD (conditions e–h), including conditions with perception errors (simulation 4 in Table 6 and Table 7, conditions g and h). However, Shunners, based on sugden, were invaded by Defecting-Reciprocators several times when Cooperating-Reciprocators and Defecting-Reciprocators invaded (simulation 7 in Table 6). On the other hand, Shunners were not invaded under kandori (simulation 7 in Table 7). Shunners, based on the strict discriminator, were invaded by Cooperating-Reciprocators when the condition allowed for the presence of perception errors (conditions g and h; simulation 4 in Table 8). Therefore, the linkage strategies based on kandori were more robust against perception errors than those based on standing. Although the strategies based on sugden were slightly more robust than those based on standing, they did not have sufficient evolutionary stability to resist effectively against invasion from Cooperating-Reciprocators. The linkage strategy based on both standing and the strict discriminator was weak against perception errors.
In order to observe details of the evolutionary dynamics between Shunners and Cooperating-Reciprocators, we calculated each strategy’s average payoff in a population that consisted of 96 Shunners and four Cooperating-Reciprocators without any selections or mutations. Figure 1 shows the payoff advantages of Shunners against Cooperating-Reciprocators in each condition for each norm. With sugden, and when perception errors existed (conditions g and h), the Shunners’ payoff advantages against the Cooperating-Reciprocators were approximately equal to their payoff advantages in standing. These results indicate that the sugden linkage strategy, in comparison to standing, was not more robust against perception errors. When kandori was applied as the norm, the difference in payoffs between the Shunners and the Cooperating-Reciprocators was dramatically enlarged when conditions c, d, g and h were met. Thus, the kandori linkage strategy was more robust against perception errors. On the other hand, when strict discriminator was used as the norm, Shunners had a smaller advantage against Cooperating-Reciprocators than under any other norm. It was common to all norms that the linkage’s advantage decreased when perception errors existed.
We summarize the results in Table 9. What causes these differences between norms? First, the only feature that makes sugden different from standing is that sugden judges the donor as good when those who had a bad reputation did not help a bad recipient (d4b in Table 1). This feature increases the possibility of recovering from bad to good if a player is badly evaluated due to a perception error. This mechanism seems to have slightly reduced the payoff difference due to perception errors.
Among the linkage strategies under consideration, kandori was the most successful norm. Kandori is different from standing and sugden because it judges a donor as bad if the donor helped a bad recipient (d3* in Table 1). As a result of this feature, kandori Shunners did not help the Cooperating-Reciprocators who helped SD defectors because these Shunners viewed such defectors as bad. For the linkage strategies based on standing and sugden, the following process is necessary for Shunners to refuse to help Cooperating-Reciprocators: first, Cooperating-Reciprocators do not help Shunners who do not help defectors in the SD, then Shunners stop helping Cooperating-Reciprocators who do not help a Shunner. However, with linkage strategies based on kandori, Shunners stop helping Cooperating-Reciprocators directly without going through such a process. For this reason, the Shunners’ payoff based on kandori outperforms the Cooperating-Reciprocators’ payoffs when Shunners are the majority group.
The strict discriminator was the weakest norm for attaining cooperation among all of the norms that we considered. The Shunners who used the strict discriminator rule were invaded by Defectors and Cooperating-Reciprocators under some conditions. The payoff differences between Shunners and Cooperating-Reciprocators were even smaller when conditions c and d were applied, in which cases Shunners were not invaded in the cases of other norms. This indicates that strict discriminators are vulnerable to both implementation and perception errors. Since the strict discriminator’s criterion of assigning a good score is very strict, strict discriminators are prone to judge the other players who are using the same norm as bad. Thus, strict discriminators cannot form successful indirect reciprocity when errors exist. In general, the payoff difference between Shunners and Cooperating-Reciprocators depends on the frequency of each strategy’s use [48]. Thus, the more they can build a successful ISE with players who engage in the same strategy, the more payoffs they can earn. However, because strict discriminators cannot build a profitable exchange, Shunners do not have an advantage against Cooperating-Reciprocators even when the frequency of their frequency is high.

4. Discussion

Previous research has proposed that linkage is a promising solution of SDs only if players do not suffer from perception errors [48]. However, since perception errors usually exist in our society, it is necessary that people overcome these errors so that groups can achieve cooperation. Therefore, we searched for other linkage strategies that are not affected by perception errors. We found several strategies that could sustain cooperation in SDs by linkage with ISEs even when perception errors existed. Linkage strategies with kandori in ISEs were most robust against perception errors. Thus, our study shows that cooperation in SDs can be maintained by linkage strategies with ISEs even when perception errors exist. We conclude that our results strongly support the view that a linkage strategy is one of the most effective solutions to the SD problem.
Kandori evaluates as bad a donor who helped a bad recipient. Consequently, one who adopts a linkage strategy based on kandori judges cooperation in the nonlinkage strategy as bad because the nonlinkage strategy helps defectors in SDs. This is the source of the linkage strategy’s advantage against the nonlinkage strategies under kandori. As a result, linkage was robust when perception errors exist. In order to identify violators of the linkage norm early in the game, it was important to assign bad scores to those who helped bad recipients (d3* in Table 1). It is known that kandori has an evolutionary advantage over other strategies [53,64,65,71]. The reason for this advantage is that kandori adjusts reputations quickly. It has one good action and one bad action for each type of encounter so that it becomes possible for players to readily punish bad players and to quickly forgive good ones [64]. Our results show that even in a linkage situation, this feature appeared as applying a direct punishment to others who had different norms (i.e., nonlinkage norm) and this led kandori players to their striking success.
As mentioned in the introduction, Ohtsuki and Iwasa [53] showed that kandori is not evolutionarily stable when perception errors exist. This result seems to contradict both the results of Takahashi and Mashima [63] and also our own results. There are two possible reasons for this inconsistency. First, Ohtsuki and Iwasa [53] investigated the robustness of norms against perception errors in a situation where implementation errors occur in one way. Second, Ohtsuki and Iwasa [53] stated that an agent who made a perception error mistakenly perceived the reputation score (i.e., good or bad), whereas in the current study and in that of Takahashi and Mashima [63], a perception error caused an agent to misperceive the action of the target (i.e., helped or not). Future studies should address how these differences affect the evolutionary stability of each norm.
We used the giving game as an ISE instead of the mutual aid game that had been used in previous linkage studies [46,48]. This alteration did not affect the results. Therefore, we assert that the results of our study can be generalized for other indirect reciprocity exchanges.
The limitation of this study is that we did not consider evolutionary dynamics between different norms [e.g., S[ST] vs. C-R[KAN]]. Pacheko, Santos, and Chalub [64] showed that kandori has an evolutionary advantage over other norm in ISE. On the other hand, Uchida and Sigmund [66] showed that sugden and kandori can coexist in ISE. Therefore, it is not clear what rule evolves when different norms exist within a society where an SD and an ISE coexist.
On the other hand, we may not need to consider the situation in which different norms coexist. Since cooperation cannot be achieved in SD without a supporting mechanisms such as sanction or linkage, it may be more appropriate to conceive that an ISE is formed first and then an SD can be established by linkage during the course of the development of human society. In that case, it is natural to consider whether the linkage strategy whose norm was originally evolved in ISEs can invade the society of the nonlinkage strategy employing the same norm.
It follows, then, the next step is to examine whether the linkage strategy can invade the nonlinkage strategy. Our simulation started with a population in which all players adopted a linkage strategy. If a population starts with a nonlinkage norm, the linkage strategies cannot invade that population. As previous linkage studies have mentioned [46,48], there is a need to examine the equilibrium selection process that enables the transition from a nonlinkage norm to a linkage norm. There are several candidates that might be useful for examining this issue, such as interactions with similar strategies [46], small population sizes [72], higher mutation rates [73], between-group competitions [74], selective immigration [75,76] and learning [77,78]. Future research should investigate whether a linkage norm could spontaneously emerge from a nonlinkage equilibrium.

Author Contributions

M.I. and N.T. designed the research, conducted the simulations, and wrote the paper.

Funding

This research was funded by JSPS KAKENHI Grant Numbers JP13J03067 and JP18J00870 to M.I., JP24653161 to N.T.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Boyd, R.; Richerson, P.J. The evolution of reciprocity in sizeable groups. J. Theor. Biol. 1988, 132, 337–356. [Google Scholar] [CrossRef]
  2. Dawes, R.M. Social dilemmas. Annu. Rev. Psychol. 1980, 31, 169–193. [Google Scholar] [CrossRef]
  3. Rand, D.G.; Dreber, A.; Ellingsen, T.; Fudenberg, D.; Nowak, M.A. Positive interactions promote public cooperation. Science 2009, 325, 1272–1275. [Google Scholar] [CrossRef] [PubMed]
  4. Hardin, G. The tragedy of the commons. Science 1968, 162, 1243–1248. [Google Scholar] [CrossRef] [PubMed]
  5. Perc, M.; Jordan, J.J.; Rand, D.G.; Wang, Z.; Boccaletti, S.; Szolnoki, A. Statistical physics of human cooperation. Phys. Rep. 2017, 687, 1–51. [Google Scholar] [CrossRef]
  6. Taylor, P.D. Altruism in viscous populations—An inclusive fitness model. Evol. Ecol. 1992, 6, 352–356. [Google Scholar] [CrossRef]
  7. Hamilton, W.D. The genetical evolution of social behaviour. II. J. Theor. Biol. 1964, 7, 17–52. [Google Scholar] [CrossRef]
  8. West, S.A.; Pen, I.; Griffin, A.S. Cooperation and Competition between Relatives. Science 2002, 296, 72–75. [Google Scholar] [CrossRef] [PubMed]
  9. Foster, K.; Wenseleers, T.; Ratnieks, F. Kin selection is the key to altruism. Trends Ecol. Evol. 2006, 21, 57–60. [Google Scholar] [CrossRef] [PubMed]
  10. May, R.M. Network structure and the biology of populations. Trends Ecol. Evol. 2006, 21, 394–399. [Google Scholar] [CrossRef] [PubMed]
  11. Nowak, M.A.; May, R.M. Evolutionary Games and Spatial Chaos. Nature 1992, 359, 826–829. [Google Scholar] [CrossRef]
  12. Wang, Z.; Wang, L.; Szolnoki, A.; Perc, M. Evolutionary games on multilayer networks: A colloquium. Eur. Phys. J. B 2015, 88. [Google Scholar] [CrossRef]
  13. Perc, M.; Szolnoki, A. Coevolutionary games—A mini review. BioSystems 2010, 99, 109–125. [Google Scholar] [CrossRef] [PubMed]
  14. Szolnoki, A.; Perc, M.; Danku, Z. Making new connections towards cooperation in the prisoner’s dilemma game. EPL 2008, 84, 50007. [Google Scholar] [CrossRef]
  15. Pacheco, J.M.; Traulsen, A.; Nowak, M.A. Coevolution of Strategy and Structure in Complex Networks with Dynamical Linking. Phys. Rev. Lett. 2006, 97, 258103. [Google Scholar] [CrossRef] [PubMed]
  16. Szolnoki, A.; Perc, M. Resolving social dilemmas on evolving random networks. EPL 2009, 86, 30007. [Google Scholar] [CrossRef]
  17. Shen, C.; Chu, C.; Shi, L.; Perc, M.; Wang, Z. Aspiration-based coevolution of link weight promotes cooperation in the spatial prisoner’s dilemma game. R. Soc. Open Sci. 2018, 5, 180199. [Google Scholar] [CrossRef] [PubMed]
  18. Wang, Z.; Szolnoki, A.; Perc, M. Self-organization towards optimally interdependent networks by means of coevolution. New J. Phys. 2014, 16, 033041. [Google Scholar] [CrossRef]
  19. Zschaler, G.; Traulsen, A.; Gross, T. A homoclinic route to asymptotic full cooperation in adaptive networks and its failure. New J. Phys. 2010, 12, 093015. [Google Scholar] [CrossRef]
  20. Trivers, R.L. The evolution of reciprocal altruism. Q. Rev. Biol. 1971, 46, 35–57. [Google Scholar] [CrossRef]
  21. Axelrod, R. The Evolution of Cooperation; Basic Book: New York, NY, USA, 1981; ISBN 978-0-465-02121-5. [Google Scholar]
  22. Axelrod, R.; Hamilton, W. The evolution of cooperation. Science 1981, 211, 1390–1396. [Google Scholar] [CrossRef] [PubMed]
  23. Boerlijst, M.C.; Nowak, M.A.; Sigmund, K. The Logic of Contrition. J. Theor. Biol. 1997, 185, 281–293. [Google Scholar] [CrossRef] [PubMed]
  24. Boyd, R. Mistakes allow evolutionary stability in the repeated prisoner’s dilemma game. J. Theor. Biol. 1989, 136, 47–56. [Google Scholar] [CrossRef]
  25. Nowak, M.A.; Sigmund, K. Tit for tat in heterogeneous populations. Nature 1992, 355, 250–253. [Google Scholar] [CrossRef]
  26. Nowak, M.; Sigmund, K. A strategy of win-stay, lose-shift that outperforms tit-for-tat in the Prisoner’s Dilemma game. Nature 1993, 364, 56–58. [Google Scholar] [CrossRef] [PubMed]
  27. Wu, J.; Axelrod, R. How to cope with noise in the iterated prisoner’s dilemma. J. Confl. Resolut. 1995, 39, 183–189. [Google Scholar] [CrossRef]
  28. Olson, M. The Logic of Collective Action: Public Goods and the Theory of Groups, Second Printing with a New Preface and Appendix; Harvard University Press: Cambridge, MA, USA, 1965; ISBN 978-0-674-04166-0. [Google Scholar]
  29. Yamagishi, T. The provision of a sanctioning system as a public good. J. Pers. Soc. Psychol. 1986, 51, 110–116. [Google Scholar] [CrossRef]
  30. Fehr, E.; Gächter, S. Altruistic punishment in humans. Nature 2002, 415, 137–140. [Google Scholar] [CrossRef] [PubMed]
  31. Van Lange, P.A.M.; Rockenbach, B.; Yamagishi, T. Reward and Punishment in Social Dilemmas; Oxford University Press: Oxford, UK, 2014; ISBN 0-19-930074-7. [Google Scholar]
  32. Oliver, P. Rewards and punishments as selective incentives for collective action: Theoretical investigations. Am. J. Sociol. 1980, 85, 1356–1375. [Google Scholar] [CrossRef]
  33. Yamagishi, T. Seriousness of social dilemmas and the provision of a sanctioning system. Soc. Psychol. Q. 1988, 51, 32–42. [Google Scholar] [CrossRef]
  34. Axelrod, R. An evolutionary approach to norms. Am. Political Sci. Rev. 1986, 80, 1095–1111. [Google Scholar] [CrossRef]
  35. Boyd, R.; Richerson, P.J. Punishment allows the evolution of cooperation (or anything else) in sizable groups. Ethol. Sociobiol. 1992, 13, 171–195. [Google Scholar] [CrossRef]
  36. Okada, I.; Yamamoto, H.; Toriumi, F.; Sasaki, T. The effect of incentives and meta-incentives on the evolution of cooperation. PLoS Comput. Biol. 2015, 11, e1004232. [Google Scholar] [CrossRef] [PubMed]
  37. Yamagishi, T.; Takahashi, N. Evolution of norms without metanorms. In Social Dilemmas and Cooperation; Schulz, U., Albers, W., Mueller, U., Eds.; Springer: Berlin, Germany, 1994; pp. 311–326. ISBN 978-3-642-78862-8, 978-3-642-78860-4. [Google Scholar]
  38. Barclay, P. Strategies for cooperation in biological markets, especially for humans. Evol. Hum. Behav. 2013, 34, 164–175. [Google Scholar] [CrossRef]
  39. Barclay, P. Competitive helping increases with the size of biological markets and invades defection. J. Theor. Biol. 2011, 281, 47–55. [Google Scholar] [CrossRef] [PubMed]
  40. Gintis, H.; Smith, E.A.; Bowles, S. Costly signaling and cooperation. J. Theor. Biol. 2001, 213, 103–119. [Google Scholar] [CrossRef] [PubMed]
  41. Roberts, G. Competitive altruism: From reciprocity to the handicap principle. Proc. R. Soc. Lond. B Biol. Sci. 1998, 265, 427–431. [Google Scholar] [CrossRef]
  42. Szolnoki, A.; Perc, M. Second-order free-riding on antisocial punishment restores the effectiveness of prosocial punishment. Phys. Rev. X 2017, 7, 041027. [Google Scholar] [CrossRef]
  43. Szolnoki, A.; Perc, M. Correlation of positive and negative reciprocity fails to confer an evolutionary advantage: Phase transitions to elementary strategies. Phys. Rev. X 2013, 3, 041021. [Google Scholar] [CrossRef]
  44. Wang, Z.; Xia, C.Y.; Meloni, S.; Zhou, C.S.; Moreno, Y. Impact of social punishment on cooperative behavior in complex networks. Sci. Rep. 2013, 3, 3055. [Google Scholar] [CrossRef] [PubMed]
  45. Aoki, M. Toward a Comparative Institutional Analysis; The MIT Press: Cambridge, MA, USA, 2001; ISBN 0-262-01187-5. [Google Scholar]
  46. Panchanathan, K.; Boyd, R. Indirect reciprocity can stabilize cooperation without the second-order free rider problem. Nature 2004, 432, 499–502. [Google Scholar] [CrossRef] [PubMed]
  47. Takagi, E. Solving social dilemmas is easy in a communal society. In Resolving Social Dilemmas: Dynamics, Structural, and Intergroup Aspects; Foddy, M., Smithon, M., Hogg, M., Schneider, S., Eds.; Psychology Press: London, UK, 1999; pp. 33–54. [Google Scholar]
  48. Inaba, M.; Takahashi, N.; Ohtsuki, H. Robustness of linkage strategy that leads to large-scale cooperation. J. Theor. Biol. 2016, 409, 97–107. [Google Scholar] [CrossRef] [PubMed]
  49. Nowak, M.A.; Sigmund, K. Evolution of indirect reciprocity. Nature 2005, 437, 1291–1298. [Google Scholar] [CrossRef] [PubMed]
  50. Nowak, M.A.; Sigmund, K. The dynamics of indirect reciprocity. J. Theor. Biol. 1998, 194, 561–574. [Google Scholar] [CrossRef] [PubMed]
  51. Ohtsuki, H.; Iwasa, Y. The leading eight: Social norms that can maintain cooperation by indirect reciprocity. J. Theor. Biol. 2006, 239, 435–444. [Google Scholar] [CrossRef] [PubMed]
  52. Ohtsuki, H.; Iwasa, Y. How should we define goodness?—Reputation dynamics in indirect reciprocity. J. Theor. Biol. 2004, 231, 107–120. [Google Scholar] [CrossRef] [PubMed]
  53. Ohtsuki, H.; Iwasa, Y. Global analyses of evolutionary dynamics and exhaustive search for social norms that maintain cooperation by reputation. J. Theor. Biol. 2007, 244, 518–531. [Google Scholar] [CrossRef] [PubMed]
  54. Brandt, H.; Sigmund, K. Indirect reciprocity, image scoring, and moral hazard. Proc. Natl. Acad. Sci. USA 2005, 102, 2666–2670. [Google Scholar] [CrossRef] [PubMed]
  55. Panchanathan, K.; Boyd, R. A tale of two defectors: The importance of standing for evolution of indirect reciprocity. J. Theor. Biol. 2003, 224, 115–126. [Google Scholar] [CrossRef]
  56. Leimar, O.; Hammerstein, P. Evolution of cooperation through indirect reciprocity. Proc. Biol. Sci. 2001, 268, 745–753. [Google Scholar] [CrossRef] [PubMed]
  57. Nowak, M.A.; Sigmund, K. Evolution of indirect reciprocity by image scoring. Nature 1998, 393, 573–577. [Google Scholar] [CrossRef] [PubMed]
  58. Brandt, H.; Sigmund, K. The good, the bad and the discriminator—Errors in direct and indirect reciprocity. J. Theor. Biol. 2006, 239, 183–194. [Google Scholar] [CrossRef] [PubMed]
  59. Sigmund, K. Moral assessment in indirect reciprocity. J. Theor. Biol. 2012, 299, 25–30. [Google Scholar] [CrossRef] [PubMed]
  60. Santos, F.P.; Santos, F.C.; Pacheco, J.M. Social norm complexity and past reputations in the evolution of cooperation. Nature 2018, 555, 242–245. [Google Scholar] [CrossRef] [PubMed]
  61. Nax, H.H.; Perc, M.; Szolnoki, A.; Helbing, D. Stability of cooperation under image scoring in group interactions. Sci. Rep. 2015, 5, 12145. [Google Scholar] [CrossRef] [PubMed]
  62. Sugden, R. The Economics of Rights, Co-Operation and Welfare; Basil Blackwell: Oxford, UK, 1986; ISBN 978-0-230-53679-1. [Google Scholar]
  63. Takahashi, N.; Mashima, R. The importance of subjectivity in perceptual errors on the emergence of indirect reciprocity. J. Theor. Biol. 2006, 243, 418–436. [Google Scholar] [CrossRef] [PubMed]
  64. Pacheco, J.M.; Santos, F.C.; Chalub, F.A.C.C. Stern-judging: A simple, successful norm which promotes cooperation under indirect reciprocity. PLoS Comput. Biol. 2006, 2, 1634–1638. [Google Scholar] [CrossRef] [PubMed]
  65. Chalub, F.A.C.C.; Santos, F.C.; Pacheco, J.M. The evolution of norms. J. Theor. Biol. 2006, 241, 233–240. [Google Scholar] [CrossRef] [PubMed]
  66. Uchida, S.; Sigmund, K. The competition of assessment rules for indirect reciprocity. J. Theor. Biol. 2010, 263, 13–19. [Google Scholar] [CrossRef] [PubMed]
  67. Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998; ISBN 9780521623650. [Google Scholar]
  68. Grefenstette, J. Proportional selection and sampling algorithms. In Evolutionary Computation 1: Basic Algorithms and Operators; Bäck, T., Fogel, D.B., Michalewicz, Z., Eds.; Institute of Physics Publishing: Bristol, UK, 2000; pp. 172–180. [Google Scholar]
  69. Baker, J.E. Reducing bias and inefficiency in the selection algorithm. In Proceedings of the 2nd International Conference on Genetic Algorithms; Grefenstette, J., Ed.; L. Erlbaum Associates Inc.: Hillsdale, NJ, USA, 1987; pp. 14–21. [Google Scholar]
  70. Brandt, H.; Sigmund, K. The logic of reprobation: Assessment and action rules for indirect reciprocation. J. Theor. Biol. 2004, 231, 475–486. [Google Scholar] [CrossRef] [PubMed]
  71. Nowak, M.A. Evolutionary Dynamics: Exploring the Equations of Life; Harvard University Press: Cambridge, UK, 2006; ISBN 0-8058-0158-8. [Google Scholar]
  72. Samuelson, L. Evolutionary Games and Equilibrium Selection; The MIT Press: Cambridge, UK, 1998; ISBN 978-0-262-69219-9. [Google Scholar]
  73. Boyd, R.; Gintis, H.; Bowles, S.; Richerson, P.J. The evolution of altruistic punishment. Proc. Natl. Acad. Sci. USA 2003, 100, 3531–3535. [Google Scholar] [CrossRef] [PubMed]
  74. Boyd, R.; Richerson, P.J. Voting with your feet: Payoff biased migration and the evolution of group beneficial behavior. J. Theor. Biol. 2009, 257, 331–339. [Google Scholar] [CrossRef] [PubMed]
  75. Rockenbach, B.; Milinski, M. The efficient interaction of indirect reciprocity and costly punishment. Nature 2006, 444, 718–723. [Google Scholar] [CrossRef] [PubMed]
  76. Boyd, R.; Richerson, P.J. Group beneficial norms can spread rapidly in a structured population. J. Theor. Biol. 2002, 215, 287–296. [Google Scholar] [CrossRef] [PubMed]
  77. Henrich, J.; Boyd, R. Why People Punish Defectors: Weak Conformist Transmission can Stabilize Costly Enforcement of Norms in Cooperative Dilemmas. J. Theor. Biol. 2001, 208, 79–89. [Google Scholar] [CrossRef] [PubMed]
  78. Shimura, H.; Nakamaru, M. Large group size promotes the evolution of cooperation in the mutual-aid game. J. Theor. Biol. 2018, 451. in press. [Google Scholar] [CrossRef] [PubMed]
1
The results of the robustness of norms against perception errors obtained in Ohtsuki and Iwasa [53] and Takahashi and Mashima [63] may seem to contradict each other. We will return to this point in the discussion.
2
In the mutual aid game, one member of the group is chosen randomly as the aid recipient, and all other members decide whether to help the same recipient. An insurance system is one example of mutual aid game. On the other hand, in the giving game, one donor and one recipient are chosen randomly, and interaction occurs between two persons. Shimura and Nakamaru [67] found that the group size and the number of repetitions of the game were theoretically important for the evolution of cooperation when the mutual aid game was played.
Games 10 00010 g001 550
Figure 1. Difference between Shunners’ payoffs and Cooperating-Reciprocators’ payoffs. Shunners of standing, sugden and kandori had evolutionary advantage in simulations with SD and ISE errors (conditions c, d, g, h). The advantage was smaller when perception errors existed (comparing g and h to c and d). The advantage was also smaller when two-way errors existed (comparing condition d and h to c and g).
Figure 1. Difference between Shunners’ payoffs and Cooperating-Reciprocators’ payoffs. Shunners of standing, sugden and kandori had evolutionary advantage in simulations with SD and ISE errors (conditions c, d, g, h). The advantage was smaller when perception errors existed (comparing g and h to c and d). The advantage was also smaller when two-way errors existed (comparing condition d and h to c and g).
Games 10 00010 g001
Table
Table 1. Assignment of reputation scores.
Table 1. Assignment of reputation scores.
Original ScoreBehavior in the Previous Period Updated Score
Standing (ST)Sugden (SUG) Kandori (KAN)Strict Discriminator (SDisc)
GoodHelping a good individual d1gGoodGoodGoodGood
Not helping a good individuald2gBadBadBadBad
Helping a bad individuald3gGoodGoodBadBad
Not helping a bad individuald4gGoodGoodGoodBad
BadHelping a good individual d1bGoodGoodGoodGood
Not helping a good individuald2bBadBadBadBad
Helping a bad individuald3bGoodGoodBadBad
Not helping a bad individuald4bBadGoodGoodBad
Table
Table 2. Strategies used in the current study.
Table 2. Strategies used in the current study.
Strategy in SD
DefectCooperate
Strategy in ISEAll-DDefector (D)-
All-C-Cooperator (C)
Original DiscriminatorDefecting-Reciprocator (D-R)Cooperating-Reciprocator (C-R)
Linkage Discriminator-Shunner (S)
Table
Table 3. Error conditions in Inaba, Takahashi, and Ohtsuki [48] and in the current study.
Table 3. Error conditions in Inaba, Takahashi, and Ohtsuki [48] and in the current study.
SD ISE
ConditionImplementation Error (δsd)Perception Error (εsd)Implementation Error (δise)Perception Error (εise)Direction
a000.050one-way
b000.050two-way
c0.0500.050one-way
d0.0500.050two-way
e000.050.05one-way
f000.050.05two-way
g0.050.050.050.05one-way
h0.050.050.050.05two-way
Table
Table 4. Which norms are evolutionary stable in the ISE?
Table 4. Which norms are evolutionary stable in the ISE?
Implementation ErrorsImplementation and Perception Errors
One Way (Corresponding to Condition a) 1Two-Way (Corresponding to Condition b)One Way (Corresponding to Condition e)Two-Way (Corresponding to Condition f) 2One-Way Implementation Error, Two-Way Perception Error 1
STY----
SUGY--NN
KANY--YN
SDiscY--YN
Note 1: Ohtsuki and Iwasa [53]. Note 2: Takahashi and Mashima [63].
Table
Table 5. Frequency of a successful invasion under standing.
Table 5. Frequency of a successful invasion under standing.
Simulation No.{Wild Type/Mutant}No Perception ErrorsWith Perception Errors
ISE ErrorsSD and ISE ErrorsISE ErrorsSD and ISE Errors
abcdefgh
1{S(ST)/D}00000000
2{S(ST)/C}00000000
3{S(ST)/D-R(ST)}00000000
4{S(ST)/C-R(ST)}970091158
5{C-R(ST)/D-R(ST)}2020202020202020
6{C-R(ST)/S(ST)}690091300
7 a{S(ST)/C-R(ST), D-R(ST)}19190019181516
Note: We conducted 20 replications for each simulation. The table shows how many times invasion was successful out of 20 replications. In simulations 1 to 6, we regarded invasion as successful when there were 10 or more players who adopted mutant strategies in the population in the last generation. In simulation 7, we regarded invasion as successful when there were 10 or more Defecting-Reciprocators. a: Only in simulation 7, g = 100,000.
Table
Table 6. Frequency of successful invasions under sugden.
Table 6. Frequency of successful invasions under sugden.
Simulation No.{Wild Type/Mutant}No Perception ErrorsWith Perception Errors
ISE ErrorsSD and ISE ErrorsISE ErrorsSD and ISE Errors
abcdefgh
1{S(SUG)/D}00000000
2{S(SUG)/C}01000000
3{S(SUG)/D-R(SUG)}00000000
4{S(SUG)/C-R(SUG)}11130013900
5{C-R(SUG)/D-R(SUG)}2020202020202020
6{C-R(SUG)/S(SUG)}1410008800
7 a{S(SUG)/C-R(SUG), D-R(SUG)}192000202006
Note: We conducted 20 replications for each simulation. The table shows how many times invasion was successful in 20 replications. In simulations 1 to 6, we regarded invasion as successful when there were 10 or more players who adopted mutant strategies in the population in the last generation. In simulation 7, we regarded invasion as successful when there were 10 or more Defecting-Reciprocators. a: Only in simulation 7, g = 100,000.
Table
Table 7. Frequency of successful invasions under kandori.
Table 7. Frequency of successful invasions under kandori.
Simulation No.{Wild Type/Mutant}No Perception ErrorsWith Perception Errors
ISE ErrorsSD and ISE ErrorsISE ErrorsSD and ISE Errors
abcdefgh
1{S(KAN)/D}00000000
2{S(KAN)/C}00000000
3{S(KAN)/D-R(KAN)}00000000
4{S(KAN)/C-R(KAN)}12110091700
5{C-R(KAN)/D-R(KAN)}2020202020202020
6{C-R(KAN)/C-S(KAN)}171100111200
7 a{S(KAN)/C-R(KAN), D-R(KAN)}181900181900
Note: We conducted 20 replications for each simulation. The table shows how many times invasion was successful in 20 replications. In simulations 1 to 6, we regarded invasion as successful when there were 10 or more players who adopted mutant strategies in the population in the last generation. In simulation 7, we regarded invasion as successful when there were 10 or more Defecting-Reciprocators. a: Only in simulation 7, g = 100,000.
Table
Table 8. Frequency of successful invasions under strict discriminator.
Table 8. Frequency of successful invasions under strict discriminator.
Simulation No.{Wild Type/Mutant}No Perception ErrorsWith Perception Errors
ISE ErrorsSD and ISE ErrorsISE ErrorsSD and ISE Errors
abcdefgh
1{S(SDisc)/D}00002002020
2{S(SDisc)/C}00000000
3{S(SDisc)/D-R(SDisc)}00000000
4{S(SDisc)/C-R(SDisc)}131400811420
5{C-R(SDisc)/D-R(SDisc)}2020202020202020
6{C-R(SDisc)/S(SDisc)}161300111500
7 a{S(SDisc)/C-R(SDisc), D-R(SDisc)}20190020181920
Note: We conducted 20 replications for each simulation. The table shows how many times invasion was successful in 20 replications. In simulations 1 to 6, we regarded invasion as successful when there were 10 or more players who adopted mutant strategies in the population in the last generation. In simulation 7, we regarded invasion as successful when there were 10 or more Defecting-Reciprocators. a: Only in simulation 7, g = 100,000.
Table
Table 9. Summary: Are Shunners evolutionary stable in the linked-game?
Table 9. Summary: Are Shunners evolutionary stable in the linked-game?
No Perception ErrorsWith Perception Errors
ISE ErrorsSD and ISE ErrorsISE ErrorsSD and ISE Errors
abcdefgh
STNNYYNNNN
SUGNNYYNNYN
KANNNYYNNYY
SDiscNNYYNNNN

Share and Cite

MDPI and ACS Style

Inaba, M.; Takahashi, N. Linkage Based on the Kandori Norm Successfully Sustains Cooperation in Social Dilemmas. Games 2019, 10, 10. https://0-doi-org.brum.beds.ac.uk/10.3390/g10010010

AMA Style

Inaba M, Takahashi N. Linkage Based on the Kandori Norm Successfully Sustains Cooperation in Social Dilemmas. Games. 2019; 10(1):10. https://0-doi-org.brum.beds.ac.uk/10.3390/g10010010

Chicago/Turabian Style

Inaba, Misato, and Nobuyuki Takahashi. 2019. "Linkage Based on the Kandori Norm Successfully Sustains Cooperation in Social Dilemmas" Games 10, no. 1: 10. https://0-doi-org.brum.beds.ac.uk/10.3390/g10010010

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop