Intentions versus Outcomes: Cooperation and Fairness in a Sequential Prisoner’s Dilemma with Nature
Abstract
:1. Introduction
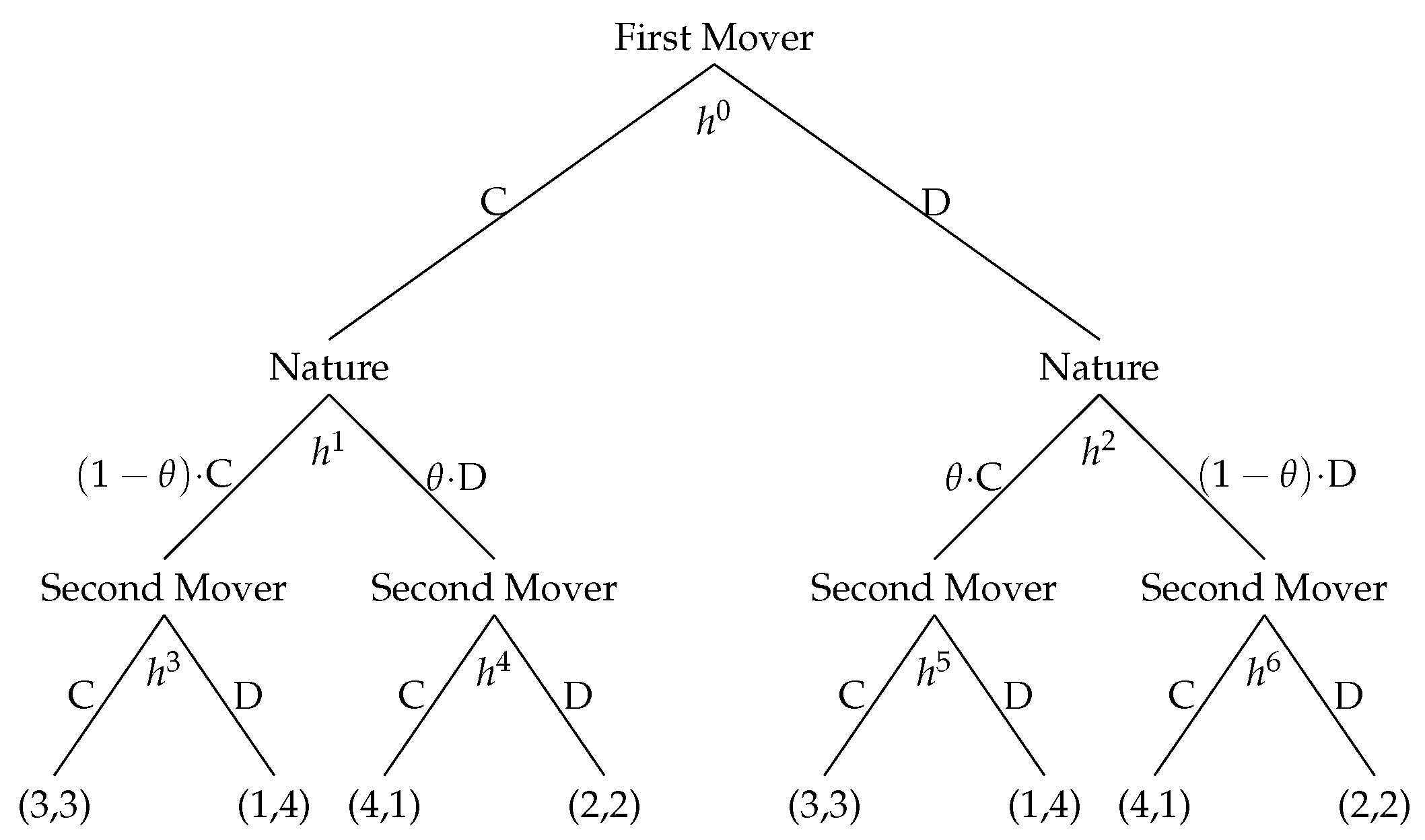
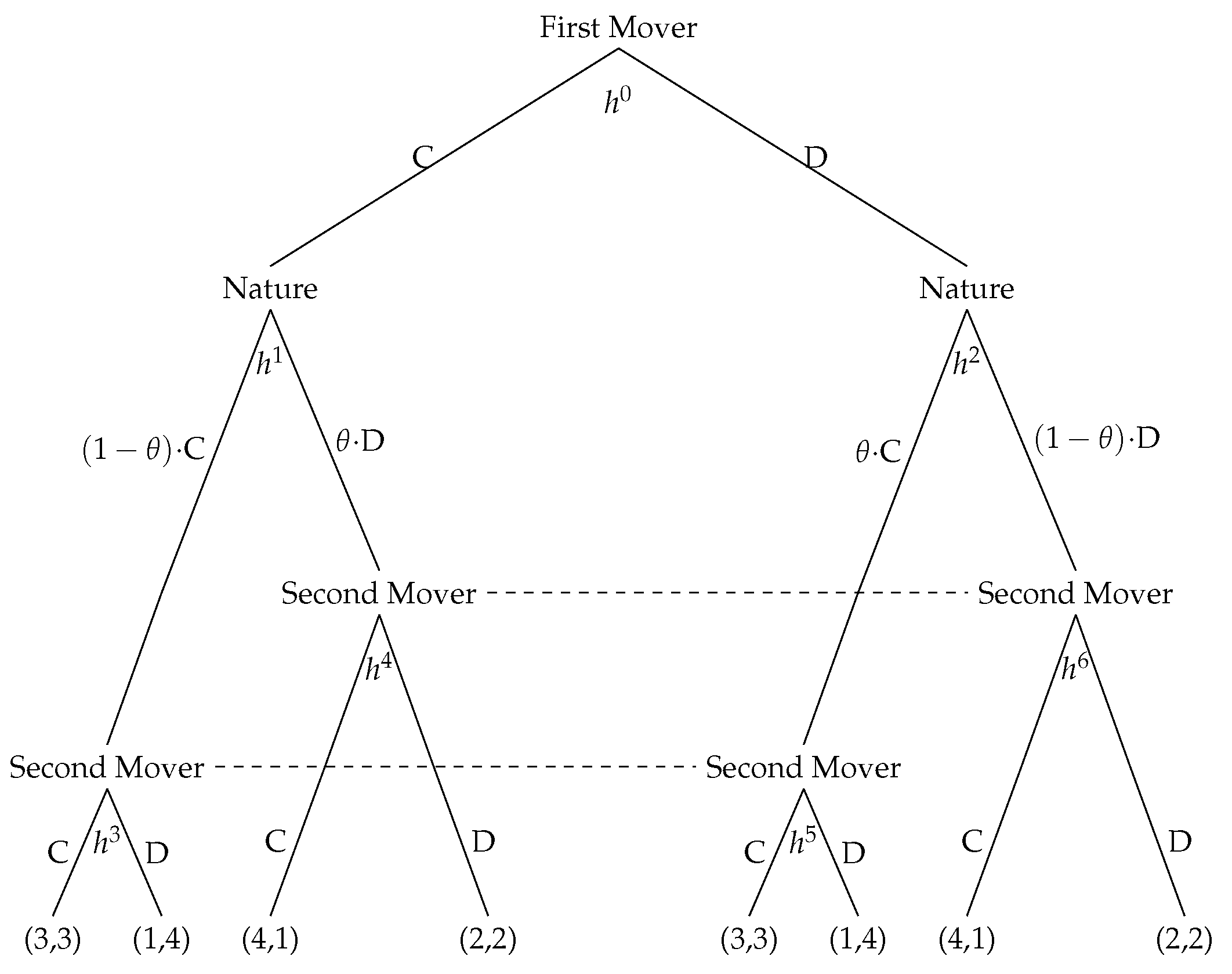
2. Sequential Prisoner’s Dilemma with Nature
3. Theories of Social Preferences
3.1. Individual Heterogeneity
3.1.1. Perspective Taking
3.1.2. Empathy
4. Experiment
4.1. Experimental Design
4.2. Questionnaire
4.3. Hypotheses
4.4. Potential Econometric Issues
5. Main Results
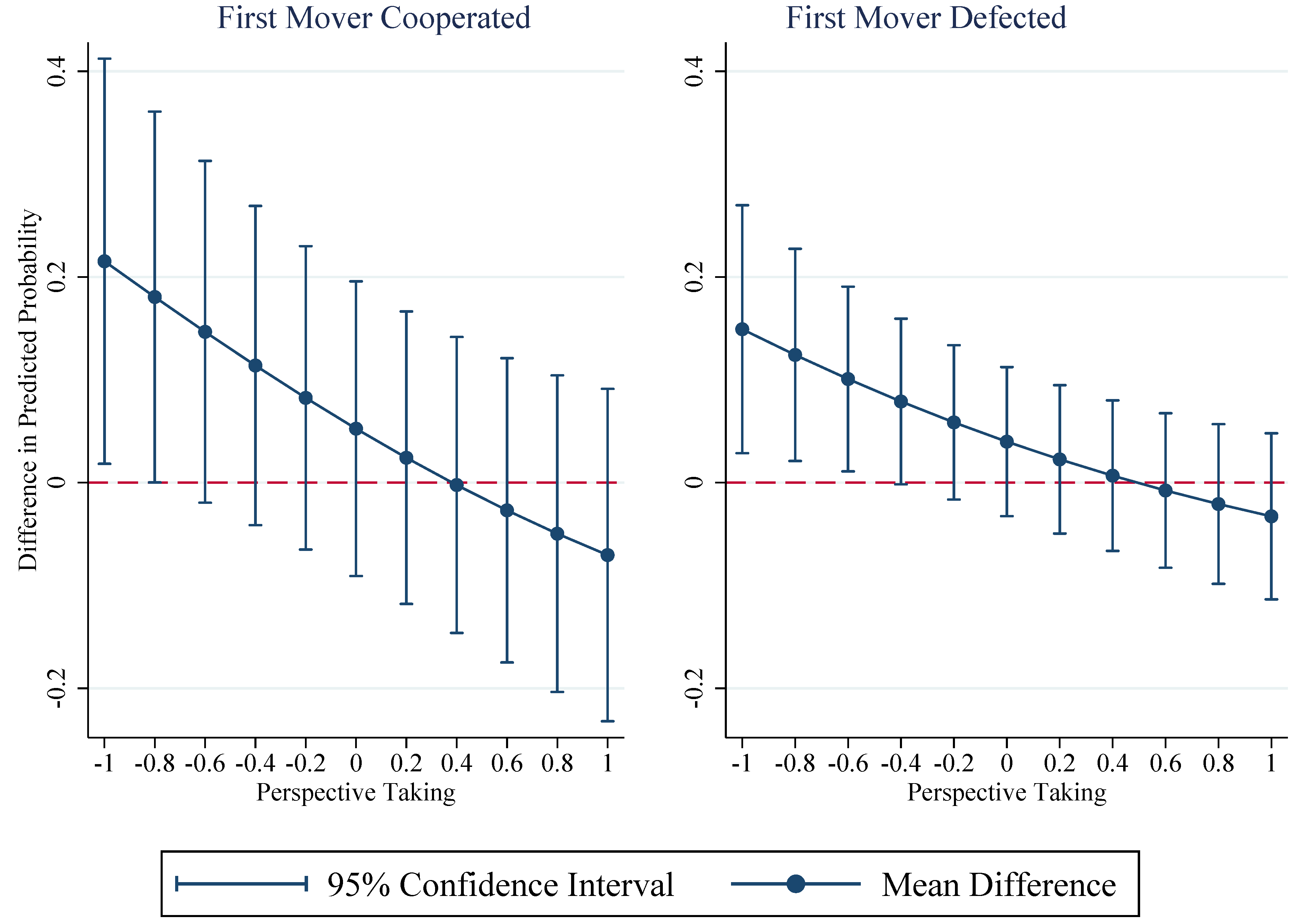
6. Additional Results
7. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Theoretical Models of Social Preferences
Appendix A.1. Inequity Aversion
- If , then player 2 will cooperate if nature cooperates and defect if nature defects.
- If , then player 2 will always defect.
Appendix A.2. Reciprocity Model
- (a)
- If , and , then player 2 will cooperate if player 1 cooperates and defect if player 1 defects.
- (b)
- , then player 2 will always defect.
- If player 1 cooperates
- (a)
- , then player 2 will always cooperate.
- (b)
- , then player 2 will always defect.
- If player 1 defects, then player 2 will always defect.
Appendix A.3. Mixed-Concerns Model
Appendix A.3.1. Perfect Information
- (a)
- If , , and , then player 2 will cooperate if player 1 cooperates and defect if player 1 defects.
- (b)
- If , , and , then player 2 will cooperate if player 1 and nature cooperates, and defect otherwise.
- (c)
- If and , then player 2 will cooperate if nature cooperates and defect if nature defects.
- (d)
- Ifand, orand, then player 2 will always defect.
Appendix A.3.2. Imperfect Information
- If player 1 cooperates
- (a)
- If and or and, then player 2 will cooperate if nature cooperates and defect if nature defects.
- (b)
- If and , then player 2 will always cooperate.
- (c)
- If and , then player 2 will always defect.
- If player 1 defects
- (a)
- If and , then player 2 will cooperate if nature cooperates and defect if nature defects.
- (b)
- If and or and , then player 2 will always defect.
Appendix A.3.3. Perfect Versus Imperfect Information
| 1 | Examples of outcome-based models include Bolton2000 and Fehr and Schmidt [6], and intention-based models include Rabin [7], and Dufwenberg and Kirchsteiger [8]. Models that combine concerns for intentions and outcomes include Levine [9], Charness and Rabin [10], Falk and Fischbacher [11], and Cox et al. [12]. |
| 2 | While this paper assumes the reversal probability is the same whether the first mover cooperates or defects. Theoretical results are similar if the reversal probabilities are allowed to differ. For clarity of presentation, a single probability is used both in the theoretical analysis and the experiment. |
| 3 | The analysis can be done without this restriction. However, if , then the choice that the first mover chooses is more likely to be switched. While this makes sense mathematically, it is not clear that this represents what occurs in most human interactions. Having means that if the first mover wants nature to be more likely to choose cooperate, then the first mover should defect. This is not say these types of situations cannot occur, but the main focus of the paper will be when a player’s intended choice matches the player’s actual choice. |
| 4 | |
| 5 | In addition, these results are robust to including age, number of economic classes, number of statistics classes, and political views. |
| 6 | Here the only difference between and is that choices in history h are made with probability one. |
| 7 | Here the equitable payoff is mathematically equivalent to (3). |
| 8 | Many different types of distributional concerns could be considered. Other forms to be included could be Rawlsian, Utilitarian, or Nash Product. |
| 9 | Assuming the standard function form for inequity aversion Fehr and Schmidt [6] gives the same equilibrium predictions for second movers in the sequential prisoner’s dilemma with nature as the restricted functional form assumed here. |
References
- Ahn, T.; Lee, M.; Ruttan, L.; Walker, J. Asymmetric payoffs in simultaneous and sequential prisoner’s dilemma games. Public Choice 2007, 132, 353–366. [Google Scholar] [CrossRef] [Green Version]
- Bolle, F.; Ockenfels, P. Prisoners’ dilemma as a game with incomplete information. J. Econ. Psychol. 1990, 11, 69–84. [Google Scholar] [CrossRef]
- Clark, K.; Sefton, M. The sequential prisoner’s dilemma: Evidence on reciprocation. Econ. J. 2001, 111, 51–68. [Google Scholar] [CrossRef]
- Ridinger, G.; McBride, M. Reciprocity in Games with Unknown Types. In Handbook of Experimental Game Theory; Capra, M., Croson, R., Rigdon, M., Rosenblatt, T., Eds.; Edward Elgar Publishing: Cheltenham, UK; Northampton, MA, USA, 2020. [Google Scholar]
- Bolton, G.E.; Okenfels, A. Erc: A theory of equity, reciprocity, and competition. Am. Econ. Rev. 2000, 90, 166–193. [Google Scholar] [CrossRef] [Green Version]
- Fehr, E.; Schmidt, K.M. A theory of fairness, competition, and cooperation. Q. J. Econ. 1999, 114, 817–868. [Google Scholar] [CrossRef]
- Rabin, M. Incorporating fairness into game theory and economics. Am. Econ. Rev. 1993, 83, 1281–1302. [Google Scholar]
- Dufwenberg, M.; Kirchsteiger, G. A theory of sequential reciprocity. Games Econ. Behav. 2004, 47, 268–298. [Google Scholar] [CrossRef] [Green Version]
- Levine, D.K. Modeling altruism and spitefulness in experiments. Rev. Econ. Dyn. 1998, 1, 593–622. [Google Scholar] [CrossRef] [Green Version]
- Charness, G.; Rabin, M. Understanding social preferences with simple tests. Q. J. Econ. 2002, 117, 817–869. [Google Scholar] [CrossRef] [Green Version]
- Falk, A.; Fischbacher, U. A theory of reciprocity. Games Econ. Behav. 2006, 54, 293–315. [Google Scholar] [CrossRef]
- Cox, J.C.; Friedman, D.; Gjerstad, S. A tractable model of reciprocity and fairness. Games Econ. Behav. 2007, 59, 17–45. [Google Scholar] [CrossRef] [Green Version]
- Chaudhuri, A. Sustaining cooperation in laboratory public goods experiments: A selective survey of the literature. Exp. Econ. 2011, 14, 47–83. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Paichayontvijit, T. Conditional cooperation and voluntary contributions to a public good. Econ. Bull. 2006, 3, 1–14. [Google Scholar]
- Fischbacher, U.; Gachter, S.; Fehr, E. Are people conditionally cooperative? evidence from a public goods experiment. Econ. Lett. 2001, 71, 397–404. [Google Scholar] [CrossRef] [Green Version]
- Herrmann, B.; Thoni, C. Measuring conditional cooperation: A replication study in russia. Exp. Econ. 2009, 12, 87–92. [Google Scholar] [CrossRef]
- Rustagi, D.; Engel, S.; Kosfeld, M. Conditional coopeation and cocost monitorying explain success in forest ccommon management. Science 2010, 330, 961–965. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dhaene, G.; Bouckaert, J. Sequential reciprocity in two-player, two-stage games: An experimental analysis. Games Econ. Behav. 2010, 70, 289–303. [Google Scholar] [CrossRef] [Green Version]
- Blanco, M.; Engelmann, D.; Normann, H.T. A within-subject analysis of other-regarding preferences. Games Econ. Behav. 2011, 72, 321–338. [Google Scholar] [CrossRef] [Green Version]
- Falk, A.; Fehr, E.; Fischbacher, U. On the nature of fair behavior. Econ. Inq. 2003, 41, 20–26. [Google Scholar] [CrossRef]
- Bolton, G.E.; Okenfels, A. A stress test of fairness measures in models of social utility. Econ. Theory 2005, 25, 2005. [Google Scholar] [CrossRef] [Green Version]
- Falk, A.; Kosfeld, M. The hidden costs of control. Am. Econ. Rev. 2006, 96, 1611–1630. [Google Scholar] [CrossRef] [Green Version]
- Stanca, L. How to be kind? Outcomes versus intentions as determinants of fairness. Econ. Lett. 2010, 106, 19–21. [Google Scholar] [CrossRef] [Green Version]
- Charness, G. Attribution and reciprocity in an experimental labor market. J. Labor Econ. 2004, 22, 665–688. [Google Scholar] [CrossRef] [Green Version]
- Falk, A.; Fehr, E.; Fischbacher, U. Testing theories of fairness- intentions matter. Games Econ. Behav. 2008, 62, 287–303. [Google Scholar] [CrossRef] [Green Version]
- Bolton, G.E.; Brandts, J.; Okenfels, A. Measuring motivations for the reciprocal responses observed in a simple dilemma game. Exp. Econ. 1998, 1, 207–219. [Google Scholar] [CrossRef]
- Charness, G.; Levine, D.I. Intention and stochastic outcomes: An experimental study. Econ. J. 2007, 117, 1051–1072. [Google Scholar] [CrossRef]
- Cox, J.C.; Deck, C.A. Assigning intentions when actions are unobservable: The impact of trembling in the trust game. South. Econ. J. 2006, 73, 307–314. [Google Scholar]
- Blanco, M.; Engelmann, D.; Koch, A.K.; Normann, H.T. Preferences and beliefs in a sequential social dilemma: A within-subject analysis. Games Econ. Behav. 2001, 87, 122–135. [Google Scholar] [CrossRef] [Green Version]
- Ridinger, G.; McBride, M. Theory of Mind Ability and Cooperation. Working Paper. 2017. Available online: https://economics.ucr.edu/wp-content/uploads/2019/10/McBride-paper-for-1-31-18-seminar.pdf (accessed on 10 January 2020).
- Sher, I.; Koenig, M.; Rustichini, A. Children’s strategic theory of mind. Proc. Natl. Acad. Sci. USA 2014, 111, 13307–13312. [Google Scholar] [CrossRef] [Green Version]
- Batson, D. These things called empathy: Eight related but distinct phenomenon. In The Social Neuroscience of Empathy; Decety, J., Ickes, W., Eds.; MIT Press: Cambridge, UK, 2011. [Google Scholar]
- Ridinger, G.; McBride, M. Money Affects Theory of Mind Differently by Gender. PLoS ONE 2015, 10, e0143973. [Google Scholar] [CrossRef]
- Ridinger, G. Shame and Theory-of-Mind Predicts Rule-following Behavior. Games 2020, 11, 36. [Google Scholar] [CrossRef]
- Singer, T. Neuroeconomics: Decision Making and the Brain. In Understanding Others: Brain Mechanisms of Theory of Mind and Empathy; Academic Press: London, UK, 2009; pp. 251–265. [Google Scholar]
- Smith, A. The Theory of Moral Sentiments. London: A. Millar. Library of Economics and Liberty. 1790. Available online: http://www.econlib.org/library/Smith/smMS.html (accessed on 24 September 2014).
- Singer, T.; Steinbeis, N. Differential roles of fairness- and compassion-based motivations for cooperation, defection, and punishment. Ann. N. Y. Acad. Sci. 2009, 1167, 41–50. [Google Scholar] [CrossRef]
- Batson, D.C.; Eklund, J.H.; Chermok, V.L.; Hoyt, J.L.; Ortiz, B.G. An additional antecedent of empathic concern: Valuing the welfare of the person in need. J. Personal. Soc. Psychol. 2007, 93, 65–74. [Google Scholar] [CrossRef]
- Bekkers, R. Traditional and health-related philanthropy: The role of resources and personality. Soc. Psychol. Q. 2006, 69, 349–366. [Google Scholar] [CrossRef] [Green Version]
- Ridinger, G. Empathetic Concern, Altruism, and the Pursuit of Distributive Justice. Master’s Thesis, California State University, Fullerton, CA, USA, 2011. [Google Scholar]
- Kruger, D.J. Evolution and altruism: Combining psychological mediators with naturally selected tendences. Evol. Hum. Behav. 2003, 24, 118–125. [Google Scholar] [CrossRef]
- Bartels, D.M.; Kvaran, T.; Nichols, S. Selfless giving. Cognition 2013, 129, 392–403. [Google Scholar] [CrossRef]
- Leliveld, M.C.; Vandijk, E.; Vanbeest, I. Punishing and compensating others at your own expense: The role of empathic concern on reactions to distributive justice. Eur. J. Soc. Psychol. 2012, 42, 135–140. [Google Scholar] [CrossRef]
- Batson, D.C.; Batson, J.G.; Todd, M.R.; Brummett, B.H.; Shaw, L.L.; Aldeguer, C.M.R. Empathy and the collective good: Caring for one of the others in a social dilemma. J. Personal. Soc. Psychol. 1995, 68, 619–631. [Google Scholar] [CrossRef]
- Oceja, L.; Jimenez, I. Beyond egoism and gruop identity: Empathy toward the other and awareness of others in a social dilemma. Span. J. Psychol. 2007, 10, 369–379. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Batson, D.C.; Moran, T. Empathy-induced altruism in a prisoner’s dilemma. Eur. J. Soc. Psychol. 1999, 22, 474–482. [Google Scholar] [CrossRef]
- Rumble, A.C.; Lange, P.A.M.V.; Parks, C.D. The benefits of empathy: When empathy may sustain cooperation in social dilemmas. Eur. J. Soc. Psychol. 2010, 40, 856–866. [Google Scholar] [CrossRef]
- Batson, D.; Ahmad, N. Empathy-induced altruism in a prisoner’s dilemma ii: What if the target of empathy has defected? Eur. J. Soc. Psychol. 2001, 31, 25–36. [Google Scholar] [CrossRef]
- Fischbacher, U. z-tree: Zurich toolbox for ready-made economic experiments. Exp. Econ. 2007, 10, 171–178. [Google Scholar] [CrossRef] [Green Version]
- Davis, M.H. Measuring individual differences in empathy: Evidence for a multidimensional approach. J. Personal. Soc. Psychol. 1983, 44, 113–126. [Google Scholar] [CrossRef]
- Bicchieri, C. The Grammar of Society: The Nature and Dynamics of Social Norms; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Ridinger, G. Ownership, punishment, and norms in a real-effort bargaining experiment. J. Econ. Behav. 2018, 155, 382–402. [Google Scholar] [CrossRef]
- Rand, D.G.; Greene, J.D.; Nowak, M.A. Spontaneous giving and calculated greed. Nature 2005, 489, 427–430. [Google Scholar] [CrossRef]
- Dana, J.; Weber, R.A.; Kuang, J.X. Exploting moral wiggle room: Experiments demonstrating an illusory preference for fairness. Econ. Theory 2007, 33, 67–80. [Google Scholar] [CrossRef]
- Camerer, C.F. Behavioral Game Theory: Experiments in Strategic Interaction; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Battigalli, P.; Dufwenberg, M. Dynamic psychological games. J. Econ. Theory 2009, 144, 1–35. [Google Scholar] [CrossRef]
- Geanakoplos, J.; Pearce, D.; Stacchetti, E. Psychological games and sequential rationality. Games Econ. Behav. 1989, 1, 60–79. [Google Scholar] [CrossRef] [Green Version]
- Sebald, A. Attribution and reciprocity. Games Econ. Behav. 2010, 68, 339–352. [Google Scholar] [CrossRef]

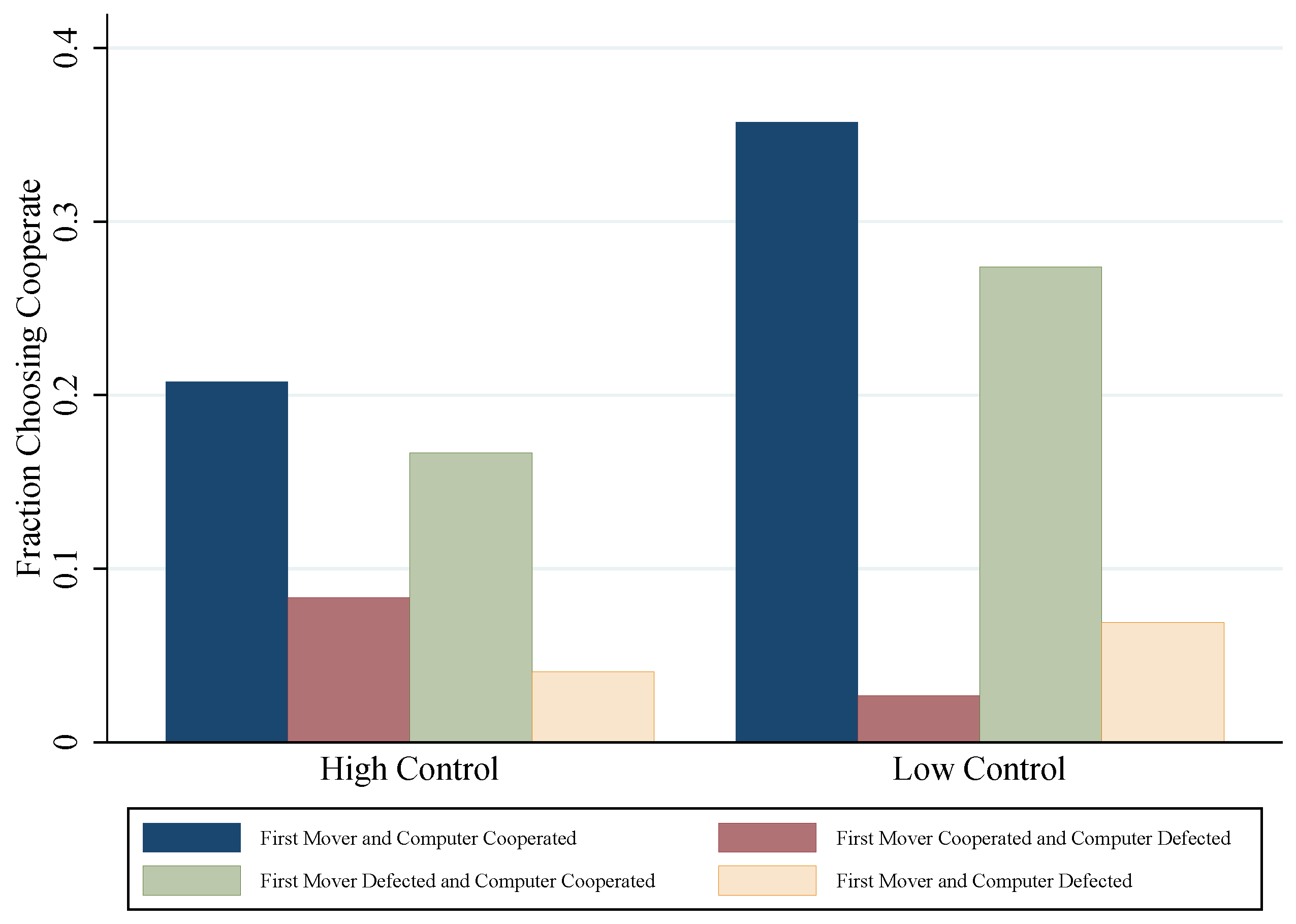



| High Control First | Low Control First | Total | |||
|---|---|---|---|---|---|
| Known | Uncertain | Known | Uncertain | ||
| Average: | |||||
| Age | 20.34 | 20.53 | 20.56 | 20.24 | 20.42 |
| Number of Economics Classes | 1.18 | 1.33 | 1.26 | 1.53 | 1.32 |
| Number of Statistics Classes | 1.05 | 1.08 | 1.16 | 0.93 | 1.06 |
| Take Home Earnings | 13.66 | 13.83 | 13.76 | 13.84 | 13.77 |
| Female (Fraction) | 0.63 | 0.64 | 0.52 | 0.67 | 0.61 |
| Number of Subjects | 62 | 64 | 62 | 58 | 246 |
| First Mover | Second Mover | |||
|---|---|---|---|---|
| Cooperation | Predicted Probability | Cooperation | Predicted Probability | |
| Uncertain | −0.01 | −0.00 | 0.47 * | 0.06 * |
| (0.13) | (0.04) | (0.21) | (0.03) | |
| Low Control | 0.42 ** | 0.15 ** | 0.46 * | 0.06 * |
| (0.13) | (0.04) | (0.21) | (0.03) | |
| First Mover and | 1.30 *** | 0.26 *** | ||
| Computer cooperated | (0.15) | (0.04) | ||
| First Mover cooperated | 0.10 | 0.01 | ||
| and Computer defected | (0.24) | (0.03) | ||
| First Mover defected | 1.20 *** | 0.27 *** | ||
| and Computer cooperated | (0.17) | (0.05) | ||
| Female | 0.10 | 0.04 | −0.21 | −0.03 |
| (0.13) | (0.05) | (0.21) | (0.03) | |
| Intercept | −0.11 | −1.52 *** | ||
| (0.18) | (0.27) | |||
| N | 1230 | 1230 | 1230 | 1230 |
| 0.23 *** | 0.23 *** | 0.45 *** | 0.45 *** | |
| Model | 70.76 | 70.76 | 135.90 | 135.90 |
| Known | Uncertain | |||
|---|---|---|---|---|
| High Control | Low Control | High Control | Low Control | |
| First Mover and | 1.61 | 1.84 | 1.42 | 1.50 |
| Computer cooperated | (0.25) | (0.28) | (0.23) | (0.29) |
| First Mover cooperated | −0.03 | −0.32 | 0.07 | 0.33 |
| and Computer defected | (0.63) | (0.46) | (0.64) | (0.33) |
| First Mover defected | 1.02 | 1.42 | 1.75 | 1.57 |
| and Computer Cooperated | (0.31) | (0.29) | (0.33) | (0.27) |
| Low Control First | 0.29 | 1.44 | −0.16 | 2.11 |
| (0.50) | (0.61) | (0.53) | (0.69) | |
| Female | −0.15 | 0.18 | −0.63 | −0.21 |
| (0.34) | (0.40) | (0.36) | (0.51) | |
| Intercept | −1.74 | −3.01 | −1.19 | −2.65 |
| (0.44) | (0.62) | (0.44) | (0.70) | |
| N | 620 | 620 | 610 | 610 |
| 0.51 | 0.62 | 0.50 | 0.68 | |
| Model | 59.61 | 66.98 | 61.45 | 65.73 |
| Hypothesis Tests | ||||
| Inequity Aversion (Prob ) | 0.07 | 0.07 | 0.31 | 0.78 |
| Reciprocity (Prob ) | 0.01 | 0.00 | 0.04 | 0.00 |
| All Treatments | Known | |||
|---|---|---|---|---|
| (1) Second Mover Cooperation | (2) Second Mover Cooperation | (3) Second Mover Cooperation | (4) Second Mover Cooperation | |
| Empathic Concern | 0.30 | 0.31 | 0.41 | 0.39 |
| (0.13) | (0.13) | (0.23) | (0.22) | |
| Perspective Taking | 0.04 | 0.18 | −0.21 | 0.14 |
| (0.13) | (0.15) | (0.23) | (0.28) | |
| Low Control | 0.55 | 0.56 | 0.45 | 0.38 |
| (0.21) | (0.22) | (0.34) | (0.33) | |
| Low Control X | −0.37 | −0.87 | ||
| Perspective Taking | (0.24) | (0.34) | ||
| Uncertain | 0.52 | 0.52 | ||
| (0.21) | (0.21) | |||
| First Mover and | 1.33 | 1.33 | 1.43 | 1.42 |
| Computer cooperated | (0.18) | (0.18) | (0.28) | (0.28) |
| First Mover cooperated | 0.04 | 0.03 | −0.38 | −0.39 |
| and Computer defected | (0.24) | (0.24) | (0.48) | (0.50) |
| First Mover defected | 1.23 | 1.23 | 1.14 | 1.17 |
| and Computer Cooperated | (0.19) | (0.19) | (0.28) | (0.28) |
| Female | −0.34 | −0.32 | −0.21 | −0.07 |
| (0.21) | (0.22) | (0.34) | (0.31) | |
| Intercept | −1.53 | −1.57 | −1.54 | −1.63 |
| (0.29) | (0.29) | (0.47) | (0.46) | |
| N | 1200 | 1200 | 610 | 610 |
| 0.43 | 0.42 | 0.50 | 0.46 | |
| Model | 137.51 | 138.86 | 64.17 | 65.65 |
| First Mover Cooperated | First Mover Defected | |
|---|---|---|
| Second Mover Cooperation | Second Mover Cooperation | |
| Empathic Concern | 0.64 | 0.25 |
| (0.31) | (0.21) | |
| Perspective Taking | 0.07 | 0.09 |
| (0.41) | (0.23) | |
| Low Control | 0.37 | 0.34 |
| (0.53) | (0.30) | |
| Low Control X | −0.97 | −0.68 |
| Perspective Taking | (0.48) | (0.34) |
| Computer cooperated | 2.18 | 1.14 |
| (0.89) | (0.27) | |
| Female | −0.16 | −0.10 |
| (0.47) | (0.36) | |
| Intercept | −2.77 | −0.90 |
| (1.13) | (0.50) | |
| N | 209 | 306 |
| 0.61 | 0.34 | |
| Model | 21.95 | 29.68 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ridinger, G. Intentions versus Outcomes: Cooperation and Fairness in a Sequential Prisoner’s Dilemma with Nature. Games 2021, 12, 58. https://0-doi-org.brum.beds.ac.uk/10.3390/g12030058
Ridinger G. Intentions versus Outcomes: Cooperation and Fairness in a Sequential Prisoner’s Dilemma with Nature. Games. 2021; 12(3):58. https://0-doi-org.brum.beds.ac.uk/10.3390/g12030058
Chicago/Turabian StyleRidinger, Garret. 2021. "Intentions versus Outcomes: Cooperation and Fairness in a Sequential Prisoner’s Dilemma with Nature" Games 12, no. 3: 58. https://0-doi-org.brum.beds.ac.uk/10.3390/g12030058






