This section is devoted to the stability analysis of the system (
1). We start by addressing the stability of the eutrophication dynamics in a more general setting, which facilitates the stability analysis of the system, which is considered without chemical input and fishery activities, i.e.,
3.1. Stability Analysis of the Eutrophication Process
Here, we consider the dynamics of the pollutant, described by the following nonlinear equation:
with
and the integer
. Remark that the mapping
is nonnegative and increasing for
, which implies that the semi-flow generated by (
4) is monotone with respect to the initial conditions in
. In this sequel, we will denote by
the unique solution of the Cauchy problem (
4) with data
. The monotonicity of (
4), for two initial conditions,
and
, is given by:
To establish the causality of the function
k on the existence of the equilibrium points and their asymptotic behaviors, we look at the variation of
k and find that
k is increasing on
and decreasing on
, where
is the global maximum of
kWe now introduce the basic reproduction number
of the chemical eutrophication process:
In contrast to the epidemiological approach of defining
as an amplification factor—see [
15,
16]—we assign to
the rate of generating new chemical components as a result of the reactions between the components during eutrophication. We note that
; thus, for
, the total amount of generated chemicals during eutrophication is less than the number of involved input chemicals. If
, the eutrophication tends to increase the amount and the number of chemicals, while
means that the toxicity level, given by the amount of residual chemicals, stays constant because it is not affected by the eutrophication. We enumerate the equilibrium points of (
4) according to
.
Proposition 1. The number of equilibrium points of the eutrophication dynamics (4) is given by as follows: If , the only stationary point is the free-pollution equilibrium .
If , additional to the free-pollution equilibrium , there is one equilibrium point , which is positive.
If , additional to the free-pollution equilibrium , there are two equilibrium points and , which are positive. For , they are given by:
It is clear that the pollution-free equilibrium
is always a stationary solution of (
4). Furthermore, the other equilibrium of (
4) is obtained by solving
in
. Indeed, using the variation of
k stated earlier in this section, we observe that the graph of
k intersects the abscissa
once at
when
and twice at
and
when
.
The following lemmas concern the behavior of the equilibrium points given in Proposition 1. In fact, Lemma 2 states that when , the pollution-free equilibrium is globally asymptotically stable. The case is given in Lemma 3. In this latter case, the dynamics converges to or whether the initial condition is in or in . When , we have in Lemma 4 that is a uniform repeller. In addition, the dynamics converges to or whether the initial condition is in or in .
Lemma 2. If , then the pollution-free equilibrium point is globally asymptotically stable. Moreover, for initial state , the mapping is exponentially decreasing at the rate of , i.e., Proof. Let us consider a positive initial condition
; we use the monotonicity property (
5) with
and
to show that the solution
satisfies:
since 0 is an equilibrium point.
In short, we have for all , and for ; this means for all . □
Lemma 3. If , the notion of stability is weakened because there is no basin of attraction covering the neighborhood of any two equilibrium points. However, the following properties hold:
- (1)
For all , the solution is decreasing and as .
- (2)
For all , the solution is decreasing and as .
Proof. We recall that when
, the global maximum of
k is attained at
, which is also an equilibrium of the dynamical system (
4), i.e.,
For an initial condition
, the monotonicity property (
5) applied to
,
and to
,
gives us:
which, because the function
k is increasing in
, implies that:
Multiplying by
, we find that:
which implies that:
This shows that the mapping is decreasing, and since it is bounded from below by the pollution-free equilibrium , we have as .
For an initial condition greater than
,
, it yields from the monotonicity condition (
5) with
,
that:
and since
k is decreasing in
, we obtain:
Multiplying by
, we obtain:
which means
is decreasing since it is bounded from below by the equilibrium
. We conclude that
as
. □
Lemma 4. If , then is a uniform repeller and we have the following properties:
- (1)
For all , the solution is decreasing and as .
- (2)
The solution is increasing if and decreasing if . Moreover, as for all .
It is worth mentioning that the fact that is a repeller, for , is a consequence of (1) and (2). It is therefore sufficient to prove (1) and (2). However, the proof of (1) is similar to that of Lemma 3; therefore, we elaborate only the proof of (2). We will do so stepwise, by considering first the initial conditions in and then those in .
Proof. Note that the global maximum of
k, given by
, satisfies
. Then, for initial condition
, either
or
. For
, we apply the monotonicity property (
5) to
,
and to
,
, to obtain:
Using the fact that the function
k is increasing in
, we obtain:
By arguing similarly for
and using the fact that the function
k is decreasing in
, we have:
Multiplying the terms of the previous inequality by
, we obtain in both cases:
meaning that
is increasing since it is bounded from above by
. This implies that
as
.
For an initial condition greater than
,
, it yields from the monotonicity condition (
5) with
,
that:
Since
k is decreasing in
, we obtain:
Hence, is decreasing and bounded from below by the equilibrium . Therefore, as . □
3.2. Stability Analysis of the Fish Pollution Dynamic
Here, we focus on the analysis of the dynamical system (
3), i.e.,
where
K is a non-increasing function of
. The following results give the equilibrium points related to the fish pollution dynamic. These points are obtained by combining the equilibrium points of the eutrophication process (
Section 3.1) with the equilibrium points of the second equation of Equation (
8), which are
and
, where
is
,
,
or
.
Proposition 5. The number of equilibrium points of the fish pollution dynamics (8) depends on as follows: If , the only equilibrium points are thetrivial equilibrium
and the best-case scenario equilibrium, which are given, respectively, by: If , additional to the trivial equilibrium and the best-case scenario equilibrium, there are two equilibrium points, which are: If , additional to the trivial equilibrium and the best-case scenario equilibrium, there are four equilibrium points, which are:
Here, , , and are given in Proposition (1).
Since the second equation of (
8) is a Bernoulli differential equation, we consider the following Lemma, which will be used together with the results of
Section 3.1 to analyze the fish pollution dynamics.
Lemma 6. Let be a given continuous function and the solution of the following Bernoulli differential equation: If v is a monotone function with as , then, for each , we have: Proof. The solution to the Bernoulli differential equation is:
We recall that K is a non-increasing function of . As , . Let be given and fixed. Then, there exists such that for all .
Hence, for all
, we have:
Since is arbitrary, we obtain that as . □
We have now all the technical elements in order to completely describe the asymptotic behavior of the solutions of (
8). In the following, we refer to
,
and
as
extinction-fish equilibrium and
,
,
and
as
persistent-fish equilibrium. Furthermore,
will be called the
worst-case scenario equilibrium.
Next, we list in a series of lemmas the results concerning the asymptotic behavior of the system (
8) in terms of the threshold
. Lemma 8 states that when
, the
best-case scenario equilibrium is globally asymptotically stable. When
(Lemma 8), the
extinction-fish equilibrium is unstable while the dynamics of the system converges either to the
best-case scenario equilibrium or to the
persistent-fish equilibrium
depending on the initial condition. For the case
(Lemma 9), the
extinction-fish equilibrium and
are unstable. In this case, the dynamics of the system converges either to the
best-case scenario equilibrium or to the
worst-case scenario equilibrium depending also on the initial condition.
Lemma 7. If , then the fish is uniformly persistent. More precisely, there exists such that for each , we have: Proof. Let
be given. Using the results of
Section 3.1, we know that, independently of
,
is monotone and converges to some
, where
is either
,
,
or
. Therefore, we deduce from Lemma 6 that
as
. The proof is completed. □
Lemma 8. If , then the best-case scenario equilibrium is globally asymptotically stable in . More precisely, for each , we have: Proof. Let be given. If , then, from Lemma 2, is monotone and converges to 0 as . Thus, Lemma 6 implies that as . □
Lemma 9. If , then the extinction-fish equilibrium is unstable and we have the following properties:
- (i)
For each with , we have:i.e., converges to the best-case scenario equilibrium . - (ii)
For each with , we have:i.e., converges to the persistent-fish equilibrium .
Proof. The fact that
is unstable is a consequence of (i) and (ii). The proof of (i) follows the same lines of the proof of Lemma 8 and thus we only prove (ii). Let
with
be given. Then, Lemma 3 ensures that
is monotone and converges to
as
. Hence, we infer from Lemma 6 that:
□
The proof of the next lemma uses the same arguments of the proofs of Lemmas 7–9.
Lemma 10. If , then the extinction-fish equilibrium and are unstable and we have the following properties:
- (i)
For each with , we have:i.e., converges to the best-case scenario equilibrium . - (ii)
For each with , we have:i.e., converges to the worst-case scenario equilibrium .
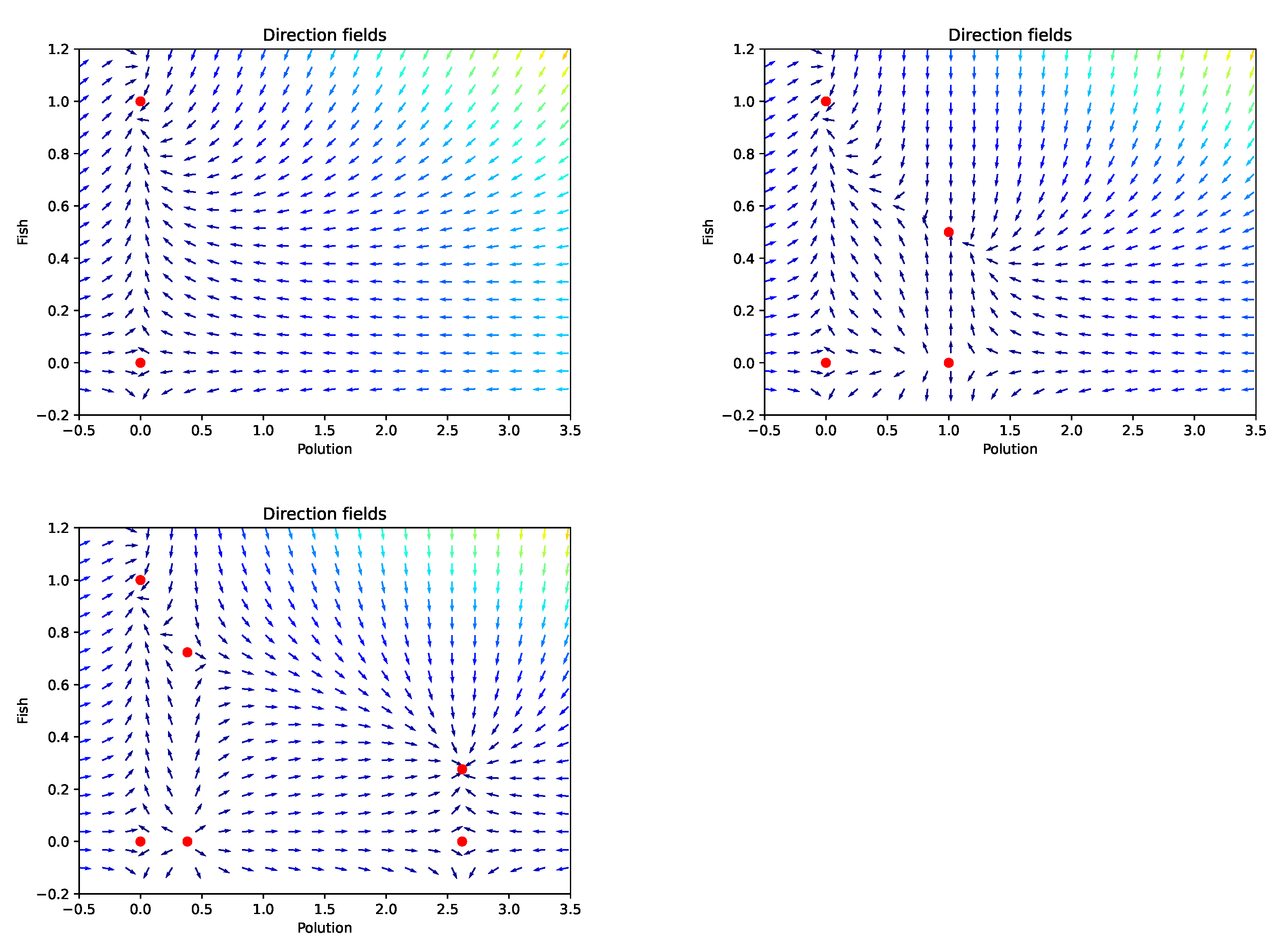
3.3. Numerical Illustrations
For illustration, we consider the capacity function
and the following values:
,
,
, and
. Therefore, the value of
will depend on
b. For
and 3, we have
,
and
, respectively. The dynamic of the model is given in
Figure 1.
As stated in Proposition 5, the number of equilibrium points depends on
We have the trivial equilibrium and the best-case scenario equilibrium , which is a nodal sink and globally asymptotically stable. It characterizes non-pollution for a perfect natural growth of the fish population.
. Here, additionally to the trivial equilibrium and the best-case scenario equilibrium , we have , which is unstable, and . In this case, we see that if the initial condition is in , the dynamic converges to as stated by Lemma 9. For initial condition starting at , is a stable point and behaves as a nodal sink. The level of pollution is damping at half the level of fish population growth.
. Additionally to the trivial equilibrium and best-case scenario equilibrium , we have , , and . The equilibrium point is unstable (as well as and ) and behaves as a source. This stands for a very low pollution state, where the pollutants are not yet damping or at least not at an alarming level regarding the fish population growth. The stationary point is a nodal sink and is locally asymptotically stable. It illustrates the impact of a high level of pollution on the fish population. This leads asymptotically to the survival of the fish population after the total disintegration of the pollutant.
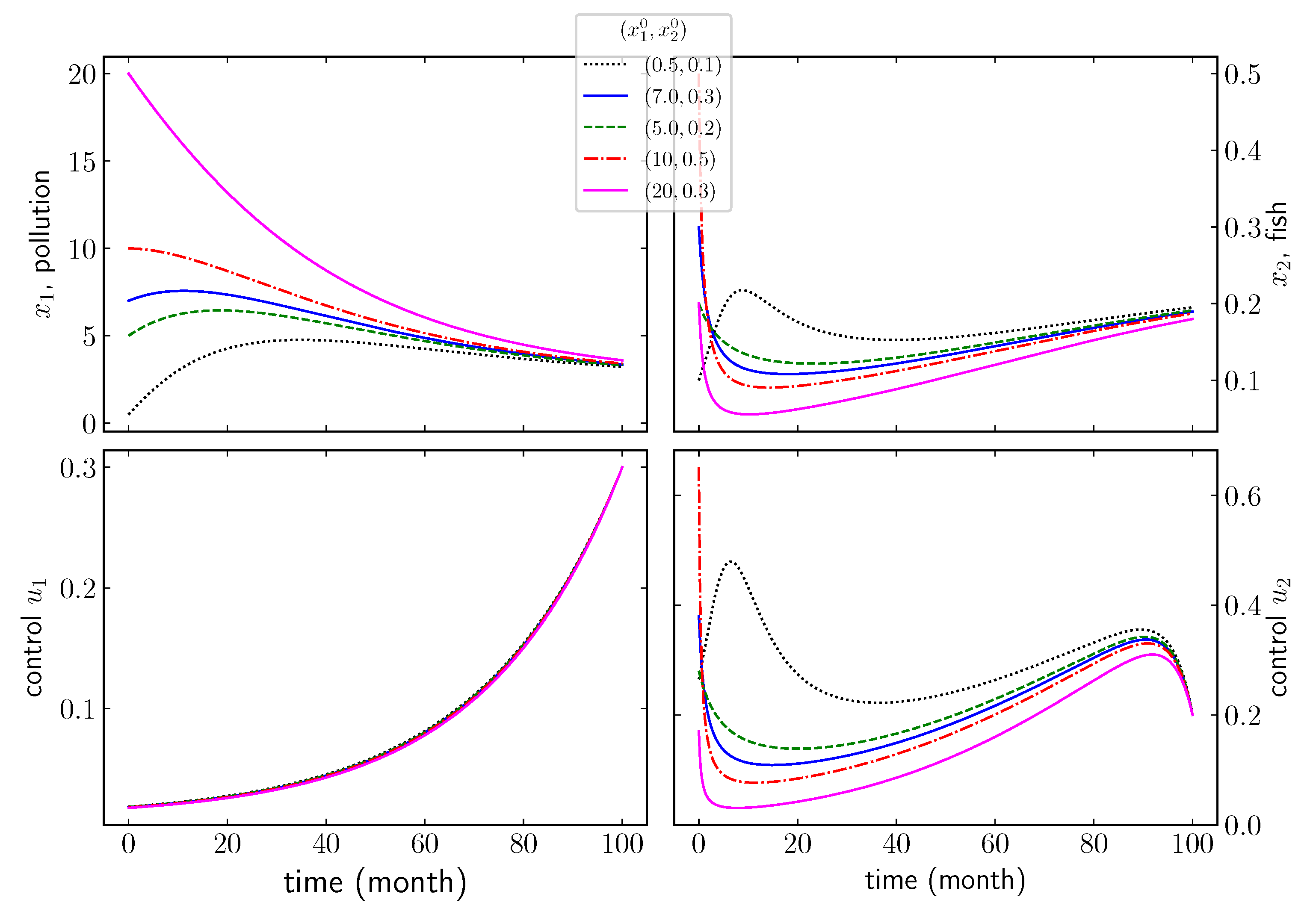
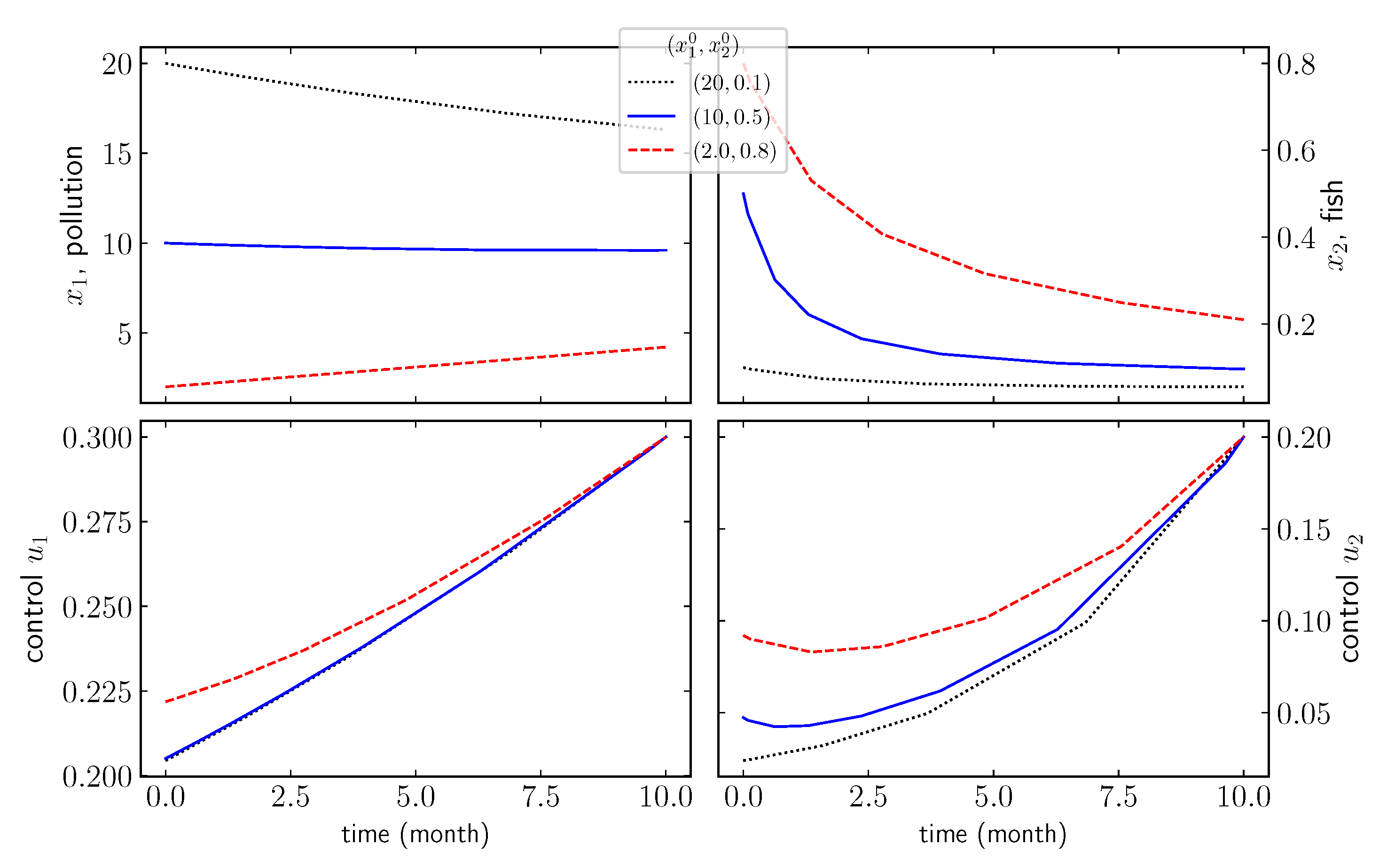
The main issue that we address in this paper is to design a fishing/pollution policy that satisfies all parties. The outcome is to have the best positioning of the stable (asymptotically stable) stationary point for both fishermen and polluters and to be able to bring and/or maintain the system state around this equilibrium. Before designing this stability policy, we must determine the feasibility, i.e., the controllability issue.
3.4. Controllability
In the rest of the paper, we consider
and
as control variables and we intend to investigate their optimal dynamics to preserve the fish population and to generate a consistent gain for both of the players in terms of business outcomes. Here, we look at the feasibility of designing such dynamics for
and
by investigating the controllability of the model. The feasibility of a mutually beneficial strategy for all the players agrees with the controllability of system (
2). The first-order controllability around an equilibrium point implies its short-term controllability. In this sense, we announce the condition for the fish population preservation policy as a controllability result.
Proposition 11. The regulation of the total pollution is a necessary and sufficient condition on the feasibility of the stability policy.
Proof. The linear tangent system of (
2) around the equilibrium point
is given by:
where
We denote by
,
and
the Kalman controllability matrices of (
11) with respect to
,
and
, respectively. They are given by:
Since the state variable
is positive at any time, then rank(
) = rank(
) = 2 while rank(
) = 1. Consequently, the system (
1) is, in the short term, controllable by
while not being locally controllable by
. □
The non-controllability of (
1) by
is due to the fact that the effect of this control is limited only to the fish population, while the control
acts on both dynamics, directly on the pollution level and via the limit growth rate
K of the fish population. In spite of this evidence of regulating the pollution in the river, it will be politically difficult to attribute full responsibility to industries and farmers. Therefore, a cooperative strategy to yield them for the preservation of the fish population is required.
In the next sections, we investigate the evolution of the fish population as the consequence of unilateral/bilateral strategies adopted by the players. The unilateral strategies yield from a non-cooperative situation while the bilateral strategies are led by a third entity that decides the threshold of fish stock to be harvested, the tolerated level of pollution, and the tax to be paid by the players.