A Stress Orientation Analysis Framework for Dislocation Glide in Face-Centred Cubic Metals
Abstract
:1. Introduction
2. Stress Orientation Framework
3. Deformation Twinning
3.1. Copley-Kear-Byun Mechanism
3.2. McCabe’s Twin Nucleation Criterion
4. Conclusions
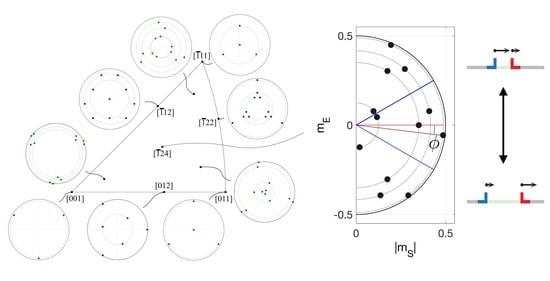
- The stress orientation maps: graphical interpretations that simultaneously capture the resolved shear stress on all the slip systems.
- A one parameter description via angle that determines the orientation effects of the stress on an octahedral slip plane.
- The normal stress can be incorporated into the graphical representations via an extension of the Mohr’s circles.
Author Contributions
Funding
Conflicts of Interest
References
- Stroh, A.N. Constrictions and Jogs in Extended Dislocations. Proc. Phys. Soc. B 1954, 67, 427–436. [Google Scholar] [CrossRef]
- Tschopp, M.A.; Spearot, D.E.; McDowell, D.L. Atomistic simulations of homogeneous dislocation nucleation in single crystal copper. Modell. Simul. Mater. Sci. Eng. 2007, 15, 693–709. [Google Scholar] [CrossRef]
- Spearot, D.E.; Tschopp, M.A.; Jacob, K.I.; McDowell, D.L. Tensile strength of <100> and <110> tilt bicrystal copper interfaces. Acta Mater. 2007, 55, 705–714. [Google Scholar] [CrossRef]
- Wyman, R.D.; Fullwood, D.T.; Wagoner, R.H.; Homer, E.R. Variability of non-Schmid effects in grain boundary dislocation nucleation criteria. Acta Mater. 2017, 124, 588–597. [Google Scholar] [CrossRef] [Green Version]
- Burbery, N.; Das, R.; Ferguson, G. Mobility of dissociated mixed dislocations under an Escaig stress. Modell. Simul. Mater. Sci. Eng. 2017, 25, 045001. [Google Scholar] [CrossRef]
- Dang, K.; Spearot, D. Pressure Dependence of the Peierls Stress in Aluminum. JOM 2018, 70, 1094–1099. [Google Scholar] [CrossRef]
- Byun, T. On the stress dependence of partial dislocation separation and deformation microstructure in austenitic stainless steels. Acta Mater. 2003, 51, 3063–3071. [Google Scholar] [CrossRef]
- Tsuno, N.; Shimabayashi, S.; Kakehi, K.; Rae, C.M.F.; Reed, R.C. Tension/Compression asymmetry in yield and creep strengths of Ni-based superalloys. Superalloys 2008, 2008, 433–442. [Google Scholar]
- Escaig, B. Sur le glissement dévié des dislocations dans la structure cubique à faces centrées. J. Phys. 1968, 29, 225–239. [Google Scholar] [CrossRef]
- Kang, K.; Yin, J.; Cai, W. Stress dependence of cross slip energy barrier for face-centered cubic nickel. J. Mech. Phys. Solids 2014, 62, 181–193. [Google Scholar] [CrossRef]
- Malka-Markovitz, A.; Mordehai, D. Cross-slip in face-centered cubic metals: A general Escaig stress-dependent activation energy line tension model. Philos. Mag. 2018, 98, 347–370. [Google Scholar] [CrossRef]
- Baudouin, J.B.; Monnet, G.; Perez, M.; Domain, C.; Nomoto, A. Effect of the applied stress and the friction stress on the dislocation dissociation in face centered cubic metals. Mater. Lett. 2013, 97, 93–96. [Google Scholar] [CrossRef]
- Oren, E.; Yahel, E.; Makov, G. Kinetics of dislocation cross-slip: A molecular dynamics study. Comput. Mater. Sci. 2017, 138, 246–254. [Google Scholar] [CrossRef]
- Malka-Markovitz, A.; Mordehai, D. Cross-slip in face centred cubic metals: A general full stress-field dependent activation energy line-tension model. Philos. Mag. 2019, 99, 1460–1480. [Google Scholar] [CrossRef]
- Thompson, N. Dislocation Nodes in Face-Centred Cubic Lattices. Proc. Phys. Soc. B 1953, 66, 481–492. [Google Scholar] [CrossRef]
- Anderson, P.M.; Hirth, J.P.; Lothe, J. Theory of Dislocations, 3rd ed.; Cambridge University Press: New York, NY, USA, 2017. [Google Scholar]
- Kuprekova, E.I.; Chumlyakov, Y.I.; Chernov, I.P. Dependence of critical cleavage stresses as a function of orientation and temperature in single crystals of Fe-18% Cr-14% Ni-2% Mo austenitic stainless steel containing hydrogen. Met. Sci. Heat Treat. 2008, 50, 282–288. [Google Scholar] [CrossRef]
- De Cooman, B.C.; Estrin, Y.; Kim, S.K. Twinning-induced plasticity (TWIP) steels. Acta Mater. 2018, 142, 283–362. [Google Scholar] [CrossRef]
- Geissler, D.; Freudenberger, J.; Kauffmann, A.; Krautz, M.; Klauss, H.; Voss, A.; Eickemeyer, J.; Schultz, L. Appearance of dislocation-mediated and twinning-induced plasticity in an engineering-grade FeMnNiCr alloy. Acta Mater. 2011, 59, 7711–7723. [Google Scholar] [CrossRef]
- De Koning, M.; Cai, W.; Bulatov, V.V. Anomalous Dislocation Multiplication in FCC Metals. Phys. Rev. Lett. 2003, 91, 025503. [Google Scholar] [CrossRef] [Green Version]
- Douin, J.; Pettinari-Sturmel, F.; Coujou, A. Dissociated dislocations in confined plasticity. Acta Mater. 2007, 55, 6453–6458. [Google Scholar] [CrossRef]
- Deutchman, H.; Phillips, P.; Zhou, N.; Samal, M.; Ghosh, S.; Wang, Y.; Mills, M. Deformation Mechanisms Coupled with Phase Field and Crystal Plasticity Modeling in a High-Temperature Polycrystalline Ni-Based Superalloy. Superalloys 2012, 2012, 25–33. [Google Scholar] [CrossRef]
- Qin, Q.; Bassani, J.L. Non-Schmid yield behavior in single crystals. J. Mech. Phys. Solids 1992, 40, 813–833. [Google Scholar] [CrossRef]
- Barba, D.; Alabort, E.; Pedrazzini, S.; Collins, D.; Wilkinson, A.; Bagot, P.; Moody, M.; Atkinson, C.; Jérusalem, A.; Reed, R. On the microtwinning mechanism in a single crystal superalloy. Acta Mater. 2017, 135, 314–329. [Google Scholar] [CrossRef]
- Gutierrez-Urrutia, I.; Raabe, D. Dislocation and twin substructure evolution during strain hardening of an Fe–22wt.% Mn–0.6wt.% C TWIP steel observed by electron channeling contrast imaging. Acta Mater. 2011, 59, 6449–6462. [Google Scholar] [CrossRef]
- Gutierrez-Urrutia, I.; Raabe, D. Study of Deformation Twinning and Planar Slip in a TWIP Steel by Electron Channeling Contrast Imaging in a SEM. Mater. Sci. Forum 2012, 702–703, 523–529. [Google Scholar] [CrossRef]
- Narita, N.; Takamura, J. Deformation twinning in silver-and copper-alloy crystals. Philos. Mag. 1974, 29, 1001–1028. [Google Scholar] [CrossRef]
- Karaman, I.; Sehitoglu, H.; Chumlyakov, Y.; Maier, H.; Kireeva, I. Extrinsic stacking faults and twinning in Hadfield manganese steel single crystals. Scr. Mater. 2001, 44, 337–343. [Google Scholar] [CrossRef]
- Karaman, I.; Sehitoglu, H.; Chumlyakov, Y.I.; Maier, H.J. The deformation of low-stacking-fault-energy austenitic steels. JOM 2002, 54, 31–37. [Google Scholar] [CrossRef]
- Sato, S.; Kwon, E.P.; Imafuku, M.; Wagatsuma, K.; Suzuki, S. Microstructural characterization of high-manganese austenitic steels with different stacking fault energies. Mater. Charact. 2011, 62, 781–788. [Google Scholar] [CrossRef]
- Choi, W.S.; De Cooman, B.C.; Sandlöbes, S.; Raabe, D. Size and orientation effects in partial dislocation-mediated deformation of twinning-induced plasticity steel micro-pillars. Acta Mater. 2015, 98, 391–404. [Google Scholar] [CrossRef]
- Cai, S.; Li, X.; Tao, N. Orientation dependence of deformation twinning in Cu single crystals. J. Mater. Sci. Technol. 2018, 34, 1364–1370. [Google Scholar] [CrossRef]
- Gutierrez-Urrutia, I.; Zaefferer, S.; Raabe, D. The effect of grain size and grain orientation on deformation twinning in a Fe–22wt.% Mn–0.6wt.% C TWIP steel. Mater. Sci. Eng. A 2010, 527, 3552–3560. [Google Scholar] [CrossRef]
- Cohen, J.; Weertman, J. A dislocation model for twinning in f.c.c. metals. Acta Metall. 1963, 11, 996–998. [Google Scholar] [CrossRef]
- Fujita, H.; Mori, T. A formation mechanism of mechanical twins in F.C.C. Metals. Scr. Metall. 1975, 9, 631–636. [Google Scholar] [CrossRef]
- Copley, S.; Kear, B. The dependence of the width of a dissociated dislocation on dislocation velocity. Acta Metall. 1968, 16, 227–231. [Google Scholar] [CrossRef]
- Li, B.; Sui, M.; Mao, S. Twinnability Predication for fcc Metals. J. Mater. Sci. Technol. 2011, 27, 97–100. [Google Scholar] [CrossRef]
- McCabe, R.J.; Beyerlein, I.J.; Carpenter, J.S.; Mara, N.A. The critical role of grain orientation and applied stress in nanoscale twinning. Nat. Commun. 2014, 5, 3806. [Google Scholar] [CrossRef]
- Suzuki, H.; Barrett, C. Deformation twinning in silver-gold alloys. Acta Metall. 1958, 6, 156–165. [Google Scholar] [CrossRef]
- Meyers, M.; Vöhringer, O.; Lubarda, V. The onset of twinning in metals: A constitutive description. Acta Mater. 2001, 49, 4025–4039. [Google Scholar] [CrossRef]
- Kamaya, M.; Kawamura, Y.; Kitamura, T. Three-dimensional local stress analysis on grain boundaries in polycrystalline material. Int. J. Solids Struct. 2007, 44, 3267–3277. [Google Scholar] [CrossRef] [Green Version]








| ( , ) | (m , ) | (, ) | |
| ( , ) | - | ||
| (m , ) | - | ||
| ( , ) | - | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
León-Cázares, F.D.; Rae, C.M.F. A Stress Orientation Analysis Framework for Dislocation Glide in Face-Centred Cubic Metals. Crystals 2020, 10, 445. https://0-doi-org.brum.beds.ac.uk/10.3390/cryst10060445
León-Cázares FD, Rae CMF. A Stress Orientation Analysis Framework for Dislocation Glide in Face-Centred Cubic Metals. Crystals. 2020; 10(6):445. https://0-doi-org.brum.beds.ac.uk/10.3390/cryst10060445
Chicago/Turabian StyleLeón-Cázares, Fernando Daniel, and Catherine Mary Fiona Rae. 2020. "A Stress Orientation Analysis Framework for Dislocation Glide in Face-Centred Cubic Metals" Crystals 10, no. 6: 445. https://0-doi-org.brum.beds.ac.uk/10.3390/cryst10060445