Molecular Modeling Insights into the Structure and Behavior of Integrins: A Review
Abstract
:1. Introduction
2. Computational Modeling Methods
2.1. Quantum Chemistry Methods
2.2. Molecular Mechanics (Force Fields) Methods
2.3. Molecular Dynamics Simulations
2.4. Enhanced Sampling Algorithms
2.5. Protein Structure Prediction
2.6. Molecular Docking
3. Structure of Integrins
3.1. Glycosylation of Integrins
3.2. 3D structures of Integrins
3.3. Molecular Modeling of Integrins’ Structures
4. The Biological Function of Integrins
4.1. Molecular Simulations of Integrins’ Conformational Dynamics
4.2. Integrins’ Activation
5. Integrins as Therapeutic Targets
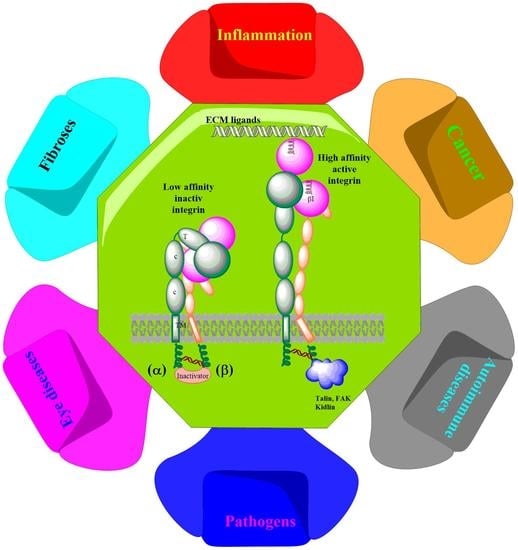
Integrins in Diseases
6. Integrin-Based Therapeutics
6.1. Marketed Drugs

6.2. RGD-Binding Integrins
6.3. Leukocyte Integrins
6.4. Integrin-Based Biomaterials for Bone and Tissue Repair
6.5. Molecular Modeling in the Design and Development of Integrin Antagonists
7. Summary and Perspectives
Author Contributions
Funding
Conflicts of Interest
References
- Harjunpää, H.; Asens, M.L.; Guenther, C.; Fagerholm, S.C. Cell Adhesion Molecules and Their Roles and Regulation in the Immune and Tumor Microenvironment. Front. Immunol. 2019, 10, 1078. [Google Scholar] [CrossRef] [Green Version]
- Chothia, C.; Jones, E. The molecular structure of cell adhesion molecules. Ann. Rev. Biochem. 1997, 66, 823–862. [Google Scholar] [CrossRef] [Green Version]
- Hynes, R.O.; Lander, A.D. Contact and adhesive specificities in the associations, migrations, and targeting of cells and axons. Cell 1992, 68, 303–322. [Google Scholar] [CrossRef] [Green Version]
- Ley, K. (Ed.) Adhesion Molecules: Function and Inhibition; Birkhäuser: Basel, Switzerland, 2007. [Google Scholar] [CrossRef]
- Schreiber, R.D.; Old, L.J.; Smyth, M.J. Cancer immunoediting: Integrating immunity’s roles in cancer suppression and promotion. Science 2011, 331, 1565–1570. [Google Scholar] [CrossRef] [Green Version]
- Tvaroska, I.; Selvaraj, C.; Koca, J. Selectins-The Two Dr. Jekyll and Mr. Hyde Faces of Adhesion Molecules-A Review. Molecules 2020, 25, 2835. [Google Scholar] [CrossRef]
- Luo, B.H.; Carman, C.V.; Springer, T.A. Structural basis of integrin regulation and signaling. Annu. Rev. Immunol. 2007, 25, 619–647. [Google Scholar] [CrossRef] [Green Version]
- Hynes, R.O. Integrins: Bidirectional, allosteric signaling machines. Cell 2002, 110, 673–687. [Google Scholar] [CrossRef] [Green Version]
- Pan, L.; Zhao, Y.; Yuan, Z.; Qin, G. Research advances on structure and biological functions of integrins. Springerplus 2016, 5, 1094. [Google Scholar] [CrossRef] [Green Version]
- Gahmberg, C.G.; Fagerholm, S.C.; Nurmi, S.M.; Chavakis, T.; Marchesan, S.; Gronholm, M. Regulation of integrin activity and signalling. Biochim. Biophys. Acta 2009, 1790, 431–444. [Google Scholar] [CrossRef]
- Shattil, S.J.; Kim, C.; Ginsberg, M.H. The final steps of integrin activation: The end game. Nat. Rev. Mol. Cell Biol. 2010, 11, 288–300. [Google Scholar] [CrossRef] [Green Version]
- Kechagia, J.Z.; Ivaska, J.; Roca-Cusachs, P. Integrins as biomechanical sensors of the microenvironment. Nat. Rev. Mol. Cell Biol. 2019, 20, 457–473. [Google Scholar] [CrossRef]
- Bachmann, M.; Kukkurainen, S.; Hytonen, V.P.; Wehrle-Haller, B. Cell Adhesion by Integrins. Physiol. Rev. 2019, 99, 1655–1699. [Google Scholar] [CrossRef]
- Raab-Westphal, S.; Marshall, J.F.; Goodman, S.L. Integrins as Therapeutic Targets: Successes and Cancers. Cancers 2017, 9, 110. [Google Scholar] [CrossRef] [Green Version]
- Barczyk, M.; Carracedo, S.; Gullberg, D. Integrins. Cell Tissue Res. 2010, 339, 269–280. [Google Scholar] [CrossRef] [Green Version]
- Arnaout, M.A.; Goodman, S.L.; Xiong, J.P. Structure and mechanics of integrin-based cell adhesion. Curr. Opin. Cell Biol. 2007, 19, 495–507. [Google Scholar] [CrossRef] [Green Version]
- Bennett, J.S.; Berger, B.W.; Billings, P.C. The structure and function of platelet integrins. J. Thromb. Haemost. 2009, 7 (Suppl. 1), 200–205. [Google Scholar] [CrossRef]
- Askari, J.A.; Buckley, P.A.; Mould, A.P.; Humphries, M.J. Linking integrin conformation to function. J. Cell Sci. 2009, 122, 165–170. [Google Scholar] [CrossRef] [Green Version]
- van der Flier, A.; Sonnenberg, A. Function and interactions of integrins. Cell Tissue Res. 2001, 305, 285–298. [Google Scholar] [CrossRef]
- Zheng, Y.; Leftheris, K. Insights into Protein-Ligand Interactions in Integrin Complexes: Advances in Structure Determinations. J. Med. Chem. 2020, 63, 5675–5696. [Google Scholar] [CrossRef]
- Campbell, I.D.; Humphries, M.J. Integrin structure, activation, and interactions. Cold Spring Harb. Perspect. Biol. 2011, 3, a004994. [Google Scholar] [CrossRef] [Green Version]
- Arnaout, M.A.; Mahalingam, B.; Xiong, J.P. Integrin structure, allostery, and bidirectional signaling. Annu. Rev. Cell Dev. Biol. 2005, 21, 381–410. [Google Scholar] [CrossRef] [Green Version]
- Hamidi, H.; Ivaska, J. Every step of the way: Integrins in cancer progression and metastasis. Nat. Rev. Cancer 2018, 18, 533–548. [Google Scholar] [CrossRef] [Green Version]
- Slack, R.J.; Macdonald, S.J.F.; Roper, J.A.; Jenkins, R.G.; Hatley, R.J.D. Emerging therapeutic opportunities for integrin inhibitors. Nat. Rev. Drug Discov. 2022, 21, 60–78. [Google Scholar] [CrossRef]
- De Marco, R.; Tolomelli, A.; Juaristi, E.; Gentilucci, L. Integrin Ligands with alpha/beta-Hybrid Peptide Structure: Design, Bioactivity, and Conformational Aspects. Med. Res. Rev. 2016, 36, 389–424. [Google Scholar] [CrossRef]
- Mrugacz, M.; Bryl, A.; Falkowski, M.; Zorena, K. Integrins: An Important Link between Angiogenesis, Inflammation and Eye Diseases. Cells 2021, 10, 1703. [Google Scholar] [CrossRef]
- Baiula, M.; Spampinato, S.; Gentilucci, L.; Tolomelli, A. Novel Ligands Targeting alpha4beta1 Integrin: Therapeutic Applications and Perspectives. Front. Chem. 2019, 7, 489. [Google Scholar] [CrossRef]
- Su, C.Y.; Li, J.Q.; Zhang, L.L.; Wang, H.; Wang, F.H.; Tao, Y.W.; Wang, Y.Q.; Guo, Q.R.; Li, J.J.; Liu, Y.; et al. The Biological Functions and Clinical Applications of Integrins in Cancers. Front. Pharmacol. 2020, 11, 579068. [Google Scholar] [CrossRef]
- Bicho, D.; Ajami, S.; Liu, C.; Reis, R.L.; Oliveira, J.M. Peptide-biofunctionalization of biomaterials for osteochondral tissue regeneration in early stage osteoarthritis: Challenges and opportunities. J. Mater. Chem. B 2019, 7, 1027–1044. [Google Scholar] [CrossRef]
- Shekaran, A.; Garcia, A.J. Extracellular matrix-mimetic adhesive biomaterials for bone repair. J. Biomed. Mater. Res. A 2011, 96, 261–272. [Google Scholar] [CrossRef]
- Zhao, J.; Santino, F.; Giacomini, D.; Gentilucci, L. Integrin-Targeting Peptides for the Design of Functional Cell-Responsive Biomaterials. Biomedicines 2020, 8, 307. [Google Scholar] [CrossRef]
- Young, D. A Practical Guide for Applying Techniques to real World problems; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Dykstra, C.E.; Franking, G.; Kim, K.S.; Scuseria, G.E. (Eds.) Theory and Applications of Computational Chemistry; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Levine, I.N. Quantum Chemistry, 6th ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2009; 751p. [Google Scholar]
- Parr, R.G.; Yang, W. Density-Functional Theory of Atoms and Molecules; Oxford University Press: Oxford,UK; Clarendon Press: New York, NY, USA; Oxford, UK, 1989; p. 333. [Google Scholar]
- Scuseria, G.E.; Staroverov, V.N. Progress in the development of exchange-correlation functionals. In Theory and Applications of Computational Chemistry; Elsevier: Amsterdam, The Netherlands, 2005; pp. 669–724. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Schultz, N.E.; Truhlar, D.G. Design of density functionals by combining the method of constraint satisfaction with parametrization for thermochemistry, thermochemical kinetics, and noncovalent interactions. J. Chem. Theor. Comput. 2006, 2, 364–382. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Density functionals with broad applicability in chemistry. Acc. Chem. Res. 2008, 41, 157–167. [Google Scholar] [CrossRef]
- Zheng, J.J.; Zhao, Y.; Truhlar, D.G. The DBH24/08 Database and Its Use to Assess Electronic Structure Model Chemistries for Chemical Reaction Barrier Heights. J. Chem. Theory Comput. 2009, 5, 808–821. [Google Scholar] [CrossRef]
- Xu, X.F.; Alecu, I.M.; Truhlar, D.G. How Well Can Modern Density Functionals Predict Internuclear Distances at Transition States? J. Chem. Theory Comput. 2011, 7, 1667–1676. [Google Scholar] [CrossRef]
- Warshel, A.; Levitt, M. Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. J. Mol. Biol. 1976, 103, 227–249. [Google Scholar] [CrossRef]
- Senn, H.M.; Thiel, W. QM/MM methods for biological systems. In Atomistic Approaches in Modern Biology: From Quantum Chemistry to Molecular Simulations; Springer: Berlin/Heidelberg, Germany, 2007; Volume 268, pp. 173–290. [Google Scholar] [CrossRef]
- Tvaroska, I. QM/MM Insight on Enzymatic Reactions of Glycosyltransferases. Mini-Rev. Org. Chem. 2011, 8, 263–269. [Google Scholar] [CrossRef]
- Lin, H.; Truhlar, D.G. QM/MM: What have we learned, where are we, and where do we go from here? Theor. Chem. Acc. 2007, 117, 185–199. [Google Scholar] [CrossRef]
- Murphy, R.B.; Philipp, D.M.; Friesner, R.A. A mixed quantum mechanics/molecular mechanics (QM/MM) method for large-scale modeling of chemistry in protein environments. J. Comput. Chem. 2000, 21, 1442–1457. [Google Scholar] [CrossRef]
- Groenhof, G. Introduction to QM/MM simulations. Methods Mol. Biol. 2013, 924, 43–66. [Google Scholar] [CrossRef] [Green Version]
- Perez, S.; Tvaroska, I. Carbohydrate-protein interactions: Molecular modeling insights. Adv. Carbohydr. Chem. Biochem. 2014, 71, 9–136. [Google Scholar] [CrossRef]
- Tvaroska, I. Glycosyltransferases as targets for therapeutic intervention in cancer and inflammation: Molecular modeling insights. Chem. Pap. 2022, 76, 1953–1988. [Google Scholar] [CrossRef]
- Kitaura, K.; Ikeo, E.; Asada, T.; Nakano, T.; Uebayasi, M. Fragment molecular orbital method: An approximate computational method for large molecules. Chem. Phys. Lett. 1999, 313, 701–706. [Google Scholar] [CrossRef]
- Fedorov, D.G.; Kitaura, K. The Fragnemt Molecular Orbital Method-Practical Applications to Large Molecular Systems; CRC Press: Boca Raton, FL, USA; Taylor and Francis Group: Oxfordshire, UK, 2009. [Google Scholar]
- Fedorov, D.G.; Nagata, T.; Kitaura, K. Exploring chemistry with the fragment molecular orbital method. Phys. Chem. Chem. Phys. 2012, 14, 7562–7577. [Google Scholar] [CrossRef]
- Sladek, V.; Kona, J.; Tokiwa, H. In silico analysis of interaction pattern switching in ligandreceptor binding in Golgi alpha-mannosidase II induced by the protonated states of inhibitors. Phys. Chem. Chem. Phys. 2017, 19, 12527–12537. [Google Scholar] [CrossRef]
- Sladek, V.; Tokiwa, H.; Shimano, H.; Shigeta, Y. Protein Residue Networks from Energetic and Geometric Data: Are They Identical? J. Chem. Theory Comput. 2018, 14, 6623–6631. [Google Scholar] [CrossRef]
- Takaya, D.; Niwa, H.; Mikuni, J.; Nakamura, K.; Handa, N.; Tanaka, A.; Yokoyama, S.; Honma, T. Protein ligand interaction analysis against new CaMKK2 inhibitors by use of X-ray crystallography and the fragment molecular orbital (FMO) method. J. Mol. Graph. Model. 2020, 99, 107599. [Google Scholar] [CrossRef]
- Kona, J.; Sestak, S.; Wilson, I.B.H.; Polakova, M. 1,4-Dideoxy-1,4-imino-D- and L-lyxitol-based inhibitors bind to Golgi alpha-mannosidase II in different protonation forms. Org. Biomol. Chem. 2022, 20, 8932–8943. [Google Scholar] [CrossRef]
- Sladek, V.; Fedorov, D.G. The Importance of Charge Transfer and Solvent Screening in the Interactions of Backbones and Functional Groups in Amino Acid Residues and Nucleotides. Int. J. Mol. Sci. 2022, 23, 13514. [Google Scholar] [CrossRef]
- Anan, R.; Nakamura, T.; Shimamura, K.; Matsushita, Y.; Ohyama, T.; Kurita, N. Change in binding states between catabolite activating protein and DNA induced by ligand-binding: Molecular dynamics and ab initio fragment molecular orbital calculations. J. Mol. Model. 2019, 25, 192. [Google Scholar] [CrossRef]
- Lim, H.; Chun, J.; Jin, X.; Kim, J.; Yoon, J.; No, K.T. Investigation of protein-protein interactions and hot spot region between PD-1 and PD-L1 by fragment molecular orbital method. Sci. Rep. 2019, 9, 16727. [Google Scholar] [CrossRef] [Green Version]
- Lindorff-Larsen, K.; Maragakis, P.; Piana, S.; Eastwood, M.P.; Dror, R.O.; Shaw, D.E. Systematic validation of protein force fields against experimental data. PLoS ONE 2012, 7, e32131. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Rauscher, S.; Nawrocki, G.; Ran, T.; Feig, M.; de Groot, B.L.; Grubmuller, H.; MacKerell, A.D., Jr. CHARMM36m: An improved force field for folded and intrinsically disordered proteins. Nat. Methods 2017, 14, 71–73. [Google Scholar] [CrossRef] [Green Version]
- Robustelli, P.; Piana, S.; Shaw, D.E. Developing a molecular dynamics force field for both folded and disordered protein states. Proc. Natl. Acad. Sci. USA 2018, 115, E4758–E4766. [Google Scholar] [CrossRef] [Green Version]
- Dauber-Osguthorpe, P.; Hagler, A.T. Biomolecular force fields: Where have we been, where are we now, where do we need to go and how do we get there? J. Comput.-Aided Mol. Des. 2019, 33, 133–203. [Google Scholar] [CrossRef]
- Nerenberg, P.S.; Head-Gordon, T. New developments in force fields for biomolecular simulations. Curr. Opin. Struct. Biol. 2018, 49, 129–138. [Google Scholar] [CrossRef] [Green Version]
- Maier, J.A.; Martinez, C.; Kasavajhala, K.; Wickstrom, L.; Hauser, K.E.; Simmerling, C. ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. [Google Scholar] [CrossRef] [Green Version]
- Diem, M.; Oostenbrink, C. Hamiltonian Reweighing To Refine Protein Backbone Dihedral Angle Parameters in the GROMOS Force Field. J. Chem. Inf. Model. 2020, 60, 279–288. [Google Scholar] [CrossRef]
- Harder, E.; Damm, W.; Maple, J.; Wu, C.; Reboul, M.; Xiang, J.Y.; Wang, L.; Lupyan, D.; Dahlgren, M.K.; Knight, J.L.; et al. OPLS3: A Force Field Providing Broad Coverage of Drug-like Small Molecules and Proteins. J. Chem. Theory Comput. 2016, 12, 281–296. [Google Scholar] [CrossRef]
- Inakollu, V.S.; Geerke, D.P.; Rowley, C.N.; Yu, H. Polarisable force fields: What do they add in biomolecular simulations? Curr. Opin. Struct. Biol. 2020, 61, 182–190. [Google Scholar] [CrossRef]
- Drude, P. The Theory of Optics; Dover: New York, NY, USA, 1959. [Google Scholar]
- Lemkul, J.A.; Huang, J.; Roux, B.; MacKerell, A.D., Jr. An Empirical Polarizable Force Field Based on the Classical Drude Oscillator Model: Development History and Recent Applications. Chem. Rev. 2016, 116, 4983–5013. [Google Scholar] [CrossRef]
- Kognole, A.A.; Aytenfisu, A.H.; MacKerell, A.D., Jr. Extension of the CHARMM Classical Drude Polarizable Force Field to N- and O-Linked Glycopeptides and Glycoproteins. J. Phys. Chem. B 2022, 126, 6642–6653. [Google Scholar] [CrossRef] [PubMed]
- van Duin, A.C.T.; Dasgupta, S.; Lorant, S.; Goddard, W.A. ReaxFF: A Reactive Force Field for Hydrocarbons. J. Phys. Chem. A 2001, 105, 9396–9409. [Google Scholar] [CrossRef] [Green Version]
- Chenoweth, K.; van Duin, A.C.; Goddard, W.A., 3rd. ReaxFF reactive force field for molecular dynamics simulations of hydrocarbon oxidation. J. Phys. Chem. A 2008, 112, 1040–1053. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Trnka, T.; Tvaroska, I.; Koca, J. Automated Training of ReaxFF Reactive Force Fields for Energetics of Enzymatic Reactions. J. Chem. Theory Comput. 2018, 14, 291–302. [Google Scholar] [CrossRef] [PubMed]
- Rahnamoun, A.; Kaymak, M.C.; Manathunga, M.; Gotz, A.W.; van Duin, A.C.T.; Merz, K.M., Jr.; Aktulga, H.M. ReaxFF/AMBER-A Framework for Hybrid Reactive/Nonreactive Force Field Molecular Dynamics Simulations. J. Chem. Theory Comput. 2020, 16, 7645–7654. [Google Scholar] [CrossRef]
- Monti, S.; Carravetta, V.; Agren, H. Simulation of Gold Functionalization with Cysteine by Reactive Molecular Dynamics. J. Phys. Chem. Lett. 2016, 7, 272–276. [Google Scholar] [CrossRef]
- Monti, S.; Corozzi, A.; Fristrup, P.; Joshi, K.L.; Shin, Y.K.; Oelschlaeger, P.; van Duin, A.C.; Barone, V. Exploring the conformational and reactive dynamics of biomolecules in solution using an extended version of the glycine reactive force field. Phys. Chem. Chem. Phys. 2013, 15, 15062–15077. [Google Scholar] [CrossRef]
- Trnka, T.; Kozmon, S.; Tvaroska, I.; Koca, J. Stepwise catalytic mechanism via short-lived intermediate inferred from combined QM/MM MERP and PES calculations on retaining glycosyltransferase ppGalNAcT2. PLoS Comput. Biol. 2015, 11, e1004061. [Google Scholar] [CrossRef]
- Moerman, E.; Furman, D.; Wales, D.J. Systematic Evaluation of ReaxFF Reactive Force Fields for Biochemical Applications. J. Chem. Theory Comput. 2021, 17, 497–514. [Google Scholar] [CrossRef]
- Dama, J.F.; Sinitskiy, A.V.; McCullagh, M.; Weare, J.; Roux, B.; Dinner, A.R.; Voth, G.A. The Theory of Ultra-Coarse-Graining. 1. General Principles. J. Chem. Theory Comput. 2013, 9, 2466–2480. [Google Scholar] [CrossRef]
- Machado, M.R.; Zeida, A.; Darre, L.; Pantano, S. From quantum to subcellular scales: Multi-scale simulation approaches and the SIRAH force field. Interface Focus 2019, 9, 20180085. [Google Scholar] [CrossRef]
- Marrink, S.J.; Tieleman, D.P. Perspective on the Martini model. Chem. Soc. Rev. 2013, 42, 6801–6822. [Google Scholar] [CrossRef] [Green Version]
- de Jong, D.H.; Singh, G.; Bennett, W.F.; Arnarez, C.; Wassenaar, T.A.; Schafer, L.V.; Periole, X.; Tieleman, D.P.; Marrink, S.J. Improved Parameters for the Martini Coarse-Grained Protein Force Field. J. Chem. Theory Comput. 2013, 9, 687–697. [Google Scholar] [CrossRef]
- Marrink, S.J.; Monticelli, L.; Melo, M.N.; Alessandri, R.; Tieleman, D.P.; Souza, P.C.T. Twodecades of Martini: Better beads, broader scope. WIREs Comput. Mol. Sci. 2022, 12, e1620. [Google Scholar] [CrossRef]
- Spiwok, V.; Sucur, Z.; Hosek, P. Enhanced sampling techniques in biomolecular simulations. Biotechnol. Adv. 2015, 33, 1130–1140. [Google Scholar] [CrossRef]
- Karplus, M.; McCammon, J.A. Molecular dynamics simulations of biomolecules. Nat. Struct. Biol. 2002, 9, 646–652. [Google Scholar] [CrossRef]
- Lindahl, E. Molecular dynamics simulations. Methods Mol. Biol. 2015, 1215, 3–26. [Google Scholar] [CrossRef]
- Hospital, A.; Goni, J.R.; Orozco, M.; Gelpi, J.L. Molecular dynamics simulations: Advances and applications. Adv. Appl. Bioinform. Chem. 2015, 8, 37–47. [Google Scholar] [CrossRef] [Green Version]
- Zhao, G.; Perilla, J.R.; Yufenyuy, E.L.; Meng, X.; Chen, B.; Ning, J.; Ahn, J.; Gronenborn, A.M.; Schulten, K.; Aiken, C.; et al. Mature HIV-1 capsid structure by cryo-electron microscopy and all-atom molecular dynamics. Nature 2013, 497, 643–646. [Google Scholar] [CrossRef] [Green Version]
- Torri, G.M.; Valleau, J.P. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Swendsen, R.H.; Wang, J.S. Replica Monte Carlo simulation of spin glasses. Phys. Rev. Lett. 1986, 57, 2607–2609. [Google Scholar] [CrossRef] [PubMed]
- Sugita, Y.; Okamoto, Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999, 314, 141–151. [Google Scholar] [CrossRef]
- Laio, A.; Parrinello, M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barducci, A.; Bonomi, M.; Parrinello, M. Metadynamics. Wires Comput. Mol. Sci. 2011, 1, 826–843. [Google Scholar] [CrossRef]
- Valsson, O.; Parrinello, M. Variational approach to enhanced sampling and free energy calculations. Phys. Rev. Lett. 2014, 113, 090601. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Liu, C.W.; Shao, Q.; Zhang, J.; Gao, Y.Q. From thermodynamics to kinetics: Enhanced sampling of rare events. Acc. Chem. Res. 2015, 48, 947–955. [Google Scholar] [CrossRef]
- Gao, Y.Q. An integrate-over-temperature approach for enhanced sampling. J. Chem. Phys. 2008, 128, 064105. [Google Scholar] [CrossRef]
- Bussi, G.; Laio, A. Using metadynamics to explore complex free-energy landscapes. Nat. Rev. Phys. 2020, 2, 200–212. [Google Scholar] [CrossRef]
- Oborsky, P.; Tvaroska, I.; Kralova, B.; Spiwok, V. Toward an Accurate Conformational Modeling of Iduronic Acid. J. Phys.Chem. B 2013, 117, 1003–1009. [Google Scholar] [CrossRef]
- Spiwok, V.; Hlat-Glembova, K.; Tvaroska, I.; Kralova, B. Conformational Free Energy Modeling of Druglike Molecules by Metadynamics in the WHIM Space. J. Chem. Inf. Model. 2012, 52, 804–813. [Google Scholar] [CrossRef]
- Salomon-Ferrer, R.; Case, D.A.; Walker, R.C. An overview of the Amber biomolecular simulation package. WIRE Comput. Mol. Sci. 2013, 3, 198–210. [Google Scholar] [CrossRef]
- Pronk, S.; Pall, S.; Schulz, R.; Larsson, P.; Bjelkmar, P.; Apostolov, R.; Shirts, M.R.; Smith, J.C.; Kasson, P.M.; van der Spoel, D.; et al. GROMACS 4.5: A high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 2013, 29, 845–854. [Google Scholar] [CrossRef] [Green Version]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [Green Version]
- Phillips, J.C.; Hardy, D.J.; Maia, J.D.C.; Stone, J.E.; Ribeiro, J.V.; Bernardi, R.C.; Buch, R.; Fiorin, G.; Henin, J.; Jiang, W.; et al. Scalable molecular dynamics on CPU and GPU architectures with NAMD. J. Chem. Phys. 2020, 153, 044130. [Google Scholar] [CrossRef]
- Hénin, J.; Lelièvre, T.; Shirts, M.R.; Valsson, O.; Delemotte, L. Enhanced sampling methods for molecular dynamics simulations [Article v1.0]. axrXiv 2022, arXiv:2202.04164v2. [Google Scholar]
- Allison, J.R. Computational methods for exploring protein conformations. Biochem. Soc. Trans. 2020, 48, 1707–1724. [Google Scholar] [CrossRef]
- Bernardi, R.C.; Melo, M.C.R.; Schulten, K. Enhanced sampling techniques in molecular dynamics simulations of biological systems. Biochim. Biophys. Acta 2015, 1850, 872–877. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.I.; Shao, Q.; Zhang, J.; Yang, L.; Gao, Y.Q. Enhanced sampling in molecular dynamics. J. Chem. Phys. 2019, 151, 070902. [Google Scholar] [CrossRef]
- Floudas, C.A. Computational methods in protein structure prediction. Biotechnol. Bioeng. 2007, 97, 207–213. [Google Scholar] [CrossRef]
- Kuhlman, B.; Bradley, P. Advances in protein structure prediction and design. Nat. Rev. Mol. Cell Biol. 2019, 20, 681–697. [Google Scholar] [CrossRef]
- Lushington, G.H. Comparative modeling of proteins. Methods Mol. Biol. 2015, 1215, 309–330. [Google Scholar] [CrossRef] [PubMed]
- Webb, B.; Sali, A. Protein Structure Modeling with MODELLER. Methods Mol. Biol. 2021, 2199, 239–255. [Google Scholar] [CrossRef] [PubMed]
- Schrödinger. Schrödinger; LLC: New York, NY, USA, 2021. [Google Scholar]
- Prime. Prime, 3rd ed.; Schrodinger, LLC: New York, NY, USA, 2011. [Google Scholar]
- Waterhouse, A.; Bertoni, M.; Bienert, S.; Studer, G.; Tauriello, G.; Gumienny, R.; Heer, F.T.; de Beer, T.A.P.; Rempfer, C.; Bordoli, L.; et al. SWISS-MODEL: Homology modelling of protein structures and complexes. Nucleic Acids Res. 2018, 46, W296–W303. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Godzik, A. Fold recognition methods. Methods Biochem. Anal. 2003, 44, 525–546. [Google Scholar] [CrossRef]
- Jones, D.T.; Miller, R.T.; Thornton, J.M. Successful protein fold recognition by optimal sequence threading validated by rigorous blind testing. Proteins 1995, 23, 387–397. [Google Scholar] [CrossRef]
- Kallberg, M.; Wang, H.; Wang, S.; Peng, J.; Wang, Z.; Lu, H.; Xu, J. Template-based protein structure modeling using the RaptorX web server. Nat. Protoc. 2012, 7, 1511–1522. [Google Scholar] [CrossRef] [Green Version]
- Taylor, W.R.; Bartlett, G.J.; Chelliah, V.; Klose, D.; Lin, K.; Sheldon, T.; Jonassen, I. Prediction of protein structure from ideal forms. Proteins 2008, 70, 1610–1619. [Google Scholar] [CrossRef]
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Zidek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef]
- Tunyasuvunakool, K.; Adler, J.; Wu, Z.; Green, T.; Zielinski, M.; Zidek, A.; Bridgland, A.; Cowie, A.; Meyer, C.; Laydon, A.; et al. Highly accurate protein structure prediction for the human proteome. Nature 2021, 596, 590–596. [Google Scholar] [CrossRef]
- Baek, M.; DiMaio, F.; Anishchenko, I.; Dauparas, J.; Ovchinnikov, S.; Lee, G.R.; Wang, J.; Cong, Q.; Kinch, L.N.; Schaeffer, R.D.; et al. Accurate prediction of protein structures and interactions using a three-track neural network. Science 2021, 373, 871–876. [Google Scholar] [CrossRef]
- Baek, M.; Baker, D. Deep learning and protein structure modeling. Nat. Methods 2022, 19, 13–14. [Google Scholar] [CrossRef]
- Sulimov, V.B.; Kutov, D.C.; Sulimov, A.V. Advances in Docking. Curr. Med. Chem. 2019, 26, 7555–7580. [Google Scholar] [CrossRef]
- Pinzi, L.; Rastelli, G. Molecular Docking: Shifting Paradigms in Drug Discovery. Int. J. Mol. Sci. 2019, 20, 4331. [Google Scholar] [CrossRef] [Green Version]
- Kitchen, D.B.; Decornez, H.; Furr, J.R.; Bajorath, J. Docking and scoring in virtual screening for drug discovery: Methods and applications. Nat. Rev. Drug Discov. 2004, 3, 935–949. [Google Scholar] [CrossRef]
- De Vivo, M.; Cavalli, A. Recent advances in dynamic docking for drug discovery. WIREs Comput. Mol. Sci. 2017, 7, e1320. [Google Scholar] [CrossRef]
- Ewing, T.J.; Makino, S.; Skillman, A.G.; Kuntz, I.D. DOCK 4.0: Search strategies for automated molecular docking of flexible molecule databases. J. Comput.-Aided Mol. Des. 2001, 15, 411–428. [Google Scholar] [CrossRef]
- Rarey, M.; Kramer, B.; Lengauer, T.; Klebe, G. A fast flexible docking method using an incremental construction algorithm. J. Mol. Biol. 1996, 261, 470–489. [Google Scholar] [CrossRef] [Green Version]
- Friesner, R.A.; Banks, J.L.; Murphy, R.B.; Halgren, T.A.; Klicic, J.J.; Mainz, D.T.; Repasky, M.P.; Knoll, E.H.; Shelley, M.; Perry, J.K.; et al. Glide: A new approach for rapid, accurate docking and scoring. 1. Method and assessment of docking accuracy. J. Med. Chem. 2004, 47, 1739–1749. [Google Scholar] [CrossRef]
- Goodsell, D.S.; Lauble, H.; Stout, C.D.; Olson, A.J. Automated docking in crystallography: Analysis of the substrates of aconitase. Proteins 1993, 17, 1–10. [Google Scholar] [CrossRef]
- Spitaleri, A.; Ghitti, M.; Mari, S.; Alberici, L.; Traversari, C.; Rizzardi, G.P.; Musco, G. Use of metadynamics in the design of isoDGR-based alphavbeta3 antagonists to fine-tune the conformational ensemble. Angew. Chem. Int. Ed. Engl. 2011, 50, 1832–1836. [Google Scholar] [CrossRef]
- Hogervorst, F.; Kuikman, I.; von dem Borne, A.E.; Sonnenberg, A. Cloning and sequence analysis of beta-4 cDNA: An integrin subunit that contains a unique 118 kd cytoplasmic domain. EMBO J. 1990, 9, 765–770. [Google Scholar] [CrossRef] [PubMed]
- Cai, X.; Thinn, A.M.M.; Wang, Z.; Shan, H.; Zhu, J. The importance of N-glycosylation on beta3 integrin ligand binding and conformational regulation. Sci. Rep. 2017, 7, 4656. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gu, J.; Taniguchi, N. Regulation of integrin functions by N-glycans. Glycoconj. J. 2004, 21, 9–15. [Google Scholar] [CrossRef] [PubMed]
- Marsico, G.; Russo, L.; Quondamatteo, F.; Pandit, A. Glycosylation and Integrin Regulation in Cancer. Trends Cancer 2018, 4, 537–552. [Google Scholar] [CrossRef] [PubMed]
- Paszek, M.J.; DuFort, C.C.; Rossier, O.; Bainer, R.; Mouw, J.K.; Godula, K.; Hudak, J.E.; Lakins, J.N.; Wijekoon, A.C.; Cassereau, L.; et al. The cancer glycocalyx mechanically primes integrin-mediated growth and survival. Nature 2014, 511, 319–325. [Google Scholar] [CrossRef] [Green Version]
- Thomas, R.; Menon, V.; Mani, R.; Pruszak, J. Glycan Epitope and Integrin Expression Dynamics Characterize Neural Crest Epithelial-to-Mesenchymal Transition (EMT) in Human Pluripotent Stem Cell Differentiation. Stem Cell Rev. Rep. 2022, 18, 2952–2965. [Google Scholar] [CrossRef]
- Zhao, Y.; Sato, Y.; Isaji, T.; Fukuda, T.; Matsumoto, A.; Miyoshi, E.; Gu, J.; Taniguchi, N. Branched N-glycans regulate the biological functions of integrins and cadherins. FEBS J. 2008, 275, 1939–1948. [Google Scholar] [CrossRef]
- Janik, M.E.; Litynska, A.; Vereecken, P. Cell migration-The role of integrin glycosylation. Biochim. Et Biophys. Acta-Gen. Subj. 2010, 1800, 545–555. [Google Scholar] [CrossRef]
- Varki, A. Biological roles of glycans. Glycobiology 2017, 27, 3–49. [Google Scholar] [CrossRef] [Green Version]
- Reily, C.; Stewart, T.J.; Renfrow, M.B.; Novak, J. Glycosylation in health and disease. Nat. Rev. Nephrol. 2019, 15, 346–366. [Google Scholar] [CrossRef]
- Costa, A.F.; Campos, D.; Reis, C.A.; Gomes, C. Targeting Glycosylation: A New Road for Cancer Drug Discovery. Trends Cancer 2020, 6, 757–766. [Google Scholar] [CrossRef]
- Vasconcelos-Dos-Santos, A.; Oliveira, I.A.; Lucena, M.C.; Mantuano, N.R.; Whelan, S.A.; Dias, W.B.; Todeschini, A.R. Biosynthetic Machinery Involved in Aberrant Glycosylation: Promising Targets for Developing of Drugs Against Cancer. Front Oncol. 2015, 5, 138. [Google Scholar] [CrossRef] [Green Version]
- Isaji, T.; Sato, Y.; Zhao, Y.; Miyoshi, E.; Wada, Y.; Taniguchi, N.; Gu, J. N-glycosylation of the beta-propeller domain of the integrin alpha5 subunit is essential for alpha5beta1 heterodimerization, expression on the cell surface, and its biological function. J. Biol. Chem. 2006, 281, 33258–33267. [Google Scholar] [CrossRef] [Green Version]
- Luo, B.H.; Springer, T.A.; Takagi, J. Stabilizing the open conformation of the integrin headpiece with a glycan wedge increases affinity for ligand. Proc. Natl. Acad. Sci. USA 2003, 100, 2403–2408. [Google Scholar] [CrossRef] [Green Version]
- Xiong, J.P.; Stehle, T.; Diefenbach, B.; Zhang, R.; Dunker, R.; Scott, D.L.; Joachimiak, A.; Goodman, S.L.; Arnaout, M.A. Crystal structure of the extracellular segment of integrin alpha Vbeta3. Science 2001, 294, 339–345. [Google Scholar] [CrossRef] [Green Version]
- Xiong, J.P.; Goodman, S.L.; Arnaout, M.A. Purification, analysis, and crystal structure of integrins. Methods Enzymol. 2007, 426, 307–336. [Google Scholar] [CrossRef]
- Srichai, M.B.; Zent, R. Integrin Structure and Function. In Cell-Extracellular Matrix Interactions in Cancer; Pozzi, A., Ed.; Springer: New York, NY, USA, 2009; pp. 19–41. [Google Scholar]
- Liddington, R.C. Structural aspects of integrins. Adv. Exp. Med. Biol. 2014, 819, 111–126. [Google Scholar] [CrossRef]
- Ley, K.; Laudanna, C.; Cybulsky, M.I.; Nourshargh, S. Getting to the site of inflammation: The leukocyte adhesion cascade updated. Nat. Rev. Immunol. 2007, 7, 678–689. [Google Scholar] [CrossRef]
- Xie, C.; Zhu, J.; Chen, X.; Mi, L.; Nishida, N.; Springer, T.A. Structure of an integrin with an alphaI domain, complement receptor type 4. EMBO J. 2010, 29, 666–679. [Google Scholar] [CrossRef]
- Huang, J.; Li, X.; Shi, X.; Zhu, M.; Wang, J.; Huang, S.; Huang, X.; Wang, H.; Li, L.; Deng, H.; et al. Platelet integrin alphaIIbbeta3: Signal transduction, regulation, and its therapeutic targeting. J. Hematol. Oncol. 2019, 12, 26. [Google Scholar] [CrossRef] [Green Version]
- Xiong, J.P.; Mahalingham, B.; Alonso, J.L.; Borrelli, L.A.; Rui, X.; Anand, S.; Hyman, B.T.; Rysiok, T.; Muller-Pompalla, D.; Goodman, S.L.; et al. Crystal structure of the complete integrin alphaVbeta3 ectodomain plus an alpha/beta transmembrane fragment. J. Cell Biol. 2009, 186, 589–600. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Choi, W.S.; Rice, W.J.; Stokes, D.L.; Coller, B.S. Three-dimensional reconstruction of intact human integrin alphaIIbbeta3: New implications for activation-dependent ligand binding. Blood 2013, 122, 4165–4171. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhu, J.; Zhu, J.; Springer, T.A. Complete integrin headpiece opening in eight steps. J. Cell Biol. 2013, 201, 1053–1068. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, J.; Su, Y.; Xia, W.; Qin, Y.; Humphries, M.J.; Vestweber, D.; Cabanas, C.; Lu, C.; Springer, T.A. Conformational equilibria and intrinsic affinities define integrin activation. EMBO J. 2017, 36, 629–645. [Google Scholar] [CrossRef] [PubMed]
- Springer, T.A.; Dustin, M.L. Integrin inside-out signaling and the immunological synapse. Curr. Opin. Cell Biol. 2012, 24, 107–115. [Google Scholar] [CrossRef] [Green Version]
- Hughes, P.E.; Diaz-Gonzalez, F.; Leong, L.; Wu, C.; McDonald, J.A.; Shattil, S.J.; Ginsberg, M.H. Breaking the integrin hinge. A defined structural constraint regulates integrin signaling. J. Biol. Chem. 1996, 271, 6571–6574. [Google Scholar] [CrossRef] [Green Version]
- Kim, C.; Ye, F.; Hu, X.; Ginsberg, M.H. Talin activates integrins by altering the topology of the beta transmembrane domain. J. Cell Biol. 2012, 197, 605–611. [Google Scholar] [CrossRef] [Green Version]
- Shimaoka, M.; Takagi, J.; Springer, T.A. Conformational regulation of integrin structure and function. Annu. Rev. Biophys. Biomol. Struct. 2002, 31, 485–516. [Google Scholar] [CrossRef]
- Changede, R.; Xu, X.; Margadant, F.; Sheetz, M.P. Nascent Integrin Adhesions Form on All Matrix Rigidities after Integrin Activation. Dev. Cell 2015, 35, 614–621. [Google Scholar] [CrossRef] [Green Version]
- Shimaoka, M.; Xiao, T.; Liu, J.H.; Yang, Y.; Dong, Y.; Jun, C.D.; McCormack, A.; Zhang, R.; Joachimiak, A.; Takagi, J.; et al. Structures of the alpha L I domain and its complex with ICAM-1 reveal a shape-shifting pathway for integrin regulation. Cell 2003, 112, 99–111. [Google Scholar] [CrossRef] [Green Version]
- Emsley, J.; Knight, C.G.; Farndale, R.W.; Barnes, M.J.; Liddington, R.C. Structural basis of collagen recognition by integrin alpha2beta1. Cell 2000, 101, 47–56. [Google Scholar] [CrossRef]
- Sen, M.; Yuki, K.; Springer, T.A. An internal ligand-bound, metastable state of a leukocyte integrin, alphaXbeta2. J. Cell Biol. 2013, 203, 629–642. [Google Scholar] [CrossRef]
- Bajic, G.; Yatime, L.; Sim, R.B.; Vorup-Jensen, T.; Andersen, G.R. Structural insight on the recognition of surface-bound opsonins by the integrin I domain of complement receptor 3. Proc. Natl. Acad. Sci. USA 2013, 110, 16426–16431. [Google Scholar] [CrossRef] [Green Version]
- Potin, D.; Launay, M.; Monatlik, F.; Malabre, P.; Fabreguettes, M.; Fouquet, A.; Maillet, M.; Nicolai, E.; Dorgeret, L.; Chevallier, F.; et al. Discovery and development of 5-[(5S,9R)-9-(4-cyanophenyl)-3-(3,5-dichlorophenyl)-1-methyl-2,4-dioxo-1,3,7-tria zaspiro [4.4]non-7-yl-methyl]-3-thiophenecarboxylic acid (BMS-587101)--a small molecule antagonist of leukocyte function associated antigen-1. J. Med. Chem. 2006, 49, 6946–6949. [Google Scholar] [CrossRef]
- Tuckwell, D.S.; Brass, A.; Humphries, M.J. Homology modelling of integrin EF-hands. Evidence for widespread use of a conserved cation-binding site. Biochem. J. 1992, 285 Pt 1, 325–331. [Google Scholar] [CrossRef] [Green Version]
- Shimaoka, M.; Shifman, J.M.; Jing, H.; Takagi, J.; Mayo, S.L.; Springer, T.A. Computational design of an integrin I domain stabilized in the open high affinity conformation. Nat. Struct. Biol. 2000, 7, 674–678. [Google Scholar] [CrossRef]
- You, T.J.; Maxwell, D.S.; Kogan, T.P.; Chen, Q.; Li, J.; Kassir, J.; Holland, G.W.; Dixon, R.A. A 3D structure model of integrin alpha 4 beta 1 complex: I. Construction of a homology model of beta 1 and ligand binding analysis. Biophys. J. 2002, 82, 447–457. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.O.; Rieu, P.; Arnaout, M.A.; Liddington, R. Crystal structure of the A domain from the alpha subunit of integrin CR3 (CD11b/CD18). Cell 1995, 80, 631–638. [Google Scholar] [CrossRef]
- Marinelli, L.; Gottschalk, K.E.; Meyer, A.; Novellino, E.; Kessler, H. Human integrin alphavbeta5: Homology modeling and ligand binding. J. Med. Chem. 2004, 47, 4166–4177. [Google Scholar] [CrossRef]
- Filizola, M.; Hassan, S.A.; Artoni, A.; Coller, B.S.; Weinstein, H. Mechanistic insights from a refined three-dimensional model of integrin alphaIIbbeta3. J. Biol. Chem. 2004, 279, 24624–24630. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiong, J.P.; Stehle, T.; Zhang, R.; Joachimiak, A.; Frech, M.; Goodman, S.L.; Arnaout, M.A. Crystal structure of the extracellular segment of integrin alpha Vbeta3 in complex with an Arg-Gly-Asp ligand. Science 2002, 296, 151–155. [Google Scholar] [CrossRef] [PubMed]
- Shi, M.; Foo, S.Y.; Tan, S.M.; Mitchell, E.P.; Law, S.K.; Lescar, J. A structural hypothesis for the transition between bent and extended conformations of the leukocyte beta2 integrins. J. Biol. Chem. 2007, 282, 30198–30206. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gottschalk, K.E. A coiled-coil structure of the alphaIIbbeta3 integrin transmembrane and cytoplasmic domains in its resting state. Structure 2005, 13, 703–712. [Google Scholar] [CrossRef] [Green Version]
- Vinogradova, O.; Vaynberg, J.; Kong, X.; Haas, T.A.; Plow, E.F.; Qin, J. Membrane-mediated structural transitions at the cytoplasmic face during integrin activation. Proc. Natl. Acad. Sci. USA 2004, 101, 4094–4099. [Google Scholar] [CrossRef] [Green Version]
- Vinogradova, O.; Haas, T.; Plow, E.F.; Qin, J. A structural basis for integrin activation by the cytoplasmic tail of the alpha IIb-subunit. Proc. Natl. Acad. Sci. USA 2000, 97, 1450–1455. [Google Scholar] [CrossRef] [Green Version]
- Ulmer, T.S.; Yaspan, B.; Ginsberg, M.H.; Campbell, I.D. NMR analysis of structure and dynamics of the cytosolic tails of integrin alpha IIb beta 3 in aqueous solution. Biochemistry 2001, 40, 7498–7508. [Google Scholar] [CrossRef]
- Rosano, C.; Rocco, M. Solution properties of full-length integrin alpha(IIb)beta3 refined models suggest environment-dependent induction of alternative bent /extended resting states. FEBS J. 2010, 277, 3190–3202. [Google Scholar] [CrossRef]
- Zhu, J.; Luo, B.H.; Xiao, T.; Zhang, C.; Nishida, N.; Springer, T.A. Structure of a complete integrin ectodomain in a physiologic resting state and activation and deactivation by applied forces. Mol. Cell 2008, 32, 849–861. [Google Scholar] [CrossRef]
- Lau, T.L.; Kim, C.; Ginsberg, M.H.; Ulmer, T.S. The structure of the integrin alphaIIbbeta3 transmembrane complex explains integrin transmembrane signalling. EMBO J. 2009, 28, 1351–1361. [Google Scholar] [CrossRef]
- Kozmon, S. Homology model of alfa4beta1 integriins. 2022; unpublished results. [Google Scholar]
- Rose, D.M.; Alon, R.; Ginsberg, M.H. Integrin modulation and signaling in leukocyte adhesion and migration. Immunol. Rev. 2007, 218, 126–134. [Google Scholar] [CrossRef]
- Horton, E.R.; Byron, A.; Askari, J.A.; Ng, D.H.J.; Millon-Fremillon, A.; Robertson, J.; Koper, E.J.; Paul, N.R.; Warwood, S.; Knight, D.; et al. Definition of a consensus integrin adhesome and its dynamics during adhesion complex assembly and disassembly. Nat. Cell Biol. 2015, 17, 1577–1587. [Google Scholar] [CrossRef] [Green Version]
- Mehrbod, M.; Mofrad, M.R.K. Localized Lipid Packing of Transmembrane Domains Impedes Integrin Clustering. PLoS Comput. Biol. 2013, 9, e1002948. [Google Scholar] [CrossRef]
- Mehrbod, M.; Trisno, S.; Mofrad, M.R. On the activation of integrin alphaIIbbeta3: Outside-in and inside-out pathways. Biophys. J. 2013, 105, 1304–1315. [Google Scholar] [CrossRef] [Green Version]
- Kulke, M.; Langel, W. Molecular dynamics simulations to the bidirectional adhesion signaling pathway of integrin alphaV beta3. Proteins 2020, 88, 679–688. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, C.E.; Chen, T.; Lauffenburger, D.A. Simulation of Integrin-Cytoskeletal Interactions in Migrating Fibroblasts. Biophys. J. 1994, 67, 461–474. [Google Scholar] [CrossRef] [Green Version]
- Bidone, T.C.; Polley, A.; Jin, J.; Driscoll, T.; Iwamoto, D.V.; Calderwood, D.A.; Schwartz, M.A.; Voth, G.A. Coarse-Grained Simulation of Full-Length Integrin Activation. Biophys. J. 2019, 116, 1000–1010. [Google Scholar] [CrossRef] [Green Version]
- Craig, D.; Gao, M.; Schulten, K.; Vogel, V. Structural insights into how the MIDAS ion stabilizes integrin binding to an RGD peptide under force. Structure 2004, 12, 2049–2058. [Google Scholar] [CrossRef] [Green Version]
- Driscoll, T.P.; Bidone, T.C.; Ahn, S.J.; Yu, A.; Groisman, A.; Voth, G.A.; Schwartz, M.A. Integrin-based mechanosensing through conformational deformation. Biophys. J. 2021, 120, 4349–4359. [Google Scholar] [CrossRef]
- D’Ursi, P.; Orro, A.; Morra, G.; Moscatelli, M.; Trombetti, G.; Milanesi, L.; Rovida, E. Molecular dynamics and docking simulation of a natural variant of Activated Protein C with impaired protease activity: Implications for integrin-mediated antiseptic function. J. Biomol. Struct. Dyn. 2015, 33, 85–92. [Google Scholar] [CrossRef]
- Gaillard, T.; Dejaegere, A.; Stote, R.H. Dynamics of beta3 integrin I-like and hybrid domains: Insight from simulations on the mechanism of transition between open and closed forms. Proteins 2009, 76, 977–994. [Google Scholar] [CrossRef]
- Chen, W.; Lou, J.; Hsin, J.; Schulten, K.; Harvey, S.C.; Zhu, C. Molecular dynamics simulations of forced unbending of integrin alpha(v)beta(3). PLoS Comput. Biol. 2011, 7, e1001086. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Puklin-Faucher, E.; Gao, M.; Schulten, K.; Vogel, V. How the headpiece hinge angle is opened: New insights into the dynamics of integrin activation. J. Cell Biol. 2006, 175, 349–360. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, N.; Qiu, S.; Fang, Y.; Wu, J.; Li, Q. Comparison of Linear vs. Cyclic RGD Pentapeptide Interactions with Integrin alphavbeta3 by Molecular Dynamics Simulations. Biology 2021, 10, 688. [Google Scholar] [CrossRef] [PubMed]
- Chng, C.P.; Tan, S.M. Leukocyte integrin alphaLbeta2 transmembrane association dynamics revealed by coarse-grained molecular dynamics simulations. Proteins 2011, 79, 2203–2213. [Google Scholar] [CrossRef] [PubMed]
- Jallu, V.; Poulain, P.; Fuchs, P.F.; Kaplan, C.; de Brevern, A.G. Modeling and molecular dynamics simulations of the V33 variant of the integrin subunit beta3: Structural comparison with the L33 (HPA-1a) and P33 (HPA-1b) variants. Biochimie 2014, 105, 84–90. [Google Scholar] [CrossRef]
- Liu, J.; Das, M.; Yang, J.; Ithychanda, S.S.; Yakubenko, V.P.; Plow, E.F.; Qin, J. Structural mechanism of integrin inactivation by filamin. Nat. Struct. Mol. Biol. 2015, 22, 383–389. [Google Scholar] [CrossRef] [Green Version]
- Provasi, D.; Negri, A.; Coller, B.S.; Filizola, M. Talin-driven inside-out activation mechanism of platelet alphaIIbbeta3 integrin probed by multimicrosecond, all-atom molecular dynamics simulations. Proteins 2014, 82, 3231–3240. [Google Scholar] [CrossRef] [Green Version]
- Stavrakoudis, A. Conformational Studies of the 313–320 and 313–332 Peptide Fragments Derived from the aIIb Subunit of Integrin Receptor with Molecular Dynamics Simulations. Int. J. Pept. Res. Ther. 2009, 15, 263–272. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, J. Structural determinants of the integrin transmembrane domain required for bidirectional signal transmission across the cell membrane. J. Biol. Chem. 2021, 297, 101318. [Google Scholar] [CrossRef]
- Xiao, T.; Takagi, J.; Coller, B.S.; Wang, J.H.; Springer, T.A. Structural basis for allostery in integrins and binding to fibrinogen-mimetic therapeutics. Nature 2004, 432, 59–67. [Google Scholar] [CrossRef] [Green Version]
- Murcia, M.; Jirouskova, M.; Li, J.; Coller, B.S.; Filizola, M. Functional and computational studies of the ligand-associated metal binding site of beta3 integrins. Proteins 2008, 71, 1779–1791. [Google Scholar] [CrossRef] [Green Version]
- Kóňa, J. Comparative study of interaction energies between the integrin aIIbb3 and the peptidic, peptidomimetic and non-peptidic ligands by quantum mechanics FMO-PIEDA calculations. 2022; unpublished results. [Google Scholar]
- Puklin-Faucher, E.; Vogel, V. Integrin activation dynamics between the RGD-binding site and the headpiece hinge. J. Biol. Chem. 2009, 284, 36557–36568. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Pan, D.; Yan, Q.; Song, Y. Activation mechanisms of alphaVbeta3 integrin by binding to fibronectin: A computational study. Protein Sci. 2017, 26, 1124–1137. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Pan, D.; Bellis, S.L.; Song, Y. Effect of altered glycosylation on the structure of the I-like domain of beta1 integrin: A molecular dynamics study. Proteins 2008, 73, 989–1000. [Google Scholar] [CrossRef]
- Xiong, J.P.; Stehle, T.; Goodman, S.L.; Arnaout, M.A. A novel adaptation of the integrin PSI domain revealed from its crystal structure. J. Biol. Chem. 2004, 279, 40252–40254. [Google Scholar] [CrossRef] [Green Version]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [Green Version]
- Monticelli, L.; Kandasamy, S.K.; Periole, X.; Larson, R.G.; Tieleman, D.P.; Marrink, S.J. The MARTINI Coarse-Grained Force Field: Extension to Proteins. J. Chem. Theory Comput. 2008, 4, 819–834. [Google Scholar] [CrossRef]
- Jallu, V.; Poulain, P.; Fuchs, P.F.; Kaplan, C.; de Brevern, A.G. Modeling and molecular dynamics of HPA-1a and -1b polymorphisms: Effects on the structure of the beta3 subunit of the alphaIIbbeta3 integrin. PLoS One 2012, 7, e47304. [Google Scholar] [CrossRef]
- MacKerell, A.D.; Bashford, D.; Bellott, M.; Dunbrack, R.L.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef]
- Yang, J.; Ma, Y.Q.; Page, R.C.; Misra, S.; Plow, E.F.; Qin, J. Structure of an integrin alphaIIb beta3 transmembrane-cytoplasmic heterocomplex provides insight into integrin activation. Proc. Natl. Acad. Sci. USA 2009, 106, 17729–17734. [Google Scholar] [CrossRef] [Green Version]
- Elosegui-Artola, A.; Bazellieres, E.; Allen, M.D.; Andreu, I.; Oria, R.; Sunyer, R.; Gomm, J.J.; Marshall, J.F.; Jones, J.L.; Trepat, X.; et al. Rigidity sensing and adaptation through regulation of integrin types. Nat. Mater. 2014, 13, 631–637. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dong, X.; Mi, L.Z.; Zhu, J.; Wang, W.; Hu, P.; Luo, B.H.; Springer, T.A. alpha(V)beta(3) integrin crystal structures and their functional implications. Biochemistry 2012, 51, 8814–8828. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.; Lin, Z.; Fang, Y.; Wu, J. Prediction of Catch-Slip Bond Transition of Kindlin2/beta3 Integrin via Steered Molecular Dynamics Simulation. J. Chem. Inf. Model. 2020, 60, 5132–5141. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Deng, Y.; Sun, K.; Yang, H.; Liu, J.; Wang, M.; Zhang, Z.; Lin, J.; Wu, C.; Wei, Z.; et al. Structural basis of kindlin-mediated integrin recognition and activation. Proc. Natl. Acad. Sci. USA 2017, 114, 9349–9354. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van Agthoven, J.F.; Xiong, J.P.; Alonso, J.L.; Rui, X.; Adair, B.D.; Goodman, S.L.; Arnaout, M.A. Structural basis for pure antagonism of integrin alphaVbeta3 by a high-affinity form of fibronectin. Nat. Struct. Mol. Biol. 2014, 21, 383–388. [Google Scholar] [CrossRef] [Green Version]
- Li, N.; Zhang, X.; Li, P.; Yang, H.; Tong, C.; Lü, S.; Zhang, Y.; Ye, Z.; Pan, J.; Long, M. Mechanical S trength and S tructural B asis of β 2 I ntegrin to Mediate Neutrophil Accumulation on L iver Sinusoidal Endothelial Cells: A Study Using Atomic Force Microscopy and Molecular Dynamics Simulations. Comput. Model. Eng. Sci. (CMES) 2018, 216, 263–279. [Google Scholar] [CrossRef]
- Lee, J.O.; Bankston, L.A.; Arnaout, M.A.; Liddington, R.C. Two conformations of the integrin A-domain (I-domain): A pathway for activation? Structure 1995, 3, 1333–1340. [Google Scholar] [CrossRef] [Green Version]
- Lu, F.; Zhu, L.; Bromberger, T.; Yang, J.; Yang, Q.; Liu, J.; Plow, E.F.; Moser, M.; Qin, J. Mechanism of integrin activation by talin and its cooperation with kindlin. Nat. Commun. 2022, 13, 2362. [Google Scholar] [CrossRef]
- Humphries, J.D.; Chastney, M.R.; Askari, J.A.; Humphries, M.J. Signal transduction via integrin adhesion complexes. Curr. Opin. Cell Biol. 2019, 56, 14–21. [Google Scholar] [CrossRef] [Green Version]
- Bouti, P.; Webbers, S.D.S.; Fagerholm, S.C.; Alon, R.; Moser, M.; Matlung, H.L.; Kuijpers, T.W. beta2 Integrin Signaling Cascade in Neutrophils: More Than a Single Function. Front. Immunol. 2020, 11, 619925. [Google Scholar] [CrossRef]
- Bouvard, D.; Pouwels, J.; De Franceschi, N.; Ivaska, J. Integrin inactivators: Balancing cellular functions in vitro and in vivo. Nat. Rev. Mol. Cell Biol. 2013, 14, 430–442. [Google Scholar] [CrossRef]
- Sun, Z.; Guo, S.S.; Fassler, R. Integrin-mediated mechanotransduction. J. Cell Biol. 2016, 215, 445–456. [Google Scholar] [CrossRef] [Green Version]
- Seetharaman, S.; Etienne-Manneville, S. Integrin diversity brings specificity in mechanotransduction. Biol. Cell 2018, 110, 49–64. [Google Scholar] [CrossRef]
- Iskratsch, T.; Wolfenson, H.; Sheetz, M.P. Appreciating force and shape-the rise of mechanotransduction in cell biology. Nat. Rev. Mol. Cell Biol. 2014, 15, 825–833. [Google Scholar] [CrossRef]
- Humphries, J.D.; Byron, A.; Humphries, M.J. Integrin ligands at a glance. J. Cell Sci. 2006, 119, 3901–3903. [Google Scholar] [CrossRef] [Green Version]
- Park, E.J.; Myint, P.K.; Ito, A.; Appiah, M.G.; Darkwah, S.; Kawamoto, E.; Shimaoka, M. Integrin-Ligand Interactions in Inflammation, Cancer, and Metabolic Disease: Insights Into the Multifaceted Roles of an Emerging Ligand Irisin. Front. Cell Dev. Biol. 2020, 8, 588066. [Google Scholar] [CrossRef]
- Ley, K.; Rivera-Nieves, J.; Sandborn, W.J.; Shattil, S. Integrin-based therapeutics: Biological basis, clinical use and new drugs. Nat. Rev. Drug Discov. 2016, 15, 173–183. [Google Scholar] [CrossRef] [Green Version]
- Mezu-Ndubuisi, O.J.; Maheshwari, A. The role of integrins in inflammation and angiogenesis. Pediatr. Res. 2021, 89, 1619–1626. [Google Scholar] [CrossRef]
- Kourtzelis, I.; Mitroulis, I.; von Renesse, J.; Hajishengallis, G.; Chavakis, T. From leukocyte recruitment to resolution of inflammation: The cardinal role of integrins. J. Leukoc. Biol. 2017, 102, 677–683. [Google Scholar] [CrossRef] [Green Version]
- Bianchi, E.; Molteni, R.; Pardi, R.; Dubini, G. Microfluidics for in vitro biomimetic shear stress-dependent leukocyte adhesion assays. J. Biomech. 2013, 46, 276–283. [Google Scholar] [CrossRef]
- Abram, C.L.; Lowell, C.A. Leukocyte adhesion deficiency syndrome: A controversy solved. Immunol. Cell Biol. 2009, 87, 440–442. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nair, S.; Ghosh, K.; Kulkarni, B.; Shetty, S.; Mohanty, D. Glanzmann’s thrombasthenia: Updated. Platelets 2002, 13, 387–393. [Google Scholar] [CrossRef] [PubMed]
- Bardhan, A.; Bruckner-Tuderman, L.; Chapple, I.L.C.; Fine, J.D.; Harper, N.; Has, C.; Magin, T.M.; Marinkovich, M.P.; Marshall, J.F.; McGrath, J.A.; et al. Epidermolysis bullosa. Nat. Rev. Dis. Prim. 2020, 6, 78. [Google Scholar] [CrossRef] [PubMed]
- Greenlee-Wacker, M.C. Clearance of apoptotic neutrophils and resolution of inflammation. Immunol. Rev. 2016, 273, 357–370. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dotan, I.; Allez, M.; Danese, S.; Keir, M.; Tole, S.; McBride, J. The role of integrins in the pathogenesis of inflammatory bowel disease: Approved and investigational anti-integrin therapies. Med. Res. Rev. 2020, 40, 245–262. [Google Scholar] [CrossRef] [Green Version]
- de Souza, H.S.; Fiocchi, C. Immunopathogenesis of IBD: Current state of the art. Nat. Rev. Gastroenterol. Hepatol. 2016, 13, 13–27. [Google Scholar] [CrossRef]
- Orr, C.; Vieira-Sousa, E.; Boyle, D.L.; Buch, M.H.; Buckley, C.D.; Canete, J.D.; Catrina, A.I.; Choy, E.H.S.; Emery, P.; Fearon, U.; et al. Synovial tissue research: A state-of-the-art review. Nat. Rev. Rheumatol. 2017, 13, 463–475. [Google Scholar] [CrossRef]
- Jang, S.; Kwon, E.J.; Lee, J.J. Rheumatoid Arthritis: Pathogenic Roles of Diverse Immune Cells. Int. J. Mol. Sci. 2022, 23, 905. [Google Scholar] [CrossRef]
- Lowin, T.; Straub, R.H. Integrins and their ligands in rheumatoid arthritis. Arthritis Res. Ther. 2011, 13, 244. [Google Scholar] [CrossRef] [Green Version]
- Wollheim, F.A. Predictors of joint damage in rheumatoid arthritis. APMIS 1996, 104, 81–93. [Google Scholar] [CrossRef]
- Conroy, K.P.; Kitto, L.J.; Henderson, N.C. alphav integrins: Key regulators of tissue fibrosis. Cell Tissue Res. 2016, 365, 511–519. [Google Scholar] [CrossRef] [Green Version]
- Herrera, J.; Henke, C.A.; Bitterman, P.B. Extracellular matrix as a driver of progressive fibrosis. J. Clin. Investig. 2018, 128, 45–53. [Google Scholar] [CrossRef] [Green Version]
- Henderson, N.C.; Rieder, F.; Wynn, T.A. Fibrosis: From mechanisms to medicines. Nature 2020, 587, 555–566. [Google Scholar] [CrossRef]
- Sciurba, J.C.; Gieseck, R.L.; Jiwrajka, N.; White, S.D.; Karmele, E.P.; Redes, J.; Vannella, K.M.; Henderson, N.C.; Wynn, T.A.; Hart, K.M. Fibroblast-specific integrin-alpha V differentially regulates type 17 and type 2 driven inflammation and fibrosis. J. Pathol. 2019, 248, 16–29. [Google Scholar] [CrossRef] [Green Version]
- Finney, A.C.; Stokes, K.Y.; Pattillo, C.B.; Orr, A.W. Integrin signaling in atherosclerosis. Cell. Mol. Life Sci. 2017, 74, 2263–2282. [Google Scholar] [CrossRef]
- Kong, P.; Cui, Z.Y.; Huang, X.F.; Zhang, D.D.; Guo, R.J.; Han, M. Inflammation and atherosclerosis: Signaling pathways and therapeutic intervention. Signal Transduct. Target. Ther. 2022, 7, 131. [Google Scholar] [CrossRef]
- Zhi, K.; Li, M.; Zhang, X.; Gao, Z.; Bai, J.; Wu, Y.; Zhou, S.; Li, M.; Qu, L. alpha4beta7 Integrin (LPAM-1) is upregulated at atherosclerotic lesions and is involved in atherosclerosis progression. Cell. Physiol. Biochem. 2014, 33, 1876–1887. [Google Scholar] [CrossRef]
- Oksala, N.; Parssinen, J.; Seppala, I.; Klopp, N.; Illig, T.; Laaksonen, R.; Levula, M.; Raitoharju, E.; Kholova, I.; Sioris, T.; et al. Kindlin 3 (FERMT3) is associated with unstable atherosclerotic plaques, anti-inflammatory type II macrophages and upregulation of beta-2 integrins in all major arterial beds. Atherosclerosis 2015, 242, 145–154. [Google Scholar] [CrossRef]
- Wu, H.; Gower, R.M.; Wang, H.; Perrard, X.Y.; Ma, R.; Bullard, D.C.; Burns, A.R.; Paul, A.; Smith, C.W.; Simon, S.I.; et al. Functional role of CD11c+ monocytes in atherogenesis associated with hypercholesterolemia. Circulation 2009, 119, 2708–2717. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Green, J.; Yurdagul, A., Jr.; Albert, P.; McInnis, M.C.; Orr, A.W. alphavbeta3 Integrins Mediate Flow-Induced NF-kappaB Activation, Proinflammatory Gene Expression, and Early Atherogenic Inflammation. Am. J. Pathol. 2015, 185, 2575–2589. [Google Scholar] [CrossRef] [Green Version]
- Yurdagul, A., Jr.; Green, J.; Albert, P.; McInnis, M.C.; Mazar, A.P.; Orr, A.W. alpha5beta1 integrin signaling mediates oxidized low-density lipoprotein-induced inflammation and early atherosclerosis. Arter. Thromb. Vasc. Biol. 2014, 34, 1362–1373. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, W.; Hutcheon, A.E.K.; Sriram, S.; Tran, J.A.; Zieske, J.D. Initiation of fibrosis in the integrin Alphavbeta6 knockout mice. Exp. Eye Res. 2019, 180, 23–28. [Google Scholar] [CrossRef] [PubMed]
- Weller, J.M.; Zenkel, M.; Schlotzer-Schrehardt, U.; Bachmann, B.O.; Tourtas, T.; Kruse, F.E. Extracellular matrix alterations in late-onset Fuchs’ corneal dystrophy. Investig. Ophthalmol. Vis. Sci. 2014, 55, 3700–3708. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Storm, R.J.; Persson, B.D.; Skalman, L.N.; Frangsmyr, L.; Lindstrom, M.; Rankin, G.; Lundmark, R.; Domellof, F.P.; Arnberg, N. Human Adenovirus Type 37 Uses alphaVbeta1 and alpha3beta1 Integrins for Infection of Human Corneal Cells. J. Virol. 2017, 91, e02019-16. [Google Scholar] [CrossRef] [Green Version]
- Wang, A.G.; Yen, M.Y.; Hsu, W.M.; Fann, M.J. Induction of vitronectin and integrin alphav in the retina after optic nerve injury. Mol. Vis. 2006, 12, 76–84. [Google Scholar]
- Labelle, M.; Hynes, R.O. The initial hours of metastasis: The importance of cooperative host-tumor cell interactions during hematogenous dissemination. Cancer Discov. 2012, 2, 1091–1099. [Google Scholar] [CrossRef] [Green Version]
- Chambers, A.F.; Groom, A.C.; MacDonald, I.C. Dissemination and growth of cancer cells in metastatic sites. Nat. Rev. Cancer 2002, 2, 563–572. [Google Scholar] [CrossRef]
- Hanahan, D.; Weinberg, R.A. Hallmarks of cancer: The next generation. Cell 2011, 144, 646–674. [Google Scholar] [CrossRef] [Green Version]
- Obenauf, A.C.; Massague, J. Surviving at a Distance: Organ-Specific Metastasis. Trends Cancer 2015, 1, 76–91. [Google Scholar] [CrossRef]
- Desgrosellier, J.S.; Cheresh, D.A. Integrins in cancer: Biological implications and therapeutic opportunities. Nat. Rev. Cancer 2010, 10, 9–22. [Google Scholar] [CrossRef] [Green Version]
- Cooper, J.; Giancotti, F.G. Integrin Signaling in Cancer: Mechanotransduction, Stemness, Epithelial Plasticity, and Therapeutic Resistance. Cancer Cell 2019, 35, 347–367. [Google Scholar] [CrossRef]
- Seguin, L.; Desgrosellier, J.S.; Weis, S.M.; Cheresh, D.A. integrins and cancer: Regulators of cancer stemness, metastasis, and drug resistance. Trends Cell Biol. 2015, 25, 234–240. [Google Scholar] [CrossRef] [Green Version]
- Nieberler, M.; Reuning, U.; Reichart, F.; Notni, J.; Wester, H.J.; Schwaiger, M.; Weinmuller, M.; Rader, A.; Steiger, K.; Kessler, H. Exploring the Role of RGD-Recognizing Integrins in Cancer. Cancers 2017, 9, 116. [Google Scholar] [CrossRef] [Green Version]
- Hamidi, H.; Pietila, M.; Ivaska, J. The complexity of integrins in cancer and new scopes for therapeutic targeting. Br. J. Cancer 2016, 115, 1017–1023. [Google Scholar] [CrossRef] [Green Version]
- Seguin, L.; Kato, S.; Franovic, A.; Camargo, M.F.; Lesperance, J.; Elliott, K.C.; Yebra, M.; Mielgo, A.; Lowy, A.M.; Husain, H.; et al. An integrin beta(3)-KRAS-RalB complex drives tumour stemness and resistance to EGFR inhibition. Nat. Cell Biol. 2014, 16, 457–468. [Google Scholar] [CrossRef] [Green Version]
- White, D.E.; Kurpios, N.A.; Zuo, D.; Hassell, J.A.; Blaess, S.; Mueller, U.; Muller, W.J. Targeted disruption of beta1-integrin in a transgenic mouse model of human breast cancer reveals an essential role in mammary tumor induction. Cancer Cell 2004, 6, 159–170. [Google Scholar] [CrossRef] [Green Version]
- Ramirez, N.E.; Zhang, Z.; Madamanchi, A.; Boyd, K.L.; O’Rear, L.D.; Nashabi, A.; Li, Z.; Dupont, W.D.; Zijlstra, A.; Zutter, M.M. The alpha(2)beta(1) integrin is a metastasis suppressor in mouse models and human cancer. J. Clin. Investig. 2011, 121, 226–237. [Google Scholar] [CrossRef] [Green Version]
- Kannan, N.; Nguyen, L.V.; Eaves, C.J. Integrin beta3 links therapy resistance and cancer stem cell properties. Nat. Cell Biol. 2014, 16, 397–399. [Google Scholar] [CrossRef]
- Laubli, H.; Borsig, L. Selectins promote tumor metastasis. Semin. Cancer Biol. 2010, 20, 169–177. [Google Scholar] [CrossRef]
- Wirtz, D.; Konstantopoulos, K.; Searson, P.C. The physics of cancer: The role of physical interactions and mechanical forces in metastasis. Nat. Rev. Cancer 2011, 11, 512–522. [Google Scholar] [CrossRef] [Green Version]
- Ramovs, V.; Te Molder, L.; Sonnenberg, A. The opposing roles of laminin-binding integrins in cancer. Matrix Biol. 2017, 57–58, 213–243. [Google Scholar] [CrossRef] [PubMed]
- Ramovs, V.; Secades, P.; Song, J.Y.; Thijssen, B.; Kreft, M.; Sonnenberg, A. Absence of integrin alpha3beta1 promotes the progression of HER2-driven breast cancer in vivo. Breast Cancer Res. 2019, 21, 63. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.L.; Xing, X.; Cai, L.B.; Zhu, L.; Yang, X.M.; Wang, Y.H.; Yang, Q.; Nie, H.Z.; Zhang, Z.G.; Li, J.; et al. Integrin alpha9 Suppresses Hepatocellular Carcinoma Metastasis by Rho GTPase Signaling. J. Immunol. Res. 2018, 2018, 4602570. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Z.; Li, Y.; Xiao, Y.; Lin, H.P.; Yang, P.; Humphries, B.; Gao, T.; Yang, C. Integrin alpha9 depletion promotes beta-catenin degradation to suppress triple-negative breast cancer tumor growth and metastasis. Int. J. Cancer 2019, 145, 2767–2780. [Google Scholar] [CrossRef] [PubMed]
- Attieh, Y.; Clark, A.G.; Grass, C.; Richon, S.; Pocard, M.; Mariani, P.; Elkhatib, N.; Betz, T.; Gurchenkov, B.; Vignjevic, D.M. Cancer-associated fibroblasts lead tumor invasion through integrin-beta3-dependent fibronectin assembly. J. Cell Biol. 2017, 216, 3509–3520. [Google Scholar] [CrossRef] [Green Version]
- Erdogan, B.; Ao, M.; White, L.M.; Means, A.L.; Brewer, B.M.; Yang, L.; Washington, M.K.; Shi, C.; Franco, O.E.; Weaver, A.M.; et al. Cancer-associated fibroblasts promote directional cancer cell migration by aligning fibronectin. J. Cell Biol. 2017, 216, 3799–3816. [Google Scholar] [CrossRef] [Green Version]
- Peng, C.; Zou, X.; Xia, W.; Gao, H.; Li, Z.; Liu, N.; Xu, Z.; Gao, C.; He, Z.; Niu, W.; et al. Integrin alphavbeta6 plays a bi-directional regulation role between colon cancer cells and cancer-associated fibroblasts. Biosci. Rep. 2018, 38, BSR20180243. [Google Scholar] [CrossRef] [Green Version]
- Ota, D.; Kanayama, M.; Matsui, Y.; Ito, K.; Maeda, N.; Kutomi, G.; Hirata, K.; Torigoe, T.; Sato, N.; Takaoka, A.; et al. Tumor-alpha9beta1 integrin-mediated signaling induces breast cancer growth and lymphatic metastasis via the recruitment of cancer-associated fibroblasts. J. Mol. Med. 2014, 92, 1271–1281. [Google Scholar] [CrossRef]
- Foubert, P.; Varner, J.A. Integrins in tumor angiogenesis and lymphangiogenesis. Methods Mol. Biol. 2012, 757, 471–486. [Google Scholar] [CrossRef]
- Eke, I.; Cordes, N. Focal adhesion signaling and therapy resistance in cancer. Semin. Cancer Biol. 2015, 31, 65–75. [Google Scholar] [CrossRef]
- Kim, Y.J.; Jung, K.; Baek, D.S.; Hong, S.S.; Kim, Y.S. Co-targeting of EGF receptor and neuropilin-1 overcomes cetuximab resistance in pancreatic ductal adenocarcinoma with integrin beta1-driven Src-Akt bypass signaling. Oncogene 2017, 36, 2543–2552. [Google Scholar] [CrossRef]
- Yang, D.; Tang, Y.; Fu, H.; Xu, J.; Hu, Z.; Zhang, Y.; Cai, Q. Integrin beta1 promotes gemcitabine resistance in pancreatic cancer through Cdc42 activation of PI3K p110beta signaling. Biochem. Biophys. Res. Commun. 2018, 505, 215–221. [Google Scholar] [CrossRef]
- Stewart, P.L.; Nemerow, G.R. Cell integrins: Commonly used receptors for diverse viral pathogens. Trends Microbiol. 2007, 15, 500–507. [Google Scholar] [CrossRef]
- Scibelli, A.; Roperto, S.; Manna, L.; Pavone, L.M.; Tafuri, S.; Della Morte, R.; Staiano, N. Engagement of integrins as a cellular route of invasion by bacterial pathogens. Vet. J. 2007, 173, 482–491. [Google Scholar] [CrossRef]
- Hussein, H.A.; Walker, L.R.; Abdel-Raouf, U.M.; Desouky, S.A.; Montasser, A.K.; Akula, S.M. Beyond RGD: Virus interactions with integrins. Arch. Virol. 2015, 160, 2669–2681. [Google Scholar] [CrossRef]
- Hauck, C.R.; Borisova, M.; Muenzner, P. Exploitation of integrin function by pathogenic microbes. Curr. Opin. Cell Biol. 2012, 24, 637–644. [Google Scholar] [CrossRef]
- Chiu, C.Y.; Mathias, P.; Nemerow, G.R.; Stewart, P.L. Structure of adenovirus complexed with its internalization receptor, alphavbeta5 integrin. J. Virol. 1999, 73, 6759–6768. [Google Scholar] [CrossRef] [Green Version]
- Philpott, N.J.; Nociari, M.; Elkon, K.B.; Falck-Pedersen, E. Adenovirus-induced maturation of dendritic cells through a PI3 kinase-mediated TNF-alpha induction pathway. Proc. Natl. Acad. Sci. USA 2004, 101, 6200–6205. [Google Scholar] [CrossRef] [Green Version]
- Akula, S.M.; Pramod, N.P.; Wang, F.Z.; Chandran, B. Integrin alpha3beta1 (CD 49c/29) is a cellular receptor for Kaposi’s sarcoma-associated herpesvirus (KSHV/HHV-8) entry into the target cells. Cell 2002, 108, 407–419. [Google Scholar] [CrossRef]
- Gavrilovskaya, I.N.; Brown, E.J.; Ginsberg, M.H.; Mackow, E.R. Cellular entry of hantaviruses which cause hemorrhagic fever with renal syndrome is mediated by beta3 integrins. J. Virol. 1999, 73, 3951–3959. [Google Scholar] [CrossRef] [Green Version]
- Geimonen, E.; Neff, S.; Raymond, T.; Kocer, S.S.; Gavrilovskaya, I.N.; Mackow, E.R. Pathogenic and nonpathogenic hantaviruses differentially regulate endothelial cell responses. Proc. Natl. Acad. Sci. USA 2002, 99, 13837–13842. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shakeel, S.; Seitsonen, J.J.; Kajander, T.; Laurinmaki, P.; Hyypia, T.; Susi, P.; Butcher, S.J. Structural and functional analysis of coxsackievirus A9 integrin alphavbeta6 binding and uncoating. J. Virol. 2013, 87, 3943–3951. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barillari, G.; Sgadari, C.; Fiorelli, V.; Samaniego, F.; Colombini, S.; Manzari, V.; Modesti, A.; Nair, B.C.; Cafaro, A.; Sturzl, M.; et al. The Tat protein of human immunodeficiency virus type-1 promotes vascular cell growth and locomotion by engaging the alpha5beta1 and alphavbeta3 integrins and by mobilizing sequestered basic fibroblast growth factor. Blood 1999, 94, 663–672. [Google Scholar] [PubMed]
- Arthos, J.; Cicala, C.; Martinelli, E.; Macleod, K.; Van Ryk, D.; Wei, D.; Xiao, Z.; Veenstra, T.D.; Conrad, T.P.; Lempicki, R.A.; et al. HIV-1 envelope protein binds to and signals through integrin alpha4beta7, the gut mucosal homing receptor for peripheral T cells. Nat. Immunol. 2008, 9, 301–309. [Google Scholar] [CrossRef]
- Barillari, G.; Gendelman, R.; Gallo, R.C.; Ensoli, B. The Tat protein of human immunodeficiency virus type 1, a growth factor for AIDS Kaposi sarcoma and cytokine-activated vascular cells, induces adhesion of the same cell types by using integrin receptors recognizing the RGD amino acid sequence. Proc. Natl. Acad. Sci. USA 1993, 90, 7941–7945. [Google Scholar] [CrossRef] [Green Version]
- Schornberg, K.L.; Shoemaker, C.J.; Dube, D.; Abshire, M.Y.; Delos, S.E.; Bouton, A.H.; White, J.M. Alpha5beta1-integrin controls ebolavirus entry by regulating endosomal cathepsins. Proc. Natl. Acad. Sci. USA 2009, 106, 8003–8008. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Zhang, Q.; Tiwari, S.K.; Lichinchi, G.; Yau, E.H.; Hui, H.; Li, W.; Furnari, F.; Rana, T.M. Integrin alphavbeta5 Internalizes Zika Virus during Neural Stem Cells Infection and Provides a Promising Target for Antiviral Therapy. Cell. Rep. 2020, 30, 969–983. [Google Scholar] [CrossRef] [Green Version]
- Guerrero, C.A.; Mendez, E.; Zarate, S.; Isa, P.; Lopez, S.; Arias, C.F. Integrin alpha(v)beta(3) mediates rotavirus cell entry. Proc. Natl. Acad. Sci. USA 2000, 97, 14644–14649. [Google Scholar] [CrossRef] [Green Version]
- Kotecha, A.; Wang, Q.; Dong, X.; Ilca, S.L.; Ondiviela, M.; Zihe, R.; Seago, J.; Charleston, B.; Fry, E.E.; Abrescia, N.G.A.; et al. Rules of engagement between alphavbeta6 integrin and foot-and-mouth disease virus. Nat. Commun. 2017, 8, 15408. [Google Scholar] [CrossRef]
- Sigrist, C.J.; Bridge, A.; Le Mercier, P. A potential role for integrins in host cell entry by SARS-CoV-2. Antiviral. Res. 2020, 177, 104759. [Google Scholar] [CrossRef]
- Carvacho, I.; Piesche, M. RGD-binding integrins and TGF-beta in SARS-CoV-2 infections-novel targets to treat COVID-19 patients? Clin. Transl. Immunol. 2021, 10, e1240. [Google Scholar] [CrossRef]
- La Linn, M.; Eble, J.A.; Lubken, C.; Slade, R.W.; Heino, J.; Davies, J.; Suhrbier, A. An arthritogenic alphavirus uses the alpha1beta1 integrin collagen receptor. Virology 2005, 336, 229–239. [Google Scholar] [CrossRef]
- Graham, K.L.; Fleming, F.E.; Halasz, P.; Hewish, M.J.; Nagesha, H.S.; Holmes, I.H.; Takada, Y.; Coulson, B.S. Rotaviruses interact with alpha4beta7 and alpha4beta1 integrins by binding the same integrin domains as natural ligands. J. Gen. Virol. 2005, 86, 3397–3408. [Google Scholar] [CrossRef]
- Graham, K.L.; Halasz, P.; Tan, Y.; Hewish, M.J.; Takada, Y.; Mackow, E.R.; Robinson, M.K.; Coulson, B.S. Integrin-using rotaviruses bind alpha2beta1 integrin alpha2 I domain via VP4 DGE sequence and recognize alphaXbeta2 and alphaVbeta3 by using VP7 during cell entry. J. Virol. 2003, 77, 9969–9978. [Google Scholar] [CrossRef] [Green Version]
- Graham, K.L.; Zeng, W.; Takada, Y.; Jackson, D.C.; Coulson, B.S. Effects on rotavirus cell binding and infection of monomeric and polymeric peptides containing alpha2beta1 and alphaxbeta2 integrin ligand sequences. J. Virol. 2004, 78, 11786–11797. [Google Scholar] [CrossRef] [Green Version]
- Bergelson, J.M.; Shepley, M.P.; Chan, B.M.; Hemler, M.E.; Finberg, R.W. Identification of the integrin VLA-2 as a receptor for echovirus 1. Science 1992, 255, 1718–1720. [Google Scholar] [CrossRef]
- Hamzaoui, N.; Kerneis, S.; Caliot, E.; Pringault, E. Expression and distribution of beta1 integrins in in vitro-induced M cells: Implications for Yersinia adhesion to Peyer’s patch epithelium. Cell. Microbiol. 2004, 6, 817–828. [Google Scholar] [CrossRef]
- Kwok, T.; Zabler, D.; Urman, S.; Rohde, M.; Hartig, R.; Wessler, S.; Misselwitz, R.; Berger, J.; Sewald, N.; Konig, W.; et al. Helicobacter exploits integrin for type IV secretion and kinase activation. Nature 2007, 449, 862–866. [Google Scholar] [CrossRef]
- Coburn, J.; Cugini, C. Targeted mutation of the outer membrane protein P66 disrupts attachment of the Lyme disease agent, Borrelia burgdorferi, to integrin alphavbeta3. Proc. Natl. Acad. Sci. USA 2003, 100, 7301–7306. [Google Scholar] [CrossRef]
- Joh, D.; Wann, E.R.; Kreikemeyer, B.; Speziale, P.; Hook, M. Role of fibronectin-binding MSCRAMMs in bacterial adherence and entry into mammalian cells. Matrix Biol. 1999, 18, 211–223. [Google Scholar] [CrossRef]
- Fowler, T.; Wann, E.R.; Joh, D.; Johansson, S.; Foster, T.J.; Hook, M. Cellular invasion by Staphylococcus aureus involves a fibronectin bridge between the bacterial fibronectin-binding MSCRAMMs and host cell beta1 integrins. Eur. J. Cell Biol. 2000, 79, 672–679. [Google Scholar] [CrossRef] [PubMed]
- Cue, D.; Southern, S.O.; Southern, P.J.; Prabhakar, J.; Lorelli, W.; Smallheer, J.M.; Mousa, S.A.; Cleary, P.P. A nonpeptide integrin antagonist can inhibit epithelial cell ingestion of Streptococcus pyogenes by blocking formation of integrin alpha 5beta 1-fibronectin-M1 protein complexes. Proc. Natl. Acad. Sci. USA 2000, 97, 2858–2863. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yilmaz, O.; Watanabe, K.; Lamont, R.J. Involvement of integrins in fimbriae-mediated binding and invasion by Porphyromonas gingivalis. Cell. Microbiol. 2002, 4, 305–314. [Google Scholar] [CrossRef] [PubMed]
- Leroy-Dudal, J.; Gagniere, H.; Cossard, E.; Carreiras, F.; Di Martino, P. Role of alphavbeta5 integrins and vitronectin in Pseudomonas aeruginosa PAK interaction with A549 respiratory cells. Microbes Infect. 2004, 6, 875–881. [Google Scholar] [CrossRef]
- Dehio, M.; Gomez-Duarte, O.G.; Dehio, C.; Meyer, T.F. Vitronectin-dependent invasion of epithelial cells by Neisseria gonorrhoeae involves alpha(v) integrin receptors. FEBS Lett. 1998, 424, 84–88. [Google Scholar] [CrossRef] [Green Version]
- Cox, D.; Brennan, M.; Moran, N. Integrins as therapeutic targets: Lessons and opportunities. Nat. Rev. Drug Discov. 2010, 9, 804–820. [Google Scholar] [CrossRef]
- Hatley, R.J.D.; Macdonald, S.J.F.; Slack, R.J.; Le, J.; Ludbrook, S.B.; Lukey, P.T. An alphav-RGD Integrin Inhibitor Toolbox: Drug Discovery Insight, Challenges and Opportunities. Angew. Chem. Int. Ed. Engl. 2018, 57, 3298–3321. [Google Scholar] [CrossRef]
- Danhier, F.; Le Breton, A.; Preat, V. RGD-based strategies to target alpha(v) beta(3) integrin in cancer therapy and diagnosis. Mol. Pharm. 2012, 9, 2961–2973. [Google Scholar] [CrossRef]
- Fiorino, G.; Correale, C.; Fries, W.; Repici, A.; Malesci, A.; Danese, S. Leukocyte traffic control: A novel therapeutic strategy for inflammatory bowel disease. Expert Rev. Clin. Immunol. 2010, 6, 567–572. [Google Scholar] [CrossRef]
- Major, E.O. Progressive multifocal leukoencephalopathy in patients on immunomodulatory therapies. Annu. Rev. Med. 2010, 61, 35–47. [Google Scholar] [CrossRef] [Green Version]
- van den Kerkhof, D.L.; van der Meijden, P.E.J.; Hackeng, T.M.; Dijkgraaf, I. Exogenous Integrin alphaIIbbeta3 Inhibitors Revisited: Past, Present and Future Applications. Int. J. Mol. Sci. 2021, 22, 3366. [Google Scholar] [CrossRef]
- Chew, D.P.; Bhatt, D.L.; Sapp, S.; Topol, E.J. Increased mortality with oral platelet glycoprotein IIb/IIIa antagonists: A meta-analysis of phase III multicenter randomized trials. Circulation 2001, 103, 201–206. [Google Scholar] [CrossRef]
- Lin, F.Y.; Li, J.; Xie, Y.; Zhu, J.; Huong Nguyen, T.T.; Zhang, Y.; Zhu, J.; Springer, T.A. A general chemical principle for creating closure-stabilizing integrin inhibitors. Cell 2022, 185, 3533–3550.e27. [Google Scholar] [CrossRef]
- Kereiakes, D.J.; Henry, T.D.; DeMaria, A.N.; Bentur, O.; Carlson, M.; Seng Yue, C.; Martin, L.H.; Midkiff, J.; Mueller, M.; Meek, T.; et al. First Human Use of RUC-4: A Nonactivating Second-Generation Small-Molecule Platelet Glycoprotein IIb/IIIa (Integrin alphaIIbbeta3) Inhibitor Designed for Subcutaneous Point-of-Care Treatment of ST-Segment-Elevation Myocardial Infarction. J. Am. Heart Assoc. 2020, 9, e016552. [Google Scholar] [CrossRef]
- Nakamura, I.; Duong, L.T.; Rodan, S.B.; Rodan, G.A. Involvement of alpha(v)beta3 integrins in osteoclast function. J. Bonev Miner. Metab. 2007, 25, 337–344. [Google Scholar] [CrossRef]
- Stupp, R.; Hegi, M.E.; Gorlia, T.; Erridge, S.C.; Perry, J.; Hong, Y.K.; Aldape, K.D.; Lhermitte, B.; Pietsch, T.; Grujicic, D.; et al. Cilengitide combined with standard treatment for patients with newly diagnosed glioblastoma with methylated MGMT promoter (CENTRIC EORTC 26071-22072 study): A multicentre, randomised, open-label, phase 3 trial. Lancet Oncol. 2014, 15, 1100–1108. [Google Scholar] [CrossRef] [Green Version]
- Auzzas, L.; Zanardi, F.; Battistini, L.; Burreddu, P.; Carta, P.; Rassu, G.; Curti, C.; Casiraghi, G. Targeting alphavbeta3 integrin: Design and applications of mono- and multifunctional RGD-based peptides and semipeptides. Curr. Med. Chem. 2010, 17, 1255–1299. [Google Scholar] [CrossRef]
- Dhavalikar, P.; Robinson, A.; Lan, Z.; Jenkins, D.; Chwatko, M.; Salhadar, K.; Jose, A.; Kar, R.; Shoga, E.; Kannapiran, A.; et al. Review of Integrin-Targeting Biomaterials in Tissue Engineering. Adv. Healthc Mater. 2020, 9, e2000795. [Google Scholar] [CrossRef]
- Karimi, F.; O’Connor, A.J.; Qiao, G.G.; Heath, D.E. Integrin Clustering Matters: A Review of Biomaterials Functionalized with Multivalent Integrin-Binding Ligands to Improve Cell Adhesion, Migration, Differentiation, Angiogenesis, and Biomedical Device Integration. Adv. Healthc. Mater. 2018, 7, e1701324. [Google Scholar] [CrossRef]
- Marie, P.J. Targeting integrins to promote bone formation and repair. Nat. Rev. Endocrinol. 2013, 9, 288–295. [Google Scholar] [CrossRef]
- Anderson, J.M.; Rodriguez, A.; Chang, D.T. Foreign body reaction to biomaterials. Semin. Immunol. 2008, 20, 86–100. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Petrie, T.A.; Raynor, J.E.; Dumbauld, D.W.; Lee, T.T.; Jagtap, S.; Templeman, K.L.; Collard, D.M.; Garcia, A.J. Multivalent integrin-specific ligands enhance tissue healing and biomaterial integration. Sci. Transl. Med. 2010, 2, 45ra60. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perdih, A.; Dolenc, M.S. Small molecule antagonists of integrin receptors. Curr. Med. Chem. 2010, 17, 2371–2392. [Google Scholar] [CrossRef] [PubMed]
- Sheldrake, H.M.; Patterson, L.H. Strategies to inhibit tumor associated integrin receptors: Rationale for dual and multi-antagonists. J. Med. Chem. 2014, 57, 6301–6315. [Google Scholar] [CrossRef] [PubMed]
- Paolillo, M.; Russo, M.A.; Serra, M.; Colombo, L.; Schinelli, S. Small molecule integrin antagonists in cancer therapy. Mini Rev. Med. Chem. 2009, 9, 1439–1446. [Google Scholar] [CrossRef]
- Pierschbacher, M.D.; Ruoslahti, E. Cell attachment activity of fibronectin can be duplicated by small synthetic fragments of the molecule. Nature 1984, 309, 30–33. [Google Scholar] [CrossRef]
- Komoriya, A.; Green, L.J.; Mervic, M.; Yamada, S.S.; Yamada, K.M.; Humphries, M.J. The minimal essential sequence for a major cell type-specific adhesion site (CS1) within the alternatively spliced type III connecting segment domain of fibronectin is leucine-aspartic acid-valine. J. Biol. Chem. 1991, 266, 15075–15079. [Google Scholar] [CrossRef]
- Nagae, M.; Re, S.; Mihara, E.; Nogi, T.; Sugita, Y.; Takagi, J. Crystal structure of alpha5beta1 integrin ectodomain: Atomic details of the fibronectin receptor. J. Cell Biol. 2012, 197, 131–140. [Google Scholar] [CrossRef] [Green Version]
- Gentilucci, L.; Cardillo, G.; Spampinato, S.; Tolomelli, A.; Squassabia, F.; De Marco, R.; Bedini, A.; Baiula, M.; Belvisi, L.; Civera, M. Antiangiogenic effect of dual/selective alpha(5)beta(1)/alpha(v)beta(3) integrin antagonists designed on partially modified retro-inverso cyclotetrapeptide mimetics. J. Med. Chem. 2010, 53, 106–118. [Google Scholar] [CrossRef]
- Frank, A.O.; Otto, E.; Mas-Moruno, C.; Schiller, H.B.; Marinelli, L.; Cosconati, S.; Bochen, A.; Vossmeyer, D.; Zahn, G.; Stragies, R.; et al. Conformational control of integrin-subtype selectivity in isoDGR peptide motifs: A biological switch. Angew. Chem. Int. Ed. Engl. 2010, 49, 9278–9281. [Google Scholar] [CrossRef] [Green Version]
- Mingozzi, M.; Dal Corso, A.; Marchini, M.; Guzzetti, I.; Civera, M.; Piarulli, U.; Arosio, D.; Belvisi, L.; Potenza, D.; Pignataro, L.; et al. Cyclic isoDGR peptidomimetics as low-nanomolar alphavbeta3 integrin ligands. Chemistry 2013, 19, 3563–3567. [Google Scholar] [CrossRef]
- Maltsev, O.V.; Marelli, U.K.; Kapp, T.G.; Di Leva, F.S.; Di Maro, S.; Nieberler, M.; Reuning, U.; Schwaiger, M.; Novellino, E.; Marinelli, L.; et al. Stable Peptides Instead of Stapled Peptides: Highly Potent alphavbeta6-Selective Integrin Ligands. Angew. Chem. Int. Ed. Engl. 2016, 55, 1535–1539. [Google Scholar] [CrossRef]
- Bakthavatsalam, D.; Craft, J.W., Jr.; Kazansky, A.; Nguyen, N.; Bae, G.; Caivano, A.R.; Gundlach, C.W.; Aslam, A.; Ali, S.; Gupta, S.; et al. Identification of Inhibitors of Integrin Cytoplasmic Domain Interactions With Syk. Front. Immunol. 2020, 11, 575085. [Google Scholar] [CrossRef]
- Ghitti, M.; Spitaleri, A.; Valentinis, B.; Mari, S.; Asperti, C.; Traversari, C.; Rizzardi, G.P.; Musco, G. Molecular dynamics reveal that isoDGR-containing cyclopeptides are true alphavbeta3 antagonists unable to promote integrin allostery and activation. Angew. Chem. Int. Ed. Engl. 2012, 51, 7702–7705. [Google Scholar] [CrossRef]
- Marinelli, L.; Lavecchia, A.; Gottschalk, K.E.; Novellino, E.; Kessler, H. Docking studies on alphavbeta3 integrin ligands: Pharmacophore refinement and implications for drug design. J. Med. Chem. 2003, 46, 4393–4404. [Google Scholar] [CrossRef]
- Guest, E.E.; Oatley, S.A.; Macdonald, S.J.F.; Hirst, J.D. Molecular Simulation of alphavbeta6 Integrin Inhibitors. J. Chem. Inf. Model. 2020, 60, 5487–5498. [Google Scholar] [CrossRef]
- Liu, Y.; Pan, Y.; Xu, Y. Binding investigation of integrin alphavbeta3 with its inhibitors by SPR technology and molecular docking simulation. J. Biomol. Screen 2010, 15, 131–137. [Google Scholar] [CrossRef]
- Marinelli, L.; Meyer, A.; Heckmann, D.; Lavecchia, A.; Novellino, E.; Kessler, H. Ligand binding analysis for human alpha5beta1 integrin: Strategies for designing new alpha5beta1 integrin antagonists. J. Med. Chem. 2005, 48, 4204–4207. [Google Scholar] [CrossRef]
- Oglic, D.; Oatley, S.A.; Macdonald, S.J.F.; McInally, T.; Garnett, R.; Hirst, J.D.; Gartner, T. Active Search for Computer-aided Drug Design. Mol. Inform 2018, 37, 1700130. [Google Scholar] [CrossRef]
- Turaga, R.C.; Yin, L.; Yang, J.J.; Lee, H.; Ivanov, I.; Yan, C.; Yang, H.; Grossniklaus, H.E.; Wang, S.; Ma, C.; et al. Rational design of a protein that binds integrin alphavbeta3 outside the ligand binding site. Nat. Commun. 2016, 7, 11675. [Google Scholar] [CrossRef] [Green Version]
- Bochen, A.; Marelli, U.K.; Otto, E.; Pallarola, D.; Mas-Moruno, C.; Di Leva, F.S.; Boehm, H.; Spatz, J.P.; Novellino, E.; Kessler, H.; et al. Biselectivity of isoDGR peptides for fibronectin binding integrin subtypes alpha5beta1 and alphavbeta6: Conformational control through flanking amino acids. J. Med. Chem. 2013, 56, 1509–1519. [Google Scholar] [CrossRef]
- Marchini, M.; Mingozzi, M.; Colombo, R.; Guzzetti, I.; Belvisi, L.; Vasile, F.; Potenza, D.; Piarulli, U.; Arosio, D.; Gennari, C. Cyclic RGD peptidomimetics containing bifunctional diketopiperazine scaffolds as new potent integrin ligands. Chemistry 2012, 18, 6195–6207. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- da Ressurreicao, A.S.; Vidu, A.; Civera, M.; Belvisi, L.; Potenza, D.; Manzoni, L.; Ongeri, S.; Gennari, C.; Piarulli, U. Cyclic RGD-peptidomimetics containing bifunctional diketopiperazine scaffolds as new potent integrin ligands. Chemistry 2009, 15, 12184–12188. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guarnieri, F.; Still, W.C. A rapidly convergent simulation method: Mixed Monte Carlo/stochastic dynamics. J. Comput. Chem. 1994, 15, 1302–1310. [Google Scholar] [CrossRef]
- Still, W.C.; Tempczyk, A.; Hawley, R.C.; Hendrickson, T. Semianalytical treatment of solvation for molecular mechanics and dynamics. J. Am. Chem. Soc. 1990, 112, 6127–6129. [Google Scholar] [CrossRef]
- Dong, X.; Hudson, N.E.; Lu, C.; Springer, T.A. Structural determinants of integrin beta-subunit specificity for latent TGF-beta. Nat. Struct. Mol. Biol. 2014, 21, 1091–1096. [Google Scholar] [CrossRef] [Green Version]
- Logan, D.; Abu-Ghazaleh, R.; Blakemore, W.; Curry, S.; Jackson, T.; King, A.; Lea, S.; Lewis, R.; Newman, J.; Parry, N.; et al. Structure of a major immunogenic site on foot-and-mouth disease virus. Nature 1993, 362, 566–568. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, Y.; Yang, F.; Guo, J.; He, J.; Wu, Q.; Cao, W.; Lv, L.; Zheng, H.; Zhang, Z. Induction of partial protection against foot and mouth disease virus in guinea pigs by neutralization with the integrin beta6-1 subunit. Viruses 2013, 5, 1114–1130. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Bell, K.; Mousa, S.A.; Varner, J.A. Regulation of angiogenesis in vivo by ligation of integrin alpha5beta1 with the central cell-binding domain of fibronectin. Am. J. Pathol. 2000, 156, 1345–1362. [Google Scholar] [CrossRef]
- Heckmann, D.; Meyer, A.; Laufer, B.; Zahn, G.; Stragies, R.; Kessler, H. Rational design of highly active and selective ligands for the alpha5beta1 integrin receptor. ChemBioChem 2008, 9, 1397–1407. [Google Scholar] [CrossRef]
- Macchiarulo, A.; Costantino, G.; Meniconi, M.; Pleban, K.; Ecker, G.; Bellocchi, D.; Pellicciari, R. Insights into phenylalanine derivatives recognition of VLA-4 integrin: From a pharmacophoric study to 3D-QSAR and molecular docking analyses. J. Chem. Inform. Comput. Sci. 2004, 44, 1829–1839. [Google Scholar] [CrossRef]
- Martins-Da Silva, J.H.M.; Dardenne, L.E.; Savino, W.; Savino, E.R. Analysis of α4β1 Integrin Specific Antagonists Binding Modes: Structural Insights by Molecular Docking, Molecular Dynamics and Linear Interaction Energy Method for Free Energy Calculations. J. Braz. Chem. Soc. 2010, 21, 546–555. [Google Scholar] [CrossRef] [Green Version]
- Thangapandian, S.; John, S.; Sakkiah, S.; Lee, K.W. Discovery of potential integrin VLA-4 antagonists using pharmacophore modeling, virtual screening and molecular docking studies. Chem. Biol. Drug Des. 2011, 78, 289–300. [Google Scholar] [CrossRef]
- Venkatraman, S.; Lebsack, A.D.; Alves, K.; Gardner, M.F.; James, J.; Lingham, R.B.; Maniar, S.; Mumford, R.A.; Si, Q.; Stock, N.; et al. Discovery of N-{N-[(3-cyanobenzene) sulfonyl]-4(R)-(3,3-difluoropiperidin-1-yl)-(l)-prolyl}-4-[(3′,5′-dichloro-isonic otinoyl) amino]-(l)-phenylalanine (MK-0617), a highly potent and orally active VLA-4 antagonist. Bioorg. Med. Chem. Lett. 2009, 19, 5803–5806. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Y.; Hyde, D.M.; Gotwals, P.J.; Lobb, R.R.; Ryan, S.T.; Giri, S.N. Effect of antibody against integrin alpha4 on bleomycin-induced pulmonary fibrosis in mice. Biochem. Pharmacol. 2000, 60, 1949–1958. [Google Scholar] [CrossRef]
- Woodside, D.G.; Vanderslice, P. Cell adhesion antagonists: Therapeutic potential in asthma and chronic obstructive pulmonary disease. BioDrugs 2008, 22, 85–100. [Google Scholar] [CrossRef]
- Vasconcelos, D.; Chaves, B.; Albuquerque, A.; Andrade, L.; Henriques, A.; Sartori, G.; Savino, W.; Caffarena, E.; Martins-Da-Silva, J.H. Development of New Potential Inhibitors of beta1 Integrins through In Silico Methods-Screening and Computational Validation. Life 2022, 12, 932. [Google Scholar] [CrossRef]
- Carlevaro, C.M.; Martins-Da Silva, J.H.; Savino, E.R.; Caffarena, E.R. Plausible Binding Mode of the Active a4b1 Antagonist, MK-0617, Determined by Docking and Free Energy Calculations. J. Theor. Comput. Chem. 2013, 12, 1250108. [Google Scholar] [CrossRef]
- Pourbasheer, E.; Aalizadeh, R.; Ganjali, M.R.; Norouzi, P. QSAR study of a1b4 integrin inhibitors by GA-MLR and GA-SVM methods. Struct. Chem. 2014, 25, 355–370. [Google Scholar] [CrossRef]
- Singh, J.; van Vlijmen, H.; Lee, W.C.; Liao, Y.; Lin, K.C.; Ateeq, H.; Cuervo, J.; Zimmerman, C.; Hammond, C.; Karpusas, M.; et al. 3D QSAR (COMFA) of a series of potent and highly selective VLA-4 antagonists. J. Comput.-Aided Mol. Des. 2002, 16, 201–211. [Google Scholar] [CrossRef]












Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tvaroška, I.; Kozmon, S.; Kóňa, J. Molecular Modeling Insights into the Structure and Behavior of Integrins: A Review. Cells 2023, 12, 324. https://0-doi-org.brum.beds.ac.uk/10.3390/cells12020324
Tvaroška I, Kozmon S, Kóňa J. Molecular Modeling Insights into the Structure and Behavior of Integrins: A Review. Cells. 2023; 12(2):324. https://0-doi-org.brum.beds.ac.uk/10.3390/cells12020324
Chicago/Turabian StyleTvaroška, Igor, Stanislav Kozmon, and Juraj Kóňa. 2023. "Molecular Modeling Insights into the Structure and Behavior of Integrins: A Review" Cells 12, no. 2: 324. https://0-doi-org.brum.beds.ac.uk/10.3390/cells12020324