Electron Symmetry Breaking during Attosecond Charge Migration Induced by Laser Pulses: Point Group Analyses for Quantum Dynamics

Abstract

Quantum simulations of the electron dynamics of oriented benzene and Mg-porphyrin driven by short (<10 fs) laser pulses yield electron symmetry breaking during attosecond charge migration. Nuclear motions are negligible on this time domain, i.e., the point group symmetries G = D_6h and D_4h of the nuclear scaffolds are conserved. At the same time, the symmetries of the one-electron densities are broken, however, to specific subgroups of G for the excited superposition states. These subgroups depend on the polarization and on the electric fields of the laser pulses. They can be determined either by inspection of the symmetry elements of the one-electron density which represents charge migration after the laser pulse, or by a new and more efficient group-theoretical approach. The results agree perfectly with each other. They suggest laser control of symmetry breaking. The choice of the target subgroup is restricted, however, by a new theorem, i.e., it must contain the symmetry group of the time-dependent electronic Hamiltonian of the oriented molecule interacting with the laser pulse(s). This theorem can also be applied to confirm or to falsify complementary suggestions of electron symmetry breaking by laser pulses.

1. Introduction

This paper focuses on the interplay of two domains of research in molecular quantum dynamics: charge migration in molecules on the time scale from a few hundred attoseconds (1 as = 10⁻¹⁸ s) to few femtoseconds (1 fs = 10⁻¹⁵ s), and electron symmetry breaking by laser pulses; the nuclear symmetry is conserved on this time scale. Here, the term “electron symmetry” means the point group symmetry of the observable one-electron density. The complementary term “nuclear symmetry” means the point group of the nuclear scaffold attained at the global minimum structure in the electronic ground state.

The paper should be of interest also to experts and young scientists in neighboring fields, e.g., quantum control and quantum chemistry. Quantum chemists, for example, are familiar with the assignment of the nuclear symmetry to the electronic eigenstates, with corresponding irreducible representations (IRREPs) in the standard time-independent scenario. From this perspective, one may ask how a laser pulse could ever induce different electron and nuclear symmetries, as suggested by the title and the Abstract of this paper. An important purpose is, therefore, to confirm that this is possible indeed. The phenomenon shall be demonstrated on the ultrashort time scale of laser-driven quantum dynamics when the nuclei still do not move, i.e., they conserve nuclear symmetry. At the same time, however, the electrons may already exhibit laser-induced transitions from the initial ground state to specific superpositions of eigenstates which imply electron symmetry breaking. Moreover, we aim at the derivation of practical rules for assigning the broken symmetries of the relevant one-electron densities of the superposition states which represent charge migration initiated by laser pulses, in co-existence with the conserved nuclear symmetry. The derivations will be presented in a step-by-step manner for two examples, namely for the effects of linearly polarized laser pulses on oriented benzene molecule, and on oriented Mg-porphyrin. The term “oriented” means the specific orientation of the nuclear scaffold with respect to the laboratory frame; the latter may be determined by a linearly polarized laser pulse. Occasionally, we shall also refer to analogous effects of circularly polarized laser pulses in oriented benzene, Mg-porphyrin or other molecules, but without any detailed derivations. The present non-linear model systems are chosen because their high nuclear point group symmetries G = D_6h and D_4h support two-dimensional (2d) IRREPs for degenerate electronic states. We shall show below that this offers new opportunities for laser control of electron symmetry breaking. The new phenomenon calls for the present significant extension of the previous theory and applications [1,2,3,4,5].

This Introduction starts with a historical overview of the topic. This sets the stage for a list of the next challenges which we try to master in the rest of this paper. The historical overview centers attention on just five publications [1,2,3,4,5]. To the best of our knowledge, these are the only ones that assign different point group symmetries of the relevant one-electron densities of the initial states of the oriented molecules—this is always the electronic ground state, and its electronic symmetry is the same as the nuclear symmetry —and after symmetry breaking by the laser pulse. In retrospect, one may find various other publications that document the phenomenon implicitly, but without any specification of the relevant point groups. We shall refer to some of this implicit evidence in the next Sections.

Electron symmetry breaking by laser pulses, with an explicit comparison of the symmetries before and after the laser pulses, was documented first by Ulusoy and Nest in their fundamental work on quantum control of aromaticity, with application to the benzene molecule with a specific orientation of its nuclear scaffold [1]. For this example, the nuclear point group symmetry is D_6h; the corresponding IRREPs of the electronic ground state S₀ and the first and second excited electronic singlet states S₁ and S₂ are ¹A_1g, ¹B_2u and ¹B_1u, respectively. The key result of their publication is that the aromaticity of benzene in state S₀ can be extinguished by means of well-designed laser pulses which prepare the non-aromatic (1/√2)*(S₀ + S₁) (i) or the (1/√2)*(S₀ + S₂) (ii) superposition states. Ulusoy and Nest noted that in spite of the robust nuclear symmetry D_6h, these electronic superposition states transform according to IRREPs of different D_3d (i) and D_3h (ii) point group symmetries, and they exhibit different types of periodic charge migrations between neighboring CC bonds (i) or carbon atoms (ii), with periods of 520 as and 720 as, respectively [1]. Recent work has demonstrated, however, that these findings do not hold in the molecular reference frame but only in the reference frame of the laser field [6]. With this understanding, Ref. [1] has the full set of the sub-topics of the title of this paper: Electron symmetry breaking D_6h →D_3d (i) or D_6h → D_3h (ii) versus nuclear symmetry conservation (D_6h) during attosecond charge migration induced by laser pulses. However, Ulusoy and Nest focused on laser control of aromaticity, without any explicit note of electron symmetry breaking, even though it was clearly documented. They also did not present any rigorous derivations of their assignments of the broken electron symmetries of the non-aromatic superposition states.

The work of Ulusoy and Nest [1] stimulated quantum dynamics simulation of another electron symmetry breaking in oriented benzene, specifically D_6h → C_s, with robust nuclear D_6h symmetry, followed by C_s → D_6h electron symmetry restoration, simply by time-reversed circularly polarized laser pulses with proper phase relations. Refs. [3,4] document the same type of laser-driven electron symmetry breaking, but different strategies for symmetry restoration. In Refs. [2,3,4], the electron symmetries D_6h and C_s were assigned just by empirical inspection of the relevant one-electron densities. Ref. [5] refers to preparations of electronic superposition states with different IRREPs in oriented molecules by laser pulses, but without explicit quantum dynamics simulations. The superposition states present attosecond charge migration. Ref. [5] has the first rigorous derivation of the point group symmetries of the one-electron densities of the target states. The applications are for rather simple prototypes, namely D_∞h → C_∞v electron symmetry breaking and attosecond charge migration in the σ_g + σ_u superposition state of oriented H₂⁺, with robust nuclear symmetry D_∞h, and by analogy for C_2v → C_s electron symmetry breaking and attosecond charge migration in the A₁ + B₂ superposition state of oriented H₂O, with robust nuclear symmetry C_2v.

The pioneering papers [1,2,3,4,5] call for the following extensions: (a) Rigorous assignments of electron symmetry breaking in supplementary examples for oriented benzene and for oriented Mg-porphyrin. For this purpose, we design linearly polarized laser pulses that initiate selective types of attosecond charge migration with corresponding electron symmetry breaking while conserving nuclear symmetry. The results are demonstrated by quantum dynamics simulations of laser excitations of electronic superposition states with different combinations of IRREPs. As a constraint, the duration of the laser pulses should be shorter than 10 fs, as in Refs. [2,3,4], because in this time domain, the nuclear motions may be considered as frozen, i.e., they conserve nuclear symmetry [7,8]. For comparison, the laser pulses which were designed in Ref. [1] take 80 fs or even longer times. (b) Derivation of simple yet rigorous rules for the assignments of symmetries of the relevant one-electron densities of the resulting electronic superposition states in the oriented molecules. These rules (b) will be applied not only to the new examples (a), but they will also be used to check the previous assignments of electron symmetry breaking in Ref. [1]. This calls for a significant extension of the previous rules for superpositions of non-degenerate electronic states with one-dimensional (1d) IRREPs [5] to superpositions of non-degenerate plus degenerate electronic states with 1d plus 2d IRREPs in oriented molecules. The present applications serve as examples that should enable analogous derivations of rigorous rules for the assignments of laser-induced symmetry breaking in electronic superposition states in other oriented systems.

The subsequent Section 2 presents the models, methods and techniques. Section 3 has the results and discussions. The conclusions are in Section 4. Appendix A derives various general theorems for electron symmetry breaking induced by short linearly polarized laser pulses in oriented molecules with arbitrary point groups of the frozen nuclear scaffolds. Appendix B has additional results for the two model systems, benzene and Mg-porphyrine.

2. Models, Methods and Techniques

This section has nine subsections. The first one (Section 2.1) presents a convenient analytical, parametrized expression for the electric fields $ℰ$_p(t) of various linearly polarized laser pulses labeled p = 1, 2, 3, … which achieve different types of electron symmetry breaking in oriented molecules, ready for applications to the two examples, oriented benzene and Mg-porphyrin. For each system, the “first” laser pulse (p = 1) is used for specifying the laboratory frame. Section 2.2 defines the orientations of the nuclear scaffolds with respect to the laboratory frame. The scaffolds have the symmetries of the familiar nuclear point groups G. Section 2.3 specifies the nomenclature for the corresponding symmetry elements and the related symmetry operations—this task is mandatory, in view of two different conventions in the literature, with different assignments of the symmetry operations which yield different IRREPs of some of the electronic states in the laser-induced target superposition states. Section 2.4 defines the electronic Hamiltonian H_e of the oriented molecules and summarizes the methods of quantum chemistry for the evaluations of the electronic eigenstates with the energies, wavefunctions, assignments of IRREPs of G, and the related dipole transition matrix elements. Section 2.5 defines the time-dependent Hamiltonians H_p(t) for the oriented molecules interacting with the linearly polarized laser pulses labeled p, or two sequential laser pulses, and determines the subgroups S(H_p(t)) of G by those symmetry operations of H_e which are conserved in H_p(t). Section 2.6 summarizes the methods of quantum dynamics for the laser-driven time evolution of the electronic states, starting from the electronic ground state. Section 2.7 discovers some symmetry relations of the wavefunctions which are driven by laser pulses with different linear polarizations. The quantum chemical method for calculating the one-electron densities of these superposition states is in Section 2.8. Section 2.9 adds some details for the design of the laser pulses for selective types of electron symmetry breaking.

The order of presentations of Section 2.1, Section 2.2, Section 2.3, Section 2.4, Section 2.5, Section 2.6, Section 2.7, Section 2.8 and Section 2.9 is convenient, for the present purpose, but it suffers from the dilemma that several Sections depend on each other in various ways. Unfortunately, there is no unique “logic” or “ideal” order of the presentations which could avoid this problem.

2.1. Linearly Polarized Laser Pulses in the Laboratory Frame

The subsequent applications use several linearly polarized laser pulses. They are labeled by p = 1, 2, 3, ... The first one (p = 1) is used for the definition of the right-handed set of Cartesian coordinates x, y, z of the laboratory frame. All laser pulses—including the first one—propagate along the same direction: this defines the z-direction along the unit-vector e_z of the laboratory frame. All laser pulses are linearly polarized, with polarization (unit) vector e_p perpendicular to e_z. In the present applications, the polarization vector of the “first” laser pulse (p = 1) defines the x-direction, e_x ≡ e_p=1. The y-direction is along the unit vector e_y perpendicular to e_x and e_z.

The time-(t)-dependent electric fields $ℰ$_p(t) of the linearly polarized laser pulses are modeled as products of the polarization vectors e_p times scalar fields $ℰ$_p(t) with sin²-shapes of the carrier envelopes,

$$\begin{array}{cccc}{\mathsf{ℰ}}_{\mathrm{p}}\left(t\right)& =& {\mathbf{e}}_{\mathrm{p}} {\mathsf{ℰ}}_{\mathrm{p}}\left(\mathrm{t}\right)\hfill & \\ & \equiv & {\mathbf{e}}_{\mathrm{p}} {\mathsf{ℰ}}_{0_{\mathrm{p}}} {\sin }^2[\pi (\mathrm{t}-{\mathrm{t}}_{\mathrm{i}\mathrm{p}})/{\mathsf{\tau }}_{\mathrm{p}}] \sin [{\mathsf{\omega }}_{\mathrm{p}} (\mathrm{t}-{\mathrm{t}}_{\mathrm{i}\mathrm{p}}-{\mathsf{\tau }}_{\mathrm{p}}/2\left)\right]\hfill & \mathrm{for} {\mathrm{t}}_{\mathrm{i}\mathrm{p}} \le \mathrm{t} \le {\mathrm{t}}_{\mathrm{i}\mathrm{p}} + {\mathsf{\tau }}_{\mathrm{p}}\hfill \\ & =& 0\hfill & \mathrm{else}\hfill \end{array}$$

(1)

Here $ℰ$_0p denotes the electric field strength, t_ip and t_ip + τ_p are the initial and final times of the laser pulse, τ_p is its (total) duration. For applications of a single laser pulse, we set t_ip = 0. For two sequential laser pulses p and p + 1, the second pulse is fired right after the first one, hence t_i,p+1 = t_ip + τ_p. The carrier frequency is denoted ω_p: the corresponding periods, wavelength, and photon energy are T_p= 2π/ω_p, λ_p = c T_p and ℏω_p, respectively; c and ℏ = h/2π denote the velocity of light in vacuum and Planck’s reduced constant, respectively. The carrier-envelope phases ω_p (t_ip + τ_p/2) are fixed such that the sin[…] term is antisymmetric with respect to the maximum of the sin²-shape function. The corresponding maximum mean intensity (i.e., the maximum of the intensity time-averaged over one period) is at t = t_ip + τ_p/2. Its value is approximated almost perfectly by

I_mp = 0.5 ϵ₀ c $ℰ$_0p²,

(2)

where ϵ₀ is the permittivity of vacuum. In the present applications, the values of the photon energies are in the domain of several eV. The corresponding wavelengths are in the domain of several hundred nanometers—more than four orders of magnitude larger than the size of the molecules. As consequence, the electric fields are almost perfectly homogeneous in the molecular domains, as modeled in Equation (1).

Some methods for the determination of the laser parameters in Equation (1) for control of the electron symmetry breaking and charge migration are presented in Section 2.9.

2.2. Orientations of the Nuclear Scaffolds

The present scenario of the nuclear scaffold of benzene (¹²C₆H₆) is adapted from Ref. [1]. The scaffold has the familiar D_6h symmetry. It is oriented with respect to the laboratory frame as shown in Figure 1, with its center of mass at the origin. Specifically, the molecular plane is in the laboratory x-y-plane, and two carbon nuclei are on the y-axis. This scenario has also been used in Refs. [2,3,4,6,9,10,11,12]. An alternative orientation of the nuclear scaffold—i.e., again with the molecular plane in the laboratory x-y-plane, but with two carbon nuclei on the x-axis instead of the y-axis—is considered in Refs. [13,14].

The quantum mechanical indistinguishability of the carbon nuclei (bosons), as well as the protons (fermions) implies that one cannot assign individual nuclei to any specific sites of the nuclear frame. Instead, the probabilities of occupying the carbon and proton sites are the same (=1/6) for all carbon nuclei and protons, respectively [6]. This renders the presentation of the results rather easy, e.g., one can talk about charge migration from the “left” (x < 0) to the “right” (x > 0) CC bonds, or from the “bottom” (y < 0) to the “top” (y > 0) domains of carbon nuclei, without labeling the individual carbon nuclei.

For the nuclear scaffold of oriented Mg-porphyrin (²⁴Mg¹⁴N₄¹²C₂₀H₁₂) we adapt the scenario of Ref. [15], also used in Ref. [16]. It has the familiar D_4h symmetry. It is oriented with respect to the laboratory frame as shown in Figure 2, with its center of mass at the origin. The molecular plane is again in the laboratory x-y-plane, and the four nitrogen nuclei are on the x and y-axes.

2.3. Nomenclature of Selected Symmetry Elements, Symmetry Operations and Subgroups of the Point Groups D_6h and D_4h of the Oriented Benzene and Mg-Porphyrin

The laser pulses (Section 2.1) shall be designed (Section 2.9) to break the original electron symmetries of the oriented molecules, i.e., from D_6h for benzene and D_4h for Mg-porphyrin (Section 2.2) to selective subgroups. Here, we explain the nomenclature for some important symmetry operations which are necessary to specify those subgroups. The related symmetry elements include the inversion center which coincides with the center of mass at the origin, the horizontal symmetry plane σ_h which coincides with the laboratory x-y-plane, and few others which are illustrated in Figure 1 and Figure 2. Specifically, benzene (analogous results for Mg-porphyrin are in brackets) has three plus three (two plus two) axes for binary rotations C’₂₁, C’₂₂, C’₂₃ and C”₂₁, C”₂₂, C”₂₃ (C’₂₁, C’₂₂ and C”₂₁, C”₂₂). These coincide with the lines of intersections of the horizontal plane σ_h and the vertical and dihedral planes σ_v1, σ_v2, σ_v3 and σ_d1, σ_d2, σ_d3, (σ_v1, σ_v2 and σ_d1, σ_d2), respectively. The symmetry elements correspond to symmetry operations which may be written with the same notations, i.e., binary rotations C’₂₁, C’₂₂, C’₂₃ and C”₂₁, C”₂₂, C”₂₃ (C’₂₁, C’₂₂ and C”₂₁, C”₂₁), the vertical and dihedral reflections σ_v1, σ_v2, σ_v3 and σ_d1, σ_d2, σ_d3, (σ_v1, σ_v2 and σ_d1, σ_d2), respectively, the horizontal reflection σ_h, etc. Six (four) sets of four symmetry operations of the type {E, C₂, σ_h, σ}, namely the identity (E), one of the two-fold rotations, the horizontal reflection and the associated vertical or dihedral reflection, establish six (four) different C_2v subgroups—these are written with notations that remind of the rotations, i.e., C_2v’₁, C_2v’₂, C_2v’₃ and C_2v”₁, C_2v”₂, C_2v”₃ (C_2v’₁, C_2v’₂ and C_2v”₁, C_2v”₂), respectively. For example, C_2v’₁ = {E,C’₂₁,σ_h,σ_v1}, C_2v’₂ = {E,C’₂₂,σ_h,σ_v2}, ….., C_2v”₁ = {E,C”₂₁,σ_h,σ_d1}, …, etc. Analogous notations apply for other subgroups S of the point group G = D_6h (D_4h) of the oriented benzene (Mg-porphyrin).

Table 1. Symmetry operations of point group D_6h and various subgroups for the oriented benzene ^(a).

$$\begin{array}{l}{D}_{6\mathrm{h}} =\{E, 2C_6, 2C_3, C_2, 3C_2^{\prime }, 3C_2^{″}, i, 2S_3, 2S_6,{\sigma }_h, 3{\sigma }_d, 3{\sigma }_v\}\\ D_{3\mathrm{h}}^{\prime } =\{E, 2C_3, 3C_2^{\prime },{\sigma }_h, 2S_3, 3{\sigma }_v\}\\ D_{3\mathrm{h}}^{″} =\{E, 2C_3, 3C_2^{″},{\sigma }_h, 2S_3, 3{\sigma }_d\}\\ D_{3\mathrm{d}}^{\prime } =\{E, 2C_3, 3C_2^{\prime },i, 2S_6, 3{\sigma }_d\}\\ D_{3\mathrm{d}}^{″} =\{E, 2C_3, 3C_2^{″},i, 2S_6, 3{\sigma }_v\}\\ D_{2\mathrm{h},\mathrm{k}}=\{E, C_2, C_{2k}^{\prime }, C_{2k}^{″}, i, {\sigma }_h, {\sigma }_{dk}, {\sigma }_{vk}\},\hspace{1em}k=1,2,3\\ C_{2\mathrm{v},\mathrm{k}}^{\prime }=\{E, C_{2k}^{\prime },{\sigma }_h,{\sigma }_{vk}\},\hspace{1em}k=1,2,3,\hspace{1em} \subset \hspace{1em}{D}_{2\mathrm{h},\mathrm{k}}, D_{3\mathrm{h}}^{\prime }\\ C_{2\mathrm{v},\mathrm{k}}^{″}=\{E, C_{2k}^{″},{\sigma }_h,{\sigma }_{vk}\},\hspace{1em}k=1,2,3,\hspace{1em} \subset \hspace{1em}{D}_{2\mathrm{h},\mathrm{k}}, D_{3\mathrm{h}}^{″}\\ C_{2h} =\{E, C_2,i,{\sigma }_h\}\hspace{1em} \subset \hspace{1em}{D}_{2\mathrm{h},\mathrm{k}}, k=1,2,3\\ C_s\hspace{1em}=\{E, {\sigma }_h\}\hspace{1em} \subset \hspace{1em}{C}_{2\mathrm{h}}\end{array}$$

^(a) Most of the related symmetry elements are illustrated in Figure 1.

has a list of the symmetry operations, i.e., of the group elements g of the group G = D_6h and various subgroups S, with specification of the selected subsets of elements g contained in S.

It is also useful to define unit vectors e’₁, e’₂, e’₃ and e”₁, e”₂, e”₃ (e’₁, e’₂ and e”₁, e”₂) along the rotational axes C’₂₁, C’₂₂, C’₂₃ and C”₂₁, C”₂₂, C”₂₃ (C’₂₁, C’₂₂ and C”₂₁, C”₂₂) of the oriented benzene (Mg-porphyrin) in the laboratory frame. These are listed in

Table 2. Linear polarizations of laser pulses for symmetry breaking of the electronic Hamiltonian of the oriented benzene and Mg-porphyrin ^(a).

	Benzene (G = $D_{6h})$ (b)								Mg-Porphyrin (G = $D_{4h})$
Polarization vectors		$e_1^{\prime }$	$e_2^{\prime }$	$e_3^{\prime }$	$e_1^{″}$	$e_2^{″}$	$e_3^{″}$	$e_1^{\prime }$ & $e_1^{″}$		$e_1^{\prime }$	$e_2^{\prime }$	$e_1^{″}$	$e_2^{″}$
	=	$e_y$	$C_3{e}_y$	$C_3^2{e}_y$	$e_x$	$C_3{e}_x$	$C_3^2{e}_x$	$e_y$ & $e_x$	=	$e_x$	$e_y$	$C_8{e}_x$	$C_8{e}_y$
parallel to binary rotation axes		$C_{21}^{\prime }$	$C_{22}^{\prime }$	$C_{23}^{\prime }$	$C_{21}^{″}$	$C_{22}^{″}$	$C_{23}^{″}$	$C_{21}^{\prime },C_{21}^{″}$		$C_{21}^{\prime }$	$C_{22}^{\prime }$	$C_{21}^{″}$	$C_{22}^{″}$
associated symmetry planes		${\sigma }_{v1}$	${\sigma }_{v2}$	${\sigma }_{v3}$	${\sigma }_{d1}$	${\sigma }_{d2}$	${\sigma }_{d3}$	${\sigma }_h$		${\sigma }_{v1}$	${\sigma }_{v2}$	${\sigma }_{d1}$	${\sigma }_{d2}$
resulting subgroup S (${\mathrm{H}}_{\mathrm{e}}\left(\mathrm{t}\right))$		$C_{2v,1}^{\prime }$	$C_{2v,2}^{\prime }$	$C_{2v,3}^{\prime }$	$C_{2v,1}^{″}$	$C_{2v,2}^{″}$	$C_{2v,3}^{″}$	$C_s$		$C_{2v,1}^{\prime }$	$C_{2v,2}^{\prime }$	$C_{2v,1}^{″}$	$C_{2v,2}^{″}$
with symmetry operations	$C_{2v,k}^{\prime }$ = {E, $C_{2k}^{\prime }$, ${\sigma }_h,$ ${\sigma }_{vk}$}, $k$= 1, 2, 3           {E,${\sigma }_h\}$ $C_{2v,k}^{″}$ = {E, $C_{2k}^{″},{\sigma }_h$, ${\sigma }_{dk}$}, $k$ = 1, 2, 3								$C_{2v,k}^{\prime }$ = {E, $C_{2k}^{\prime }, {\sigma }_h$, ${\sigma }_{vk}$}, $k$= 1, 2 $C_{2v,k}^{″}$ = {E, $C_{2k}^{″}, {\sigma }_h$, ${\sigma }_{dk}$}, $k$ = 1, 2

^(a) The field-free electronic Hamiltonians H_e of the oriented benzene and Mg-porphyrin have molecular point group symmetries G = D_6h and D_4h. The interaction with the laser pulses with polarization e changes H_e to H_e(t) and breaks G to the subgroup S(H_e(t)) depending on e. ^(b) The symbol e’₁&e”₁ denotes sequential applications of two laser pulses with polarizations e’₁ and e”₁.

. Note that for benzene, e’₁ = e_y and e”₁ = e_x (this is a consequence of our adaption of the orientation of benzene used in Ref. [1], as in Refs. [2,3,4,6,9,10,11,12], cf. Figure 1), whereas for Mg-porphyrin, e’₁ = e_x and e’₂ = e_y (this is in accord with Refs. [13,15,16], cf. Figure 2). In the applications below, these unit vectors will serve as polarization vectors of the linearly polarized laser pulses, Equation (1).

2.4. Quantum Chemical Methods for the Electronic States with Their Energies, Wavefunctions, IRREPs, and Transition Dipole Matrix Elements

The present project calls for quantum chemical ab initio calculations of various properties of the oriented model systems benzene and Mg-porphyrin.

(i) The nuclear scaffolds are determined as global minimum structures in the electronic ground state. They confirm the familiar nuclear symmetries (D_6h and D_4h, respectively.) The scaffolds are oriented in the laboratory frame as shown in Figure 1 and Figure 2, respectively (Section 2.2). With these orientations, the laboratory frame also serves as a molecular frame. The corresponding electronic Hamiltonians H_e = T_e + V_e account for the kinetic energies T_e of all electrons and for the Coulomb interactions V_e of all particles (electrons and nuclei). Proper nuclear charges are assigned to the respective positions provided by the rigid nuclear scaffold. This rule avoids any labeling of the nuclei, in accord with Ref. [6], and at the same time, it imposes the respective nuclear symmetry on H_e, which means H_e commutes with all symmetry operations (=group elements g) of the point groups G = D_6h or D_4h of the oriented benzene or Mg-porphyrin, respectively,

[H_e,g] = 0 for g ϵ G = D_6h (oriented benzene) or D_4h (oriented Mg-porphyrin).

(3)

As consequence, H_e also commutes with the symmetry projection operators of the groups G of order |G|,

P^Γm(G) = (d^Γm/|G|) Σ_gϵG χ^Γm(g)^* g

(4)

for the IRREPs Γ_m with dimension d^Γm and characters χ^Γm(g),

[H_e, P^Γm(G)] = 0.

(5)

(ii) The singlet ground and low-lying electronic excited states of the oriented model systems with rigid nuclear frames are evaluated with their eigenenergies E_m and eigenfunctions |m> (using Dirac notation) in the laboratory (≡molecular) frame. The Dirac notation |m> is a short-hand notation that specifies the energy and IRREP quantum numbers of the eigenstate; for example, the electronic ground state is denoted |0> = |1A_1g> (≡ |1¹A_1g>, dropping the notation “¹” for singlet states). They are obtained as real-valued solutions of the time-independent electronic Schrödinger equation (TISE)

H_e |m> = E_m |m>.

(6)

For convenience, we set E₀ = 0 eV for the ground state, cf. Figure 3 and Figure 4. For benzene, the computations are carried out as in Refs. [6,11,12], i.e., by means of the state-averaged CASSCF(6,6) method with an aug-cc-pVTZ basis [17] as implemented in MOLPRO [18]. The energies of the 22 lowest excited states are corrected by multireference configuration interaction with single and double excitations. The energies are found to be in fair agreement with the literature [19]. The IRREPs of the electronic eigenfunctions are assigned by means of the symmetry projection operators (4) for the point group G = D_6h,

|m> transforms as IRREP Γ_m of G ↔ P^Γm(G) |m> = |m>.

(7)

The resulting electronic energy levels of the ground and lowest singlet states of the oriented benzene are shown in Figure 3, together with the IRREPs of G = D_6h.

For Mg-porphyrin, the 20 lowest-lying excited states up to 5.5 eV are calculated using linear-response time-dependent density functional theory with the CAM-B3LYP functional [20] and a correlation-consistent aug-cc-pVTZ basis [17,21] as implemented in Gaussian 16 [22]. The resulting energy levels of the ground and lowest singlet states of the oriented Mg-porphyrin are shown in Figure 4, together with the assignments of IRREPs of G = D_4h. The energies compare well with literature values [23].

(iii) The electronic transition dipole matrix elements of the oriented model systems

d_mn = <m|d|n>

(8)

are calculated with dipole operator

d = −e Σ_j r_j

(9)

where −e denotes the electron charge. The sum Σ_j is over all electrons with coordinates r_j = (x_j, y_j, z_j) in the laboratory (≡molecular) frame. For the oriented benzene, the corresponding Cartesian components d_x, d_y and d_z of d transform according to IRREPs E_1u (with basis E_1u^x_, E_1u^y) and A_2u; for the oriented Mg-porphyrin, they transform according to E_u (with basis E_u^x, E_u^y) and A_2u, respectively. Many x, y, or z-components of the transition dipole matrix elements (8) are equal to zero, due to the symmetry selection rules [1]. This supports selective laser-induced transitions between states |m> and |n> with non-zero matrix elements <m| d |n>, as illustrated in Figure 3 and Figure 4. Detailed group theoretical derivations of symmetry rules for the transition dipole matrix elements are in Appendix B. The results of the quantum chemical calculations of selected non-zero values of the transition dipole matrix elements are listed in

Table A2. Transition dipole moments 〈${\Psi }_i^{\alpha }$|$d_j^{\beta }|$ ${\Phi }_k^{\gamma }$〉, j = x, y, for some $D_{6h}$ and $D_{4h}$states.

Transition |Ψ〉 → |Φ〉 (a)	Integrals (b,c)	$$\left|c_{mn}^{\left(i\right)}\right|$$ [ea0]	cf. Fig.
$$D_{6h}$$
$$|A_{1g}\rangle \to |B_{2u}\rangle$$	(f)
$$\hspace{1em}\hspace{1em} \to |B_{1u}\rangle$$	(f)
$$\hspace{1em}\hspace{1em} \to |E_{1u}\rangle$$	$$\begin{gathered} \hspace{1em}\hspace{1em}\left(\mathrm{a}\right) \langle m{A}_{1g}|d_x n{E}_{1u}^x\rangle = \langle m{A}_{1g}|d_y n{E}_{1u}^y\rangle = c_{mn}^{\left(1\right)} {}^{\left(\mathrm{d}\right)} \\ \left(\mathrm{f}\right) \langle m{A}_{1g}|d_x n{E}_{1u}^y\rangle = \langle m{A}_{1g}|d_y n{E}_{1u}^x\rangle = 0 \end{gathered}$$	$$\begin{gathered} \left|c_{11}^{\left(1\right)}\right|= 2.36 \\ \left|c_{12}^{\left(1\right)}\right|= 0.16 \\ \left|c_{13}^{\left(1\right)}\right|= 0.03 \\ \left|c_{21}^{\left(1\right)}\right|=0.93 \\ \left|c_{22}^{\left(1\right)}\right|= 0.51 \end{gathered}$$	5,9
$$\hspace{1em}\hspace{1em} \to |E_{2g}\rangle$$	(f)
$$|E_{1u}\rangle \to |B_{2u}\rangle$$	(f)
$$\hspace{1em}\hspace{1em} \to |B_{1u}\rangle$$	(f)
$$\hspace{1em}\hspace{1em} \to |E_{2g}\rangle$$	$$\begin{gathered} \hspace{1em}\hspace{1em}\hspace{1em}\left(\mathrm{a}\right) \langle m{E}_{1u}^x|d_x n{E}_{2g}^{x^2-y^2}\rangle = \langle m{E}_{1u}^x|d_y n{E}_{2g}^{xy}\rangle = c_{mn}^{\left(2\right)} \\ = -\langle m{E}_{1u}^y|d_y n{E}_{2g}^{x^2-y^2}\rangle = \langle m{E}_{1u}^y|d_x n{E}_{2g}^{xy}\rangle \\ \left(\mathrm{f}\right) \langle m{E}_{1u}^x|d_y n{E}_{2g}^{x^2-y^2}\rangle = \langle m{E}_{1u}^x|d_x n{E}_{2g}^{xy}\rangle \\ = \langle m{E}_{1u}^y|d_x n{E}_{2g}^{x^2-y^2}\rangle = \langle m{E}_{1u}^y|d_y n{E}_{2g}^{xy}\rangle = 0 \end{gathered}$$	$$\begin{gathered} \left|c_{11}^{\left(2\right)}\right|= 0.38 \\ \left|c_{21}^{\left(2\right)}\right|=0.67 \end{gathered}$$	9
$$D_{4\mathrm{h}}$$
$$|A_{1g}\rangle \to |E_{1u}\rangle$$	$$\begin{gathered} \hspace{1em}\hspace{1em} \left(\mathrm{a}\right) \langle m{A}_{1g}|d_x n{E}_u^x\rangle =\langle m{A}_{1g}|d_y n{E}_u^y\rangle =c_{mn}^{\left(3\right)} {}^{\left(\mathrm{d}\right)} \\ \left(\mathrm{f}\right) \langle m{A}_{1g}|d_x n{E}_u^y\rangle =\langle m{A}_{1g}|d_y n{E}_u^x\rangle =0 \end{gathered}$$	$$\left|c_{11}^{\left(3\right)}\right|=5.41$$	11

^(a) For real-valued wavefunctions 〈${\Psi }_i^{\alpha }$| $d_j^{\beta }|$ ${\Phi }_k^{\gamma }$〉 = 〈${\Phi }_k^{\gamma }$| $d_j^{\beta }|$ ${\Psi }_i^{\alpha }$〉. For the discussion of the integral on the right hand side the Kronecker product $D^{\beta }$⦻ $D^{\gamma }$ has to be replaced by $D^{\beta }$⦻ $D^{\alpha }.$ ^(b) (a) = symmetry allowed, (f) = forbidden. ^(c) The present discrimination of symmetry allowed and forbidden transitions agrees with Ref. [1]. ^(d) The integrals are invariant under rotation of $d_j^{\beta }{\Phi }_k^{\gamma }$ about the z axis, in particular 〈$A_{1g}|d_x{E}_u^x$〉 = 〈$A_{1g}|d_{x\prime }{E}_u^{x\prime }$〉 where $e_{x\prime }$= $C_8{e}_x$; see Section 3.

therein. For the methods of calculating the integral (8), see Section 2.8.

2.5. Symmetry Breaking of the Electronic Hamiltonians for the Oriented Model Benzene or Mg-Porphyrin by Linearly Polarized Laser Pulses

The time-dependent total electronic model Hamiltonian H_p(t) of the oriented molecule (benzene or Mg-porphyrin) interacting with the electric field $ℰ$_p(t) of the linearly polarized laser pulse labeled “p” (Section 2.1) consists of two terms for the electronic Hamiltonian H_e and for the laser-dipole interaction—$ℰ$_p(t) * d. In semiclassical dipole approximation

H_p(t) = H_e − $ℰ$_p(t) * d = H_e − e_p * d * $ℰ$_p(t).

(10)

The scalar product e_p * d breaks the symmetry of the point group G = D_6h or D_4h for the oriented benzene or Mg-porphyrin) of H_e down to a subgroup S(H_p(t)) of G. For example, in the case of the oriented benzene interacting with the “first” (p = 1) laser pulse with polarization vector e₁ ≡ e_x = e”₁, the full set of commutations (3) of the electronic Hamiltonian H_e with all symmetry operations ( = all group elements g ϵ G) is reduced to a much smaller set of commutations of the total Hamiltonian H_p(t) ≡ H_e”1(t) with only four symmetry operations of the subgroup S(H_p=1(t)) ≡ S(H_e”1(t)) = C_2v”₁, specifically

[H_e”1(t), g] = 0 for g ϵ S(H_e”1(t)) = C_2v”₁ = {E, C₂”, σ_h, σ_d1}
≠ 0 else

(11)

As consequence, the electronic Hamiltonian H_e”1(t) of the oriented benzene molecule interacting with the linearly e”₁ polarized laser pulse conserves the symmetry elements {E, C₂”, σ_h, σ_d1} of the subgroup S(H_e”1(t)) = C_2v”₁ of the point group G = D_6h of the Hamiltonian H_e of the non-interacting molecule. In brief, the e”₁ polarized laser pulse breaks the symmetry G = D_6h of the electronic Hamiltonian H_e down to S(H_e”1(t)) = C_2v”₁ symmetry of H_e”1(t). This implies that H_e”1(t) also commutes with the symmetry projection operators P^Γm(C_2v”₁) = (1/4) Σ_gϵC2v”1 χ^Γm(g)* g for the IRREPs Γ_m = A₁, A₂, B₁, B₂ of C_2v”₁,

[H_e”1(t), P^Γm(C_2v”₁)] = 0 for Γ_m = A₁, A₂, B₁, B₂.

(12)

By analogy, interactions of the oriented benzene (or Mg-porphyrin, in brackets) with laser pulses with linear polarization vectors e = e’₁, e’₂, e’₃ and e”₁, e”₂, e”₃ (e’₁, e’₂ and e”₁, e”₂) along the rotational axes C’₂₁, C’₂₂, C’₂₃ and C”₂₁, C”₂₂, C”₂₃ (C’₂₁, C’₂₂ and C”₂₁, C”₂₂) conserve the symmetry elements of the subgroups S(H_e(t)) = C_2v’₁, C_2v’₂, C_2v’₃ and C_2v”₁, C_2v”₂, C_2v”₃ (C_2v’₁, C_2v’₂ and C_2v”₁, C_2v”₂), respectively, with commutation relations analogous to Equations (11) and (12), or in brief, those e polarized laser pulses break the symmetry G = D_6h (D_4h) of H_e down to those C_2v-type symmetries S(H_e(t)). These results also hold for applications of two sequential laser pulses with the same polarization vectors e_p = e_p’. In contrast, interactions with laser pulses with other polarizations e_p perpendicular to e_z, or two sequential laser pulses labeled p&p’ (also called e_p&e_p’) with different polarizations e_p ≠ e_p’, reduce the commutations (11) further to

[H_e(t), g] = 0 for g ϵ S(H_e(t)) = C_s = {E, σ_h}
  ≠ 0 for laser polarizations e_p different from
   e’₁, e’₂, e’₃ and e”₁, e”₂, e”₃ for oriented benzene

(13)

(e’₁, e’₂ and e”₁, e”₂ for oriented Mg-porphyrin),
  or for two sequential laser pulses with different polarizations

and this implies the commutations

[H_e’1(t), P^Γm(C_s)] = 0 for Γm = A’, A”

(14)

analogous to Equation (12).

The subgroup symmetries S(H_e(t)) of the time-dependent Hamiltonians H_e(t) of the oriented molecules interacting with laser pulses with linear polarizations e, or with two sequential laser pulses, are listed in Table 2.

2.6. Quantum Dynamical Methods for the Propagation of the Laser-Driven Electronic Superposition States

The laser pulse with linear polarization e = e_p, or two sequential linearly polarized laser pulses (Section 2.1) drive the electronic wave functions of the oriented model systems from their initial (t = 0) electronic ground state

|Ψ_e(t = 0)> = |1A_1g> ≡ |0>

(15)

to time-dependent excited states |Ψ_e(t)> = |Ψ_ep(t)> = |Ψ_p(t)>. The different but equivalent notations are used below, depending on the context. The subscripts “e” and “p” remind of the polarization vectors e = e_p of the laser pulse labeled p. The wavefunctions are expanded in terms of the electronic eigenstates (Section 2.4),

|Ψ_e(t)> = Σ_m c_em(t) |m>

(16)

with complex time-dependent coefficients c_em(t). The initial state (15) corresponds to the initial coefficients

c_em(t = 0) = δ_m0

(17)

where δ denotes Kronecker’s symbol. The coefficients c_em(t) yield the time-dependent probabilities P_em(t) of occupying the electronic eigenstates |m>,

P_em(t) = |c_em(t)|².

(18)

These occupation probabilities are normalized,

Σ_m P_em(t) = 1.

(19)

Initially, the ground state is populated exclusively,

P_em(t = 0) = δ_m0.

(20)

The time evolution of the electronic wave function (16) is obtained as solution of the time-dependent Schrödinger equation (TDSE)

iℏ d/dt |Ψ_e(t)> = H_e(t) |Ψ_e(t)>

(21)

with initial value (15). The expansion in terms of electronic eigenstates (16) yields the equivalent algebraic version of the TDSE,

iℏ d/dt c_e(t) = H_e(t) c_e(t)

(22)

with initial values (17) of the components c_em(t) of the vector c_e(t). In practice, Equation (22) is applied with a finite set of eigenstates in the expansion (16). The numerical results are converged with respect to the number of eigenstates shown in Figure 3 and Figure 4. The Hamilton matrix H_e(t) for the oriented molecule interacting with the e = e_p polarized laser pulse has elements

H_e,mn(t) = <m| H_e(t) |n> = E_m δ_mn − e_p * d_mn * $ℰ$_p(t),

(23)

cf. Equations (6), (8) and (10). The formal solution of Equation (22) is

c_e(t) = U_e(t) c_e(0)

(24)

with unitary time evolution operator

$${\mathbf{U}}_{\mathbf{e}}(\mathrm{t}) = \widehat{T} \exp [-\mathrm{i} {\int }_0^{\mathrm{t}} \mathrm{d}\mathrm{t}\prime {\mathbf{H}}_{\mathbf{e}}(\mathrm{t}\prime )/\mathsf{\hslash }]$$

(25)

where $\widehat{T}$ is the time ordering operator. Equations (24) and (25) are propagated numerically by means of the methods and programs which were developed in Refs. [24,25,26,27]. In a nutshell, the lowest-lying eigenstates of the many-body electronic Hamiltonian are calculated as linear combinations of Slater determinants at a chosen level of theory (i.e., MRCISD for benzene, and LR-TDDFT for magnesium porphyrin). This step is performed used standard quantum chemistry programs (MOLPRO and Gaussian 16). All matrix elements required to represent the time-dependent Hamiltonian are computed using the open-source toolbox detCI@ORBKIT [28,29,30]. Note that the many-body electronic Hamiltonian is considered diagonal in the basis at the chosen level of theory. The coefficients (i.e., the contributions of the different Slater determinants) extracted from the quantum chemistry programs as solutions of the time-independent many-body Hamiltonian are first pruned by removing all contributions below 0.001, and then renormalized. The matrix elements of the dipole moment operator are computed by numerical integration using these pseudo-eigenstate wave functions. Finally, the time-evolution of the coefficients c_e(t) in Equation (24) is performed by direct numerical integration of the time-dependent Schrödinger equation using a preconditioned adaptive step size Runge–Kutta algorithm [31]. For more detail on the implementation, the propagation, and the calculation of the required matrix elements, the reader is referred to the cited literature.

After the end of the laser pulse (t ≥ t_f where t_f = τ_p for a single pulse, or t_f = τ_p + τ_p’ for two pulses p, p’) the wave functions (16) represent charge migration in the field-free systems, see the examples in Section 3. They evolve with constant amplitudes and with linearly increasing phases of the coefficients

c_em(t) = |c_em(t_f)| * exp[−i E_m (t − t_m)/ℏ] for t ≥ t_f

(26)

and with constant population probabilities of the electronic eigenstates |m>,

P_em(t) = P_em(t_f) = |c_em(t_f)|² for t ≥ t_f.

(27)

The phase of the coefficient c_e0(t) of the ground state is equal to zero because we set E₀ = 0 eV, cf. Figure 3 and Figure 4. The phases of the coefficients (26) for the excited states (E_m > 0 eV) are written such that exp[…] = 1 at t = t_m, t_m + h/E_m, t_m +2 h/E_m, etc. The specific choice of t_m is irrelevant; for convenience, one may choose the first event t_m after the end of the laser pulse, t_f < t_m < t_f + h/E_m which satisfies the equality exp[…] = 1.

2.7. Some Symmetry Relations of the Wavefunctions Driven by Laser Pulses with Different Linear Polarizations

In the applications to electron symmetry breaking in oriented benzene below, we shall compare the effects of laser pulses with different polarizations. In this Section, we assume that they are labeled p = 1 and 2, e.g., e_p=1 ≡ e₁ = e_x = e”₁ and e_p=2 ≡ e₂ = C₃ e₁ = e”₂, with the same amplitudes of the electric fields, $ℰ$₁(t) = $ℰ$₂(t) ≡ $ℰ$ (t). (Note that the real applications in Section 3.1. use different labels, as specified at the end of this Section.) The purpose of this Section is to prove that the laser-driven population dynamics is robust with respect to threefold rotations C₃ of the polarization vectors. The corresponding electronic wavefunctions are denoted Ψ_e1({r_i},t) and Ψ_e2({r_i},t), depending on the Cartesian coordinates {r_i} of all electrons in the laboratory frame. In Dirac notation,

Ψ_e1({r_i},t) ≡ <{r_i} | Ψ_e1(t)>.

(28)

Analogous notations hold for the electronic eigenfunctions <{r_i}| m> ≡ Ψ_m({r_i}), e.g., the wave function of the ground state |0> = |1A_1g> depending on {r_i} is written as <{r_i}|1A_1g> ≡ Ψ_1A1g({r_i}). The electronic wavefunctions also depend on the electronic spins, and they depend parametrically on the nuclear charges and coordinates at the proper places of the oriented nuclear scaffold, but these dependencies are not written explicitly in Equation (28).

The electronic wavefunctions (28) are obtained as solutions of the electronic TDSEs

           iℏ d/dt Ψ_e1({r_i},t) = H_e1(t) Ψ_e1({r_i},t) = [H_e({r_i}) + e e₁ * Σ_i r_i * $ℰ$(t)] Ψ_e1({r_i},t),

(29)

           iℏ d/dt Ψ_e2({r_i},t) = H_e2(t) Ψ_e2({r_i},t) = [H_e({r_i}) + e e₂ * Σ_i r_i * $ℰ$(t)] Ψ_e2({r_i},t)
             = [H_e({r_i}) + e C₃ e₁ * Σ_i r_i * $ℰ$(t)] Ψ_e2({r_i},t)
    = [H_e({r_i(t)})] Ψ_e2({r_i},t)

              = [H_e({C₃⁻¹r_i}) + e e₁ * Σ_i C₃⁻¹r_i * $ℰ$(t)] Ψ_e2({r_i},t)

(30)

The last Equation (30) holds because of the D_6h symmetry of the electronic Hamiltonian H_e. The two wave functions have the same initial values,

Ψ_e1({r_i},t = 0) = Ψ_e2({r_i},t = 0) = Ψ_A1g({r_i})
   = C₃ Ψ_A1g({r_i}) = Ψ_e1({C₃⁻¹ r_i},t = 0).

(31)

The last Equation (31) holds because of the IRREP A_1g of the initial electronic wave function of the oriented benzene in its ground state, with all characters equal to 1. Comparison of the last Equations (30) and (29) together with Equation (31) shows that the solution of Equation (30) is

Ψ_e2({r_i},t) = Ψ_e1({C₃⁻¹r_i},t) = C₃ Ψ_e1({r_i},t).

(32)

That means rotation of the linear polarization e”₁ of the laser pulse by 120° to C₃ e”₁ = e”₂ without any changes of the electric field amplitude $ℰ$(t) rotates the laser-driven electronic wave function by the same angle 120°. In brief e”₁ → e”₂ = C₃ e”₁ yields the rotation of the wave function Ψ_e”1({r_i},t) → Ψ_e”2({r_i},t) = C₃ Ψ_e”1({r_i},t).

The expansion (16) of the time-dependent wave function in terms of the eigenfunction implies the relation

Ψ_e”1({r_i},t) = Σ_m c_e“1m(t) Ψ_m({r_i}) → Ψ_e”2({r_i},t) = C₃ Ψ_e”1({r_i},t).
   = Σ_m c_e“1m(t) C₃ Ψ_m({r_i}).

(33)

The third Equation (33) means that rotation of the laser pulse polarization vector e”₁ by 120° to C₃ e”₁ = e”₂ yields the same coefficients for the expansion in terms of the rotated eigenfunctions. The relation (33) also implies that the quantum dynamics of the populations of the rotated eigenfunctions is the same as Equation (18) for the non-rotated eigenfunctions.

Analogous symmetry relations for laser-driven wavefunctions of the oriented benzene hold for analogous rotations of polarizations

e’₁ → e’₂ = C₃ e’₁ yields the rotation Ψ_e’1({r_i},t) → Ψ_e’2({r_i},t) = C₃ Ψ_e’1({r_i},t),
e’₁ → e’₃ = C₃² e’₁ yields the rotation Ψ_e’1({r_i},t) → Ψ_e’3({r_i},t) = C₃² Ψ_e’1({r_i},t),

(34)

e”₁ → e”₂ = C₃ e”₁ yields the rotation Ψ_e“1({r_i},t) → Ψ_e“2({r_i},t) = C₃ Ψ_e“1({r_i},t),
e”₁ → e”₃ = C₃² e”₁ yields the rotation Ψ_e“1({r_i},t) → Ψ_e“3({r_i},t) = C₃² Ψ_e“1({r_i},t),

(35)

with consequences for the expansions of the wavefunctions in terms of the rotated eigenfunctions analogous to Equation (33).

Likewise, rotations of the linear polarizations of the laser pulses for electron symmetry breaking in the oriented Mg-porphyrin, without any changes of the amplitude of the electric field, yield the following symmetry relations of the resulting electronic wave functions:

e’₁ → e’₂ = C₄ e’₁  yields the rotation Ψ_e’1({r_i},t) → Ψ_e’2({r_i},t) = C₄ Ψ_e’1({r_i},t),

(36)

e”₁ → e”₂ = C₄ e”₁  yields the rotation Ψ_e“1({r_i},t) → Ψ_e“2({r_i},t) = C₄ Ψ_e“1({r_i},t),

(37)

again with consequences for the expansions of the wavefunctions in terms of the rotated eigenfunctions analogous to Equation (33), except that the rotation C₃ is replaced by C₄.

In Section 3.1 below, we shall show that six different laser pulses labeled p = 1, …,6 with the same electric field amplitudes $ℰ$₁(t) = … = $ℰ$₆(t) but with different polarizations yield the same population dynamics (cf. Figure 5 below) but different electron symmetry breakings and different attosecond charge migrations in benzene. This equality of all six population dynamics is proven in two steps. First, the Equations (34) and (35) prove the equality of the population dynamics of the laser pulses with polarization vectors e₁”, e₂”, e₃” (corresponding to p = 1, 3, 4) and independently also for the polarization vectors e₁’, e₂’, e₃’ (p = 2, 5, 6). Second, Appendix B has additional group theoretical derivations for the transition dipole matrix elements which imply the equality of the population dynamics of the laser pulses with polarization vectors e₁” and e₁’. Likewise, in Section 3.2 and Section 3.4 we shall show that four different laser pulses labeled p = 1, …, 4 with the same electric field amplitudes $ℰ$₁(t) = … = $ℰ$₄(t) but with different polarizations yield the same population dynamics (cf. Section 3.4) but different electron symmetry breakings and different attosecond charge migrations in Mg-porphyrin. The equality of all four population dynamics is again proven in two steps. First, the Equations (36) and (37) prove the equality of the population dynamics of the laser pulses with polarization vectors e₁’, e₂’ (corresponding to p = 1, 3) and independently also for the polarization vectors e₁”, e₂” (p = 2, 4). Second, Appendix B implies the proof for the equality of the population dynamics of the laser pulses with polarization vectors e₁’ and e₁”.

2.8. Calculation of the One-Electron Density of the Time-Dependent Electronic Superposition State

The electronic wavefunction (16) and (28) of the oriented model system driven by the laser pulse with linear polarization e_p (or by two sequential laser pulses) yields the one-electron density

ρ_p(r,t) = ∫|Ψ_ep({r_i},t)|² dr₂ dr₃ .... |_{r = r1}

(38)

The integration (38) is over the Cartesian coordinates {r_i} of all anti-symmetrized electrons but one. The integration is also over all electron spins, but this is not written explicitly in Equation (38). It is carried out numerically by means of detCI@ORBKIT [28,29,30] and plotted using Matplotlib [32]. This method is also used to calculate the integrals for transition dipole matrix elements (8).

The linear expansion of the electronic wavefunction (16) allows to decompose the one-electron density into “diagonal” (dia, m = n) and “off-diagonal” (odi, mǂn) contributions,

ρ_p(r,t) = ρ_p,dia(r,t) + ρ_p,odi(r,t),
ρ_p,dia(r,t) = Σ_m |c_ep,m(t)|² ∫|Ψ_m({r_i})|² dr₂ dr₃ .... |_{r = r1},
ρ_p,odi(r,t) = ΣΣ_m<n [c_ep,m(t)^* * c_ep,n(t) ∫Ψ_m({r_i})^* * Ψ_n({r_i}) dr₂ dr₃ .... |_{r = r1}
+ c_ep,m(t) * c_ep,n(t)^* ∫Ψ_m({r_i}) * Ψ_n({r_i})^* dr₂ dr₃ .... |_{r = r1}.

(39)

For times t after the end t_f of the laser pulse, or of two sequential laser pulses, the field-free evolution of the expansion coefficients (26) renders these parts time-independent and time-dependent, respectively,

ρ_p(r,t) = <ρ_p(r)> + Δρ_p(r,t) for t ≥ t_f,

<ρ_p(r)> = ρ_p,dia(r,t_f) = Σ_m P_ep,m(t_f) ∫|Ψ_m({r_i})|² dr₂ dr₃ .... |_{r = r1},
≡ Σ_m P_ep,m(t_f) ρ_m(r),

Δρ_p(r,t) = ρ_p,odi(r,t) = ΣΣ_m<n |c_ep,m(t_f)| * |c_ep,n(t_f)|
 * {exp[ i (E_m − E_n) t / ℏ] ∫Ψ_m({r_i})^* * Ψ_n({r_i}) dr₂ dr₃ .... |_{r = r1}
 + exp[ i (E_n − E_m) t / ℏ] ∫Ψ_m({r_i}) * Ψ_n({r_i})^* dr₂ dr₃ .... |_{r = r1}}
 = ΣΣ_m<n |c_ep,m(t_f)| * |c_ep,n(t_f)|
 * 2 cos(ω_mn t) * ∫Ψ_m({r_i}) * Ψ_n({r_i}) dr₂ dr₃ .... |_{r = r1}

(40)

The notation in the first and second Equation (40) indicates that <ρ_p(r)> is the long time mean average of ρ_p(r,t)

$$<{\mathsf{\rho }}_{\mathrm{p}}(\mathbf{r})> = {\lim }_{\mathrm{t}}{\to }_{\infty }[1/(\mathrm{t} - {\mathrm{t}}_{\mathrm{f}}){]}^{ }{{\displaystyle \int }}_{t_f}^t{\mathsf{\rho }}_p\left(r,{\mathrm{t}}^{\prime }\right)d{t}^{\prime }$$

(41)

whereas Δρ_p(r,t) is the time-dependent deviation from the mean. The ρ_m(r) in Equation (40) is the one-electron densities of the eigenstates |m>, e.g., ρ₀(r) = ρ_1A1g(r) is the one-electron density of the ground state |0> = |1A_1g>, illustrated in Figure 1 and Figure 2 for the oriented benzene and Mg-porphyrin, respectively. The last Equation (40) with transition frequencies

ω_mn = (E_m − E_n)/ℏ

(42)

and transition periods

T_mn= 2π/ω_mn

(43)

holds because we use real-valued electronic eigenfunctions.

2.9. Re-Optimized π/2- and π-Laser Pulses for Control of Electron Symmetry Breaking and Charge Migration

The applications in Section 3 shall demonstrate electron symmetry breaking in the oriented model systems, benzene and Mg-porphyrin, by means of short linearly polarized laser pulses labeled p = 1, 2, 3, …, or by two sequential laser pulses. The total pulse duration should be below 10 fs so that the nuclear scaffolds are still frozen [7,8] with the conservation of nuclear symmetry. Initially, the systems are in the electronic ground state with IRREP A_1g. The initial electron symmetry is, therefore, the same as the nuclear symmetry, namely G = D_6h and D_4h, respectively. After the laser pulse, or after two sequential laser pulses, the symmetry of the one-electron density (Section 2.8) is broken from G down to a subgroup S(ρ_p(r,t)) of G. The subgroup S(ρ_p(r,t)) depends on the one-electron density ρ_p(r,t) which is generated by the laser pulse labeled p. It is determined in the field-free environment immediately after the laser pulse, when the oriented model system still keeps the original nuclear symmetry of the frozen scaffold, but the electrons already exhibit charge migration, on typical time scales from a few hundred as to a few fs. One of the purposes of the applications is to demonstrate that the different linearly polarized laser pulses can prepare the electrons in a rather large variety of symmetries with different subgroups S(ρ_p(r,t)) of G. This means that one can use the laser pulses to control electron symmetry while conserving nuclear symmetry. In many cases (but by no means in all cases), this type of laser control of electron symmetry is achieved by means of laser pulses which excite the oriented systems from the electronic ground state to a selective superposition of the ground plus one excited states, with equal population probabilities. The laser pulses which achieve this goal are so-called π/2 pulses, or re-optimized π/2 pulses.

The general theory for π/2 pulses is presented, e.g., in Ref. [33]; for applications, see, e.g., Refs. [1,2,10,15]. Here, we adapt the specific result for linearly polarized laser pulses with sin²—shapes, electric field amplitude $ℰ$₀ and duration τ, cf. Section 2.1. Accordingly, the π/2 laser pulse for the selective transition from the initial state |Ψ_i> = |Ψ_A1g> to the superposition state (1/√2)*(|Ψ_i> + |Ψ_f>) should be resonant to the energy gap between the states, i.e., the photon energy is tuned to

ℏω = ℏω_if ≡ E_f − E_i

(44)

with period

T = T_if = 2π/ω_if

(45)

Moreover, the electric field amplitude $ℰ$₀ and the duration τ should satisfy the condition [10,15,33]

| d_if |* $ℰ$₀ *τ / (2 *ℏ) = π/2 for π/2 pulses

(46)

where |d_if| denotes the absolute value of the transition dipole matrix element <Ψ_i|d|Ψ_f> for the initial state |Ψ_i> and the target state |Ψ_f>.

For a target transition |Ψ_i> → (1/√2)*(|Ψ_i> + |Ψ_f>) with specific value of |d_if|, the rule (46) calls for the proper value of the product $ℰ$₀ *τ. Accordingly, large values of |d_if| are favourable because they allow small values $ℰ$₀ *τ. The rule (46) allows some flexibility for the choice of the individual laser parameters, e.g., one could use either long weak pulses or short intense ones. The present applications call for a compromise, i.e., the laser pulses must be short (τ ≤ 10 fs) but not all too short, to avoid exceedingly large values of the maximum intensities I_m, cf. Section 2.1.

The rules (44)–(46) were derived for the ideal so-called two-state scenario with exclusive transitions between just two states, |Ψ_i> and |Ψ_f> [33]. Moreover, they hold for laser pulses with large numbers of optical cycles,

N_c = τ/T » 1.

(47)

In contrast, the present multi-state quantum dynamics simulations (Section 2.6) allow—in principle, at least—many other transitions, and some of the pulses are just few-cycle pulses. For these more realistic scenarios, the rules (44)–(47) serve as a zero-order approximation. Systematic re-optimization of the laser parameters, e.g., slight detuning of the resonance frequency combined with variations of the field strength, then yields re-optimized π/2 pulses for the target transitions [15].

The subsequent discussions also refer to so-called π laser pulses. These achieve complete population transfer from the initial state |Ψ_i> to |Ψ_f>. They require the same conditions (44) and (47) as for the π/2 pulses, but the condition (46) is replaced by [10,15,32]

|d_if|* $ℰ$₀ *τ/(2 *ℏ) = π for π pulses.

(48)

3. Results

This Section for the results is divided into three major parts: The first part has Section 3.1 and Section 3.2. They demonstrate “empirical” numerical results for electron symmetry breaking by short linearly polarized laser pulses, from the groups G of the rigid nuclear scaffolds of the oriented model systems, benzene (G = D_6h) and Mg-porphyrin (G = D_4h), respectively, to various subgroups S(ρ_p(r,t)) of G. These results are based on the evidence of the symmetry elements of the one-electron density ρ_p(r,t) which represents charge migration right after the laser pulses labeled p. The pulses are illustrated in the set of Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12, in particular in Figure 5, Figure 9 and Figure 11 below. Their mathematical expression is in Equation (1). The laser polarizations are listed in Table 2. All other laser parameters, i.e., the final values of the amplitudes, frequencies and pulse durations are in Figure 5, Figure 9 and Figure 11 below. The resulting one-electron densities are illustrated in Figure 6, Figure 7, Figure 8, Figure 10 and Figure 12 below. Their electron symmetries are listed in

Table 3. Electronic superposition states of oriented benzene and the characters (=1) of the totally symmetric representations of their symmetry subgroups.

	|Ψ〉 = |0〉    +     |m〉 (a)	|A1g〉 + $\mathbf{|}{\mathit{E}}_{\mathbf{1}\mathit{u}}^{\mathit{x}}\mathbf{\rangle }$	$\mathbf{|}{\mathit{A}}_{\mathbf{1}\mathit{g}}\mathbf{\rangle }$ + ${\mathit{C}}_{\mathbf{3}}\mathbf{|}{\mathit{E}}_{\mathbf{1}\mathit{u}}^{\mathit{x}}\mathbf{\rangle }$	$\mathbf{|}{\mathit{A}}_{\mathbf{1}\mathit{g}}\mathbf{\rangle }$ + ${\mathit{C}}_{\mathbf{3}}^{\mathbf{2}}$$\mathbf{|}{\mathit{E}}_{\mathbf{1}\mathit{u}}^{\mathit{x}}\mathbf{\rangle }$	$\mathbf{|}{\mathit{A}}_{\mathbf{1}\mathit{g}}\mathbf{\rangle }$ + $\mathbf{|}{\mathit{E}}_{\mathbf{1}\mathit{u}}^{\mathit{y}}\mathbf{\rangle }$	$\mathbf{|}{\mathit{A}}_{\mathbf{1}\mathit{g}}\mathbf{\rangle }$ + ${\mathit{C}}_{\mathbf{3}}$$\mathbf{|}{\mathit{E}}_{\mathbf{1}\mathit{u}}^{\mathit{y}}\mathbf{\rangle }$	$\mathbf{|}{\mathit{A}}_{\mathbf{1}\mathit{g}}\mathbf{\rangle }$ + ${\mathit{C}}_{\mathbf{3}}^{\mathbf{2}}$$\mathbf{|}{\mathit{E}}_{\mathbf{1}\mathit{u}}^{\mathit{y}}\mathbf{\rangle }$	$\mathbf{|}{\mathit{A}}_{\mathbf{1}\mathit{g}}\mathbf{\rangle }$ + $\mathbf{|}{\mathit{E}}_{\mathbf{2}\mathit{g}}^{{\mathit{x}}^{\mathbf{2}}\mathbf{-}{\mathit{y}}^{\mathbf{2}}}\mathbf{\rangle }$	$\mathbf{|}{\mathit{A}}_{\mathbf{1}\mathit{g}}\mathbf{\rangle }$ + $\mathbf{|}{\mathit{E}}_{\mathbf{2}\mathit{g}}^{\mathit{x}\mathit{y}}\mathbf{\rangle }$	$\mathbf{|}{\mathit{A}}_{\mathbf{1}\mathit{g}}\mathbf{\rangle }$ + $\mathbf{|}{\mathit{B}}_{\mathbf{2}\mathit{u}}\mathbf{\rangle }$	$\mathbf{|}{\mathit{A}}_{\mathbf{1}\mathit{g}}\mathbf{\rangle }$ + $\mathbf{|}{\mathit{B}}_{\mathbf{1}\mathit{u}}\mathbf{\rangle }$
g ∈ D6h (b)
E		1	1	1	1	1	1	1	1	1	1
2 C6
2 C3										1	1
C2z								1	1
C21‘					1			1			1
C22‘						1					1
C23‘							1				1
C21‘‘		1						1		1
C22‘‘			1							1
C23‘‘				1						1
i								1	1
2 S3										1	1
2 S6
σh		1	1	1	1	1	1	1	1	1	1
σv1					1			1			1
σv2						1					1
σv3							1				1
σd1		1						1		1
σd2			1							1
σd3				1						1
${\mathrm{S}}_{\mathsf{\Psi }}\subseteq {\mathbf{D}}_{6\mathrm{h}}$ $\mathrm{IRREP} \mathrm{of} {\mathrm{S}}_{\mathsf{\Psi }} {}^{\left(\mathrm{c}\right)}$		$C_{2v,1}^{″}$ $A_1$	$C_{2v,2}^{″}$ $A_1$	$C_{2v,3}^{″}$ $A_1$	$C_{2v,1}^{\prime }$ $A_1$	$C_{2v,2}^{\prime }$ $A_1$	$C_{2v,3}^{\prime }$ $A_1$	$D_{2h,1}$ $A_g$	$C_{2h}$ $A_g$	$D_{3h}^{″}$ $A_1^{\prime }$	$D_{3h}^{\prime }$ $A_1^{\prime }$
${\mathrm{S}}_{\mathsf{\rho }}\subseteq {\mathrm{D}}_{6\mathrm{h}}$		$C_{2v,1}^{″}$	$C_{2v,2}^{″}$	$C_{2v,3}^{″}$	$C_{2v,1}^{\prime }$	$C_{2v,2}^{\prime }$	$C_{2v,3}^{\prime }$	$D_{2h,1}$	$C_{2h}$	$D_{3h}^{″}$	$D_{3h}^{\prime }$
Laser pulses p (d)		1	3	4	2	5	6	7&8	7&9	Ref. [1]	Ref. [1]

^(a) The expression |A〉 +|B〉 denotes the superposition of two non-vanishing electronic wave functions with IRREP A_1g and another IRREP. The superposition states are prepared by selective laser pulses, and they depend on the laser polarizations and on the time after the laser pulses, cf. Section 3.1. ^(b) Some important symmetry elements corresponding to the symmetry operations g are illustrated in Figure 1. ^(c) The electronic superposition state |Ψ> transforms according to the totally symmetric IRREP of the subgroup ${\mathrm{S}}_{\mathsf{\Psi }}$ ≡ S(Ψ) of D_6h. The subgroups are specified in Table 1 and Table 2. ^(d) Cf. Section 3.1.

and

Table 4. Electronic superposition states of oriented Mg-porphyrin and the characters (=1) of the totally symmetric representations of their symmetry subgroups.

	$$\begin{gathered} \mathbf{|}\mathsf{\Psi }\mathbf{\rangle }\mathbf{=}\mathbf{|}\mathbf{0}\mathbf{\rangle } \\ \mathbf{\hspace{1em}\hspace{1em}\hspace{1em}+} \end{gathered}$$    |m〉 (a)	$$\begin{gathered} \mathbf{|}{\mathit{A}}_{\mathbf{1}\mathit{g}}\mathbf{\rangle } \\ \mathbf{+} \\ \mathbf{|}{\mathit{E}}_{\mathit{u}\mathbf{1}}^{\mathbf{\prime }}\mathbf{\rangle } \end{gathered}$$	$$\begin{gathered} \mathbf{|}{\mathit{A}}_{\mathbf{1}\mathit{g}}\mathbf{\rangle } \\ \mathbf{+} \\ \mathbf{|}{\mathit{E}}_{\mathit{u}\mathbf{2}}^{\mathbf{\prime }}\mathbf{\rangle } \end{gathered}$$	$$\begin{gathered} \mathbf{|}{\mathit{A}}_{\mathbf{1}\mathit{g}}\mathbf{\rangle } \\ \mathbf{+} \\ \mathbf{|}{\mathit{E}}_{\mathit{u}\mathbf{1}}^{\mathbf{″}}\mathbf{\rangle } \end{gathered}$$	$$\begin{gathered} \mathbf{|}{\mathit{A}}_{\mathbf{1}\mathit{g}}\mathbf{\rangle } \\ \mathbf{+} \\ \mathbf{|}{\mathit{E}}_{\mathit{u}\mathbf{2}}^{\mathbf{″}}\mathbf{\rangle } \end{gathered}$$
g ∈ D4h (b)
E		1	1	1	1
C4+ C4−
C2z
C21‘		1
C22‘			1
C21‘‘				1
C22‘‘					1
i
S4− S4+
σh		1	1	1	1
σv1		1
σv2			1
σd1				1
σd2					1
$${\mathrm{S}}_{\mathsf{\Psi }}\subseteq {\mathbf{D}}_{4\mathrm{h}}$$		$$C_{2v,1}^{\prime }$$	$$C_{2v,2}^{\prime }$$	$$C_{2v,1}^{\prime \prime }$$	$$C_{2v,2}^{\prime \prime }$$
$$\mathrm{IRREP} \mathrm{of} {\mathrm{S}}_{\mathsf{\Psi }} {}^{\left(\mathrm{c}\right)}$$		A1	A1	A1	A1
Sρ ⊆ D4h		$$C_{2v,1}^{\prime }$$	$$C_{2v,2}^{\prime }$$	$$C_{2v,1}^{\prime \prime }$$	$$C_{2v,2}^{\prime \prime }$$
Laser pulses p (d)		1	2	3	4

^(a) The expression |A〉 +|B〉 denotes the superposition of two non-vanishing electronic wave functions with IRREP A_1g and another IRREP, e.g., $E_{u1}^{\prime }$ ≡ $E_u^x$, $E_{u2}^{\prime }$ ≡ $E_u^y$, etc. The superposition states are prepared by selective laser pulses, and they depend on the laser polarizations and on the time after the laser pulses, cf. Section 3.2. ^(b) Some important symmetry elements corresponding to the symmetry operations g are illustrated in Figure 2. ^(c) The electronic superposition state |Ψ> transforms according to the totally symmetric IRREP of the subgroup ${\mathrm{S}}_{\mathsf{\Psi }}$ ≡ S(Ψ) of. The subgroups are specified in Table 2. The corresponding one-electron density ρ has the same subgroup ${\mathrm{S}}_{\mathsf{\rho } }$≡ S(ρ) =${ \mathrm{S}}_{\mathsf{\Psi }}$. ^(d) Cf. Section 3.2 and Section 3.4.

below. The second part has Section 3.3 and Section 3.4. They present the theory of electron symmetry breaking, to explain the phenomena of Section 3.1 and Section 3.2, respectively. The third part has Section 3.5—this discovers a simple general rule for electron symmetry breaking by short linearly polarized laser pulses which comprise all cases presented in Section 3.1, Section 3.2, Section 3.3 and Section 3.4

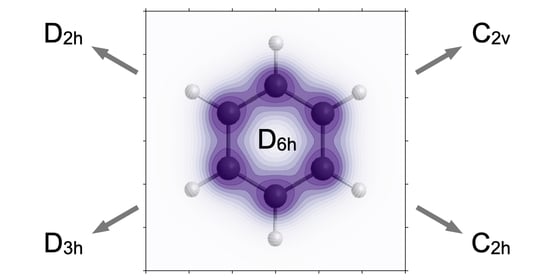
3.1. Electron Symmetry Breaking and Charge Migration Induced by Linearly Polarized Laser Pulses in Oriented Benzene with D_6h Nuclear Scaffold

This Section presents the results of quantum dynamics simulations (cf. Section 2.6) of eight different examples of electron symmetry breaking in the oriented model benzene (cf. Section 2.2) induced by eight different linearly polarized laser pulses labeled p = 1, 2, 3, …, or two sequential laser pulses (cf. Section 2.1). The symmetry breakings G = D_6h → S(ρ_p(r,t)) yield eight different point subgroups S(ρ_p(r,t)) of G for the one-electron densities ρ_p(r,t) (cf. Section 2.8) which present eight different types of attosecond charge migration, right after the end of the laser pulse(s). The durations of the laser pulses, or two sequential laser pulses, are restricted to 10 fs, such that the nuclear scaffolds may be considered as frozen [7,8], implying conservation of nuclear D_6h symmetry.

The first two examples (labeled p = 1, 2) are motivated by the results of Ref. [10] which discovered quantum control of electronic fluxes during attosecond charge migration in superposition states of oriented benzene. The charge migration is illustrated in Ref. [10] by means of snapshots of the one-electron density. As a byproduct, but without explicit observation (even without mentioning the word “symmetry”!), Ref. [10] demonstrates two different C_2v-type symmetries of the time-dependent one-electron densities which are generated by two different linearly e_x and e_y polarized π/2 laser pulses with Gaussian shapes. Here, we employ two similar re-optimized π/2 laser pulses with sin²-shapes (cf. Section 2.1 and Section 2.9), labeled p = 1 and 2, which are tailored to selective transitions from the initial (t = 0) electronic ground state |1A_1g> to the superposition states (1/√2)*(|1A_1g> + |1E_1u^x>) and (1/√2)*(|1A_1g> + |1E_1u^y>), respectively. The notation {|1E_1u^x>, |1E_1u^y>} denotes the doublet of two orthogonal degenerate states with IRREP E_1u and with the lowest energy E_1E1u which transform as the functions x and y (in brief: as x and y), respectively [13]. The target transitions are illustrated schematically by vertical arrows from the energy level E_1A1g to E_1E1u in Figure 3. The energy gap between their eigenenergies is ΔE_1A1g,1E1u = E_1E1u − E_1A1g = 8.17 eV with corresponding transition frequency ω_1A1g,1E1u = ΔE_1A1g,1E1u /ℏ and period T = T_1A1g,1E1u = 2π/ω_1A1g,1E1u = h/ ΔE_1A1g,1E1u = 506 as, cf. Equations (42) and (43). The pulses have the same electric field amplitudes $ℰ$₁(t) = $ℰ$₂(t) ≡ $ℰ$(t) which is shown in Figure 5, but different polarization vectors e₁ = e_x = e”₁ and e₂ = e_y = e’₁. The identical laser parameters are specified in Figure 5; the frequencies ω₁ = ω₂ are resonant with the transition frequency ω_1A1g,1E1u. Figure 5 also shows the resulting two-state population dynamics P_1A1g(t) and P_1E1ux(t) = P_1E1uy(t) ≡ P_1E1u(t), documenting perfect preparation of the target superposition states, with the same amplitudes (= 1/√2) of the ground and degenerate excited states at the end (t= τ₁ = τ₂ ≡ τ) of the laser pulses. The populations of all other states are entirely negligible.

Figure 6a,b illustrate the field-free time evolutions of the one-electron densities ρ_p(r,t) after the end of the re-optimized π/2 laser pulses labeled p=1 and 2, respectively. They are represented by three snapshots of ρ_p(r,t) − ρ_p(r,t=0) = ρ_p(r,t) − ρ_1A1g(r) integrated over z, i.e., ∫ [ρ_p(r,t) − ρ_1A1g(r)]dz. The snapshots are taken at t= t₀, t₀ + T/4 and t₀ + T/2, with period T = T_1A1g,1E1u. Here, t₀ is the first time after the end of the laser pulse when the phase factor exp[….] of c_e,1E1u(t) is equal to 1, cf. Equation (26). This equality is obtained during the first period T after the end of the laser pulse, t_f = τ ≤ t₀ ≤ τ + T, such that the nuclei can still be considered as frozen, conserving nuclear symmetry. Sequel snapshots at t = t₀ + (3/4)T and at t₀ + T look the same as those at t = t₀ + T/4 and at t₀, respectively. The subtraction of the initial one-electron density ρ_p(r,t = 0) = ρ_1A1g(r) from ρ_p(r,t) yields what may be called the “swapping one-electron density”, i.e., that part of the one-electron density which is driven by the laser pulse away from the original reference ρ_1A1g(r). It facilitates recognition of the time evolution and the symmetry of the one-electron density after the laser pulse; in contrast, the temporal changes of ρ_p(r,t) would be hardly recognizable. Appendix A proves that the electron symmetry of ρ_p(r,t) is the same as for the swapping one-electron density, ρ_p(r,t) − ρ_1A1g(r).

Altogether, the time evolution of the laser-driven one-electron densities illustrated in Figure 6a,b demonstrate two different types of periodic charge migrations, essentially from the left to the right CC bonds (and back, p = 1), or from the domains of the bottom to the top C-atoms (and back, p = 2), respectively, with period T = T_1A1g,1E1u. At time t = t₀, the swapping one-electron densities are accumulated in the left CC bond (p = 1), or in the domain of the bottom C-atom (p = 2). At t = t₀ + T/4, they “tunnel” [34] between the sites, and at t₀ + T/2, they arrive on the opposite sites. At t = t₀ + (3/4) T, they tunnel back (snapshot identical to the one for t = t₀ + T/4), and at t = t₀ + T, they are back to the densities at t= t₀, completing the first cycle of periodic charge migration.

Inspection of the swapping one-electron density ρ_p=1(r,t) − ρ_1A1g(r) ≡ ρ_e”1 (r,t) − ρ_1A1g(r) (Figure 6a) which is prepared by the e₁ = e_x = e”₁ polarized re-optimized π/2 laser pulse reveals that it conserves three and only three symmetry elements of the frozen nuclear symmetry point group G = D_6h, namely the binary rotation axis C₂”₁, the related dihedral plane σ_d1, and the horizontal plane σ_h. The corresponding symmetry operations constitute the subgroup S(ρ_p=1(r,t)) = C_2v”₁ = {E, C₂”₁, σ_h, σ_d1}. Accordingly, the one-electron density ρ_e”1 (r,t) evolves with C_2v”₁ symmetry. In conclusion, the e₁ = e_x = e”₁ polarized re-optimized π/2 laser pulse yields electron symmetry breaking G=D_6h → S(ρ_p=1(r,t)) = C_2v”₁.

By analogy, inspection of the swapping one-electron density ρ_p=2(r,t) − ρ_1A1g(r) (Figure 6b) which is prepared by the e₂ = e_y = e’₁ polarized re-optimized π/2 laser pulse reveals that it conserves a different set of three symmetry elements. The corresponding symmetry operations constitute the subgroup S(ρ_p=2(r,t)) = C_2v’₁ = {E, C₂’₁, σ_h, σ_v1} of G = D_6h. In conclusion, the e₂ = e_y = e’₁ polarized re-optimized π/2 laser pulse yields electron symmetry breaking G = D_6h → S(ρ_p=2(r,t)) = C_2v’₁.

Figure 7a,b show the effects of two other re-optimized π/2 laser pulses labeled p = 3,4. They have the same electric field amplitudes $ℰ$₃(t) = $ℰ$₄(t) = $ℰ$(t) with the same laser parameters as the previous ones (p = 1,2, cf. Figure 5), but different polarizations, e₃ = e”₂ = C₃ e”₁ and e₄ = e”₃ = C₃² e”₁, respectively. As shown in Section 2.7 (cf. the rule (35)), the rotations of the laser polarizations cause corresponding rotations of the laser-driven wave functions which may be expanded in terms of corresponding rotated eigenfunctions. The resulting population dynamics is the same as for the non-rotated wave functions, cf. Figure 5. Accordingly, the resulting time evolutions of the one-electron densities appear as images of the one shown in Figure 6a, rotated by 120° (C₃) and by 240° (C₃²), respectively. By analogy with the previous analyses, inspection of the resulting swapping one-electron densities ρ₃(r,t) − ρ_1A1g(r) ≡ ρ_e”2 (r,t) − ρ_1A1g(r) and ρ₄(r,t) − ρ_1A1g(r) ≡ ρ_e”3 (r,t) − ρ_1A1g(r) show that the laser pulses labeled p = 3 and 4 yield electron symmetry breaking from G = D_6h to two subgroups S(ρ_p=3(r,t)) = C_2v”₂ = {E, C₂”₂, σ_h, σ_d2} and S(ρ_p=4(r,t)) = C_2v”₃ = {E, C₂”₃, σ_h, σ_d3}—these are different from the previous subgroups S(ρ_p=1(r,t)) and S(ρ_p=2(r,t))_.

Likewise, Figure 8a,b show the effects of two other re-optimized π/2 laser pulses labeled p = 5, 6. They have the same electric field amplitudes $ℰ$₅(t) = $ℰ$₆(t) = $ℰ$(t) and the same laser parameters as the previous ones (p = 1, 2, 3, 4, cf. Figure 5), but different polarizations, e₅ = e’₂ = C₃ e’₁ and e₆ = e’₃ = C₃² e’₁, respectively. The resulting time evolutions of the swapping one-electron densities appear as images of the one shown in Figure 6b, rotated by 120° (C₃) and by 240° (C₃²), respectively, in accord with the rule (34). By analogy with the previous analyses, inspection of the resulting swapping one-electron densities ρ₅(r,t) − ρ_1A1g(r) ≡ ρ_e’2(r,t) − ρ_1A1g(r) and ρ₆(r,t) − ρ_1A1g(r) ≡ ρ_e’3(r,t) − ρ_1A1g(r) show that the re-optimized π/2 laser pulses labeled p=5 and 6 yield electron symmetry breaking G=D_6h → S(ρ_p=5(r,t)) = C_2v’₂ = {E, C₂’₂, σ_h, σ_v2} and S(ρ_p=6(r,t)) = C_2v’₃ = {E, C₂’₃, σ_h, σ_v3}, different from the previous ones.

Finally, we present two additional electron symmetry breakings in the oriented benzene, which are achieved by two different sequences of two linearly polarized laser pulses. The first example is motivated by a specific result of Ref. [1] for laser preparation of oriented benzene in selective non-aromatic (“na”) superposition states

|Ψ_na,1> = (1/√2)*(|1A_1g> + |1B_2u>)

(49)

or

|Ψ_na,2> = (1/√2)*(|1A_1g> + |1B_1u>).

(50)

For the orientation of benzene adapted from Ref. [1], cf. Figure 1, the excited states |1B_2u> and |1B_1u> transform as x(x² − 3y²) and y(3x² − y²), respectively [13]. Symmetry selection rules do not allow direct excitations of the ground state to these target states [1,13], but Ulusoy and Nest succeeded in designing sequences of three e_x and e_y linearly polarized laser pulses, or alternative re-optimized pulses which reach the goals. Our first example is stimulated by their series of three e_y polarized laser pulses which prepare the target state (50) by means of three transitions which are all symmetry allowed. The first one is a π/2 laser pulses which excites the aromatic ground state |1A_1g> to the superposition state (1/√2)*(|1A_1g> + |1E_1u^y>), analogous to the present laser pulse labeled p = 2. The second one is a π laser pulse which transfers the excited state |1E_1u^y> into |1E_2g^x2−y2>. This state is one of two degenerate 1E_2g states {|1E_2g^x2−y2>, |1E_2g^xy>} with energy E_1E2g which transform as x² − y² and xy, respectively [13]. The third one is another π laser pulse which transfers |1E_2g^x2−y2> into |1B_1u>. Consequently, at the ends of the second and third laser pulses, the oriented benzene is in the superposition state (1/√2) (|1A_1g> + |1E_2g^x2−y2>) and finally in the target state (50), respectively.

As set off in the Introduction, Ulusoy and Nest already noted that their three-step approach to laser control of aromaticity in oriented benzene breaks electron symmetry [1]. Our original plan was to investigate laser-induced electron symmetry breaking already after two steps, i.e., after excitation of the ground state (|1A_1g> first to the superposition state (1/√2)*(|1A_1g> + |1E_1u^y>) and then to (1/√2)*(|1A_1g> + |1E_2g^x2−y2>), by means of two e_y polarized π/2 and π laser pulses, but now under the constraint of the conservation of nuclear symmetry. In the context of this manuscript, these laser pulses shall be labeled p = 7 and 8, or briefly 7&8. The constraint requires that their durations should add up to τ₇ + τ₈ ≤ 10 fs. [7,8].

Unfortunately, however, the plan cannot be realized, because of the following dilemma: Ulusoy and Nest’s “intermediate” excited states |1E_1u^y> and |1E_2g^x2−y2> are near-degenerate, cf. Figure 3. The narrow energy gap E_1E1u − E_1E2g = ℏω_1E1u,1E2g = 0.306 eV implies the rather long period T_1E1u,1E2g = 2π/ω_1E1g,1E2g = 13.52 fs, cf. Equation (45). The condition (47) thus requires that the second π laser pulse should take too long to transfer the “intermediate” excited state |1E_1u^y> into |1E_2g^x2−y2>. This is far beyond the upper limit, 10 fs, for the conservation of nuclear symmetry, i.e., for our purpose, it is unacceptable.

To overcome this problem, it is essential to get rid of the near degeneracy of the levels E_1E1u and E_1E2g. For this purpose, we decided that the “first” intermediate state |1E_1u^y> should be replaced by the more excited state |2E_1u^y> with much higher energy E_2E1u compared to E_1E1u. The corresponding sequence of two laser-induced target transitions is illustrated schematically by two sequential arrows in Figure 3. The previous near degeneracy is clearly lifted. Specifically, the energy gap between states |2E_1u^y> and |1E_2g^x2−y2> is E_2E1u − E_1E2g = 5.75 eV, with corresponding period T_2E1u,1E2g = 719 as. Likewise, the energy gap between states |2E_1u^y> and |1A_1g > is E_2E1u − E_1A1g = 14.23 eV, with period T_2E1u,1A1g = 291 as. These two periods are short enough to satisfy condition (47) for two laser pulses with durations τ₇ = 2.5 fs and τ₈ = 7.5 fs, respectively. Their durations add up to t_f = τ₇ + τ₈ = 10 fs, in accord with the constraint for the conservation of nuclear symmetry [7,8]. The smaller value of τ₇ compared to τ₈ is suggested by condition (47), due to the smaller value of T_2E1u,1A1g compared to T_2E1u,1E2g.

The replacement of the intermediate state |1E_1u^y> by the more excited state |2E_1u^y> with the same IRREP raises another problem, however, namely the absolute values of the y-components of the transition matrix element |<1A_1g|d_y|2E_1u^y>| = 0.161 e a₀ for the target transitions |1A_1g> → |2E_1u^y> via |2E_1uy> is significantly smaller than |<1A_1g|d_y|1E_1u^y>| = 2.339 e a₀ for Ulusoy and Nest’s transitions via |1E_1u^y>. At the same time, the required durations τ₇ = 2.5 fs and τ₈ = 7.5 fs are an order of magnitude smaller than the values used in Ref. [1]. Consequently, the conditions (46) and (48) for a hypothetical sequence of π/2 and π laser pulses for sequential transitions|1A_1g> → |2E_1u^y> → |1E_2g^x2−y2> call for exceedingly large field strengths and intensities—this is, again, unacceptable.

The way out of this dilemma is pointed by Ref. [2] which shows that for the present purpose, i.e., for laser-induced electron symmetry breaking, it is not really necessary to use π/2 and π laser pulses. Instead, it suffices to employ weaker pulses p = 7 and/or 8 which prepare superposition states such as c_e’1,1A1g(τ₇) |1A_1g> + c_e’1,2E1uy(τ₇) |2E_1u^y> and subsequently c_{e’1&e’1,1A1g}(t_f) |1A_1g> + c_{e’1&e’1,1E2g}(t_f) |1E_2g^x2−y2>, with rather small populations of the excited states compared to the ground states, P_e’1,2E1uy(τ₇) = |c_e’1,2E1uy(τ₇)|² « P_e’1,1A1g(τ₇) = |c_e’1,1A1g(τ₇)|² and P_{e’1&e’1,1E2g^x2-y2}(t_f) = |c_{e’1&e’1,1E2g^x2-y2}(t_f)|² « P_{e’1&e’1,1A1g}(t_f) = |c_{e’1&e’1,1A1g}(t_f)|². Consequently, we employ two sequential linearly e₇ = e₈ = e_y = e’₁ polarized laser pulses with durations τ₇ =2.5 fs and τ₈ = 7.5 fs, with the same form of the electric fields, Equation (1), as before, with the carrier frequencies slightly detuned from the resonance frequencies, yet with electric field strengths well below the values for hypothetical π/2 and π pulses. The electric fields $ℰ$_p(t) of the laser pulses p = 7, 8 are illustrated in Figure 9. The laser parameters are listed in the Figure 9. The resulting population dynamics are also shown in Figure 9.

Figure 9 shows that at the end (τ₇ = 2.5 fs) of the first e_p=7 = e’₁ = e_y polarized laser pulse p = 7, the oriented benzene is excited from the initial ground state |1A_1g> to the intermediate target superposition state c_e’1,1A1g(τ₇) |1A_1g> + c_e’1,1E1uy(τ₇) |1E_1u^y>, with populations P_e’1,1E1uy(τ₇) = |c_e’1,1E1uy(τ₇)|² = 0.105 « P_e’1,1A1g(τ₇) = |c_e’1,1A1g(τ₇)|² = 0.890. Subsequently, at t_f = τ₇ + τ₈ = 10 fs, the second e_p=8 = e’₁ = e_y polarized laser pulse p = 8 yields the superposition of three eigenstates (cf. Equation (16))

|Ψ_e’1&e’1(t_f = τ₇ + τ₈)> = c_{e’1&e’1,1A1g} (t_f) |1A_1g>
+ c_{e’1&e’1,2A1g} (t_f) |2A_1g> + c_{e‘1&e‘1,1E2g^x2-y2} (t_f) |1E_2g^x2−y2>

(51)

with populations P_{e’1&e’1,1A1g} (t_f) = |c_{e’1&e’1,1A1g} (t_f)|² = 0.664, P_{e’1&e’1,2A1g} (t_f) = |c_{e’1&e’1,2A1g} (t_f)|² = 0.225 and P_{e‘1&e‘1,1E2g^x2-y2} (t_f) = |c_{e‘1&e‘1,1E2g^x2-y2} (t_f)|² = 0.098. The subscript “e’₁&e’₁” indicates that the wavefunction (51) is prepared by a sequence of two polarized laser pulses with the same polarizations, e’₁ and again e’₁. The population of state |2A_1g> is added unexpectedly to those of the two target states |1A_1g> and |1E_2g^x2−y2>. However, this does not harm the present purpose. What matters for the new example of electron symmetry breaking is that the final state (51) is prepared as superposition of states which transform according to two different IRREPs—here this is A_1g (the same for states |1A_1g> and |2A_1g>) and E_2g^x2−y2 (for state|1E_2g^x2−y2>). Apparently, Figure 9 shows that the pulses p = 7 and 8 also cause transient populations of complementary states, in particular |1E_1u^y>. This is caused by non-linear effects—but this is irrelevant for the present purpose, and beyond the scope of this paper.

After the sequence of two laser pulses 7 and 8 with the same polarizations e’₁ and again e’₁, for times t ≥ t_f = τ₇ + τ₈ = 10 fs, the wavefunction (51) evolves in field-free environments, with coefficients specified in Equation (26). The corresponding swapping part of the one-electron densities ρ_e’1&e’1(r,t) − ρ_1A1g(r) is illustrated in Figure 10a by snapshots analogous to those shown in Figure 6, Figure 7 and Figure 8. Corresponding inspection and analyses of these snapshots reveal that ρ_e’1&e’1(r,t) displays charge migration with conservation of the symmetry elements of the subgroup D_2h,1 = {E,C₂,C₂’₁,C₂”₁,i,σ_h, σ_v1,σ_d1} of D_6h. Hence, as resume of the combined Figure 1 and Figure 10a, the series of two laser pulses 7 and 8, also called e’₁&e’₁ (Figure 9) yield electron symmetry breaking D_6h → S(ρ_e’1&e’1(r,t)) =D_2h,1 in the oriented model benzene, with conservation of nuclear symmetry. This is quite different from the six previous examples which are documented in the combined Figure 1 and Figure 6, Figure 7 or Figure 8.

Our last example of electron symmetry breaking in oriented benzene is achieved by another sequence of two laser pulses—this time they are labeled 7 and 9. The first laser pulse (p = 7) is the same as the first laser pulse in the previous series of laser pulses 7 and 8, cf. Figure 9. The second pulse (p = 9) has the same electric field as the previous pulse labeled p=8, i.e., $ℰ$_p=9(t) = $ℰ$_p=8(t), cf. Figure 9, but the laser polarization is e₉ = e”₁ = e_x instead of e₈ = e’₁ = e_y. Hence the series of laser pulses 7 and 9 will also be denoted e’₁&e”₁. The resulting population probabilities P_{e’1&e“1,m} (t) of eigenstates |m> are shown in Figure 9. Since the two series of laser pulses 7 and 8 and 7 and 9 employ the same first pulse (p = 7), they yield the same populations during the time 0 ≤ t < τ₇ = 2.5 fs of the first laser pulse. During the time τ₇ = 2.5 fs ≤ t ≤ t_f = τ₇ + τ₈ = τ₇ + τ₉ = 10 fs of the second pulses, p = 8 or 9, the equality of their electric fields $ℰ$_p=8(t) = $ℰ$_p=9(t) but orthogonality of the laser polarizations e₈ = e’₁ = e_y ⊥ e₉ = e”₁ = e_x yields the same populations P_{e’1&e“1,m”}(t) = P_{e’1&e’1,m’}(t) for the non-degenerate states |m”> = |m’> = |1A_1g> and |2A_1g>, but require proper modifications of the quantum numbers of the degenerate states, i.e., the series of pulses 7 and 8 excite the transient and final states |1E_1u^y> and |1E_2g^x2−y2> whereas pulses 7 and 9 excite |1E_1u^x> and |1E_2g^xy>, respectively. Accordingly, at the end (t = t_f = τ₇ + τ₉ = 10 fs) of the sequence of laser pulses 7 and 9, also called e’₁&e”₁, the oriented benzene is prepared in the superposition state

|Ψ_e’1&e”1(t_f = τ₇ + τ₈)> = c_{e’1&e”1,1A1g} (t_f) |1A_1g>
+ c_{e’1&e”1,2A1g} (t_f) |2A_1g> + c_{e‘1&e“1,1E2g^xy} (t_f) |1E_2g^xy>

(52)

with the same populations of the states |1A_1g>, |2A_1g>, |1E_2g^xy> as those (|1A_1g>, |2A_1g>, |1E_2g^x2−y2>) for pulses 7 and 8.

The field-free time evolution of the wave function (52) after the sequence laser pulses 7 and 9, also called e’₁&e”₁, i.e., for t ≥ t_f = 10 fs, yields the swapping one-electron density ρ_e’1&e’1(r,t) − ρ_1A1g(r) which is illustrated in Figure 10b by snapshots, analogous to those shown in Figure 10a for the laser pulses 7 and 8. They reveal a new type of charge migration, with the conservation of the symmetry elements of the subgroup C_2h = {E,C₂,i,σ_h} of D_6h. Hence, as a result of the combined Figure 1 and Figure 10b, the series of laser pulses 7 and 9 with polarizations e’₁ and e”₁ (Figure 9) yield electron symmetry breaking D_6h → S(ρ_e’1&e”1(r,t)) = C_2h in the oriented model benzene, with the conservation of nuclear symmetry.

To summarize, all the different electron symmetry breakings D_6h → S(ρ_p(r,t)) from the point group G = D_6h to different subgroups S(ρ_p(r,t)) of G, p = 1, …, 9 are achieved by means of different linearly polarized laser pulses, or two sequential laser pulses, which excite the initial electronic ground state |1A_1g> to different superpositions (16) of the electronic ground state plus one (p = 1, …, 6) or two different excited states (p = 7&8 and 7&9). An important common property of the different sets of the electronic ground and excited states which constitute the different superpositions is that (at least) two of them have different IRREPs, e.g., A_1g and E_1u or A_1g and E_2g. In the case of doubly degenerate IRREPs, preparations of superposition states with different sets of basis functions yield different point subgroups S(ρ_p(r,t)) of G.

3.2. Electron Symmetry Breaking and Charge Migration Induced by Linearly Polarized Laser Pulses in Oriented Mg-Porphyrin with D_4h Nuclear Scaffold

This Section heightens the impression which was gained in the previous Section 3.1, namely different well designed short linearly polarized laser pulses labeled p = 1, 2, 3, … can achieve different types of charge migrations with different electron symmetry breakings, from the point group of the electronic ground state G to various subgroups S(ρ_p(r,t)) of G. For this purpose, we present additional examples, with applications to another oriented molecule with nuclear point group symmetry G different from D_6h. Specifically, we choose oriented Mg-porphyrin with G = D_4h, cf. Figure 2 and Figure 4, and demonstrate different electron symmetry breakings D_4h→ S(ρ_p(r,t)) by means of different linearly polarized laser pulses. The oriented model Mg-porphyrin is suggested by Ref. [15] which discovers the stimulation of a specific type of charge migration, namely electron circulation, by means of a circularly polarized laser pulse. As a byproduct, Ref. [15] has a series of snapshots of the time-dependent one-electron density after the laser-pulse. In retrospect, those snapshots clearly document electron symmetry breaking D_4h → C_s = {E, σ_h} by a short laser pulse, with the conservation of the nuclear symmetry D_4h. However, this effect was not noted in Ref. [15]—the word “symmetry” is not even mentioned therein. In contrast with Ref. [15], here we are heading for the explicit discovery of electron symmetry breaking D_4h → S(ρ_p(r,t)) in oriented Mg-porphyrin, by means of selective linearly polarized laser pulses. The effects are analogous to those for D_6h → S(ρ_p(r,t)) electron symmetry breaking in oriented benzene, as documented in Section 3.1. This analogy allows a rather brief presentation of the results for Mg-porphyrin, without any repetition of the detailed derivations of Section 3.1. Moreover, we restrict the presentation to just two cases of electron symmetry breaking D_4h → S(ρ_p(r,t)) by means of two different laser pulses labeled p = 1, 2. The rich examples D_6h → S(ρ_p(r,t)), p = 1, …, 9, for benzene should then suffice to stimulate the reader’s imagination to invent additional cases, also for oriented Mg-porphyrin.

As in Section 3.1, we start with the demonstration of electron symmetry breaking in oriented Mg-porphyrin, by means of a e_p=1 = e_x = e’₁ polarized re-optimized π/2 laser pulse. The laser pulse labeled p = 1 has the familiar form of the electric field $ℰ$_p=1(t), Equation (1). It is illustrated in Figure 11, with the laser parameters in Figure 11. The resulting population dynamics are also shown in Figure 11. Apparently, the first laser pulse p = 1 with duration τ₁ = 10 fs excites the oriented Mg-porphyrin from the initial (t = 0) electronic ground state |1A_1g> to the superposition state $\left(1/\sqrt{2}\right)$*(|1A_1g> + |2E_u^x>). The notation |2E_u^x> refers to the doublet {|2E_u^x>, |2E_u^y>} ≡ {|2E_u’₁>, |2E_u’₂>} of two orthogonal degenerate states with IRREP E_u with the second-lowest energy E_2Eu which transform as x and y, respectively [13]. The target transitions is illustrated schematically by the vertical arrow from the energy level E_1A1g to E_2Eu in Figure 4. The energy gap between their eigenenergies is ΔE_1A1g,2Eu = E_2Eu − E_1A1g = 3.60 eV with corresponding transition frequency ω_1A1g,2Eu = ΔE_1A1g,2Eu /ℏ and period T = T_1A1g,2Eu = 2π/ω_1A1g,2Eu = h/ΔE_1A1g,2Eu = 1.147 fs, cf. Equations (42) and (43).

The subsequent (t ≥ τ₁ = 10 fs) time evolution of the swapping one-electron density ρ_p=1(r,t) − ρ_1A1g(r) is illustrated in Figure 12a by three snapshots, analogous to the previous Figure 6 for oriented benzene. Apparently, the oriented Mg-porphyrin exhibits periodic charge migration from the left to the right, and back, with period T. Analogous inspection and analyses show that the migrating one-electron density conserves three symmetry elements, namely C₂’₁, σ_h, σ_v1, cf. Figure 2. Accordingly, the combined Figure 2 and Figure 12a document electron symmetry breaking induced by the e’₁ polarized laser pulse p = 1, namely D_4h → S(ρ_p=1(r,t)) = C_2v’₁ = {E, C₂’₁, σ_h, σ_v1}.

The second example for electron symmetry breaking in oriented Mg-porphyrin employs another re-optimized π/2 laser pulse labeled p = 2. It has the same electric field as the first pulse p = 1, i.e., $ℰ$₂(t) = $ℰ$₁(t), cf. Figure 11, but different polarization e₂ = e”₁ = (1/√2)* (e_x +e_y) = C₈ e”₁. It prepares the superposition state (1/√2)*(|1A_1g> + |2E_u”₁>], analogous to the superposition state (1/√2)*(|1A_1g> + |2E_u’₁>] which is prepared by the e’₁ polarized pulse p = 1. The e’₁ (p = 1) and e”₁ (p = 2) polarized pulses yield the same population dynamics, cf. Figure 11. The periodic charge migration which is initiated by the e”₁ (p = 2) polarized pulse is illustrated in Figure 12b. It has the same period T as for the charge migration initiated by pulse p = 1, but it is from the lower left to the upper right of the oriented scaffold, and back. Apparently, it conserves three symmetry elements, namely C₂”₁, σ_h, σ_d1, cf. Figure 2. Accordingly, the combined Figure 2 and Figure 12b document electron symmetry breaking induced by the e”₁ polarized laser pulse p = 2, namely D_4h→ S(ρ_p=2(r,t)) = C_2v”₁ = {E, C₂”₁, σ_h, σ_d1}.

The summary of this Section 3.2 with application to oriented Mg-porphyrin is analogous to the summary for Section 3.1 for oriented benzene. Different electron symmetry breakings D_4h → S(ρ_p(r,t)) from the point group G = D_4h to different subgroups S(ρ_p(r,t)) of G, p = 1, 2 are achieved by means of different linearly polarized laser pulses which excite the initial electronic ground state |1A_1g> to different superpositions (16) of the electronic ground state plus an excited state with different IRREP E_u. Preparations of superposition states with different basis functions yield different point subgroups S(ρ_p(r,t)) of G.

3.3. Symmetry of One-Electron Densities of Superposition States in Oriented Benzene

Section 3.1 shows that different short laser pulses, or two sequential laser pulses with linear polarization(s) e and with total durations t_f = 10 fs, initiate different charge migrations in the oriented benzene which are represented by different one-electron densities ρ_e(t > t_f) with different electron symmetries S(ρ_e(t)) depending on e. All those electron symmetry breakings G = D_6h → S(ρ_e(t)) conserve nuclear symmetry D_6h. Until now, the symmetries S(ρ_e(t)) were determined by inspection of the symmetry elements of G which are conserved in ρ_e(t > t_f).

The purpose of this Section is to derive a recipe for the rigorous determination of the subgroup S(ρ_e(t > t_f)), starting from the superposition state (16) which was prepared by the laser pulse, or two sequential laser pulses with polarization(s) e, without any empirical inspection of the symmetry elements of ρ_e(t). For this purpose, to simplify the notation, we rewrite the superposition state (16) as

|Ψ_e(t > t_f)> ≡ |Ψ> = Σ_m c_m |m> = ΣΣ_n,k c_n,k |n,k> = Σ_k|Ψ_k>

(53)

i.e., we keep in mind that the wavefunctions |Ψ> and |Ψ_k> as well as the expansion coefficients c_m and c_n,k depend on the laser polarization(s) e and on the time after the laser pulse, t > t_f, cf. Equation (26), but this dependence is no longer written explicitly. Equation. (53) also replaces the energy quantum number m by two quantum numbers n,k. Here, k denotes the IRREP Γ_m = Γ_k of the basis function |m> = |n,k> ≡ |n, Γ_k >, and n specifies the energetic order of the basis functions with IRREP Γ_k. The wave functions

|Ψ_k> = Σ_n c_n,k |n, Γ_k >

(54)

in Equation (53) are in general linear combinations of basis functions |n, Γ_k > which have the same IRREP Γ_k and non-zero coefficients c_n,k. The wave function |Ψ> and the basis functions |m> = |n, Γ_k > in Equations (53) and (54) are normalized, whereas the |Ψ_k> are not normalized. In fact, normalization of the |Ψ_k> is not necessary, for the present purpose.

The derivation of the subgroup S(ρ_e(t > t_f)) of the one electron density for t > t_f after the laser pulse(s) with polarization(s) e proceeds in three steps, cf. Appendix A: First we determine the subgroup S(|Ψ_e(t > t_f)>) of the superposition state (53). Next we derive the subgroup S(Ψ_e(t > t_f)^* Ψ_e(t > t_f)) of the electron density Ψ_e(t > t_f)^* Ψ_e(t > t_f), and finally the target subgroup S(ρ_e(t > t_f)) of the one-electron density ρ_e(t > t_f). The derivations are general, in principle, but the presentation focuses on the present applications (cf. Section 3.1) where the laser pulses prepare superposition states (16), (53) with non-vanishing contributions of the ground state |1A_1g> plus possibly excited states |nA_1g> with the same IRREP A_1g plus one excited basis function |n,k> ≡ |n, Γ_k ≠A_1g > with IRREP Γ_k ≠A_1g, thus

|Ψ_e(t > t_f)> ≡ |Ψ_A1g> +|Ψ_{Γk ǂ A1g}>.

(55)

The Appendix A proves that for such cases (and also for various other cases), the subgroups are all identical,

S(ρ_e(t > t_f)) = S(Ψ_e(t > t_f)^* Ψ_e(t > t_f)) = S(|Ψ_e(t > t_f)>),

(56)

and the IRREP of ρ_e(t > t_f) in the subgroup S(ρ_e(t > t_f)) is always the totally symmetric one. For this reason, the subsequent presentation focuses on the derivation of the subgroup S(|Ψ_e(t > t_f)>). Once S(|Ψ_e(t > t_f)>) is determined, the theorem (56) tells us that the target subgroup S(ρ_e(t > t_f)) is the same as S(|Ψ_e(t > t_f)>).

The general theory is presented in Appendix A. It ends up with a simple recipe. It is demonstrated here for the cases which were presented in Section 3.1. The results are summarized in Table 3. This Table 3 may be recognized as a collection of special parts of the character tables of the subgroups S(|Ψ_e(t > t_f)>) of the superpositions |Ψ_e(t > t_f)>, Equation (55), namely for the characters of the totally symmetric IRREPs. These characters are all equal to 1. Thus Table 3 lists the number “1” for all symmetry operations g ϵ S(|Ψ_e(t > t_f)>). Turning the table, the task is to determine the symmetry elements g with “marks 1” in Table 3. These sets of symmetry operations identify the subgroups S(|Ψ_e(t > t_f)>). At the same time, the theorem (56) for superpositions (55) makes those subgroups S(|Ψ_e(t > t_f)>) equal to the target subgroup S(ρ_e(t > t_f)) of the one-electron density ρ_e(t > t_f).

Here we present step-by-step applications of the general theory (cf. Appendix A) to two (out of eight) examples which were presented in Section 3.1. Table 3 also lists analogous results for the other six cases of Section 3.1, and also for the non-aromatic states (49), (50) of the oriented benzene which are prepared by three linearly polarized laser pulses or by re-optimized laser pulses designed by Ulusoy and Nest [1].

Our first example is for the electronic superposition state |Ψ_e”1(t > t_f)> = c_e”1,A1g(t) |1A_1g> + c_e”1,1E1ux(t) |1E_1u^x> which is prepared by the e”₁ = e_x polarized π/2 laser pulse shown in Figure 5, cf. Section 3.1. Using the simplified notation of Equations (53) and (55), this superposition state is rewritten

|Ψ> = |A_1g> + |E_1u^x>.

(57)

It consists of two partial waves with IRREPs A_1g and E_1u^x of the group G=D_6h. According to the general theory (cf. Appendix A), the subgroup S(|Ψ>) of |Ψ> is the subset of the symmetry operations g of G which satisfy the same symmetry properties for all components,

S(|Ψ>) = {g ϵ G| g|Ψ_k> = χ(g) |Ψ_k>}

(58)

with the same characters χ(g) for all wave functions |Ψ_k> in the expansion (53). In the present case (57), S(|Ψ>) consists of all g which satisfy g|A_1g> = χ(g) |A_1g> as well as g|E_1u^x> = χ(g) |E_1u^x >. The characters χ(g) of the totally symmetric IRREP A_1g are all equal to 1. Hence the operations g of G must satisfy the symmetry property g|E_1u^x> =|E_1u^x >,

S(|Ψ>) = {g ϵ G| g|E_1u^x> =|E_1u^x >} for the case (57).

(59)

Since the electronic wave function |E_1u^x > transforms as x, the operations g of G must satisfy g x = x, or g e_x = e_x. There are only four operations g of G which map x on x, or the unit vector e_x on e_x, namely g = E, C₂₁”, σ_h and σ_d1, cf. Figure 1. The set of operations {E, C₂₁”, σ_h, σ_d1} is the subgroup C_2v”_1, cf. Table 1. Hence S(|Ψ>) = C_2v”₁. Accordingly, the entry |Ψ> = |A_1g> + |E_1u^x> in Table 3 marks the characters “1” for the operations g = E, C₂₁”, σ_h and σ_d1, and these yield the subgroup S(|Ψ>) = C_2v”₁ with totally symmetric IRREP A_1g. The theorem (56) implies that the corresponding one-electron density ρ_e(t > t_f) has the same symmetry C_2v”₁.

Our second example is for the superposition state |Ψ_e’1&e”1(t >t_f)> = c_{e’1&e”1,1A1g} (t) |1A_1g> + c_{e’1&e”1,2A1g} (t) |2A_1g> + c_{e‘1&e“1,1E2g^xy} (t) |1E_2g^xy>, cf. Equation (52), which is prepared by the series of two laser pulses with different polarizations e’₁ and e”₁, cf. Figure 9. Using again the simplified notation of Equations (53) and (55), this superposition state is rewritten

|Ψ> = |A_1g> + |E_2g^xy>.

(60)

where

|A_1g> = c_{e’1&e”1,1A1g} (t) |1A_1g> + c_{e’1&e”1,2A1g} (t) |2A_1g>,
|E_2g^xy> = c_{e‘1&e“1,1E2g^xy} (t) |1E_2g^xy>.

(61)

It consists of two partial waves with IRREPs A_1g and E_2g^xy of the group G=D_6h. According to the general theory (cf. Appendix A), and by analogy with the first example, the subgroup S(|Ψ>) of |Ψ> is the subset of the symmetry operations g of G which satisfy the symmetry property g|E_2g^xy> =|E_2g^xy>,

S(|Ψ>) = {g ϵ G| g|E_2g^xy> =|E_2g^xy>} for the case (60).

(62)

Since the electronic wave function |E_2g^xy > transforms as xy, the operations g of G must satisfy g xy = xy. There are only four operations g of G which map xy on xy, namely g = E, C₂^z, i and σ_h, cf. Figure 1. The set of operations {E, C₂^z, i, σ_h} is the subgroup C_2h, cf. Table 1. Hence S(|Ψ>) = C_2h. Accordingly, the entry |Ψ> = |A_1g> + |E_2g^xy> in Table 3 marks the characters “1” for the operations g = E, C₂^z, i, σ_h, and these yield the subgroup S(|Ψ>) = C_2h with totally symmetric IRREP A_g. The theorem (56) implies that the corresponding one-electron density ρ_e(t > t_f) has the same symmetry S(ρ_e(t > t_f)) = C_2h.

To summarize, the applications of the general theory (cf. Appendix A) to the cases (57) and (60) demonstrate a simple recipe for the approach from the laser-driven electronic superposition state (53) via its symmetry subgroup (58) to the same symmetry subgroup of the one-electron density. The same approach can be applied to all other cases which were presented in Section 3.1. The resulting electron symmetry breakings due to laser pulses p are also listed in Table 3. They are in perfect agreement with the empirical results which were obtained in Section 3.1, by inspection of the symmetry elements of the one-electron densities.

Table 3 also presents analogous results for the symmetry subgroups of the one-electron densities of two non-aromatic superposition states (49) and (50) which are prepared by laser pulses designed by Ulusoy and Nest [1]. Accordingly, our result S(|A_1g> + |B_1u>) = D_3h’ for the superposition state |A_1g> + |B_1u> and for its one-electron density confirms their assignment. However, for the other case, our approach yields S(|A_1g> + |B_2u>) = D_3h”, different from their result D_3d [1]. In retrospect, close inspection of their cartoons of the one-electron density and of the corresponding Lewis structures verifies the present result.

3.4. Symmetry of One-Electron Densities of Superposition States in Oriented Mg-Porphyrin

This Section for the derivation of the symmetries of one-electron densities of laser-driven superposition states in oriented Mg-porphyrin (D_4h) is entirely analogous to the corresponding Section 3.3 for oriented benzene (D_6h). The previous Section 3 has detailed presentations of two applications of the general theory (cf. Appendix A) to two different superposition states which are prepared by a linearly polarized laser pulse, or by two sequential linearly polarized pulses, as illustrated in Figure 5 and Figure 9, respectively, cf. Section 3.1. The results are summarized in Table 3, together with the results for six additional cases. The present Section 3.4 summarizes the corresponding results for four applications to laser-driven superposition states in Mg-porphyrin in Table 4, complemented by the analogous step-by-step presentation of one example.

Specifically, let us derive the symmetry subgroup of the one-electron density of the superposition state |Ψ_e’1(t > t_f)> = c_e’1,A1g(t) |1A_1g> + c_e’1,1Eux(t) |1E_u^x> which is prepared by the e’₁ = e_x polarized π/2 laser pulse shown in Figure 11, cf. Section 3.2. Using the simplified notation of Equations (53) and (55), this superposition state is rewritten

|Ψ> = |A_1g> + |E_u^x> ≡ |A_1g> + |E_u1’>

(63)

It consists of two partial waves with IRREPs A_1g and E_u^x ≡ E_u1’ of the group G = D_4h; the two equivalent notations remind of the two notations of the laser polarizations, e_x = e’₁. According to the general theory (cf. Appendix A) and its application in Section 3.3, the symmetry subgroup S(|Ψ>) of the wavefunction (63) consists of the operations g of G which satisfy the symmetry property g|E_u^x> =|E_u^x>,

S(|Ψ>) = {g ϵ G| g|E_u^x> =|E_u^x >} for the case (63).

(64)

Since the electronic wave function |E_1u^x > ≡ |E_u1’> transforms as x, the operations g of G must satisfy g x = x, or g e’₁ = e’₁. There are four operations g of G which map x on x, or the unit vector e’₁ on e’₁, namely g = E, C₂₁’, σ_h and σ_v1, cf. Figure 2. Accordingly, the entry |Ψ> = |A_1g> + |E_u1’> in Table 4 marks the characters “1” for the operations g = E, C₂₁’, σ_h and σ_v1, and these yield the subgroup S(|Ψ>) = C_2v’₁ with totally symmetric IRREP A_1g. The theorem (56) implies that the corresponding one-electron density ρ_e’1(t > t_f) has the same symmetry C_2v’₁. Table 4 summarizes this result, together with three additional applications. The empirical results which were derived by inspection of the symmetry elements of the one-electron densities of two laser-driven superposition states in Section 3.2 (cf. Figure 12) are confirmed by the group-theoretical results of Table 4.

Table 4 also comprises the results for two cases of electron symmetry breaking in the oriented Mg-porphyrin which have not been demonstrated in Section 3.2. We use these cases to explain two applications of the general approach (cf. Appendix A) which was exemplified in Section 3.3 and Section 3.4. First, it provides an efficient and firm method to determine the subgroup S(ρ_e(t > t_f)) of electron symmetry breaking G → S(ρ_e(t > t_f)) by a laser pulse. As example, consider the (hypothetical) preparation of the superposition state |Ψ_e”2(t > t_f)> = c_e”2,A1g(t) |1A_1g > + c_{e”2,1Eu2”}(t) |1E_u2” > by means of a e”₂ polarized π/2 laser pulse, labeled p = 3. It would represent a new type of charge migration. The traditional way of determining the related electron symmetry breaking G = D_4h → S(ρ_e”2(t > t_f)) would cost quantum dynamics simulations of the laser excitation |1A_1g> → |Ψ_e”2(t > t_f)>, calculation of the one-electron density ρ_e”2(t > t_f), an inspection of ρ_e”2(t > t_f) to determine the symmetry elements of G which are conserved in ρ_e”2(t > t_f), and finally, the determination of the subgroup S(ρ_e”2(t > t_f)) as the set of the corresponding symmetry operations, cf. Section 3.1 and Section 3.2. In contrast, the recipe which was exemplified in Section 3.3 and Section 3.4 just calls for rewriting the target wavefunction as

|Ψ_e”2(t > t_f)> = |Ψ> = |A_1g> +|E_u2”>

(65)

and then to determine the symmetry group of this wavefunction as the set of symmetry operations g which satisfy g |E_u2”> =|E_u2”>. The recipe of Section 3.3 and Section 3.4 yields the result

S(ρ_e”2(t > t_f)) = S(|Ψ_e”2(t > t_f)>) = {g ϵ D_4h| g |E_u2”> =|E_u2”>}
 = {g=E,C₂”_2, σ_h, σ_d2} = C_2v”₂

(66)

without any inspection of the one-electron density ρ_e”2(t > t_f), cf. Table 4.

The second application is for laser control of electron symmetry. This task is motivated, e.g., by the Woodward–Hoffmann rules for the control of chemical reactions by preparations of the reactants with different electron symmetries in the electronic ground and excited states [35]. For example, let us assume that the goal is to design the laser pulse, or series of laser pulses with total duration t_f ≤ 10 fs and polarization(s) e which achieve(s) electron symmetry breaking G = D_4h → S(ρ_e(t > t_f)) = C_2v’₂ in the oriented Mg-porphyrin. The recipe of Section 3.3 and Section 3.4 suggests that for this purpose, the laser pulse(s) should prepare the superposition state

|Ψ_e(t > t_f)> = |Ψ> = |A_1g> +| Γ_k >

(67)

which consists of basis functions with IRREP A_1g and another IRREP Γ_k ǂ A_1g such that

S(ρ_e(t > t_f)) = S(|Ψ_e(t > t_f)>) = {g ϵ D_4h| g | Γ_k > =| Γ_k >} = C_2v’₂
 = {g=E, C₂‘₂, σ_h, σ_v2}

(68)

cf. Table 1 and Table 4 and Figure 2.

The first challenge then is to determine the IRREP Γ_k of the wavefunction | Γ_k > which satisfies Equation (68). For this purpose, one should check the D_4h character Table for the characters for the one-dimensional (1d) IRREPs and—in the case of 2d IRREPs—also the diagonal elements of the 2 × 2 representation matrices for all symmetry operations of D_4h, see, e.g., Ref. [13]. The target IRREP Γ_k must have characters or diagonal elements of the representation matrices equal to “1” precisely for the symmetry elements {g=E,C₂‘_2, σ_h, σ_v2}. Table 4 shows that this condition is satisfied exclusively by the basis function |nE_u2’> for IRREP Γ_k = E_u. Hence the wavefunction | Γ_k > in the target superposition state (67) should be a linear combination of basis functions |nE_u2’>. Likewise, the other wavefunction | A_1g > in the superposition state (67) should be a linear combination of basis functions |nA_1g>. These two conditions for Equation (67) allow many choices. The simplest linear combination is

|Ψ_e(t > t_f)> = |A_1g> +| Γ_k > = c_e,1A1g |1A_1g> + c_e,1Eu2’ |1E_u2’>

(69)

with time-dependent coefficients, cf. Equation (26).

The second challenge is to design the laser pulse, or series of laser pulses, with polarization(s) e which prepares the target state (69), within less than t_f = 10 fs. Again, there is no unique solution for this task. In the present case, experience with |Ψ_e’1(t > t_f) > = c_e1’,1A1g|1A_1g > + c_e1’,Eu1’|1E_u1’ > (cf. Section 3.2, Figure 11) suggests that one should employ the corresponding π/2 laser pulse, labeled p = 4, with polarization e₄ = e’₂ = e_y and with the same electric field $ℰ$(t) as the one shown in Figure 11.

3.5. Symmetry of One-Electron Densities of Oriented Molecules Driven by One or Several Linearly Polarized Laser Pulses

The previous Section 3.1, Section 3.2, Section 3.3 amd Section 3.4 contain ten plus four examples of electron symmetry breaking G → S(ρ_e(t > t_f)) by short (t_f = 10 fs) laser pulses, or two sequential laser pulses with polarizations e in the oriented benzene (G = D_6h) and Mg-porphyrin (G = D_4h). The results are summarized in Table 3 and Table 4. Comparison with Table 2 reveals the rule

S(H_e(t)) ⊆ S(ρ_e(t > t_f)) = S(|Ψ_e(t > t_f)) ⊆ G

(70)

The corresponding orders |...| of the groups and subgroups satisfy

|S(H_e(t))| ≤ |S(ρ_e(t > t_f))| = |S(|Ψ_e(t > t_f))| ≤ |G|.

(71)

The equality in the middle of relations (70), (71) is adapted from Equation (56). It holds for superposition states (53) which are prepared by the laser pulse(s) such that they contain the ground state and/or an excited basis function with the IRREP A_1g of the initial state, plus one (or more) excited states with different IRREPs, see, e.g., Equation (55) and all the examples in Table 3 and Table 4.

The right hand side of the relations (70), (71) simply means that S(ρ_e(t > t_f))=S(|Ψ_e(t > t_f)>) is a subgroup of G. It may even be the same as G: In this case, the laser pulse does not break the symmetry G at all. This may be called the “largest case”, i.e., |S(ρ_e(t > t_f))| = |S(|Ψ_e(t > t_f)>)| = |G|. This case holds for well-designed sequences of laser pulses with polarization vectors e which break and restore electron symmetry [2,3,4], or which induce attosecond charge migration represented by superpositions of electronic eigenstates with the same IRREP as the ground state, see, e.g., Refs. [36,37,38]. The left hand side of the relations (70) and (71) is an important restriction. It means that the subgroup S(ρ_e(t > t_f)) = S(|Ψ_e(t > t_f)) of laser-broken electron symmetry must contain the subgroup S(H_e(t)) of the time-dependent electronic Hamiltonian of the molecule interacting with the laser pulse(s), cf. Section 2.5 and Table 2. The subgroup S(ρ_e(t > t_f)) = S(|Ψ_e(t > t_f)) may even be the same as S(H_e(t)). This may be called the “smallest case”, i.e., |S(ρ_e(t > t_f))| = |S(|Ψ_e(t > t_f))| = |S(H_e(t))|. In general, however, the order of the subgroup S(ρ_e(t > t_f)) = S(|Ψ_e(t > t_f)) can be larger than S(H_e(t)), and smaller than G. Comparison of all results in Table 3 and Table 4 with Table 2 confirm the rule (70) and (71) for all ten plus four examples of Section 3.1, Section 3.2, Section 3.3 and Section 3.4

The purpose of this Section 3.5 is to prove the relation (70), and to discuss some consequences. The proof of the equality in the middle of relation (70) is in Appendix A, cf. Equation (56). The right-hand side of the relations (70) and (71) is proven by empirical evidence: The previous investigations [2,3,4] show that series of two laser pulses with the same polarizations can break and restore the original symmetry of the electronic ground state. From the viewpoint of this paper, Refs. [2,3,4] present the “largest cases” where S(ρ_e(t > t_f)) = S(|Ψ_e(t > t_f)) = G.

For the proof of the left-hand side of the relations (70) and (71), we use the fact that the Hamilton operator H_e(t) commutes with the group elements g ϵ S(H_e(t))

[H_e(t), g] = 0 for g ϵ S(H_e(t))

(72)

cf. Section 2.5, Equations (11) and (13). The initial (t = 0) wavefunction is the electronic ground state, Equation (15). Since it is totally symmetric with respect to all symmetry elements of the group G,

g |Ψ_e(t=0)> = g |1A_1g> = |1A_1g> = |Ψ_e(t = 0)> for g ϵ S(H_e(t)).

(73)

After the laser pulse (t > t_f), the laser-driven wave function has evolved to

|Ψ_e(t)> = U_e(t) |Ψ_e(t = 0)>

(74)

with time evolution operator

$${\mathrm{U}}_{\mathbf{e}}(\mathrm{t}) = \widehat{T} \exp [-\mathrm{i} {\int }_0^{\mathrm{t}} \mathrm{d}{\mathrm{t}}^{\prime } {\mathbf{H}}_{\mathbf{e}}({\mathrm{t}}^{\prime })/\mathsf{\hslash }]$$

(75)

cf. Equation (25). Since the symmetry operations g ϵ S(H_e(t)) commute with H_e(t), cf. Equation (72), they also commute with U_e(t). Hence

g |Ψ_e(t)> = g U_e(t) |Ψ_e(t = 0)>
  = U_e(t) g |Ψ_e(t = 0)>
  = U_e(t)|Ψ_e(t = 0)>
  = |Ψ_e(t)> for g ϵ S(H_e(t)).

(76)

This means that |Ψ_e(t)> has at least the symmetry S(H_e(t)) of the time-dependent Hamilton operator H_e(t). However, at times t ≥ t_f after the laser pulse, the relation (76) may also hold for additional group elements g^~ ϵ G which do not belong to S(H_e(t)). Let S(|Ψ_e(t > t_f)>) = {g, g^~} be the subgroup of G which contains the elements g ϵ S(H_e(t)) and g^~ ∉ S(H_e(t)) which satisfy the relation (76). Now there may be two cases: either there are such “additional elements” g^~, or not. Accordingly, either |S(H_e(t))| = |S(|Ψ_e(t > t_f))| and S(H_e(t)) = S(|Ψ_e(t > t_f)), or |S(H_e(t))| < |S(|Ψ_e(t > t_f))| and S(H_e(t)) ⊆ S(|Ψ_e(t > t_f)), respectively. This completes the proof of the left hand side of the relations (70) and (71). In any case, the IRREP of |Ψ_e(t)> is always the totally symmetric IRREP of the subgroup S(|Ψ_e(t)>), because all elements g ϵ S(H_e(t)) and the other ones (if any) g^~ satisfy the equation (76), i.e., all the characters of |Ψ_e(t)> are equal to 1.

The rule (70) and (71) has (at least) two consequences, not only for the present examples, electron symmetry breaking by short (typically t_f ≤ 10 fs) laser pulses, or two sequential laser pulses with polarization(s) e in the oriented benzene of Mg-porphyrin, but by analogy also in other oriented molecules with symmetry group G of the nuclear scaffold. On the one hand, if one starts from the electronic ground state with totally symmetric IRREP and applies laser pulse(s) with polarization vector(s) e, then the knowledge of the symmetry S(H_e(t)) of the time-dependent electronic Hamilton operator H_e(t) of the molecule interacting with the laser pulse(s) (in semiclassical dipole approximation), does not suffice to determine the electron symmetry breaking G → S(ρ_e(t > t_f)) = S(|Ψ_e(t > t_f)). On the other hand, one has some important information about S(ρ_e(t > t_f)) = S(|Ψ_e(t > t_f)), namely it has to be a subgroup of G, and it must contain the symmetry group S(H_e(t)) as a subgroup. For example, if one applies an e = e_y = e₁’ polarized laser pulse (or series of pulses) on the oriented benzene, then S(H_e(t)) = C_2v’₁, cf. Table 2. Hence it is impossible to design any electric fields $ℰ$(t) of e_y polarized laser pulses which would achieve electron symmetry breakings D_6h → C_s, C₂, or C_i because these hypothetical target subgroups have order 2, below the order 4 of S(H_e(t)), which is the minimum according to the rule (71). Instead, there is a large variety of possible symmetry breakings D_6h → S(ρ_e(t > t_f)) = S(|Ψ_e(t > t_f)) which satisfy the rule (70), (71), from the “smallest” case S(ρ_e(t > t_f)) = S(|Ψ_e(t > t_f)) = C_2v’₁ (cf. Table 3, entry for |Ψ_e(t > t_f)> = |A_1g> + |E_1u^y>) via larger subgroups D_2h,1 (cf. Table 3, |Ψ_e(t > t_f)> = |A_1g> + |E_1u^x2−y2>) or D_3h’ (cf. Table 3, |Ψ_e(t > t_f)> = |A_1g> + |B_1u>) to G = D_6h, in the extreme case of symmetry restoration—these examples are all in accord with the rule (70), (71). Likewise, if one applies an e = e_x = e₁” polarized laser pulse (or series of pulses) on the oriented benzene, then S(H_e(t)) = C_2v”₁, and the rule (70), (71) again opens many possibilities, from the smallest possible subgroup C_2v”₁ (cf. Table 3, entry for |Ψ_e(t > t_f)> = |A_1g> + |E_1u^x>) via the larger subgroup D_3h” (cf. Table 3, |Ψ_e(t > t_f)> = |A_1g> + |B_2u>) to G = D_6h. However, the rule (70), (71) also excludes many hypothetical cases, not only the subgroups of order 2 which must be discarded because this is below the order 4 of the minimum group C_2v”₁, but also larger ones such as D_3d’ or D_3d^”—such symmetry groups (suggested in Ref. [1]) are excluded because they do not contain the subgroup S(H_e(t)) = C_2v”₁, i.e., they violate the theorem (70).

4. Conclusions

This work does not only confirm the discovery of Refs. [1,2,3,4,5], namely short laser pulses, or series of laser pulses can break electron symmetry during attosecond charge migration while conserving the symmetry group G of the nuclear scaffold, but it provides also important extensions:

(a)

Specific designs of laser pulses with selective polarization vectors and electric fields yield a large variety of electron symmetry breakings, from the original symmetry point group G of the electron density for the electronic ground state to various subgroups of G for excited superposition states. This is demonstrated here by eight plus four examples for different laser pulses applied to oriented benzene and Mg-porphyrin, cf. Table 3 and Table 4, respectively. The target subgroups of the electron symmetry breaking are determined by two different approaches. First, the laser pulse(s) induce(s) intramolecular charge migration which is represented by the time-dependent one-electron density. Its symmetry can be determined by inspection of its symmetry elements, cf. Section 3.1 and Section 3.2 and Figure 6, Figure 7 and Figure 8, Figure 10 and Figure 12. Alternatively, the symmetry subgroup can be determined by means of a systematic group-theoretical approach which is developed in Appendix A and exemplified in Section 3.3 and Section 3.4. The results of the two approaches agree perfectly with each other.

(b)

One can make use of this variety (a) for laser control of electron symmetry.

(c)

Laser control of electron symmetry is, however, not ad libitum: For any chosen polarization(s) of the laser pulse, or series of laser pulses, the target electron symmetry must obey the theorem (70), (71), cf. Section 3.5, which means it must be a subgroup of G, and it must contain the symmetry elements of the symmetry group of the time-dependent electronic Hamiltonian for the oriented molecule interacting with the laser pulse. All examples in Table 3 and Table 4 in Section 3.3 and Section 3.4 satisfy this rule. It may also be used to check previous assignments of laser-driven symmetry breakings, see the discussion at the end of Section 3.5.

In retrospect, electron symmetry breaking can also be recognized in snapshots of the laser-driven one-electron densities presented in various previous publications, see, e.g., Refs. [15,36,39], but those publications centered attention on different phenomena, without any analyses or any methods for rigorous assignments of the laser-selective symmetry breaking from the original molecular point group G to specific subgroups.

The present advances should stimulate various additional extensions of the field:

(d)

The present examples are for linearly polarized laser pulses which prepare superpositions of electronic basis functions with two different IRREPs. One of these IRREPs is the totally symmetric one, cf. Table 3 and Table 4 in Section 3.3 and Section 3.4. This scenario makes the symmetry of the superposition state equal to the symmetry of the one-electron density, and this facilitates the applications. The general group-theoretical derivation in Appendix A is, however, ready for applications to more general cases. It is thus a challenge to design laser pulse(s) which break electron symmetry by preparation of superpositions of basis functions that do not belong to the totally symmetry IRREP, and/or with more than two IRREPs.

(e)

Another challenge is to extend the present approach to applications of circularly polarized laser pulses, see, e.g., Refs. [2,3,4,15], or to laser pulses with different, preferably commensurable frequencies for two orthogonal components, see, e.g., Ref. [40].

(f)

At longer times, typically for t > 10 fs, the laser-driven electron density representing attosecond charge migration with broken electron symmetry will induce nuclear motions away from their initial equilibrium positions. As a working hypothesis, the nuclear and electron symmetries should adapt to each other, somewhat analogous to dynamical Jahn–Teller distortion on much longer time scales [14]. The underlying fundamental point group analyses for coupled electron and nuclear quantum dynamics driven by short laser pulses in the time domain from a few hundred to a few fs is largely terra incognita.

(g)

The literature has fascinating concepts for monitoring electron symmetry breaking in oriented molecules by short laser pulses, e.g., by attosecond photoionization of the superposition state [41], by time-resolved measurements of the asymmetries in photoelectron angular distributions [36,42], by high harmonic spectroscopy which is sensitive to electron symmetry [40,43,44] or by electron diffraction induced by ultrashort X-ray pulses [6,45,46]. The present predictions call for experimental applications or extensions of the concepts. The pioneering Ref. [47] points even to practical applications, i.e., photodissociation of molecules with broken electron symmetry may cause asymmetric distributions of the photoproducts in the laboratory—ultimately this could pave the way to photo-separation of the products.