Fracture of Fe95Ni5 Alloys with Gradient-Grained Structure under Uniaxial Tension
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
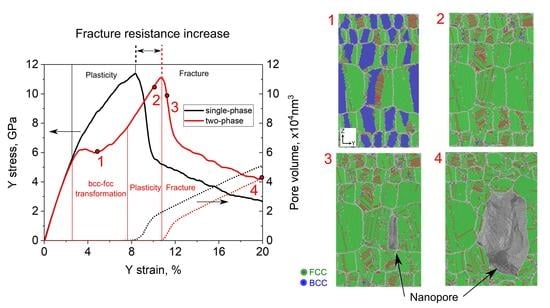
3.1. Fracture of Single- and Two-Phase Samples with a Gradient-Grained Structure
3.2. Fracture of Nanocrystalline Fcc and Bcc Samples
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ovid’ko, I.A. Review on the Fracture Processes in Nanocrystalline Materials. J. Mater. Sci. 2007, 42, 1694–1708. [Google Scholar] [CrossRef]
- Kumar, K.S.; Van Swygenhoven, H.; Suresh, S. Mechanical Behavior of Nanocrystalline Metals and Alloys. Acta Mater. 2003, 51, 5743–5774. [Google Scholar] [CrossRef]
- Cheng, S.; Ma, E.; Wang, Y.M.; Kecskes, L.J.; Youssef, K.M.; Koch, C.C.; Trociewitz, U.P.; Han, K. Tensile Properties of in Situ Consolidated Nanocrystalline Cu. Acta Mater. 2005, 53, 1521–1533. [Google Scholar] [CrossRef]
- Youssef, K.M.; Scattergood, R.O.; Murty, K.L.; Horton, J.A.; Koch, C.C. Ultrahigh Strength and High Ductility of Bulk Nanocrystalline Copper. Appl. Phys. Lett. 2005, 87, 091904. [Google Scholar] [CrossRef]
- Li, H.; Ebrahimi, F. Transition of Deformation and Fracture Behaviors in Nanostructured Face-Centered-Cubic Metals. Appl. Phys. Lett. 2004, 84, 4307–4309. [Google Scholar] [CrossRef]
- Wolf, D.; Yamakov, V.; Phillpot, S.R.; Mukherjee, A.; Gleiter, H. Deformation of Nanocrystalline Materials by Molecular-Dynamics Simulation: Relationship to Experiments? Acta Mater. 2005, 53, 1–40. [Google Scholar] [CrossRef]
- Lu, C.; Mai, Y.W.; Shen, Y.G. Recent Advances on Understanding the Origin of Superhardness in Nanocomposite Coatings: A Critical Review. J. Mater. Sci. 2006, 41, 937–950. [Google Scholar] [CrossRef]
- Korchuganov, A.V.; Zolnikov, K.P.; Kryzhevich, D.S. The Contribution of Various Plasticity Mechanisms to the Deformation Behavior of Gradient Nanograined FeNi Alloy. Metals 2022, 12, 573. [Google Scholar] [CrossRef]
- Korchuganov, A.; Kryzhevich, D.; Zolnikov, K. Deformation Behavior of Two-Phase Gradient Nanograined Fe95Ni5 Alloys under Different Types of Loading. Metals 2022, 12, 1492. [Google Scholar] [CrossRef]
- Wu, X.L.; Zhu, Y.T.; Ma, E. Predictions for Partial-Dislocation-Mediated Processes in Nanocrystalline Ni by Generalized Planar Fault Energy Curves: An Experimental Evaluation. Appl. Phys. Lett. 2006, 88, 121905. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Zhang, Q.; Huang, R.; Li, X.; Gao, H. Towards Understanding the Structure–Property Relationships of Heterogeneous-Structured Materials. Scr. Mater. 2020, 186, 304–311. [Google Scholar] [CrossRef]
- Li, X.; Lu, L.; Li, J.; Zhang, X.; Gao, H. Mechanical Properties and Deformation Mechanisms of Gradient Nanostructured Metals and Alloys. Nat. Rev. Mater. 2020, 5, 706–723. [Google Scholar] [CrossRef]
- Yang, M.; Pan, Y.; Yuan, F.; Zhu, Y.; Wu, X. Back Stress Strengthening and Strain Hardening in Gradient Structure. Mater. Res. Lett. 2016, 4, 145–151. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Weng, G.J.; Chen, S.; Wu, X. On Strain Hardening Mechanism in Gradient Nanostructures. Int. J. Plast. 2017, 88, 89–107. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Chen, R.; Yang, Y.; Guo, J.; Su, Y.; Ding, H.; Fu, H. Effects of Grain Size and Precipitated Phases on Mechanical Properties in TiAl Gradient Materials. Mater. Sci. Eng. A 2018, 731, 634–641. [Google Scholar] [CrossRef]
- Liu, X.C.; Zhang, H.W.; Lu, K. Strain-Induced Ultrahard and Ultrastable Nanolaminated Structure in Nickel. Science 2013, 342, 337–340. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.W.; Wang, Z.B.; Lu, J.; Lu, K. Fatigue Behaviors of AISI 316L Stainless Steel with a Gradient Nanostructured Surface Layer. Acta Mater. 2015, 87, 150–160. [Google Scholar] [CrossRef]
- An, X.; Bao, W.; Zhang, Z.; Jiang, Z.; Yuan, S.; You, Z.; Zhang, Y. Gradient Enhanced Strain Hardening and Tensile Deformability in a Gradient-Nanostructured Ni Alloy. Nanomaterials 2021, 11, 2437. [Google Scholar] [CrossRef]
- Hasan, M.N.; Liu, Y.F.; An, X.H.; Gu, J.; Song, M.; Cao, Y.; Li, Y.S.; Zhu, Y.T.; Liao, X.Z. Simultaneously Enhancing Strength and Ductility of a High-Entropy Alloy via Gradient Hierarchical Microstructures. Int. J. Plast. 2019, 123, 178–195. [Google Scholar] [CrossRef]
- Lin, Y.; Pan, J.; Zhou, H.F.; Gao, H.J.; Li, Y. Mechanical Properties and Optimal Grain Size Distribution Profile of Gradient Grained Nickel. Acta Mater. 2018, 153, 279–289. [Google Scholar] [CrossRef]
- Liu, X.C.; Zhang, H.W.; Lu, K. Formation of Nano-Laminated Structure in Nickel by Means of Surface Mechanical Grinding Treatment. Acta Mater. 2015, 96, 24–36. [Google Scholar] [CrossRef]
- Xu, W.; Liu, X.C.; Lu, K. Strain-Induced Microstructure Refinement in Pure Al below 100 nm in Size. Acta Mater. 2018, 152, 138–147. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, Z.; Wang, Y.; Ma, G.; Huang, T.; Wu, G.; Jensen, D.J. Fabricating Interstitial-Free Steel with Simultaneous High Strength and Good Ductility with Homogeneous Layer and Lamella Structure. Scr. Mater. 2017, 141, 111–114. [Google Scholar] [CrossRef]
- Ren, X.D.; Zhou, W.F.; Liu, F.F.; Ren, Y.P.; Yuan, S.Q.; Ren, N.F.; Xu, S.D.; Yang, T. Microstructure Evolution and Grain Refinement of Ti-6Al-4V Alloy by Laser Shock Processing. Appl. Surf. Sci. 2016, 363, 44–49. [Google Scholar] [CrossRef]
- Li, J.; Lu, W.; Gibson, J.; Zhang, S.; Chen, T.; Korte-Kerzel, S.; Raabe, D. Eliminating Deformation Incompatibility in Composites by Gradient Nanolayer Architectures. Sci. Rep. 2018, 8, 16216. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Z.; Zhou, H.; Lu, Q.; Gao, H.; Lu, L. Extra Strengthening and Work Hardening in Gradient Nanotwinned Metals. Science 2018, 362, eaau1925. [Google Scholar] [CrossRef] [Green Version]
- Tan, X.; Kok, Y.; Tan, Y.J.; Descoins, M.; Mangelinck, D.; Tor, S.B.; Leong, K.F.; Chua, C.K. Graded Microstructure and Mechanical Properties of Additive Manufactured Ti-6Al-4V via Electron Beam Melting. Acta Mater. 2015, 97, 1–16. [Google Scholar] [CrossRef]
- Zeng, Z.; Li, X.; Xu, D.; Lu, L.; Gao, H.; Zhu, T. Gradient Plasticity in Gradient Nano-Grained Metals. Extrem. Mech. Lett. 2016, 8, 213–219. [Google Scholar] [CrossRef] [Green Version]
- Gao, H.; Huang, Y. Geometrically Necessary Dislocation and Size-Dependent Plasticity. Scr. Mater. 2003, 48, 113–118. [Google Scholar] [CrossRef]
- Zhao, J.; Lu, X.; Yuan, F.; Kan, Q.; Qu, S.; Kang, G.; Zhang, X. Multiple Mechanism Based Constitutive Modeling of Gradient Nanograined Material. Int. J. Plast. 2020, 125, 314–330. [Google Scholar] [CrossRef]
- Wu, X.; Jiang, P.; Chen, L.; Yuan, F.; Zhu, Y.T. Extraordinary Strain Hardening by Gradient Structure. Proc. Natl. Acad. Sci. USA 2014, 111, 7197–7201. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wei, Y.; Yang, W.; Gao, H. Competing Grain-Boundary- and Dislocation-Mediated Mechanisms in Plastic Strain Recovery in Nanocrystalline Aluminum. Proc. Natl. Acad. Sci. USA 2009, 106, 16108–16113. [Google Scholar] [CrossRef] [PubMed]
- Hasnaoui, A.; Van Swygenhoven, H.; Derlet, P.M. Dimples on Nanocrystalline Fracture Surfaces as Evidence for Shear Plane Formation. Science 2003, 300, 1550–1552. [Google Scholar] [CrossRef]
- Schäfer, J.; Albe, K. Competing Deformation Mechanisms in Nanocrystalline Metals and Alloys: Coupled Motion versus Grain Boundary Sliding. Acta Mater. 2012, 60, 6076–6085. [Google Scholar] [CrossRef]
- Fang, T.H.; Li, W.L.; Tao, N.R.; Lu, K. Revealing Extraordinary Intrinsic Tensile Plasticity in Gradient Nano-Grained Copper. Science 2011, 331, 1587–1590. [Google Scholar] [CrossRef] [Green Version]
- Fang, Q.; Li, L.; Li, J.; Wu, H. Strengthening Mechanism of Gradient Nanostructured Body-Centred Cubic Iron Film: From Inverse Hall-Petch to Classic Hall-Petch. Comput. Mater. Sci. 2018, 152, 236–242. [Google Scholar] [CrossRef]
- Sun, J.; Ye, H.; Tao, J.; Li, Q.; Zhang, J.; Shen, L.; Zheng, Y.; Zhang, H. Gradient Structure Regulated Plastic Deformation Mechanisms in Polycrystalline Nanotwinned Copper. J. Phys. D Appl. Phys. 2019, 52, 365304. [Google Scholar] [CrossRef]
- Cao, P. The Strongest Size in Gradient Nanograined Metals. Nano Lett. 2020, 20, 1440–1446. [Google Scholar] [CrossRef]
- He, C.Y.; Yang, X.F.; Chen, H.; Zhang, Y.; Yuan, G.J.; Jia, Y.F.; Zhang, X.C. Size-Dependent Deformation Mechanisms in Copper Gradient Nano-Grained Structure: A Molecular Dynamics Simulation. Mater. Today Commun. 2022, 31, 103198. [Google Scholar] [CrossRef]
- Xu, L.; Huang, Z.; Shen, Q.; Chen, F. Atomistic Simulations of Plasticity Heterogeneity in Gradient Nano-Grained FCC Metals. Mater. Des. 2022, 221, 110929. [Google Scholar] [CrossRef]
- Zhou, K.; Zhang, T.; Liu, B.; Yao, Y. Molecular Dynamics Simulations of Tensile Deformation of Gradient Nano-Grained Copper Film. Comput. Mater. Sci. 2018, 142, 389–394. [Google Scholar] [CrossRef]
- Wang, P.; Yang, X.; Tian, X. Fracture Behavior of Precracked Nanocrystalline Materials with Grain Size Gradients. J. Mater. Res. 2015, 30, 709–716. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, F.; Zhang, J. Effects of the Grain Size Gradient on the Microstructural Evolution in Gradient Nano-grained Copper with Initial Central Crack. Mater. Des. Process. Commun. 2019, 2, e122. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Yang, F.; Zhang, X.; Zhang, J.; Zhong, Z. Crack Propagation in Gradient Nano-Grained Metals with Extremely Small Grain Size Based on Molecular Dynamic Simulations. Int. J. Fract. 2022, 233, 71–83. [Google Scholar] [CrossRef]
- Ma, Z.; Liu, J.; Wang, G.; Wang, H.; Wei, Y.; Gao, H. Strength Gradient Enhances Fatigue Resistance of Steels. Sci. Rep. 2016, 6, 22156. [Google Scholar] [CrossRef] [Green Version]
- Long, J.; Pan, Q.; Tao, N.; Dao, M.; Suresh, S.; Lu, L. Improved Fatigue Resistance of Gradient Nanograined Cu. Acta Mater. 2019, 166, 56–66. [Google Scholar] [CrossRef]
- Jing, L.; Pan, Q.; Long, J.; Tao, N.; Lu, L. Effect of Volume Fraction of Gradient Nanograined Layer on High-Cycle Fatigue Behavior of Cu. Scr. Mater. 2019, 161, 74–77. [Google Scholar] [CrossRef]
- Pan, Q.; Lu, L. Improved Fatigue Resistance of Gradient Nanograined Metallic Materials: Suppress Strain Localization and Damage Accumulation. Scr. Mater. 2020, 187, 301–306. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, L.; Zhang, S.; Sun, C.; Wang, W.; Yang, G.; Li, Q.; Wei, Y. The Influence of Combined Gradient Structure with Residual Stress on Crack-Growth Behavior in Medium Carbon Steel. Eng. Fract. Mech. 2019, 209, 369–381. [Google Scholar] [CrossRef] [Green Version]
- Cao, R.; Yu, Q.; Pan, J.; Lin, Y.; Sweet, A.; Li, Y.; Ritchie, R.O. On the Exceptional Damage-Tolerance of Gradient Metallic Materials. Mater. Today 2020, 32, 94–107. [Google Scholar] [CrossRef]
- Lin, Y.; Yu, Q.; Pan, J.; Duan, F.; Ritchie, R.O.; Li, Y. On the Impact Toughness of Gradient-Structured Metals. Acta Mater. 2020, 193, 125–137. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.W.; Foster, M.E.; Sills, R.B. An Fe-Ni-Cr Embedded Atom Method Potential for Austenitic and Ferritic Systems. J. Comput. Chem. 2018, 39, 2420–2431. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://www.ctcms.nist.gov/potentials/entry/2018--Zhou-X-W-Foster-M-E-Sills-R-B--Fe-Ni-Cr/2018--Zhou-X-W--Fe-Ni-Cr--LAMMPS--ipr1.html (accessed on 13 July 2023).
- Wang, H.; Liu, Q.; Zhang, J.; Hsu, T.Y. The Size Effect on the Phase Stability of Nanograined Fe-12Ni Powders and the Magnetic Separation of Face-Centred-Cubic-Body-Centered-Cubic Phases. Nanotechnology 2003, 14, 696–700. [Google Scholar] [CrossRef]
- Nishiyama, Z. X-ray Investigation of the Mechanism of the Transformation from Face Centered Cubic Lattice to Body Centered Cubic. Sci. Rep. Tohoku Univ. 1934, 23, 637. [Google Scholar]
- Hiroshi, I.; Masao, I.; Kazuo, M. Voronoi Diagram in the Laguerre Geometry and Its Applications. SIAM J. Comput. 1985, 14, 93–105. [Google Scholar] [CrossRef]
- Voronoi, G.F. Nouvelles applications des paramètres continus à la théorie de formes quadratiques. J. Für Die Reine Angew. Math. 1908, 134, 198–287. [Google Scholar] [CrossRef]
- Honeycutt, J.D.; Andersen, H.C. Molecular Dynamics Study of Melting and Freezing of Small Lennard-Jones Clusters. J. Phys. Chem. 1987, 91, 4950–4963. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and Analysis of Atomistic Simulation Data with OVITO-the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korchuganov, A.; Kryzhevich, D.; Zolnikov, K. Fracture of Fe95Ni5 Alloys with Gradient-Grained Structure under Uniaxial Tension. Metals 2023, 13, 1308. https://0-doi-org.brum.beds.ac.uk/10.3390/met13071308
Korchuganov A, Kryzhevich D, Zolnikov K. Fracture of Fe95Ni5 Alloys with Gradient-Grained Structure under Uniaxial Tension. Metals. 2023; 13(7):1308. https://0-doi-org.brum.beds.ac.uk/10.3390/met13071308
Chicago/Turabian StyleKorchuganov, Aleksandr, Dmitrij Kryzhevich, and Konstantin Zolnikov. 2023. "Fracture of Fe95Ni5 Alloys with Gradient-Grained Structure under Uniaxial Tension" Metals 13, no. 7: 1308. https://0-doi-org.brum.beds.ac.uk/10.3390/met13071308