1. Introduction
General system theory (GST) [
1,
2] appeared as a paradigm shift from reductionism to address in a holistic way all aspects of different type of systems and the interdependence between these using an input-state-output description, analysis and dynamics. This approach has proven to be very beneficial in the control engineering of systems leading to the control theory of systems. However, GST failed to have the same impact in the modeling, analysis and control of humanistic complex systems in which human judgment, perception and emotions play an important role because either the systems include human components like in economic and social systems or because the systems are meant to be human-like intelligent and act human-like as in the various fields of artificial intelligence. The reason for this was simple: the humanistic systems could not be dealt with the same tools as technical engineering systems.
Fuzzy sets and fuzzy system theory (FST) development initiated by Lotfi Zadeh allowed to approach the approximate reasoning in natural language (words, concepts) specific to humanistic systems [
3,
4,
5]. The evolution from GST to a FST for humanistic and human-like systems was a great progress leading to new but limited advances in artificial intelligence [
5] because FST had no tools to incorporate in an integrated way human cognitive, emotional and behavioral aspects. This is exactly one of the theses of postmodernism for which deconstruction provided a possible solution.
Postmodernism appeared in philosophy, literature, science and arts as a reaction to the limitations of modern science and philosophy to discovering the absolute objective truth about reality. This opened the door to subjectivity, uncertainty and relativity [
6,
7], to the realization that reality is not just objectively represented in our minds through perception but it is ultimately subjectively re-constructed. It became clear that truth is not absolute but fragmented, with nuances given by our subjectivity. A postmodern science must quantify and incorporate human subjectivity in the measurement of truth and the description of reality.
In our view, a postmodern system theory must be concerned with re-capturing what was lost behind during the paradigm shift from reductionism to holism: the role of human cognitive, emotional and behavioral aspects in assessing the multi-faceted nature of truth. Postmodernism offers a possible methodology, which appeared in philosophy and literature: deconstruction of concepts in terms of unities of opposites, deconstruction of truth in a fragmented, multi-faceted synthesis of nuances [
6,
7]. We formalize deconstruction in general system theory, fuzzy set theory and fuzzy system theory as a return from holism back to reductionism in order to incorporate human cognitive, emotional and behavioral aspects in system controlled dynamics and output maps, in fuzzy membership functions of fuzzy state, control and output subsets.
This is the path we followed in formulating a Kabbalah system theory (KST) [
8] based on the analytical philosophy and methodology of Kabbalah, which offers an integrated cognitive, emotional- and behavioral framework for humanistic systems characterized by exactly these three levels. We used Kabbalah to deconstruct general system theory very much like we use in optics a prism to decompose light that goes through the prism into a full spectrum of colors. KST was formulated as a deconstructed version of GST, a postmodern GST in which humanistic system dynamics breaks into three interconnected hierarchical sub-systems: cognitive, emotional and behavioral. The Kabbalah Tree of Life model offers a fractal structural model for each of these sub-systems. In order to open the door of KST to the complexity and imprecision of humanistic system applications we developed Kabbalistic fuzzy sets (KFS) [
9] as a deconstructed version of fuzzy set theory [
3], a postmodern fuzzy set theory. Fuzzy set theory is based on a fuzzy membership function taking nuanced truth-values due to human subjectivity, yet we see nowhere human cognitive, emotional and behavioral aspects featuring in the fuzzy membership function formulas. Kabbalah structural model allowed us to propose a possible worlds frame of modal logics type in order to deconstruct fuzzy membership functions.
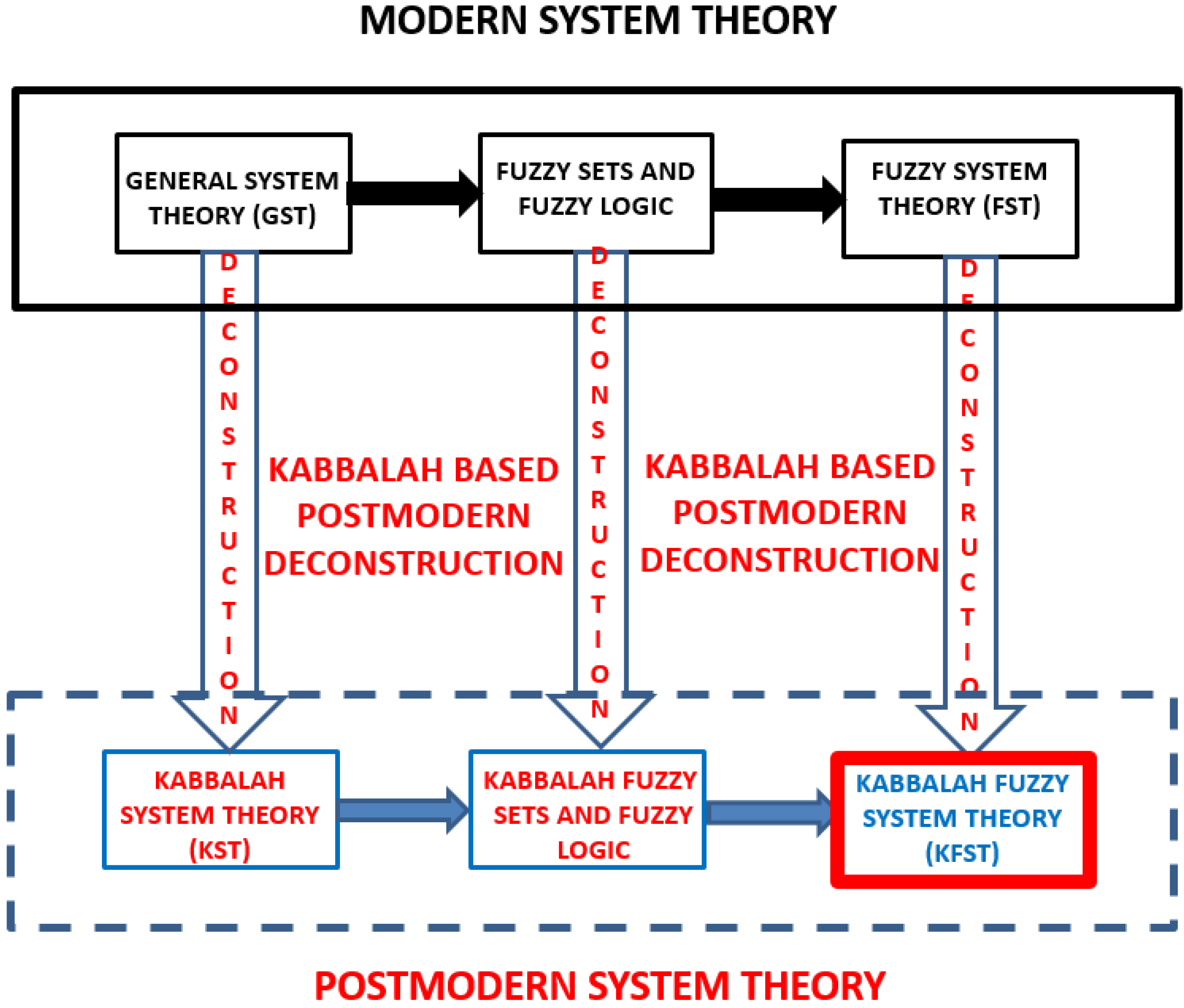
Figure 1.
Our methodology for building a postmodern fuzzy system theory, KFST, via a Kabbalah based postmodern “deconstruction” of (modern) general system theory (GST) and, of fuzzy sets, fuzzy logic and of fuzzy system theory (FST). The deconstruction incorporates cognitive, emotional and behavioral components in GST and fuzzy sets theory using a Kabbalah Tree of Life possible worlds model. Our previously built Kabbalah system theory (KST) and Kabbalah fuzzy set theory are used in this paper according to this deconstruction chain to construct a Kabbalah fuzzy system theory (KFST).
Figure 1.
Our methodology for building a postmodern fuzzy system theory, KFST, via a Kabbalah based postmodern “deconstruction” of (modern) general system theory (GST) and, of fuzzy sets, fuzzy logic and of fuzzy system theory (FST). The deconstruction incorporates cognitive, emotional and behavioral components in GST and fuzzy sets theory using a Kabbalah Tree of Life possible worlds model. Our previously built Kabbalah system theory (KST) and Kabbalah fuzzy set theory are used in this paper according to this deconstruction chain to construct a Kabbalah fuzzy system theory (KFST).
We will use here Kabbalah based KFS to deconstruct FST in order to obtain a postmodern fuzzy system theory which we will call “Kabbalah fuzzy system theory” (KFST). In KFST, the canonic deconstruction result will show how the fuzzy system dynamics is decomposed into its humanistic cognitive, emotional and behavioral fuzzy sub-systems.
Figure 1 represents the flowchart of the process that was highlighted here, which will be pursued in this paper. KFST is one possible approach in the search for a postmodern second generation GST, the theme of this special issue of Systems journal. The purpose of this paper is, to quote from Prof. Minati and Prof. Pessa’s call for papers, to focus on a “new unitary theoretical understanding” and to provide a “new theoretical framework to deal with the challenges of the post-GST age”, However, only future applications to humanistic systems can establish this new theoretical framework into a new direction of a “second generation GST”.
2. The Tree of Life of Kabbalah as a General System Model
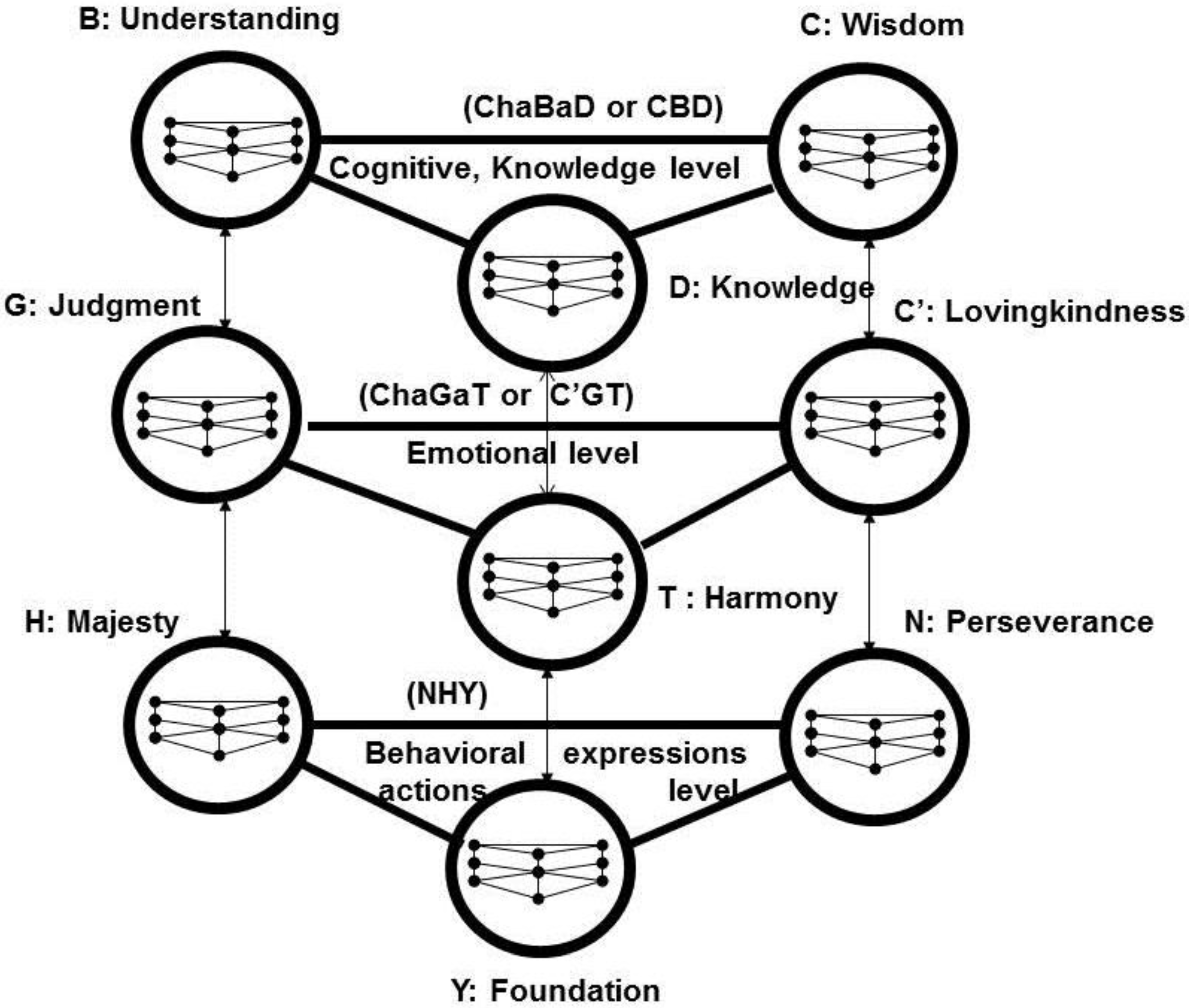
According to Kabbalah, any system, including humanistic systems with their cognitive, emotional and behavioral aspects, can be represented by a set, S, of ten interconnected fundamental general components/properties/attributes called “sefirot” (counts or units in Hebrew, sefira singular, sefirot plural), grouped in the Sefirotic Tree of Life (T) which is a graph with S, the node set, and edges representing a specific binary relation between sefirot as a subset of S × S, see
Figure 2. T has three triadic levels [
10,
11,
12]:
(1) Knowledge and cognitive level: Sefirot Wisdom (Chochmah in Hebrew), Understanding (Binah) and Knowledge (Da’at) which in fact prepares the transition and implementation of understanding at the next emotional level. These three sefirot form a triad ChaBaD, from the initials of the three sefirot, which we will denote by CBD.
(2) Emotional level: Sefirot Lovingkindness (Chesed), Judgment/Justice/Strength/Rigor or Severity (Gevurah) and Harmony or Beauty (Tiferet). These three sefirot form the triad ChaGaT which we will denote by C’GT where C’ is used for sefira Chesed
(3) Behavioral, expressions and actions level: Sefirot Perseverance or Endurance (Netzach), Victory or Majesty (Hod), Foundation (Yesod) and Kingship (Malchut). We will represent sefirot Yesod and Malchut as one sefirot, Yesod. The triadic level for behavior and physical actions will be denoted by NHY.
These nine sefirot, form a very general coordinate system of nine general basic attributes or properties that can be used to describe complex humanistic systems in general just like the Cartesian (Einstein-Minkowski) system X, Y, Z (T) is used for physics. The names are symbolic and metaphoric.
Each sefira is made of a Tree of Life with nine sub-sefirot of the same type as the original nine sefirot. The Sefirotic Tree of Life has a fractal, self-similar structure, see
Figure 2.
The sub-structure of sefirot in the fractal Tree of Life in
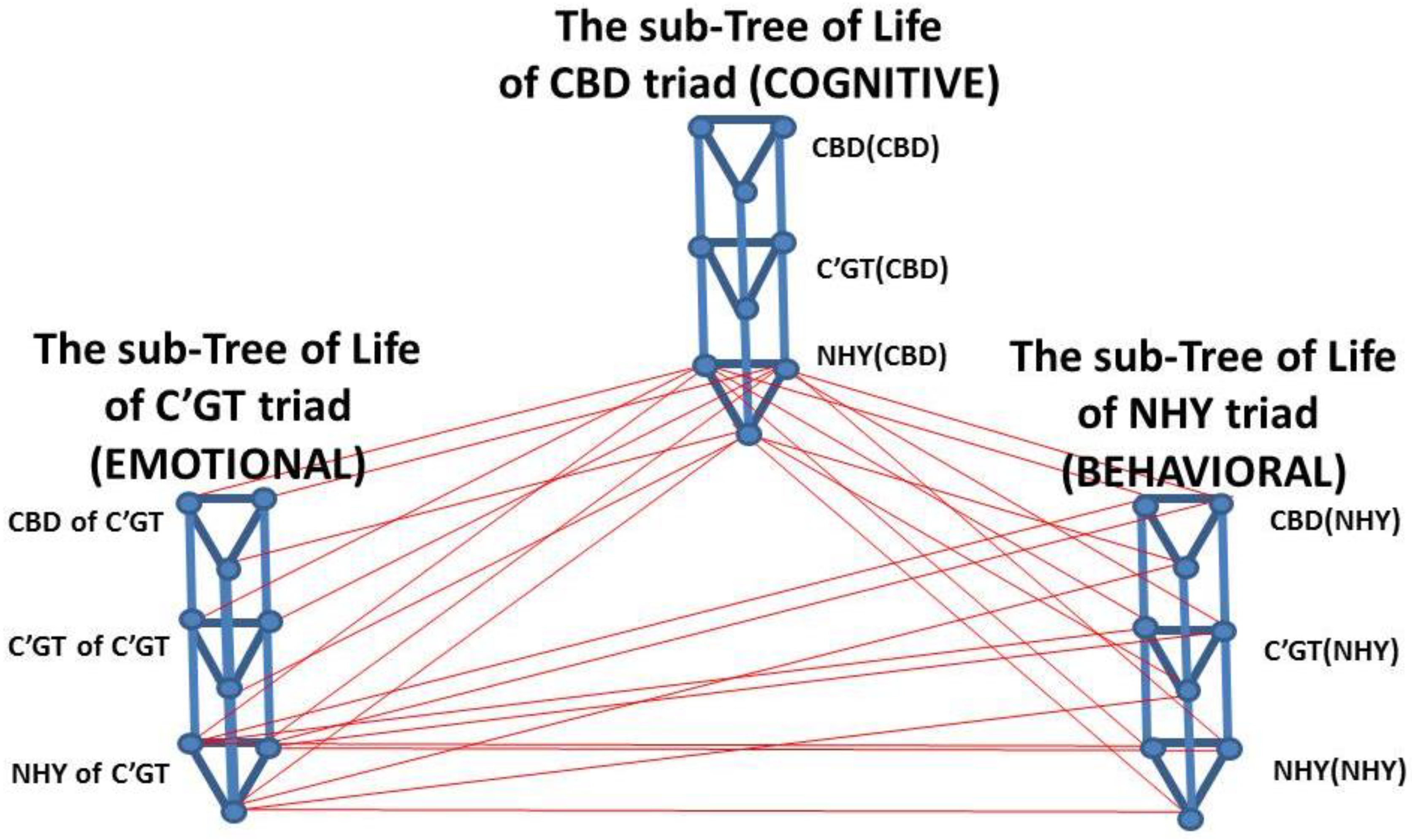
Figure 2 induces a sub-structure of the hierarchic triads of sefirot CBD, C’GT, NHY. Let’s take for example sefirot C, B, D of CBD triad. Each sefirot has its own CBD sub-triad inside its sub-structure: we have a sub-CBD of C, sub-CBD of B and sub-CBD of D. These three sub-triads of cognitive CBD type are forming together the CBD sub-triad of CBD denoted CBD(CBD). Similarly we have C’GT(CBD). NHY(CBD). This way CBD has its own sub-Tree of Life structure made of CBD(CBD), C’GT(CBD), NHY(CBD). NHY(CBD), for example, refers to the behavioral expression and action oriented part of the cognitive triad CBD. Just like the Tree of Life has a sefirotic fractal structure in terms of sefirot in
Figure 2 so too it has a triadic fractal structure in terms of triadic hierarchic levels as shown in
Figure 3.
Figure 2.
The fractal sefirotic structure of the Tree of Life of Kabbalah as a general system model: nine interconnected sefirot units organized in three interconnected hierarchical levels or sub-systems corresponding to the cognitive triad of sefirot CBD, emotional triad of sefirot C’GT and behavioral, expressions and actions triad of sefirot NHY. Each sefirot unit is made up similarly of nine sub-sefirot connected according to a Tree of Life structure. (
Source: [
9]).
Figure 2.
The fractal sefirotic structure of the Tree of Life of Kabbalah as a general system model: nine interconnected sefirot units organized in three interconnected hierarchical levels or sub-systems corresponding to the cognitive triad of sefirot CBD, emotional triad of sefirot C’GT and behavioral, expressions and actions triad of sefirot NHY. Each sefirot unit is made up similarly of nine sub-sefirot connected according to a Tree of Life structure. (
Source: [
9]).
The links between the triads CBD, C’GT, NHY, shown in
Figure 3 with their sub-levels, are based on the hierarchical inner organization of the Tree of Life of Kabbalah [
13]: CBD, through its behavior, expression and action oriented sub-level, NHY(CBD), controls both C’GT and NHY levels of the Tree of Life. Similarly, C’GT, through its behavior, expressions and actions sub-component NHY(C’GT), is part of the control of NHY, the behavior, expressions and actions level of the Tree of Life structure. [
13] is one of the fundamental presentations of Kabbalah methodology focused among other on exploring the hierarchical relations and coordination among the triadic levels of sefirot of the Tree of Life.
Figure 3.
The hierarchical fractal triadic structure of the Tree of Life, in terms of the sub-triads of each triad of sefirot, corresponds to the fractal sefirotic structure of the Tree of Life in terms of sefirot from
Figure 2. The CBD sub-levels of sefirot C, B, D form the CBD sub-triad of CBD denoted by CBD(CBD). Similarly we have C’GT(CBD) and NHY(CBD) which together with CBD(CBD) form the sub-Tree of Life of CBD. The same applies for the sub-Trees of Life of C’GT and NHY. The connections between the sub-Trees of Life of CBD, C’GT, NHY are based on the hierarchical system organization of the Tree of Life of Kabbalah: CBD controls C’GT and NHY by means of its NHY(CBD), the behavior, actions and expressions oriented sub-triad of the cognitive triad CBD. C’GT controls NHY through NHY(C’GT), the behavior, expressions and actions oriented sub-triad of the emotions triad C’GT.
Figure 3.
The hierarchical fractal triadic structure of the Tree of Life, in terms of the sub-triads of each triad of sefirot, corresponds to the fractal sefirotic structure of the Tree of Life in terms of sefirot from
Figure 2. The CBD sub-levels of sefirot C, B, D form the CBD sub-triad of CBD denoted by CBD(CBD). Similarly we have C’GT(CBD) and NHY(CBD) which together with CBD(CBD) form the sub-Tree of Life of CBD. The same applies for the sub-Trees of Life of C’GT and NHY. The connections between the sub-Trees of Life of CBD, C’GT, NHY are based on the hierarchical system organization of the Tree of Life of Kabbalah: CBD controls C’GT and NHY by means of its NHY(CBD), the behavior, actions and expressions oriented sub-triad of the cognitive triad CBD. C’GT controls NHY through NHY(C’GT), the behavior, expressions and actions oriented sub-triad of the emotions triad C’GT.
3. Kabbalah Fuzzy Set Theory: The Postmodern Deconstruction Based on Kabbalah and on the Possible Worlds Semantic Model of Modal Logic
We introduce next the postmodern fuzzy set version, Kabbalistic fuzzy sets, the next step in our construction process of a postmodern fuzzy system theory described in
Figure 1. Our approach to create a Kabbalah fuzzy set theory [
9] is based on the “possible worlds” semantic model of modal logic [
14], which is used to construct fuzzy set membership functions [
15,
16]. We will develop a modified Kabbalah fuzzy set theory in this paper that is better suitable for fuzzy system theory: a new hierarchic Kabbalah possible worlds model will be developed here based on
Figure 3 with a new possible world “importance” weighting function based on the structure of the graph in
Figure 3 [0,1] will be used instead of a lattice L to make calculations more intuitive.
A fuzzy subset of X, A is described by a set membership function, m(A,⋅) taking values in the interval [0,1] as opposed to just the two value set {0, 1} corresponding to “true” and “false”:
Fuzzy sets arise when considering fuzzy concepts having a universe of discourse X. For example: A = “tall men”, X= “men”; A = “smart people”, X = “people”; A = “beautiful women”, X = “women”. Systems with human components or involving human judgment, reasoning, decisions
etc. are often fuzzy systems using fuzzy concepts specific to our thinking in terms of natural language. The fuzzy concept A, as a fuzzy subset of X, is described by its membership function m (A,⋅) which indicates the truth value of the proposition:
The assessment of the truth value of proposition P (x, A), and hence of the membership function m(x, A), can be done from different modal logic angles [
14]: modal (“it is possible that x belongs to A”), epistemic (“it is known that x belongs to A”), doxastic (“it is believed that x belongs to A”)
etc. This suggests linking classical fuzzy set theory [
3] with modal logic [
14], as it was done in [
15,
16] in order to get a “meta-theory” of fuzzy sets and fuzzy logic based on the “possible worlds” semantic model of modal logic. The merit of such an approach is that it brings semantics in fuzzy set theory and it also gives a construction methodology for fuzzy set membership functions.
The possible worlds model, M, of modal logic is linked to the names of Kripke and Hintikka [
14] and is defined as a M = < W, R, V, w > where W is a set of “possible N worlds” W= {W(1),…,W(N)} meaning in our context possible points of view, facets of looking at the truth of a logical proposition, statement, predicate such as P(x, A) related to a complex, fuzzy concept A having universe of discourse or values X. W can be also the set of agents or experts assessing the truth of P(x, A). R is a binary relation between the worlds W, called “accessibility relation” given by a subset of W × W according to which W(i) R W(j) means W(j) is accessible to W(i). This relationship is assumed to be reflexive: a world is accessible of course to itself. <W, R> is called a Kripke frame of possible worlds. w is a weighting function assigning weights of importance or reliability to each possible world of W. V is a valuation function of the truth of simple (atomic) propositions P (x, A) ϵ Prop, the set of atomic propositions:
Of course, we can generalize V like we did in in [
6] to have it take values in a lattice. w is a weighting function taking values in [0,1] assigned to each world W(i) of W, according to the importance of the world W(i) such that w(W(i)), i = 1,…,N sum up to 1. In our Kabbalah postmodern deconstruction approach to fuzzy set theory, we chose the sefirot to be the possible worlds and the binary relation between them is given by the Tree of Life graph in
Figure 3. We will denote both the graph and the binary “accessibility” relation between worlds in
Figure 3 by R. Sefirot represent the “worlds”: points of view, angles, facets of a system or concept such as the fuzzy concept A. The three levels of the Tree of Life, cognitive, emotional/motivational, behavioral are in direct correspondence with modal logics: the cognitive CBD level is linked to epistemic logic where truth is assessed based on knowledge, the C’GT emotional, subjective level is linked to beliefs which are subjective reflections of knowledge in CBD or are simply subjective, emotional, linked to motivation, behavioral/action level NHY is linked to dynamic logic of action of modal logic.
We are proposing here a new weighting function w for the possible worlds model. The weight of a world, represented by a sefirot S(i) in the frame given by the graph R and its underlying binary relation shown in
Figure 3, is defined as:
deg(S(i),R) is the degree of the node S(i) in the graph R and is equal to the number of nodes, worlds (sefirot) S(j) which are linked to S(i) (accessible to S(i)). deg(R) is the total degree of the graph R defined to be the sum of the degrees of its nodes:
w(S(i)) gives the relative importance of S(i) as a world in R: the more worlds or sefirot S(j) are accessible to a given sefirot S(i), the more reliable, documented, important is the assessment of truth performed by S(i) as it is based on more information. We have by definition of w(S(i)):
Using the possible worlds semantic frame of sefirot in
Figure 3 we can define a calculation methodology for the membership function m(⋅,A) of a fuzzy set as follows:
In the sequel, we shall omit square brackets [ ] from (5) to simplify notation.
The idea of introducing a possible world weighting function belongs to the modal logic meta-theory of fuzzy sets approach of [
15], see also [
16]. The problem with that approach is that the construction of the fuzzy set membership function does not depend on the binary “accessibility” relation or the graph linking the possible worlds. The structure of the interconnection between possible worlds has no say in the fuzzy membership function. That is why we introduced here an “importance” weighting function w that weighs the worlds based on the count of “accessibility” links that connect any world to some of the rest of the worlds in
Figure 3: a measure of importance or informational reliability. The other original contribution here is to introduce a specific possible worlds architecture based on the three level hierarchic fractal structure of the Tree of Life of sefirot which we constructed here in in
Figure 3: cognitive, emotional and behavioral/expressions/actions levels. Based on Equation (5) we can introduce operations with fuzzy sets: intersection, union and bounded sum of fuzzy sets. Given two fuzzy sets:
The union A⋃B, intersection A⋂B and bounded sum A⊕B are fuzzy sets (fuzzy subsets of X) given by membership functions of x ϵ X:
We can also introduce the Cartesian product A × B of two fuzzy subsets of two different universes of discourse X and Y:
We can now state the postmodern deconstruction result for fuzzy sets via Kabbalah logic and semantics, which opens the door to a postmodern fuzzy set theory:
Proposition 1. (Postmodern fuzzy set deconstruction canonic form) Let m(A,⋅) be the membership function of a fuzzy set A (fuzzy subset of universe of discourse X), given by formula (5) relative to a possible worlds model M = < W, R, V, w >, with frame < W, R > of sefirot possible worlds W(i) = S(i), i = 1,…,27 connected like in the graph of the binary accessibility relation R from
Figure 3. Then the membership function m (A, x) for all x ϵ X can be canonically decomposed as:
A fuzzy set with fuzzy membership function expressed by Equation (12) is called a Kabbalistic fuzzy set (KFS).
The sums are each taken over the nine sefirot of the respective levels CBD, C’GT, NHY. The weights w(S) are defined by (3’) and (3”) and hence the weight of a sefirot is normalized relative to the sum of all 27 weights of the 27 sefirot in
Figure 3. In our case the bounded sum ⊕ by 1 is actually the usual sum + since the weights w(S) add up to 1 according to Equation (5) and the valuation function V(P(x, A),S) is either 0 or 1, false or truth.
The postmodern fuzzy set deconstruction formula represents a fuzzy set membership function as a bounded sum (sum) of an epistemic, cognitive estimate with an emotional, doxastic estimate and with a behavioral, action estimate of the fuzzy membership function. These three fuzzy membership function estimates, representing three fuzzy subsets of A, correspond to the three assessments of the truth of the proposition P(x, A) = {x ϵ A} at the three different modal semantic levels as follows:
Postmodernism is about the multifaceted nature of truth [
6] and our deconstruction formula for a fuzzy set captures that by showing how the fuzzy membership function is made up by summing the three different estimates, assessments or facets of truth at the three modal levels. This formula unveils the cognitive, emotional and behavioral components embedded in the subjective assessment of a fuzzy concept A. m(A, ⋅ ∣
CBD) is the cognitive, epistemic modal estimate of m(A, ⋅), m(A, ⋅ ∣
C’GT) is the emotional, doxastic modal estimate while m(A, ⋅ ∣
NHY) is the behavioral, action modal estimate of the fuzzy membership function m(A, ⋅). Remark that these estimates or fuzzy subsets are interconnected since weights w(S) at one level are normalized relative to the weights of all 27 sefirot and not just relative to the weights of the nine sefirot forming that level. According to the process described in
Figure 1, the postmodern fuzzy set theory, which deconstructs fuzzy sets along the cognitive, emotional and behavioral dimensions, will allow us next to introduce fuzzy systems where the basic concepts of general system theory, input-state-output, are Kabbalistic fuzzy sets.
4. Postmodern Fuzzy System Theory
In its most abstract form, a general system is a 5–uple <U, X, Y, F, G> where U is the set of controls, X is the state set and Y is the output set, F: X× U → X is the controlled state dynamics map, G: X → Y is the output map. A fuzzy general system, in its most abstract form is a 9-uple ∑ = <U, X, Y, F, G, m, n, q, p > where m : X → [0, 1] , n : Y → [0,1] , q : U → [0,1] are respectively the fuzzy state set, fuzzy output set and fuzzy control set and p (x, u) = (m(x) × q(u)) = min (m(x), q(u)) such that the diagram on the left side of
Figure 4 is commutative in a “fuzzy sense” [
3]:
It is explained in detail in [
3], (pp. 22–23) why the usual equality condition of commutativity of diagrams of maps is replaced by inequality in the case of fuzzy sets and maps of fuzzy sets (very similar to sub-additivity
versus additivity which is why we can call this inequality “sub-commutativity” if we want). The 9-uple ∑ = <U, X, Y, F, G, m, n, q, p > only defines a fuzzy general system if (19) is satisfied otherwise it is just an 9-uple of sets and maps. ∑ = <U, X, Y, F, G, m, n, q, p > is one way to define general fuzzy systems. There are few other ways of defining fuzzy systems including replacing U, X, Y respectively with all fuzzy subsets of U denoted
![Systems 02 00590 i001]()
(U), all fuzzy subsets of X denoted
![Systems 02 00590 i001]()
(X), all fuzzy subsets of Y denoted
![Systems 02 00590 i001]()
(Y) and using fuzzy maps F and G or using fuzzy relations on X × U × X and X × Y to define dynamics and output [
3].
By applying Proposition 1 (postmodern deconstruction canonic form) to each of m, n, q, p fuzzy membership functions defining ∑ and taking into account (19) defining ∑ we obtain:
Proposition 2. (postmodern deconstruction canonic form for fuzzy general systems) Let < U, X, Y, F, G, m, n, q, p > be a 9-uple of maps and sets as above without relations (19) assumed to hold. Define 9-uples ∑
CBD, ∑
C’GT, ∑
NHY as follows (see
Figure 4):
where
are the canonic postmodern fuzzy membership function deconstruction forms for m, n, p, q based on Proposition 1, formula (12).
If (20)–(22) satisfy each the commutativity inequalities of type (19) (so that ∑
CBD, ∑
C’GT, ∑
NHY are general fuzzy systems as defined above and their diagrams in the right side of
Figure 4 commute) then ∑ = <U, X, Y, F, G, m, n, q, p > is a general fuzzy system satisfying the commutativity of the diagram on the left side of
Figure 4 given by relations (19).
Figure 4.
A postmodern deconstruction of a fuzzy general system
∑ (represented by the diagram on the left side of figure) into its cognitive
∑CBD, emotional
∑C’GT and behavioral/expressions/actions
∑NHY fuzzy subsystems or estimates (represented by the corresponding diagrams on the right side of figure) based on the Kabbalah possible worlds architecture of
Figure 3 and Proposition 1 (the postmodern fuzzy set deconstruction canonic form).
Figure 4.
A postmodern deconstruction of a fuzzy general system
∑ (represented by the diagram on the left side of figure) into its cognitive
∑CBD, emotional
∑C’GT and behavioral/expressions/actions
∑NHY fuzzy subsystems or estimates (represented by the corresponding diagrams on the right side of figure) based on the Kabbalah possible worlds architecture of
Figure 3 and Proposition 1 (the postmodern fuzzy set deconstruction canonic form).
Proof. If we sum the commutativity inequality conditions of type (19) for ∑CBD, ∑C’GT, ∑NHY which are assumed to hold and we use Equations (23)–(26) then we get exactly the commutativity condition for ∑ = <U, X, Y, F, G, m, n, q, p > proving it is a fuzzy general system.
We can symbolically write:
and think of
∑CBD,
∑C’GT,
∑NHY as a factorization, decomposition or “realization” for
∑ (not in the classical input-output map realization sense [
3]). Note however that
∑ can have many other possible “realizations”.
∑CBD,
∑C’GT,
∑NHY are respectively the cognitive/epistemic, emotional/doxastic and behavioral/action fuzzy estimates or fuzzy subsystems of
∑.
A fuzzy general system defined by (19) with state, control or input and output KFS defined by (23)–(26) will be called a Kabbalistic fuzzy system.
Postmodern fuzzy system theory KFST is about working with Kabbalistic fuzzy system ∑ in its deconstructed form from (27) and about relating the structural properties of ∑ to those of ∑
CBD, ∑
C’GT, ∑
NHY and of the Kabbalah based possible world frame in
Figure 3. Fuzzy system theory FST was all stopping at ∑ level and its structural properties. Although fuzzy sets and fuzzy systems arise from human subjectivity and knowledge imprecision, this humanistic nature behind fuzzy systems was not visible in the FST but will now become incorporated in KFST according to the deconstruction process in
Figure 1 which was carried out in this paper.
We would like to approach next the most popular model for fuzzy systems, the most implemented model which was launched by Zadeh in [
17]: fuzzy systems as fuzzy rules based systems (∑):
where
![Systems 02 00590 i002]()
,
![Systems 02 00590 i003]()
,
![Systems 02 00590 i004]()
,
![Systems 02 00590 i005]()
are fuzzy subsets of U, X, Y that is they belong to
![Systems 02 00590 i001]()
(U),
![Systems 02 00590 i001]()
(X),
![Systems 02 00590 i001]()
(Y). We used the system notation ∑ here for fuzzy rules just to emphasize that this is another model for fuzzy systems. A fuzzy rules based system contains several rules of the (28) type linked between them by “OR” connectives. Fuzzy rules are modeled as fuzzy relations between fuzzy subsets [
3,
14] using fuzzy Cartesian product and fuzzy intersection operations. ∑ is thus seen as a fuzzy subset of:
with membership function given by:
“OR” connectives between several rules of the type (28) are modelled by union of fuzzy sets of (29) type and thus by the “max” operator between their respective membership functions of (30) type. The result of (30) is equal to one of the membership function values m(
![Systems 02 00590 i002]()
, u), m(
![Systems 02 00590 i003]()
, x), m(
![Systems 02 00590 i004]()
, x’), m(
![Systems 02 00590 i005]()
, y) which can be written in the postmodern deconstruction canonic form for fuzzy sets from Proposition 1. This way we ultimately get a deconstruction canonic form for the fuzzy rule (∑):
where r = (u, x, x’, y) and we used a Kabbalistic possible worlds model M = < W, R, V, w > like in Proposition 1, with sefirotic Tree of Life frame < W, R > given by
Figure 3. Again here we have the three cognitive, emotional/doxastic, behavioral/action estimates of ∑ in the deconstruction formula (31).
The structure of the possible worlds (sefirot) accessibility relation in
Figure 3 plays a key role in KFST. First, it allows to deconstruct here fuzzy systems based on (1) cognitive, (2) emotional and (3) behavioral components as it was done in Propositions 1 and 2. This will display the multi-faceted humanistic nature behind fuzzy systems and fuzzy sets.
Second, the structure of the accessibility relation of possible worlds does not only reveal the multi-faceted humanistic structure of a fuzzy general system but it also relates these facets to each other. Denote by Acc (CBD), Acc (C’GT) and Acc (NHY) the possible worlds accessible in
Figure 3 respectively from CBD, C’GT, NHY (which include respectively CBD, C’GT, NHY themselves due to reflexivity). Based on the Tree of Life possible worlds accessibility relation, R, shown
Figure 3, we have the following filtration or sequence of nested subsets of possible worlds in R:
We can define extensions ∑ (Acc (CBD)), ∑ (Acc (C’GT)), ∑ (Acc (NHY)) of ∑
CBD , ∑
C’GT, ∑
NHY by using respectively Acc (CBD), Acc (C’GT) and Acc (NHY) instead of just CBD, C’GT and NHY’ respectively. This gives us an idea how the structure of the possible world accessibility relation introduced in
Figure 3 allows us to explore a fuzzy system from different partial and progressive information angles, restricting it to just CBD, C’GT, NHY or progressively extending it to Acc (CBD), Acc (C’GT), Acc (NHY). This shows how the Kabbalistic possible world frame <W,R> constructed in
Figure 3 is a tool for developing different deconstructed postmodern fuzzy system models based on the structure of information embedded in <W,R>.
5. Example: Application of Postmodern Fuzzy System Theory to Create Kabbalistic Fuzzy System Models for Fuzzy Agents
An agent computer system is an autonomous system, which based on observing or perceiving its environment can decide, based on its objectives, which actions to take in order to achieve the objectives. Agents can be organized in distributed agent structures and can be used, among others, to model and simulate complex systems. Fuzzy agents address the complexity and imprecision of the environment in which they operate by making fuzzy observations, by taking fuzzy decisions leading to implementing fuzzy actions [
18].
There are many models for agents but the most basic are based on the sequence observe or perceive —decide—act. We will use here fuzzy control systems to create a model for fuzzy agents. A fuzzy agent can be modeled by a Kabbalistic fuzzy general system ∑ = <O, D, A, d, a, m, n, q, p > given by a commuting diagram like the one on the left of
Figure 4 where:
O = the observation set or universe of discourse
D = the decision set or decision state space of the agent based on his objectives
A = the set of actions of the agent based on his objectives
d is the state dynamics of the decision process based on agent’s objectives and inputs from O
a is the output action function of the agent dependent on the decisions of the agent
m is the fuzzy membership function of the Kabbalistic fuzzy decision set
n is the fuzzy membership function of the Kabbalistic fuzzy action set
q is the fuzzy membership function of the Kabbalistic fuzzy observation set
p = m × q
By using the postmodern deconstruction canonic forms from Propositions 1 and 2, based on a possible worlds frame like in
Figure 3, for m, n, q, p and ∑ we obtain the ∑ (COGNITIVE), ∑ (EMOTIONAL) and ∑ (BEHAVIORAL) models for the fuzzy agent cognitive, emotional and behavioral fuzzy sub-systems of ∑ = <O, D, A, d, a, m, n, q, p > given by commuting diagrams of the types ∑
CBD, ∑
C’GT, ∑
NHY displayed on the right side of
Figure 4.
Postmodern fuzzy system theory can thus provide theoretical deconstructed fuzzy agent models to quantify and help design the humanistic type cognitive, emotional and behavioral mechanisms behind the observation, decision and action processes of fuzzy agents.
 (U), all fuzzy subsets of X denoted
(U), all fuzzy subsets of X denoted  (X), all fuzzy subsets of Y denoted
(X), all fuzzy subsets of Y denoted  (Y) and using fuzzy maps F and G or using fuzzy relations on X × U × X and X × Y to define dynamics and output [3].
(Y) and using fuzzy maps F and G or using fuzzy relations on X × U × X and X × Y to define dynamics and output [3]. 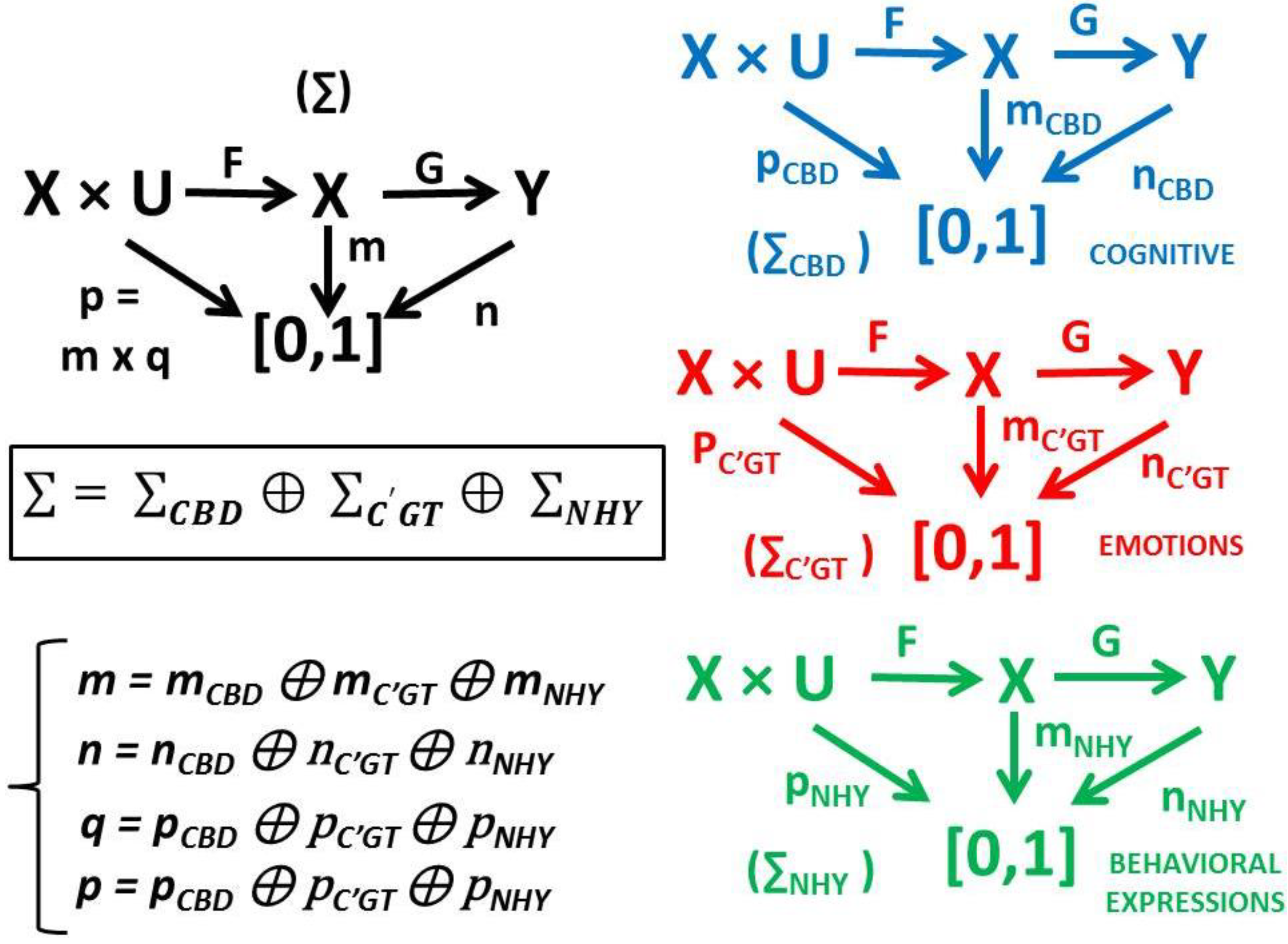
 ; AND STATE
; AND STATE  THEN NEXT STATE
THEN NEXT STATE  AND OUTPUT
AND OUTPUT 
 ,
,  ,
,  ,
,  are fuzzy subsets of U, X, Y that is they belong to
are fuzzy subsets of U, X, Y that is they belong to  (U),
(U),  (X),
(X),  (Y). We used the system notation ∑ here for fuzzy rules just to emphasize that this is another model for fuzzy systems. A fuzzy rules based system contains several rules of the (28) type linked between them by “OR” connectives. Fuzzy rules are modeled as fuzzy relations between fuzzy subsets [3,14] using fuzzy Cartesian product and fuzzy intersection operations. ∑ is thus seen as a fuzzy subset of:
(Y). We used the system notation ∑ here for fuzzy rules just to emphasize that this is another model for fuzzy systems. A fuzzy rules based system contains several rules of the (28) type linked between them by “OR” connectives. Fuzzy rules are modeled as fuzzy relations between fuzzy subsets [3,14] using fuzzy Cartesian product and fuzzy intersection operations. ∑ is thus seen as a fuzzy subset of:
 ⋂
⋂  ) × (
) × (  ⋂
⋂  )
)
 , u), m(
, u), m(  , x)], min [m(
, x)], min [m(  , x’), m(
, x’), m(  , y)]}
, y)]}
 , u), m(
, u), m(  , x), m(
, x), m(  , x’), m(
, x’), m(  , y) which can be written in the postmodern deconstruction canonic form for fuzzy sets from Proposition 1. This way we ultimately get a deconstruction canonic form for the fuzzy rule (∑):
, y) which can be written in the postmodern deconstruction canonic form for fuzzy sets from Proposition 1. This way we ultimately get a deconstruction canonic form for the fuzzy rule (∑):




