The Influence of s-Wave Interactions on Focussing of Atoms
Abstract
:1. Introduction
2. Materials and Methods
2.1. Classical Trajectories Approach
2.2. Gross–Pitaevskii Equation Methodology
2.3. The BEC Ground State
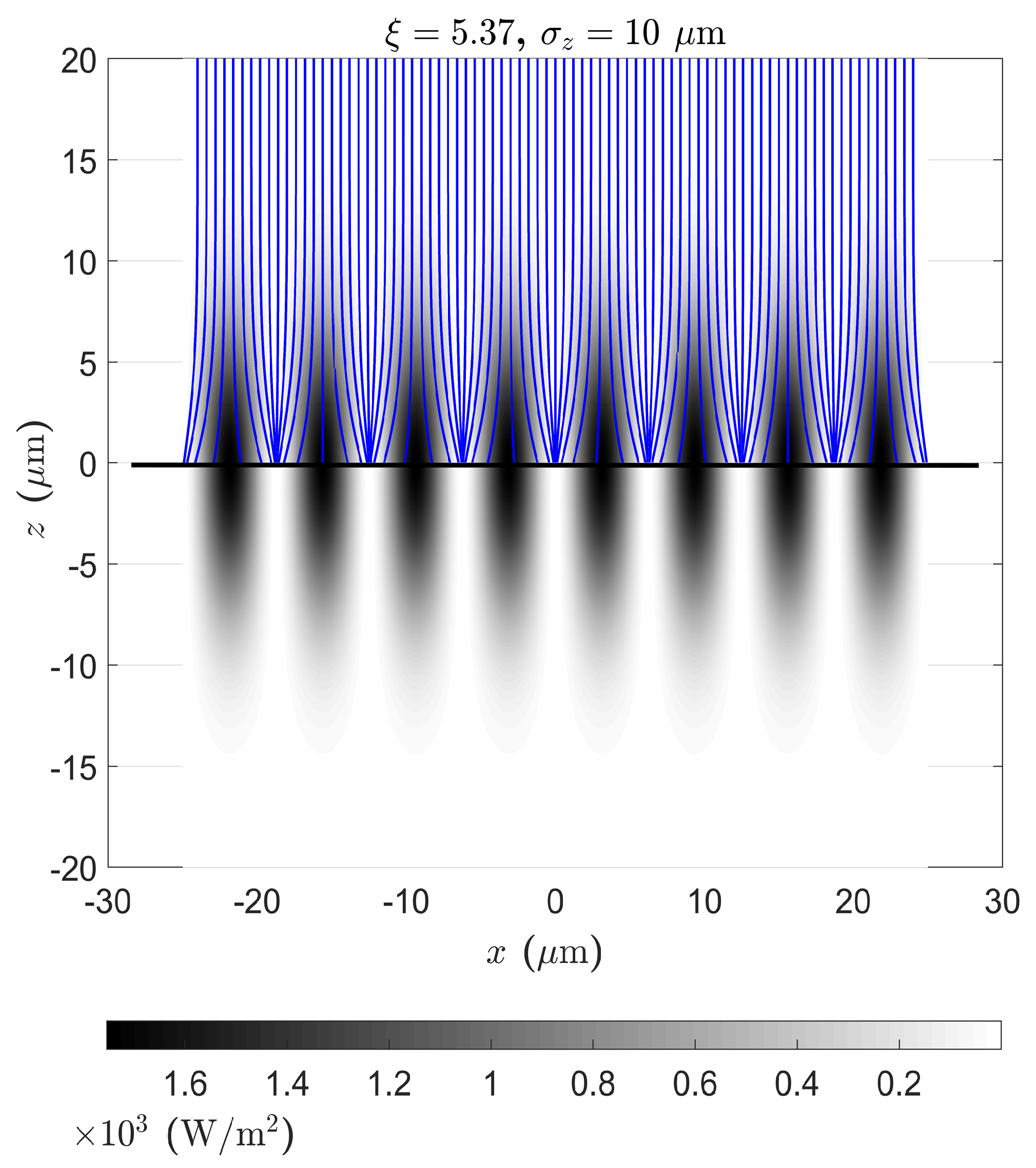
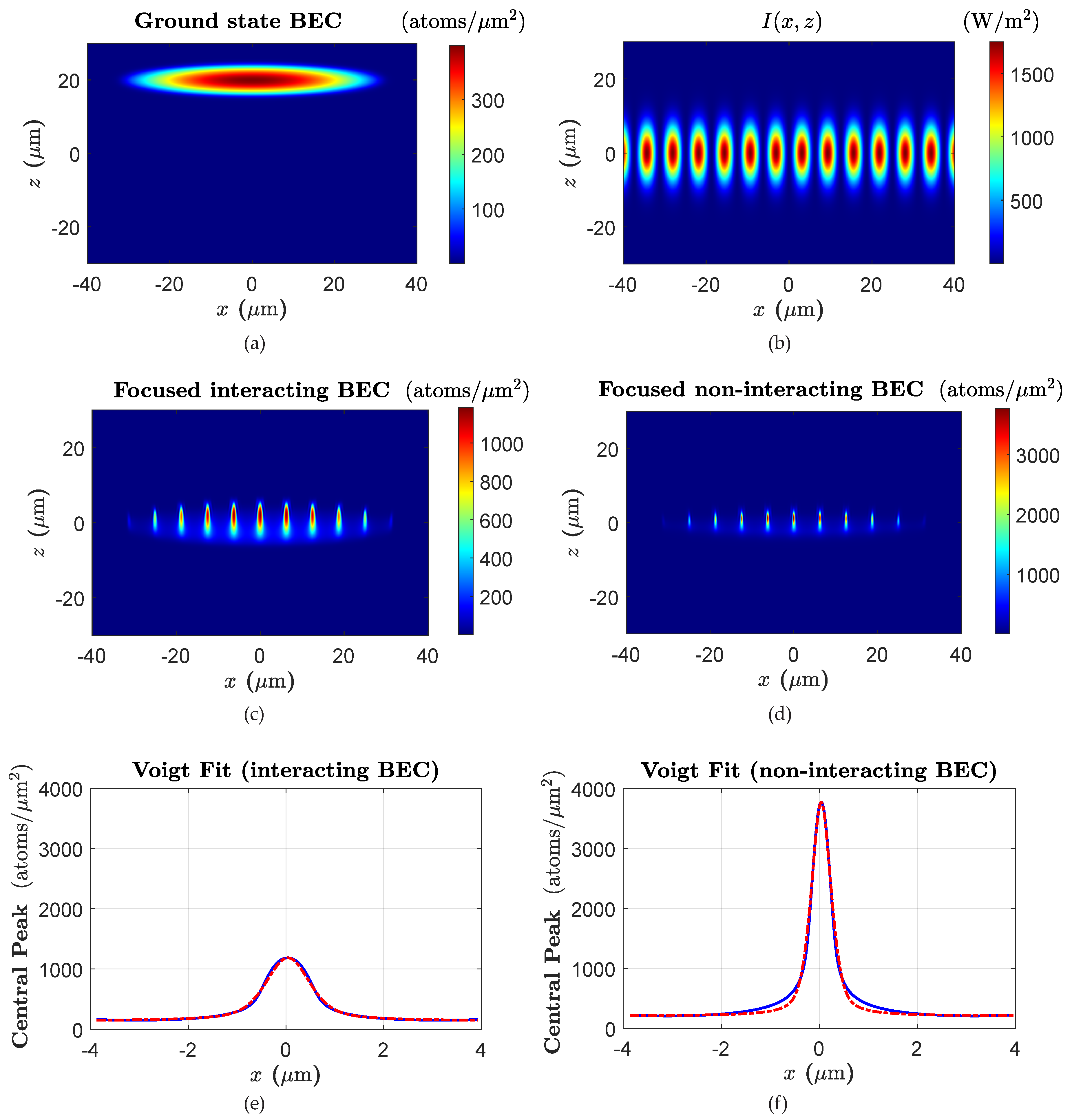
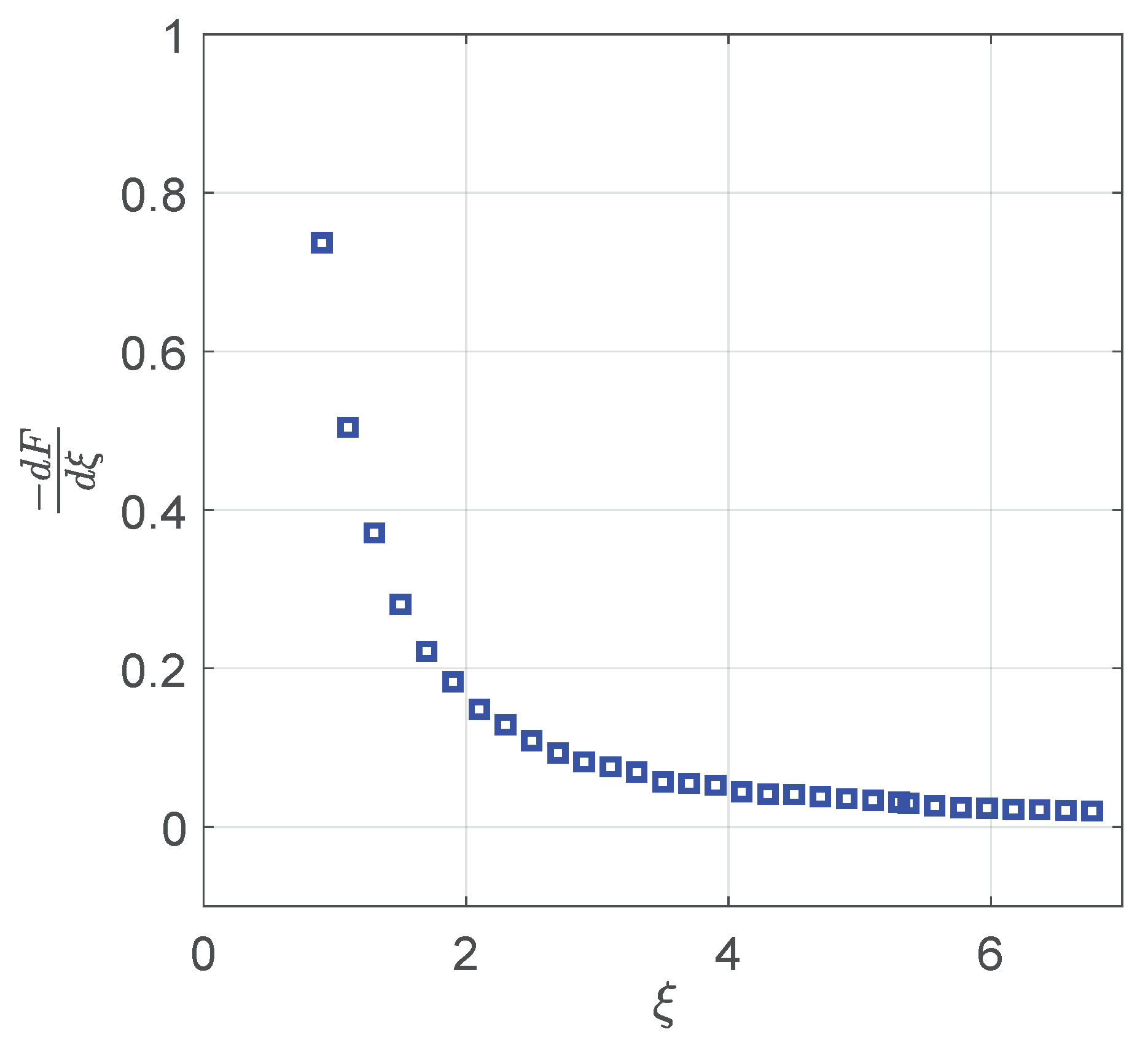
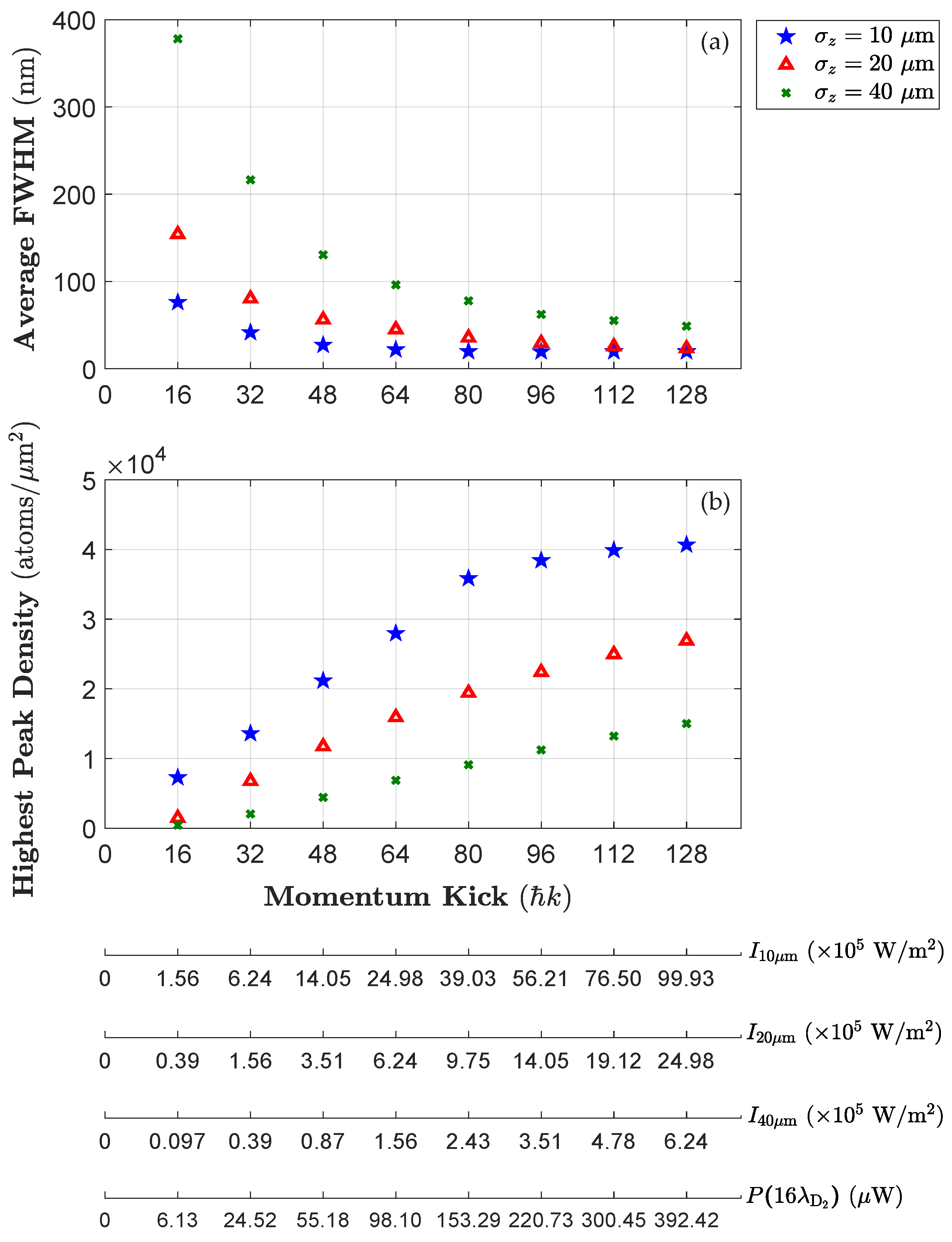
3. Results and Discussion
3.1. Time Dependent Focusing Potential
3.2. The Variation of BEC and Potential Factors
3.3. Velocity Distribution of a BEC
3.4. Chromatic Aberration in Classical Trajectories Model
3.5. Angular Divergence in Classical Trajectories Model
3.6. GPE and Classical Trajectories Agreement
3.7. Numerical Investigation of Focusing
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Timp, G.; Behringer, R.; Tennant, D.; Cunningham, J.; Prentiss, M.; Berggren, K. Using light as a lens for submicron, neutral-atom lithography. Phys. Rev. Lett. 1992, 69, 1636. [Google Scholar] [CrossRef]
- McClelland, J.J.; Scholten, R.; Palm, E.; Celotta, R.J. Laser-focused atomic deposition. Science 1993, 262, 877–880. [Google Scholar] [CrossRef]
- Meschede, D. Atomic nanofabrication: Perspectives for serial and parallel deposition. J. Phys. 2005, 19, 118. [Google Scholar] [CrossRef]
- Balykin, V.; Melentiev, P. Nanolithography with atom optics. Nanotechnol. Russ. 2009, 4, 425–447. [Google Scholar] [CrossRef]
- Balykin, V.; Letokhov, V. The possibility of deep laser focusing of an atomic beam into the Å-region. Opt. Commun. 1987, 64, 151–156. [Google Scholar] [CrossRef]
- Balykin, V.; Letokhov, V. Deep focusing of an atomic beam in the Angstrom region by laser radiation. Zh. Eksp. Teor. Fiz 1988, 94, 150. [Google Scholar]
- McClelland, J.J.; Scheinfein, M. Laser focusing of atoms: A particle-optics approach. JOSA B 1991, 8, 1974–1986. [Google Scholar] [CrossRef]
- Oberthaler, M.K.; Pfau, T. One-, two-and three-dimensional nanostructures with atom lithography. J. Phys. Condens. Matter 2003, 15, R233. [Google Scholar] [CrossRef]
- Ohmukai, R.; Urabe, S.; Watanabe, M. Atom lithography with ytterbium beam. Appl. Phys. B 2003, 77, 415–419. [Google Scholar] [CrossRef]
- Myszkiewicz, G.; Hohlfeld, J.; Toonen, A.; Van Etteger, A.; Shklyarevskii, O.; Meerts, W.; Rasing, T.; Jurdik, E. Laser manipulation of iron for nanofabrication. Appl. Phys. Lett. 2004, 85, 3842–3844. [Google Scholar] [CrossRef] [Green Version]
- Smeets, B.; van der Straten, P.; Meijer, T.; Fabrie, C.; van Leeuwen, K. Atom lithography without laser cooling. Appl. Phys. B 2010, 98, 697–705. [Google Scholar] [CrossRef] [Green Version]
- Bjorkholm, J.; Freeman, R.; Ashkin, A.; Pearson, D. Observation of focusing of neutral atoms by the dipole forces of resonance-radiation pressure. Phys. Rev. Lett. 1978, 41, 1361. [Google Scholar] [CrossRef]
- Bjorkholm, J.E.; Freeman, R.R.; Ashkin, A.; Pearson, D. Experimental observation of the influence of the quantum fluctuations of resonance-radiation pressure. Opt. Lett. 1980, 5, 111–113. [Google Scholar] [CrossRef] [PubMed]
- Balykin, V.; Letokhov, V.; Ovchinnikov, Y.B.; Sidorov, A. Focusing of an atomic beam and imaging of atomic sources by means of a laser lens based on resonance-radiation pressure. J. Mod. Opt. 1988, 35, 17–34. [Google Scholar] [CrossRef]
- Ammann, H.; Christensen, N. Delta Kick Cooling: A New Method for Cooling Atoms. Phys. Rev. Lett. 1997, 78, 2088. [Google Scholar] [CrossRef] [Green Version]
- Kovachy, T.; Hogan, J.; Sugarbaker, A.; Dickerson, S.; Donnelly, C.; Overstreet, C.; Kasevich, M. Matter Wave Lensing to Picokelvin Temperatures. Phys. Rev. Lett. 2015, 114, 143004. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Henn, E.; Seman, J.; Seco, G.; Olimpio, E.; Castilho, P.; Roati, G.; Magalhaes, D.V.; Magalhaes, K.M.F.; Bagnato, V.S. Bose–Einstein condensation in 87Rb: Characterization of the Brazilian experiment. Braz. J. Phys. 2008, 38, 279–286. [Google Scholar] [CrossRef]
- Ziegler, K.; Shukla, A. Erratum: Bose–Einstein condensation in a trap: The case of a dense condensate. Phys. Rev. A 1998, 57, 1464. [Google Scholar] [CrossRef]
- Murray, D.; Öhberg, P. Matter wave focusing. J. Phys. B At. Mol. Opt. Phys. 2005, 38, 1227. [Google Scholar] [CrossRef]
- Boegel, P.; Meister, M.; Siemß, J.N.; Gaaloul, N.; Efremov, M.; Schleich, W. Diffractive focusing of a uniform Bose–Einstein condensate. arXiv 2021, arXiv:2102.08682. [Google Scholar]
- Richberg, R.; Szigeti, S.S.; Martin, A.M. Optical focusing of Bose-Einstein condensates. Phys. Rev. A 2021, 103, 063304. [Google Scholar] [CrossRef]
- Grimm, R.; Weidemüller, M.; Ovchinnikov, Y.B. Optical dipole traps for neutral atoms. In Advances in Atomic, Molecular, and Optical Physics; Elsevier: San Diego, CA, USA, 2000; Volume 42, pp. 95–170. [Google Scholar]
- Gordon, J.; Ashkin, A. Motion of atoms in a radiation trap. Phys. Rev. A 1980, 21, 1606. [Google Scholar] [CrossRef]
- McClelland, J.J. Atom-optical properties of a standing-wave light field. JOSA B 1995, 12, 1761–1768. [Google Scholar] [CrossRef]
- Grivet, P.; Hawkes, P.W.; Septier, A. Electron Optics; Elsevier: New York, NY, USA, 2013. [Google Scholar]
- McGloin, D.; Spalding, G.C.; Melville, H.; Sibbett, W.; Dholakia, K. Applications of spatial light modulators in atom optics. Opt. Express 2003, 11, 158–166. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Wang, J. Arbitrary manipulation of spatial amplitude and phase using phase-only spatial light modulators. Sci. Rep. 2014, 4, 7441. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hecht, E. Optics, 5th ed.; Pearson Education Limited: London, UK, 2017. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Cambridge University Press: London, UK, 2013. [Google Scholar]
- Shiono, T.; Setsune, K.; Yamazaki, O.; Wasa, K. Rectangular-apertured micro-Fresnel lens arrays fabricated by electron-beam lithography. Appl. Opt. 1987, 26, 587–591. [Google Scholar] [CrossRef] [PubMed]
- Rozaliya, B.; Gene, I. Strain and Dislocation Gradients from Diffraction: Spatially-Resolved Local Structure and Defects; Imperial College Press: London, UK, 2014. [Google Scholar]
- Griffin, A.; Snoke, D.W.; Stringari, S. Bose–Einstein Condensation; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Pethick, C.J.; Smith, H. Bose–Einstein Condensation in Dilute Gases; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Gross, E.P. Structure of a quantized vortex in boson systems. Il Nuovo Cim. (1955–1965) 1961, 20, 454–477. [Google Scholar] [CrossRef] [Green Version]
- Pitaevskii, L. Vortex lines in an imperfect Bose gas. Sov. Phys. JETP 1961, 13, 451–454. [Google Scholar]
- Pitaevskii, L. PITAEVSKII LP. Zh. Eksp. Teor. Fiz 1961, 40, 646. [Google Scholar]
- Gross, E.P. Unified theory of interacting bosons. Phys. Rev. 1957, 106, 161. [Google Scholar] [CrossRef]
- Ginzburg, V.; Pitaevskii, L. On the theory of superfluidity. Sov. Phys. JETP 1958, 7, 858–861. [Google Scholar]
- Dalfovo, F.; Giorgini, S.; Pitaevskii, L.P.; Stringari, S. Theory of Bose–Einstein condensation in trapped gases. Rev. Mod. Phys. 1999, 71, 463. [Google Scholar] [CrossRef] [Green Version]
- Leggett, A.J. Bose–Einstein condensation in the alkali gases: Some fundamental concepts. Rev. Mod. Phys. 2001, 73, 307. [Google Scholar] [CrossRef] [Green Version]
- Pitaevskii, L.; Stringari, S. Bose–Einstein Condensation and Superfluidity; Cambridge University Press: New York, NY, USA, 2016; Volume 164. [Google Scholar]
- McDonald, G.D.; Kuhn, C.C.; Hardman, K.S.; Bennetts, S.; Everitt, P.J.; Altin, P.A.; Debs, J.E.; Close, J.D.; Robins, N.P. Bright solitonic matter-wave interferometer. Phys. Rev. Lett. 2014, 113, 013002. [Google Scholar] [CrossRef] [Green Version]
- Thøgersen, M.; Zinner, N.T.; Jensen, A.S. Thomas–Fermi approximation for a condensate with higher-order interactions. Phys. Rev. A 2009, 80, 043625. [Google Scholar] [CrossRef] [Green Version]
- Balac, S.; Mahé, F. Embedded Runge–Kutta scheme for step-size control in the interaction picture method. Comput. Phys. Commun. 2013, 184, 1211–1219. [Google Scholar] [CrossRef] [Green Version]
- Kruger, P.B.; Mathews, S.; Aggarwala, K.R.; Sanchez, N. Chromatic aberration and ocular focus: Fincham revisited. Vis. Res. 1993, 33, 1397–1411. [Google Scholar] [CrossRef]









| Example | (μW) | (W/m2) | (μm) | (μm) | (Peak) (atoms/μm2) | (Peak) (atoms/μm2) |
|---|---|---|---|---|---|---|
| μm cm/s | 1185 | 3771 | ||||
| μm cm/s | 543 | 1598 | ||||
| μm cm/s | 3181 | 6028 |
| Example | ||||
|---|---|---|---|---|
| μm cm/s | ||||
| μm cm/s | ||||
| μm cm/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Richberg, R.; Martin, A.M. The Influence of s-Wave Interactions on Focussing of Atoms. Atoms 2021, 9, 37. https://0-doi-org.brum.beds.ac.uk/10.3390/atoms9030037
Richberg R, Martin AM. The Influence of s-Wave Interactions on Focussing of Atoms. Atoms. 2021; 9(3):37. https://0-doi-org.brum.beds.ac.uk/10.3390/atoms9030037
Chicago/Turabian StyleRichberg, Roham, and Andrew M. Martin. 2021. "The Influence of s-Wave Interactions on Focussing of Atoms" Atoms 9, no. 3: 37. https://0-doi-org.brum.beds.ac.uk/10.3390/atoms9030037






