Nonprofits and Pass-Throughs: Performance Comparison
Abstract
:1. Introduction
2. Background and Literature Review
2.1. Key Features of Nonprofits (NPs) and Pass-Throughs (PTs)
2.2. Equity and Debt Financing for Nonprofits (NPs) and Pass-Throughs (PTs)
2.3. Assignment of Unlevered and Levered Tax Rates for Nonprofits (NPs) and Pass-Throughs (PTs)
2.4. Capital Structure Models
3. Methodology
3.1. Capital Structure Model (CSM)
3.2. Identifying the Optimal P Choice
3.3. CSM Approach to Growth
3.4. P Choices, Costs of Borrowing, and Betas
4. Results Using Low (L) Tax Rates under TCJA with Historical Growth
4.1. Variables and Computations
4.2. Illustrations of NP and PT Outcomes
4.3. Five Illustrative Figures Using TCJA Tax Rates and Growth of 3.12%
5. Results Incorporating High Tax Rates (H), Pre-TCJA Tax Rates, and Increased Growth
5.1. H and L Results with TCJA Tax Rates and 3.12% Growth
5.1.1. Credit Spread Results
5.1.2. Results for 2018–2019 Period
5.2. H and L Results with Pre-TCJA Tax Rates and 3.90% Growth
5.3. Five Illustrative Figures of H and L Results with Pre-TCJA Tax Rates and 3.90% Growth
5.4. Key Comparisons
5.5. Limitations and Future Research
6. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Acronym Glossary
| Acronym: Term | Definition and/or Meaning for This Study’s Purpose | Main Location |
| NP: nonprofit | Ownership form characterized by its tax-exempt status | Exhibit 1 |
| PT: pass-through | Ownership form where taxes on paid at the personal level | Exhibit 1 |
| FP: for-profit | A business whose earnings are subject to taxes because they fall within either the C corp or pass-through ownership form. | Section 1 |
| CC: C corp | Ownership form where taxes on paid at both the corporate and personal levels | Section 1 |
| TCJA: Tax Cuts and Jobs Act | US revenue act that favors C corps relative to pass-throughs by reducing corporate tax rates more than personal tax rates. | Section 1 |
| CSM: Capital Structure Model | A trade-off model that identifies the maximum firm value from a series of increasing debt issues that retire unlevered equity | Section 3.1 |
| CFBT: cash flows before taxes | Cash flows available before federal taxes are paid and before any applicable tax shield lowers business taxes. | Section 3.1 |
| PBRBT: before-tax plowback ratio | The amount of retained earnings (RE) divided by cash flows before taxes (CFBT) | Section 3.1 |
| OCR: Optimal credit rating | Credit rating that corresponds to max VL and ODV. | Section 3.2 |
| RE: retained earnings | Before-tax cash flows from operations used strictly for growth that leads to increased production of goods and/or services. | Section 3.3 |
| Costs of borrowing | Cost of debt (rD), cost of unlevered equity(rU), cost of levered equity (rL) | Table 1 |
| ICR: interest coverage ratio | Comes in three firm categories of small, large, and financial service and are used to compute leverage choices. | Table 1 |
| αI and α2: alphas | Coefficients that capture the effects of tax rates | Table 2 |
| EU: unlevered equity value | EU is the same as unlevered firm value (VU) because unlevered means no debt. Thus, value consists only of equity. | Table 2 |
| gU: unlevered equity growth rate | The growth rate for an unlevered growth firm. | Table 2 |
| gL: levered equity growth rate | The growth rate for a levered growth firm. This rate ties together the plowback-payout and debt-equity choices. | Table 3 |
| Max GL: maximum gain to leverage | The greatest gain to leverage among all feasible leverage choices. | Table 3 |
| VL: firm value | VL = EL + D where EL is levered equity value and D is debt value. For our application of the CSM, VL is also EU + GL. | Table 3 |
| Max VL: maximum firm value | Max VL = EU + max GL where max VL can also be identified by the greatest VL among all feasible VL outputs. | Table 3 |
| DV: debt-to-firm value ratio | A leverage ratio computed as D/VL where D is debt value and VL is firm value. | Table 3 |
| ODV: optimal DV | The optimal DV associated with the greatest attainable firm value among feasible DV choices, which is max VL. | Table 3 |
References
- Amirkhanyan, Anna. 2010. Monitoring across sectors: Examining the effects of nonprofits and for-profits contractor ownership on performance monitoring in state and local contacts. Public Administration Review 70: 742–755. [Google Scholar] [CrossRef]
- Anheier, Helmut. 2014. Nonprofit Organizations. Theory, Management, Policy, 2nd ed. New York: Routledge, pp. 1–594. [Google Scholar]
- Baxter, Nevins. 1967. Leverage risk of ruin and the cost of capital. Journal of Finance 22: 395–403. [Google Scholar]
- Berk, Jonathan, Richard Stanton, and Josef Zechner. 2010. Human capital, bankruptcy and capital structure. Journal of Finance 65: 891–926. [Google Scholar] [CrossRef] [Green Version]
- Bowman, Woods. 2002. The uniqueness of NP finance and the decision to borrow. NP Management and Leadership 23: 293–311. [Google Scholar] [CrossRef]
- Bowman, Woods. 2015. The Price of NPO Debt. NP Quarterly. Available online: https://NPquarterly.org/2015/08/06/the-price-of-NP-debt/ (accessed on 31 December 2019).
- Brookings. 2017. 9 Facts about Pass-through Businesses. Available online: https://www.brookings.edu/research/9-facts-about-pass-through-businesses/#fact5 (accessed on 19 December 2019).
- Calabrese, Thad. 2011. Testing competing capital structure theories of nonprofit organizations. Public Budgeting and Finance 31: 119–43. [Google Scholar] [CrossRef]
- Calabrese, Thad, and Todd Ely. 2016. Borrowing for the public good: The growing importance of tax-exempt bonds for public charities. Nonprofit and Voluntary Sector Quarterly 45: 458–77. [Google Scholar] [CrossRef]
- Damodaran, Aswath. 2019. Damodaran Online: Home Page for Aswath Damodaran. Available online: http://pages.stern.nyu.edu/~adamodar/New_Home_Page/dataarchived.html (accessed on 25 November 2019).
- Damodaran, Aswath. 2020. Damodaran Online: Home Page for Aswath Damodaran. Available online: http://pages.stern.nyu.edu/~adamodar/New_Home_Page/datacurrent.html (accessed on 15 January 2020).
- DeAngelo, Harry, and Ronald Masulis. 1980. Optimal capital structure under corporate and personal taxes. Journal of Financial Economics 8: 3–29. [Google Scholar] [CrossRef]
- DeSimone, Rebecca. 2019. Can an LLC Be a Nonprofit? Available online: https://www.legalzoom.com/articles/can-an-llc-be-a-nonprofit (accessed on 5 May 2019).
- Donaldson, Gordon. 1961. Corporate Debt Capacity: A Study of Corporate Debt Policy and the Determination of Corporate Debt Capacity. Boston: Harvard Business School, pp. 1–294. [Google Scholar]
- Federal Reserve Economic Data. 2020. 30-Year Treasury Constant Maturity Rate. Federal Reserve Bank of St. Louis. Available online: https://fred.stlouisfed.org/series/DGS30 (accessed on 25 July 2020).
- Graham, John. 2000. How big are the tax benefits of debt? Journal of Finance 55: 1901–41. [Google Scholar] [CrossRef]
- Graham, John, and Campbell Harvey. 2001. The theory and practice of corporate finance: Evidence from the field. Journal of Financial Economics 60: 187–243. [Google Scholar] [CrossRef]
- Hackbarth, Dirk, Christopher Hennessy, and Hayne Leland. 2007. Can the trade-off theory explain debt structure? Review of Financial Studies 20: 1389–428. [Google Scholar] [CrossRef] [Green Version]
- Hull, Robert. 2010. A capital structure model with growth. Investment Management and Financial Innovation 7: 26–40. [Google Scholar]
- Hull, Robert. 2012. A capital structure model with wealth transfers. Investment Management and Financial Innovation 9: 19–32. [Google Scholar]
- Hull, Robert. 2014. A capital structure model (CSM) with tax rate changes. Investment Management and Financial Innovations 11: 8–21. [Google Scholar]
- Hull, Robert. 2018. Capital structure model (CSM): Correction, constraints, and applications. Investment Management and Financial Innovation 15: 245–62. [Google Scholar] [CrossRef] [Green Version]
- Hull, Robert. 2019. Business wealth and tax policy. Theoretical Economics Letters 9: 1020–39. [Google Scholar] [CrossRef] [Green Version]
- Hull, Robert. 2020a. Credit ratings and firm value. Investment Management and Financial Innovation 17: 157–68. [Google Scholar] [CrossRef]
- Hull, Robert. 2020b. Pass-through and C corp outputs under TCJA. International Journal of Financial Studies 18: 46–78. [Google Scholar] [CrossRef]
- Hull, Robert, and John Hull. 2020. Taxpayer wealth and federal tax revenue under a tax policy that shields retained earnings used for growth from taxes. eJournal of Tax Research. Forthcoming. [Google Scholar]
- Hull, Robert, and David Price. 2015. Pass-through valuation. The Journal of Entrepreneurial Finance 17: 82–116. [Google Scholar]
- Jegers, Marc, and Else Verschueren. 2006. On the capital structure of nonprofit organisations: An empirical study for Californian organisations. Financial Accountability & Management 22: 309–29. [Google Scholar]
- Jensen, Michael. 1986. Agency costs of free cash flow, corporate finance, and takeovers. American Economic Review 76: 323–29. [Google Scholar]
- Jensen, Michael, and William Meckling. 1976. Theory of the firm: Managerial behavior, agency costs and ownership structure. Journal of Financial Economics 3: 305–60. [Google Scholar] [CrossRef]
- Keatinge, Robert. 2009. LLCs and nonprofit organizations—For-profits, nonprofits, and hybrids. Suffolk University Law Review 42: 553–86. [Google Scholar]
- Kisgen, Darren. 2006. Credit ratings and capital structure. Journal of Finance 61: 1035–72. [Google Scholar] [CrossRef]
- Korteweg, Arthur. 2010. The net benefits of leverage. Journal of Finance 65: 2137–70. [Google Scholar] [CrossRef]
- Manne, Geoffrey. 1999. Agency costs and the oversight of charitable organizations. Wisconsin Law Review 227: 227–90. [Google Scholar]
- McBride, William. 2012. CRS, at Odds with Academic Studies, Continues to Claim No Harm in Raising Top Earners Tax Rates. Tax Foundation. Available online: https://taxfoundation.org/crs-odds-academic-studies-continues-claim-no-harm-raising-top-earners-tax-rates (accessed on 1 February 2020).
- Miller, Clara. 2003. Hidden in plain sight: Nonprofit capital structure. Nonprofit Quarterly March: 1–8. [Google Scholar]
- Morningstar. 2019. Credit Ratings. Available online: https://ratingagency.morningstar.com/mcr/ratings-surveillance/corporate-financial%20institutions (accessed on 21 July 2019).
- Myers, Stewart. 1977. Determinants of corporate borrowing. Journal of Financial Economics 5: 147–75. [Google Scholar] [CrossRef] [Green Version]
- Myers, Stewart, and Nicholas Majluf. 1984. Corporate financing and investment decisions when firms have information that investors do not have. Journal of Financial Economics 13: 187–221. [Google Scholar] [CrossRef] [Green Version]
- National Center for Charitable Statistics. 2018. The Nonprofit Sector in Brief 2018. Available online: https://nccs.urban.org/publication/nonprofit-sector-brief-2018#the-nonprofit-sector-in-brief-2018-public-charites-giving-and-volunteering (accessed on 2 February 2020).
- National Federation of Independent Business. 2013. Entity Choice and Effective Tax Rates. Available online: http://www.s-corp.org/wp-content/uploads/2013/08/Quantria_Study_ETR_8-6-13_Final_pm.pdf (accessed on 7 October 2019).
- Pomerleau, Kyle. 2015. An Overview of Pass-through Businesses in the United States. Tax Foundation, Special Report, Number 227. January 24. Available online: https://taxfoundation.org/overview-pass-through-businesses-united-states (accessed on 10 December 2019).
- Rao, Sumedh. 2015. Is the Private Sector more Efficient? A Cautionary Tale. United Nations Development Programme (UNDP): Global Centre for Public Service Excellence (GCPSE). Available online: https://www.undp.org/content/dam/undp/library/capacity-development/English/Singapore%20Centre/GCPSE_Efficiency.pdf (accessed on 20 February 2021).
- SBA Office of Advocacy. 2009. Effective Federal Income Tax Rates Faced By Small Businesses in the United States. Small Business Administration. April. Available online: https://www.sba.gov/sites/default/files/advocacy/rs343tot.pdf (accessed on 28 October 2019).
- Tax Foundation. 2018. The Tax Foundation’s Tax and Growth Model, April. Available online: https://taxfoundation.org/overview-tax-foundations-taxes-growth-model/ (accessed on 20 May 2020).
- Tax Policy Center. 2016. T16-0181—Distribution of Business Income, by Expanded Cash Income Percentile; Current Law. August 23. Available online: https://www.taxpolicycenter.org/model-estimates/distribution-business-income-august-2016/t16-0181-distribution-business-income (accessed on 18 January 2020).
- Tax Policy Center. 2018. Key Elements of the U.S. Tax System. Available online: http://www.taxpolicycenter.org/taxvox/25-percent-rate-pass-through-businesses-helps-rich-investors-not-small-businesses (accessed on 20 May 2018).
- Tax Policy Center. 2020. How Do Taxes Affect the Economy in the Long Run? Available online: https://www.taxpolicycenter.org/briefing-book/how-do-taxes-affect-economy-long-run (accessed on 20 May 2020).
- Trussell, John. 2012. A comparison of the capital structures of nonprofit and proprietary healthcare organizations. Journal of Healthcare and Finance 39: 1–12. [Google Scholar]
- U.S. Bureau of Economic Analysis. 2018. US Real GDP Growth Rate by Year. Available online: http://www.multpl.com/us-real-gdp-growth-rate/table/by-year (accessed on 11 January 2020).
- U.S. Bureau of Economic Analysis. 2020. US Real GDP Growth Rate by Year. Available online: http://www.multpl.com/us-real-gdp-growth-rate/table/by-year (accessed on 11 January 2020).
- Van Binsbergen, Jules, John Graham, and Jie Yang. 2010. Cost of debt. Journal of Finance 65: 2089–136. [Google Scholar] [CrossRef]
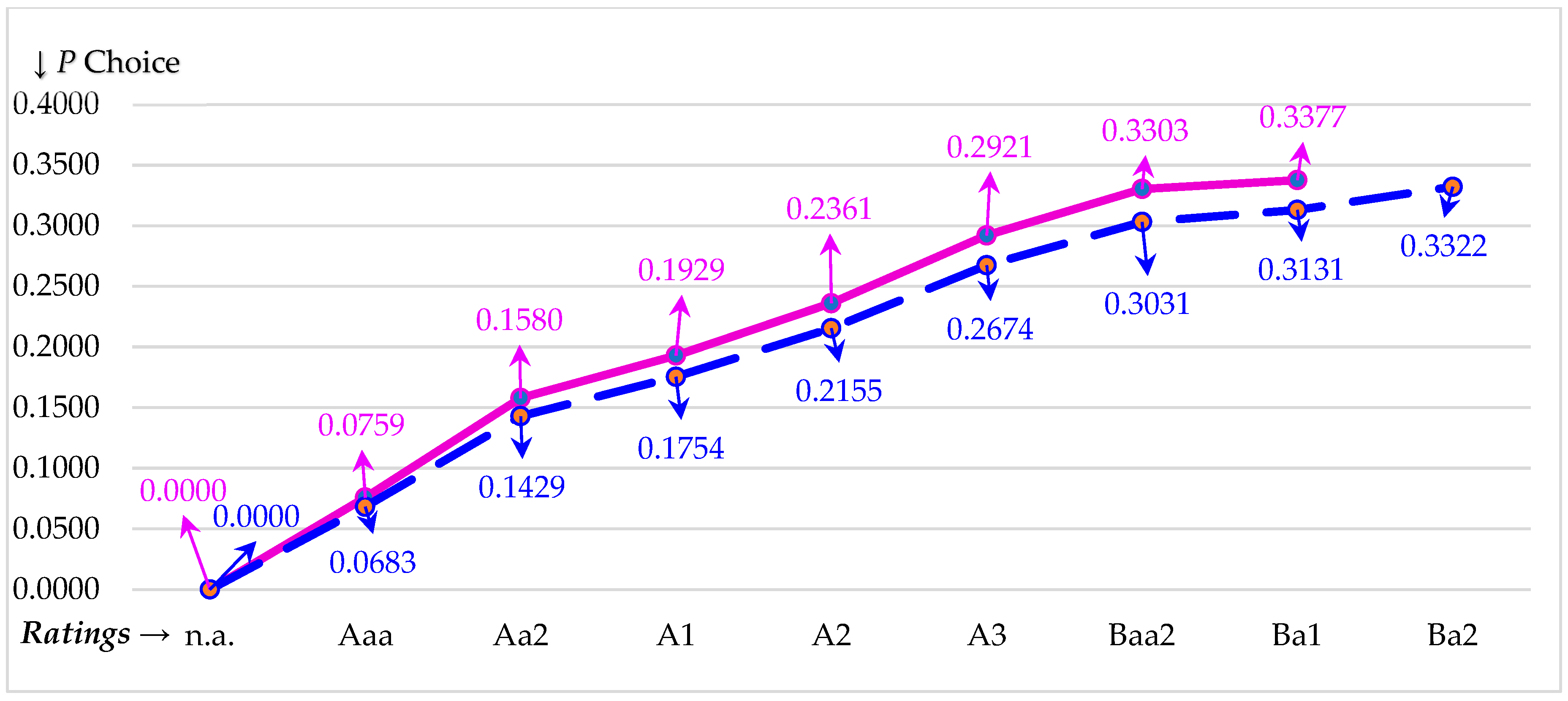
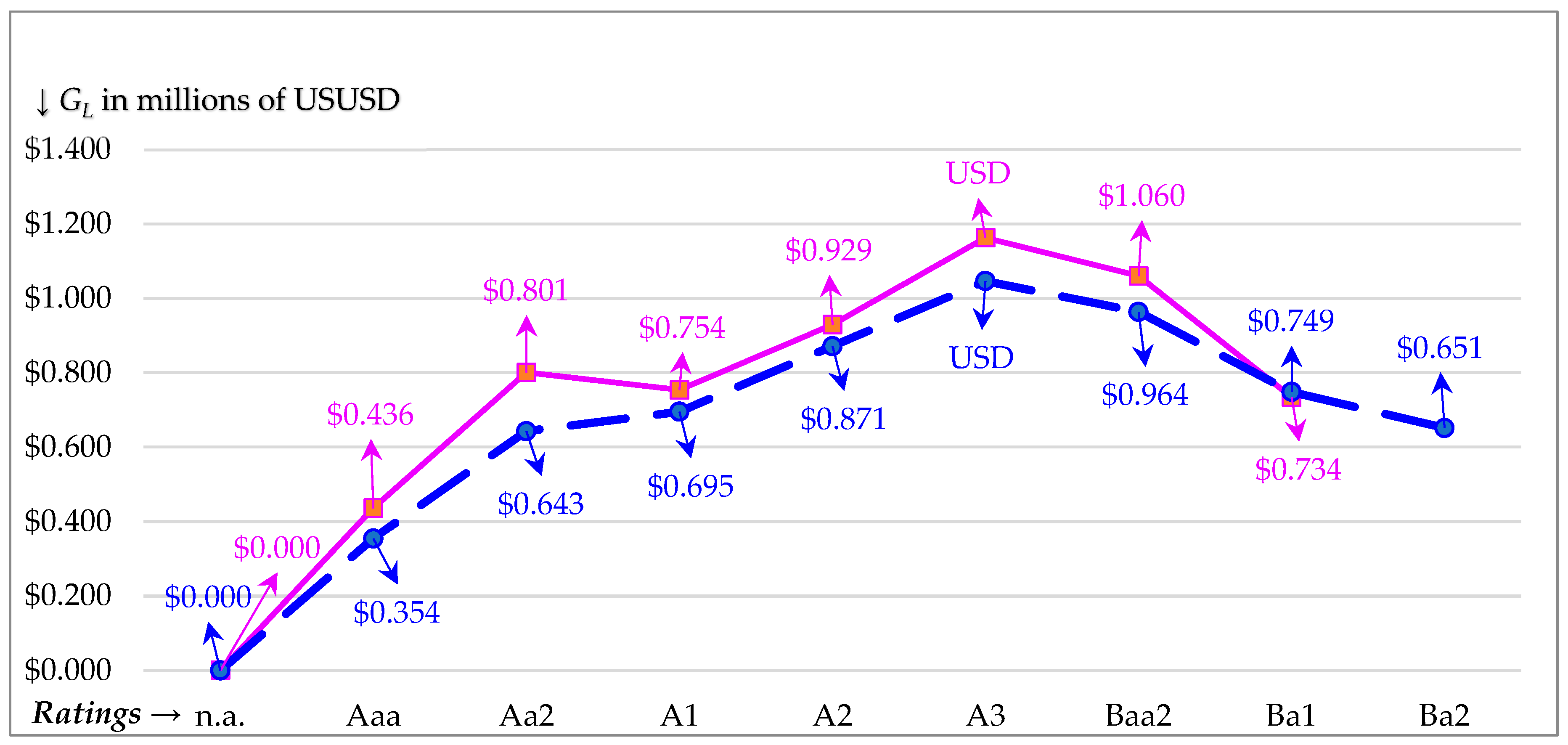
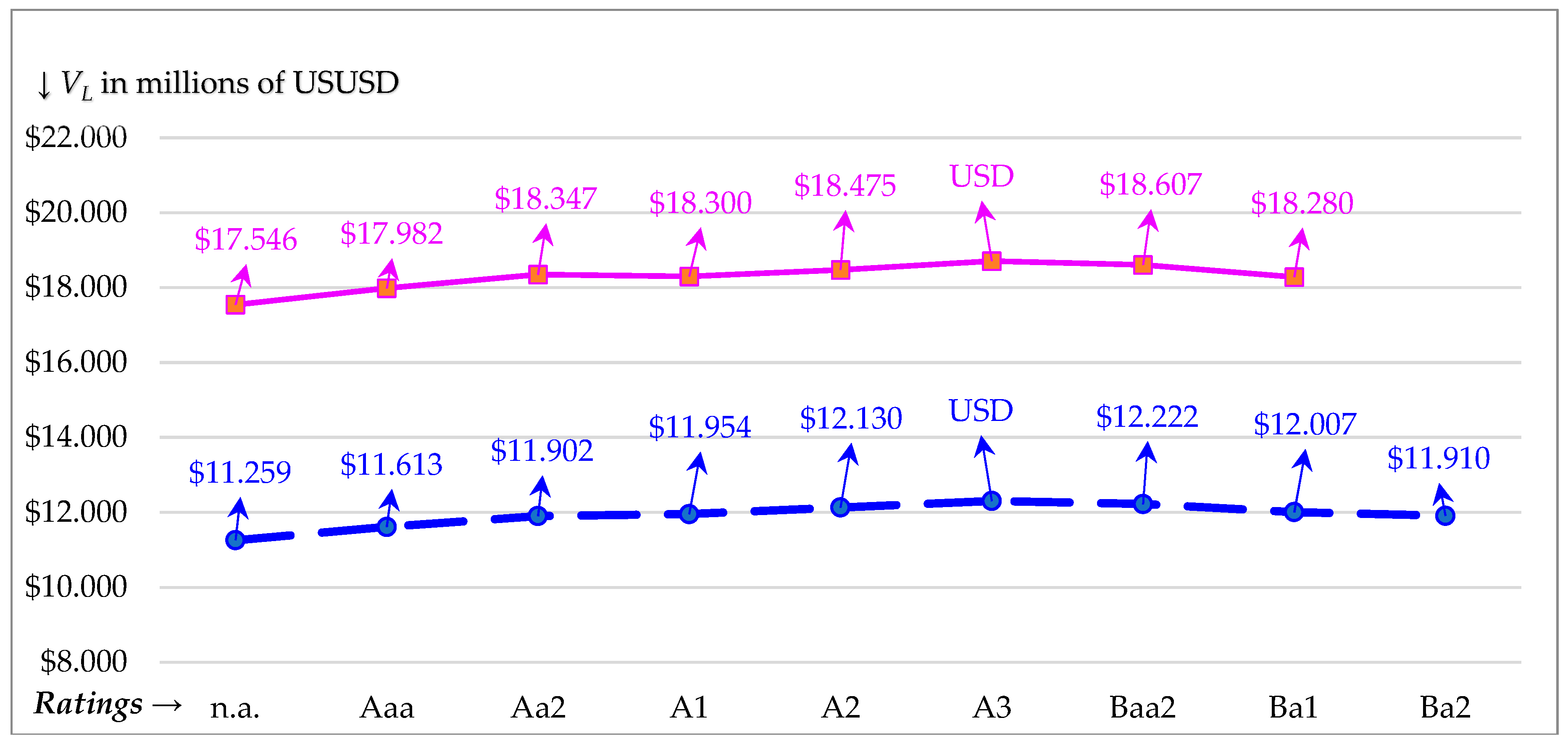
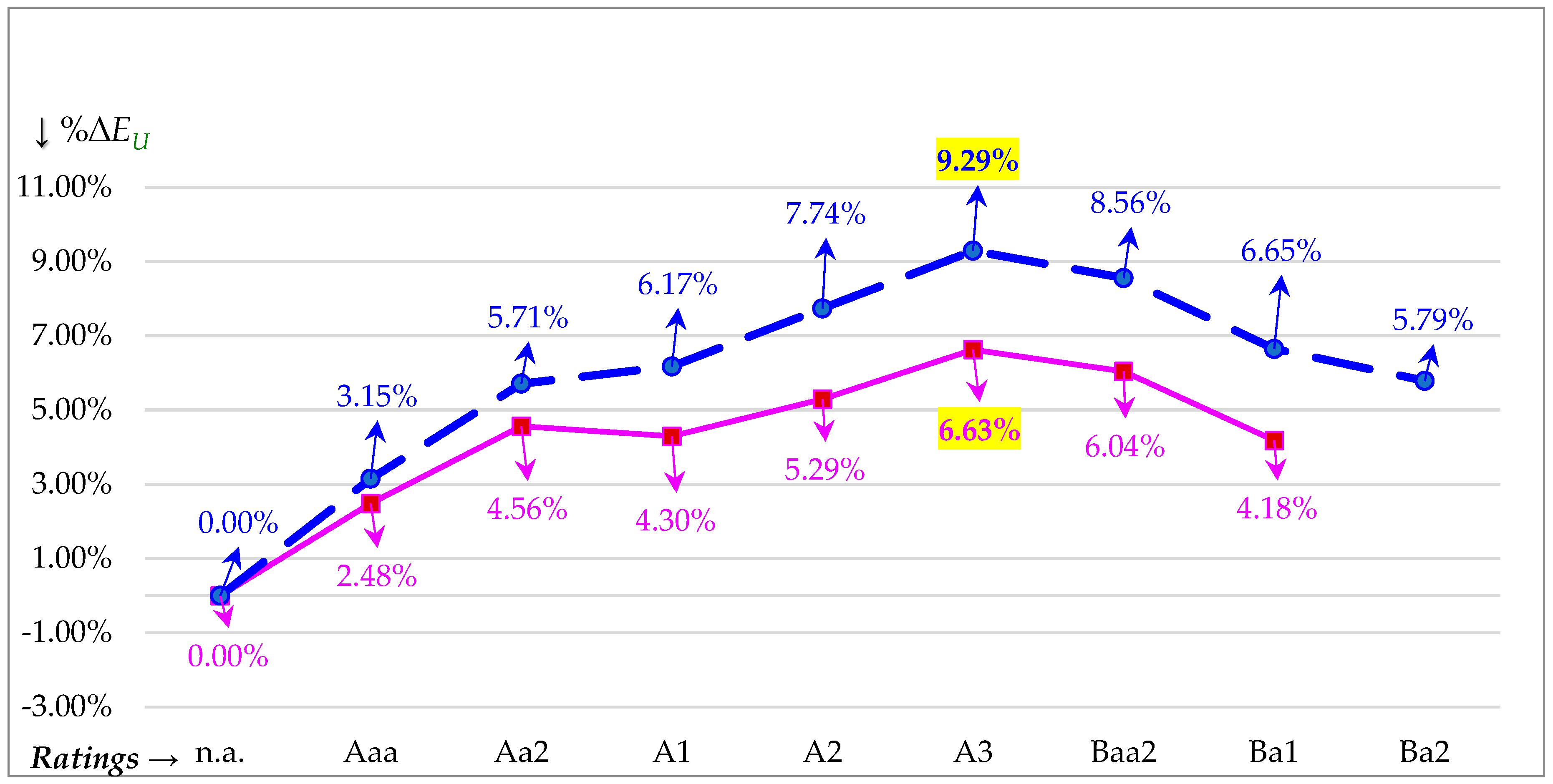




| P Choice | ICR | Moody’s Rating | Credit Spread | rD | rL | βD | βL |
|---|---|---|---|---|---|---|---|
| 0.0759 | 24.000 | Aaa | 0.6300% | 3.1300% | 6.5800% | 0.1260 | 0.8160 |
| 0.1580 | 11.000 | Aa2 | 0.7800% | 3.2800% | 6.7300% | 0.1560 | 0.8460 |
| 0.1929 | 8.500 | A1 | 0.9750% | 3.4750% | 6.9250% | 0.1950 | 0.8850 |
| 0.2361 | 6.750 | A2 | 1.0764% | 3.5764% | 7.0264% | 0.2153 | 0.9053 |
| 0.2921 | 5.250 | A3 | 1.2168% | 3.7168% | 7.1668% | 0.2434 | 0.9334 |
| 0.3303 | 4.250 | Baa2 | 1.5600% | 4.0600% | 7.5100% | 0.3120 | 1.0020 |
| 0.3370 | 3.750 | Ba1 | 2.0000% | 4.5000% | 7.9500% | 0.4000 | 1.0900 |
| 0.3579 | 3.250 | Ba2 | 2.4000% | 4.9000% | 8.3500% | 0.4800 | 1.1700 |
| 0.3448 | 2.750 | B1 | 3.5100% | 6.0100% | 9.4600% | 0.7020 | 1.3920 |
| 0.3774 | 2.250 | B2 | 4.2120% | 6.7120% | 10.1620% | 0.8424 | 1.5324 |
| 0.4258 | 1.750 | B3 | 5.1480% | 7.6480% | 11.0980% | 1.0296 | 1.7296 |
| 0.3874 | 1.375 | Caa | 8.2000% | 10.7000% | 14.1500% | 1.6400 | 2.3300 |
| 0.4994 | 1.025 | Ca2 | 8.6424% | 11.1424% | 14.5924% | 1.7285 | 2.4185 |
| 0.6335 | 0.650 | C2 | 11.3412% | 13.8412% | 17.2912% | 2.2682 | 2.9582 |
| 0.8541 | 0.380 | D2 | 15.1164% | 17.6164% | 21.0664% | 3.0233 | 3.7133 |
| Panel A. Alpha Computations |
| Nonprofit (NP) Alpha Computations: |
| For our L tax rate tests for NPs, α1 = α2 = 1 for all P choices because these tests assume NP tax rates are all zero. To illustrate with TE1 = TE2 = 0; TC1 = TC2 = 0; TD1 = TD2 = 0, we have: α1 = (1 − TE2)/(1 − TD2) = (1 − 0)(1 − 0)/(1 − 0) = 1.00. α2 = (1 − TE1)/(1 − TE2) = (1 − 0)/(1 − 0) = 1.00. |
| Pass-Through (PT) Alpha Computations: |
| The unlevered personal debt tax rate (TD1) only exist hypothetically for an unlevered situation, which is a way of saying we assign a beginning value to achieved an effective levered personal tax rate on debt (TD2) at the optimal P choice. For an unlevered situation, the unlevered personal equity tax rate (TE1) is 0.3, TD1 = 0.18, and the unlevered corporate tax rate (TC1) = 0. The latter is zero because PTs do not pay corporate taxes. For a levered situation, levered personal equity tax rate (TE2) is less than TE1 since TE2 decreases by 0.03 with each increasing P choice. TD2 is greater than TD1 since TD2 increases by 0.03 with each increasing P choice. For the first debt-for-equity choice using TE1 = 0.3, TD2 = TD1(1 + ΔTD1) = 0.18(1 + 0.03) = 0.1854, and TE2 = TE2(1 − ΔTE2) = 0.3(1 − 0.03) = 0.291, we have (to ten digits so later computations can minimize rounding off errors): α1 = (1 − TE2)/(1 − TD2) = (1 − 0.291)/(1 − 0.1854) = 0.8703658237. α2 = (1 − TE2)/(1 − TE1) = (1 − 0.291) (1 − 0.3) = 1.0128571429. For the fifth debt-for-equity choice using TD2 = TD1(1 + 0.03)5 = 0.18(1.1592740743) = 0.2086693 and TE2 = TE1(1 − 0.03)5 = 0.3(0.8587340257) = 0.25762021, we have: α1 = (1 − TE2)/(1 − TD2) = (1 − 0.25762021)/(1 − 0.2086693) = 0.9381410624. α2 = (1 − TE2)/(1 − TE1) = (1 − 0.25762021)/(1 − 0.3) = 1.0605425604. |
| Panel B. Unlevered Firm Value (EU) Computations |
| NP example using CC definitions given in Section 3.1: PBRBT = 0.2598; CFBT = USD 1,000,000; RE = PBRBT(CFBT) = 0.2598(USD 1,000,000) = USD 259,800. Cost to use RE (CRE) = TC2(RE) = 0(USD 259,800) = USD 0. %CRE per USD 1,000,000 of CFBT = USD 0/USD 1,000,000 = 0.00 or 0%. C = (1 − PBRBT)(CFBT) = (1 − 0.2598)(USD 1,000,000) = USD 740,200. gU = rU(1 − TC1)RE/C = 0.065(1 − 0)USD 259,800/USD 740,200 = 2.28141043%. EU = (1 − PBRBT)(1 − TE1)(1 − TC1)CFBT/(rU − gU) = (1 − 0.2598)(1 − 0)(1 − 0)USD 1,000,000/(0.065 − 0.0228141043) = USD 17,546,149. |
| PT example using PT definitions given in Section 3.1: PBRBT = 0.3519; CFBT = USD 1,000,000; RE = PBRBT(CFBT) = 0.3519(USD 1,000,000) = USD 351,900. Cost to use RE (CRE) = TE2(RE) = 0.25762021(USD 259,800) = USD 90,657. %CRE per USD 1,000,000 of CFBT = USD 90,657/USD 1,000,000 = 0.090657 or about 9.07%. C = (1 − PBRBT)(CFBT) = (1 − 0.3519)(USD 1,000,000) = USD 648,100. gU = rU(1 − TE1)RE/C = 0.065(1 − 0.3)USD 351,900/USD 648,100 = 0.0247052152 or 2.47052152%. EU = (1 − PBRBT)(1 − TE1)CFBT/(rU − gU) = (1 − 0.3519)(1 − 0.3)USD 1,000,000/(0.065 − 0.0247052152) = USD 11,258,777. |
| Panel A. Key Outcomes for P Choices (Optimal Outcomes in Bold Print) | |||||||||
| P Choice = Proportion of Unlevered Firm Value (EU) Retired by Debt (D) | |||||||||
| Outcomes | 0.0000 | 0.0759 | 0.1580 | 0.1929 | 0.2361 | 0.2921 | 0.3303 | 0.3377 | 0.3579 |
| Moody’s Rating | n.a. | Aaa | Aa2 | A1 | A2 | A3 | Baa2 | Ba1 | Ba2 |
| Debt (D) | 0.000 | 1.331 | 2.772 | 3.386 | 4.42 | 5.125 | 5.795 | 5.926 | n.a. |
| Equity growth rate: gL | 2.28% | 2.38% | 2.56% | 2.75% | 2.90% | 3.12% | 3.57% | 4.12% | n.a. |
| 1st component of GL | 0.000 | 0.338 | 0.591 | 0.567 | 0.556 | 0.418 | −0.175 | −1.031 | n.a. |
| 2nd component of GL | 0.000 | 0.098 | 0.210 | 0.187 | 0.373 | 0.745 | 1.235 | 1.765 | n.a. |
| Gain to leverage: GL | 0.000 | 0.436 | 0.801 | 0.754 | 0.929 | 1.163 | 1.060 | 0.734 | n.a. |
| Firm value: VL | 17.546 | 17.982 | 18.347 | 18.300 | 18.475 | 18.709 | 18.607 | 18.280 | n.a. |
| Equity value: EL | 17.546 | 16.651 | 15.575 | 14.914 | 14.333 | 13.584 | 12.811 | 12.354 | n.a. |
| %∆EU | 0.00% | 2.48% | 4.56% | 4.30% | 5.29% | 6.63% | 6.04% | 4.18% | n.a. |
| NB | 0.00% | 32.74% | 28.88% | 22.27% | 22.42% | 22.69% | 18.30% | 12.39% | n.a. |
| DV | 0.0000 | 0.0740 | 0.1511 | 0.1850 | 0.2242 | 0.2739 | 0.3115 | 0.3242 | n.a. |
| Panel B. Computations for Optimal Outcomes at P = 0.2921 | |||||||||
| D = P = 0.2921(USD 17,546,148.72) = USD 5,124,736.08 or D = (1 − TD2)I/rD = (1 − 0)USD 190,476.19/0.037168 = USD 5,124,736.08. gL = rL(1 − TC2)RE/[C + G − (1 − TC2)I] = 0.71668(1 − 0)USD 259,800/[USD 740,200 + USD 47,052.52 − (1 − 0)USD 190,476.19] = 0.0311998742 or about 3.12%. Max GL = (1 − αIrD/rLg)D + (1 − α2rUg/rLg)EU = [1 − 1.00000(0.037168)/0.0404681258]USD 5,124,736.08 + [1 − 1.00(0.0421858957)/0.0404681258]USD 17,546,148.72 = USD 417,915.91 − USD 744,789.77 = USD 1,162,706. Max VL = EU + Max GL = USD 17,546,149 + USD 1,162,706 = USD 18,708,854. EL = VL − D = USD 18,708,854 − USD 5,124,736.08 = USD 13,584,118. Max %∆EU = Max GL/EU = USD 1,162,706/USD 17,546,149 = 0.0663 or 6.63%. NB = Max GL/D = USD 1,162,706/USD 5,124,736.08 = 0.2269 or 22.69%. ODV = D/Max VL = USD 5,124,736.08/USD 18,708,854 = 0.2739. | |||||||||
| Panel A. Key Outcomes for P Choices (Optimal Outcomes in Bold Print) | |||||||||
| P Choice = Proportion of Unlevered Firm Value (EU) Retired by Debt (D) | |||||||||
| Outcomes | 0.0000 | 0.0683 | 0.1429 | 0.1754 | 0.2155 | 0.2674 | 0.3031 | 0.3131 | 0.3322 |
| Moody’s Rating | n.a. | Aaa | Aa2 | A1 | A2 | A3 | Baa2 | Ba1 | Ba2 |
| Debt (D) | 0.000 | 0.769 | 1.609 | 1.975 | 2.426 | 3.011 | 3.413 | 3.525 | 3.740 |
| Equity growth rate: gL | 2.47% | 2.54% | 2.67% | 2.83% | 2.94% | 3.12% | 3.49% | 3.97% | 4.49% |
| 1st component of GL | 0.000 | 0.251 | 0.457 | 0.460 | 0.468 | 0.417 | 0.116 | −0.317 | −0.919 |
| 2nd component of GL | 0.000 | 0.104 | 0.186 | 0.235 | 0.403 | 0.629 | 0.848 | 1.066 | 1.570 |
| Gain to leverage: GL | 0.000 | 0.354 | 0.643 | 0.695 | 0.871 | 1.046 | 0.964 | 0.749 | 0.651 |
| Firm value: VL | 11.259 | 11.613 | 11.902 | 11.954 | 12.130 | 12.305 | 12.222 | 12.007 | 11.910 |
| Equity value: EL | 11.259 | 10.844 | 10.292 | 9.979 | 9.704 | 9.294 | 8.810 | 8.483 | 8.170 |
| %∆EU | 0.00% | 3.15% | 5.71% | 6.17% | 7.74% | 9.29% | 8.56% | 6.65% | 5.79% |
| NB | 0.00% | 46.11% | 39.96% | 35.20% | 35.91% | 34.75% | 28.23% | 21.24% | 17.42% |
| DV | 0.0000 | 0.0662 | 0.1352 | 0.1652 | 0.2000 | 0.2447 | 0.2792 | 0.2935 | 0.3140 |
| Panel B. Computations for Optimal Outcomes at P = 0.2674 | |||||||||
| D = P(EU) = 0.2674(USD 11,258,777.1) = USD 3,010,617.92 or D = (1 − TD2)I/rD = (1 − 0.208669333)USD 141,405.67/0.037168 = USD 3,010,617.92. gL = rL(1 − TC2)RE/[C + G − (1 − TC2)I] = 0.071668(1 − 0.25762021)USD 351,900/[USD 648,100 + USD 57,036.74 − (1 − 0.25762021)USD 141,405.67] = 0.0311963388 or about 3.12%. Max GL = (1 − αIrD/rLg)D + (1 − α2rUg/rLg)EU = [1 − 0.9381410624(0.037168)/0.04029478476]USD 3,010,617.92 + [1 − 1.0605425604(0.04029478476)/0.0404716612]USD 11,258,777.1 = USD 416,785 − USD 629,451 = USD 1,046,236. Max VL = EU + Max GL = USD 11,258,777 + USD 1,046,236 = USD 12,305,013. EL = VL − D = USD 12,305,013 − USD 3,010,617.92 = USD 9,294,396. Max %∆EU = Max GL/EU = USD 1,046,236/USD 11,258,777 = 0.0929 or 9.29%. NB = Max GL/D = USD 1,046,236/USD 3,010,617.92 = 0.3475 or 34.75%. ODV = D/Max VL = USD 3,010,617.92/USD 12,305,013 = 0.2447. | |||||||||
| P | PBRBT | gU | EU | Max VL | Max GL | Max %∆EU | NB | ODV | OCR | DGN | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2014: NP-L | 0.1499 | 0.3025 | 2.819% | USD 18.949 | USD 20.027 | USD 1.078 | 5.69% | 37.96% | 0.1419 | Aa2 | USD 3.516 |
| 2014: NP-H | 0.1474 | 0.3073 | 2.826% | USD 18.107 | USD 19.129 | USD 1.022 | 5.64% | 38.27% | 0.1395 | Aa2 | USD 3.274 |
| 2014: PT-L | 0.2683 | 0.3528 | 2.480% | USD 11.270 | USD 12.340 | USD 1.070 | 9.49% | 35.38% | 0.2451 | A3 | USD 0.401 |
| 2014: PT- H | 0.2806 | 0.3786 | 2.535% | USD 10.029 | USD 11.211 | USD 1.182 | 11.78% | 41.99% | 0.2510 | A3 | USD 0.006 |
| 2015: NP-L | 0.1810 | 0.2778 | 2.500% | USD 18.056 | USD 18.649 | USD 0.592 | 3.28% | 18.18% | 0.1752 | A1 | USD 2.865 |
| 2015: NP-H | 0.1777 | 0.2826 | 2.509% | USD 17.265 | USD 17.828 | USD 0.563 | 3.26% | 18.36% | 0.1721 | A1 | USD 2.668 |
| 2015: PT-L | 0.2047 | 0.3551 | 2.505% | USD 11.301 | USD 11.964 | USD 0.663 | 5.86% | 28.65% | 0.1934 | A2 | USD 0.560 |
| 2015: PT- H | 0.2137 | 0.3800 | 2.550% | USD 10.045 | USD 10.815 | USD 0.770 | 7.67% | 35.88% | 0.1985 | A2 | USD 0.161 |
| 2016: NP-L | 0.2902 | 0.2582 | 2.262% | USD 17.505 | USD 18.594 | USD 1.089 | 6.22% | 21.43% | 0.2732 | A3 | USD 2.271 |
| 2016: NP-H | 0.2843 | 0.2630 | 2.273% | USD 16.746 | USD 17.776 | USD 1.031 | 6.15% | 21.65% | 0.2678 | A3 | USD 2.111 |
| 2016: PT-L | 0.2656 | 0.3501 | 2.451% | USD 11.236 | USD 12.235 | USD 1.000 | 8.90% | 33.50% | 0.2439 | A3 | USD 0.399 |
| 2016: PT- H | 0.2777 | 0.3759 | 2.506% | USD 10.000 | USD 11.117 | USD 1.118 | 11.18% | 40.25% | 0.2498 | A3 | USD 0.008 |
| 2017: NP-L | 0.3608 | 0.2495 | 2.161% | USD 17.296 | USD 18.809 | USD 1.513 | 8.75% | 24.25% | 0.3318 | Baa2 | USD 1.977 |
| 2017: NP-H | 0.3531 | 0.2543 | 2.172% | USD 16.549 | USD 17.975 | USD 1.426 | 8.62% | 24.40% | 0.3251 | Baa2 | USD 1.836 |
| 2017: PT-L | 0.3295 | 0.3433 | 2.379% | USD 11.154 | USD 12.462 | USD 1.308 | 11.73% | 35.60% | 0.2949 | Baa2 | USD 0.231 |
| 2017: PT- H | 0.3452 | 0.3698 | 2.441% | USD 9.937 | USD 11.378 | USD 1.441 | 14.50% | 42.00% | 0.3015 | Baa2 | −USD 0.152 |
| 2018: NP-L | 0.2733 | 0.2431 | 2.088% | USD 17.154 | USD 17.584 | USD 0.430 | 2.51% | 9.18% | 0.2666 | A3 | USD 2.120 |
| 2018: NP-H | 0.2677 | 0.2479 | 2.100% | USD 16.415 | USD 16.819 | USD 0.404 | 2.46% | 9.20% | 0.2613 | A3 | USD 1.974 |
| 2018: PT-L | 0.2493 | 0.3335 | 2.277% | USD 11.047 | USD 11.630 | USD 0.583 | 5.28% | 21.18% | 0.2368 | A3 | USD 0.391 |
| 2018: PT- H | 0.2606 | 0.3590 | 2.330% | USD 9.838 | USD 10.576 | USD 0.739 | 7.51% | 28.83% | 0.2424 | A3 | USD 0.027 |
| 2019: NP-L | 0.2921 | 0.2598 | 2.281% | USD 17.546 | USD 18.709 | USD 1.163 | 6.63% | 22.69% | 0.2739 | A3 | USD 2.289 |
| 2019: NP-H | 0.2861 | 0.2647 | 2.293% | USD 16.786 | USD 17.888 | USD 1.102 | 6.56% | 22.94% | 0.2685 | A3 | USD 2.130 |
| 2019: PT-L | 0.2674 | 0.3519 | 2.471% | USD 11.259 | USD 12.305 | USD 1.046 | 9.29% | 34.75% | 0.2447 | A3 | USD 0.401 |
| 2019: PT-H | 0.2796 | 0.3777 | 2.525% | USD 10.019 | USD 11.179 | USD 1.160 | 11.58% | 41.41% | 0.2506 | A3 | USD 0.006 |
| 2014-17: NP-L | 0.2455 | 0.2720 | 2.44% | USD 17.952 | USD 19.020 | USD 1.068 | 5.99% | 25.44% | 0.2305 | A2 | USD 2.657 |
| 2014-17: NP-H | 0.2406 | 0.2768 | 2.45% | USD 17.167 | USD 18.177 | USD 1.010 | 5.92% | 25.67% | 0.2261 | A2 | USD 2.472 |
| 2014-17: PT-L | 0.2670 | 0.3503 | 2.45% | USD 11.240 | USD 12.250 | USD 1.010 | 9.00% | 33.28% | 0.2443 | A3 | USD 0.398 |
| 2014-17: PT-H | 0.2793 | 0.3761 | 2.51% | USD 10.003 | USD 11.130 | USD 1.128 | 11.28% | 40.03% | 0.2502 | A3 | USD 0.006 |
| 2018-19: NP-L | 0.2827 | 0.2515 | 2.185% | USD 17.350 | USD 18.147 | USD 0.796 | 4.57% | 15.93% | 0.2703 | A3 | USD 2.204 |
| 2018-19: NP-H | 0.2769 | 0.2563 | 2.196% | USD 16.601 | USD 17.354 | USD 0.753 | 4.51% | 16.07% | 0.2649 | A3 | USD 2.052 |
| 2018-19: PT-L | 0.2584 | 0.3427 | 2.374% | USD 11.153 | USD 11.968 | USD 0.815 | 7.29% | 27.96% | 0.2407 | A3 | USD 0.396 |
| 2018-19: PT-H | 0.2701 | 0.3684 | 2.427% | USD 9.928 | USD 10.878 | USD 0.950 | 9.55% | 35.12% | 0.2465 | A3 | USD 0.017 |
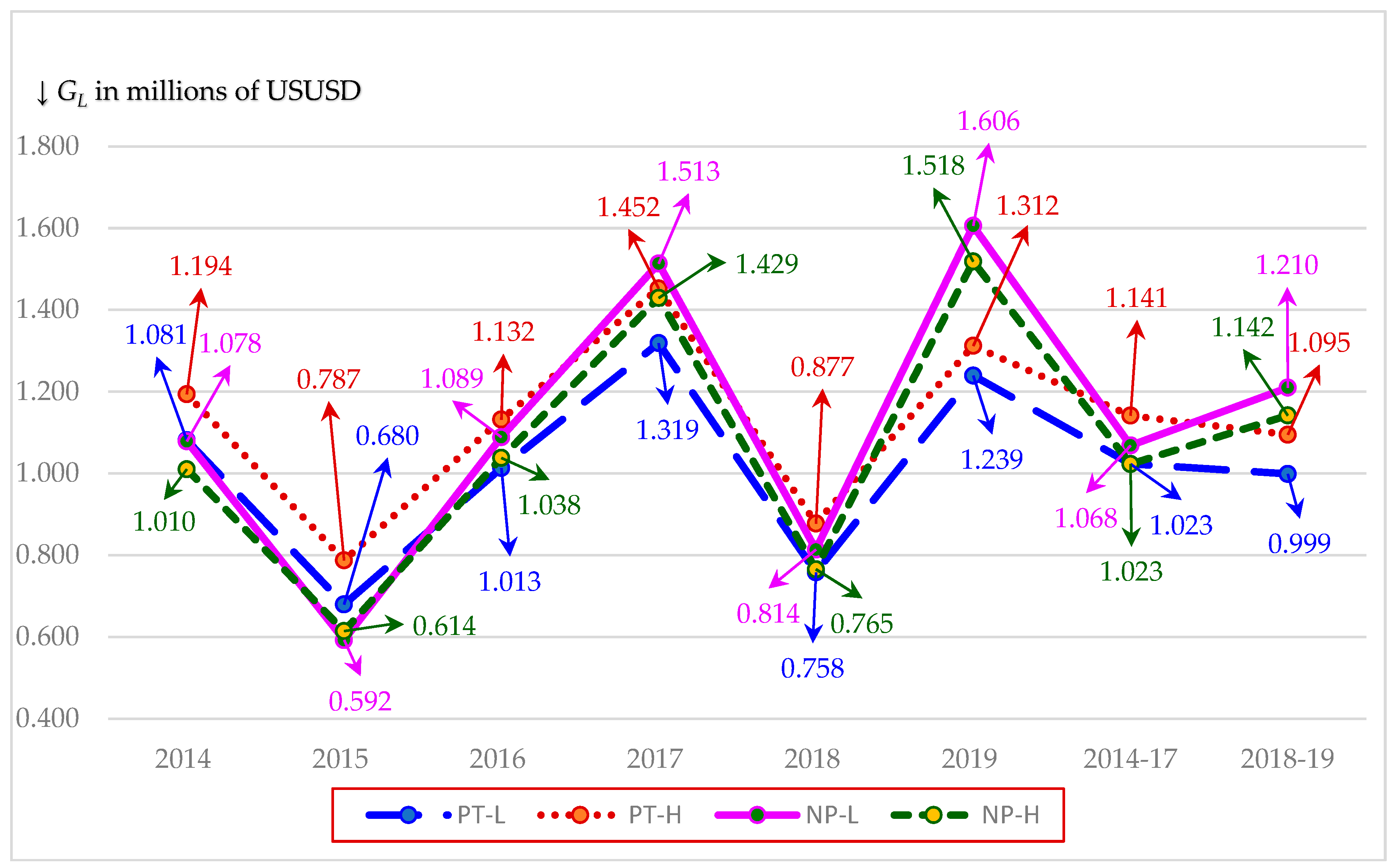
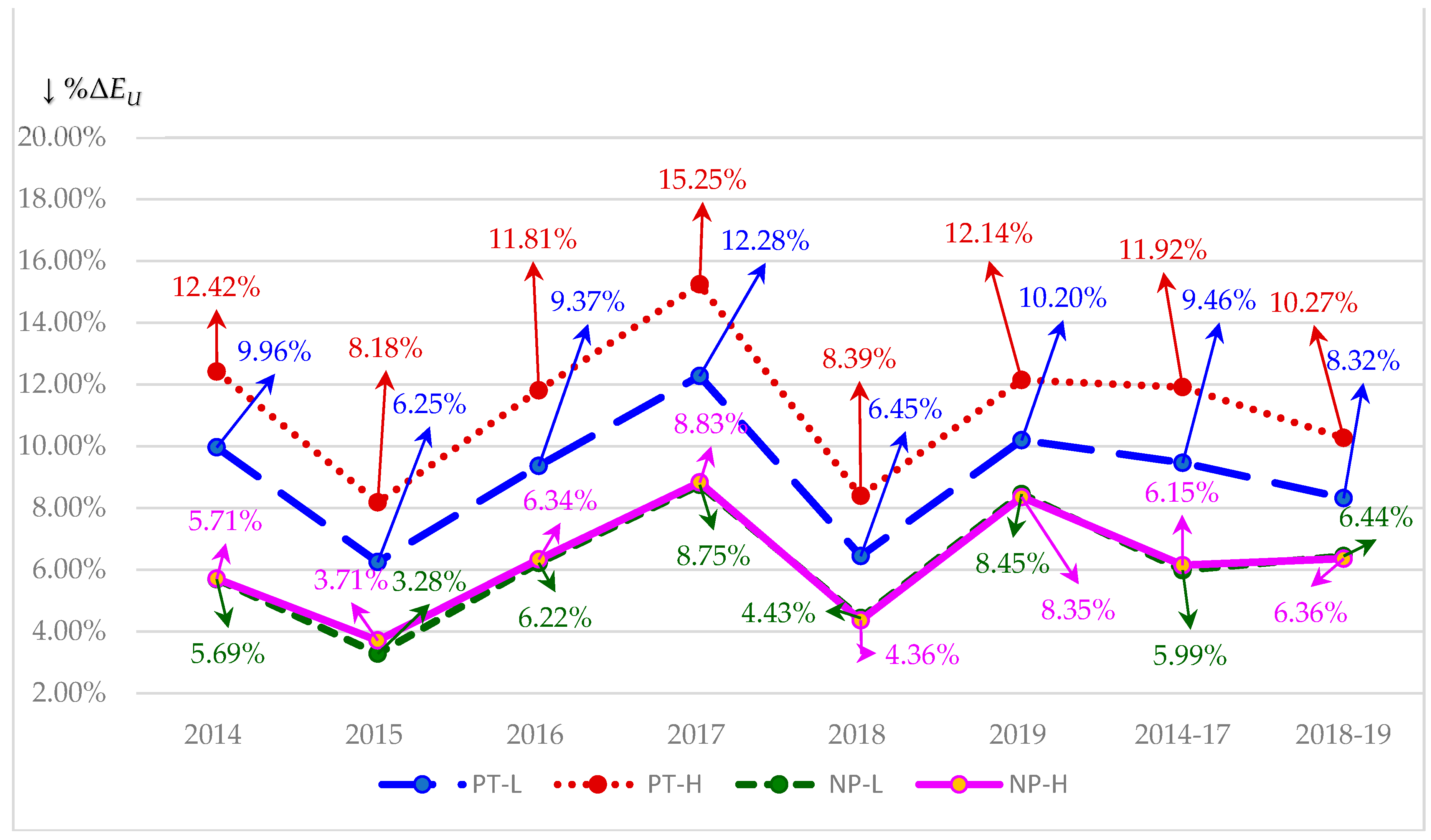
| P | PBRBT | gU | EU | Max VL | Max GL | Max %∆EU | NB | ODV | OCR | DGN | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2014: NP-L | 0.1499 | 0.3025 | 2.819% | USD 18.949 | USD 20.027 | USD 1.078 | 5.69% | 37.96% | 0.1419 | Aa2 | USD 3.516 |
| 2014: NP-H | 0.1477 | 0.3099 | 2.831% | USD 17.699 | USD 18.709 | USD 1.010 | 5.71% | 38.64% | 0.1397 | Aa2 | USD 3.149 |
| 2014: PT-L | 0.2683 | 0.3606 | 2.493% | USD 10.850 | USD 11.931 | USD 1.081 | 9.96% | 37.14% | 0.2440 | A3 | USD 0.279 |
| 2014: PT- H | 0.2814 | 0.3872 | 2.546% | USD 9.610 | USD 10.803 | USD 1.194 | 12.42% | 44.14% | 0.2503 | A3 | −USD 0.114 |
| 2015: NP-L | 0.1810 | 0.2778 | 2.500% | USD 18.056 | USD 18.649 | USD 0.592 | 3.28% | 18.13% | 0.1752 | A1 | USD 2.865 |
| 2015: NP-H | 0.2193 | 0.2729 | 2.366% | USD 16.551 | USD 17.165 | USD 0.614 | 3.71% | 16.92% | 0.2114 | A2 | USD 2.273 |
| 2015: PT-L | 0.2047 | 0.3627 | 2.516% | USD 10.876 | USD 11.556 | USD 0.680 | 6.25% | 30.53% | 0.1926 | A2 | USD 0.433 |
| 2015: PT- H | 0.2142 | 0.3884 | 2.559% | USD 9.622 | USD 10.410 | USD 0.787 | 8.18% | 38.19% | 0.1980 | A2 | USD 0.038 |
| 2016: NP-L | 0.2902 | 0.2582 | 2.262% | USD 17.505 | USD 18.594 | USD 1.089 | 6.22% | 21.43% | 0.2732 | A3 | USD 2.271 |
| 2016: NP-H | 0.2846 | 0.2659 | 2.284% | USD 16.382 | USD 17.420 | USD 1.038 | 6.34% | 22.27% | 0.2676 | A3 | USD 2.022 |
| 2016: PT-L | 0.2655 | 0.3579 | 2.464% | USD 10.817 | USD 11.831 | USD 1.013 | 9.37% | 35.27% | 0.2428 | A3 | USD 0.277 |
| 2016: PT- H | 0.2785 | 0.3844 | 2.516% | USD 9.581 | USD 10.713 | USD 1.132 | 11.81% | 42.42% | 0.2491 | A3 | −USD 0.111 |
| 2017: NP-L | 0.3608 | 0.2495 | 2.161% | USD 17.296 | USD 18.809 | USD 1.513 | 8.75% | 24.25% | 0.3318 | Baa2 | USD 1.977 |
| 2017: NP-H | 0.3534 | 0.2573 | 2.184% | USD 16.192 | USD 17.621 | USD 1.429 | 8.83% | 24.98% | 0.3247 | Baa2 | USD 1.753 |
| 2017: PT-L | 0.3295 | 0.3511 | 2.392% | USD 10.740 | USD 12.059 | USD 1.319 | 12.28% | 37.26% | 0.2935 | Baa2 | USD 0.144 |
| 2017: PT- H | 0.3463 | 0.3785 | 2.454% | USD 9.524 | USD 10.977 | USD 1.452 | 15.25% | 44.04% | 0.3004 | Baa2 | −USD 0.265 |
| 2018: NP-L | 0.2555 | 0.2867 | 2.613% | USD 18.349 | USD 19.163 | USD 0.814 | 4.43% | 17.36% | 0.2447 | A3 | USD 3.698 |
| 2018: NP-H | 0.2503 | 0.2919 | 2.626% | USD 17.554 | USD 18.320 | USD 0.765 | 4.36% | 17.42% | 0.2399 | A3 | USD 3.474 |
| 2018: PT-L | 0.2342 | 0.3835 | 2.830% | USD 11.760 | USD 12.518 | USD 0.758 | 6.45% | 27.52% | 0.2200 | A3 | USD 1.279 |
| 2018: PT- H | 0.2451 | 0.4097 | 2.887% | USD 10.457 | USD 11.335 | USD 0.877 | 8.39% | 34.23% | 0.2261 | A3 | USD 0.785 |
| 2019: NP-L | 0.2697 | 0.3038 | 2.836% | USD 19.003 | USD 20.609 | USD 1.606 | 8.45% | 31.33% | 0.2487 | A3 | USD 4.189 |
| 2019: NP-H | 0.2642 | 0.3091 | 2.850% | USD 18.178 | USD 19.697 | USD 1.518 | 8.35% | 31.61% | 0.2439 | A3 | USD 3.939 |
| 2019: PT-L | 0.2477 | 0.4016 | 3.054% | USD 12.154 | USD 13.394 | USD 1.239 | 10.20% | 41.17% | 0.2248 | A3 | USD 1.489 |
| 2019: PT-H | 0.2593 | 0.4279 | 3.111% | USD 10.805 | USD 12.118 | USD 1.312 | 12.14% | 46.83% | 0.2312 | A3 | USD 0.945 |
| 2014-17: NP-L | 0.2259 | 0.2778 | 2.52% | USD 18.232 | USD 19.268 | USD 1.035 | 5.74% | 32.43% | 0.2121 | A2 | USD 2.657 |
| 2014-17: NP-H | 0.2320 | 0.2823 | 2.50% | USD 16.962 | USD 17.953 | USD 0.992 | 5.90% | 32.77% | 0.2178 | A2 | USD 2.299 |
| 2014-17: PT-L | 0.2670 | 0.3581 | 2.47% | USD 10.821 | USD 11.844 | USD 1.023 | 9.46% | 35.05% | 0.2432 | A3 | USD 0.276 |
| 2014-17: PT-H | 0.2801 | 0.3846 | 2.52% | USD 9.584 | USD 10.726 | USD 1.141 | 11.92% | 42.20% | 0.2495 | A3 | −USD 0.113 |
| 2018-19: NP-L | 0.2626 | 0.2953 | 2.724% | USD 18.676 | USD 19.886 | USD 1.210 | 6.44% | 24.34% | 0.2467 | A3 | USD 3.944 |
| 2018-19: NP-H | 0.2573 | 0.3005 | 2.738% | USD 17.866 | USD 19.008 | USD 1.142 | 6.36% | 24.52% | 0.2419 | A3 | USD 3.707 |
| 2018-19: PT-L | 0.2410 | 0.3926 | 2.942% | USD 11.957 | USD 12.956 | USD 0.999 | 8.32% | 34.34% | 0.2224 | A3 | USD 1.384 |
| 2018-19: PT-H | 0.2522 | 0.4188 | 2.999% | USD 10.631 | USD 11.726 | USD 1.095 | 10.27% | 40.53% | 0.2287 | A3 | USD 0.865 |
| P | PBRBT | gU | EU | Max VL | Max GL | Max %∆EU | NB | ODV | OCR | DGN | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| T5-L | 9.42% | −26.63% | −7.97% | 55.57% | 51.63% | −2.25% | −37.32% | −43.03% | 12.27% | A3 | USD 1.808 |
| T5-H | 2.53% | −30.42% | −9.52% | 67.20% | 59.53% | −20.69% | −52.72% | −54.24 | 7.47% | A3 | USD 2.035 |
| T6-L | 8.98% | −24.79% | −7.39% | 56.19% | 53.49% | 21.14% | −22.58% | −29.11% | 10.91% | A3 | USD 2.841 |
| T6-H | 2.01% | −28.25% | −8.72% | 68.05% | 62.10% | 4.30% | −38.09% | −39.52% | 5.77% | A3 | USD 2.841 |
| Mean | 5.73% | −27.52% | −8.40% | 61.75% | 56.69% | 0.62% | −37.68% | −41.48% | 9.10% | A3 | USD 2.311 |
| StDev | 4.01% | 2.39% | 0.92% | 6.80% | 4.94% | 17.29% | 12.31% | 10.36% | 3.00% | n.a. | USD 0.445 |
| Nonprofit | Pass-Through |
|---|---|
| Owned By: No one | Owned By: Investors |
| Ownership types: Corporation (501c3), association, trust | Ownership types: Sole proprietorship, partnership, LLC, S corp |
| Board Members: Nominated | Board Members: Elected by owners (if applicable) |
| Official obligations: Fulfill duties related to goals involving service, education, and research | Official obligations: Increase ownership wealth by providing profitable services and products |
| Major Goal: Maximize value in terms of service distributions | Major Goal: Maximize value in terms of monetary distributions |
| Mission: Described largely in terms of service, education, research, and growth | Mission: Described largely in terms of profit, efficiency, service, growth |
| Decision-making and implementation: Cautiously proceeds to satisfy mission and constituencies | Decision-making and implementation: Quickly responds to profitable opportunities |
| Sources of Revenues: Services, contributions, grants, and investments (including endowment income) | Sources of Revenues: Business activities (sales and services) and investments in other businesses |
| Equity Distributions: Non-monetary distributions in form of services rendered to those in need | Equity Distributions: Monetary distributions to owners in form of cash payouts and capital gains |
| Sources of Equity Financing: Internal equity (eligible revenues, investment/endowment income); External equity (contributions, grants, government) | Sources of Equity Financing: Internal equity (retained earnings); External equity (new partners, new issuances, venture capital) |
| Sources of Debt Financing: Personal tax-exempt debt, nonfinancial debt (mortgages), short-term debt (trade credit, bank borrowings avoided) | Sources of Debt Financing: Bond issues, mezzanine debt, Small Business Administration loans, short-term debt (trade credit, bank borrowings) |
| Corporate Taxes: Zero or very little taxes resulting from minor taxable profitable ventures | Corporate Taxes: None as PTs do not pay corporate taxes |
| Personal Equity Taxes: Zero or very little taxes from minor taxable for-profit ventures | Personal Equity Taxes: Personal taxes paid on business income (even if undistributed) |
| Personal Debt Taxes: Zero or minor due to issuing mostly tax-exempt debt | Personal Debt Taxes: Personal taxes paid on interest from debt |
| Interest Tax Shield: Zero or very little business tax shield (typically at corporate tax level) | Interest Tax Shield: Full business tax shield (at personal tax level) |
| Nonprofit (Unlevered and Levered Tax Rates) | Pass-Through (Unlevered and Levered Tax Rates) |
|---|---|
| Panel A: Low (L) Tax Rates | |
| Pre-TCJA | Pre-TCJA |
| TC1 = 0 and TC2 = 0 | TC1 = 0 and TC2 = 0 |
| TE1 = 0 and TE2 = 0 | TE1 = 0.320 and TE2 = 0.275 |
| TD1 = 0 and TD2 = 0 | TD1 = 0.190 and TD2 = 0.220 |
| TCJA | TCJA |
| TC1 = 0 and TC2 = 0 | TC1 = 0 and TC2 = 0 |
| TE1 = 0 and TE2 = 0 | TE1 = 0.300 and TE2 = 0.255 |
| TD1 = 0 and TD2 = 0 | TD1 = 0.180 and TD2 = 0.210 |
| Panel B: High (H) Tax Rates | |
| Pre-TCJA | Pre-TCJA |
| TC1 = 0.030 and TC2 = 0.025 | TC1 = 0 and TC2 = 0 |
| TE1 = 0.030 and TE2 = 0.025 | TE1 = 0.380 and TE2 = 0.330 |
| TD1 = 0.050 and TD2 = 0.060 | TD1 = 0.190 and TD2 = 0.220 |
| TCJA | TCJA |
| TC1 = 0.020 and TC2 = 0.020 | TC1 = 0 and TC2 = 0 |
| TE1 = 0.020 and TE2 = 0.020 | TE1 = 0.360 and TE2 = 0.310 |
| TD1 = 0.040 and TD2 = 0.045 | TD1 = 0.180 and TD2 = 0.210 |
| Credit Ratings Moody’s/S&P | Credit Spreads by Years/Periods (Means for the Two Periods in the Last Two Columns) | |||||||
|---|---|---|---|---|---|---|---|---|
| 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2014–2017 | 2018–2019 | |
| Aaa/AAA | 0.4000% | 0.7500% | 0.6000% | 0.5400% | 0.7500% | 0.6300% | 0.5725% | 0.6900% |
| Aa2/AA | 0.7000% | 1.0000% | 0.8000% | 0.7200% | 1.0000% | 0.7800% | 0.8050% | 0.8900% |
| A1/A+ | 0.9000% | 1.1000% | 1.0000% | 0.9000% | 1.2500% | 0.9750% | 0.9750% | 1.1125% |
| A2/A | 1.0000% | 1.2500% | 1.1000% | 0.9900% | 1.3750% | 1.0764% | 1.0850% | 1.2257% |
| A3/A- | 1.2000% | 1.7500% | 1.2500% | 1.1300% | 1.5625% | 1.2168% | 1.3325% | 1.3897% |
| Baa2/BBB | 1.7500% | 2.2500% | 1.6000% | 1.2700% | 2.0000% | 1.5600% | 1.7175% | 1.7800% |
| Ba1/BB+ | 2.7500% | 3.2500% | 2.5000% | 1.9800% | 3.0000% | 2.0000% | 2.6200% | 2.5000% |
| Ba2/BB | 3.2500% | 4.2500% | 3.0000% | 2.3800% | 3.6000% | 2.4000% | 3.2200% | 3.0000% |
| B1/B+ | 4.0000% | 5.5000% | 3.7500% | 2.9800% | 4.5000% | 3.5100% | 4.0575% | 4.0050% |
| B2/B | 5 0000% | 6.5000% | 4.5000% | 3.5700% | 5.4000% | 4.2120% | 4.8925% | 4.8060% |
| B3/B- | 6.0000% | 7.5000% | 5.5000% | 4.3700% | 6.6000% | 5.1480% | 5.8425% | 5.8740% |
| Caa/CCC | 7.0000% | 9.0000% | 6.5000% | 8.6400% | 9.0000% | 8.2000% | 7.7850% | 8.6000% |
| Ca2/CC | 8.0000% | 12.0000% | 8.0000% | 10.6300% | 11.0800% | 8.6424% | 9.6575% | 9.8612% |
| C2/C | 10.0000% | 16.0000% | 10.5000% | 13.9500% | 14.5400% | 11.3412% | 12.6125% | 12.9406% |
| D2/D | 12.0000% | 20.0000% | 14.0000% | 18.6000% | 19.3800% | 15.1164% | 16.1500% | 17.2482% |
| Mean | 4.2633% | 6.1400% | 4.3067% | 4.8433% | 5.6692% | 4.4539% | 4.8883% | 5.0615% |
| StDev | 3.6493% | 5.8879% | 3.9770% | 5.5558% | 5.5745% | 4.4309% | 4.7429% | 4.9991% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hull, R.; Van Dalsem, S. Nonprofits and Pass-Throughs: Performance Comparison. Int. J. Financial Stud. 2021, 9, 13. https://0-doi-org.brum.beds.ac.uk/10.3390/ijfs9010013
Hull R, Van Dalsem S. Nonprofits and Pass-Throughs: Performance Comparison. International Journal of Financial Studies. 2021; 9(1):13. https://0-doi-org.brum.beds.ac.uk/10.3390/ijfs9010013
Chicago/Turabian StyleHull, Robert, and Shane Van Dalsem. 2021. "Nonprofits and Pass-Throughs: Performance Comparison" International Journal of Financial Studies 9, no. 1: 13. https://0-doi-org.brum.beds.ac.uk/10.3390/ijfs9010013







