Investigation of Combining Logitboost(M5P) under Active Learning Classification Tasks
Abstract
:1. Introduction
- inductive/transductive approaches, where an explicit learning rule is formatted using the train set during the former one, trying to apply this on a distinct test set, while these two sets are both provided in advance during the latter;
- incomplete/inaccurate supervision, where both labeled and unlabeled examples are initially gathered regarding the first category, on contrast with the second one which is distinguished because of the noise that may govern the provided labeled examples, a fact that would cause intense deterioration on learning a specific task; and
- active/semi-supervised learning, where there is a straightforward separation of the approaches that need or demand human intervention so as to blend human’s knowledge into their total learning kernel for acquiring safer decisions instead of being based solely on a base learner’s predictions building a more automated learning chain but with greater risks.
2. Materials and Methods
- heterogeneity-based,
- performance-based,
- representativeness-based, and
- hybrid ones,
| Algorithm 1Active learning scheme |
| 1: Mode: |
| 2: Pool-based scenario over a provided dataset D = Xn x N ⋃ Yn x 1 |
| 3: xi—i-th instance vector with N features xi: <x1, x2, … xN> ∀ 1 ≤ i ≤ n |
| 4: yi—scalar class variable with yi ∊ {0, 1} or unknown ∀ 1 ≤ i ≤ n |
| 5: n—number of instances n = size(L) + size(U) |
| 6: B—batch of unlabeled samples that are labeled per iteration |
| 7: Input: |
| 8: Liter (Uiter)—(un)labeled instances during the iter-th iteration, Liter ⊂ D, Uiter ⊂ D |
| 9: k—number of executed iterations |
| 10: base learner—the selected classifier |
| 11: QS(metric)—the selected Query Strategy along with its embedded metric |
| 12: Preprocess: |
| 13: b—size of batch B computed by Equation (10) |
| 14: Main Procedure: |
| 15: Set iter = 1 |
| 16: While iter < k do |
| 17: Train base learner on Liter |
| 18: Assign class probabilities over each ui ∊ Uiter |
| 19: Rank ui according to QS(metric) |
| 20:Select the top-b ranked ui formatting current B |
| 21: Provide batch B to human oracle and obtain their pseudo-labels: |
| 22: Update L: Liter+1 ← Liter ⋃ {B, } |
| 23: Update U: Uiter+1 ← Uiter\{B} |
| 24: iter = iter + 1 |
| 25: Output: |
| 26: Train base learner on Lk for predicting class labels of test data |
3. Results
3.1. Data
3.2. Active Learning Components
3.2.1. Classifiers
- k-Nearest Neighbors [47], the most representative classification algorithm from the family of lazy learners, also referred to as an instance-based algorithm since it does not consume any resources during the training stage. Instead, it computes based on appropriate distance metrics the k-nearest neighbors of each test instance and exports its decision through a simple majority vote about the class of the latter one. Three different variants of this algorithm were included: 1-NN, 3-NN and 5-NN, increasing the value of the k parameter;
- Decision Trees (DTs) [48], where J48 and Random tree algorithms from this category were preferred. The first one constitutes a popular implementation of C4.5 generating a pruned variant that exploits Gain Ratio to determine how to split the tree, while the second one considers just a randomly chosen subset of the initial feature space before growing an unpruned decision tree. Logistic Model Trees (LMT) [49] was also employed as a powerful ensemble algorithm. Based on this, a tree structure is suitably grown, but proper logistic regression models are built at its leaves, exploiting in this manner only the most relevant attributes;
- JRip [50], a rule-based learner that tries to produce rules so as to capture all the included instances into the provided training set;
- Naive Bayes (NB) [51], a simple Bayesian-based method that assumes that all the features inside the original feature space are independent. Although this assumption seldom holds, especially in real-life cases, this generative approach has found great acceptance at the literature; and
- AdaBoost (Ada) [18], the most popular boosting algorithm that minimizes exponential loss.
3.2.2. Experiment Details
- Logitboost(M5P) vs. 1-NN vs. 3-NN vs. 5-NN vs. J48 vs. JRip vs. NB vs. RandomTree
- Logitboost(M5P) vs. Logitboost(DStump) vs. Bagging(J48) vs. Ada(DStump) vs. LMT
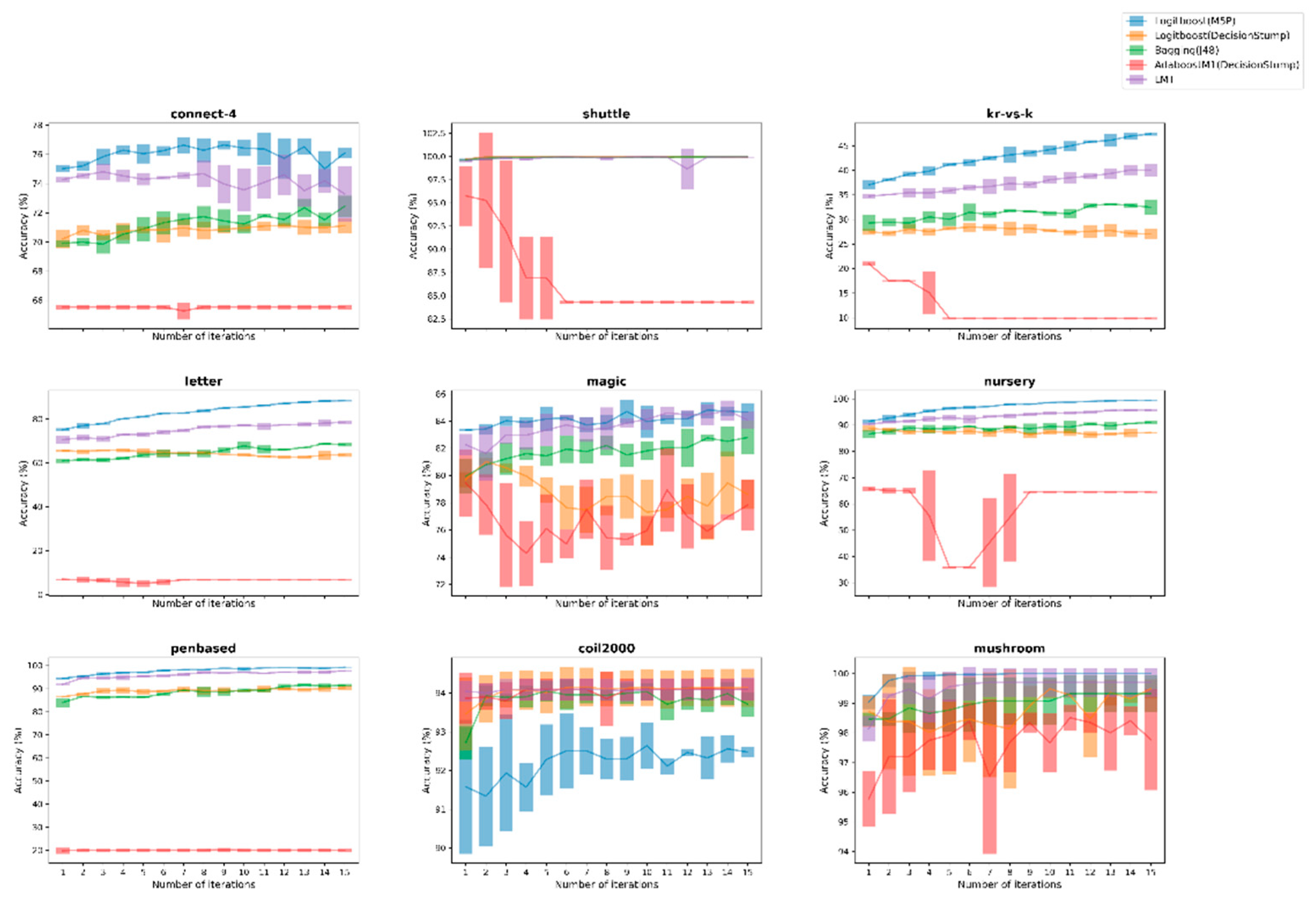
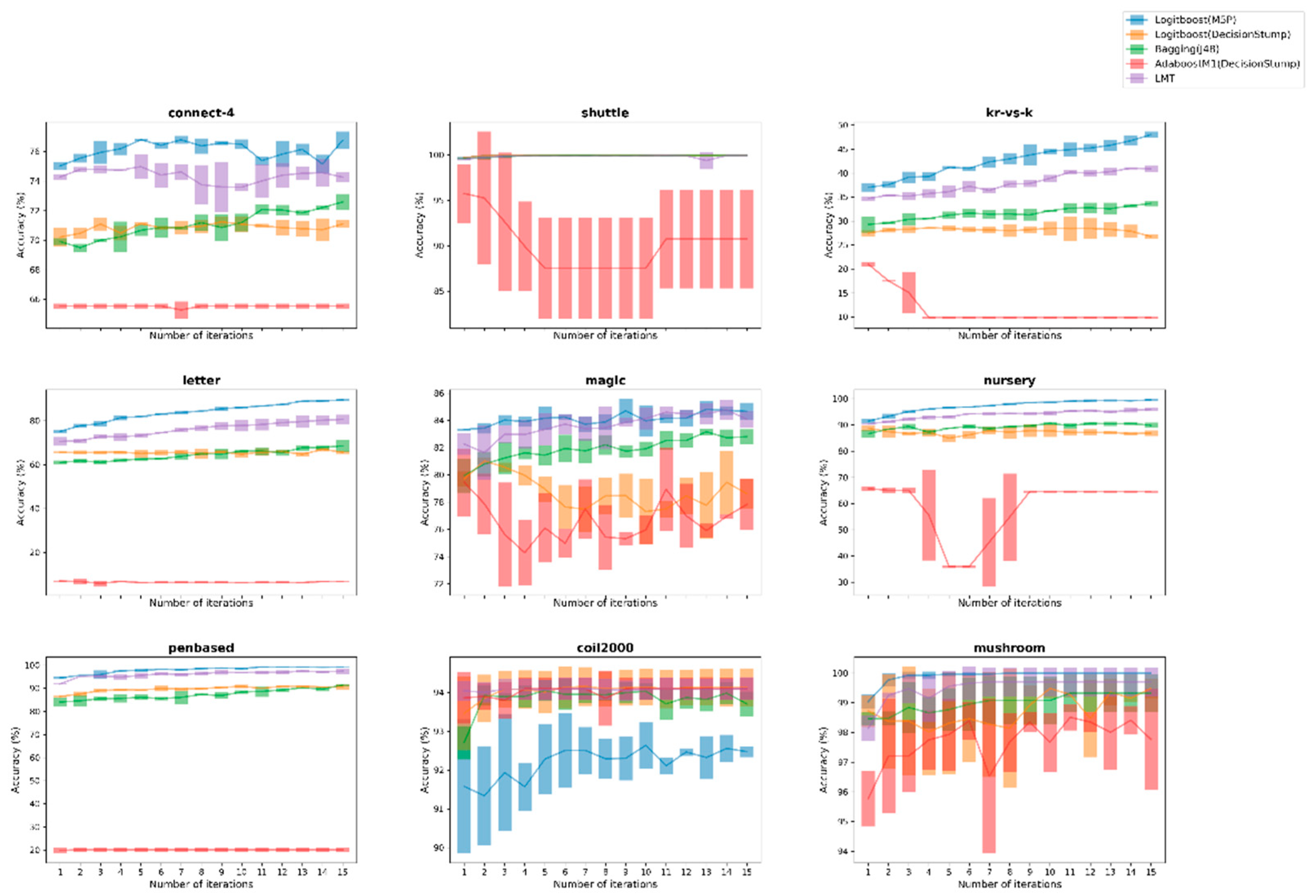
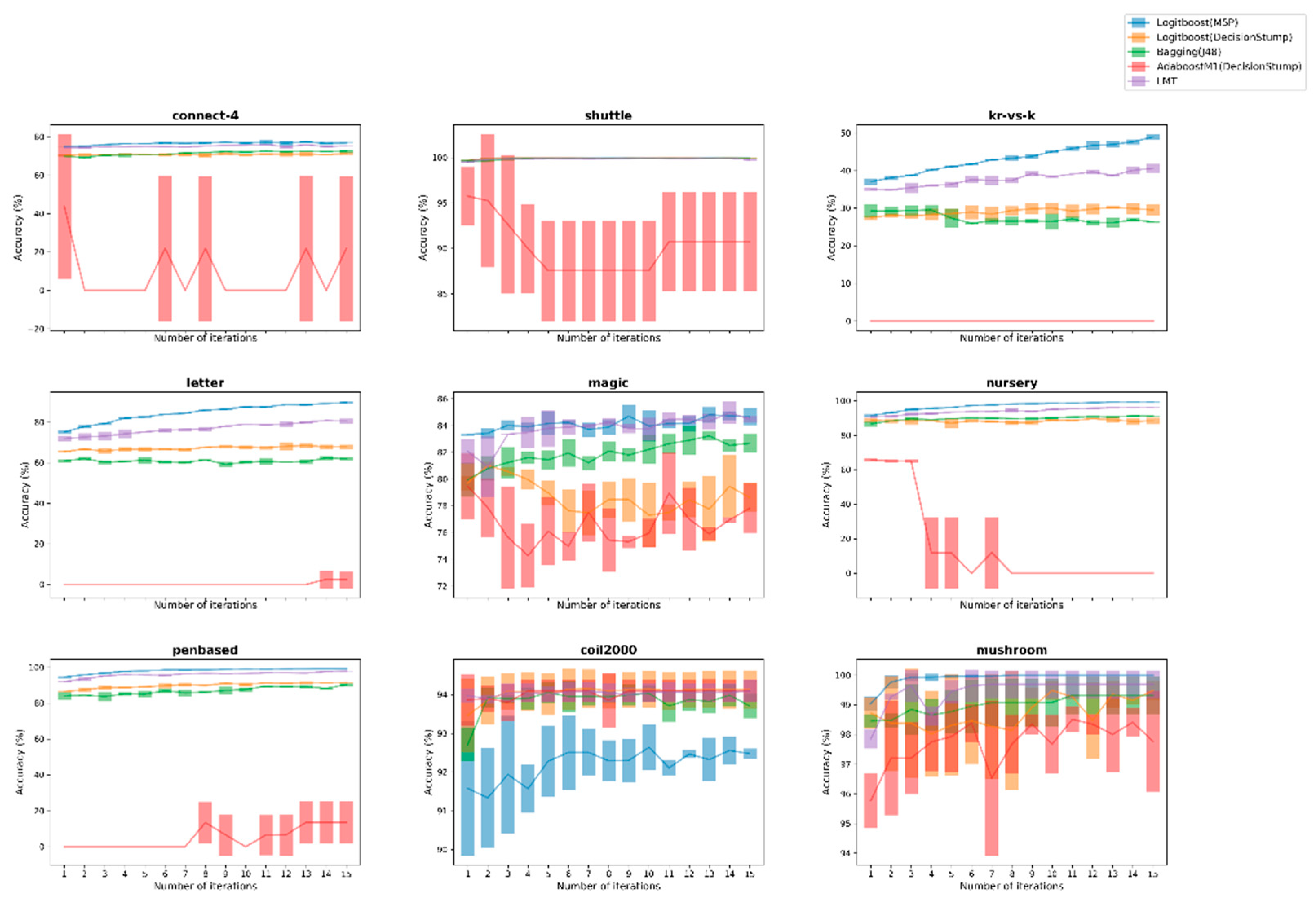
3.3. Figures, Tables and Schemes
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Papadakis, G.; Tsekouras, L.; Thanos, E.; Giannakopoulos, G.; Palpanas, T.; Koubarakis, M. The return of jedAI: End-to-End Entity Resolution for Structured and Semi-Structured Data. Proc. VLDB Endow. 2018, 11, 1950–1953. [Google Scholar] [CrossRef]
- Charton, E.; Meurs, M.-J.; Jean-Louis, L.; Gagnon, M. Using Collaborative Tagging for Text Classification: From Text Classification to Opinion Mining. Informatics 2013, 1, 32–51. [Google Scholar] [CrossRef] [Green Version]
- Vanhoeyveld, J.; Martens, D.; Peeters, B. Value-added tax fraud detection with scalable anomaly detection techniques. Appl. Soft Comput. 2020, 86, 105895. [Google Scholar] [CrossRef]
- Masood, A.; Al-Jumaily, A. Semi advised learning and classification algorithm for partially labeled skin cancer data analysis. In Proceedings of the 2017 12th International Conference on Intelligent Systems and Knowledge Engineering (ISKE), Nanjing, China, 24–26 November 2017; pp. 1–4. [Google Scholar]
- Haseeb, M.; Hussain, H.I.; Ślusarczyk, B.; Jermsittiparsert, K. Industry 4.0: A Solution towards Technology Challenges of Sustainable Business Performance. Soc. Sci. 2019, 8, 154. [Google Scholar] [CrossRef] [Green Version]
- Schwenker, F.; Trentin, E. Pattern classification and clustering: A review of partially supervised learning approaches. Pattern Recognit. Lett. 2014, 37, 4–14. [Google Scholar] [CrossRef]
- Jain, S.; Kashyap, R.; Kuo, T.-T.; Bhargava, S.; Lin, G.; Hsu, C.-N. Weakly supervised learning of biomedical information extraction from curated data. BMC Bioinform. 2016, 17, 1–12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, Z.-H. A brief introduction to weakly supervised learning. Natl. Sci. Rev. 2017, 5, 44–53. [Google Scholar] [CrossRef] [Green Version]
- Ullmann, S.; Tomalin, M. Quarantining online hate speech: Technical and ethical perspectives. Ethic- Inf. Technol. 2019, 22, 69–80. [Google Scholar] [CrossRef] [Green Version]
- Settles, B. Active Learning; Morgan & Claypool Publishers: San Rafael, CA, USA, 2012; Volume 6. [Google Scholar]
- Karlos, S.; Fazakis, N.; Kotsiantis, S.B.; Sgarbas, K.; Karlos, G. Self-Trained Stacking Model for Semi-Supervised Learning. Int. J. Artif. Intell. Tools 2017, 26. [Google Scholar] [CrossRef]
- Zhang, Z.; Cummins, N.; Schuller, B. Advanced Data Exploitation in Speech Analysis: An overview. IEEE Signal Process. Mag. 2017, 34, 107–129. [Google Scholar] [CrossRef]
- Sabata, T.; Pulc, P.; Holena, M. Semi-supervised and Active Learning in Video Scene Classification from Statistical Features. In IAL@PKDD/ECML; Springer: Dublin, Ireland, 2018; Volume 2192, pp. 24–35. Available online: http://ceur-ws.org/Vol-2192/ialatecml_paper1.pdf (accessed on 30 October 2020).
- Karlos, S.; Kanas, V.G.; Aridas, C.; Fazakis, N.; Kotsiantis, S. Combining Active Learning with Self-Train Algorithm for Classification of Multimodal Problems. In Proceedings of the 2019 10th International Conference on Information, Intelligence, Systems and Applications (IISA), Patras, Greece, 15–17 July 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Senthilnath, J.; Varia, N.; Dokania, A.; Anand, G.; Benediktsson, J.A. Deep TEC: Deep Transfer Learning with Ensemble Classifier for Road Extraction from UAV Imagery. Remote Sens. 2020, 12, 245. [Google Scholar] [CrossRef] [Green Version]
- Menze, B.H.; Kelm, B.M.; Splitthoff, D.N.; Koethe, U.; Hamprecht, F.A. On Oblique Random Forests; Springer Science and Business Media LLC: Heidelberg/Berlin, Germany, 2011; pp. 453–469. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting. Ann. Stat. 2000, 28, 337–407. Available online: http://projecteuclid.org/euclid.aos/1016218223 (accessed on 15 March 2016). [CrossRef]
- Freund, Y.; Schapire, R.E. Experiments with a New Boosting Algorithm. In ICML; Morgan Kaufmann: Bari, Italy, 1996; pp. 148–156. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.133.1040 (accessed on 1 October 2019).
- Reitmaier, T.; Sick, B. Let us know your decision: Pool-based active training of a generative classifier with the selection strategy 4DS. Inf. Sci. 2013, 230, 106–131. [Google Scholar] [CrossRef]
- Sharma, M.; Bilgic, M. Evidence-based uncertainty sampling for active learning. Data Min. Knowl. Discov. 2016, 31, 164–202. [Google Scholar] [CrossRef]
- Grau, I.; Sengupta, D.; Lorenzo, M.M.G.; Nowe, A. An Interpretable Semi-Supervised Classifier Using Two Different Strategies for Amended Self-Labeling 2020. Available online: http://arxiv.org/abs/2001.09502 (accessed on 7 June 2020).
- Otero, J.; Sánchez, L. Induction of descriptive fuzzy classifiers with the Logitboost algorithm. Soft Comput. 2005, 10, 825–835. [Google Scholar] [CrossRef]
- Burduk, R.; Bożejko, W. Modified Score Function and Linear Weak Classifiers in LogitBoost Algorithm. In Advances in Intelligent Systems and Computing; Springer: Bydgoszcz, Poland, 2019; pp. 49–56. [Google Scholar] [CrossRef]
- Kotsiantis, S.B.; Pintelas, P.E. Logitboost of simple bayesian classifier. Informatica 2005, 29, 53–59. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.136.2277 (accessed on 18 October 2019).
- Leathart, T.; Frank, E.; Holmes, G.; Pfahringer, B.; Noh, Y.-K.; Zhang, M.-L. Probability Calibration Trees. In Proceedings of the Ninth Asian Conference on Machine Learning, Seoul, Korea, 15–17 November 2017; pp. 145–160. Available online: http://proceedings.mlr.press/v77/leathart17a/leathart17a.pdf (accessed on 30 October 2020).
- Goessling, M. LogitBoost autoregressive networks. Comput. Stat. Data Anal. 2017, 112, 88–98. [Google Scholar] [CrossRef] [Green Version]
- Li, P. Robust LogitBoost and Adaptive Base Class (ABC) LogitBoost. arXiv 2012, arXiv:1203.3491. [Google Scholar]
- Reid, M.D.; Zhou, J. An improved multiclass LogitBoost using adaptive-one-vs-one. Mach. Learn. 2014, 97, 295–326. [Google Scholar] [CrossRef]
- Quinlan, J.R. Learning with continuous classes. Mach. Learn. 1992, 92, 343–348. [Google Scholar] [CrossRef]
- Deshpande, N.; Londhe, S.; Kulkarni, S. Modeling compressive strength of recycled aggregate concrete by Artificial Neural Network, Model Tree and Non-linear Regression. Int. J. Sustain. Built Environ. 2014, 3, 187–198. [Google Scholar] [CrossRef] [Green Version]
- Karlos, S.; Fazakis, N.; Kotsiantis, S.; Sgarbas, K. Self-Train LogitBoost for Semi-supervised Learning” in Engineering Applications of Neural Networks. In Communications in Computer and Information Science; Springer: Rhodes, Greece, 2015; Volume 517, pp. 139–148. [Google Scholar] [CrossRef] [Green Version]
- Iba, W.; Langley, P. Induction of One-Level Decision Trees (Decision Stump). In Proceedings of the Ninth International Conference on Machine Learning, Aberdeen, Scotland, 1–3 July 1992; pp. 233–240. [Google Scholar]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software. ACM SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Fung, G. Active Learning from Crowds. In ICML; Springer: Bellevue, WA, USA, 2011; pp. 1161–1168. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Data Classification: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Elakkiya, R.; Selvamani, K. An Active Learning Framework for Human Hand Sign Gestures and Handling Movement Epenthesis Using Enhanced Level Building Approach. Procedia Comput. Sci. 2015, 48, 606–611. [Google Scholar] [CrossRef] [Green Version]
- Pozo, M.; Chiky, R.; Meziane, F.; Métais, E. Exploiting Past Users’ Interests and Predictions in an Active Learning Method for Dealing with Cold Start in Recommender Systems. Informatics 2018, 5, 35. [Google Scholar] [CrossRef] [Green Version]
- Souza, R.R.; Dorn, A.; Piringer, B.; Wandl-Vogt, E. Towards A Taxonomy of Uncertainties: Analysing Sources of Spatio-Temporal Uncertainty on the Example of Non-Standard German Corpora. Informatics 2019, 6, 34. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, V.-L.; Destercke, S.; Hüllermeier, E. Epistemic Uncertainty Sampling. In Lecture Notes in Computer Science; Springer: Split, Croatia, 2019; pp. 72–86. [Google Scholar] [CrossRef] [Green Version]
- Tang, E.K.; Suganthan, P.N.; Yao, X. An analysis of diversity measures. Mach. Learn. 2006, 65, 247–271. [Google Scholar] [CrossRef] [Green Version]
- Olson, D.L.; Wu, D. Regression Tree Models. In Predictive Data Mining Models; Springer: Singapore, 2017; pp. 45–54. [Google Scholar]
- Wang, Y.; Witten, I.H. Inducing Model Trees for Continuous Classes. In European Conference on Machine Learning; Springer: Athens, Greece, 1997; pp. 1–10. [Google Scholar]
- Alipour, A.; Yarahmadi, J.; Mahdavi, M. Comparative Study of M5 Model Tree and Artificial Neural Network in Estimating Reference Evapotranspiration Using MODIS Products. J. Clim. 2014, 2014, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Behnood, A.; Olek, J.; Glinicki, M.A. Predicting modulus elasticity of recycled aggregate concrete using M5′ model tree algorithm. Constr. Build. Mater. 2015, 94, 137–147. [Google Scholar] [CrossRef]
- Schapire, R.E. The Boosting Approach to Machine Learning: An Overview. In Nonlinear Estimation and Classification; Denison, D.D., Hansen, M.H., Holmes, C.C., Mallick, B., Yu, B., Eds.; Springer: New York, NY, USA; Volume 171, Lecture Notes in Statistics. [CrossRef]
- Linchman, M. UCI Machine Learning Repository. 2013. Available online: http://archive.ics.uci.edu/ml/ (accessed on 30 October 2020).
- Zhang, S.; Li, X.; Zong, M.; Zhu, X.; Wang, R. Efficient kNN Classification with Different Numbers of Nearest Neighbors. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 1774–1785. [Google Scholar] [CrossRef]
- Kotsiantis, S.B. Decision trees: A recent overview. Artif. Intell. Rev. 2013, 39, 261–283. [Google Scholar] [CrossRef]
- Landwehr, N.; Hall, M.; Frank, E. Logistic Model Trees. Mach. Learn. 2005, 59, 161–205. [Google Scholar] [CrossRef] [Green Version]
- Hühn, J.; Hüllermeier, E. FURIA: An algorithm for unordered fuzzy rule induction. Data Min. Knowl. Discov. 2009, 19, 293–319. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Jiang, L.; Yu, L. Class-specific attribute value weighting for Naive Bayes. Inf. Sci. 2020, 508, 260–274. [Google Scholar] [CrossRef]
- Reyes, O.; Pérez, E.; Del, M.; Rodríguez-Hernández, C.; Fardoun, H.M.; Ventura, S. JCLAL: A Java Framework for Active Learning. J. Mach. Learn. Res. 2016, 17, 95-1. Available online: http://www.jmlr.org/papers/volume17/15-347/15-347.pdf (accessed on 20 April 2017).
- Quinlan, J.R. Bagging, Boosting, and C4.5; AAAI Press: Portland, OR, USA, 1996. [Google Scholar]
- Baumgartner, D.; Serpen, G. Performance of global–local hybrid ensemble versus boosting and bagging ensembles. Int. J. Mach. Learn. Cybern. 2012, 4, 301–317. [Google Scholar] [CrossRef]
- Eisinga, R.; Heskes, T.; Pelzer, B.; Grotenhuis, M.T. Exact p-values for pairwise comparison of Friedman rank sums, with application to comparing classifiers. BMC Bioinform. 2017, 18, 68. [Google Scholar] [CrossRef] [Green Version]
- Hollander, M.; Wolfe, D.A.; Chicken, E. Nonparametric Statistical Methods. In Simulation and the Monte Carlo Method, 3rd ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Ramirez-Loaiza, M.E.; Sharma, M.; Kumar, G.; Bilgic, M. Active learning: An empirical study of common baselines. Data Min. Knowl. Discov. 2016, 31, 287–313. [Google Scholar] [CrossRef]
- Li, J.; Zhu, Q. A boosting Self-Training Framework based on Instance Generation with Natural Neighbors for K Nearest Neighbor. Appl. Intell. 2020, 50, 3535–3553. [Google Scholar] [CrossRef]
- Kamarudin, M.H.; Maple, C.; Watson, T.; Safa, N.S. A LogitBoost-Based Algorithm for Detecting Known and Unknown Web Attacks. IEEE Access 2017, 5, 26190–26200. [Google Scholar] [CrossRef]
- Araújo, B.; Zhao, L. Data heterogeneity consideration in semi-supervised learning. Expert Syst. Appl. 2016, 45, 234–247. [Google Scholar] [CrossRef]
- Platanios, E.A.; Kapoor, A.; Horvitz, E. Active Learning amidst Logical Knowledge. arXiv 2017, arXiv:1709.08850. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef] [Green Version]
- Santos, D.; Prudêncio, R.B.C.; Carvalho, A.C.P.L.F.; Dos Santos, D.P. Empirical investigation of active learning strategies. Neurocomputing 2019, 326–327, 15–27. [Google Scholar] [CrossRef]
- Lughofer, E. On-line active learning: A new paradigm to improve practical useability of data stream modeling methods. Inf. Sci. 2017, 415, 356–376. [Google Scholar] [CrossRef]

| Dataset | n | # of Classes | N | Categorical/Numerical Features | Majority/Minority Class |
|---|---|---|---|---|---|
| appendicitis | 106 | 2 | 7 | 0/7 | 80.189/19.811% |
| banana | 5300 | 2 | 2 | 0/2 | 55.17/44.83% |
| bands | 365 | 2 | 19 | 0/19 | 63.014/36.986% |
| breast-cancer | 286 | 2 | 9 | 9/0 | 70.28/29.72% |
| breast-w | 699 | 2 | 9 | 0/9 | 65.522/34.478% |
| breast | 277 | 2 | 9 | 9/0 | 70.758/29.242% |
| bupa | 345 | 2 | 6 | 0/6 | 57.971/42.029% |
| chess | 3196 | 2 | 36 | 36/0 | 52.222/47.778% |
| coil2000 | 9822 | 2 | 85 | 0/85 | 94.034/5.966% |
| colic | 368 | 2 | 22 | 15/7 | 63.043/36.957% |
| colic.orig | 368 | 2 | 27 | 20/7 | 66.304/33.696% |
| credit-a | 690 | 2 | 15 | 9/6 | 55.507/44.493% |
| credit-g | 1000 | 2 | 20 | 13/7 | 70.0/30.0% |
| crx | 653 | 2 | 15 | 9/6 | 54.671/45.329% |
| diabetes | 768 | 2 | 8 | 0/8 | 65.104/34.896% |
| german | 1000 | 2 | 20 | 13/7 | 70.0/30.0% |
| haberman | 306 | 2 | 3 | 0/3 | 73.529/26.471% |
| heart-statlog | 270 | 2 | 13 | 0/13 | 55.556/44.444% |
| heart | 270 | 2 | 13 | 0/13 | 55.556/44.444% |
| hepatitis | 155 | 2 | 19 | 13/6 | 79.355/20.645% |
| housevotes | 232 | 2 | 16 | 16/0 | 53.448/46.552% |
| ionosphere | 351 | 2 | 34 | 0/34 | 64.103/35.897% |
| kr-vs-kp | 3196 | 2 | 36 | 36/0 | 52.222/47.778% |
| labor | 57 | 2 | 16 | 8/8 | 64.912/35.088% |
| magic | 19,020 | 2 | 10 | 0/10 | 64.837/35.163% |
| mammographic | 830 | 2 | 5 | 0/5 | 51.446/48.554% |
| monk-2 | 432 | 2 | 6 | 0/6 | 52.778/47.222% |
| mushroom | 8124 | 2 | 22 | 22/0 | 51.797/48.203% |
| phoneme | 5404 | 2 | 5 | 0/5 | 70.651/29.349% |
| pima | 768 | 2 | 8 | 0/8 | 65.104/34.896% |
| ring | 7400 | 2 | 20 | 0/20 | 50.486/49.514% |
| saheart | 462 | 2 | 9 | 1/8 | 65.368/34.632% |
| sick | 3772 | 2 | 29 | 22/7 | 93.876/6.124% |
| sonar | 208 | 2 | 60 | 0/60 | 53.365/46.635% |
| spambase | 4597 | 2 | 57 | 0/57 | 60.583/39.417% |
| spectfheart | 267 | 2 | 44 | 0/44 | 79.401/20.599% |
| tic-tac-toe | 958 | 2 | 9 | 9/0 | 65.344/34.656% |
| titanic | 2201 | 2 | 3 | 0/3 | 67.697/32.303% |
| twonorm | 7400 | 2 | 20 | 0/20 | 50.041/49.959% |
| vote | 435 | 2 | 16 | 16/0 | 61.379/38.621% |
| wdbc | 569 | 2 | 30 | 0/30 | 62.742/37.258% |
| wisconsin | 683 | 2 | 9 | 0/9 | 65.007/34.993% |
| Dataset | n | # of Classes | N | Categorical/Numerical Features | Majority /Minority Class |
|---|---|---|---|---|---|
| abalone | 4174 | 28 | 8 | 1/7 | 16.507/0.048% |
| anneal | 898 | 6 | 38 | 32/6 | 76.169/0.891% |
| anneal.orig | 898 | 6 | 38 | 32/6 | 76.169/0.891% |
| audiology | 226 | 24 | 69 | 69/0 | 25.221/0.884% |
| automobile | 159 | 6 | 25 | 10/15 | 30.189/10.063% |
| autos | 205 | 7 | 25 | 10/15 | 32.683/1.463% |
| balance-scale | 625 | 3 | 4 | 0/4 | 46.08/53.92% |
| balance | 625 | 3 | 4 | 0/4 | 46.08/53.92% |
| car | 1728 | 4 | 6 | 6/0 | 70.023/7.755% |
| cleveland | 297 | 5 | 13 | 0/13 | 53.872/16.162% |
| connect-4 | 67,557 | 3 | 42 | 42/0 | 65.83/34.17% |
| dermatology | 358 | 6 | 34 | 0/34 | 31.006/18.995% |
| ecoli | 336 | 8 | 7 | 0/7 | 42.56/1.19% |
| flare | 1066 | 6 | 11 | 11/0 | 31.051/12.946% |
| glass | 214 | 7 | 9 | 0/9 | 35.514/4.206% |
| hayes-roth | 160 | 3 | 4 | 0/4 | 40.625/59.375% |
| heart-c | 303 | 5 | 13 | 7/6 | 54.455/0.0% |
| heart-h | 294 | 5 | 13 | 7/6 | 63.946/0.0% |
| hypothyroid | 3772 | 4 | 29 | 22/7 | 92.285/2.572% |
| iris | 150 | 3 | 4 | 0/4 | 33.333/66.666% |
| kr-vs-kp | 28,056 | 18 | 6 | 6/0 | 16.228/0.374% |
| led7digit | 500 | 10 | 7 | 0/7 | 11.4/16.4% |
| letter | 20,000 | 26 | 16 | 0/16 | 4.065/7.34% |
| lymph | 148 | 4 | 18 | 15/3 | 54.73/4.054% |
| lymphography | 148 | 4 | 18 | 15/3 | 54.73/4.054% |
| marketing | 6876 | 9 | 13 | 0/13 | 18.252/15.008% |
| movement_libras | 360 | 15 | 90 | 0/90 | 6.667/13.334% |
| newthyroid | 215 | 3 | 5 | 0/5 | 69.767/30.232% |
| nursery | 12,960 | 5 | 8 | 8/0 | 33.333/2.546% |
| optdigits | 5620 | 10 | 64 | 0/64 | 10.178/19.716% |
| page-blocks | 5472 | 5 | 10 | 0/10 | 89.784/2.102% |
| penbased | 10,992 | 10 | 16 | 0/16 | 10.408/19.196% |
| post-operative | 87 | 3 | 8 | 8/0 | 71.264/28.735% |
| primary-tumor | 339 | 22 | 17 | 17/0 | 24.779/0.295% |
| satimage | 6435 | 7 | 36 | 0/36 | 23.823/9.728% |
| segment | 2310 | 7 | 19 | 0/19 | 14.286/28.572% |
| shuttle | 57,999 | 7 | 9 | 0/9 | 78.598/0.039% |
| soybean | 683 | 19 | 35 | 35/0 | 13.47/3.221% |
| tae | 151 | 3 | 5 | 0/5 | 34.437/65.563% |
| texture | 5500 | 11 | 40 | 0/40 | 9.091/18.182% |
| thyroid | 7200 | 3 | 21 | 0/21 | 92.583/7.417% |
| vehicle | 846 | 4 | 18 | 0/18 | 25.768/48.581% |
| Datasets | Logitboost (M5P) | 1NN | 3NN | 5-NN | J48 | JRip | Random Tree | NB |
|---|---|---|---|---|---|---|---|---|
| appendicitis | 75.84 | 80.56 | 82.07 | 81.13 | 80.16 | 80.47 | 79.59 | 78.63 |
| banana | 87.06 | 84.86 | 84.69 | 86.64 | 71.54 | 78.87 | 83.30 | 83.08 |
| bands | 58.63 | 46.76 | 40.08 | 39.00 | 50.96 | 39.09 | 42.56 | 46.76 |
| breast-cancer | 66.08 | 72.15 | 70.63 | 69.82 | 70.15 | 70.40 | 67.03 | 67.84 |
| breast-w | 95.66 | 88.75 | 93.66 | 94.90 | 87.94 | 86.55 | 88.08 | 90.10 |
| breast | 69.92 | 72.31 | 71.71 | 72.68 | 69.67 | 69.18 | 69.32 | 69.47 |
| bupa | 61.26 | 48.21 | 44.25 | 44.06 | 49.37 | 43.29 | 52.17 | 52.24 |
| chess | 97.68 | 80.44 | 79.81 | 79.62 | 92.98 | 88.64 | 82.64 | 89.66 |
| coil2000 | 92.63 | 92.49 | 93.71 | 93.99 | 94.03 | 94.02 | 91.54 | 92.73 |
| colic.ORIG | 66.39 | 64.77 | 66.75 | 65.67 | 66.13 | 69.85 | 67.21 | 67.82 |
| colic | 78.54 | 72.47 | 66.56 | 69.84 | 63.05 | 64.95 | 62.05 | 68.51 |
| credit-a | 81.74 | 67.83 | 63.86 | 67.54 | 84.30 | 70.58 | 64.30 | 72.21 |
| credit-g | 69.47 | 69.43 | 70.53 | 70.13 | 67.27 | 69.87 | 67.27 | 68.87 |
| crx | 79.48 | 68.30 | 62.62 | 67.59 | 86.17 | 70.48 | 60.59 | 70.18 |
| diabetes | 71.22 | 67.62 | 65.93 | 65.67 | 68.32 | 66.62 | 68.84 | 68.89 |
| german | 69.23 | 69.34 | 70.57 | 70.47 | 69.97 | 69.83 | 67.14 | 68.73 |
| haberman | 72.22 | 43.14 | 32.57 | 31.92 | 42.16 | 31.70 | 40.74 | 48.22 |
| heart-c | 77.23 | 68.32 | 66.12 | 70.85 | 64.25 | 58.64 | 60.62 | 65.49 |
| heart-h | 73.36 | 73.47 | 74.94 | 69.05 | 65.99 | 67.12 | 66.78 | 69.09 |
| heart-statlog | 75.06 | 72.96 | 63.21 | 63.95 | 70.25 | 59.26 | 65.68 | 66.67 |
| heart | 74.81 | 72.35 | 61.98 | 65.93 | 63.95 | 62.35 | 63.58 | 66.91 |
| hepatitis | 78.28 | 59.84 | 61.76 | 64.37 | 54.01 | 46.23 | 44.93 | 56.48 |
| housevotes | 96.11 | 90.51 | 89.50 | 90.80 | 88.49 | 93.81 | 87.04 | 92.32 |
| ionosphere | 84.52 | 79.68 | 73.03 | 69.80 | 65.62 | 53.37 | 59.45 | 65.78 |
| kr-vs-kp | 97.48 | 80.09 | 80.03 | 80.04 | 90.93 | 91.28 | 83.07 | 90.61 |
| labor | 76.02 | 53.80 | 74.27 | 49.71 | 42.69 | 44.44 | 52.05 | 57.50 |
| magic | 84.53 | 76.82 | 74.21 | 77.20 | 80.64 | 79.67 | 79.44 | 81.21 |
| mammographic | 81.65 | 65.46 | 63.38 | 61.21 | 66.75 | 64.58 | 70.20 | 72.14 |
| monk-2 | 98.30 | 73.53 | 71.60 | 70.14 | 97.22 | 95.52 | 81.40 | 91.74 |
| mushroom | 99.77 | 99.98 | 99.98 | 99.98 | 98.52 | 99.20 | 99.10 | 99.36 |
| phoneme | 81.49 | 78.23 | 74.17 | 76.17 | 73.30 | 72.48 | 76.49 | 76.82 |
| pima | 71.09 | 65.45 | 66.71 | 65.58 | 66.84 | 65.32 | 69.70 | 68.71 |
| ring | 89.20 | 76.50 | 73.08 | 69.57 | 81.28 | 65.74 | 79.53 | 78.16 |
| saheart | 62.63 | 63.35 | 65.44 | 66.09 | 64.86 | 66.02 | 63.28 | 63.97 |
| sick | 98.37 | 94.72 | 95.23 | 95.09 | 95.64 | 96.34 | 94.87 | 96.53 |
| sonar | 65.71 | 55.77 | 49.35 | 48.56 | 56.89 | 48.22 | 56.07 | 56.67 |
| spambase | 90.80 | 75.26 | 71.53 | 71.03 | 85.87 | 84.48 | 79.52 | 84.93 |
| spectfheart | 73.03 | 47.44 | 49.56 | 44.57 | 56.05 | 45.44 | 49.94 | 56.14 |
| tic-tac-toe | 83.61 | 76.23 | 71.99 | 70.84 | 65.62 | 68.23 | 68.09 | 73.31 |
| titanic | 77.92 | 77.62 | 77.09 | 77.16 | 73.80 | 73.30 | 77.34 | 76.19 |
| twonorm | 96.23 | 91.39 | 91.25 | 93.58 | 78.45 | 79.34 | 77.03 | 84.20 |
| vote | 95.10 | 92.03 | 93.33 | 93.87 | 93.03 | 89.35 | 88.58 | 91.01 |
| wdbc | 95.66 | 88.69 | 88.70 | 91.04 | 84.29 | 81.43 | 86.18 | 87.76 |
| wisconsin | 96.10 | 87.85 | 95.17 | 95.90 | 87.26 | 87.94 | 88.96 | 91.00 |
| Datasets | Logitboost (M5P) | 1NN | 3NN | 5NN | J48 | JRip | Random Tree | NB |
|---|---|---|---|---|---|---|---|---|
| abalone | 22.03 | 17.42 | 17.38 | 21.92 | 20.84 | 11.48 | 17.25 | 16.92 |
| anneal.ORIG | 84.71 | 83.93 | 84.52 | 83.48 | 75.54 | 73.64 | 81.99 | 80.12 |
| anneal | 92.80 | 75.24 | 82.14 | 86.23 | 85.86 | 84.59 | 86.37 | 87.92 |
| audiology | 48.84 | 34.93 | 39.56 | 34.67 | 55.76 | 26.72 | 32.02 | 35.86 |
| automobile | 47.59 | 34.38 | 33.54 | 26.21 | 36.27 | 17.82 | 39.83 | 35.08 |
| autos | 43.74 | 28.61 | 21.95 | 18.84 | 37.88 | 11.21 | 35.93 | 30.29 |
| balance-scale | 85.60 | 73.39 | 77.60 | 79.78 | 64.37 | 61.55 | 67.68 | 71.61 |
| balance | 87.62 | 71.57 | 77.39 | 79.68 | 65.23 | 64.47 | 67.89 | 73.33 |
| car | 89.91 | 79.24 | 80.71 | 80.34 | 71.74 | 71.28 | 73.53 | 78.24 |
| cleveland | 50.84 | 55.44 | 55.56 | 55.22 | 52.97 | 53.20 | 52.19 | 52.08 |
| connect-4 | 76.32 | 70.65 | 72.57 | 73.07 | 71.36 | 69.24 | 64.40 | 69.99 |
| dermatology | 93.95 | 80.43 | 90.79 | 91.72 | 66.88 | 53.79 | 63.98 | 70.57 |
| ecoli | 73.12 | 58.83 | 69.35 | 69.44 | 62.00 | 52.08 | 57.84 | 61.01 |
| flare | 72.95 | 66.57 | 67.10 | 63.44 | 61.92 | 67.86 | 64.20 | 68.33 |
| glass | 51.87 | 39.38 | 38.13 | 40.96 | 36.93 | 36.47 | 41.00 | 43.11 |
| hayes-roth | 51.89 | 44.54 | 43.13 | 40.61 | 41.69 | 41.88 | 49.64 | 47.80 |
| hypothyroid | 99.43 | 91.25 | 92.82 | 92.54 | 97.92 | 97.68 | 94.29 | 97.13 |
| iris | 83.78 | 85.33 | 85.11 | 83.56 | 64.22 | 43.78 | 71.56 | 66.37 |
| kr-vs-kp | 47.88 | 39.74 | 40.16 | 39.96 | 30.66 | 15.50 | 28.88 | 30.75 |
| led7digit | 56.00 | 61.34 | 51.48 | 47.53 | 41.33 | 25.39 | 47.40 | 42.93 |
| letter | 88.49 | 79.07 | 75.23 | 73.98 | 62.63 | 58.19 | 56.75 | 67.81 |
| lymph | 74.77 | 65.51 | 69.82 | 69.57 | 55.90 | 55.64 | 61.49 | 63.96 |
| lymphography | 70.72 | 66.41 | 72.29 | 69.45 | 59.46 | 57.19 | 61.71 | 63.21 |
| marketing | 26.88 | 26.87 | 25.16 | 26.84 | 26.52 | 23.27 | 25.56 | 25.24 |
| movement_libras | 38.15 | 39.54 | 33.98 | 32.22 | 24.44 | 10.37 | 20.56 | 23.02 |
| newthyroid | 83.84 | 81.87 | 83.41 | 85.86 | 76.87 | 71.48 | 79.86 | 78.39 |
| nursery | 99.57 | 85.59 | 87.92 | 86.25 | 88.12 | 82.81 | 83.16 | 88.51 |
| optdigits | 97.16 | 92.89 | 96.52 | 97.11 | 72.25 | 68.79 | 61.92 | 75.96 |
| page-blocks | 96.52 | 93.07 | 94.67 | 94.54 | 94.35 | 94.24 | 93.75 | 94.84 |
| penbased | 99.05 | 95.60 | 98.39 | 98.38 | 86.70 | 82.17 | 82.27 | 87.83 |
| post-operative | 68.20 | 68.58 | 70.88 | 71.26 | 71.26 | 71.26 | 67.43 | 68.97 |
| primary-tumor | 30.29 | 29.99 | 29.79 | 27.63 | 24.29 | 25.66 | 28.12 | 28.02 |
| satimage | 87.38 | 68.38 | 85.92 | 85.39 | 70.01 | 64.72 | 61.53 | 71.21 |
| segment | 94.49 | 86.81 | 88.74 | 86.58 | 85.11 | 77.52 | 78.14 | 83.38 |
| shuttle | 99.98 | 99.72 | 99.83 | 99.79 | 99.79 | 99.81 | 99.69 | 99.82 |
| soybean | 76.53 | 78.67 | 66.96 | 57.30 | 46.18 | 46.91 | 47.28 | 56.91 |
| tae | 45.26 | 38.41 | 34.24 | 37.95 | 36.41 | 33.80 | 40.59 | 39.88 |
| texture | 98.21 | 90.79 | 94.53 | 95.28 | 80.82 | 75.14 | 70.76 | 81.37 |
| thyroid | 99.60 | 62.75 | 81.70 | 87.46 | 98.92 | 98.60 | 93.14 | 97.11 |
| vehicle | 70.57 | 45.90 | 40.70 | 45.11 | 45.63 | 39.95 | 46.22 | 52.25 |
| vowel | 49.43 | 26.33 | 14.04 | 15.79 | 35.35 | 18.72 | 26.73 | 31.63 |
| waveform-5000 | 82.65 | 63.79 | 68.40 | 75.93 | 68.51 | 62.35 | 59.89 | 68.30 |
| wine | 96.63 | 77.70 | 84.62 | 86.15 | 60.07 | 46.28 | 55.10 | 66.00 |
| winequalityRed | 51.53 | 33.25 | 47.07 | 47.59 | 37.92 | 35.81 | 31.08 | 39.48 |
| winequalityWhite | 49.16 | 37.31 | 45.12 | 45.15 | 41.00 | 35.08 | 34.18 | 39.47 |
| yeast | 51.84 | 37.71 | 39.92 | 46.45 | 36.07 | 30.21 | 33.76 | 38.61 |
| zoo | 26.43 | 75.55 | 81.55 | 68.26 | 60.24 | 41.24 | 50.69 | 39.45 |
| Datasets | Logitboost (M5P) | Logitboost (DStump) | Bagging (J48) | Ada (DStump) | LMT |
|---|---|---|---|---|---|
| banana | 87.06 | 84.48 | 83.35 | 59.25 | 71.91 |
| bands | 58.63 | 49.32 | 47.21 | 55.14 | 57.90 |
| breast-w | 95.66 | 91.28 | 90.32 | 92.61 | 95.52 |
| chess | 97.68 | 90.00 | 95.78 | 84.38 | 98.14 |
| coil2000 | 92.63 | 92.30 | 93.49 | 94.03 | 94.03 |
| credit-a | 81.74 | 72.75 | 81.06 | 84.88 | 79.76 |
| credit-g | 69.47 | 68.53 | 69.53 | 70.63 | 69.80 |
| german | 69.23 | 68.37 | 68.73 | 70.47 | 69.47 |
| heart-statlog | 75.06 | 69.14 | 60.25 | 70.49 | 70.25 |
| housevotes | 96.11 | 91.82 | 94.67 | 94.82 | 95.25 |
| ionosphere | 84.52 | 69.92 | 62.20 | 74.45 | 83.86 |
| kr-vs-kp | 97.48 | 90.39 | 95.58 | 86.57 | 98.04 |
| magic | 84.53 | 81.73 | 82.88 | 77.14 | 84.33 |
| mammographic | 81.65 | 74.66 | 79.52 | 79.92 | 80.97 |
| monk-2 | 98.30 | 90.48 | 97.22 | 95.76 | 93.98 |
| mushroom | 99.77 | 99.41 | 99.36 | 97.58 | 99.60 |
| phoneme | 81.49 | 78.26 | 80.47 | 72.25 | 79.42 |
| pima | 71.09 | 69.84 | 69.01 | 70.66 | 73.13 |
| ring | 89.20 | 82.30 | 87.62 | 49.51 | 83.88 |
| sick | 98.37 | 96.59 | 98.12 | 97.52 | 98.34 |
| sonar | 65.71 | 59.48 | 52.57 | 60.73 | 60.28 |
| spambase | 90.80 | 85.08 | 89.66 | 83.76 | 92.70 |
| spectfheart | 73.03 | 59.70 | 49.44 | 69.91 | 72.28 |
| tic-tac-toe | 83.61 | 75.01 | 67.40 | 69.07 | 72.41 |
| titanic | 77.92 | 77.15 | 78.27 | 77.66 | 77.56 |
| twonorm | 96.23 | 85.82 | 86.36 | 84.81 | 97.79 |
| vote | 95.10 | 91.56 | 88.35 | 92.72 | 85.06 |
| wdbc | 95.66 | 89.87 | 85.76 | 94.38 | 97.01 |
| wisconsin | 96.10 | 92.02 | 92.97 | 92.97 | 96.58 |
| Datasets | Logitboost (M5P) | Logitboost (DStump) | Bagging (J48) | Ada (DStump) | LMT |
|---|---|---|---|---|---|
| abalone | 22.03 | 18.73 | 19.94 | 16.73 | 22.73 |
| anneal.ORIG | 84.71 | 82.27 | 76.80 | 75.57 | 82.75 |
| anneal | 92.80 | 89.03 | 85.15 | 77.02 | 92.28 |
| audiology | 48.84 | 38.91 | 49.10 | 33.90 | 54.27 |
| automobile | 47.59 | 40.83 | 37.11 | 23.48 | 43.40 |
| balance-scale | 85.60 | 74.96 | 71.84 | 49.81 | 84.00 |
| balance | 87.62 | 76.28 | 66.98 | 55.90 | 85.49 |
| car | 89.91 | 80.56 | 78.34 | 70.79 | 87.29 |
| cleveland | 50.84 | 51.70 | 53.87 | 53.98 | 53.20 |
| connect-4 | 76.32 | 70.24 | 72.67 | 65.83 | 73.44 |
| dermatology | 93.95 | 76.17 | 86.31 | 48.70 | 93.02 |
| ecoli | 73.12 | 63.99 | 68.15 | 62.00 | 71.73 |
| flare | 72.95 | 68.49 | 68.73 | 53.47 | 69.20 |
| glass | 51.87 | 45.33 | 40.80 | 38.95 | 42.39 |
| hayes-roth | 51.89 | 49.78 | 45.24 | 48.12 | 46.27 |
| hypothyroid | 99.43 | 96.95 | 99.51 | 93.83 | 99.11 |
| iris | 83.78 | 73.90 | 70.22 | 80.00 | 73.56 |
| kr-vs-kp | 47.88 | 35.84 | 33.56 | 10.04 | 40.32 |
| led7digit | 56.00 | 48.78 | 47.00 | 14.94 | 57.00 |
| letter | 88.49 | 71.02 | 68.15 | 6.91 | 78.27 |
| marketing | 26.88 | 25.89 | 26.59 | 18.64 | 29.35 |
| movement_libras | 38.15 | 27.24 | 24.35 | 10.93 | 40.37 |
| newthyroid | 83.84 | 80.70 | 78.79 | 81.26 | 89.15 |
| nursery | 99.57 | 90.41 | 90.74 | 64.54 | 95.40 |
| optdigits | 97.16 | 78.35 | 81.60 | 18.74 | 95.07 |
| page-blocks | 96.52 | 95.04 | 96.06 | 92.60 | 96.64 |
| penbased | 99.05 | 89.72 | 91.95 | 20.52 | 97.45 |
| primary-tumor | 30.29 | 28.81 | 24.39 | 25.86 | 24.98 |
| satimage | 87.38 | 73.37 | 81.66 | 33.63 | 83.01 |
| segment | 94.49 | 85.34 | 89.25 | 28.51 | 91.53 |
| shuttle | 99.98 | 99.83 | 99.96 | 84.23 | 99.92 |
| soybean | 76.53 | 60.24 | 43.88 | 13.47 | 74.73 |
| tae | 45.26 | 41.91 | 35.76 | 35.74 | 37.08 |
| texture | 98.21 | 83.45 | 84.93 | 16.08 | 99.59 |
| thyroid | 99.60 | 96.62 | 99.36 | 96.87 | 99.54 |
| vehicle | 70.57 | 56.34 | 52.44 | 26.04 | 68.36 |
| vowel | 49.43 | 35.93 | 39.66 | 14.14 | 50.10 |
| waveform-5000 | 82.65 | 70.28 | 75.00 | 55.37 | 86.33 |
| wine | 96.63 | 72.58 | 64.28 | 69.14 | 80.56 |
| winequalityRed | 51.53 | 40.70 | 46.32 | 42.21 | 50.49 |
| winequalityWhite | 49.16 | 40.94 | 47.39 | 31.19 | 49.24 |
| yeast | 51.84 | 41.40 | 47.15 | 21.29 | 54.09 |
| QS (metric) | Logitboost (M5P) | 1NN | 3NN | 5NN | J48 | Random Tree | JRip | NB |
|---|---|---|---|---|---|---|---|---|
| Binary Datasets | ||||||||
| R = 5% | ||||||||
| UncS(Ent) | 32 | 2 | 4 | 3 | 3 | 0 | 1 | 0 |
| UncS(LConf) | 33 | 2 | 4 | 3 | 2 | 0 | 1 | 0 |
| UncS(SMar) | 33 | 2 | 4 | 3 | 2 | 1 | 0 | 0 |
| R = 10% | ||||||||
| UncS(Ent) | 30 | 0 | 3 | 7 | 2 | 0 | 3 | 0 |
| UncS(LConf) | 30 | 0 | 3 | 7 | 2 | 0 | 3 | 0 |
| UncS(SMar) | 31 | 0 | 3 | 7 | 3 | 1 | 0 | 0 |
| R = 15% | ||||||||
| UncS(Ent) | 26 | 0 | 6 | 8 | 3 | 0 | 2 | 0 |
| UncS(LConf) | 26 | 0 | 6 | 8 | 3 | 0 | 2 | 0 |
| UncS(SMar) | 27 | 0 | 6 | 9 | 3 | 0 | 0 | 0 |
| R = 20% | ||||||||
| UncS(Ent) | 23 | 2 | 6 | 4 | 5 | 1 | 4 | 0 |
| UncS(LConf) | 23 | 2 | 6 | 4 | 5 | 1 | 4 | 0 |
| UncS(SMar) | 26 | 2 | 6 | 5 | 5 | 1 | 0 | 0 |
| Multi-Class Datasets | ||||||||
| R = 5% | ||||||||
| UncS(Ent) | 37 | 4 | 3 | 2 | 2 | 0 | 1 | 0 |
| UncS(LConf) | 38 | 3 | 3 | 1 | 2 | 1 | 1 | 0 |
| UncS(SMar) | 37 | 3 | 4 | 1 | 2 | 1 | - | 0 |
| R = 10% | ||||||||
| UncS(Ent) | 36 | 2 | 4 | 5 | 0 | 0 | 0 | 0 |
| UncS(LConf) | 38 | 1 | 6 | 2 | 0 | 0 | 0 | 0 |
| UncS(SMar) | 38 | 0 | 7 | 1 | 1 | 0 | - | 0 |
| R = 15% | ||||||||
| UncS(Ent) | 34 | 5 | 3 | 4 | 1 | 0 | 1 | 0 |
| UncS(LConf) | 35 | 3 | 6 | 2 | 1 | 0 | 1 | 0 |
| UncS(SMar) | 35 | 3 | 3 | 5 | 1 | 0 | - | 0 |
| R = 20% | ||||||||
| UncS(Ent) | 35 | 1 | 3 | 3 | 4 | 1 | 0 | 0 |
| UncS(LConf) | 35 | 1 | 4 | 2 | 5 | 1 | 0 | 0 |
| UncS(SMar) | 36 | 2 | 2 | 2 | 4 | 1 | - | 0 |
| Total | 774 | 40 | 105 | 98 | 61 | 10 | 24 | 0 |
| QS (metric) | Logitboost (M5P) | Logitboost (DStump) | Bagging (J48) | Ada (DStump) | LMT |
|---|---|---|---|---|---|
| Binary Datasets | |||||
| R = 5% | |||||
| UncS(Ent) | 17 | 0 | 1 | 4 | 8 |
| UncS(LConf) | 16 | 0 | 1 | 2 | 10 |
| UncS(SMar) | 16 | 0 | 1 | 2 | 10 |
| R = 10% | |||||
| UncS(Ent) | 16 | 0 | 3 | 3 | 9 |
| UncS(LConf) | 18 | 0 | 3 | 3 | 7 |
| UncS(SMar) | 18 | 0 | 2 | 4 | 7 |
| R = 15% | |||||
| UncS(Ent) | 14 | 0 | 4 | 3 | 9 |
| UncS(LConf) | 12 | 0 | 4 | 4 | 11 |
| UncS(SMar) | 12 | 0 | 4 | 3 | 12 |
| R = 20% | |||||
| UncS(Ent) | 10 | 1 | 1 | 3 | 14 |
| UncS(LConf) | 10 | 1 | 1 | 3 | 14 |
| UncS(SMar) | 12 | 0 | 1 | 3 | 14 |
| Multi-Class Datasets | |||||
| R = 5% | |||||
| UncS(Ent) | 28 | 1 | 0 | 1 | 12 |
| UncS(LConf) | 27 | 1 | 0 | 1 | 13 |
| UncS(SMar) | 27 | 1 | 0 | 0 | 14 |
| R = 10% | |||||
| UncS(Ent) | 28 | 5 | 0 | 0 | 9 |
| UncS(LConf) | 28 | 3 | 0 | 0 | 11 |
| UncS(SMar) | 26 | 2 | 0 | 0 | 14 |
| R = 15% | |||||
| UncS(Ent) | 29 | 1 | 0 | 1 | 12 |
| UncS(LConf) | 26 | 1 | 0 | 0 | 15 |
| UncS(SMar) | 27 | 2 | 0 | 0 | 13 |
| R = 20% | |||||
| UncS(Ent) | 28 | 1 | 0 | 0 | 13 |
| UncS(LConf) | 26 | 4 | 0 | 0 | 12 |
| UncS(SMar) | 28 | 3 | 0 | 0 | 11 |
| Total | 499 | 51 | 2 | 40 | 274 |
| Active Learning Approaches | Binary | Multiclass | Average | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R(%) | 5% | 10% | 15% | 20% | 5% | 10% | 15% | 20% | |
| UncS(Logitboost(M5P)) | 2.138 | 2.511 | 2.477 | 3.040 | 2.270 | 1.948 | 1.921 | 2.270 | 2.322 |
| UncS(LMT) | 3.787 | 3.000 | 2.563 | 2.328 | 3.321 | 2.813 | 2.528 | 3.321 | 2.958 |
| RS(LMT) | 4.437 | 4.230 | 4.540 | 3.632 | 3.468 | 3.603 | 3.659 | 3.468 | 3.880 |
| RS(Logitboost(M5P)) | 4.851 | 5.109 | 4.839 | 4.983 | 3.079 | 3.016 | 3.452 | 3.079 | 4.051 |
| RS(Ada(DStump)) | 5.437 | 6.132 | 6.943 | 6.977 | 8.238 | 8.889 | 9.246 | 8.238 | 7.513 |
| RS(Bagging(J48)) | 5.833 | 6.672 | 6.483 | 6.316 | 5.921 | 6.298 | 6.286 | 5.921 | 6.216 |
| UncS(Ada(DStump)) | 6.626 | 5.707 | 5.931 | 6.575 | 9.381 | 9.381 | 8.937 | 9.381 | 7.740 |
| UncS(Bagging(J48)) | 6.339 | 5.282 | 4.695 | 4.908 | 6.560 | 5.583 | 5.440 | 6.560 | 5.671 |
| RS((Logitboost(DStump))) | 7.080 | 7.678 | 7.793 | 8.241 | 5.516 | 6.111 | 6.214 | 5.516 | 6.769 |
| UncS((Logitboost(DStump))) | 8.471 | 8.678 | 8.736 | 8.000 | 7.246 | 7.357 | 7.317 | 7.246 | 7.881 |
| Active Learning Approaches | Binary | Multiclass | Average | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R(%) | 5% | 10% | 15% | 20% | 5% | 10% | 15% | 20% | |
| Ent(5 iterations) | 3.32 | 3.88 | 3.69 | 3.50 | 3.94 | 3.82 | 3.95 | 3.83 | 3.74 |
| Ent(10 iterations) | 3.38 | 2.86 | 3.09 | 2.93 | 2.47 | 3.07 | 2.89 | 3.39 | 3.01 |
| Ent(15 iterations) | 3.01 | 2.98 | 2.58 | 3.20 | 3.15 | 3.07 | 3.02 | 2.60 | 3.00 |
| Ent(20 iterations) | 2.36 | 2.75 | 2.74 | 2.51 | 2.73 | 2.74 | 2.66 | 2.78 | 2.66 |
| Ent(25 iterations) | 2.93 | 2.53 | 2.90 | 2.85 | 2.71 | 2.29 | 2.48 | 2.40 | 2.64 |
| LConf(5 iterations) | 3.39 | 3.83 | 3.65 | 3.51 | 3.46 | 4.00 | 3.95 | 3.86 | 3.71 |
| LConf(10 iterations) | 3.31 | 2.95 | 3.05 | 3.18 | 2.90 | 2.82 | 2.99 | 2.66 | 2.98 |
| LConf(15 iterations) | 3.02 | 2.93 | 2.94 | 2.94 | 3.20 | 2.88 | 3.20 | 3.59 | 3.09 |
| LConf(20 iterations) | 2.30 | 2.77 | 2.63 | 2.51 | 2.81 | 2.73 | 2.51 | 2.60 | 2.61 |
| LConf(25 iterations) | 2.99 | 2.51 | 2.74 | 2.85 | 2.63 | 2.56 | 2.35 | 2.30 | 2.62 |
| SMar(5 iterations) | 3.35 | 3.78 | 3.65 | 3.47 | 3.83 | 3.99 | 3.82 | 3.89 | 3.72 |
| SMar(10 iterations) | 3.33 | 2.95 | 3.09 | 2.90 | 2.98 | 2.95 | 3.17 | 3.23 | 3.08 |
| SMar(15 iterations) | 3.03 | 2.93 | 2.60 | 3.15 | 2.72 | 2.80 | 2.63 | 2.57 | 2.80 |
| SMar(20 iterations) | 2.30 | 2.80 | 2.73 | 2.49 | 2.78 | 2.83 | 3.07 | 2.76 | 2.72 |
| SMar(25 iterations) | 2.99 | 2.53 | 2.93 | 3.00 | 2.69 | 2.44 | 2.31 | 2.54 | 2.68 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kazllarof, V.; Karlos, S.; Kotsiantis, S. Investigation of Combining Logitboost(M5P) under Active Learning Classification Tasks. Informatics 2020, 7, 50. https://0-doi-org.brum.beds.ac.uk/10.3390/informatics7040050
Kazllarof V, Karlos S, Kotsiantis S. Investigation of Combining Logitboost(M5P) under Active Learning Classification Tasks. Informatics. 2020; 7(4):50. https://0-doi-org.brum.beds.ac.uk/10.3390/informatics7040050
Chicago/Turabian StyleKazllarof, Vangjel, Stamatis Karlos, and Sotiris Kotsiantis. 2020. "Investigation of Combining Logitboost(M5P) under Active Learning Classification Tasks" Informatics 7, no. 4: 50. https://0-doi-org.brum.beds.ac.uk/10.3390/informatics7040050







