Statistical Characteristics of a Twisted Anisotropic Gaussian Schell-Model Beam in Turbulent Ocean
Abstract
:1. Introduction
2. The CSD Function of a TAGSM Beam Passing through in Turbulent Ocean
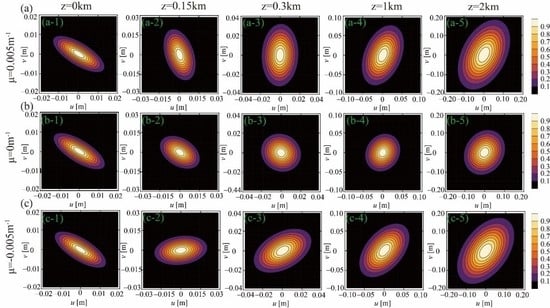
3. Numerical Simulation and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Simon, R.; Mukunda, N. Twisted Gaussian Schell-model beams. J. Opt. Soc. Am. A 1993, 10, 95–109. [Google Scholar] [CrossRef]
- Serna, J.; Movilla, J.M. Orbital angular momentum of partially coherent beams. Opt. Lett. 2001, 26, 405–407. [Google Scholar] [CrossRef] [Green Version]
- Lin, Q.; Cai, Y. Tensor ABCD law for partially coherent twisted anisotropic Gaussian-Schell model beams. Opt. Lett. 2002, 27, 216–218. [Google Scholar] [CrossRef]
- Cai, Y.; Hu, L. Propagation of partially coherent twisted anisotropic Gaussian Schell-model beams through an apertured astigmatic optical system. Opt. Lett. 2006, 31, 685–687. [Google Scholar] [CrossRef]
- Alkelly, A.A.; Shukri, M.; Alarify, Y.S. Influences of twist phenomenon of partially coherent field with uniform-intensity diffractive axicons. J. Opt. Soc. Am. A 2012, 29, 417–425. [Google Scholar] [CrossRef]
- Shukri, M.A.; Alkelly, A.A.; Alarify, Y.S. Spatial correlation properties of twisted partially coherent light focused by diffractive axicons. J. Opt. Soc. Am. A 2012, 29, 2019–2027. [Google Scholar] [CrossRef]
- Ge, D.; Cai, Y.; Lin, Q. Propagation of partially polarized Gaussian Schell-model beams in dispersive and absorbing media. Opt. Commun. 2004, 229, 93–98. [Google Scholar] [CrossRef]
- Liu, L.; Chen, Y.; Guo, L.; Cai, Y. Twist phase-induced changes of the statistical properties of a stochastic electromagnetic beam propagating in a uniaxial crystal. Opt. Express 2015, 23, 12454–12467. [Google Scholar]
- Wang, J.; Wang, H.; Zhu, S.; Li, Z. Second-order moments of a twisted Gaussian Schell-model beam in anisotropic turbulence. J. Opt. Soc. Am. A 2018, 35, 1173–1179. [Google Scholar] [CrossRef]
- Cui, Y.; Wang, F.; Cai, Y. Propagation of a twist Gaussian-Schell model beam in non-Kolmogorov turbulence. Opt. Commun. 2014, 324, 108–113. [Google Scholar]
- Tong, Z.; Korotkova, O. Beyond the classical Rayleigh limit with twisted light. Opt. Lett. 2012, 37, 2595–2597. [Google Scholar] [CrossRef]
- Zhao, C.; Cai, Y.; Korotkova, O. Radiation force of scalar and electromagnetic twisted Gaussian Schell-model beams. Opt. Express 2009, 17, 21472–21487. [Google Scholar] [CrossRef]
- Wang, F.; Cai, Y.; Halil, T.; Eyyuboğlu; Baykal, Y. Twist phase-induced reduction in scintillation of a partially coherent beam in turbulent atmosphere. Opt. Lett. 2012, 37, 184–186. [Google Scholar] [CrossRef]
- Wang, H.; Peng, X.; Liu, L.; Wang, F.; Cai, Y.; Popov, S. Generating bona fide twisted Gaussian Schell-model beams. Opt. Lett. 2019, 44, 3709–3712. [Google Scholar] [CrossRef]
- Borghi, R.; Gori, F.; Guattari, G.; Santarsiero, M. Twisted Schell-model beams with axial symmetry. Opt. Lett. 2015, 40, 4504–4507. [Google Scholar] [CrossRef]
- Borghi, R. Twisting partially coherent light. Opt. Lett. 2018, 43, 1627–1630. [Google Scholar] [CrossRef]
- Mei, Z.; Korotkova, O. Random sources for rotating spectral densities. Opt. Lett. 2017, 42, 255–258. [Google Scholar] [CrossRef]
- Gori, F.; Santarsiero, M. Devising genuine twisted cross-spectral densities. Opt. Lett. 2018, 43, 595–598. [Google Scholar] [CrossRef]
- Wu, G. Propagation properties of a radially polarized partially coherent twisted beam in free space. J. Opt. Soc. Am. A 2016, 33, 345–350. [Google Scholar] [CrossRef]
- Peng, X.; Liu, L.; Wang, F.; Popov, S.; Cai, Y. Twisted Laguerre-Gaussian Schell-model beam and its orbital angular moment. Opt. Express 2018, 26, 33956–33969. [Google Scholar] [CrossRef]
- Peng, X.; Liu, L.; Yu, J.; Liu, X.; Cai, Y.; Baykal, Y.; Li, W. Propagation of a radially polarized twisted Gaussian Schell-model beam in turbulent atmosphere. J. Opt. 2016, 18, 125601. [Google Scholar] [CrossRef]
- Wan, L.; Zhao, D. Twisted Gaussian Schell-model array beams. Opt. Lett. 2018, 43, 3554–3557. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Wang, J.; Huang, H.; Wang, H.; Zhu, S.; Li, Z.; Lu, J. Propagation characteristics of a twisted cosine-Gaussian correlated radially polarized beam. Appl. Sci. 2018, 8, 1485. [Google Scholar] [CrossRef] [Green Version]
- Fu, W.; Cao, P. Second-order statistics of a radially polarized partially coherent twisted beam in a uniaxial crystal. J. Opt. Soc. Am. A 2017, 34, 1703–1710. [Google Scholar] [CrossRef] [PubMed]
- Stahl, C.S.D.; Gbur, G. Twisted vortex Gaussian Schell-model beams. J. Opt. Soc. Am. A 2018, 35, 1899–1906. [Google Scholar] [CrossRef]
- Wan, L.; Zhao, D. Controllable rotating Gaussian Schell-model beams. Opt. Lett. 2019, 44, 735–738. [Google Scholar] [CrossRef]
- Yi, X.; Li, Z.; Liu, Z. Underwater optical communication performance for laser beam propagation through weak oceanic turbulence. Appl. Opt. 2015, 54, 1273–1278. [Google Scholar] [CrossRef]
- Zilberman, A.; Golbraikh, E.; Kopeika, N.S.; Virtser, A.; Kupershmidt, I.; Shtemler, Y. Lidar study of aerosol turbulence characteristics in the troposphere: Kolmogorov and non-Kolmogorov turbulence. Atmos. Res. 2008, 88, 66–77. [Google Scholar] [CrossRef]
- Cheng, J. Ghost imaging through turbulent atmosphere. Opt. Express 2009, 17, 7916–7921. [Google Scholar] [CrossRef]
- Wang, F.; Cai, Y.; Korotkova, O. Ghost imaging with partially coherent light in turbulent atmosphere. In Proceedings of the Atmospheric and Oceanic Propagation of Electromagnetic Waves IV, San Francisco, CA, USA, 26 February 2010; Volume 7588, p. 75880F. [Google Scholar]
- Le, M.; Wang, G.; Zheng, H.; Liu, J.; Xu, Z. Underwater computational ghost imaging. Opt. Express 2017, 25, 22859–22868. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Liu, L.; Wang, F.; Zhang, Y.; Cai, Y. Ghost imaging with a partially coherent beam carrying twist phase in a turbulent ocean: A numerical approach. Appl. Sci. 2019, 9, 3023. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Liu, X.; Cai, Y. Propagation of partially coherent beam in turbulent atmosphere: A review. Prog. Electromagn. Res. 2015, 150, 123–143. [Google Scholar] [CrossRef] [Green Version]
- Gbur, G. Partially coherent beam propagation in atmospheric turbulence [Invited]. J. Opt. Soc. Am. A 2014, 31, 2028–2045. [Google Scholar]
- Korotkova, O. Light propagation in a turbulent ocean. Prog. Opt. 2018, 64, 1–43. [Google Scholar]
- Nikishov, V.V.; Nikishov, V.I. Spectrum of turbulent fluctuations of the sea-water refraction index. Int. J. Fluid Mech. Res. 2000, 27, 82–98. [Google Scholar] [CrossRef]
- Peng, X.; Liu, L.; Cai, Y.; Baykal, Y. Statistical properties of a radially polarized twisted Gaussian Schell-model beam in an underwater turbulent medium. J. Opt. Soc. Am. A 2016, 34, 133–139. [Google Scholar] [CrossRef]
- Tang, M.; Zhao, D. Propagation of radially polarized beams in the oceanic turbulence. Appl. Phys. B 2013, 111, 665–670. [Google Scholar] [CrossRef]
- Dong, Y.; Guo, L.; Liang, C.; Wang, F.; Cai, Y. Statistical properties of a partially coherent cylindrical vector beam in oceanic turbulence. J. Opt. Soc. Am. A 2015, 32, 894–901. [Google Scholar] [CrossRef]
- Lu, L.; Zhang, P.; Fan, C.; Qiao, C. Influence of oceanic turbulence on propagation of a radial Gaussian beam array. Opt. Express 2015, 23, 2827–2836. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, Y. Analysis of modal crosstalk for communication in turbulent ocean using Lommel-Gaussian beam. Opt. Express 2017, 25, 22565–22574. [Google Scholar] [CrossRef]
- Hu, B.; Shi, H.; Zhang, Y. Fiber-coupling efficiency of Gaussian–Schell model beams through an ocean to fiber optical communication link. Opt. Commun. 2018, 417, 14–18. [Google Scholar] [CrossRef]
- Korotkova, O.; Farwell, N. Effect of oceanic turbulence on polarization of stochastic beams. Opt. Commun. 2011, 284, 1740–1746. [Google Scholar]
- Xu, J.; Zhao, D. Propagation of a stochastic electromagnetic vortex beam in the oceanic turbulence. Opt. Laser Technol. 2014, 57, 189–193. [Google Scholar]
- Zhou, Y.; Zhao, D. Propagation properties of a twisted rectangular multi-Gaussian Schell-model beam in free space and oceanic turbulence. Appl. Opt. 2018, 57, 8978–8983. [Google Scholar] [CrossRef]
- Lu, W.; Liu, L.; Sun, J. Influence of temperature and salinity fluctuations on propagation behavior of partially coherent beams in oceanic turbulence. J. Opt. A-Pure Appl. Opt. 2006, 8, 1052–1058. [Google Scholar] [CrossRef]
- Kashani, F.; Yousefi, M. Analyzing the propagation behavior of coherence and polarization degrees of a phase-locked partially coherent radial flat-topped array laser beam in underwater turbulence. Appl. Opt. 2016, 55, 6311–6320. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Y.; Yin, H. Evolution properties of partially coherent flat-topped vortex hollow beam in oceanic turbulence. Appl. Opt. 2015, 54, 10510–10516. [Google Scholar]
- Baykal, Y. Scintillation index in strong oceanic turbulence. Opt. Commun. 2016, 375, 15–18. [Google Scholar]
- Huang, X.; Deng, Z.; Shi, X.; Bai, Y.; Fu, X. Average intensity and beam quality of optical coherence lattices in oceanic turbulence with anisotropy. Opt. Express 2018, 26, 4786–4797. [Google Scholar]
- Sun, C.; Lv, X.; Ma, B.; Zhang, J.; Deng, D.; Hong, W. Statistical properties of partially coherent radially and azimuthally polarized rotating elliptical Gaussian beams in oceanic turbulence with anisotropy. Opt. Express 2019, 27, A245–A256. [Google Scholar] [CrossRef]
- Wang, F.; Cai, Y. Second-order statistics of a twisted Gaussian Schell-model beam in turbulent atmosphere. Opt. Express 2010, 18, 24661–24672. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; He, S. Propagation of a partially coherent twisted anisotropic Gaussian Schell-model beam in a turbulent atmosphere. Appl. Phys. Lett. 2006, 89, 041117. [Google Scholar] [CrossRef]
- Wolf, E.; Collett, E. Partially coherent sources which produce the same far-field intensity distribution as a laser. Opt. Commun. 1978, 25, 293–296. [Google Scholar] [CrossRef]
- Simon, R. Anisotropic Gaussian Schell-model beams: Passage through optical systems and associated invariants. Phys. Rev. A. 1985, 1, 2419–2434. [Google Scholar] [CrossRef]
- Cai, Y.; Zhu, S. Orbital angular moment of a partially coherent beam propagating through an astigmatic ABCD optical system with loss or gain. Opt. Lett. 2014, 39, 1968–1971. [Google Scholar] [CrossRef]







© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhao, Y.; Liu, X.; Liang, C.; Liu, L.; Wang, F.; Cai, Y. Statistical Characteristics of a Twisted Anisotropic Gaussian Schell-Model Beam in Turbulent Ocean. Photonics 2020, 7, 37. https://0-doi-org.brum.beds.ac.uk/10.3390/photonics7020037
Liu Y, Zhao Y, Liu X, Liang C, Liu L, Wang F, Cai Y. Statistical Characteristics of a Twisted Anisotropic Gaussian Schell-Model Beam in Turbulent Ocean. Photonics. 2020; 7(2):37. https://0-doi-org.brum.beds.ac.uk/10.3390/photonics7020037
Chicago/Turabian StyleLiu, Yonglei, Yuefeng Zhao, Xianlong Liu, Chunhao Liang, Lin Liu, Fei Wang, and Yangjian Cai. 2020. "Statistical Characteristics of a Twisted Anisotropic Gaussian Schell-Model Beam in Turbulent Ocean" Photonics 7, no. 2: 37. https://0-doi-org.brum.beds.ac.uk/10.3390/photonics7020037