Novel Stopping Criteria for Optimization-Based Microwave Breast Imaging Algorithms
Abstract
:1. Introduction
2. Materials and Methods
2.1. DGM-CSI Algorithm
2.2. Frequency-Cycling Tissue-Dependent Mapping Technique
2.3. Stopping Criteria for Single-Frequency Reconstructions
2.4. Global Termination of Multi-Frequency Reconstructions
2.5. Full Description of Multi-Frequency Imaging Procedure
- The real and imaginary parts of the complex permittivity are reconstructed using the lowest frequency data available (e.g., 1.0 GHz). The termination point of this reconstruction is dictated by the results of successive two-sample K-S tests performed on both the real and imaginary parts of the data error separately, comparing the current iteration to those of a sliding window of past iterations, governed by a choice of parameters for p-value, window size, and percentage of windowed iterations reaching this p-value threshold. For robustness, a back-up termination condition may be implemented, either related to the relative change in domain error for CSI-based algorithms as described in Section 2.4, or a maximum number of iterations.
- A point-by-point search through the reconstructed real part of each nodal basis coefficient in the DGM-CSI mesh (or more generally, each mesh element or pixel of the reconstructed image) classifies the type of breast tissue. This classification is based solely on the range of expected values of dielectric constant at that frequency, as outlined in [25].
- An initial guess for the next imaging frequency (e.g., 2.0 GHz) is generated using the tissue-dependent mapping process [24,25]. It consists of the unmodified real parts of the reconstructed at the mesh nodal points, and a new imaginary part created from a simple linear interpolation of the expected range of dielectric loss values, based on the appropriate Cole-Cole models of tissues classified in Step 2. This technique preserves the geometry of the real and imaginary parts of the solution.
- This new initial guess for the complex permittivity is used to run the inversion algorithm at the next frequency (e.g., 2.0 GHz). As per the procedure outlined in [25], the user may choose to keep the imaginary part constant during this inversion and update only the real part to converge to a new solution. This “anchoring” process has been shown to improve overall imaging results due to the tendency of CSI-based inversion algorithms to cause significant deterioration of the imaginary part at high-frequency reconstructions. Again, the aforementioned parameterized stopping criteria would be primarily employed to determine the appropriate point to halt this reconstruction.
- If more than two frequencies are used in the frequency hop, steps 2–4 are repeated as necessary until the reconstruction of the final frequency of the succession is complete (e.g., 3.0 GHz). This succession may include “frequency cycling”; that is, returning the inversion algorithm to the lowest frequency data and incrementally stepping through each frequency again [25].
- When each available dataset in the frequency cycle has been used at least once to contribute to the overall image reconstruction, a global termination criterion will become active, which will monitor the relative change in the domain error between successive iterations (Section 2.4). If this relative change falls below 0.1% at any point, the current reconstruction is halted and the frequency cycle is broken.
- Regardless of the frequency at which the algorithm was halted by this relative domain error threshold, if the imaginary part of the solution has been continuously held constant during the frequency cycle after Step 1, one last initial guess is generated as in Step 3 and a final reconstruction is run at the lowest frequency available (e.g., 1.0 GHz) with both the real and imaginary parts allowed to converge to a solution (i.e., the imaginary part is no longer “anchored”). This final inversion is terminated by the parameterized stopping criteria or a relative change of domain error between successive iterations falling below 0.1%, whichever occurs first. The purpose of this final run is to demonstrate the stability of the final solution and ensure that its imaginary part, despite being originally based on the geometry and tissue properties of the real part, does indeed satisfy full CSI optimization.
2.6. Synthetic Breast Models
2.7. Error Calculation
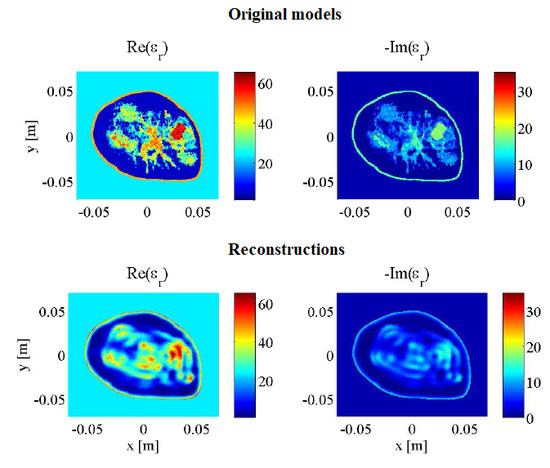
3. Results and Discussion
3.1. Imaging with Open Boundaries
3.2. Imaging with PEC Boundaries
3.3. Effect of Noise Levels
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Trentham-Dietz, A.; Kerlikowske, K.; Stout, N.K.; Miglioretti, D.L.; Schechter, C.B.; Ergun, M.A.; van den Broek, J.J.; Alagoz, O.; Sprague, B.L.; van Ravesteyn, N.T.; et al. Tailoring breast cancer screening intervals by breast density and risk for women aged 50 years or older: Collaborative modeling of screening outcomes. Ann. Intern. Med. 2016, 165, 700–712. [Google Scholar] [CrossRef] [PubMed]
- D’Orsi, C.J.; Mendelson, E.B.; Morris, E.A. (Eds.) ACR BI-RADS Atlas: Breast Imaging Reporting and Data System, 5th ed.; American College of Radiology: Reston, VA, USA, 2012. [Google Scholar]
- Boerner, W.M.; Brand, H.; Cram, L.A.; Gjessing, D.T.; Jordan, A.K.; Keydel, W.; Schwierz, G.; Vogel, M. (Eds.) Inverse Methods in Electromagnetic Imaging; D. Reidel Publishing: Dordrecht, The Netherlands, 1985. [Google Scholar]
- Larsen, L.E.; Jacobi, J.H. (Eds.) Medical Applications of Microwave Imaging; IEEE Press: New York, NY, USA, 1986. [Google Scholar]
- Kosmas, P.; Crocco, L. Introduction to Special Issue on “Electromagnetic Technologies for Medical Diagnostics: Fundamental Issues, Clinical Applications and Perspectives”. Diagnostics 2019, 9, 19. [Google Scholar] [CrossRef]
- Sill, J.M.; Fear, E.C. Tissue sensing adaptive radar for breast cancer detection—Experimental investigation of simple tumor models. IEEE Trans. Microw. Theory Tech. 2005, 53, 3312–3319. [Google Scholar] [CrossRef]
- Delbary, F.; Brignone, M.; Bozza, G.; Aramini, R.; Piana, M. A visualization method for breast cancer detection using microwaves. SIAM J. Appl. Math. 2010, 70, 2509–2533. [Google Scholar] [CrossRef]
- Cakoni, F.; Colton, D.; Monk, P. Qualitative Methods in Inverse Electromagnetic Scattering Theory: Inverse Scattering for Anisotropic Media. IEEE Antennas Propag. Mag. 2017, 59, 24–33. [Google Scholar] [CrossRef]
- Colton, D.; Kress, R. Inverse Acoustic and Electromagnetic Scattering Theory; Springer Science & Business Media: Berlin, Germany, 2012; Volume 93. [Google Scholar]
- Engl, H.W.; Hanke, M.; Neubauer, A. Regularization of Inverse Problems; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1996. [Google Scholar]
- Van den Berg, P.M.; Kleinman, R.E. A contrast source inversion method. Inverse Probl. 1997, 13, 1607–1620. [Google Scholar] [CrossRef]
- Abubakar, A.; Van den Berg, P.M.; Mallorqui, J.J. Imaging of biomedical data using a multiplicative regularized contrast source inversion method. IEEE Trans. Microw. Theory Tech. 2002, 50, 1761–1771. [Google Scholar] [CrossRef] [Green Version]
- Zakaria, A.; Gilmore, C.; LoVetri, J. Finite-element contrast source inversion method for microwave imaging. Inverse Probl. 2010, 26, 115010. [Google Scholar] [CrossRef]
- Jeffrey, I.; Geddert, N.; Brown, K.; LoVetri, J. The Time-Harmonic Discontinuous Galerkin Method as a Robust Forward Solver for Microwave Imaging Applications. Prog. Electromagn. Res. 2015, 154, 1–21. [Google Scholar] [CrossRef]
- Brown, K.G.; Geddert, N.; Asefi, M.; LoVetri, J.; Jeffrey, I. Hybridizable Discontinuous Galerkin Method Contrast Source Inversion of 2-D and 3-D Dielectric and Magnetic Targets. IEEE Trans. Microw. Theory Tech. 2019, 67, 1766–1777. [Google Scholar] [CrossRef]
- Baran, A.; Kurrant, D.; Zakaria, A.; Fear, E.; LoVetri, J. Breast Imaging Using Microwave Tomography with Radar-Based Tissue-Regions Estimation. Prog. Electromagn. Res. 2014, 149, 161–171. [Google Scholar] [CrossRef]
- Kurrant, D.J.; Baran, A.; Fear, E.C.; LoVetri, J. Integrating prior information into microwave tomography Part 1: Impact of detail on image quality. Med. Phys. 2017, 44, 6461–6481. [Google Scholar] [CrossRef]
- Kurrant, D.; Baran, A.; LoVetri, J.; Fear, E. Integrating prior information into microwave tomography part 2: Impact of errors in prior information on microwave tomography image quality. Med. Phys. 2017, 44, 6482–6503. [Google Scholar] [CrossRef]
- Abdollahi, N.; Kurrant, D.; Mojabi, P.; Omer, M.; Fear, E.; LoVetri, J. Incorporation of Ultrasonic Prior Information for Improving Quantitative Microwave Imaging of Breast. IEEE J. Multiscale Multiphys. Comput. Tech. 2019, 4, 98–110. [Google Scholar] [CrossRef]
- Nemez, K.; Baran, A.; Asefi, M.; LoVetri, J. Modeling Error and Calibration Techniques for a Faceted Metallic Chamber for Magnetic Field Microwave Imaging. IEEE Trans. Microw. Theory Tech. 2007, 65, 4347–4356. [Google Scholar] [CrossRef]
- Asefi, M.; Baran, A.; LoVetri, J. An Experimental Phantom Study for Air-Based Quasi-Resonant Microwave Breast Imaging. IEEE Trans. Microw. Theory Tech. 2019. [Google Scholar] [CrossRef]
- Shea, J.D.; Kosmas, P.; Van Veen, B.D.; Hagness, S.C. Contrast-enhanced microwave imaging of breast tumors: A computational study using 3D realistic numerical phantoms. Inverse Probl. 2010, 26, 074009. [Google Scholar] [CrossRef]
- Chew, W.; Lin, J. A frequency-hopping approach for microwave imaging of large inhomogeneous bodies. IEEE Microw. Guided Wave Lett. 1995, 5, 439–441. [Google Scholar] [CrossRef]
- Kaye, C.; Jeffrey, I.; LoVetri, J. Enhancement of multi-frequency microwave breast images using a tissue-dependent mapping technique with discontinuous Galerkin contrast source inversion. In Proceedings of the AES 2016—4th Advanced Electromagnetics Symposium, Malaga, Spain, 26–28 July 2016; pp. 37–39. [Google Scholar]
- Kaye, C.; Jeffrey, I.; LoVetri, J. Improvement of Multi-Frequency Microwave Breast Imaging through Frequency Cycling and Tissue-Dependent Mapping. IEEE Trans. Antennas Propag. 2019. submitted. [Google Scholar]
- Abubakar, A.; van den Berg, P.M.; Habashy, T.M. Application of the multiplicative regularized contrast source inversion method on TM- and TE-polarized experimental Fresnel data. Inverse Probl. 2005, 21, S5–S13. [Google Scholar] [CrossRef] [Green Version]
- Van den Berg, P.M.; van Broekhoven, A.L.; Abubakar, A. Extended contrast source inversion. Inverse Probl. 1999, 15, 1325–1344. [Google Scholar] [CrossRef]
- Bloemenkamp, R.F.; Abubakar, A.; van den Berg, P.M. Inversion of experimental multi-frequency data using the contrast source inversion method. Inverse Probl. 2001, 17, 1611–1622. [Google Scholar] [CrossRef]
- Jeffrey, I.; Zakaria, A.; LoVetri, J. Microwave Imaging by Mixed-Order Discontinuous Galerkin Contrast Source Inversion. In Proceedings of the 2014 XXXIst URSI General Assembly and Scientific Symposium (URSI GASS 2014), Beijing, China, 16–23 August 2014; pp. 255–258. [Google Scholar]
- Lazebnik, M.; Popovic, D.; McCartney, L.; Watkins, C.B.; Lindstrom, M.J.; Harter, J.; Sewall, S.; Ogilvie, T.; Magliocc, M.A.; Breslin, T.M.; et al. A large-scale study of the ultrawideband microwave dielectric properties of normal, benign and malignant breast tissues obtained from cancer surgeries. Phys. Med. Biol. 2007, 52, 6093–6115. [Google Scholar] [CrossRef] [PubMed]
- Kaye, C. Development and Calibration of Microwave Tomography Imaging Systems for Biomedical Applications Using Computational Electromagnetics. Master’s Thesis, University of Manitoba, Winnipeg, MB, Canada, 2009. [Google Scholar]
- Massey, F.J. The Kolmogorov-Smirnov Test for Goodness of Fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Miller, L.H. Table of Percentage Points of Kolmogorov Statistics. J. Am. Stat. Assoc. 1956, 51, 111–121. [Google Scholar] [CrossRef]
- Marsaglia, G.; Tsang, W.; Wang, J. Evaluating Kolmogorov’s Distribution. J. Stat. Softw. 2003, 8, 1–4. [Google Scholar] [CrossRef]
- MathWorks. Two-Sample Kolmogorov-Smirnov Test (R2018a). Available online: www.mathworks.com/help/stats/kstest2.html (accessed on 16 March 2018).
- Kurrant, D.J.; Fear, E.C. Regional estimation of the dielectric properties of inhomogeneous objects using near-field reflection data. Inverse Probl. 2012, 28, 075001. [Google Scholar] [CrossRef]
- Nemez, K.; Asefi, M.; Baran, A.; LoVetri, J. A faceted magnetic field probe resonant chamber for 3D breast MWI: A synthetic study. In Proceedings of the 2016 17th International Symposium on Antenna Technology and Applied Electromagnetics (ANTEM), Montreal, QC, Canada, 10–13 July 2016; pp. 322–324. [Google Scholar]












| Frequency: | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Scenario | TM | SC | No. of Iterations (Stopping Condition) | Total | |||||
| Components Reconstructed | |||||||||
| 1.0 GHz: | 2.0 GHz: | 3.0 GHz: | |||||||
| A | No | No | 400 (F) | 400 (F) | 400 (F) | 1200 | |||
| Re, Im | Re, Im | Re, Im | |||||||
| 1.0 GHz: | 2.0 GHz: | 3.0 GHz: | 1.0 GHz: | 2.0 GHz: | 3.0 GHz: | ||||
| B | Yes | No | 200 (F) | 200 (F) | 200 (F) | 200 (F) | 200 (F) | 200 (F) | 1200 |
| Re, Im | Re | Re | Re | Re | Re | ||||
| 1.0 GHz: | 2.0 GHz: | 3.0 GHz: | 1.0 GHz: | 2.0 GHz: | 1.0 GHz: | ||||
| C | Yes | Yes * | 140 (KS) | 190 (KS) | 255 (KS) | 53 (KS) | 89 (DE) | 41 (KS) | 768 |
| Re, Im | Re | Re | Re | Re | Re, Im | ||||
| Frequency: | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Scenario | TM | SC | No. of Iterations (Stopping Condition) | Total | |||||
| Components Reconstructed | |||||||||
| 1.0 GHz: | 1.25 GHz: | 1.5 GHz: | |||||||
| D | No | No | 400 (F) | 400 (F) | 400 (F) | 1200 | |||
| Re, Im | Re, Im | Re, Im | |||||||
| 1.0 GHz: | 1.25 GHz: | 1.5 GHz: | 1.0 GHz: | 1.25 GHz: | 1.5 GHz: | ||||
| E | Yes | No | 200 (F) | 200 (F) | 200 (F) | 200 (F) | 200 (F) | 200 (F) | 1200 |
| Re, Im | Re | Re | Re | Re | Re | ||||
| 1.0 GHz: | 1.25 GHz: | 1.5 GHz: | 1.0 GHz: | 1.0 GHz: | |||||
| F | Yes | Yes * | 123 (KS) | 124 (KS) | 97 (KS) | 14 (DE) | 48 (DE) | 406 | |
| Re, Im | Re | Re | Re | Re, Im | |||||
| Frequency: | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Scenario (Noise %) | TM | SC | No. of Iterations (Stopping Condition) | Total | |||||
| Components Reconstructed | |||||||||
| 1.0 GHz: | 2.0 GHz: | 3.0 GHz: | |||||||
| G (5%) | No | No | 400 (F) | 400 (F) | 400 (F) | 1200 | |||
| Re, Im | Re, Im | Re, Im | |||||||
| 1.0 GHz: | 2.0 GHz: | 3.0 GHz: | 1.0 GHz: | 2.0 GHz: | 1.0 GHz: | ||||
| H (3%) | Yes | Yes * | 155 (KS) | 140 (KS) | 265 (KS) | 50 (KS) | 52 (DE) | 43 (DE) | 759 |
| Re, Im | Re | Re | Re | Re | Re, Im | ||||
| 1.0 GHz: | 2.0 GHz: | 3.0 GHz: | 1.0 GHz: | 1.0 GHz: | |||||
| I (5%) | Yes | Yes * | 139 (KS) | 140 (KS) | 265 (KS) | 34 (DE) | 8 (DE) | 586 | |
| Re, Im | Re | Re | Re | Re, Im | |||||
| 1.0 GHz: | 2.0 GHz: | 3.0 GHz: | 1.0 GHz: | 1.0 GHz: | |||||
| J (7.5%) | Yes | Yes * | 91 (KS) | 112 (KS) | 234 (KS) | 37 (DE) | 13 (DE) | 487 | |
| Re, Im | Re | Re | Re | Re, Im | |||||
| 1.0 GHz: | 2.0 GHz: | 3.0 GHz: | 1.0 GHz: | 1.0 GHz: | |||||
| K (10%) | Yes | Yes * | 87 (KS) | 90 (KS) | 228 (KS) | 11 (DE) | 32 (DE) | 448 | |
| Re, Im | Re | Re | Re | Re, Im | |||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaye, C.; Jeffrey, I.; LoVetri, J. Novel Stopping Criteria for Optimization-Based Microwave Breast Imaging Algorithms. J. Imaging 2019, 5, 55. https://0-doi-org.brum.beds.ac.uk/10.3390/jimaging5050055
Kaye C, Jeffrey I, LoVetri J. Novel Stopping Criteria for Optimization-Based Microwave Breast Imaging Algorithms. Journal of Imaging. 2019; 5(5):55. https://0-doi-org.brum.beds.ac.uk/10.3390/jimaging5050055
Chicago/Turabian StyleKaye, Cameron, Ian Jeffrey, and Joe LoVetri. 2019. "Novel Stopping Criteria for Optimization-Based Microwave Breast Imaging Algorithms" Journal of Imaging 5, no. 5: 55. https://0-doi-org.brum.beds.ac.uk/10.3390/jimaging5050055