4.1. Model Output
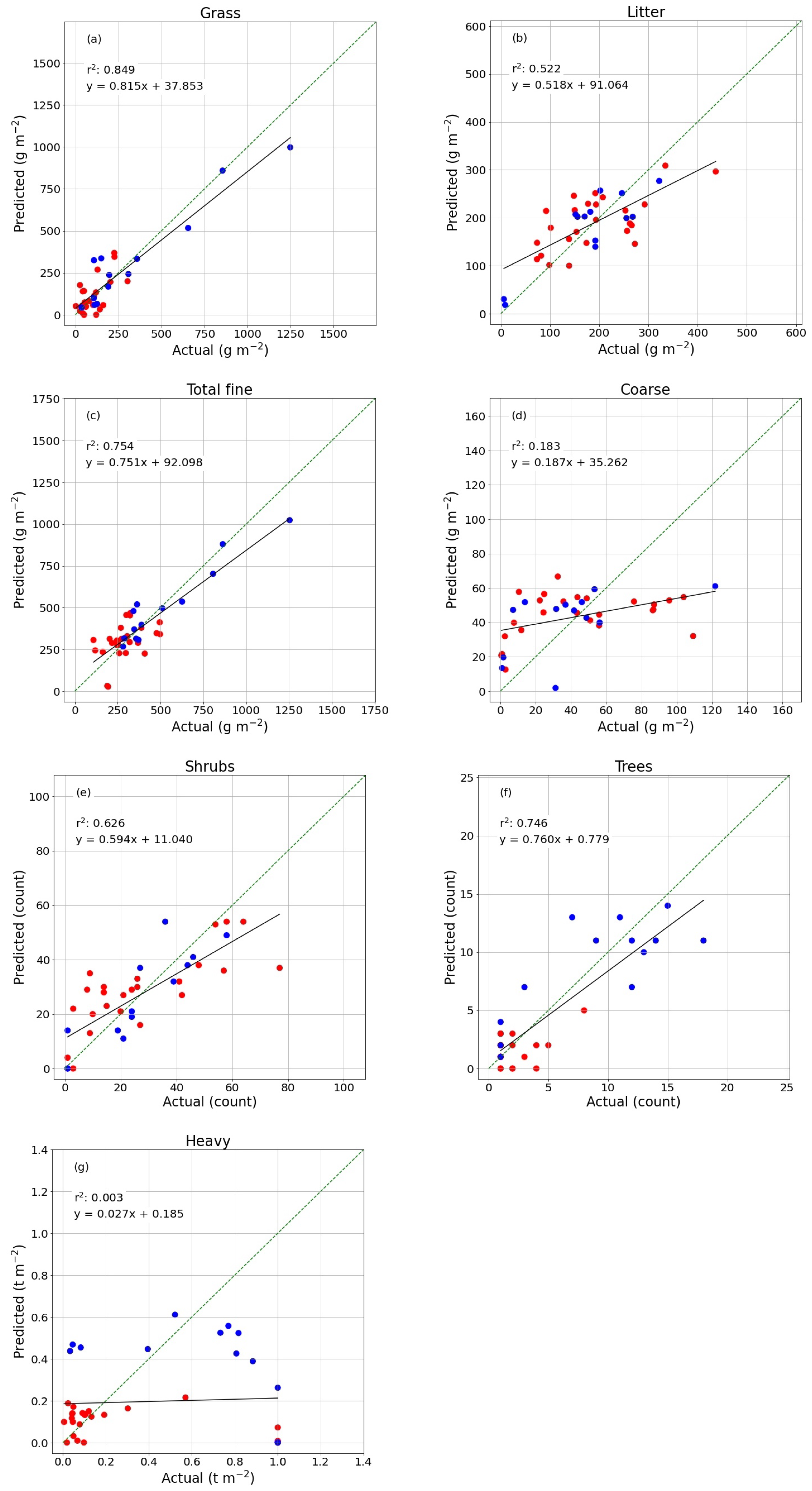
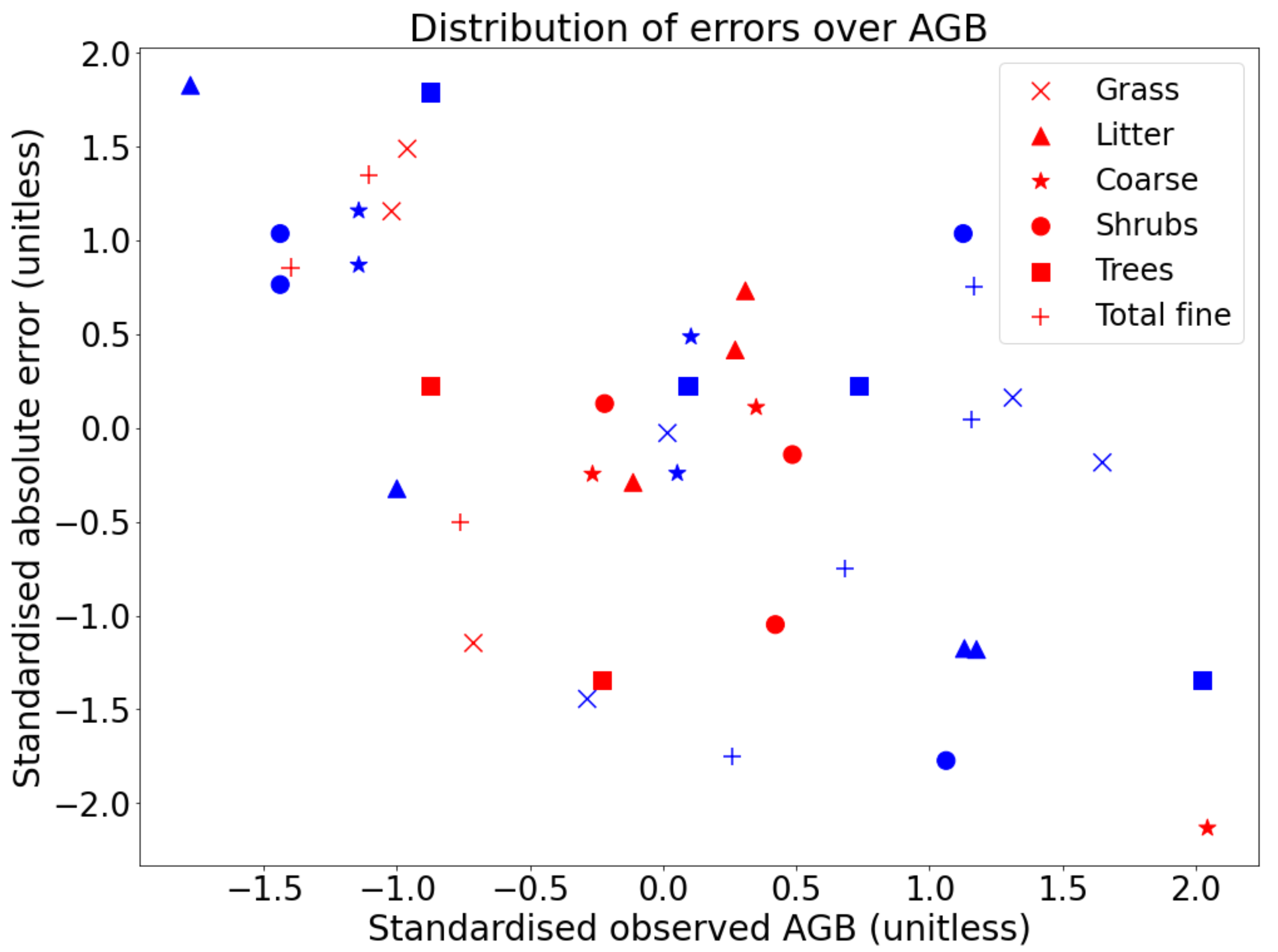
In general, prediction errors were smaller for surface fuel classes, and the total fine fuel class showed significantly smaller percentage errors than other classes. The model tended to show positive bias in low biomass regions and vice versa in high biomass regions, across all fuel classes and both study regions (
Figure 10). This would indicate perhaps that separate models may need to be developed for “low” and “high” AGB areas, which may also be reflected in the different regions; it would be an interesting extension to this study to create separate models and investigate the reasons for disparities among them. In this instance, however, there were insufficient data to perform a robust enough investigation of those effects.
For grass as well, the range of values measured on the ground in each 1×1 m quadrant was well represented by the model error range in this fuel class (
Figure 8a). Litter measurements were much more variable within each plot (
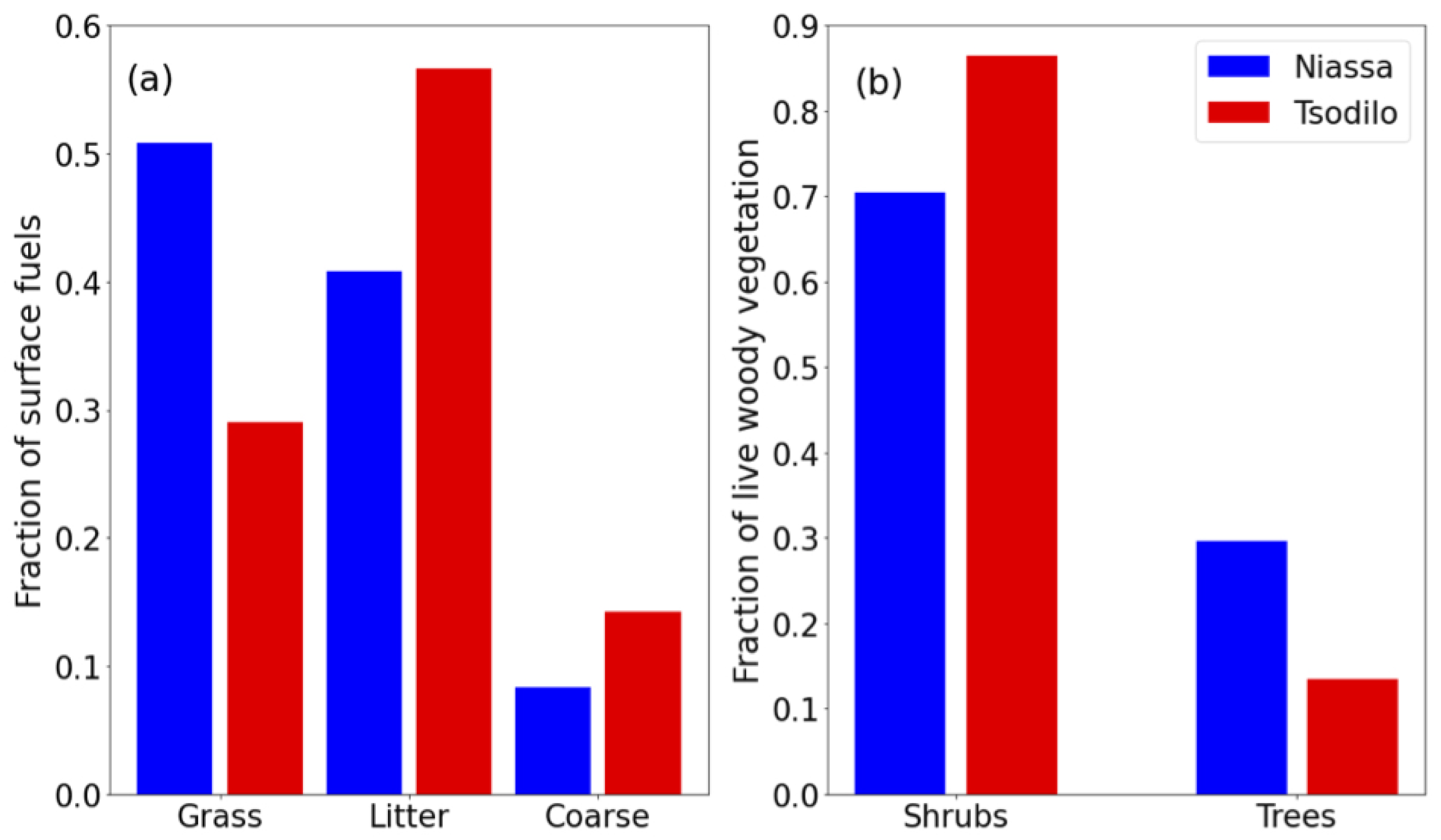
Figure 8b). Grass loading in such a small region tends to be more uniform (with the possible exception of heavily grazed areas), and litter loading in each quadrant depends heavily on the placement of the transect; should one quadrant fall precisely under a tree, then the litter loading is high, and in between two trees, then the measured value is likely to be low despite likely high loading in the surrounding area. Each plot was chosen to be a good representation of vegetation in the area, and as such, despite the large ranges measured, we think the averaged values show a reasonable representation of litter AGB in a single plot. The internal variability does present a challenge for accurate modelling however, and this effect was present (though damped by the relatively more uniform grass measurements) in the total fine class. It should also be noted that the ranges in the total fine class were calculated by adding the two lowest and two highest grass and litter loadings together, respectively, but this is not necessarily realistic. In all likelihood, areas with the highest grass loading will have the lowest litter load (pure grasslands) and vice versa for highest litter load (pure shrubland/woodland).
Noteworthy as well is that for trees, the Botswanan plots were predicted exclusively at zero. For trees, the OLS fit was far stronger when the two regions were viewed together rather than separately (which can be seen in the respective spreads of blue and especially red points in
Figure A2f). For total fine fuel in Botswana as well, the trend was not immediately obvious when blue and red points were considered separately. Perhaps, this is partially due to generally lower fine fuel loading in Tsodilo compared to Niassa, particularly for grass. Additionally, the Botswanan study site included substantial areas where the landscape is impacted by cattle and goats, the grazing of which acts as an external influence on the contribution of grass load. Efforts were made to avoid areas where cattle were known to graze intensively, but this factor cannot be ruled out completely.
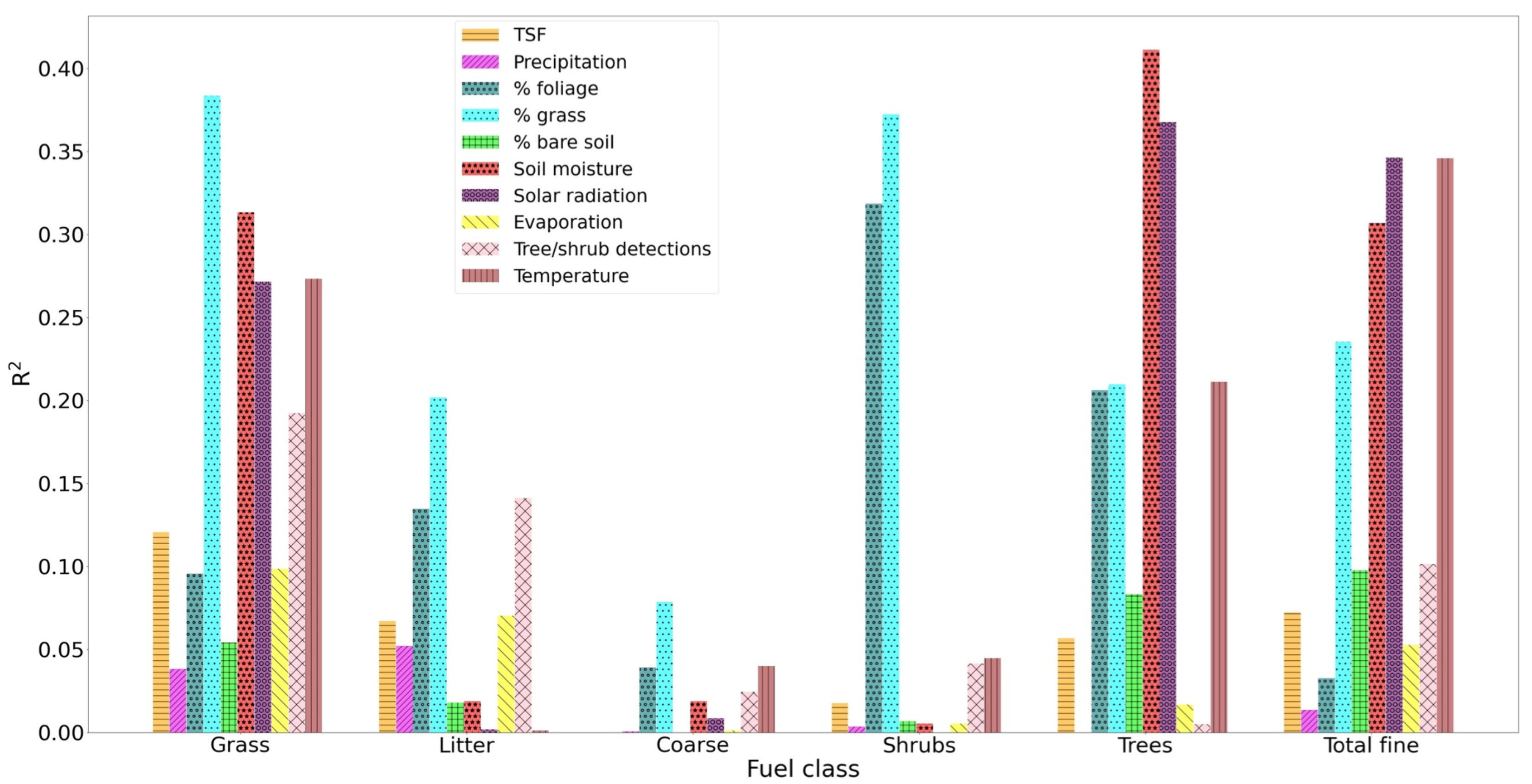
Some factors played a greater role than others in the predicted value of AGB (
Figure 11). The model for grass AGB relies on a combination of factors, most strongly the proportion of grass pixels detected by the UAS, but soil moisture, solar radiation, number of tree-like objects and temperature also play a role. For the litter class, the number of tree-like objects showed the greatest explanatory power, closely followed by % grass-covered area. The relationship between grass and litter is a complex one, and it varies between species and biome. In this instance, it was not necessarily directly causal. It is more likely that simply in areas with higher tree/shrub density and, by extension more twig/leaf litter producing species, there is generally less grass cover, and vice versa, possibly a result of less light penetration and reduced understorey growth. The tree-like object count, however, was likely to be causal, as the more individual litter-producing plants there are, the more surface litter there would be.
The explained variance of the total fine fuel class is largely dominated by the same features as grass, which would be again logical if grass contributed the most to total fine fuel AGB. This is the case for plots in Niassa, but not for those in the Tsodilo region (
Figure 9a). This explains to some extent why the fit for the predicted surface biomass in Tsodilo showed less of a clear trend (
Figure A2c) than that in Niassa, as the distribution of AGB across surface fuel classes differed and was skewed more towards litter in Tsodilo and grass in Niassa. Total AGB was generally lower in Tsodilo as well, so these data points perhaps contributed less to the fitting error, making them “less important” in a fitting context and potentially resulting in a total fine fuel model slightly better suited to more moist, grassy areas of savanna.
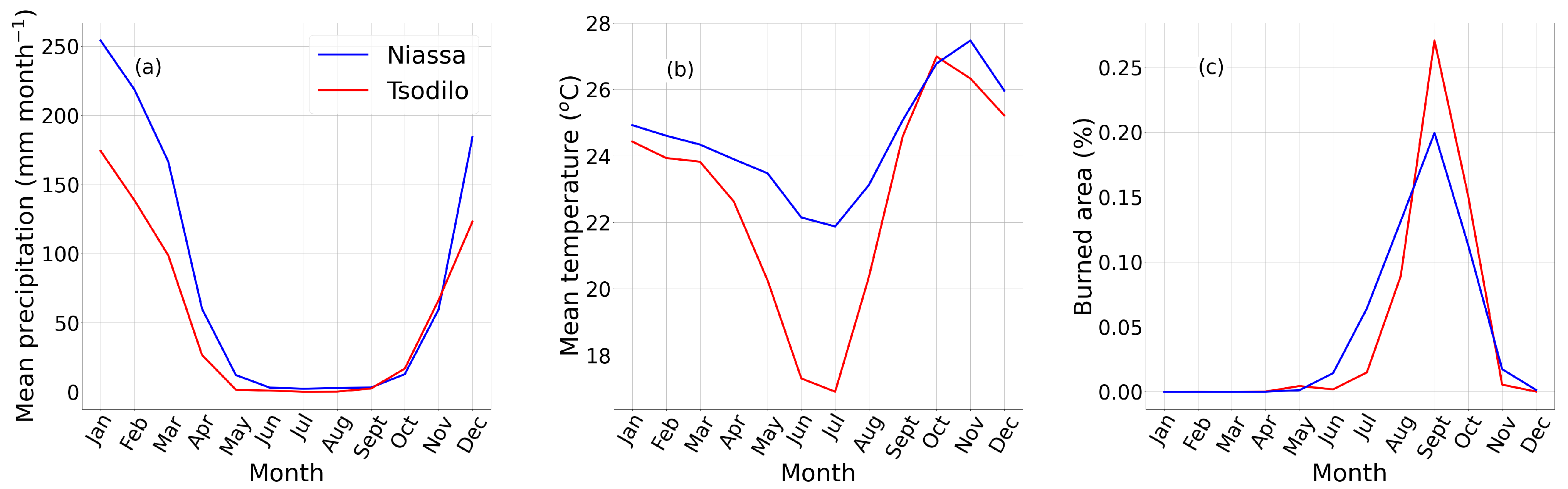
Interestingly, soil moisture was the most important explanatory variable for the number of trees in a plot, but not for the number of shrubs. This discrepancy may be a result of regular fires consuming smaller shrubs and not trees in regions like Niassa where almost all the plots burn annually, but could also be due to the difference in soil moisture between the regions. As previously mentioned, the fit in the trees class was weaker when regions were considered individually, and almost all plots in Niassa registered more trees (∼8 on average) per plot than those in Tsodilo (∼2 per plot). Since Niassa is also a warmer, wetter region in general, a correlation was found between the overall trend in tree numbers and soil moisture and used as an explanatory variable, but given that the same was not found for shrubs, it seems more likely that this was an artefact of the model design/chosen study regions. A similar effect may be observed for solar radiation and temperature, as in general, plots in Tsodilo experience a cooler climate (
Figure 3b) and somewhat more intense mean downward solar radiation (21.9 MJ m
) than Niassa (19.8 MJ m
) in ERA-5 data.
In most cases, a combination of factors, from the UAS and from meteorological input, appeared to contribute a similar proportion of the total R. One exception was in the shrubs category, where only two features (% grass and % foliage) explained significantly more of the variance than the others, both of which were extracted from UAS data. There may also be some overlap in the explained variance as a result of the proportions of foliage, grass and bare soil, as if there was a higher percentage of pixels in a given plot classed as “grass”, then there must be a smaller percentage classed as foliage or bare soil. This effect is likely to manifest itself in other variables as well. Soil moisture is also affected by temperature, evaporation, precipitation or solar radiation, and indeed, the magnitude of the explained variance for soil moisture (and to a lesser extent, temperature) and solar radiation was similar and opposite (i.e., when one was proportional, the other was inversely proportional) in every class where these features made a relatively more significant (R > 0.2) contribution. Separate models tailored to individual vegetation classes could be a further improvement in this regard, especially if the same accuracy could be achieved with fewer input variables.
4.2. Upscaling
The bounding box used to delineate plots within the model training data was 500 m
(22 m×22 m), approximately the same scale as the more recent remote sensing instruments found on LANDSAT/Sentinel-2 satellites, showing potential for the upscaling of these measurements to satellite products. An example of the grass AGB model applied to a plot in Tsodilo Hills is shown in
Figure 12. To achieve this, five-hundred meters squared tiles were delineated in the orthophoto, and the biomass for the surface fuel classes was calculated for each pixel. This dataset (along with relevant errors) was then re-gridded to the Sentinel-2 grid. With this, we can create a dataset of UAS predicted AGB, on the scale of satellite images, to act as a “truth” dataset. This dataset can be used to train a machine learning model in order to predict AGB on the basis of satellite imagery.
Direct reflectance comparison between satellite instruments and UAS data has many pitfalls (exact date/time of retrieval, atmospheric corrections/distortions, differences in scale, divergences in band definitions/widths/response curves, etc.). In this study as well, no particular effort was made to calibrate measurements with satellite overpasses, and the relevant bands in some cases barely overlapped (see
Table A1). One of the advantages of the approach detailed in this paper is that the need for reflectance data comparison was circumvented through the use of classification maps and surface cover proportions. Another potential way of connecting UAS-generated AGB maps, alternative to machine learning, would be to generate sub-pixel surface cover percentages from satellite images and feed these into the model directly in place of the UAS-generated surface cover. This approach, and the machine learning approach mentioned above, will be the subject of further research.