Attenuation and Phase Velocity of Elastic Wave in Textured Polycrystals with Ellipsoidal Grains of Arbitrary Crystal Symmetry
Abstract
:1. Introduction
2. Theoretical Background about Attenuation Modelling in Textured Polycrystals
2.1. Orientation Distribution Function (ODF)
2.1.1. Generalized Spherical Harmonics ODF
2.1.2. Gaussian form ODF
2.2. Theoretical Background of Attenuation Modelling
2.3. Two-point Statistics for Textured Polycrystals
3. Second-order Scattering Model for Textured Polycrystals with Ellipsoidal Triclinic Grains
3.1. Dispersion Equation
3.2. Analytical Equations for Attenuation Coefficient and Phase Velocity
3.2.1. Attenuation Coefficient and Phase Velocity by the Born Approximation
3.2.2. Attenuation at Rayleigh Limit
3.2.3. Quasi-Static Phase Velocity
4. Computational Results and Discussion
4.1. Comparison of the SOA Model to Available FEM and Experimental Results
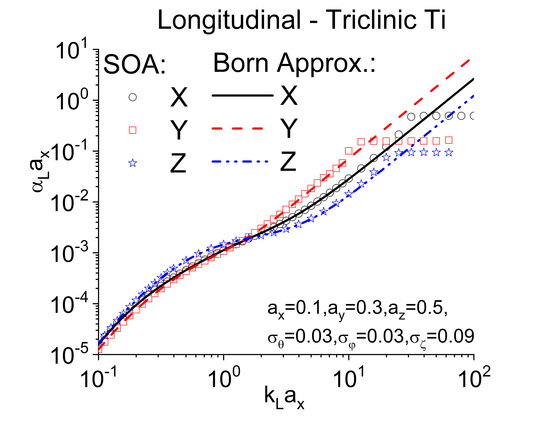
4.2. Applicability and Limitation of the Born Approximation on Textured Polycrystals
4.3. Comparison of Quasi-Static Velocity from the SOA Model with Other Velocity Bounds
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Mason, W.P.; McSkimin, H.J. Attenuation and Scattering of High Frequency Sound Waves in Metals and Glasses. J. Acoust. Soc. Am. 1947, 19, 725. [Google Scholar] [CrossRef] [Green Version]
- Papadakis, E.P. Rayleigh and Stochastic Scattering of Ultrasonic Waves in Steel. J. Appl. Phys. 1963, 34, 265–269. [Google Scholar] [CrossRef]
- Stanke, F.E.; Kino, G.S. A Unified Theory for Elastic Wave Propagation in Polycrystalline Materials. J. Acoust. Soc. Am. 1984, 75, 665. [Google Scholar] [CrossRef]
- Hirsekorn, S. The Scattering of Ultrasonic Waves by Polycrystals. J. Acoust. Soc. Am. 1982, 72, 1021–1031. [Google Scholar] [CrossRef]
- Weaver, R.L. Diffusivity of Ultrasound in Polycrystals. J. Mech. Phys. Solids 1990, 38, 55–86. [Google Scholar] [CrossRef]
- Turner, J.A. Elastic Wave Propagation and Scattering in Heterogeneous, Anisotropic Media: Textured Polycrystalline Materials. J. Acoust. Soc. Am. 1999, 106, 541. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Turner, J.A. Attenuation of Ultrasonic Waves in Rolled Metals. J. Acoust. Soc. Am. 2004, 116, 3319–3327. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Lobkis, O.I.; Rokhlin, S.I. Explicit Model for Ultrasonic Attenuation in Equiaxial Hexagonal Polycrystalline Materials. Ultrasonics 2011, 51, 303–309. [Google Scholar] [CrossRef]
- Lobkis, O.I.; Yang, L.; Li, J.; Rokhlin, S.I. Ultrasonic Backscattering in Polycrystals with Elongated Single Phase and Duplex Microstructures. Ultrasonics 2012, 52, 694–705. [Google Scholar] [CrossRef]
- Du, H.; Turner, J.A. Ultrasonic Attenuation in Pearlitic Steel. Ultrasonics 2014, 54, 882–887. [Google Scholar] [CrossRef] [PubMed]
- Papadakis, E.P. Physical Acoustics and Microstructure of Iron Alloys. Int. Met. Rev. 1984, 29, 1–24. [Google Scholar] [CrossRef]
- Guo, C.B.; Höller, P.; Goebbels, K. Scattering of Ultrasonic Waves in Anisotropic Polycrystalline Metals. Acta Acust. united with Acust. 1985, 59, 112–120. [Google Scholar]
- Gobran, N.K.; Youssef, H. Viscous Ultrasonic Attenuation in Metals. J. Appl. Phys. 1967, 38, 3291–3293. [Google Scholar] [CrossRef]
- Nowick, A.S.; Berry, B.S.; Katz, J.L. Anelastic Relaxation in Crystalline Solids; Academic Press: New York, NY, USA; London, UK, 1972; p. 667. [Google Scholar]
- Ryzy, M.; Grabec, T.; Österreicher, J.A.; Hettich, M.; Veres, I.A. Measurement of Coherent Surface Acoustic Wave Attenuation in Polycrystalline Aluminum. AIP Adv. 2018, 8, 125019. [Google Scholar] [CrossRef] [Green Version]
- Papadakis, E.P. Grain-Size Distribution in Metals and Its Influence on Ultrasonic Attenuation Measurements. J. Acoust. Soc. Am. 1961, 33, 1616–1621. [Google Scholar] [CrossRef]
- Bai, X.; Zhao, Y.; Ma, J.; Liu, Y.; Wang, Q. Grain-Size Distribution Effects on the Attenuation of Laser-Generated Ultrasound in $α$-Titanium Alloy. Materials (Basel). 2019, 12, 102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sha, G. A Simultaneous Non-Destructive Characterisation Method for Grain Size and Single-Crystal Elastic Constants of Cubic Polycrystals from Ultrasonic Measurements. Insight - Non-Destructive Test. Cond. Monit. 2018, 60, 190–193. [Google Scholar] [CrossRef]
- Li, X.; Song, Y.; Liu, F.; Hu, H.; Ni, P. Evaluation of Mean Grain Size Using the Multi-Scale Ultrasonic Attenuation Coefficient. NDT E Int. 2015, 72, 25–32. [Google Scholar] [CrossRef]
- Van Pamel, A.; Brett, C.R.; Huthwaite, P.; Lowe, M.J.S. Finite Element Modelling of Elastic Wave Scattering within a Polycrystalline Material in Two and Three Dimensions. J. Acoust. Soc. Am. 2015, 138, 2326–2336. [Google Scholar] [CrossRef] [Green Version]
- Bai, X.; Tie, B.; Schmitt, J.-H.; Aubry, D. Finite Element Modeling of Grain Size Effects on the Ultrasonic Microstructural Noise Backscattering in Polycrystalline Materials. Ultrasonics 2018, 87, 182–202. [Google Scholar] [CrossRef]
- Lhuillier, P.E.; Chassignole, B.; Oudaa, M.; Kerhervé, S.O.; Rupin, F.; Fouquet, T. Investigation of the Ultrasonic Attenuation in Anisotropic Weld Materials with Finite Element Modeling and Grain-Scale Material Description. Ultrasonics 2017, 78, 40–50. [Google Scholar] [CrossRef] [PubMed]
- Van Pamel, A.; Sha, G.; Lowe, M.J.S.; Rokhlin, S.I. Numerical and Analytic Modelling of Elastodynamic Scattering within Polycrystalline Materials. J. Acoust. Soc. Am. 2018, 14, 2394–2408. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, L.; Lobkis, O.I.; Rokhlin, S.I. Shape Effect of Elongated Grains on Ultrasonic Attenuation in Polycrystalline Materials. Ultrasonics 2011, 51, 697–708. [Google Scholar] [CrossRef] [PubMed]
- Kube, C.M.; Turner, J.A. Stress-Dependent Second-Order Grain Statistics of Polycrystals. J Acoust Soc Am 2015, 138, 2613–2625. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, L.; Turner, J.A. Wave Attenuations in Solids with Perfectly Aligned Cracks. Acoust. Res. Lett. Online 2005, 6, 99–105. [Google Scholar] [CrossRef]
- Kube, C.M.; Turner, J.A. Stress-Dependent Ultrasonic Scattering in Polycrystalline Materials. J. Acoust. Soc. Am. 2016, 139, 811–824. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, S.; Thompson, R.B.; Panetta, P.D. Ultrasonic Attenuation as Influenced by Elongated Grains. Rev. Quant. Nondestruct. Eval. ed. by D. O. Thompson D. E. Chimenti 2003, 22, 109–116. [Google Scholar]
- Karal, F.C.; Keller, J.B. Elastic, Electromagnetic, and Other Waves in a Random Medium. J. Math. Phys. 1964, 5, 537. [Google Scholar] [CrossRef]
- Hirsekorn, S. The Scattering of Ultrasonic Waves by Polycrystals. II. Shear Waves. J Acoust Soc Am 1983, 73, 1160–1163. [Google Scholar] [CrossRef]
- Page, J.H.; Sheng, P.; Schriemer, H.P.; Jones, I.; Jing, X.; Weitz, D.A. Group Velocity in Strongly Scattering Media. Science 1996, 271, 634–637. [Google Scholar] [CrossRef] [Green Version]
- Calvet, M.; Margerin, L. Velocity and Attenuation of Scalar and Elastic Waves in Random Media: A Spectral Function Approach. J. Acoust. Soc. Am. 2012, 131, 1843. [Google Scholar] [CrossRef] [PubMed]
- Kube, C.M. Iterative Solution to Bulk Wave Propagation in Polycrystalline Materials. J. Acoust. Soc. Am. 2017, 141, 1804–1811. [Google Scholar] [CrossRef] [PubMed]
- Calvet, M.; Margerin, L. Impact of Grain Shape on Seismic Attenuation and Phase Velocity in Cubic Polycrystalline Materials. Wave Motion 2016, 65, 29–43. [Google Scholar] [CrossRef]
- Frisch, U. Probabilistic Methods in Applied Mathematics; Vols. I II, Ed.; Bharucha-Reid Academic Press: New York, NY, USA, 1968. [Google Scholar]
- Rokhlin, S.I.; Li, J.; Sha, G. Far-Field Scattering Model for Wave Propagation in Random Media. J. Acoust. Soc. Am. 2015, 137, 2655–2669. [Google Scholar] [CrossRef] [PubMed]
- Kocks, U.F.; Tomé, C.N.; Wenk, H.-R. Texture and Anisotropy: Preferred Orientations in Polycrystals and Their Effect on Materials Properties; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Ahmed, S.; Thompson, R.B. Propagation of Elastic Waves in Equiaxed Stainless-Steel Polycrystals with Aligned [001] Axes. J. Acoust. Soc. Am. 1996, 99, 2086. [Google Scholar] [CrossRef]
- Yang, L.; Rokhlin, S.I. Ultrasonic Backscattering in Cubic Polycrystals with Ellipsoidal Grains and Texture. J. Nondestruct. Eval. 2013, 32, 142–155. [Google Scholar] [CrossRef]
- Li, J.; Rokhlin, S.I. Propagation and Scattering of Ultrasonic Waves in Polycrystals with Arbitrary Crystallite and Macroscopic Texture Symmetries. Wave Motion 2015, 58, 145–164. [Google Scholar] [CrossRef]
- Hirsekorn, S. The Scattering of Ultrasonic Waves in Polycrystalline Materials with Texture. J. Acoust. Soc. Am. 1985, 77, 832–843. [Google Scholar] [CrossRef]
- Norouzian, M.; Turner, J.A. Ultrasonic Wave Propagation Predictions for Polycrystalline Materials Using Three-Dimensional Synthetic Microstructures: Attenuation. J. Acoust. Soc. Am. 2019, 145, 2181–2191. [Google Scholar] [CrossRef] [PubMed]
- Bunge, H.-J. Texture Analysis in Materials Science: Mathematical Methods, 1st ed.; Armco Inc.: Middeletown, OH, USA, 1982. [Google Scholar]
- Bache, M.R.; Evans, W.J.; Suddell, B.; Herrouin, F.R.M. The Effects of Texture in Titanium Alloys for Engineering Components under Fatigue. Int. J. Fatigue 2001, 23, 153–159. [Google Scholar] [CrossRef]
- Roe, R.J.; Krigbaum, W.R. Description of Crystallite Orientation in Polycrystalline Materials Having Fiber Texture. J. Chem. Phys. 1964, 40, 2608. [Google Scholar] [CrossRef]
- Roe, R.J. Description of Crystallite Orientation in Polycrystalline Materials. III. General Solution to Pole Figure Inversion. J. Appl. Phys. 1965, 36, 2024–2031. [Google Scholar] [CrossRef]
- Cho, J.H.; Rollett, A.D.; Oh, K.H. Determination of Volume Fractions of Texture Components with Standard Distributions in Euler Space. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2004, 35, 1075–1086. [Google Scholar] [CrossRef]
- Yang, L.; Turner, J.A.; Li, Z. Ultrasonic Characterization of Microstructure Evolution during Processing. J. Acoust. Soc. Am. 2007, 121, 50. [Google Scholar] [CrossRef] [Green Version]
- Li, J.Y. Effective Electroelastic Moduli of Textured Piezoelectric Polycrystalline Aggregates. J. Mech. Phys. Solids 2000, 48, 529–552. [Google Scholar] [CrossRef]
- Li, J.; Rokhlin, S.I. Elastic Wave Scattering in Random Anisotropic Solids. Int. J. Solids Struct. 2016, 78–79, 110–124. [Google Scholar] [CrossRef]
- Mason, J.K.; Schuh, C.A. Hyperspherical Harmonics for the Representation of Crystallographic Texture. Acta Mater. 2008, 56, 6141–6155. [Google Scholar] [CrossRef]
- Huang, M. Perturbation Approach to Elastic Constitutive Relations of Polycrystals. J. Mech. Phys. Solids 2004, 52, 1827–1853. [Google Scholar] [CrossRef]
- Sha, G. Explicit Backscattering Coefficient for Ultrasonic Wave Propagating in Hexagonal Polycrystals with Fiber Texture. J. Nondestruct. Eval. 2018, 37, 37–51. [Google Scholar] [CrossRef]
- Bunge, H.J.; Esling, C.; Bechler-Ferry, E. Three- Dimensional Texture Analysis after Bunge and Roe: Correspondence between the Respective Mathematical Techniques. Textures Microstruct. 1982, 5, 95–125. [Google Scholar]
- Frisch, U. Wave Propagation in Random Media. In Probabilistic Methods in Applied Mathematics, Volume 1; Academic Press: New York, NY, USA, 1968; pp. 75–198. [Google Scholar]
- Bourret, R.C. Stochastically Perturbed Fields, with Applications to Wave Propagation in Random Media. Nuovo Cim. Ser. 10 1962, 26, 1–31. [Google Scholar] [CrossRef]
- Budreck, B.D.E. An Eigenfunction Expansion of the Elastic Wave Green ’ S Function for Anisotropic Media. Q. J. Mech. Appl. Math. 1993, 46, 1–26. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. Sect. A 2002, 65, 349–354. [Google Scholar] [CrossRef]
- Li, J.; Yang, L.; Rokhlin, S.I. Effect of Texture and Grain Shape on Ultrasonic Backscattering in Polycrystals. Ultrasonics 2014, 54, 1789–1803. [Google Scholar] [CrossRef]
- Van Pamel, A.; Sha, G.; Rokhlin, S.I.; Lowe, M.J.S. Finite-Element Modelling of Elastic Wave Propagation and Scattering within Heterogeneous Media. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20160738. [Google Scholar] [CrossRef]
- Berryman, J.G. Bounds and Self-Consistent Estimates for Elastic Constants of Random Polycrystals with Hexagonal, Trigonal, and Tetragonal Symmetries. J. Mech. Phys. Solids 2005, 53, 2141–2173. [Google Scholar] [CrossRef]
- Stanke, F.E. Spatial Autocorrelation Functions for Calculations of Effective Propagation Constants in Polycrystalline Materials. J. Acoust. Soc. Am. 1986, 80, 1479–1485. [Google Scholar] [CrossRef]
- Hu, P.; Kube, C.M.; Koester, L.W.; Turner, J.A. Mode-Converted Diffuse Ultrasonic Backscatter. J Acoust Soc Am 2015, 134, 982–990. [Google Scholar] [CrossRef]
- Yang, L.; Lobkis, O.I.; Rokhlin, S.I. An Integrated Model for Ultrasonic Wave Propagation and Scattering in a Polycrystalline Medium with Elongated Hexagonal Grains. Wave Motion 2012, 49, 544–560. [Google Scholar] [CrossRef]
- Ahmed, S.; Thompson, R.B. Attenuation of Ultrasonic Waves in Cubic Metals Having Elongated, Oriented Grains. Nondestruct. Test. Eval. 1992, 8–9, 525–531. [Google Scholar] [CrossRef]
- Wu, R.-S. Attenuation of Short Period Seismic Waves Due to Scattering. Attenuation short period Seism. waves due to Scatt. 1982, 9, 9–12. [Google Scholar]
- Hashin, Z.; Shtrikman, S. A Variational Approach to the Theory of the Elastic Behaviour of Polycrystals. J. Mech. Phys. Solids 1962, 10, 343–352. [Google Scholar] [CrossRef]
- Brown, J.M. Determination of Hashin-Shtrikman Bounds on the Isotropic Effective Elastic Moduli of Polycrystals of Any Symmetry. Comput. Geosci. 2015, 80, 95–99. [Google Scholar] [CrossRef]
- Kube, C.M.; Arguelles, A.P. Bounds and Self-Consistent Estimates of the Elastic Constants of Polycrystals. Comput. Geosci. 2016, 95, 118–122. [Google Scholar] [CrossRef]
- Li, Y.; Thompson, R.B. Relations between Elastic Constants Cij and Texture Parameters for Hexagonal Materials. J. Appl. Phys. 1990, 67, 2663–2665. [Google Scholar] [CrossRef] [Green Version]
- Man, C.S.; Huang, M. A Simple Explicit Formula for the Voigt-Reuss-Hill Average of Elastic Polycrystals with Arbitrary Crystal and Texture Symmetries. J. Elast. 2011, 105, 29–48. [Google Scholar] [CrossRef]
- Böhlke, T.; Lobos, M. Representation of Hashin-Shtrikman Bounds of Cubic Crystal Aggregates in Terms of Texture Coefficients with Application in Materials Design. Acta Mater. 2014, 67, 324–334. [Google Scholar] [CrossRef]
- Huang, M.; Man, C.S. Explicit Bounds of Effective Stiffness Tensors for Textured Aggregates of Cubic Crystallites. Math. Mech. Solids 2008, 13, 408–430. [Google Scholar] [CrossRef]
- Lobos Fernández, M.; Böhlke, T. Representation of Hashin--Shtrikman Bounds in Terms of Texture Coefficients for Arbitrarily Anisotropic Polycrystalline Materials. J. Elast. 2019, 134, 1–38. [Google Scholar] [CrossRef]
- Tane, M.; Yamori, K.; Sekino, T.; Mayama, T. Impact of Grain Shape on the Micromechanics-Based Extraction of Single-Crystalline Elastic Constants from Polycrystalline Samples with Crystallographic Texture. Acta Mater. 2017, 122, 236–251. [Google Scholar] [CrossRef]
- Rokhlin, S.I.; Chimenti, D.E.; Nagy, P.B. Physical Ultrasonics of Composites; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Gubernatis, J.E.; Krumhansl, J.A. Macroscopic Engineering Properties of Polycrystalline Materials: Elastic Properties. J. Appl. Phys. 1975, 46, 1875–1883. [Google Scholar] [CrossRef]
- Ploix, M.A.; Guy, P.; Chassignole, B.; Moysan, J.; Corneloup, G.; Guerjouma, R.E. Measurement of Ultrasonic Scattering Attenuation in Austenitic Stainless Steel Welds: Realistic Input Data for NDT Numerical Modeling. Ultrasonics 2014, 54, 1729–1736. [Google Scholar] [CrossRef] [PubMed]
- Pal, B. Pulse-Echo Method Cannot Measure Wave Attenuation Accurately. Ultrasonics 2015, 61, 6–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, L.; Rokhlin, S.I. On Comparison of Experiment and Theory for Ultrasonic Attenuation in Polycrystalline Niobium. J. Nondestruct. Eval. 2012, 31, 77–79. [Google Scholar] [CrossRef]
- Sha, G.; Rokhlin, S.I. Universal Scaling of Transverse Wave Attenuation in Polycrystals. Ultrasonics 2018, 88, 84–96. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Hurley, D.H.; Hua, Z.; Sha, G.; Raetz, S.; Gusev, V.E.; Khafizov, M. Nondestructive Characterization of Polycrystalline 3D Microstructure with Time-Domain Brillouin Scattering. Scr. Mater. 2019, 166, 34–38. [Google Scholar] [CrossRef]
- Ryzy, M.; Grabec, T.; Sedlák, P.; Veres, I.A. Influence of Grain Morphology on Ultrasonic Wave Attenuation in Polycrystalline Media with Statistically Equiaxed Grains. J. Acoust. Soc. Am. 2018, 143, 219–229. [Google Scholar] [CrossRef] [Green Version]







| Triclinic Ti | 161.6 | 67.8 | 88.2 | 1.8 | 1.1 | −0.64 | 184.4 | 68.0 | −2.5 |
| Triclinic Ti | −1.9 | −2.6 | 161.3 | −0.18 | 0.83 | 2.4 | 50.9 | −5.1 | 0.20 |
| ρ | |||||||||
| Triclinic Ti | 39.0 | −5.2 | 50.9 | 4.54 |
| Direction | X | Y | Z |
|---|---|---|---|
| Mean deviation | −13% | −9.7% | −14% |
| Departure frequency | 31.6 | 12.7 | 25.1 |
| Direction | X | Y | Z |
|---|---|---|---|
| Mean deviation | −10.9% | −7.5% | −14.4% |
| Departure frequency | 31.0 | 34.4 | 102.7 |
| Directions | Reuss | H-S Lower [73] | H-S Lower [74] | SC [73] | This work, Equation (40) | H-S Upper [74] | H-S Upper [73] | Voigt |
|---|---|---|---|---|---|---|---|---|
| X | 5.038 | 4.919 | 4.935 | 4.969 | 4.979 | 4.983 | 4.987 | 4.841 |
| Y | 4.965 | 4.834 | 4.842 | 4.883 | 4.892 | 4.897 | 4.900 | 4.743 |
| Z | 4.902 | 4.757 | 4.759 | 4.805 | 4.816 | 4.820 | 4.823 | 4.656 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sha, G. Attenuation and Phase Velocity of Elastic Wave in Textured Polycrystals with Ellipsoidal Grains of Arbitrary Crystal Symmetry. Acoustics 2020, 2, 51-72. https://0-doi-org.brum.beds.ac.uk/10.3390/acoustics2010005
Sha G. Attenuation and Phase Velocity of Elastic Wave in Textured Polycrystals with Ellipsoidal Grains of Arbitrary Crystal Symmetry. Acoustics. 2020; 2(1):51-72. https://0-doi-org.brum.beds.ac.uk/10.3390/acoustics2010005
Chicago/Turabian StyleSha, Gaofeng. 2020. "Attenuation and Phase Velocity of Elastic Wave in Textured Polycrystals with Ellipsoidal Grains of Arbitrary Crystal Symmetry" Acoustics 2, no. 1: 51-72. https://0-doi-org.brum.beds.ac.uk/10.3390/acoustics2010005