Statistical Power Law due to Reservoir Fluctuations and the Universal Thermostat Independence Principle
Abstract
:1. Introduction
2. Finite Heat Bath and Fluctuation Effects
- q > 1 and q < 1 are both possible,
- for any relative variance it is exactly q = 1,
- and for fixed E ∝ n/β we have Δβ/〈β〉 = Δn/〈n〉.
3. Deformation of the Entropy
3.1. The Additive Entropy K(S)
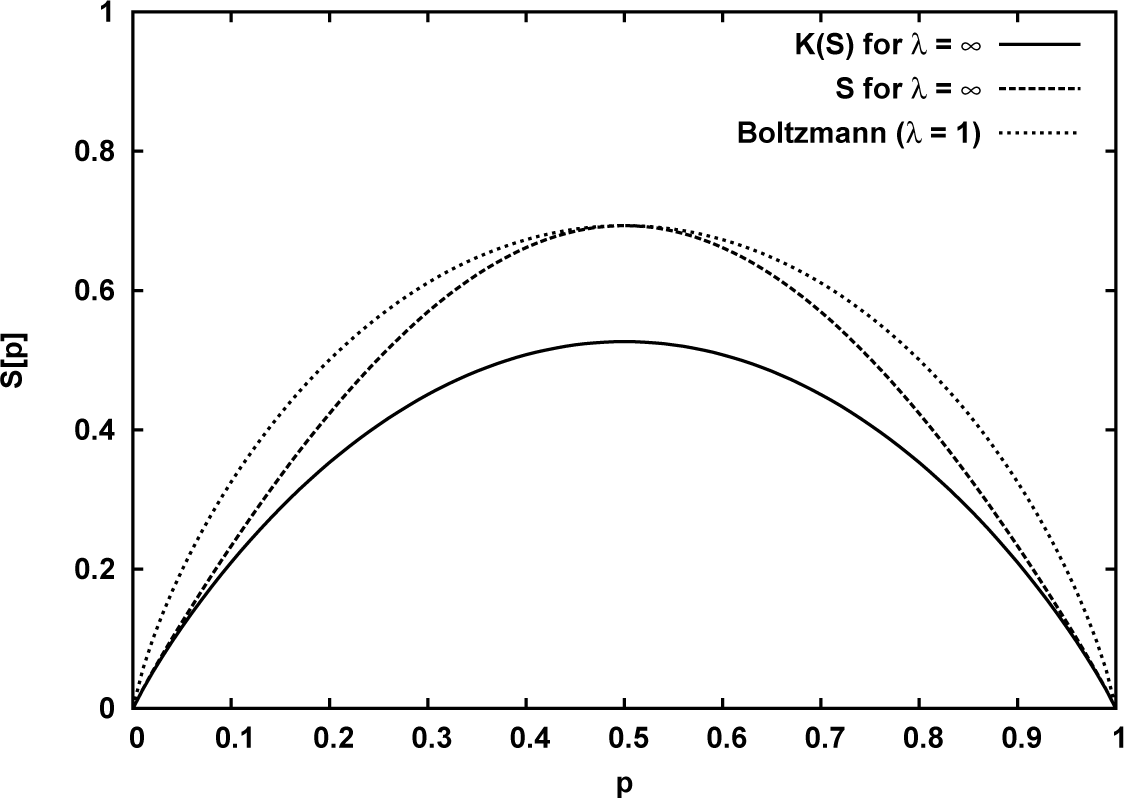
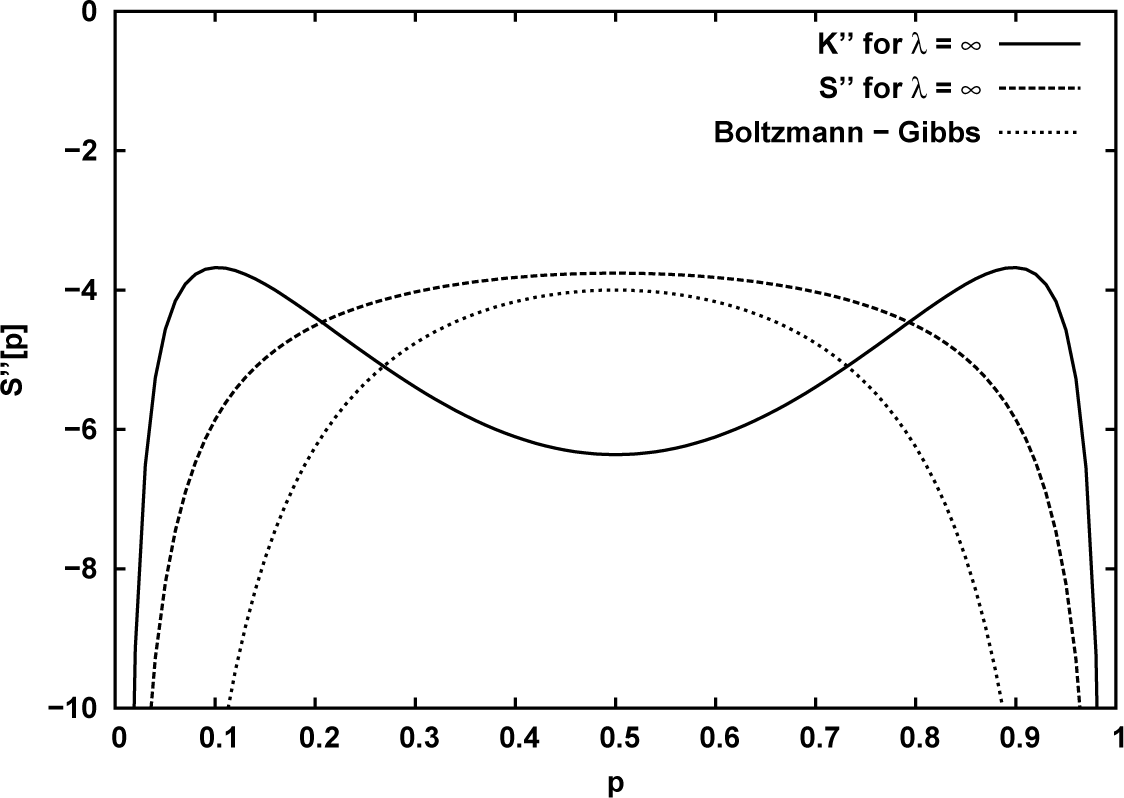
3.2. Classification by Fluctuation Models
- For λ = 1 it is obviously K1(S) = S. This is the Gaussian fluctuation model, considered in several textbooks, and also believed to lead to the smallest physically possible variance due to a “thermodynamical uncertainty” principle [55–58]. Since β = S′(E), the variances are related as Δβ = |S″(E)|ΔE = ΔE/CT2. Then from Δβ · ΔE ≥ 1 it follow and . A straightforward consequence of this is λ/C = Δβ2/〈β〉2 ≥ 1/C and therefore λ ≥ 1. We note, that if this “uncertainty” principle were correct, then only q > 1 canonical distributions of ω would exist in Nature.
- For no fluctuations λ = 0 and we get K0(S) = hC(S). We regain the Tsallis and Rényi formulas presented above in Equation (31).
- It is also very intriguing to inspect the following particular limit: C → ∞, λ → ∞ but finite. In this non-extensive limit the fluctuations are much larger than the normal Gaussian ones, and we obtain a nontrivial entropy deformation:The K-additivity, K(S12) = K(S1) + K(S2), in this case leads to the non-additivity formula , – investigated formerly in depth by Tsallis and Abe [6,54,59–64].
- For normal fluctuations K1(S) = −∑i pi ln pi is exactly the Boltzmann entropy.
- Without fluctuations is the Tsallis entropy with q = 1 − 1/C and S the corresponding Rényi entropy.
- Finally considering extreme large fluctuations and a finite heat capacity, C(S) which however may be an arbitrary function of the total entropy, S, we obtain the non-extensive result Equation (38) with :The canonical pi distribution maximizing this parameterless deformed entropy is also expressed in terms of Lambert-W function, it shows tails like the Gompertz distribution [65–67], known from extreme value statistics and nonequlibrium growth models for demography and tumors.
4. Conclusions and Outlook
Acknowledgments
Conflicts of Interest
References
- Rényi, A. On measures of entropy and information. Proceedings of 4th Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; Newman, J., Ed.; University of California Press: Berkeley, CA, USA, 1961. [Google Scholar]
- Rényi, A. Probability Theory; North Holland: Amsterdam, The Netherlands, 1970. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys 1988, 52, 479–487. [Google Scholar]
- Tsallis, C. Nonextensive statistics: Theoretical, experimental and computational evidences and connections. Braz. J. Phys 1999, 29, 1–35. [Google Scholar]
- Touchette, H. When is a quantity additive and when is it extensive? Physica A 2002, 305, 84–88. [Google Scholar]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Biró, T.S.; Jakovác, A. Power-law tails from multiplicative noise. Phys. Rev. Lett 2005, 94, 132302. [Google Scholar]
- Biró, T.S.; Rosenfeld, R. Microscopic origin of non-Gaussian distributions of finacial returns. Physica A 2008, 387, 1603–1612. [Google Scholar]
- Biró, T.S.; Purcsel, G. Non-extensive Boltzmann equation and hadronization. Phys. Rev. Lett 2005, 95, 162302. [Google Scholar]
- Biró, T.S.; Kaniadakis, G. Two generalizations of the Boltzmann equation. Eur. Phys. J. B 2006, 50, 3–6. [Google Scholar]
- Biró, T.S.; Purcsel, G. Equilibration of two non-extensive subsystems in a parton cascade model. Phys. Lett. A 2008, 372, 1174–1179. [Google Scholar]
- Biró, T.S.; Purcsel, G.; Györgyi, G.; Jakovác, A.; Schram, Z. Power-law tailed spectra from equilibrium. Nucl. Phys. A 2006, 774, 845–848. [Google Scholar]
- Biró, T.S.; Purcsel, G. Non-extensive equilibration in relativistic matter. Cent. Eur. J. Phys 2009, 7, 395–400. [Google Scholar]
- Biró, T.S.; Purcsel, G.; Ürmössy, K. Non-extensive approach to quark matter. Eur. Phys. J. A 2009, 40, 325–340. [Google Scholar]
- Biró, T.S.; Peshier, A. Limiting temperature from a parton gas with power-law tailed distribution. Phys. Lett. B 2006, 632, 247–251. [Google Scholar]
- Biró, T.S.; Ván, P. Zeroth law compatibility of non-additive thermodynamics. Phys. Rev. E 2011, 83, 061147. [Google Scholar]
- Biró, T.S. Is There a Temperature? Conceptual Challenges at High Energy, Acceleration and Complexity; Springer: New York, NY, USA, 2011. [Google Scholar]
- Ván, P.; Barnaföldi, G.G.; Biró, T.S.; Ürmössy, K. Nonadditive thermostatistics and thermodynamics. J. Phys. Conf. Ser. 2012, 394, 012002. [Google Scholar]
- Biró, T.S. Abstract composition rule for relativistic kinetic theory in the thermodynamical limit. Europhys. Lett. 2008, 84, 56003. [Google Scholar]
- Biró, T.S. Ideal gas provides q-entropy. Physica A 2013, 392, 3132–3139. [Google Scholar]
- Biró, T.S.; Barnaföldi, G.G.; Ván, P.; Ürmössy, K. Statistical power-law spectra due to reservoir fluctuations; 2014; Volume arxiv, p. 1404.1256. [Google Scholar]
- Biró, T.S.; Ván, P.; Barnaföldi, G.G. Quark-gluon plasma connected to finite heat bath. Eur. Phys. J. A 2013, 49. [Google Scholar] [CrossRef]
- Biró, T.S.; Barnaföldi, G.G.; Ván, P. New entropy formula with fluctuating reservoir. Physica A 2015, 417, 215–220. [Google Scholar]
- Wong, C.Y.; Wilk, G. Tsallis fits to pT spectra for pp collisions at the LHC. Acta Phys. Pol. B 2012, 43, 2047–2054. [Google Scholar]
- Wong, C.Y.; Wilk, G. Tsallis fits to pT spectra and multiple hard scattering in pp collisions at LHC. Phys. Rev. D 2013, 87, 114007. [Google Scholar]
- Wilk, G.; Wlodarczyk, Z. Power laws in elementary and heavy ion collisions: A story of fluctuations and non-extensivity? Eur. Phys. J. A 2009, 40, 299–312. [Google Scholar]
- Wilk, G.; Wlodarczyk, Z. Consequences of temperature fluctuations in observables measured in high-energy collisions. Eur. Phys. J. A 2012, 48. [Google Scholar] [CrossRef]
- Wilk, G.; Wlodarczyk, Z. Interpretation of the nonextensivity parameter q in some applications of Tsallis statistics and Levy distribution. Phys. Rev. Lett 2000, 84. http://0-dx-doi-org.brum.beds.ac.uk/10.1103/PhysRevLett.84.2770. [Google Scholar]
- Ürmössy, K.; Biró, T.S. Cooper–Frye Formula and non-extensive coalescence at RHIC energy. Phys. Lett. B 2010, 689, 14–17. [Google Scholar]
- Ürmössy, K.; Barnaföldi, G.G.; Biró, T.S. Microcanonical jet-fragmentation in proton-proton collisions at LHC energy. Phys. Lett. B 2012, 718, 125–129. [Google Scholar]
- Ürmössy, K.; Barnaföldi, G.G.; Biró, T.S. Generalised Tsallis statistics in electron-positron collisions. Phys. Lett. B 2011, 701, 111–116. [Google Scholar]
- Almeida, M.P. Generalized entropies from first principles. Physica A 2001, 300, 424–432. [Google Scholar]
- Begun, V.V.; Gazdzicki, M.; Gorenstein, M.I. Power-law in microcanonical ensemble with scaling volume fluctuations. Phys. Rev. C 2008, 78, 024904. [Google Scholar]
- Campisi, M.; Zahn, F.; Hänggi, P. On the origin of power laws in equilibrium. Europhys. Lett. 2012, 99, 60004. [Google Scholar]
- Bagci, G.B.; Oikonomou, T. Tsallis power-laws and finite baths with negative heat capacity. Phys. Rev. E 2013, 88, 042126. [Google Scholar]
- Parvan, A.S. Microcanonical ensemble extensive thermodynamics of Tsallis statistics. Phys. Lett. A 2006, 350, 331–338. [Google Scholar]
- Adare, A.; PHENIX Collaboration. Charged hadron multiplicity fluctuations in Au + Au and Cu + Cu collisions from to 200 GeV. Phys. Rev. C 2008, 78, 044902. [Google Scholar]
- Abelev, B.; ALICE Collaboration. Centrality dependence of π, K and p production in Pb-Pb collisions at TeV. Phys. Rev. C 2013, 88, 044910. [Google Scholar]
- Abelev, B.; ALICE Collaboration. Centrality dependence of charged particle production at large transverse momentum in Pb-Pb collisions at TeV. Phys. Lett. B 2013, 720, 52–62. [Google Scholar]
- Begun, V.V.; Gazdzicki, M.; Gorenstein, M.I. Semi-inclusive observables in statistical models. Phys. Rev. C 2009, 80, 064903. [Google Scholar]
- Jeon, S.; Koch, V.; Redlich, K.; Wang, X.N. Fluctuations of rare particles as a measure of chemical equilibrium. Nucl. Phys. A 2002, 697, 546–562. [Google Scholar]
- Begun, V.V.; Gazdzicki, M.; Gorenstein, M.I.; Zozulya, O.S. Particle number fluctuations in a canonical ensemble. Phys. Rev. C 2004, 70, 034901. [Google Scholar]
- Gorenstein, M.I. Identity method for particle number fluctuations and correlation. Phys. Rev. C 2011, 84, 024902. [Google Scholar]
- Gorenstein, M.I.; Grebieszkow, K. Strongly intensive measures for the momentum and particle number fluctuations. Phys. Rev. C 2014, 89, 034903. [Google Scholar]
- Begun, V.V.; Gorenstein, M.I. Particle number fluctuations in relativistic Bose and Fermi gases. Phys. Rev. C 2006, 73, 054904. [Google Scholar]
- Beck, C.; Cohen, E.G.D. Superstatistics. Physica A 2003, 322, 267–275. [Google Scholar]
- Abe, S.; Beck, C.; Cohen, E.G.D. Superstatistics, thermodynamics and fluctuations. Phys. Rev. E 2007, 76, 031102. [Google Scholar]
- Ma, S.K. Statistical Mechanics; World Scientific: Singapore, Singapore, 1985. [Google Scholar]
- Wilk, G.; Wlodarczyk, Z. Stohastic network view on hadron production. Acta Phys. Pol. B 2004, 35, 2141–2147. [Google Scholar]
- Wilk, G.; Wlodarczyk, Z. The imprints of superstatistics in multiparticle production processes. Cent. Eur. J. Phys 2012, 10, 568–575. [Google Scholar]
- Beck, C. Dynamical foundations of nonextensive statistical mechanics. Phys. Rev. Lett 2001, 87, 180601. [Google Scholar]
- Kodama, T.; Elze, H.T.; Aguiar, C.E.; Koide, T. Dynamical correlations as origin of nonextensive entropy. Europhys. Lett 2005, 70, 439–445. [Google Scholar]
- Tsallis, C.; Haubold, H.J. Boltzmann-Gibbs entropy is sufficient but not necessary for the likelihood factorization required by Einstein. 2014, arXiv, 1407.6052. [Google Scholar]
- Abe, S. General pseudoadditivity of composable entropy by the existence of equilibrium. Phys. Rev. E 2001, 63, 061105. [Google Scholar]
- Uffink, J.; van Lith, J. Thermodynamic uncertainty relations. Found. Phys 1999, 29, 655–692. [Google Scholar]
- Lavenda, B.H. Comments on “Thermodynamic Uncertainty Relations” by J. Uffink and J. van Lith. Found. Phys. Lett 2000, 13, 487–492. [Google Scholar]
- Uffink, J.; van Lith, J. Thermodynamic uncertainty relations again: A reply to Lavenda. Found. Phys. Lett 2001, 14, 187–193. [Google Scholar]
- Wilk, G.; Wlodarczyk, Z. Generalized thermodynamic uncertainty relations. Physica A 2011, 390, 3566–3572. [Google Scholar]
- Abe, S. Axioms and uniqueness theorem for Tsallis entropy. Phys. Lett. A 2000, 271, 74–79. [Google Scholar]
- Abe, S. A note on the q-deformation theoretic aspect of the generalized entropies in nonextensive physics. Phys. Lett. A 1997, 224, 326–330. [Google Scholar]
- Abe, S.; Rajagopal, A.K. Non-uniqueness of canonical ensemble theory entropy from microcanonical basis. Phys. Lett. A 2000, 272, 341–345. [Google Scholar]
- Abe, S.; Rajagopal, A.K. Justification of power law canonical distributions based on generalized central limit theorem. Europhys. Lett 2000, 52, 610–614. [Google Scholar]
- Abe, S.; Rajagopal, A.K. Macroscopic thermodynamics of equilibrium characterized by power law canonical distributions. Europhys. Lett 2001, 55, 6–11. [Google Scholar]
- Abe, S.; Bagci, G.B. Necessity of q-expectation value in nonextensive statistical mechanics. Phys. Rev. E 2005, 71, 016139. [Google Scholar]
- Gompertz, B. On the nature of the function expressing of the law of human mortality, and on a new mode of determining the value of life contingencies. Philos. Trans. R. Soc 1825, 115, 513–583. [Google Scholar]
- Casey, A.E. The experimental alteration of malignacy with an homologous mammalian tumour material. Am. J. Cancer 1934, 21, 760–775. [Google Scholar]
- Apostol, B.E. Euler’s transform and a generalized Omori’s law. Phys. Lett. A 2005, 351, 175–176. [Google Scholar]
- Hanel, R.; Thurner, S. A comprehensive classification of complex statsitical systems and an axiomatic derivation of their entropy and distribution functions. Europhys. Lett 2011, 93. [Google Scholar] [CrossRef]
- Andrade, J.S., Jr.; da Silva, G.F.T.; Moreira, A.A.; Nobre, F.D.; Curado, E.M.F. Thermostatistics of overdamped motion of interacting particles. Phys. Rev. Lett 2010, 105, 260601. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biró, T.S.; Ván, P.; Barnaföldi, G.G.; Ürmössy, K. Statistical Power Law due to Reservoir Fluctuations and the Universal Thermostat Independence Principle. Entropy 2014, 16, 6497-6514. https://0-doi-org.brum.beds.ac.uk/10.3390/e16126497
Biró TS, Ván P, Barnaföldi GG, Ürmössy K. Statistical Power Law due to Reservoir Fluctuations and the Universal Thermostat Independence Principle. Entropy. 2014; 16(12):6497-6514. https://0-doi-org.brum.beds.ac.uk/10.3390/e16126497
Chicago/Turabian StyleBiró, Tamás Sándor, Péter Ván, Gergely Gábor Barnaföldi, and Károly Ürmössy. 2014. "Statistical Power Law due to Reservoir Fluctuations and the Universal Thermostat Independence Principle" Entropy 16, no. 12: 6497-6514. https://0-doi-org.brum.beds.ac.uk/10.3390/e16126497




