Analyses of the Instabilities in the Discretized Diffusion Equations via Information Theory

Abstract

In a previous investigation (Bigerelle and Iost, 2004), the authors have proposed a physical interpretation of the instability λ = Δt/Δx² > 1/2 of the parabolic partial differential equations when solved by finite differences. However, our results were obtained using integration techniques based on erf functions meaning that no statistical fluctuation was introduced in the mathematical background. In this paper, we showed that the diffusive system can be divided into sub-systems onto which a Brownian motion is applied. Monte Carlo simulations are carried out to reproduce the macroscopic diffusive system. It is shown that the amount of information characterized by the compression ratio of information of the system is pertinent to quantify the entropy of the system according to some concepts introduced by the authors (Bigerelle and Iost, 2007). Thanks to this mesoscopic discretization, it is proved that information on each sub-cell of the diffusion map decreases with time before the unstable equality λ = 1/2 and increases after this threshold involving an increase in negentropy, i.e., a decrease in entropy contrarily to the second principle of thermodynamics.

1. Introduction

Numerous physical phenomena can be modeled by partial differential equations (PDE) [1] and there are many numerical methods for solving PDE [2,3]. The Finite Element Method (FEM) and the Finite Volume Method (FVM) are particularly relevant to solve PDE. The FEM or FVM are mainly useful to solve PDE in complex geometries as well as to optimize the computation times by using different mesh sizes (or different discretization times). Among all these, the Finite Difference Method (FDM) stands out as being universally appropriate and straightforward for solving both linear and nonlinear problems, particularly for uniform mesh sizes and time increments. Stability criteria are analytically easily expressed for uniform mesh sizes and time increments. As the aim of this paper consists in analyzing criteria stability of PDE via Information theory, we deal exclusively with the FDM [4]. To solve these PDE numerically, FDM consists in expanding all variables of the PDE in a Taylor series on a grid at different points of the domain and to limit this expansion to the first derivatives. Then these finite expansions are introduced into the PDE problems and finally the algebraic system of equations is solved using adequate numerical algorithms. The main problems raised in this method are that PDE become discretized and all differential elements do not tend to 0 but to a fixed value that depends on the number of discretized points. However, discretization involves local truncation errors and all rounding errors introduced during the computation due to the finite representation number might grow during the iterative process and leads to numerical instabilities. A high number of mathematical tools and theorems can be used to study the stability of the system, which we shall briefly summarize. However, no physical interpretation in term of Information theory has ever been proposed so far. The fundamental question can be summed up as follows: “Is there a link between the stability threshold and the quantity of information of the diffusive system at a given scale and how to quantify this amount of information?” Brillouin [5] proved that information could be considered as the negative of the system’s entropy called “Negentropy”. Entropy measures the lack of information; it gives the total amount of information missing in the ultramicroscopic structure of a system. In another scientific field, the Information theory can be a powerful tool to analyze data compression [6,7]. The more informative, the lower the ratio of data compression is. The discretized system will be integrally described if the size of the system after compression is minimal, regardless of the width of the data compression of all possible algorithms. Then the size of the program becomes a mathematical measure of negentropy. With regard to the numerous mathematical publications related to PDE stability, we propose to study the stability of parabolic PDE. Moreover, an important category of physical problems can easily be modeled at a microscopic scale and characterized by the Information theory concept via data compression [8].

2. Diffusion Equations

2.1. Parabolic Differential Equations

The Parabolic PDE is given by the following mathematical definition:

$$\frac{\partial u}{\partial t}-{\displaystyle \sum _{i,j}^n\frac{\partial }{\partial x_i}{a}_{i,j}\frac{\partial u}{\partial x_j}=f\left(x,t\right)}$$

(1)

where $\left(x,t\right)\in \mathsf{\Omega }\times$IR+, $\mathsf{\Omega }$ an open set of IRn.

These equations characterize a high number of transport phenomena such as heat transfer, viscous fluid mechanics, transport of atoms-vacancies, Ohm law, contagious epidemics, etc. While remaining quite general, we shall treat in this investigation the simple mono-dimensional Fick Equation [9] that reduces Equation (1) to:

$$\partial C\left(x,t\right)/\partial t=D{\partial }^{2}C\left(x,t\right)/\partial x^2$$

(2)

where $C\left(x,t\right)$ is the concentration of particles at position $x$ after a time $t$ and $D$ is the diffusion coefficient. If we impose the initial condition, $C\left(0,0\right)=C_0{\mathsf{\delta }}_0$ (explain what is ${\mathsf{\delta }}_0$?) and $\mathsf{\Omega }=\left(-\infty ,+\infty \right)$, then the well-known solution is obtained:

$$C\left(x,t\right)=\frac{C_0}{2\sqrt{\pi Dt}}\exp \left(-\frac{x^2}{4Dt}\right)$$

(3)

This equation is in fact a Gaussian probability density function (if we substitute in Equation (3) $C_0$ by Equation (1) with zero mean and $\mathsf{\sigma }\left(t\right)=\sqrt{2Dt}$ standard deviation). Using Taylor’s expansion (explicit in time and central in space), we obtain:

$$C_i^{j+1}=C_i^j+D\Delta t/{\left(\Delta x\right)}^2\left[\left(C_{i-1}^j-2C_i^j+C_{i+1}^j\right)\right]$$

(4)

where $C_i^j$ represents the concentration at point $x=i\Delta x$ and time $t=j\Delta t$.

Usually linear parabolic problems are solved via implicit or Crank–Nicolson’s schemes in order to avoid paying the price of the time step restriction. Unfortunately, implicit schemes (or mixed explicit/implicit schemes) involve that concentrations at time $t+\Delta t$ (partially or totally) depend on the gradients at time $t+\Delta t$. In 1905, Einstein proposed a physical explanation of $D$ in Equation (2) by postulating that the concentration at time $t+\Delta t$ only depends on the concentration at time t. Then the explicit scheme will be retained because it is physically causal (i.e., evolution of the system only depends on previous time). It can be noticed that microscopic simulations of diffusion mechanisms are only explicit methods (Monte Carlo methods, Cellular automata, etc.).

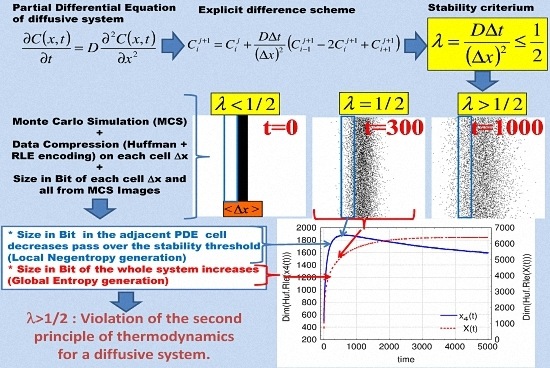
2.2. Stability Study

In this Equation (4) scheme, concentration at time $t+\Delta t$ is calculated by means of the concentration at time $t$ and then the explicit scheme becomes a dynamical system. As a result, it will be possible that this scheme becomes unstable for a set of values $D\Delta t/{\left(\Delta x\right)}^2$. The main idea behind stability is that a numerical process should limit the amplification of all components of the initial condition including rounding errors, when applied exactly. The basic analysis consider the growth of perturbations in initial data or the growth of errors introduced at mesh points at a given time level. This mathematical philosophy seems to us to be near the theory of chaos [10] and consequently we think that a duality exists between a mathematical interpretation and its physical representation. There are three common methods to investigate stability: the Von Neumann method, the matrix method, and the energy method. Using one of these three methods, it can be shown that the explicit scheme will be stable if [4]:

$$\mathsf{\lambda }=D\Delta t/{\left(\Delta x\right)}^2\le 1/2$$

(5)

2.3. Monte Carlo Simulation

The solution of the Cell-PDE could also be modeled using a Brownian motion. The discretization of the diffusion system takes place as follows. A grid of size $r_x\times r_y$, $r_x=r_y=256$, is constructed. A 2D Monte Carlo (MC) simulation was used rather than a 1D one to visualize the complexity of the discretized diffusion front. In the middle of this grid, each elementary cell is affected to the value 1 on a length $\Delta x=r_x/10$ (good approximation, result not shown) that represents the entity (we shall call “particle”), which will diffuse; elsewhere, the value 0 is given (no particle). This system constitutes the initial state at time zero (original time). Figure 1 represents this initial state ($t=0$) where black cells represent the value “1” (particle) and white ones the value “0” (no particle).

Then, for each $p$ particle, $n_s$ jumps are processed on the left or on the right with a probability of 1/2 (more precisely, a jump occurs by choosing at random one particle from all particles). This constitutes a Monte-Carlo Step (MCS). From the microscopic theory of diffusion [9], the diffusion coefficient $D$ can be expressed by:

$$D=a^2\mathsf{\Gamma }/2$$

(6)

where $\mathsf{\Gamma }$ is the particle jump frequency of length $a$ from one micro cell to one adjacent micro cell.

The stability condition then can be expressed by including Equation (5) into Equation (6):

$$\frac{\Delta t}{{\left(\Delta x\right)}^2}\le \frac{1}{a^2\mathsf{\Gamma }}$$

(7)

Then, the number of jumps $n_s$ over time $\Delta t$ is given by

$$n_s=\mathsf{\Gamma }\Delta t$$

(8)

Without any lack of generality, we shall consider $D=1$. The elementary cell size is $a=1$ (pixel unit). Then the stability criterion becomes:

$$\sqrt{n_s}\le \Delta x=r_x/10$$

(9)

Figure 1 represents the snapshots of the evolution of the diffusion system at different times, $n_s=0,10,300,655,1000$ MCS. The particular value $n_s^{sc}=\Delta x^2={(255/10)}^2=655$ corresponds to the stability–instability threshold. Firstly, we shall verify the convergence rate of the Monte Carlo simulation to the Gaussian solution. Figure 1 shows also the concentration curves for different evolution times. The theoretical Gaussian curves given by Equation (3) are plotted for each concentration map. As can be observed, convergence to the Gaussian approximation is well suited if $n_s>300$. Similar to these analyses, we shall develop and induce the Gaussian Probability Density Function approximation for the case $n_s=n_s^{sc}$; it becomes clear from the Monte-Carlo Simulation that the Gaussian PDF is an adequate assumption to model the diffusion process.

3. Quantitative Description of the System in the Area of the Information Theory

3.1. Mathematical Formalism

The system X of diffusion states is an ordered set whose dimension $\dim (X)=r_x{r}_y={256}^2$. This system contains sub-systems of the same dimension represented by $x_i$ with length equal to $\Delta x=r_x/10$ and then $\dim (x_i)=r_x{r}_y/10={256}^2/10$.

Let us note $T$, the nonlinear bijective algebra that transforms the system $x$ into a system $y$ with $y=T(x)$. Let $\left\{A\right\}$ be an algebraic set, $T_{\min }$ is said $\left\{A\right\}-\mathrm{maxi}$ contractile in $X$ if there exists one algebra noted $T_{\min }\in \left\{A\right\}$ such that:

$$\forall x\subset X,\forall T\in \left\{A\right\},\exists T_{\min }\in \left\{A\right\},\dim (T_{\min }(x))\le \dim (T(y))$$

(10)

$T_{opt}$ is said $\{\infty \}-\mathrm{maxi}$ contractile in $X$ if $T_{opt}$ is $\left\{A\right\}-\mathrm{maxi}$ contractile in $X$ where $\left\{A\right\}$ denoted all the sets of all possible algebras defined by arithmetics. Regrettably, according to the Gödel incompleteness theorem, the proposition $\ll T_{opt}$ is said $\{\infty \}-\mathrm{maxi}$ contractile in $\left(E_S,\mathsf{\Psi },G\right)\gg$ is undecidable [11] where $\left(E_S,\mathsf{\Psi },G\right)$ are, respectively, a vector space, the sets of all possible subspaces of E_S, G a relation from E_S to E_S. However, a set of $\left\{A\right\}$ algebra can be built and then $\ll \left\{A\right\}-\mathrm{maxi}$ contractile in $X\gg$ becomes decidable.

3.2. The Different Classes of Algebra

Run Length Encoding (RLE) is often used for data compression [12]. Each cell of the Monte-Carlo system is encoded by one bit, representing the existence or the absence of a particle. The efficiency of the RLE algorithm comes from the fact that selecting a cell at random, the probability that cells in the vicinity possess the same state is high under the hypothesis that physical system is not a pure random one (a pure random system possess the maximal statistical entropy). The algorithm counts the cells in rows on the grid looking for runs of cells having the same state. Encoding the number of runs rather than all individual states significantly reduces the initial size. Then we applied the Huffman algebra based on a list of the alphabetical symbols in decreasing probability order [13] on this system. This algebra allows us to better describe the structure of the diffusion that can be related to the probabilistic approach to this algebra (some statistical tools are closed to those used in statistical thermodynamics). This composition of both algebra denoted $HUF\circ RLE(X)$ is well adapted to describe the power laws met in the diffusion process [8,14].

4. Results

4.1. Compression Data Analyses

In the Monte Carlo simulation, the diffusive system $X(t)$ is composed of 10 sub-systems $x_i(t)$ with $X(t)={\displaystyle \underset{i=1}{\overset{10}{\cup }}{x}_i(t)}$. At initial time $t=0$, the cells of the sub-system $x_5(t)$ are all equal to 1 and all the other sub-system cells are equal to 0. We shall analyze by the $HUF\circ RLE$ algebra the system $X$ and the adjacent cells of $x_5$, i.e., $x_4$ (or $x_6)$ that are the cells that “received” the diffusion particles from the source located in $x_5$. To integrate the stochastic aspect of the diffusion, 1000 simulations are carried out. At $t=0$, we get $\dim (HUF\circ RLE(X))=711$ and $\dim (HUF\circ RLE(x_4))=488$ and these probability density functions are Dirac distributions (Figure 2). As it can be shown, $HUF\circ RLE$ algebra is contractile on both $X$ and $x_4$ systems because:

$$\dim (HUF\circ RLE(X(0)))<\dim (X(0))=65536 \mathrm{and} \dim (HUF\circ RLE(x_4(0)))<\dim (x_4(0))=6554$$

Then, during the diffusion process ($t>0$), $\dim (HUF\circ RLE(X(t)))$ and $\dim (HUF\circ RLE(x_4(t)))$ follow Gaussian densities meaning that the stochastic variation of the Monte Carlo is detected by the RLE and Huffman algebra. If a diffusion system is finite, the concentration $C\left(x,t\right)$ will become a random variable that will follow a Gaussian law under a pure Brownian motion assumption [15]. The measure of the reduced space dimension follows the same density probability function meaning that an isomorphism exists between space dimension and the stochastic aspect of diffusion. As the diffusion time increases, $\dim (HUF\circ RLE(X(t)))$ increases (Figure 3): in fact, during the diffusion process, the total entropy increases, which will decrease negentropy. The system tends to disorder and information can be less and less reduced.

4.2. The Relation between Stability Criteria and the Dimension of Reduced Space

Now we shall analyze the evolution of the program size for the sub-space $x_4$. Figure 3 represents the evolution of the program size versus diffusion time.

First the dimension increases to reach a maximum and then decreases after this threshold. The diffusion time corresponding to this maximum is equal to $t_{HUF\circ RLE}^{\max }={650}_{\pm 30}$. This leads to an important remark. Indeed, statistically:

$$t_{HUF\circ RLE}^{\max }=n_s^{sc}=\Delta x^2={(255/10)}^2=655$$

(11)

In the mono-dimensional diffusion problem, a PDE case gets two adjacent PDE cells that will diffuse on this cell. We shall consider particles coming from the adjacent cell. At the original time, no particle from the adjacent cell is present on the PDE cell and then the description of the cells can be summarized by an algorithmic formalism to “n rep 0” and then $\dim (HUF\circ RLE(x_4(0)))$ is minimal. Then these particles will diffuse on the cell with respect to time. Then entropy will increase thanks to the diffusion and the amount of information will increase therefore increasing $\dim (HUF\circ RLE(x_4(0)))$ until it reaches $t_{HUF\circ RLE}^{\max }$ that is the stability criterion (Figure 3). When the diffusion time is higher than the stability threshold, then $\dim (HUF\circ RLE(x_4(t)))$ decreases. This means that there exists a link between the PDE stability criterion and the amount of information characterized by this original tool. We shall now give an explanation of the decrease in the dimension after the threshold criterion.

Now let us analyze very precisely this critical density function (Figure 4).

Let us now consider the $x_2$ intervals. Concentration is the summation of all the Gaussian curves on these intervals and the concentration on the $x_2$ cell only results from the flux from cells $x_1$ and $x_3$. For the condition $\Delta x=\sqrt{2Dt}$, the inflexion points of the Gaussians $G_1$ and $G_3$ are in the middle of the interval $x_2$. Then the following expressions can be stated:

$${\partial }^2{C}_{1,0}\left(x,\Delta x^2/2D,\Delta x\right)/\partial x^2<0, {\partial }^2{C}_{3,0}\left(x,\Delta x^2/2D,\Delta x\right)/\partial x^2>0 \forall x\in \left[x_2-\Delta x/2,x_2\right]$$

(12)

$${\partial }^2{C}_{1,0}\left(x_2,\Delta x^2/2D,\Delta x\right)/\partial x^2=0, {\partial }^2{C}_{3,0}\left(x_2,\Delta x^2/2D,\Delta x\right)/\partial x^2=0$$

(13)

$${\partial }^2{C}_{1,0}\left(x,\Delta x^2/2D,\Delta x\right)/\partial x^2>0, {\partial }^2{C}_{3,0}\left(x,\Delta x^2/2D,\Delta x\right)/\partial x^2<0 \forall x\in \left[x_2,x_2+\Delta x/2\right]$$

(14)

From Equation (2), ${\partial }^2{C}_{i,j}\left(x,t,\Delta x\right)/\partial x^2\propto \partial C_{i,j}\left(x,t,\Delta x\right)/\partial t$ and it can be concluded that 50% of $dx$ micro intervals ($dx\ll \Delta x$) of $x_2$ intervals get a positive temporal gradient ($\partial C_{1,0}\left(x,t,\Delta x\right)/\partial t>0$ and $\partial C_{3,0}\left(x,t,\Delta x\right)/\partial t>0$), and 50% a negative gradient ($\partial C_{1,0}\left(x,t,\Delta x\right)/\partial t<0$ and $\partial C_{3,0}\left(x,t,\Delta x\right)/\partial t<0$). After the stability threshold, more than 50% of micro cells get a negative gradient. This clearly means that particles issued from adjacent cells $x_1$ and $x_3$ will decrease in keeping with time, which will decrease the configuration entropy of the system $x_2$ contrarily to the second principle of thermodynamics for a diffusive system. The mathematical criterion of stability of the explicit scheme is then physically related to the production of entropy characterized by our algebra operator: if the scheme is unstable, then the production of entropy on each discretized cell is negative and the size of the program will decrease.

We eventually get:

$$\partial \dim (HUF\circ RLE(x_4(t)))/\partial t>0\mathrm{if}\sqrt{2Dt}<\Delta x,t>0$$

(15)

$$\partial \dim (HUF\circ RLE(x_4(t)))/\partial t=0\mathrm{if}\sqrt{2Dt}=\Delta x$$

(16)

$$\partial \dim (HUF\circ RLE(x_4(t)))/\partial t<0\mathrm{if}\sqrt{2Dt}>\Delta x$$

(17)

To illustrate these partial differential equations, different system sizes are simulated using the Monte Carlo diffusion process (from s = 250 to 1000). Then, according to Equation (11), and if assertion $\ll \left\{HUF\circ RLE\right\}-\mathrm{maxi}$ contractile in $X\gg$ is true, the relation between the threshold that depends on the system size (because the system is always decomposed into 10 sub-systems with parts of equal length) becomes:

$$t_{HUF\circ RLE}^{\max }\left(s\right)=n_s^{sc}\left(s\right)=\Delta x^2\left(s\right)={(s/10)}^2$$

(18)

Figure 5 represents the normalized dimension obtained by $\dim (HUF\circ RLE(x_4(t)))/\dim (x_4(t))$ for the different system sizes. The maximal values for each system size are computed and compared to Equation (18).

As can be observed, data match to the theoretical equation meaning that whatever the system size, the time of maximal entropy $t_{HUF\circ RLE}^{\max }\left(s\right)$ is obtained so that it corresponds to the stability criterion. Thanks to statistical thermodynamics, it was shown that stability threshold corresponding to a violation of the second principle of the thermodynamics that confirms all results shown by the Information theory tools [16].

5. Two Examples of PDE

5.1. Non Constant Diffusion Coefficient

The problems treated by the information theory were investigated with a constant diffusion coefficient. In this case, the diffusion coefficient does not depend on the position. Thus, we will treat the following problem:

$$\frac{\partial }{\partial t}C\left(x,t\right)=\frac{\partial }{\partial x}D\left(x\right)\frac{\partial }{\partial x}C\left(x,t\right)$$

(19)

For a real positive diffusion parameter D(x) that depends on the x-position, the classical explicit first order in time and second order in space method in the one-dimensional case is stable if:

$$\mathsf{\lambda }=\frac{\max \left(D\left(x\right)\right)\Delta t}{{\left(\Delta x\right)}^2}\le 1/2$$

(20)

The x-dependence of diffusion coefficient D can be due to different variations of material properties like crystal structure, local molar concentration, vacancy gradient, etc., or external conditions like residual stress, temperature, electrical field, chemical potential, etc.

A positive perturbation $\Delta a(x)$ is introduced to the unitary jump length during the Brownian simulation process and the mean displacement of each particle becomes $1+\Delta a(x)$. By posing $a(x)=1+\Delta a(x)$ in Equation (7), one gets $D(x)={\left(a(x)\right)}^2$ and the local stability criterion becomes:

$$\sqrt{n_s(x)}\le \left(\Delta x/(1+\Delta a(x))\right)$$

(21)

Finally, the global stability criterion becomes:

$$\sqrt{n_s}\le \underset{x}{\min }\left(\Delta x/(1+\Delta a(x))\right)$$

(22)

A Gaussian function will be used to simulate the variation of diffusion coefficient:

$$\Delta a(x,c,\mathsf{\sigma })=e^{\frac{1}{2}{\left(\frac{x-c}{\mathsf{\sigma }}\right)}^2}$$

(23)

To assess nonlinearity, the size of the system is increased and resolution map will be extended to N = 1024 (rather than N = 256 for the previous simulations). The Gaussian is centered at 3/4 of the diffusion map and then c = 3 × 1024/4 = 768 (Figure 6).

The mesh size is equal to $\Delta x=1024/8=128$. At t = 0, the diffusion cell is located the middle of the map (at t = 0, x_i,j = 1 $\forall j\in \left[1,1024\right]$ if i belongs to i₄ = [448,576] otherwise x_i,j = 0). The diffusion only occurs in the x direction. Figure 7 represents snapshots of the diffusion process for two standard deviations. As can be observed, for the standard deviation of 11² pixels, a dissymmetry of the concentration appears and diffusion increases on the right of the diffusion map. Contrarily, diffusion map is symmetrical for diffusion map obtained with small standard deviation (and for high standard deviation, i.e., greater than 2²⁰ pixels, result not shown). According to Equation (21), for very small standard deviations, one gets:

$$\underset{\mathsf{\sigma }\to 0}{{\displaystyle \mathbf{lim}}}\left(n_s(x,c,\mathsf{\sigma })\right)\le \Delta {{\displaystyle x}}^2={128}^2=16384,\forall x,\forall c,$$

(24)

and for high standard deviations, one gets:

$$\underset{\mathsf{\sigma }\to \infty }{{\displaystyle \mathbf{lim}}}\left(n_s(x,c,\mathsf{\sigma })\right)\le \Delta {{\displaystyle x}}^2/4=4096,\forall x,\forall c$$

(25)

In these two cases, diffusion becomes linear and stability condition does not depend on x position.

Let us now analyze the two compression ratio, $\dim (HUF\circ RLE(i_n(t)))/\dim (i_n(t))$, of the two adjacent cells (i₃, i₅) at i₄ (i₃ = [320,448], i₅ = [576,704]) for different values of standard deviations (Figure 8). As can be observed, all curves present maximal values of compression leading to a MCS time $n_s^{sc}(x,c,\mathsf{\sigma })$ that depend on the values of the standard deviations.

From our postulate, the theoretical stability criterion is equal to $n_s^{sc}(x,c,\mathsf{\sigma })={\left(\Delta x/(1+\Delta a(x,c,\mathsf{\sigma }))\right)}^2$. Values of the theoretical stability threshold agree with simulated values (Figure 9), meaning that our method can be applied to linear PDE with non-constant diffusion coefficient.

5.2. Nonlinear PDE

The problems treated by the information theory were investigated on a linear PDE. A vast array of complex phenomena of motion, reaction, diffusion, equilibrium, conservation, and more lead to nonlinear PDE. A PDE is said to be nonlinear if the relations between the unknown functions and their partial derivatives involved in the equation are nonlinear. Thus, we will treat the following nonlinear problem:

$$\frac{\partial }{\partial t}C\left(x,t\right)=\frac{\partial }{\partial x}D\left(C\left(x,t\right)\right)\frac{\partial }{\partial x}C\left(x,t\right)$$

(26)

In our case, the diffusion coefficient depends on the concentration $C\left(x,t\right)$. Lee [17] proposed diffusion coefficients relating to the uptake of excess calcium by calcium chloride [18]. The diffusion coefficient D takes the form:

$$D\left(C\left(x,t\right)\right)=\frac{D_0}{1+aC\left(x,t\right)}$$

(27)

where a is a coefficient that represents sur-diffusion processes (a < 0) or a sub-diffusion ones (a > 0) or a classical diffusion ones (a = 0). In our simulations, $a=\left\{-1,0,1,2,3,4,5\right\}$. The stability criterion is given by:

$$\mathsf{\lambda }=\frac{\max \left(D\left(C\left(x,t\right)\right)\right)\Delta t}{{\left(\Delta x\right)}^2}\le 1/2$$

(28)

The Monte Carlo simulation is based on an explicit scheme. Jump length at time t + dt is computed from concentration at time t (Figure 10). Too validate our hypothesis, 50 simulations are performed with three sizes of the system: 128², 256² and 512² pixels. Maximal values of the dimension are extracted (Figure 11).

Values of the theoretical stability threshold agree with simulated values (Figure 12), meaning that our method can be applied to nonlinear PDE.

6. Discussion

To summarize, the mathematical criterion of stability $\mathsf{\lambda }=\Delta t/\Delta x^2>1/2$ of the explicit scheme leads to an unstable scheme due to the decrease of information versus time characterized by the reduction size of the system on each discretized cell of the whole system. In the stability vision of Von Neumann, a finite difference scheme is stable if the errors made at one time step of the calculation do not let the errors increase for the following time steps. Therefore, in our approach, this means that, for a fixed time of observation of the diffusion, an increase of the size of the sub-cells of the grid will irrevocably lead to a critical size from which discretized information will not be enough to contain information on concentration gradient described by the partial differential equation. In fact, the physical interpretation of instability of the PDE was never introduced in a high number of papers, which treat mathematical aspects of instability via information formalisms. Mishra has introduced the problems of violation of local thermodynamic laws in the transport equations via Information theory. He discretizes the transport equation via a simple centered finite difference scheme. The time derivative is replaced with a forward difference and the spatial derivative with a central difference. In this scheme of discretization, the central scheme leads to a growth of energy at every time step and is unstable whatever the size of both discretization of time and space [19]. Mishra explains why the solutions computed with the central scheme blow up. After all, the central scheme seems a reasonable approximation of the transport equation. The physical explanation can be deduced from the following argument: the exact solution moves to the right with entities speed (Figure 13).

Unfortunately, for the scheme described in this publication that we have physically proof to be physical relevant in term of the physics causality via Einstein theory of the Brownian motion [15], no justification of the conditional stabilities was found in the bibliography via Information theory. However, some results using entropy concept in PDE stability conclude [21] that many linear Partial Differential Equations or Integral equations with non-constant coefficients satisfy some entropy dissipation properties [22]. Finally, explicit time discretization leads to entropy production [23] and more specifically, explicit scheme with Lax–Friedrichs flux is entropy stable under conditions given by Equation (5) [24].

7. Conclusions

In this paper, we showed that a relation exists between the well-known stability criterion $\mathsf{\lambda }=D\Delta t/{\left(\Delta x\right)}^2\le 1/2$ applied on the explicit numerical scheme $C_x^{t+\Delta t}=C_i^t+\mathsf{\lambda }\left(C_{x-\Delta x}^t-2C_x^t+C_{x+\Delta x}^t\right)$ to guarantee the convergence of the 1D non-stationary PDE $\partial C\left(x,t\right)/\partial t=D{\partial }^{2}C\left(x,t\right)/\partial x^2$ to the solution and the quantity of information contained at a mesoscopic scale under the size of discretization $\Delta x$. Implicit and semi implicit schemes (such as the unconditionally stable scheme of Crank–Nicolson method) lead to a violation of the principle of causality: the cause must precede its effect according to all inertial observers meaning that the cause and its effect are separated by a time-like interval, and the effect belongs to the future of its cause. Jaroszkiewicz pointed out the violation of causality in the fields of discrete mechanics by analyzing the implicit and explicit Euler Schemes and deduced that the implicit scheme involves that the flow of information occurs in a temporal loop. Jaroszkiewicz concluded his argument with the following question: “we should ask, given this violation of causal implication, how could we ever use implicit Euler scheme in practical calculation” [25]. Under Causality scheme assumptions, it was proved that instability occurs during iterative process if and only if information contained inside the cell $\Delta x$ decreases with time, thus violating the second principle of the thermodynamics. As microscopic simulations of diffusion mechanisms are only explicit methods (Monte Carlo methods, Cellular automata, etc.), the criterion of sub-cell information seems to be a relevant tool to assess that a stable explicit scheme meets both the causality and the second principle of the thermodynamics.