Wigner Time-Delay and Distribution for Polarization Interaction in Strongly Coupled Semiclassical Plasmas
Abstract
:1. Introduction
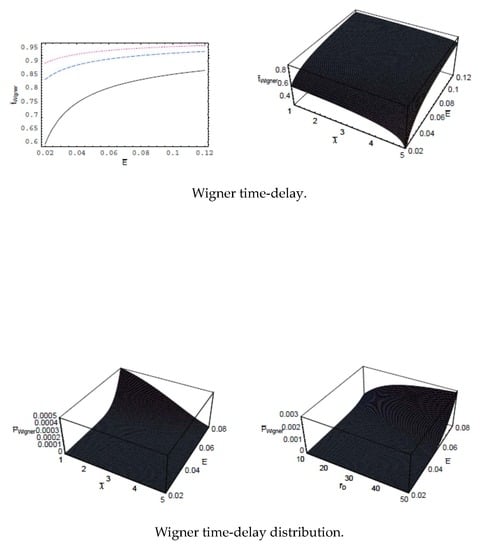
2. Theory and Calculations
3. Discussions
4. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fano, U.; Rau, A.R.P. Atomic Collisions and Spectra; Academic Press: Orlando, FL, USA, 1986. [Google Scholar]
- Friedrich, H. Theoretical Atomic Physics, 4th ed.; Springer: Berlin, Germany, 2017. [Google Scholar]
- Wigner, E.P. Lower limit for the energy derivative of the scattering phase shift. Phys. Rev. 1955, 98, 145. [Google Scholar] [CrossRef]
- Smith, F.T. Lifetime Matrix in Collision Theory. Phys. Rev. 1960, 119, 349. [Google Scholar] [CrossRef]
- de Carvalho, C.A.A.; Nussenzveig, H.M. Time delay. Phys. Rep. 2002, 364, 83. [Google Scholar] [CrossRef]
- Pazourek, R.; Feist, J.; Nagele, S.; Burgdörfer, J. Attosecond Streaking of Correlated Two-Electron Transitions in Helium. Phys. Rev. Lett. 2012, 108, 163001. [Google Scholar] [CrossRef] [Green Version]
- Pazourek, R.; Nagele, S.; Burgdörfer, J. Time-resolved photoemission on the attosecond scale: Opportunities and challenges. Faraday Disc. 2013, 163, 353. [Google Scholar] [CrossRef]
- Fujimoto, T. Plasma Spectroscopy; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Paul, S.; Ho, Y.K. Hydrogen atoms in Debye plasma environments. Phys. Plasmas 2009, 16, 063302. [Google Scholar] [CrossRef]
- Pandey, M.; Lin, Y.-C.; Ho, Y.K. Investigation of charge transfer and ionization in He-like systems (Li+, Be2+, B3+, C4+, N5+, O6+)-hydrogen atom collisions in Debye plasmas. Phys. Plasmas 2013, 20, 022104. [Google Scholar] [CrossRef]
- Pandey, M.; Lin, Y.-C.; Ho, Y.K. An investigation of antiprotons collisions with positronium atom in Debye plasma environments. Phys. Plasmas 2015, 22, 052104. [Google Scholar] [CrossRef]
- Baimbetov, B.; Nurekenov, K.T.; Ramazanov, T.S. Pseudopotential theory of classical non-ideal plasmas. Phys. Lett. A 1995, 202, 211. [Google Scholar] [CrossRef]
- Ramazanov, T.S.; Dzhumagulova, K.N.; Omarbakiyeva, Y.A. Effective polarization interaction potential “charge-atom” for partially ionized dense plasma. Phys. Plasmas 2005, 12, 092702. [Google Scholar] [CrossRef]
- Shukla, P.K.; Stenflo, L.; Bingham, R. Shielding of a slowly moving test charge in a quantum plasma. Phys. Lett. A 2006, 359, 218. [Google Scholar] [CrossRef]
- Ghoshal, A.; Ho, Y.K. Ground states of helium in exponential-cosine-screened Coulomb potentials. J. Phys. B 2009, 42, 175006. [Google Scholar] [CrossRef]
- Shevelko, V.P. Atoms and Their Spectroscopic Properties; Springer: Berlin, Germany, 1997. [Google Scholar]
- Marklund, M.; Shukla, P.K. Nonlinear collective effects in photon-photon and photon-plasma interactions. Rev. Mod. Phys. 2006, 78, 591. [Google Scholar] [CrossRef] [Green Version]
- Kobzev, G.A.; Iakubov, I.T.; Popovich, M.M. Transport and Optical Properties of Nonideal Plasma; Plenum: New York, NY, USA, 1995. [Google Scholar]
- Sitenko, A.G. Lectures in Scattering Theory; Pergamon Press: Oxford, UK, 1971. [Google Scholar]
- Smirnov, B.M. Physics of Atoms and Ions; Springer: Berlin, Germany, 2003. [Google Scholar]
- Lee, M.-J.; Jung, Y.-D. Characteristics of Polarisation in the Ramsauer–Townsend Minima in Strongly Coupled Semiclassic Plasmas. Naturforsch 2017, 72a, 995. [Google Scholar] [CrossRef]
- Smirnov, B.M. Plasma Processes and Plasma Kinetics; Wiley-VCH: Weinheim, Germany, 2007. [Google Scholar]
- Friedrich, H. Scattering Theory, 2nd ed.; Springer: Berlin, Germany, 2016. [Google Scholar]
- Texier, C.; Comtet, A. Universality of the Wigner Time Delay Distribution for One-Dimensional Random Potentials. Phys. Rev. Lett. 1999, 82, 4220. [Google Scholar] [CrossRef] [Green Version]
- Bakunin, O.G. Turbulence and Diffusion; Springer: Berlin, Germany, 2008. [Google Scholar]
- Ramazanov, T.S.; Moldabekov, Z.A.; Dzhumagulova, K.N.; Muratov, M.M. Pseudopotentials of the particles interactions in complex plasmas. Phys. Plasmas 2011, 18, 103705. [Google Scholar] [CrossRef]
- Shukla, P.K.; Eliasson, B. Colloquium: Nonlinear collective interactions in quantum plasmas with degenerate electron fluids. Rev. Mod. Phys. 2011, 83, 885. [Google Scholar] [CrossRef] [Green Version]
- Shukla, P.K.; Eliasson, B. Novel Attractive Force between Ions in Quantum Plasmas. Phys. Rev. Lett. 2012, 108, 165007. [Google Scholar] [CrossRef]
- Sayed, F.; Vladimirov, S.V.; Tyshetskiy, Y.; Ishihara, O. Modulational interactions in quantum plasmas. Phys. Plasmas 2013, 20, 072116. [Google Scholar] [CrossRef] [Green Version]
- Akbari-Moghanjoughi, M. Generalized model screening potentials for Fermi-Dirac plasmas. Phys. Plasmas 2016, 23, 042706. [Google Scholar] [CrossRef]
- Eliasson, B.; Akbari-Moghanjoughi, M. Finite temperature static charge screening in quantum plasmas. Phys. Lett. A 2016, 380, 2518. [Google Scholar] [CrossRef] [Green Version]
- Tekavec, P.F.; Dyke, T.R.; Marcus, A.H. Wave packet interferometry and quantum state reconstruction by acousto-optic phase modulation. J. Chem. Phys. 2006, 125, 194303. [Google Scholar] [CrossRef] [PubMed]
- Bruder, L.; Mudrich, M.; Stienkemeier, F. Phase-modulated electronic wave packet interferometry reveals high resolution spectra of free Rb atoms and Rb*He molecules. Phys. Chem. Chem. Phys. 2015, 17, 23877. [Google Scholar] [CrossRef] [PubMed] [Green Version]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, M.-J.; Jung, Y.-D. Wigner Time-Delay and Distribution for Polarization Interaction in Strongly Coupled Semiclassical Plasmas. Entropy 2020, 22, 910. https://0-doi-org.brum.beds.ac.uk/10.3390/e22090910
Lee M-J, Jung Y-D. Wigner Time-Delay and Distribution for Polarization Interaction in Strongly Coupled Semiclassical Plasmas. Entropy. 2020; 22(9):910. https://0-doi-org.brum.beds.ac.uk/10.3390/e22090910
Chicago/Turabian StyleLee, Myoung-Jae, and Young-Dae Jung. 2020. "Wigner Time-Delay and Distribution for Polarization Interaction in Strongly Coupled Semiclassical Plasmas" Entropy 22, no. 9: 910. https://0-doi-org.brum.beds.ac.uk/10.3390/e22090910