Noise-Robust Image Reconstruction Based on Minimizing Extended Class of Power-Divergence Measures
Abstract
:1. Introduction
2. Definitions and Notations
3. Proposed System
3.1. Definition
3.2. Theoretical Results
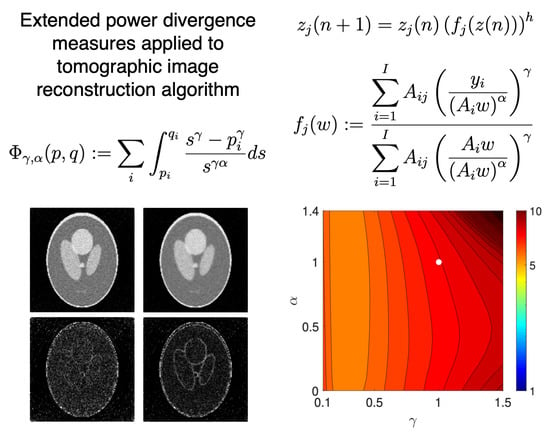
4. Experimental Results and Discussion
4.1. Reconstruction Using Numerical Phantom
4.2. Reconstruction Using Physical Phantom
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gordon, R.; Bender, R.; Herman, G.T. Algebraic reconstruction techniques (ART) for three-dimensional electron microscopy and X-ray photography. J. Theor. Biol. 1970, 29, 471–481. [Google Scholar] [CrossRef]
- Badea, C.; Gordon, R. Experiments with the nonlinear and chaotic behaviour of the multiplicative algebraic reconstruction technique (MART) algorithm for computed tomography. Phys. Med. Biol. 2004, 49, 1455–1474. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kak, A.C.; Slaney, M. Principles of Computerized Tomographic Imaging; IEEE Press: New York, NY, USA, 1988. [Google Scholar]
- Stark, H. Image Recovery: Theory and Applications; Academic Press: New York, NY, USA, 1987. [Google Scholar]
- Prakash, P.; Kalra, M.K.; Kambadakone, A.K.; Pien, H.; Hsieh, J.; Blake, M.A.; Sahani, D.V. Reducing abdominal CT radiation dose with adaptive statistical iterative reconstruction technique. Investig. Radiol. 2010, 45, 202–210. [Google Scholar] [PubMed]
- Singh, S.; Kalra, M.K.; Gilman, M.D.; Hsieh, J.; Pien, H.H.; Digumarthy, S.R.; Shepard, J.O. Adaptive statistical iterative reconstruction technique for radiation dose reduction in chest CT: A pilot study. Radiology 2011, 259, 565–573. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Kalra, M.K.; Do, S.; Thibault, J.B.; Pien, H.; O’Connor, O.J.; Blake, M.A. Comparison of hybrid and pure iterative reconstruction techniques with conventional filtered back projection: Dose reduction potential in the abdomen. J. Comput. Assist. Tomogr. 2012, 36, 347–353. [Google Scholar] [PubMed]
- Beister, M.; Kolditz, D.; Kalender, W.A. Iterative reconstruction methods in X-ray CT. Phys. Med. 2012, 28, 94–108. [Google Scholar] [PubMed]
- Huang, H.M.; Hsiao, I.T. Accelerating an Ordered-Subset Low-Dose X-Ray Cone Beam Computed Tomography Image Reconstruction with a Power Factor and Total Variation Minimization. PLoS ONE 2016, 11, e0153421. [Google Scholar]
- Shepp, L.A.; Vardi, Y. Maximum likelihood reconstruction for emission tomography. IEEE Trans. Med. Imaging 1982, 1, 113–122. [Google Scholar]
- Hudson, H.M.; Larkin, R.S. Accelerated image reconstruction using ordered subsets of projection data. IEEE Trans. Med. Imaging 1994, 13, 601–609. [Google Scholar]
- Fessler, J.A.; Hero, A.O. Penalized maximum-likelihood image reconstruction using space-alternating generalized EM algorithms. IEEE Trans. Image Process. 1995, 4, 1417–1429. [Google Scholar]
- Byrne, C. Accelerating the EMML algorithm and related iterative algorithms by rescaled block-iterative methods. IEEE Trans. Image Process. 1998, 7, 100–109. [Google Scholar] [CrossRef]
- Hwang, D.; Zeng, G.L. Convergence study of an accelerated ML-EM algorithm using bigger step size. Phys. Med. Biol. 2006, 51, 237–252. [Google Scholar] [CrossRef]
- Byrne, C. Block-iterative methods for image reconstruction from projections. IEEE Trans. Image Process. 1996, 5, 792–794. [Google Scholar] [CrossRef]
- Byrne, C. Block-iterative algorithms. Int. Trans. Oper. Res. 2009, 16, 427–463. [Google Scholar] [CrossRef]
- Tanaka, E.; Nohara, N.; Tomitani, T.; Yamamoto, M. Utilization of Non-Negativity Constraints in Reconstruction of Emission Tomograms. In Information Processing in Medical Imaging; Stephen, L.B., Ed.; Springer: Dordrecht, The Netherlands, 1986; Volume 1, pp. 379–393. [Google Scholar]
- Tanaka, E. A fast reconstruction algorithm for stationary positron emission tomography based on a modified EM algorithm. IEEE Trans. Med. Imaging 1987, 6, 98–105. [Google Scholar] [CrossRef]
- Zeng, G.L. The ML-EM algorithm is not optimal for poisson noise. In Proceedings of the 2015 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC), San Diego, CA, USA, 31 October–7 November 2015; pp. 1–3. [Google Scholar]
- Yamaguchi, Y.; Kudo, M.; Kojima, T.; Abou Al-Ola, O.M.; Yoshinaga, T. Extended Ordered-subsets Expectation-maximization Algorithm with Power Exponent for Noise-robust Image Reconstruction in Computed Tomography. Radiat. Environ. Med. 2019, 8, 105–112. [Google Scholar]
- Read, T.R.C.; Cressie, N.A.C. Goodness-of-Fit Statistics for Discrete Multivariate Data; Springer: New York, NY, USA, 1988. [Google Scholar]
- Pardo, L. Statistical Inference Based on Divergence Measures; Chapman and Hall/CRC: New York, NY, USA, 2005. [Google Scholar]
- Liese, F.; Vajda, I. On Divergences and Informations in Statistics and Information Theory. IEEE Trans. Inf. Theory 2006, 52, 4394–4412. [Google Scholar] [CrossRef]
- Pardo, L. New Developments in Statistical Information Theory Based on Entropy and Divergence Measures. Entropy 2019, 21, 391. [Google Scholar] [CrossRef] [Green Version]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Beran, R. Minimum Hellinger distance estimates for parametric models. Ann. Stat. 1977, 5, 445–463. [Google Scholar] [CrossRef]
- Basu, A.; Lindsay, B.G. Minimum disparity estimation for continuous models: Efficiency, distributions and robustness. Ann. Inst. Stat. Math. 1994, 46, 683–705. [Google Scholar] [CrossRef]
- Basu, A.; Harris, I.R.; Hjort, N.L.; Jones, M.C. Robust and efficient estimation by minimising a density power divergence. Biometrika 1998, 85, 549–559. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, A.; Basu, A. Estimation of Multivariate Location and Covariance using the S-Hellinger Distance. arXiv 2014, arXiv:1403.6304. [Google Scholar]
- Schropp, J. Using dynamical systems methods to solve minimization problems. Appl. Numer. Math. 1995, 18, 321–335. [Google Scholar] [CrossRef]
- Airapetyan, R.G.; Ramm, A.G.; Smirnova, A.B. Continuous analog of Gauss-Newton method. Math. Models Methods Appl. Sci. 1999, 9, 463–474. [Google Scholar] [CrossRef] [Green Version]
- Airapetyan, R.G.; Ramm, A.G. Dynamical systems and discrete methods for solving nonlinear ill-posed problems. In Applied Mathematics Reviews; Anastassiou, G.A., Ed.; World Scientific Publishing: Singapore, 2000; Volume 1, pp. 491–536. [Google Scholar]
- Airapetyan, R.G.; Ramm, A.G.; Smirnova, A.B. Continuous methods for solving nonlinear ill-posed problems. In Operator Theory and Its Applications; Ramm, A.G., Shivakumar, P.N., Strauss, A.V., Eds.; American Mathematical Society: Providence, RI, USA, 2000; Volume 25, pp. 111–138. [Google Scholar]
- Ramm, A.G. Dynamical systems method for solving operator equations. Commun. Nonlinear Sci. Numer. Simul. 2004, 9, 383–402. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Han, B. A dynamical system method for solving nonlinear ill-posed problems. J. Comput. Appl. Math. 2008, 197, 399–406. [Google Scholar] [CrossRef]
- Fujimoto, K.; Abou Al-Ola, O.M.; Yoshinaga, T. Continuous-time image reconstruction using differential equations for computed tomography. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1648–1654. [Google Scholar] [CrossRef]
- Abou Al-Ola, O.M.; Fujimoto, K.; Yoshinaga, T. Common Lyapunov function based on Kullback–Leibler divergence for a switched nonlinear system. Math. Probl. Eng. 2011, 2011, 723509:1–723509:12. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Fujimoto, K.; Abou Al-Ola, O.M.; Yoshinaga, T. Continuous-time image reconstruction for binary tomography. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 2081–2087. [Google Scholar] [CrossRef]
- Tateishi, K.; Yamaguchi, Y.; Abou Al-Ola, O.M.; Yoshinaga, T. Continuous Analog of Accelerated OS-EM Algorithm for Computed Tomography. Math. Probl. Eng. 2017, 2017, 1564123:1–1564123:8. [Google Scholar] [CrossRef]
- Lyapunov, A.M. Stability of Motion; Academic Press: New York, NY, USA, 1966. [Google Scholar]
- Aniszewska, D. Multiplicative Runge–Kutta methods. Nonlinear Dyn. 2007, 50, 265–272. [Google Scholar] [CrossRef]
- Bashirov, A.E.; Kurpinar, E.M.; Oezyapici, A. Multiplicative calculus and its applications. J. Math. Anal. Appl. 2008, 337, 36–48. [Google Scholar] [CrossRef] [Green Version]
- Shepp, L.A.; Logan, B.F. The Fourier reconstruction of a head section. IEEE Trans. Nucl. Sci. 1974, 21, 21–43. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [Green Version]
- Kyoto Kagaku. CT Whole Body Phantom PBU-60. Available online: https://kyotokagaku.com/en/products_introduction/ph-2b/ (accessed on 1 June 2021).











| N | |||
|---|---|---|---|
| MLEM | PDEM with | ||
| 50 | 6.44 | 6.29 | (0.8, 1.2) |
| 100 | 6.65 | 5.85 | 0.5, 1.2) |
| 200 | 7.86 | 5.70 | (0.3, 1.2) |
| N | SSIM | ||
|---|---|---|---|
| MLEM | PDEM with | ||
| 50 | 0.651 | 0.689 | (0.8, 1.2) |
| 100 | 0.581 | 0.726 | (0.5, 1.2) |
| 200 | 0.531 | 0.772 | (0.3, 1.2) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kasai, R.; Yamaguchi, Y.; Kojima, T.; Abou Al-Ola, O.M.; Yoshinaga, T. Noise-Robust Image Reconstruction Based on Minimizing Extended Class of Power-Divergence Measures. Entropy 2021, 23, 1005. https://0-doi-org.brum.beds.ac.uk/10.3390/e23081005
Kasai R, Yamaguchi Y, Kojima T, Abou Al-Ola OM, Yoshinaga T. Noise-Robust Image Reconstruction Based on Minimizing Extended Class of Power-Divergence Measures. Entropy. 2021; 23(8):1005. https://0-doi-org.brum.beds.ac.uk/10.3390/e23081005
Chicago/Turabian StyleKasai, Ryosuke, Yusaku Yamaguchi, Takeshi Kojima, Omar M. Abou Al-Ola, and Tetsuya Yoshinaga. 2021. "Noise-Robust Image Reconstruction Based on Minimizing Extended Class of Power-Divergence Measures" Entropy 23, no. 8: 1005. https://0-doi-org.brum.beds.ac.uk/10.3390/e23081005