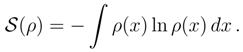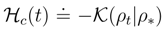Differential entropy and time
Abstract
:1. Introduction
1.1 Notions of entropy


1.2 Differential entropy
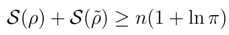
1.3 Temporal behavior-preliminaries
1.4 Outline of the paper
2. Differential entropy: uncertainty versus information
2.1 Prerequisites
 and μj = prob(Aj ) stands for a probability for an event Aj to occur in the game of chance with N possible outcomes.
and μj = prob(Aj ) stands for a probability for an event Aj to occur in the game of chance with N possible outcomes.

2.2 Events, states, microstates and macrostates
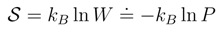
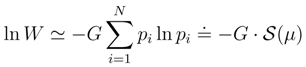
2.3 Shannon entropy and differential entropy
2.3.1 Bernoulli scheme and normal distribution
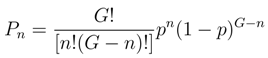

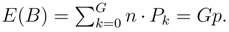 The variance E([B − E(B)]2) of B equals Gp(1 − p).
The variance E([B − E(B)]2) of B equals Gp(1 − p).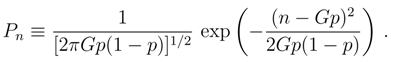
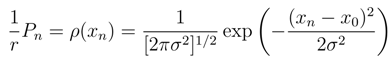
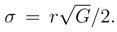 We recall that almost all of the probability ”mass” of the Gauss distribution is contained in the interval −3σ < x0 < +3σ about the mean value x0. Indeed, we have prob(|x − x0|) < 2σ) = 0.954 while prob(|x − x0|) < 3σ) = 0.998.
We recall that almost all of the probability ”mass” of the Gauss distribution is contained in the interval −3σ < x0 < +3σ about the mean value x0. Indeed, we have prob(|x − x0|) < 2σ) = 0.954 while prob(|x − x0|) < 3σ) = 0.998. in view of the above probability ”mass” estimates. Therefore, we can safely replace the Bernoulli probability measure by its (still discrete) Gaussian approximation Eq. (10) and next pass to Eq. (11) and its obvious continuous generalization.
in view of the above probability ”mass” estimates. Therefore, we can safely replace the Bernoulli probability measure by its (still discrete) Gaussian approximation Eq. (10) and next pass to Eq. (11) and its obvious continuous generalization.2.3.2 Coarse-graining
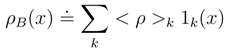

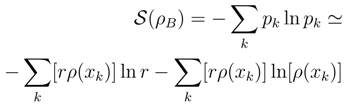
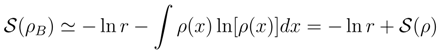
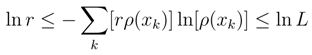


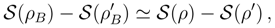
2.3.3 Coarse-graining exemplified: exponential density
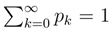 , with the well known quantum mechanical connotation.
, with the well known quantum mechanical connotation.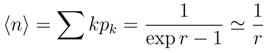
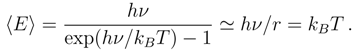

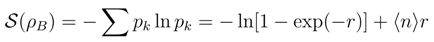
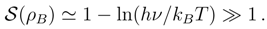
 where N and Γ is the Euler gamma function, [79], the particular cases N = 2, 3, 5 correspond to the generic level spacing distributions, based on the exploitation of the Wigner surmise. The respective histograms plus their continuous density interpolations are often reproduced in ”quantum chaos” papers, see for example [80].
where N and Γ is the Euler gamma function, [79], the particular cases N = 2, 3, 5 correspond to the generic level spacing distributions, based on the exploitation of the Wigner surmise. The respective histograms plus their continuous density interpolations are often reproduced in ”quantum chaos” papers, see for example [80].2.3.4 Spatial coarse graining in quantum mechanics
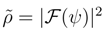 where
where
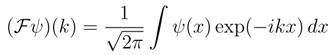
 ≪ 1 we can introduce the respective coarse grained entropies, each fulfilling an inequality Eq. (18). Combining these inequalities with Eq. (4), we get the prototype entropic inequalities for coarse grained entropies:
≪ 1 we can introduce the respective coarse grained entropies, each fulfilling an inequality Eq. (18). Combining these inequalities with Eq. (4), we get the prototype entropic inequalities for coarse grained entropies:

 .
.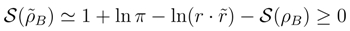
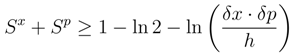
 and δx, δp with standard mean square deviation values ∆X and ∆P which are present in the canonical indeterminacy relations: ∆X · ∆P ≥ ħ/2.
and δx, δp with standard mean square deviation values ∆X and ∆P which are present in the canonical indeterminacy relations: ∆X · ∆P ≥ ħ/2.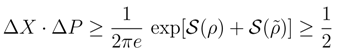
2.4 Impact of dimensional units
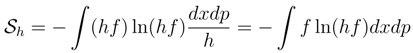

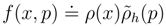
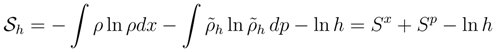
 has left us with the previously mentioned issue (Section 1.2) of ”literally taking the logarithm of a dimensional argument” i. e. that of ln h.
has left us with the previously mentioned issue (Section 1.2) of ”literally taking the logarithm of a dimensional argument” i. e. that of ln h. δp where labels r and
δp where labels r and  are dimensionless, while δx and δp stand for respective position and momentum dimensional (hitherto - resolution) units. Then:
are dimensionless, while δx and δp stand for respective position and momentum dimensional (hitherto - resolution) units. Then:
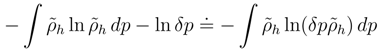
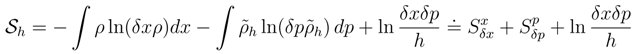
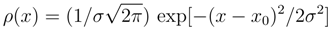
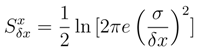
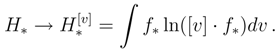

 . An obvious interpretation is that the β-scaling transformation of ρ(x − α) would broaden this density if β < 1 and would shrink when β > 1. Clearly, takes the value 0 at σ = (2πe)−1/2β in analogy with our previous dimensional considerations. If an argument of ρ is assumed to have dimensions, then the scaling transformation with the dimensional β may be interpreted as a method to restore the dimensionless differential entropy value.
. An obvious interpretation is that the β-scaling transformation of ρ(x − α) would broaden this density if β < 1 and would shrink when β > 1. Clearly, takes the value 0 at σ = (2πe)−1/2β in analogy with our previous dimensional considerations. If an argument of ρ is assumed to have dimensions, then the scaling transformation with the dimensional β may be interpreted as a method to restore the dimensionless differential entropy value.3 Localization: differential entropy and Fisher information
 in conformity with Eq. (11), but without any restriction on the value of x ∈ R.
in conformity with Eq. (11), but without any restriction on the value of x ∈ R.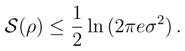

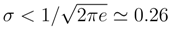 the differential entropy is negative.
the differential entropy is negative.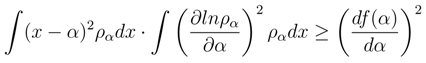


 we realize that the Fisher information is more sensitive indicator of the wave packet localization than the entropy power, Eq. (43).
we realize that the Fisher information is more sensitive indicator of the wave packet localization than the entropy power, Eq. (43). is no longer the mean value α-dependent and can be readily transformed to the conspicuously quantum mechanical form (up to a factor D2 with D = ħ/2m):
is no longer the mean value α-dependent and can be readily transformed to the conspicuously quantum mechanical form (up to a factor D2 with D = ħ/2m):
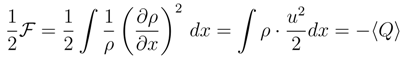
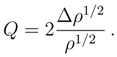

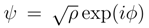 is a normalized element of L2(R), another important inequality holds true, [2,23]:
is a normalized element of L2(R), another important inequality holds true, [2,23]:

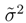 is the variance of the ”quantum mechanical momentum canonically conjugate to the position observable”, up to (skipped) dimensional factors. In the above, we have exploited the Fourier transform
is the variance of the ”quantum mechanical momentum canonically conjugate to the position observable”, up to (skipped) dimensional factors. In the above, we have exploited the Fourier transform 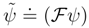 of ψ tp arrive at
of ψ tp arrive at  of Eq. (4) whose variance the above
of Eq. (4) whose variance the above 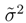 actually is.
actually is.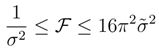
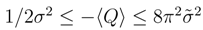 and furthermore
and furthermore

4 Asymptotic approach towards equilibrium: Smoluchowski processes
4.1 Random walk
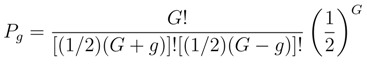
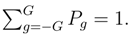


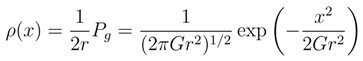
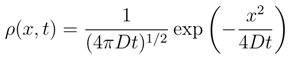


4.2 Kullback entropy versus differential entropy
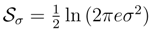 independent of α.
independent of α.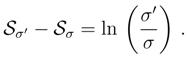
 and σ′ ≐ σ(t′) we make the non-stationary (heat kernel) density amenable to the ”absolute comparison” formula at different time instants t′ > t > 0: (σ′/σ) =
and σ′ ≐ σ(t′) we make the non-stationary (heat kernel) density amenable to the ”absolute comparison” formula at different time instants t′ > t > 0: (σ′/σ) = 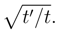
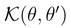 for a one-parameter family of probability densities ρθ, so that the ”distance” between any two densities in this family can be directly evaluated. Let ρθ′ stands for the prescribed (reference) probability density. We have, [6,81,88]:
for a one-parameter family of probability densities ρθ, so that the ”distance” between any two densities in this family can be directly evaluated. Let ρθ′ stands for the prescribed (reference) probability density. We have, [6,81,88]:

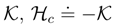 , named the conditional entropy [6], is predominantly used in the literature [6,48,92] because of its affinity (regarded as a formal generalization) to the differential entropy. Then e.g. one investigates an approach of towards its maximum (usually achieved at the value zero) when a running density is bound to have a unique stationary asymptotic, [92].
, named the conditional entropy [6], is predominantly used in the literature [6,48,92] because of its affinity (regarded as a formal generalization) to the differential entropy. Then e.g. one investigates an approach of towards its maximum (usually achieved at the value zero) when a running density is bound to have a unique stationary asymptotic, [92].
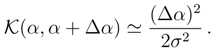
 .
.
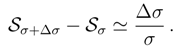
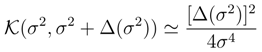

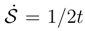 of the heat kernel differential entropy, Eq. (58) and the de Bruijn identity.
of the heat kernel differential entropy, Eq. (58) and the de Bruijn identity.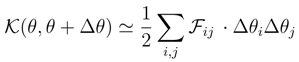
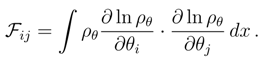

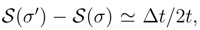 while
while 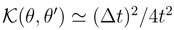 . Although, for finite increments ∆t we have
. Although, for finite increments ∆t we have

 can be defined exclusively for the differential entropy, and is meaningless in terms of the Kullback ”distance”.
can be defined exclusively for the differential entropy, and is meaningless in terms of the Kullback ”distance”.4.3 Entropy dynamics in the Smoluchowski process

 is analyzed in terms of the Fokker-Planck equation for the spatial probability density ρ(x, t), [88,89,90,91]:
is analyzed in terms of the Fokker-Planck equation for the spatial probability density ρ(x, t), [88,89,90,91]:
 , where β is interpreted as the friction (damping) parameter, T is the temperature of the bath, kB being the Boltzmann constant .
, where β is interpreted as the friction (damping) parameter, T is the temperature of the bath, kB being the Boltzmann constant .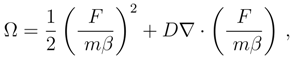
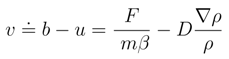
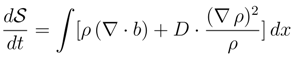
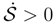 which is not true, [67,87].
which is not true, [67,87].
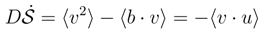
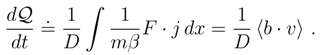
 , the ”power release” expression
, the ”power release” expression 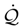 may be positive which represents the power removal to the environment, as well as negative which corresponds to the power absorption from the environment.
may be positive which represents the power removal to the environment, as well as negative which corresponds to the power absorption from the environment.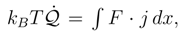 with T being the temperature of the bath. When there is no external forces, we have b = 0, and then the differential entropy time rate formula for the free Brownian motion Eq. (59) reappears.
with T being the temperature of the bath. When there is no external forces, we have b = 0, and then the differential entropy time rate formula for the free Brownian motion Eq. (59) reappears.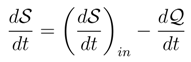
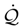 is defined in Eq. (82) while
is defined in Eq. (82) while  .
. = 0 which amounts to the existence of steady states. In the simplest case, when the diffusion current vanishes, we encounter the primitive realization of the state of equilibrium with an invariant density ρ. Then, b = u = D∇ln ρ and we readily arrive at the classic equilibrium identity for the Smoluchowski process:
= 0 which amounts to the existence of steady states. In the simplest case, when the diffusion current vanishes, we encounter the primitive realization of the state of equilibrium with an invariant density ρ. Then, b = u = D∇ln ρ and we readily arrive at the classic equilibrium identity for the Smoluchowski process:
 )in.
)in.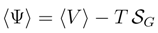
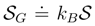 of information entropy has been introduced (actually, it is a direct configuration-space analog of the Gibbs entropy). The expectation value of the mechanical force potential 〈V〉 plays here the role of (mean) internal energy, [67,71].
of information entropy has been introduced (actually, it is a direct configuration-space analog of the Gibbs entropy). The expectation value of the mechanical force potential 〈V〉 plays here the role of (mean) internal energy, [67,71].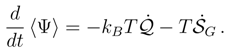

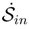 . One may expect that actualy 〈Ψ〉(t) drops down to a finite minimum as t → ∞.
. One may expect that actualy 〈Ψ〉(t) drops down to a finite minimum as t → ∞.4.4 Kullback entropy versus Shannon entropy in the Smoluchowski process

 . Let us notice that
. Let us notice that


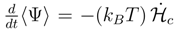 . An approach of 〈Ψ〉(t) towards the minimum proceeds in the very same rate as this of
. An approach of 〈Ψ〉(t) towards the minimum proceeds in the very same rate as this of  towards its maximum.
towards its maximum. which is non-negative, we have no growth guarantee for the differential entropy
which is non-negative, we have no growth guarantee for the differential entropy  whose sign is unspecified. Nonetheless, the balance between the time rate of entropy production/removal and the power release into or out of the environment, is definitely correct. We have
whose sign is unspecified. Nonetheless, the balance between the time rate of entropy production/removal and the power release into or out of the environment, is definitely correct. We have 
4.5 One-dimensional Ornstein-Uhlenbeck process
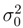 . the Fokker-Planck evolution Eq. (74) preserves the Gaussian form of ρ(x, t) while modifying the mean value α(t) = α0 exp(−γt) and variance according to
. the Fokker-Planck evolution Eq. (74) preserves the Gaussian form of ρ(x, t) while modifying the mean value α(t) = α0 exp(−γt) and variance according to

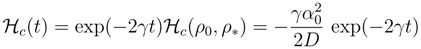

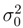 > D/γ, then
> D/γ, then  < 0, while
< 0, while 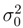 < D/γ implies
< D/γ implies  > 0. In both cases the behavior of the differential entropy is monotonic, though its growth or decay do critically rely on the choice of
> 0. In both cases the behavior of the differential entropy is monotonic, though its growth or decay do critically rely on the choice of 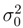 . Irrespective of
. Irrespective of 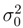 the asymptotic value of as t → ∞ reads (1/2)ln[2πe(D/γ).
the asymptotic value of as t → ∞ reads (1/2)ln[2πe(D/γ).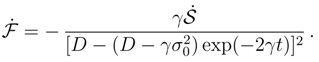
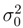 the asymptotic value of reads γ/D.
the asymptotic value of reads γ/D.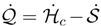 . Since
. Since

 < 0 we encounter a continual power supply
< 0 we encounter a continual power supply 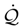 > 0 by the thermal environment.
> 0 by the thermal environment. > 0 the situation is more complicated. For example, if α0 = 0, we can easily check that
> 0 the situation is more complicated. For example, if α0 = 0, we can easily check that 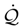 < 0, i.e. we have the power drainage from the environment for all t ∈ R+. More generally, the sign of
< 0, i.e. we have the power drainage from the environment for all t ∈ R+. More generally, the sign of 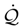 is negative for
is negative for 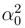 < 2(D − γ
< 2(D − γ 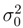 )/γ. If the latter inequality is reversed, the sign of
)/γ. If the latter inequality is reversed, the sign of 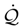 is not uniquely specified and suffers a change at a suitable time instant tchange(
is not uniquely specified and suffers a change at a suitable time instant tchange( 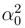 ,
, 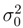 ).
).4.6 Mean energy and the dynamics of Fisher information
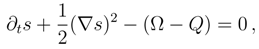
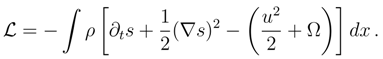

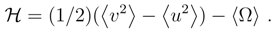
 . By invoking Eq. (86), with the time-independent V, we arrive at
. By invoking Eq. (86), with the time-independent V, we arrive at

 , in view of vρ = 0 at the integration volume boundaries, identically vanishes. Since v = −(1/mβ)∇Ψ, we define
, in view of vρ = 0 at the integration volume boundaries, identically vanishes. Since v = −(1/mβ)∇Ψ, we define
 identically.
identically.
 , we can rewrite the above formula as follows:
, we can rewrite the above formula as follows:


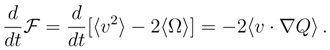

 = t(γ2
= t(γ2 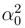 /D) exp(−2γt), hence an asymptotic value 0, while 〈u2〉(t) = (D/2)(t) → γ/D. Accordingly, we have 〈Ω〉(t) → − γ/2D.
/D) exp(−2γt), hence an asymptotic value 0, while 〈u2〉(t) = (D/2)(t) → γ/D. Accordingly, we have 〈Ω〉(t) → − γ/2D.5 Differential entropy dynamics in quantum theory
5.1 Balance equations
 with dimensions of energy. we consider the Schrödinger equation (set D = ħ/2m) in the form
with dimensions of energy. we consider the Schrödinger equation (set D = ħ/2m) in the form
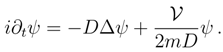
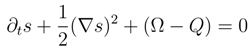
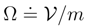 and the functional form of Q coincides with this introduced previously in Eq. (72). Notice a ”minor” sign change in Eq. (110) in comparison with Eq. (98).
and the functional form of Q coincides with this introduced previously in Eq. (72). Notice a ”minor” sign change in Eq. (110) in comparison with Eq. (98).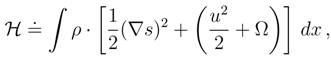

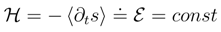
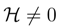 , we deal here with so-called finite energy diffusion-type processes, [51,52]. The corresponding Fokker-Planck equation propagates a probability density |ψ|2 = ρ, whose differential entropy may quite nontrivially evolve in time.
, we deal here with so-called finite energy diffusion-type processes, [51,52]. The corresponding Fokker-Planck equation propagates a probability density |ψ|2 = ρ, whose differential entropy may quite nontrivially evolve in time. )in (while assuming the validity of mathematical restrictions upon the behavior of integrands), we encounter the information entropy balance equations in their general form disclosed in Eqs. (81)-(83). The related differential entropy ”production” rate reads:
)in (while assuming the validity of mathematical restrictions upon the behavior of integrands), we encounter the information entropy balance equations in their general form disclosed in Eqs. (81)-(83). The related differential entropy ”production” rate reads:

 which implies
which implies 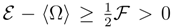 . Therefore, the localization measure has a definite upper bound: the pertinent wave packet cannot be localized too sharply.
. Therefore, the localization measure has a definite upper bound: the pertinent wave packet cannot be localized too sharply.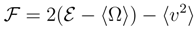
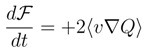
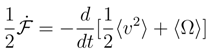
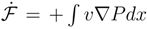 , with the same functional form for P as before. We interpret as the measure of power transfer in the course of which the (de)localization ”feeds” the diffusion current and in reverse. Here, we encounter a negative feedback between the localization and the proper energy of motion which keeps intact an overall mean energy of the quantum motion. See e.g. also [53].
, with the same functional form for P as before. We interpret as the measure of power transfer in the course of which the (de)localization ”feeds” the diffusion current and in reverse. Here, we encounter a negative feedback between the localization and the proper energy of motion which keeps intact an overall mean energy of the quantum motion. See e.g. also [53].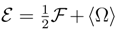 and no entropy ”production” nor dynamics of uncertainty. There holds
and no entropy ”production” nor dynamics of uncertainty. There holds  = 0 and we deal with time-reversible stationary diffusion processes and their invariant probability densities ρ(x), [52,68].
= 0 and we deal with time-reversible stationary diffusion processes and their invariant probability densities ρ(x), [52,68].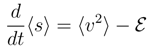
 = 0). Hence, as close as possible link with the present discussion is obtained if we re-define s into sΨ ≐ s. Then we have
= 0). Hence, as close as possible link with the present discussion is obtained if we re-define s into sΨ ≐ s. Then we have
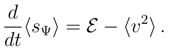
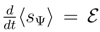 , in contrast to the standard Fokker-Planck case of
, in contrast to the standard Fokker-Planck case of  .
.5.2 Differential entropy dynamics exemplified
5.2.1 Free evolution
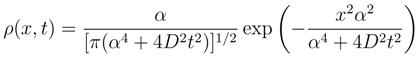
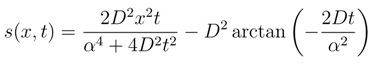
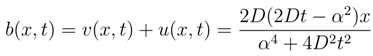
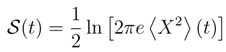
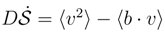 equals:
equals:
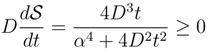
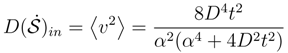

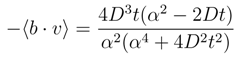
 )in ∼ 2D2/α2.
)in ∼ 2D2/α2.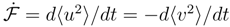 .
.5.2.2 Steady state
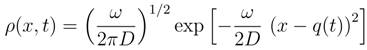

 )in = p2(t)/4m2 which is balanced by an oscillating ”dissipative” counter-term to yield
)in = p2(t)/4m2 which is balanced by an oscillating ”dissipative” counter-term to yield  .
.5.2.3 Squeezed state
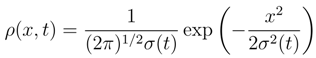
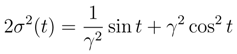
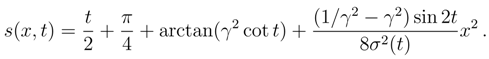
5.2.4 Stationary states
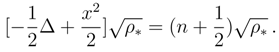
 , provided we set Ω = x2/2, define u = ∇ln
, provided we set Ω = x2/2, define u = ∇ln  and demand that Q = u2/2 + (1/2)∇ · u.
and demand that Q = u2/2 + (1/2)∇ · u.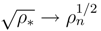 with n = 0,1,2,...). We have:
with n = 0,1,2,...). We have:
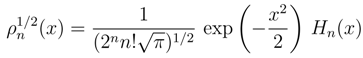
6 Outlook
Acknowledgments
Dedication
References
- Alicki, R.; Fannes, M. Quantum Dynamical Systems; Oxford University Press: Oxford, 2001. [Google Scholar]
- Ohya, M.; Petz, D. Quantum Entropy and Its use; Springer-Verlag: Berlin, 1993. [Google Scholar]
- Wehrl, A. General properties of entropy. Rev. Mod. Phys. 1978, 50, 221–260. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Techn. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: NY, 1991. [Google Scholar]
- Sobczyk, K. Information Dynamics: Premises, Challenges and Results. Mechanical Systems and Signal Processing 2001, 15, 475–498. [Google Scholar] [CrossRef]
- Yaglom, A.M.; Yaglom, I.M. Probability and Information; D. Reidel: Dordrecht, 1983. [Google Scholar]
- Hartley, R.V.L. Transmission of information. Bell Syst. Techn. J. 1928, 7, 535–563. [Google Scholar] [CrossRef]
- Brillouin, L. Science and Information Theory; Academic Press: NY, 1962. [Google Scholar]
- Ingarden, R.S.; Kossakowski, A.; Ohya, M. Information Dynamics and Open Systems; Kluwer: Dordrecht, 1997. [Google Scholar]
- Brukner, Ĉ.; Zeilinger, A. Conceptual inadequacy of the Shannon information in quantum measurements. Phys. Rev. 2002, A 63, 022113. [Google Scholar] [CrossRef]
- Mana, P.G.L. Consistency of the Shannon entropy in quantum experiments. Phys. Rev. 2004, A 69, 062108. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics.II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Stotland, A.; et al. The information entropy of quantum mechanical states. Europhys. Lett. 2004, 67, 700–706. [Google Scholar] [CrossRef]
- Partovi, M.H. Entropic formulation of uncertainty for quantum measurements. Phys. Rev. Lett. 1983, 50, 1883–1885. [Google Scholar] [CrossRef]
- Adami, C. Physics of information. 2004; arXiv:quant-ph/040505. [Google Scholar]
- Deutsch, D. Uncertainty in quantum measurement. Phys. Rev. Lett. 1983, 50, 631–633. [Google Scholar] [CrossRef]
- Garbaczewski, P.; Karwowski, W. Impenetrable barrriers and canonical quantization. Am. J. Phys. 2004, 72, 924–933. [Google Scholar] [CrossRef]
- Hirschman, I.I. A note on entropy. Am. J. Math. 1957, 79, 152–156. [Google Scholar] [CrossRef]
- Beckner, W. Inequalities in Fourier analysis. Ann. Math. 1975, 102, 159–182. [Google Scholar] [CrossRef]
- Bia-lynicki-Birula, I.; Mycielski, J. Uncertainty Relations for Information Entropy in Wave Mechanics. Commun. Math. Phys. 1975, 44, 129–132. [Google Scholar] [CrossRef]
- Bia-lynicki-Birula, I.; Madajczyk, J. Entropic uncertainty relations for angular distributions. Phys. Lett. 1985, A 108, 384–386. [Google Scholar] [CrossRef]
- Stam, A.J. Some inequalities satisfied by the quantities of information of Fisher and Shannon. Inf. and Control 1959, 2, 101–112. [Google Scholar] [CrossRef]
- Dembo, A.; Cover, T. Information theoretic inequalities. IEEE Trans. Inf. Th. 1991, 37, 1501–1518. [Google Scholar] [CrossRef]
- Maasen, H.; Uffink, J.B.M. Generalized Entropic Uncertainty Relations. Phys. Rev. Lett. 1988, 60, 1103–1106. [Google Scholar] [CrossRef] [PubMed]
- Blankenbecler, R.; Partovi, M.H. Uncertainty, entropy, and the statistical mechanics of microscopic systems. Phys. Rev. Lett. 1985, 54, 373–376. [Google Scholar] [CrossRef] [PubMed]
- Sa´nchez-Ruiz, J. Asymptotic formula for the quantum entropy of position in energy eigenstates. Phys. Lett. 1997, A 226, 7–13. [Google Scholar]
- Halliwell, J.J. Quantum-mechanical histories and the uncertainty principle: Information-theoretic inequalities. Phys. Rev. 1993, D 48, 2739–2752. [Google Scholar] [CrossRef] [Green Version]
- Gadre, S.R.; et al. Some novel characteristics of atomic information entropies. Phys. Rev. 1985, A 32, 2602–2606. [Google Scholar] [CrossRef]
- Yan˜ez, R.J.; Van Assche, W.; Dehesa, J.S. Position and information entropies of the D-dimensional harmonic oscillator and hydrogen atom. Phys. Rev. 1994, A 50, 3065–3079. [Google Scholar]
- Yan˜ez, R.J.; et al. Entropic integrals of hyperspherical harmonics and spatial entropy of D-dimensional central potentials. J. Math. Phys. 1999, 40, 5675–5686. [Google Scholar]
- Buyarov, V.; et al. Computation of the entropy of polynomials orthogonal on an interval. SIAM J. Sci. Comp. to appear (2004), also math.NA/0310238. [CrossRef]
- Majernik, V.; Opatrny´, T. Entropic uncertainty relations for a quantum oscillator. J. Phys. A: Math. Gen. 1996, 29, 2187–2197. [Google Scholar] [CrossRef]
- Majernik, V.; Richterek, L. Entropic uncertainty relations for the infinite well. J. Phys. A: Math. Gen. 1997, 30, L49–L54. [Google Scholar] [CrossRef]
- Massen, S.E.; Panos, C.P. Universal property of the information entropy in atoms, nuclei and atomic clusters. Phys. Lett. 1998, A 246, 530–532. [Google Scholar] [CrossRef]
- Massen, S.E.; et al. Universal property of information entropy in fermionic and bosonic systems. Phys. Lett. 2002, A 299, 131–135. [Google Scholar] [CrossRef]
- Massen, S.E. Application of information entropy to nuclei. Phys. Rev. 2003, C 67, 014314. [Google Scholar] [CrossRef]
- Coffey, M.W. Asymtotic relation for the quantum entropy of momentum in energy eigenstates. Phuys. Lett. 2004, A 324, 446–449. [Google Scholar] [CrossRef]
- Coffey, M.W. Semiclassical position entropy for hydrogen-like atoms. J. Phys. A: Math. Gen. 2003, 36, 7441–7448. [Google Scholar] [CrossRef]
- Dunkel, J.; Trigger, S.A. Time-dependent entropy of simple quantum model systems. Phys. Rev. 2005, A 71, 052102. [Google Scholar] [CrossRef] [Green Version]
- Santhanam, M.S. Entropic uncertainty relations for the ground state of a coupled sysytem. Phys. Rev. 2004, A 69, 042301. [Google Scholar] [CrossRef]
- Balian, R. Random matrices and information theory. Nuovo Cim. 1968, B 57, 183–103. [Google Scholar] [CrossRef]
- Werner, S.A.; Rauch, H. Neutron interferometry: Lessons in Experimental Quantum Physics; Oxford University Press: Oxford, 2000. [Google Scholar]
- Zeilinger, A.; et al. Single- and double-slit diffraction of neutrons. Rev. Mod. Phys. 1988, 60, 1067–1073. [Google Scholar] [CrossRef]
- Caves, C.M.; Fuchs, C. Quantum information: how much information in a state vector? Ann. Israel Phys. Soc. 1996, 12, 226–237. [Google Scholar]
- Newton, R.G. What is a state in quantum mechanics? Am. J. Phys. 2004, 72, 348–350. [Google Scholar] [CrossRef]
- Mackey, M.C. The dynamic origin of increasing entropy. Rev. Mod. Phys. 1989, 61, 981–1015. [Google Scholar] [CrossRef]
- Lasota, A.; Mackey, M.C. Chaos, Fractals and Noise; Springer-Verlag: Berlin, 1994. [Google Scholar]
- Berndl, K.; et al. On the global existence of Bohmian mechanics. Commun. Math. Phys. 1995, 173, 647–673. [Google Scholar] [CrossRef]
- Nelson, E. Dynamical Theories of the Brownian Motion; Princeton University Press: Princeton, 1967. [Google Scholar]
- Carlen, E. Conservative diffusions. Commun. Math. Phys. 1984, 94, 293–315. [Google Scholar] [CrossRef]
- Eberle, A. Uniqueness and Non-uniqueness of Semigroups Generated by Singular Diffusion Operators; LNM vol. 1718, Springer-Verlag: Berlin, 2000. [Google Scholar]
- Garbaczewski, P. Perturbations of noise: Origins of isothermal flows. Phys. Rev. E 1999, 59, 1498–1511. [Google Scholar] [CrossRef]
- Garbaczewski, P.; Olkiewicz, R. Feynman-Kac kernels in Markovian representations of the Schrödinger interpolating dynamics. J. Math. Phys. 1996, 37, 732–751. [Google Scholar] [CrossRef]
- Ambegaokar, V.; Clerk, A. Entropy and time. Am. J. Phys. 1999, 67, 1068–1073. [Google Scholar] [CrossRef] [Green Version]
- Tre¸bicki, J.; Sobczyk, K. Maximum entropy principle and non-stationary distributions of stochastic systems. Probab. Eng. Mechanics 1996, 11, 169–178. [Google Scholar]
- Huang, K. Statistical Mechanics; Wiley: New York, 1987. [Google Scholar]
- Cercignani, C. Theory and Application of the Boltzmann Equation; Scottish Academic Press: Edinburgh, 1975. [Google Scholar]
- Daems, D.; Nicolis, G. Entropy production and phase space volume contraction. Phys. Rev. E 1999, 59, 4000–4006. [Google Scholar] [CrossRef]
- Dorfman, J.R. An Introduction to Chaos in Nonequilibrium Statistical Physics; Cambridge Univ. Press: Cambridge, 1999. [Google Scholar]
- Gaspard, P. Chaos, Scattering and Statistical Mechanics; Cambridge Univ. Press: Cambridge, 1998. [Google Scholar]
- Deco, G.; et al. Determining the information flow of dynamical systems from continuous probability distributions. Phys. Rev. Lett. 1997, 78, 2345–2348. [Google Scholar] [CrossRef]
- Bologna, M.; et al. Trajectory versus probability density entropy. Phys. Rev. E 2001, E 64, 016223. [Google Scholar] [CrossRef] [PubMed]
- Bag, C.C.; et al. Noise properties of stochastic processes and entropy production. Phys. Rev. 2001, E 64, 026110. [Google Scholar] [CrossRef] [PubMed]
- Bag, B.C. Upper bound for the time derivative of entropy for nonequilibrium stochastic processes. Phys. Rev. 2002, E 65, 046118. [Google Scholar] [CrossRef] [PubMed]
- Hatano, T.; Sasa, S. Steady-State Thermodynamics of Langevin Systems. Phys. Rev. Lett. 2001, 86, 3463–3466. [Google Scholar] [CrossRef] [PubMed]
- Qian, H. Mesoscopic nonequilibrium thermodynamics of single macromolecules and dynamic entropy-energy compensation. Phys. Rev. 2001, E 65, 016102. [Google Scholar] [CrossRef] [PubMed]
- Jiang, D.-Q.; Qian, M.; Qian, M.-P. Mathematical theory of nonequilibrium steady states; LNM vol. 1833, Springer-Verlag: Berlin, 2004. [Google Scholar]
- Qian, H.; Qian, M.; Tang, X. Thermodynamics of the general diffusion process: time-reversibility and entropy production. J. Stat. Phys. 2002, 107, 1129–1141. [Google Scholar] [CrossRef]
- Ruelle, D. Positivity of entropy production in nonequilibrium statistical mechanics. J. Stat. Phys. 1996, 85, 1–23. [Google Scholar] [CrossRef]
- Munakata, T.; Igarashi, A.; Shiotani, T. Entropy and entropy production in simple stochastic models. Phys. Rev. 1998, E 57, 1403–1409. [Google Scholar]
- Tribus, M.; Rossi, R. On the Kullback information measure as a basis for information theory: Comments on a proposal by Hobson and Chang. J. Stat. Phys. 1973, 9, 331–338. [Google Scholar] [CrossRef]
- Smith, J.D.H. Some observations on the concepts of information-theoretic entropy and randomness. Entropy 2001, 3, 1–11. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Stochastic problems in physics and astronomy. Rev. Mod. Phys. 1943, 15, 1–89. [Google Scholar] [CrossRef]
- Hall, M.J.W. Universal geometric approach to uncertainty, entropy and infromation. Phys. Rev. 1999, A 59, 2602–2615. [Google Scholar] [CrossRef]
- Pipek, J.; Varga, I. Universal classification scheme for the spatial-localization properties of one-particle states in finite d-dimensional systems. Phys. Rev. A 1992, A 46, 3148–3163. [Google Scholar] [CrossRef] [PubMed]
- Varga, I.; Pipek, J. Rényi entropies characterizing the shape and the extension of the phase-space representation of quantum wave functions in disordered systems. Phys. Rev. 2003, E 68, 026202. [Google Scholar] [CrossRef] [PubMed]
- McClendon, M.; Rabitz, H. Numerical simulations in stochastic mechanics. Phys. Rev. 1988, A 37, 3479–3492. [Google Scholar] [CrossRef]
- Garbaczewski, P. Signatures of randomness in quantum spectra. Acta Phys. Pol. 2002, A 33, 1001–1024. [Google Scholar]
- Hu, B.; et al. Quantum chaos of a kicked particle in an infinite potential well. Phys. Rev. Lett. 1999, 82, 4224–4227. [Google Scholar] [CrossRef]
- Kullback, S. Information Theory and Statistics; Wiley: NY, 1959. [Google Scholar]
- Cramér, H. Mathematical methods of statistics; Princeton University Press: Princeton, 1946. [Google Scholar]
- Hall, M.J.W. Exact uncertainty relations. Phys. Rev. 2001, A 64, 052103. [Google Scholar] [CrossRef]
- Garbaczewski, P. Stochastic models of exotic transport. Physica 2000, A 285, 187–198. [Google Scholar] [CrossRef]
- Carlen, E.A. Superadditivity of Fisher’s information and logarithmic Sobolev inequalities. J. Funct. Anal. 1991, 101, 194–211. [Google Scholar] [CrossRef] [Green Version]
- Frieden, B.R.; Sofer, B.H. Lagrangians of physics and the game of Fisher-information transfer. Phys. Rev. 1995, E 52, 2274–2286. [Google Scholar] [CrossRef]
- Catalan, R.G.; Garay, J.; Lopez-Ruiz, R. Features of the extension of a statistical measure of complexity to continuous systems. Phys. Rev. 2002, E 66, 011102. [Google Scholar] [CrossRef] [PubMed]
- Risken, H. The Fokker-Planck Equation; Springer-Verlag: Berlin, 1989. [Google Scholar]
- Hasegawa, H. Thermodynamic properties of non-equilibrium states subject to Fokker-Planck equations. Progr. Theor. Phys. 1977, 57, 1523–1537. [Google Scholar] [CrossRef]
- Vilar, J.M.G.; Rubi, J.M. Thermodynamics ”beyond” local equilibrium. Proc. Nat. Acad. Sci. (NY) 2001, 98, 11081–11084. [Google Scholar] [CrossRef] [PubMed]
- Kurchan, J. Fluctuation theorem for stochastic dynamics. J. Phys. A: Math. Gen. 1998, 31, 3719–3729. [Google Scholar] [CrossRef]
- Mackey, M.C.; Tyran-Kamin´ska, M. Effects of noise on entropy evolution. 2005; arXiv.org preprint cond-mat/0501092. [Google Scholar]
- Mackey, M.C.; Tyran-Kaminńska, M. Temporal behavior of the conditional and Gibbs entropies. 2005; arXiv.org preprint cond-mat/0509649. [Google Scholar]
- Czopnik, R.; Garbaczewski, P. Frictionless Random Dynamics: Hydrodynamical Formalism. Physica 2003, A 317, 449–471. [Google Scholar] [CrossRef]
- Fortet, R. Résolution d’un systéme d’équations de M. Schrödingeer. J. Math. Pures Appl. 1040, 9, 83. [Google Scholar]
- Blanchard, Ph.; Garbaczewski, P. Non-negative Feynman-Kac kernels in Schrödinger’s interpolation problem. J. Math. Phys. 1997, 38, 1–15. [Google Scholar] [CrossRef]
- Jaynes, E.T. Violations of Boltzmann’s H Theorem in Real Gases. Phys. Rev. 1971, A 4, 747–750. [Google Scholar] [CrossRef]
- Voigt, J. Stochastic operators, Information and Entropy. Commun. Math. Phys. 1981, 81, 31–38. [Google Scholar] [CrossRef]
- Voigt, J. The H-Theorem for Boltzmann type equations. J. Reine Angew. Math 1981, 326, 198–213. [Google Scholar]
- Toscani, G. Kinetic approach to the asymptotic behaviour of the solution to diffusion equation. Rend. di Matematica 1996, Serie VII 16, 329–346. [Google Scholar]
- Bobylev, A.V.; Toscani, G. On the generalization of the Boltzmann H-theorem for a spatially homogeneous Maxwell gas. J. Math. Phys. 1992, 33, 2578–2586. [Google Scholar] [CrossRef]
- Arnold, A.; et al. On convex Sobolev inequalities and the rate of convergence to equilibrium for Fokker-Planck type equations. Comm. Partial Diff. Equations 2001, 26, 43–100. [Google Scholar] [CrossRef]
© 2005 by MDPI (http://www.mdpi.org). Reproduction for noncommercial purposes permitted.
Share and Cite
Garbaczewski, P. Differential entropy and time. Entropy 2005, 7, 253-299. https://0-doi-org.brum.beds.ac.uk/10.3390/e7040253
Garbaczewski P. Differential entropy and time. Entropy. 2005; 7(4):253-299. https://0-doi-org.brum.beds.ac.uk/10.3390/e7040253
Chicago/Turabian StyleGarbaczewski, Piotr. 2005. "Differential entropy and time" Entropy 7, no. 4: 253-299. https://0-doi-org.brum.beds.ac.uk/10.3390/e7040253