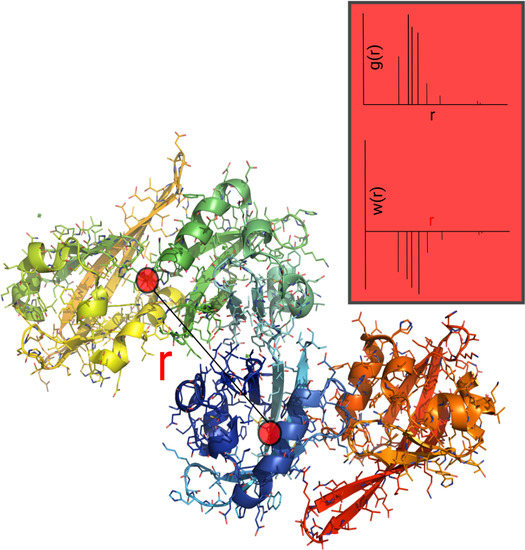
Enriched Conformational Sampling of DNA and Proteins with a Hybrid Hamiltonian Derived from the Protein Data Bank
Abstract
:1. Introduction
2. Methods
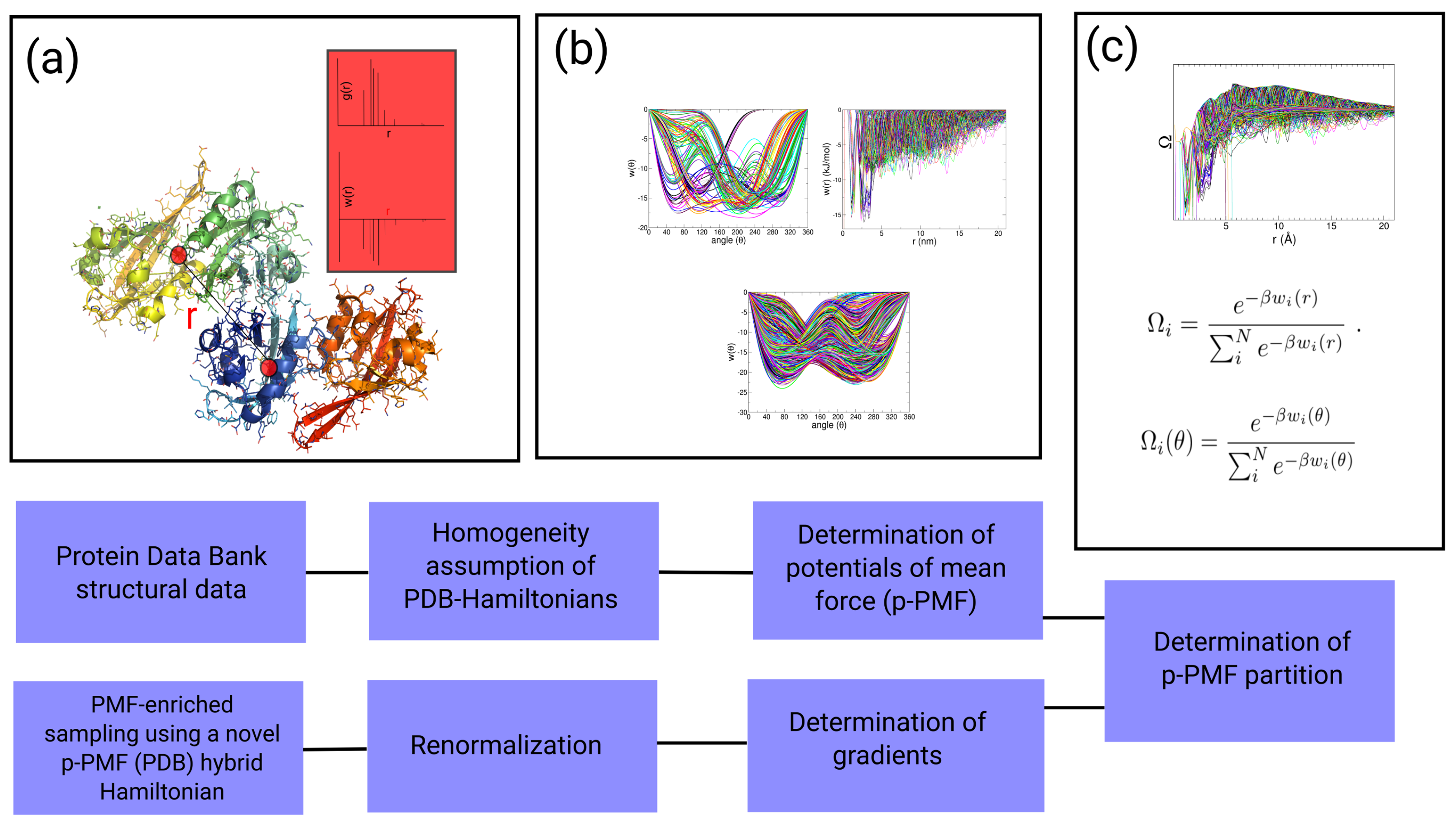
2.1. Theory
2.2. Associated Error
2.3. Renormalization of the Hamiltonian
2.4. Auxiliary p-PMF from the PDB
2.5. Statistical Partition of p-PMF for the Generation of Auxiliary Hamiltonian: PMF-Enriched Sampling
2.6. Propagator
2.7. Shift in the Free Energy Partition
2.8. Coupling Parameters and
2.9. Algorithm
- Read p-PMF data and for relevant pairs of atoms and sequence.
- Start loop over MD-steps.
- -
- Measure coordinates and .
- -
- Determine values , .
- -
- Determine partitions and for and .
- -
- Determine gradients.
- -
- Add bias after renormalization to the unbiased gradient.
2.10. Path-Sampling Method
2.11. Program and System Preparation
2.11.1. PDB Data Collection and Data Processing
2.11.2. System Preparation and Simulation Parameters
2.11.3. TrpCage
2.11.4. Dickerson–Drew DNA Dodecamer
2.11.5. Assignment of DNA Conformers with the Structural Alphabet for DNA
2.11.6. Kinetic Analysis and Analysis of Free Energy Partitions of DNA
3. Results and Discussion
3.1. Dialanine
3.2. Penta-Alanine with Ser Mutations
3.3. Simulations of TrpCage
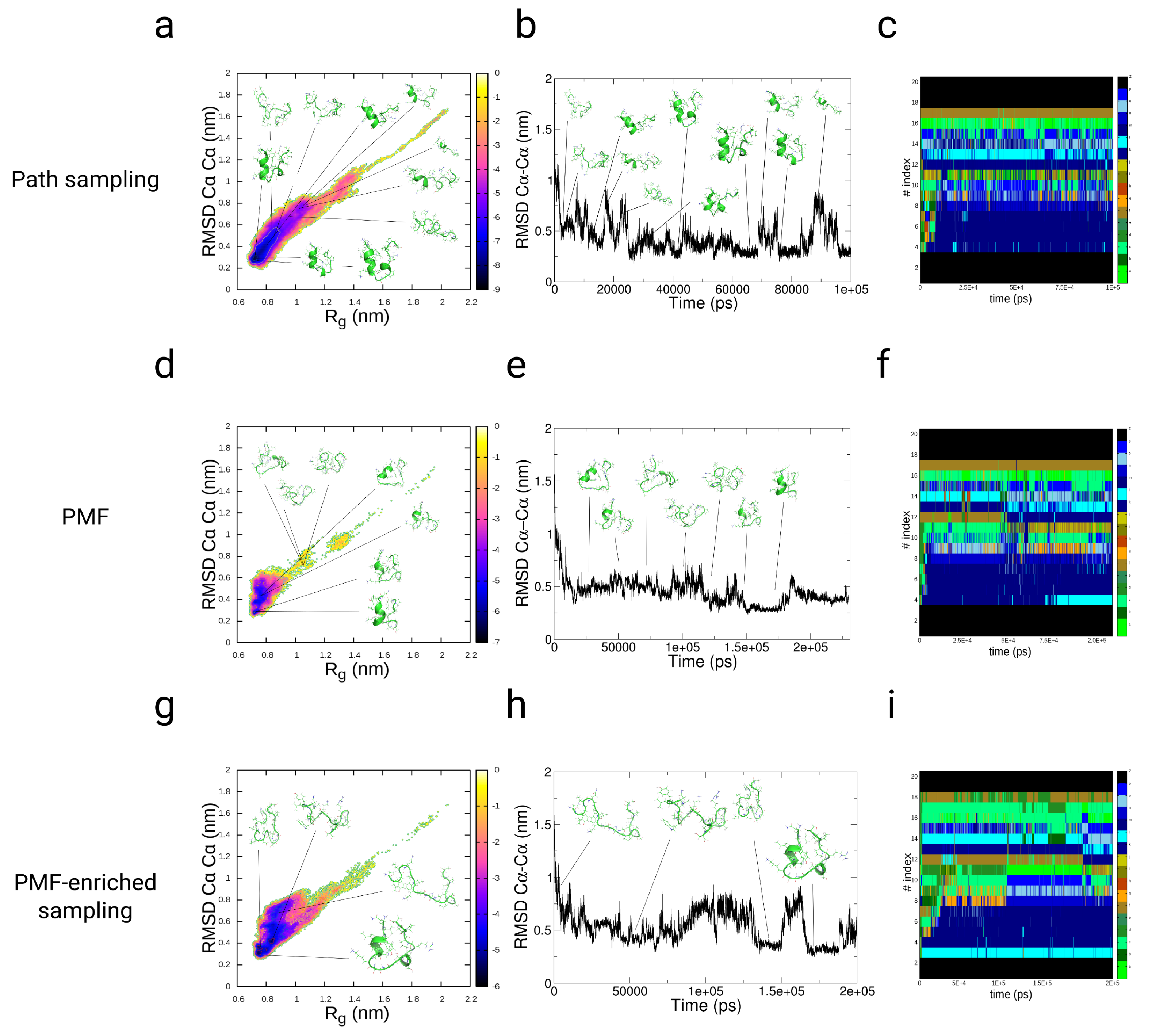
3.3.1. Path-Sampling Simulations
3.3.2. Folding of TrpCage: Direct p-PMF Simulations without Partitions and
3.3.3. Folding of TrpCage: PMF-Enriched Simulations
3.3.4. Discussion
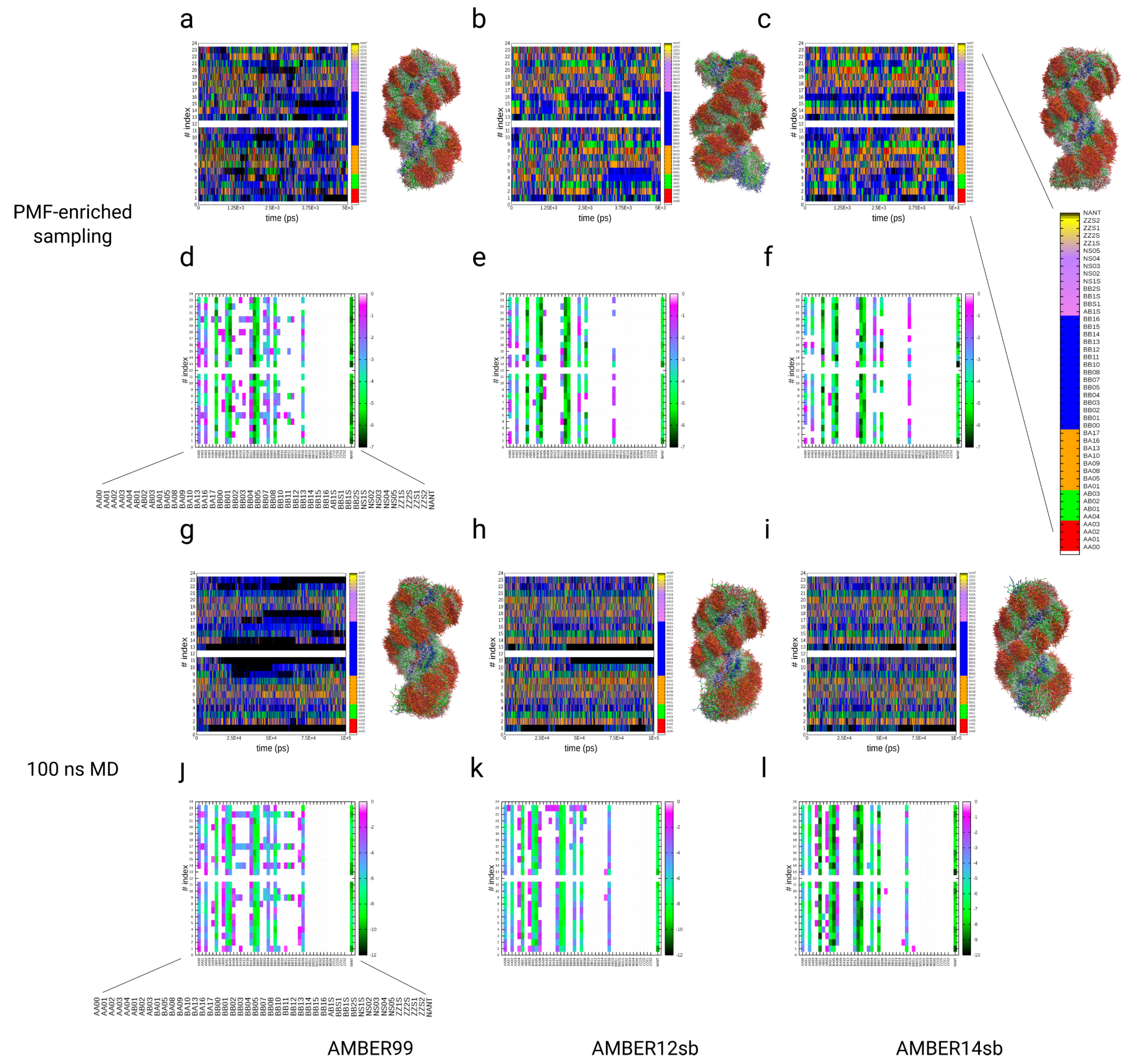
3.4. Simulations of the Dickerson–Drew DNA Dodecamer
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Karplus, M.; Kuriyan, J. Molecular dynamics and protein function. Proc. Natl. Acad. Sci. USA 2005, 102, 6679–6685. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karplus, M.; McCammon, J.A. Molecular dynamics simulations of biomolecules. Nat. Struct. Biol. 2002, 9, 646–652. [Google Scholar] [CrossRef] [PubMed]
- Durrant, J.D.; McCammon, J.A. Molecular dynamics simulations and drug discovery. BMC Biol. 2011, 9, 71. [Google Scholar] [CrossRef] [PubMed]
- Mackerell, A.D.; Feig, M.; Brooks, C.L., 3rd. Extending the treatment of backbone energetics in protein force fields: Limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comput. Chem. 2004, 25, 1400–1415. [Google Scholar] [CrossRef] [PubMed]
- Elber, R. Perspective: Computer simulations of long time dynamics. J. Chem. Phys. 2016, 144, 060901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hornak, V.; Abel, R.; Okur, A.; Strockbine, B.; Roitberg, A.; Simmerling, C. Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins Struct. Funct. Bioinf. 2006, 65, 712–725. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maier, J.; Martinez, C.; Kasavajhala, K.; Wickstrom, L.; Hauser, K.; Simmerling, C. ff14SB: improving the accuracy of protein side chain and backbone parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Case, D.; Cheatham, T.; Darden, T.; Gohlke, H.; Luo, R.; Merz, K.; Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [PubMed]
- Brooks, B.; Brooks, C.; MacKerell, A.; Nilsson, L.; Petrella, R.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S.; et al. CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- MacKerell, A.D.; Bashford, D.; Dunbrack, R.L.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; Joseph-McCarthy, D.; et al. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef] [Green Version]
- Jorgensen, W.L.; Tirado-Rives, J. The OPLS [optimized potentials for liquid simulations] potential functions for proteins, energy minimizations for crystals of cyclic peptides and crambin. J. Am. Chem. Soc. 1988, 110, 1657–1666. [Google Scholar] [CrossRef] [PubMed]
- Allen, M.; Tildesley, D. Computer Simulation of Liquids; Clarendon Pr: Oxford, UK, 1987. [Google Scholar]
- Laio, A.; Parrinello, M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sørensen, M.R.; Voter, A.F. Temperature-accelerated dynamics for simulation of infrequent events. J. Chem. Phys. 2000, 112, 9599. [Google Scholar] [CrossRef]
- Montalenti, F.; Voter, A.F. Exploiting past visits or minimum-barrier knowledge to gain further boost in the temperature-accelerated dynamics method. J. Chem. Phys. 2002, 116, 4819. [Google Scholar] [CrossRef]
- Olender, R.; Elber, R. Exact milestoning. J. Chem. Phys. 1996, 105, 9299–9315. [Google Scholar] [CrossRef]
- Ma, Q.; Izaguirre, J.A. New Algorithms for Macromolecular Simulation. Multiscale Model. Simul. 2003, 2, 1–21. [Google Scholar] [CrossRef]
- Leimkuhler, B.; Margul, D.T.; Tuckerman, M.E. Molecular dynamics based enhanced sampling of collective variables with very large time steps. Mol. Phys. 2013, 111, 3579–3594. [Google Scholar] [CrossRef]
- Bello-Rivas, J.M.; Elber, R. Exact milestoning. J. Chem. Phys. 2015, 142, 094102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schug, A.; Wenzel, W.; Hansmann, U.H.E. Energy landscape paving simulations of the trp-cage protein. J. Chem. Phys. 2005, 122, 194711. [Google Scholar] [CrossRef] [PubMed]
- Schug, A.; Herges, T.; Wenzel, W. Reproducible Protein Folding with the Stochastic Tunneling Method. Phys. Rev. Lett. 2003, 91, 158102. [Google Scholar] [CrossRef] [PubMed]
- Hamelberg, D.; Mongan, J.; McCammon, J.A. Accelerated molecular dynamics: a promising and efficient simulation method for biomolecules. J. Chem. Phys. 2004, 120, 11919. [Google Scholar] [CrossRef] [PubMed]
- Smiatek, J.; Heuer, A. Calculation of free energy landscapes: A histogram reweighted metadynamics approach. J. Comput. Chem. 2011, 32, 2084–2096. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huber, T.; Torda, A.E.; van Gunsteren, W.F. Local elevation: A method for improving the searching properties of molecular dynamics simulation. J. Comput. Aided Mol. Des. 1994, 8, 695–708. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pfaendtner, J.; Bonomi, M. Efficient Sampling of High-Dimensional Free-Energy Landscapes with Parallel Bias Metadynamics. J. Chem. Theory Comput. 2015, 11, 5062–5067. [Google Scholar] [CrossRef] [PubMed]
- Brenner, P.; Sweet, C.R.; VonHandorf, D.; Izaguirre, J.A. Accelerating the replica exchange method through an efficient all-pairs exchange. J. Chem. Phys. 2007, 126, 074103. [Google Scholar] [CrossRef] [PubMed]
- Sugita, Y.; Okamoto, Y. Replica-exchange multicanonical algorithm and multicanonical replica-exchange method for simulating systems with rough energy landscape. Chem. Phys. Lett. 2000, 329, 261–270. [Google Scholar] [CrossRef] [Green Version]
- Mitsutake, A.; Sugita, Y.; Okamoto, Y. Replica-exchange multicanonical and multicanonical replica-exchange Monte Carlo simulations of peptides. I. Formulation and benchmark test. J. Chem. Phys. 2003, 118, 6664. [Google Scholar] [CrossRef]
- Mitsutake, A.; Sugita, Y.; Okamoto, Y. Replica-exchange multicanonical and multicanonical replica-exchange Monte Carlo simulations of peptides. II. Application to a more complex system. J. Chem. Phys. 2003, 118, 6676. [Google Scholar] [CrossRef]
- Calvo, F.; Doyle, J.P.K. Entropic tempering: A method for overcoming quasiergodicity in simulation. Phys. Rev. E 2000, 63, 010902. [Google Scholar] [CrossRef]
- Faller, R.; Yan, Q.; de Pablo, J.J. Multicanonical parallel tempering. J. Chem. Phys. 2002, 116, 5419. [Google Scholar] [CrossRef]
- Fukunishi, H.; Watanabe, O.; Takada, S. On the Hamiltonian replica exchange method for efficient sampling of biomolecular systems: Application to protein structure prediction. J. Chem. Phys. 2002, 116, 9058. [Google Scholar] [CrossRef]
- Whitfield, T.W.; Bu, L.; Straub, J.E. Generalized parallel sampling. Phys. A 2002, 305, 157–171. [Google Scholar] [CrossRef]
- Jang, S.; Shin, S.; Pak, Y. Replica-exchange method using the generalized effective potential. Phys. Rev. Lett. 2003, 91, 058305. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Kim, B.; Friesner, R.A.; Berne, B.J. Replica exchange with solute tempering: A method for sampling biological systems in explicit water. Proc. Natl. Acad. Sci. USA 2005, 102, 13749–13754. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, P.; Huang, X.; Zhou, R.; Berne, B.J. Hydrophobic aided replica exchange: an efficient algorithm for protein folding in explict solvent. J. Phys. Chem. B 2006, 110, 19018–19022. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.; Cui, G.; Hornak, V.; Simmerling, C. Modified Replica Exchange Simulation Methods for Local Structure Refinement. J. Phys. Chem. B 2005, 109, 8220–8230. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lyman, E.; Ytreberg, M.; Zuckerman, D.M. Resolution Exchange Simulation. Phys. Rev. Lett. 2006, 96, 028105. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Voth, G.A. Smart resolution replica exchange: An efficient algorithm for exploring complex energy landscapes. J. Chem. Phys. 2007, 126, 045106. [Google Scholar] [CrossRef] [PubMed]
- Calvo, F. All-exchanges parallel tempering. J. Chem. Phys. 2005, 123, 124106. [Google Scholar] [CrossRef] [PubMed]
- Rick, S.W. Replica exchange with dynamical scaling. J. Chem. Phys. 2007, 126, 054102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kamberaj, H.; van der Vaart, A. Multipe scaling replica exchange for the conformational sampling of biomolecules in explicit water. J. Chem. Phys. 2007, 127, 234102. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Ma, J. Simulation via direct computation of partition functions. Phys. Rev. E 2007, 76, 036708. [Google Scholar] [CrossRef] [PubMed]
- Trebst, S.; Troyer, M.; Hansmann, U.H.E. Optimized parallel tempering simulations of proteins. J. Chem. Phys. 2006, 124, 174903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ballard, A.J.; Jarzynski, C. Replica exchange with nonequilibrium switches. Proc. Natl. Acad. Sci. USA 2009, 106, 12224–12229. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kar, P.; Nadler, W.; Hansmann, U.H.E. Microcanonical replica exchange molecular dynamics simulation of proteins. Phys. Rev. E 2009, 80, 056703. [Google Scholar] [CrossRef] [PubMed]
- Shea, J.E.; Onuchic, J.; Brooks, C. Exploring the origins of topological frustration: Design of a minimally frustrated model of fragment B of protein A. Proc. Natl. Acad. Sci. USA 1999, 96, 12512–12517. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shea, J.E.; Brooks, C.L., III. From folding theories to folding proteins: a review and assessment of simulation studies of protein folding and unfolding. Annu. Phys. Chem. Rev. 2001, 52, 499–535. [Google Scholar] [CrossRef] [PubMed]
- Kong, X.; Brooks, C.L., 3rd. λ-dynamics: A new approach to free energy calculations. J. Chem. Phys. 1996, 105, 2414. [Google Scholar] [CrossRef]
- Knight, J.L.; Brooks, C.L., 3rd. Multisite λ Dynamics for Simulated Structure–Activity Relationship Studies. J. Chem. Theory Comput. 2011, 7, 2728–2739. [Google Scholar] [CrossRef] [PubMed]
- Comer, J.; Gumbart, J.C.; Hénin, J.; Lelièvre, T.; Pohorille, A.; Chipot, C. The Adaptive Biasing Force Method: Everything You Always Wanted to Know but Were Afraid to Ask. J. Phys. Chem. B 2015, 119, 1129–1151. [Google Scholar] [CrossRef] [PubMed]
- Morris-Andrews, A.; Rottler, J.; Plotkin, S.S. A systematically coarse-grained model for DNA and its predictions for persistence length, stacking, twist, and chirality. J. Chem. Phys. 2010, 132, 035105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ouldridge, T.E.; Louis, A.A.; Doyle, J.P.K. Structural, mechanical, and thermodynamic properties of a coarse-grained DNA model. J. Chem. Phys. 2011, 134, 085101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Naôme, A.; Laaksonen, A.; Vercauteren, D.P. A Solvent-Mediated Coarse-Grained Model of DNA Derived with the Systematic Newton Inversion Method. J. Chem. Theory Comput. 2014, 10, 3541–3549. [Google Scholar] [CrossRef] [PubMed]
- Takada, S. Coarse-grained molecular simulations of large biomolecules. Curr. Opin. Struct. Biol. 2012, 22, 130–137. [Google Scholar] [CrossRef] [PubMed]
- Kmiecik, S.; Gront, D.; Kolinski, M.; Wieteska, L.; Dawid, A.E.; Kolinski, A. Coarse-Grained Protein Models and Their Applications. Chem. Rev. 2016, 116, 7898–7936. [Google Scholar] [CrossRef] [PubMed]
- Morris-Andrews, A.; Brown, F.L.; Shea, J.E. A Coarse-Grained Model for Peptide Aggregation on a Membrane Surface. J. Phys. Chem. B 2014, 118, 8420–8432. [Google Scholar] [CrossRef] [PubMed]
- Monticelli, L.; Kandasamy, S.K.; Periole, X.; Larson, R.G.; Tieleman, D.P.; Marrink, S.J. The MARTINI Coarse-Grained Force Field: Extension to Proteins. J. Chem. Theory Comput. 2008, 4, 819–834. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marrink, S.J.; Tieleman, D.P. Perspective of the Martini Model. Chem. Soc. Rev. 2013, 42, 6801–6822. [Google Scholar] [CrossRef] [PubMed]
- Rose, P.W.; Prlić, A.; Bi, C.; Bluhm, W.F.; Christie, C.H.; Dutta, S.; Green, R.K.; Goodsell, D.S.; Westbrook, J.D.; Woo, J.; et al. The RCSB Protein Data Bank: views of structural biology for basic and applied research and education. Nucleic Acids Res. 2015, 43, D345–D356. [Google Scholar] [CrossRef] [PubMed]
- Watson, J.D.; Crick, F.H.C. Molecular Structure of Nucleic Acids: A Structure for Deoxyribose Nucleic Acid. Nature 1953, 171, 737–738. [Google Scholar] [CrossRef] [PubMed]
- Svozil, D.; Kalina, J.; Omelka, M.; Schneider, B. DNA conformations and their sequence preferences. Nucleic Acids Res. 2008, 36, 3690–3706. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schneider, B.; Božíková, P.; Čech, P.; Svozil, D.; Černý, J. A DNA Structural Alphabet Distinguishes Structural Features of DNA Bound to Regulatory Proteins and in the Nucleosome Core Particle. Genes (Basel) 2017, 8, 278. [Google Scholar] [CrossRef] [PubMed]
- Schneider, B.; Božíková, P.; Nečasová, I.; Čech, P.; Svozil, D.; Černý, J. A DNA structural alphabet provides new insight into DNA flexibility. Acta Cryst. 2018, D74, 52–64. [Google Scholar] [CrossRef] [PubMed]
- Fersenfeld, G.; Davies, D.; Rich, A. Formation of a three-stranded polynucleotide molecule. J. Am. Chem. Soc. 1957, 79, 2023–2024. [Google Scholar] [CrossRef]
- Morgan, A.R. Model for DNA Replication by Kornberg’s DNA Polymerase. Nature 1970, 227, 1310–1313. [Google Scholar] [CrossRef] [PubMed]
- Beerman, T.A.; Lebowitz, J. Further analysis of the altered secondary structure of superhelical. J. Mol. Biol. 1973, 79, 451–470. [Google Scholar] [CrossRef]
- Van de Sande, J.H.; Ramsing, N.B.; Germann, M.W.; Elhorst, W.; Kalisch, B.W.; Kitzing, E.; Pon, R.T.; Clegg, R.C.; Jovin, T.M. Parallel stranded DNA. Science 1988, 241, 551–557. [Google Scholar] [CrossRef] [PubMed]
- Neidigh, J.W.; Fesinmeyer, R.M. Designing a 20-residue protei. Nat. Struct. Biol. 2002, 9, 425–430. [Google Scholar] [CrossRef] [PubMed]
- Drew, H.R.; Wing, R.M.; Takano, T.; Broka, C.; Tanaka, S.; Itakura, K.; Dickerson, R.E. Structure of a B-DNA dodecamer: conformation and dynamics. Proc. Natl. Acad. Sci. USA 1981, 78, 2179–2183. [Google Scholar] [CrossRef] [PubMed]
- Reith, D.; Pütz, M.; Müller-Plathe, F. Deriving effective mesoscale potentials from atomistic simulations. J. Comput. Chem. 2003, 24, 1624–1636. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chandler, D. Introduction to Modern Statistical Mechanics; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Mullinax, J.W.; Noid, W.G. Recovering physical potentials from a model protein databank. Proc. Natl. Acad. Sci. USA 2010, 107, 19867–19872. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alm, E.; Baker, D. Prediction of protein-folding mechanisms from free-energy landscapes derived from native structures. Proc. Natl. Acad. Sci. USA 1999, 96, 11305–11310. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liwo, A.; Olziej, S.; Pincus, M.R.; Wawak, R.J.; Rackowsky, S.; Scheraga, H.A. A united-residue force field for off-lattice protein-structure simulations. I. Functional forms and parameters of long-range side-chain interaction potentials from protein crystal data. J. Comput. Chem. 1997, 18, 849–873. [Google Scholar] [CrossRef]
- Kržišnik, K.; Urbic, T. Amino Acid Correlation Functions in Protein Structures. Acta Chim. Slov. 2015, 62, 574–581. [Google Scholar] [PubMed]
- Rackovsky, S.; Scheraga, H. Hydrophobicity, hydrophilicity, and the radial and oricntational distributions of residues in native protein. Proc. Natl. Acad. Sci. USA 1977, 74, 5248–5251. [Google Scholar] [CrossRef] [PubMed]
- Peter, E.K. Adaptive enhanced sampling with a path-variable for the simulation of protein folding and aggregation. J. Chem. Phys. 2017, 147, 214902. [Google Scholar] [CrossRef] [PubMed]
- Peter, E.K.; Shea, J.E. An adaptive bias-hybrid MD/kMC algorithm for protein folding and aggregation. Phys. Chem. Chem. Phys. 2017, 19, 17373–17382. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.J.; Kremer, K. Comparative atomistic and coarse-grained study of water: what do we lose by coarse-graining? Eur. Phys. J. E Soft Matter 2009, 28, 221–229. [Google Scholar] [CrossRef] [PubMed]
- Yan, T.; Burnham, C.J.; Popolo, M.G.D.; Voth, G.A. Molecular Dynamics Simulation of Ionic Liquids: The Effect of Electronic Polarizability. J. Phys. Chem. B 2004, 108, 11877–11881. [Google Scholar] [CrossRef]
- Best, R.B.; Buchete, N.V.; Hummer, G. Are current molecular dynamics force fields too helical? Biophys. J. 2008, 95, L07–L09. [Google Scholar] [CrossRef] [PubMed]
- Chen, A.A.; Pappu, R.V. Parameters of Monovalent Ions in the AMBER-99 Forcefield: Assessment of Inaccuracies and Proposed Improvements. J. Phys. Chem. B 2007, 111, 11884–11887. [Google Scholar] [CrossRef] [PubMed]
- Showalter, S.A.; Brüschweiler, R. Validation of Molecular Dynamics Simulations of Biomolecules Using NMR Spin Relaxation as Benchmarks: Application to the AMBER99SB Force Field. J. Chem. Theory Comput. 2007, 3, 961–975. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Klepeis, J.L.; Lindorff-Larsen, K.; Dror, R.O.; Shaw, D.E. Long-timescale molecular dynamics simulations of protein structure and function. Curr. Opin. Struct. Biol. 2009, 19, 120–127. [Google Scholar] [CrossRef] [PubMed]
- Piana, S.; Klepeis, J.L.; Shaw, D.E. Assessing the accuracy of physical models used in protein-folding simulations: quantitative evidence from long molecular dynamics simulations. Curr. Opin. Struct. Biol. 2014, 24, 98–105. [Google Scholar] [CrossRef] [PubMed]
- Piana, S.; Lindorff-Larsen, K.; Shaw, D.E. How robust are protein folding simulations with respect to force field parameterization? Biophys. J. 2011, 100, L47–L49. [Google Scholar] [CrossRef] [PubMed]
- Torrie, G.M.; Valleau, J.P. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Grubmüller, H. Predicting slow structural transitions in macromolecular systems: Conformational flooding. Phys. Rev. E 1995, 52, 2893. [Google Scholar] [CrossRef]
- Kleinert, H. Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 5th ed.; World Scientific: Singapore, 2009; pp. 1–1547. [Google Scholar]
- Feynman, R.; Hibbs, A.R. Quantum Mechanics and Path Integrals; MacGraw Hill Companies: New York, NY, USA, 1965. [Google Scholar]
- Barducci, A.; Bussi, G.; Parrinello, M. Well-Tempered Metadynamics: A Smoothly Converging and Tunable Free-Energy Method. Phys. Rev. Lett. 2008, 100, 020603. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD—Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Painter, J.; Merritt, E.A. mmLib Python toolkit for manipulating annotated structural models of biological macromolecules. J. Appl. Cryst. 2004, 37, 174–178. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef] [Green Version]
- Tobias, D.J.; Brooks, C.L., III. Conformational equilibrium in the alanine dipeptide in the gas phase and aqueous solution: A comparison of theoretical results. J. Phys. Chem. 1992, 96, 3864–3870. [Google Scholar] [CrossRef]
- Swope, W.C.; Pitera, J.W.; Suits, F.; Pitman, M.; Eleftheriou, M.; Fitch, B.G.; Germain, R.S.; Rayshubski, A.; Zhestkov, Y.; Zhou, R. Describing Protein Folding Kinetics by Molecular Dynamics Simulations. 2. Example Applications to Alanine Dipeptide and a β-Hairpin Peptide. J. Chem. Phys. B 2004, 108, 6582–6594. [Google Scholar] [CrossRef]
- Stelzl, L.S.; Hummer, G. Kinetics from Replica Exchange Molecular Dynamics Simulations. J. Chem. Theory Comput. 2017, 13, 3927–3935. [Google Scholar] [CrossRef] [PubMed]
- Tiwary, P.; Parrinello, M. From Metadynamics to Dynamics. Phys. Rev. Lett. 2013, 111, 230602. [Google Scholar] [CrossRef] [PubMed]
- Bolhuis, P.G.; Dellago, C.; Chandler, D. Reaction coordinates of biomolecular isomerization. Proc. Natl. Acad. Sci. USA 2000, 97, 5877. [Google Scholar] [CrossRef] [PubMed]
- De Bevern, A.G.; Etchebest, C.; Hazout, S. Bayesian probabilistic approach for predicting backbone structures in terms of protein blocks. Proteins 2000, 41, 271–287. [Google Scholar] [CrossRef] [Green Version]
- Culik, R.M.; Serrano, A.L.; Bunagan, M.R.; Gai, F. Achieving Secondary Structural Resolution in Kinetic Measurements of Protein Folding: A Case Study of the Folding Mechanism of Trp-cage. Angew. Chem. 2011, 123, 11076–11079. [Google Scholar] [CrossRef]
- Meuzelaar, H.; Marino, K.A.; Huerta-Viga, A.; Panman, M.R.; Smeenk, L.E.J.; Kettelarij, A.J.; van Maarseveen, P.T.; Bolhuis, P.G.; Woutersen, S. Folding Dynamics of the Trp-Cage Miniprotein: Evidence for a Native-Like Intermediate from Combined Time-Resolved Vibrational Spectroscopy and Molecular Dynamics Simulations. J. Phys. Chem. B 2013, 117, 11490–11501. [Google Scholar] [CrossRef] [PubMed]
- Juraszek, J.; Bolhuis, P.G. Sampling the multiple folding mechanisms of Trp-cage in explicit solvent. Proc. Natl. Acad. Sci. USA 2006, 103, 15859–15864. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Juraszek, J.; Bolhuis, P.G. Rate constant and reaction coordinate of Trp-cage folding in explict water. Biophys. J. 2008, 95, 4246–4257. [Google Scholar] [CrossRef] [PubMed]
- Marinelli, F.; Pietrucci, F.; Laio, A.; Piana, S. A Kinetic Model of Trp-Cage Folding from Multiple Biased Molecular Dynamics Simulations. PLoS Comput. Biol. 2009, 5, e1000452. [Google Scholar] [CrossRef] [PubMed]
- Snow, C.D.; Zagrovic, B.; Pande, V.S. The Trp Cage: Folding Kinetics and Unfolded State Topology via Molecular Dynamics Simulations. J. Am. Chem. Soc. 2002, 124, 14548–14549. [Google Scholar] [CrossRef]
- Ren, H.; Lai, Z.; Biggs, J.D.; Wang, J.; Mukamel, S. Two-dimensional stimulated resonance Raman spectroscopy study of the Trp-cage peptide folding. Phys. Chem. Chem. Phys. 2013, 15, 19457–19464. [Google Scholar] [CrossRef] [PubMed]
- Neuweiler, H.; Doose, S.; Sauer, M. A microscopic view of miniprotein folding: Enhanced folding efficiency through formation of an intermediate. Proc. Natl. Acad. Sci. USA 2005, 102, 16650–16655. [Google Scholar] [CrossRef] [PubMed]
- Qiu, L.; Pabit, S.A.; Roitberg, A.E.; Hagen, S.J. Smaller and Faster: The 20-Residue Trp-Cage Protein Folds in 4 μs. J. Am. Chem. Soc. 2002, 124, 12952–12953. [Google Scholar] [CrossRef]
- Juraszek, J.; Saladino, G.; van Erp, T.S.; Gervasio, F.L. Efficient Numerical Reconstruction of Protein Folding Kinetics with Partial Path Sampling and Pathlike Variables. Phys. Rev. Lett. 2013, 110, 108106. [Google Scholar] [CrossRef] [PubMed]
- Peter, E.K.; Shea, J.E. A hybrid MD-kMC algorithm for folding proteins in explicit solvent. Phys. Chem. Chem. Phys. 2014, 16, 6430–6440. [Google Scholar] [CrossRef] [PubMed]
- Peter, E.K.; Pivkin, I.V.; Shea, J.E. A kMC-MD method with generalized move-sets for the simulation of folding of α-helical and β-stranded peptides. J. Chem. Phys. 2015, 142, 144903. [Google Scholar] [CrossRef] [PubMed]





© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peter, E.K.; Černý, J. Enriched Conformational Sampling of DNA and Proteins with a Hybrid Hamiltonian Derived from the Protein Data Bank. Int. J. Mol. Sci. 2018, 19, 3405. https://0-doi-org.brum.beds.ac.uk/10.3390/ijms19113405
Peter EK, Černý J. Enriched Conformational Sampling of DNA and Proteins with a Hybrid Hamiltonian Derived from the Protein Data Bank. International Journal of Molecular Sciences. 2018; 19(11):3405. https://0-doi-org.brum.beds.ac.uk/10.3390/ijms19113405
Chicago/Turabian StylePeter, Emanuel K., and Jiří Černý. 2018. "Enriched Conformational Sampling of DNA and Proteins with a Hybrid Hamiltonian Derived from the Protein Data Bank" International Journal of Molecular Sciences 19, no. 11: 3405. https://0-doi-org.brum.beds.ac.uk/10.3390/ijms19113405