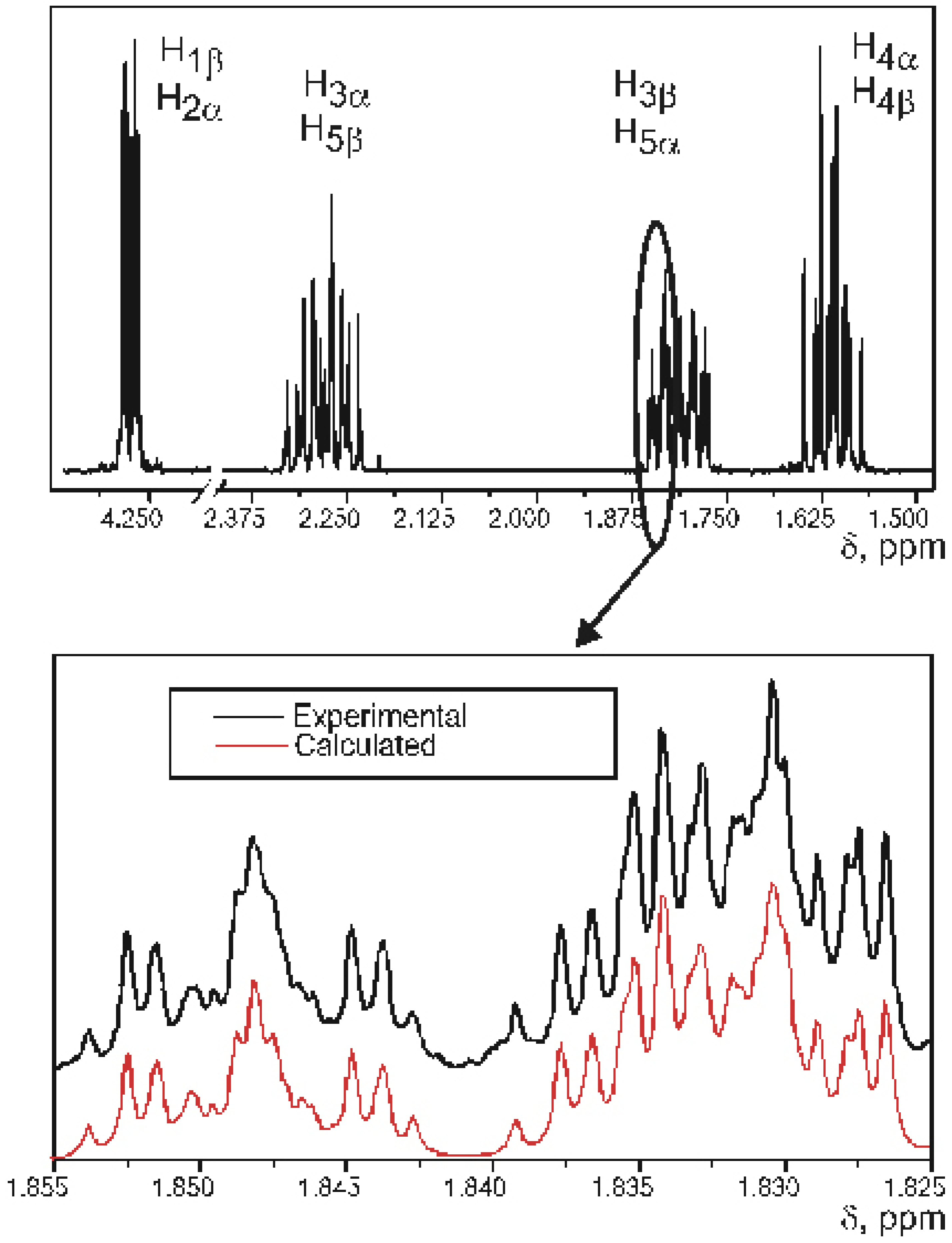
Introduction
Modern development of NMR is centered on new, more powerful, spectrometers, and multi-dimensional techniques, which aid greatly in analysis of complex first-order NMR systems [
1]. However, obtaining spin-spin coupling constants (SSCCs) from strongly coupled systems remains a non-trivial problem. Knowledge of SSCCs is vital for conformational analysis of organic molecules, but this problem hinders its experimental study even for systems as simple as cyclopentanes. To this day, there has been no experimental study of substituted cyclopentane pseudorotation in isotropic liquid phase, based on NMR data. Early attempts to analyse the spectra of these compounds [
2] produced limited information, which was insufficient for accurate conformational description.
The problem of complete analysis of tightly coupled NMR spin systems, i.e. determination of chemical shifts and SSCCs, has been addressed in a number of ways, each having its own strengths and weaknesses. One is the approach first introduced by Castellano and Bothner-By [
3], where observable peak frequencies f
i are compared to theoretical transition frequencies ψ
i, and the resulting functional (1) is iteratively minimized:
The well-known major drawback of this approach is the requirement of spectral assignment – manual procedure to establish which experimental peak corresponds to which theoretical transition. There have been successful attempts of turning the assignment procedure automatic, most promising probably being PAREMUS [
4], where it was done with help of pattern recognition theory. Another problem associated with Castellano and Bothner-By approach is the loss of spectral information. Of all data points received from the spectrometer, only a few dozens, rarely more than a hundred are actually used in the functional (1). This problem is dealt with by a group of methods known as integral transform (IT) analysis, introduced by Diel et al [
5], and developed currently by Laatikainen [
6,
7]. Here instead of discrete frequency values, the minimized functional χ
2 is built upon special functionals, known as ITs, each dependant on a fragment of spectral lineshape, surrounding a given peak.
The other classical approach is the total line shape fitting analysis, first developed by Heinzer [
8], where from the very beginning the entire NMR spectrum is treated as a single entity, without any assignments or deconvolution procedures. The minimized functional (2) depends on every data point in a uniform manner:
where y(f) is spectral amplitude at frequency f, and
p is parameter vector, which includes both common spectral parameters (chemical shifts and SSCCs) and specific lineshape parameters (scaling and linewidth, in the simplest case). We believe that the total lineshape approach is the key to the automated analysis of complex strongly coupled NMR spectra, because it does not discard any spectral information. However, being formally a typical task of multivariable function optimization, this method suffers from all relevant problems. The global minimum of the functional (2) is extremely hard to locate. Previous attempts to solve this problem, most notably algorithm DAVINS [
9] were based on complex mathematical transformations of spectral lineshape and found little use.
We found, however, that simple broadening of an NMR spectrum, performed by exponential multiplication of the FID, can eliminate local minima efficiently. Once a global minimum on such broadened spectrum has been reached, the degree of broadening can be decreased, and the procedure repeated. This approach has been implemented in our algorithm VALISA [
10], which proved to be capable of dealing with many spectral analysis problems, ranging from four to nine-spin tightly coupled systems.
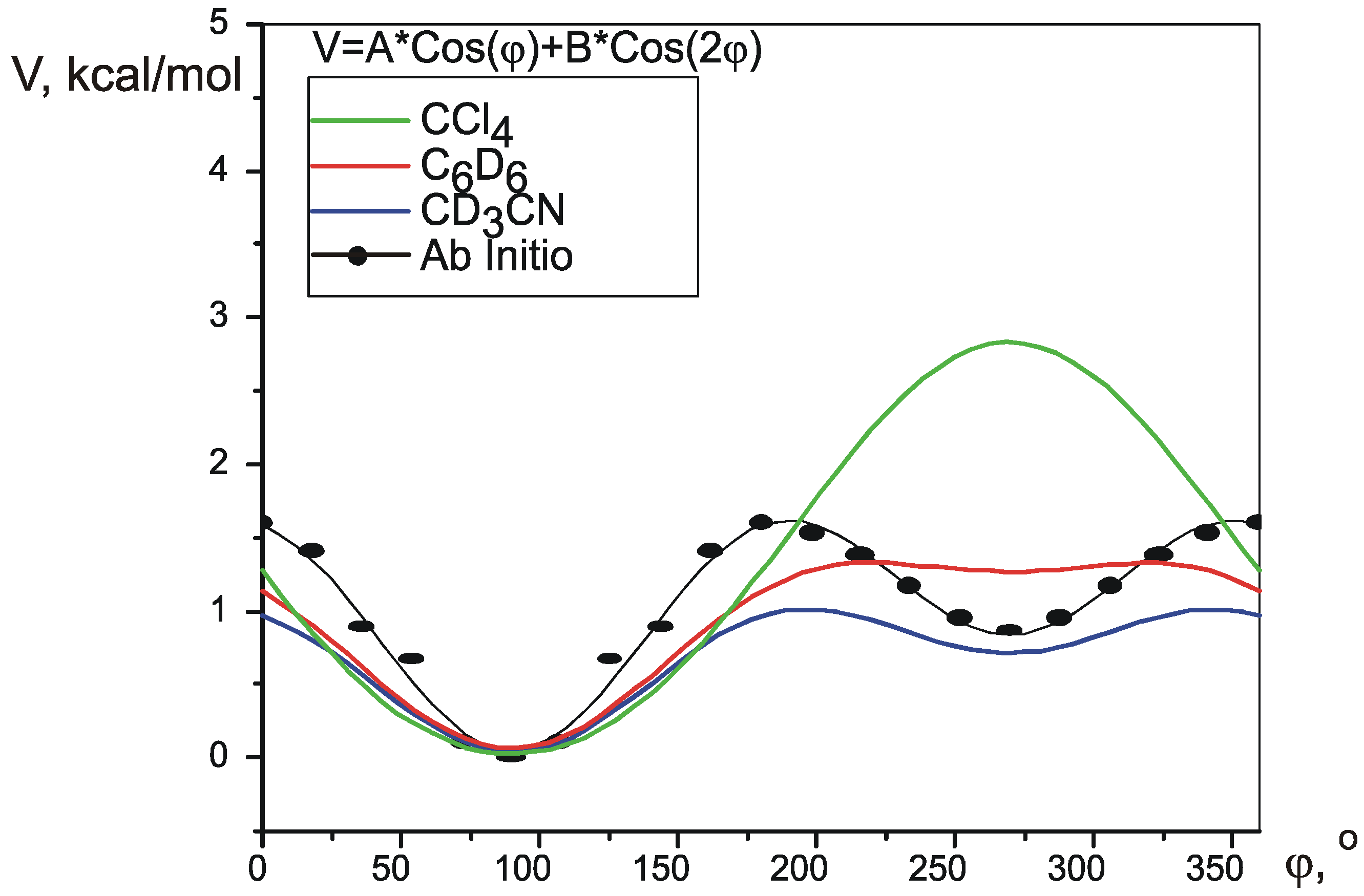
VALISA, like any total lineshape analysis, produces spectral parameters with a very high degree of precision – average values for standard error of SSCCs fall into 10-2-10-3 Hz. This precision gave us a possibility to approach the important problem of conformational analysis of substituted cyclopentanes at a whole new level of theory.
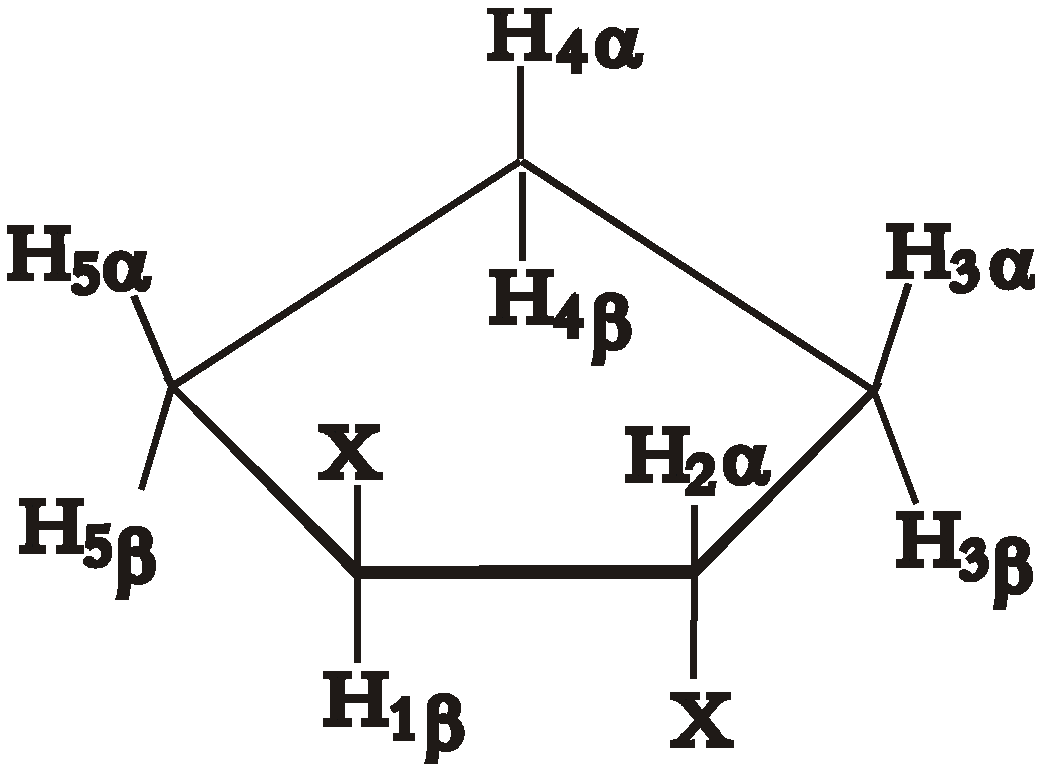
Conformational analysis of five-membered rings has been described theoretically in great detail with the advent of Cremer-Pople[
11] puckering coordinates. These coordinates, ring puckering q and phase angle of pseudorotation φ, form a basis in a two-dimensional space so that every possible conformation of a five-membered ring can be represented as a point in this space. Substituted cyclopentanes undergo a process called pseudorotation, where the most puckered part of the ring travels from one carbon to another, in a circle (
Figure 1).
Figure 1.
Pseudorotation in disubstituted cyclopentanes. Numbers in black inside the circle are values of the phase angle of pseudorotation, numbers and letters in red are the names of the basis conformations.
Figure 1.
Pseudorotation in disubstituted cyclopentanes. Numbers in black inside the circle are values of the phase angle of pseudorotation, numbers and letters in red are the names of the basis conformations.
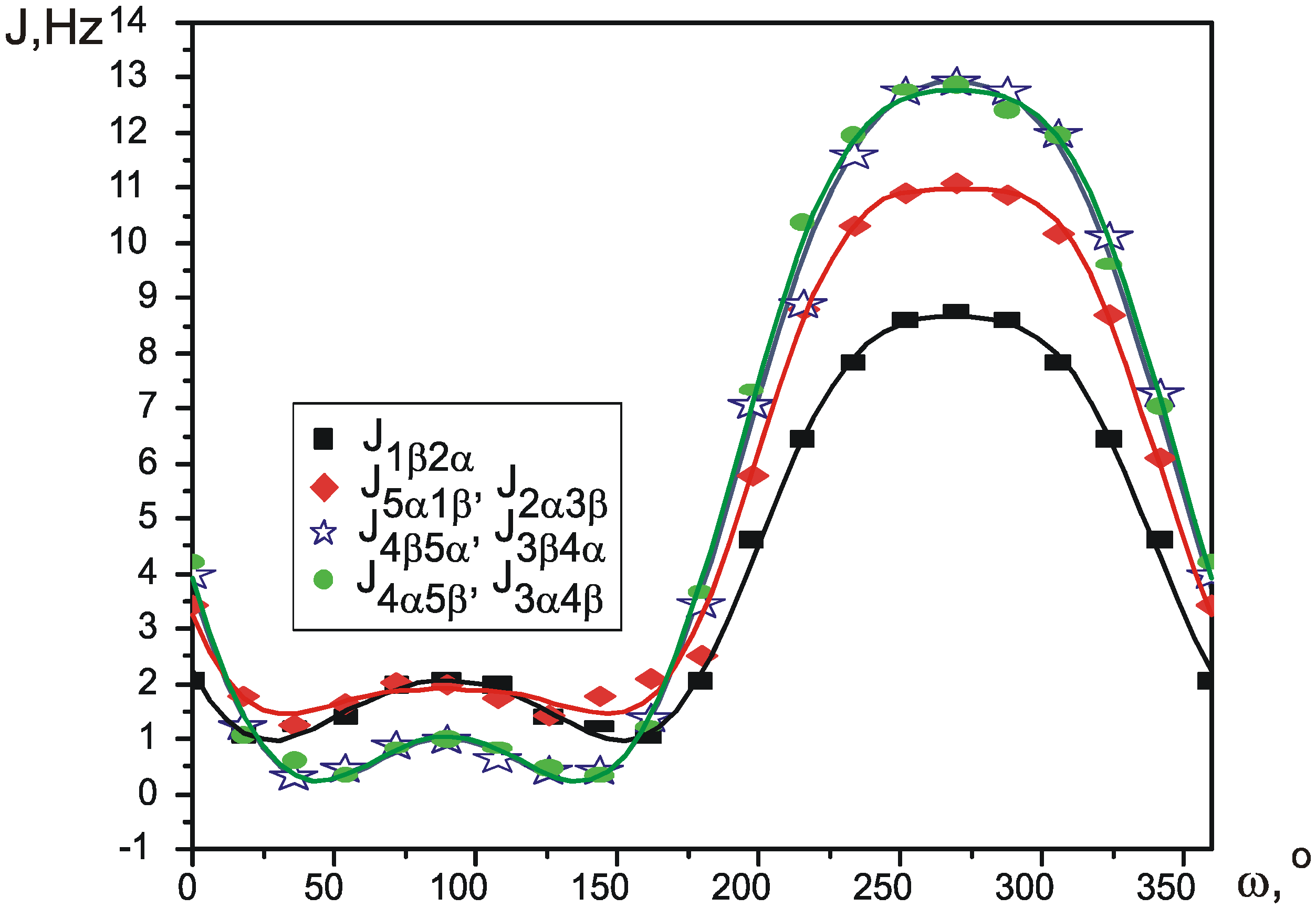
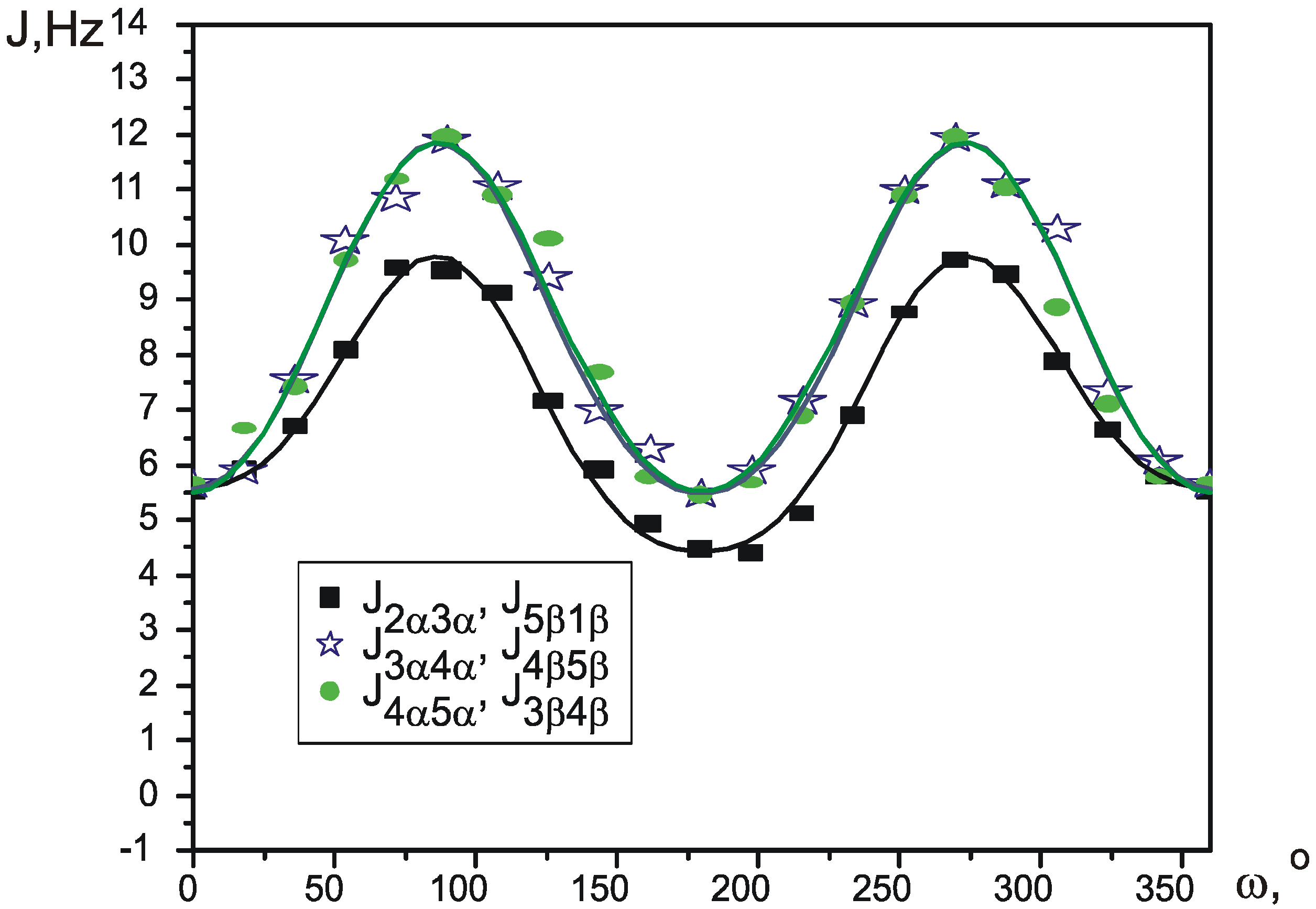
Pseudorotation is a low-energy process, which occurs fast in NMR timescale, so that normally it is only possible to measure averaged values of the spectral parameters. Wu et al. [
12] recently proposed a simple way to calculate the values of average SSCCs. Each coupling constant is parameterized as a function of Cremer-Pople pseudorotation angle φ, thus giving a different function J
i(φ) for every different SSCC. Knowing the potential of pseudorotation V(φ), an average value for each coupling constant at a given temperature can be calculated using Boltzman distribution:
Functions J
i(φ) can be produced by theoretical calculation of SSCCs in conformations, corresponding to different values of φ. The potential V(φ) can be created using one of many quantum theory methods.
Experimental studies of five-membered ring conformation seem to be lagging behind theory. In the classical works [
2] the process was reduced to an equilibrium of two fixed conformations, which was shown to be an erroneous approach later [
13], but even the most recent studies in anisotropic liquid crystal phase [
14] have been unable to give an answer more detailed than stating that the pseudorotation is limited to a sector of the
Figure 1 circle. Apparently, the reason for this is that a correct experimental description of such process requires many independent experimental parameters to be measured with sufficient precision. Ideally this could be the proton-proton coupling constants, but, for example, a disubstituted cyclopentane represents an eight-spin system of type AA’BB’CC’DD’ and contains several hundred spectral components. Complete analysis of such system could not be performed directly, without first developing a new method of spectral analysis.
The aim of this paper is to close the gap between theoretical and experimental description of substituted cyclopentane pseudorotation and to demonstrate how a continuos potential of pseudorotation can be built, based on single measurement of vicinal proton-proton coupling constants at room temperature.