The Effect of Substituents on Indirect Nuclear Spin-Spin Coupling Constants: Methan- and Ethanimine, Methanal- and Ethanaloxime
Abstract
:Introduction
Computational Aspects



- The RCN bond length is close to 128 pm in all molecules.
- The substituent -OH leads to an increase of the angle by ~ 5° and to a decrease of the and angles by 2° to 3°.
- The C=N-Z group is roughly rigid with respect to both its internal distances and angles.
Results
| Coupling | Molecule | KOD | KOP | KSD | KFC | K | J | Jexpt. |
| C-15N | methanimine | 0.04 | -28.07 | 4.59 | 30.75 | 7.30 | -2.23 | |
| (Z)-ethanimine | 0.11 | -26.70 | 4.49 | 28.51 | 6.41 | -1.96 | ||
| (E)-ethanimine | 0.11 | -27.02 | 4.40 | 33.16 | 10.65 | -3.26 | ||
| methanaloxime | 0.14 | -26.71 | 8.20 | 30.62 | 12.25 | -3.75 | |2.96| [68]a | |
| (Z)-ethanaloxime | 0.21 | -26.68 | 7.69 | 27.88 | 9.10 | -2.79 | |2.3| [68]a | |
| (E)-ethanaloxime | 0.21 | -26.34 | 7.99 | 32.59 | 14.46 | -4.43 | |4.0| [68]a | |
| 15N-HZ | methanimine | 0.11 | 0.43 | -0.14 | 40.15 | 40.55 | -49.39 | |
| (Z)-ethanimine | 0.15 | 0.72 | -0.13 | 39.45 | 40.19 | -48.95 | ||
| (E)-ethanimine | 0.14 | 0.71 | -0.11 | 40.92 | 41.65 | -50.73 | ||
| C-HX | methanimine | 0.16 | -0.12 | 0.04 | 56.80 | 56.89 | 171.86 | 172.9 [65] |
| (Z)-ethanimine | 0.25 | -0.19 | 0.03 | 55.08 | 55.17 | 166.68 | ||
| methanaloxime | 0.20 | -0.01 | -0.01 | 58.72 | 58.90 | 177.95 | ||
| (Z)-ethanaloxime | 0.28 | -0.09 | -0.02 | 57.77 | 57.94 | 175.05 | 177 ± 1 [69] | |
| C-HY | methanimine | 0.16 | -0.09 | 0.05 | 52.86 | 52.99 | 160.07 | 163.7 [66] |
| (E)-ethanimine | 0.25 | -0.18 | 0.04 | 51.66 | 51.77 | 156.41 | ||
| methanaloxime | 0.22 | -0.04 | 0.03 | 55.60 | 55.81 | 168.60 | ||
| (E)-ethanaloxime | 0.30 | -0.12 | 0.02 | 54.47 | 54.66 | 165.14 | 163 ± 1 [69] | |
| C-CX | (E)-ethanimine | 0.22 | -1.64 | 0.97 | 63.51 | 63.06 | 47.92 | |
| (E)-ethanaloxime | 0.24 | -1.35 | 0.93 | 67.94 | 67.76 | 51.49 | 48.42 [69] | |
| C-CY | (Z)-ethanimine | 0.22 | -1.56 | 0.98 | 51.72 | 51.36 | 39.02 | |
| (Z)-ethanaloxime | 0.26 | -1.43 | 0.92 | 57.18 | 56.92 | 43.25 | 40.51 [69] |
Triplet instabilities and quasi-instabilities
| Coupling | Molecule | Angles in H2C=N | KOD | KOP | KSD | KFC | K |
| 1K(C,N) | H2C=NH | Optimized | 0.04 | -28.07 | 4.59 | 30.75 | 7.30 |
| from H2C=NOH | 0.03 | -28.63 | 4.47 | 30.26 | 6.17 | ||
| H2C=NOH | Optimized | 0.14 | -26.71 | 8.20 | 30.62 | 12.25 | |
| from H2C=NH | -0.13 | -26.28 | 8.32 | 31.50 | 13.68 | ||
| 1K(C,HX) | H2C=NH | Optimized | 0.16 | -0.12 | 0.04 | 56.80 | 56.89 |
| from H2C=NOH | 0.16 | -0.13 | 0.04 | 58.08 | 58.16 | ||
| H2C=NOH | Optimized | 0.20 | -0.01 | -0.01 | 58.72 | 58.90 | |
| from H2C=NH | 0.20 | -0.00 | -0.01 | 57.66 | 57.84 | ||
| 1K(C,HY) | H2C=NH | Optimized | 0.16 | -0.09 | 0.05 | 52.86 | 52.99 |
| from H2C=NOH | 0.17 | -0.09 | 0.05 | 53.73 | 53.86 | ||
| H2C=NOH | Optimized | 0.22 | -0.04 | 0.03 | 55.60 | 55.81 | |
| from H2C=NH | 0.21 | -0.03 | 0.03 | 54.81 | 55.02 | ||
| 2K(N,HX) | H2C=NH | Optimized | -0.24 | -1.14 | 0.12 | 8.78 | 7.52 |
| from H2C=NOH | -0.23 | -1.18 | 0.13 | 7.77 | 6.49 | ||
| H2C=NOH | Optimized | -0.17 | -1.13 | 0.05 | 11.10 | 9.85 | |
| From H2C=NH | -0.18 | -1.09 | 0.04 | 12.09 | 10.85 | ||
| 2K(N,HY) | H2C=NH | Optimized | -0.29 | -0.85 | 0.19 | -2.80 | -3.75 |
| From H2C=NOH | -0.28 | -0.93 | 0.19 | -2.36 | -3.37 | ||
| H2C=NOH | Optimized | -0.23 | -0.99 | 0.06 | -1.74 | -2.90 | |
| From H2C=NH | -0.25 | -0.89 | 0.07 | -1.94 | -3.00 | ||
| 3K(HX,HY) | H2C=NH | Optimized | -0.31 | 0.31 | 0.03 | 1.27 | 1.31 |
| From H2C=NOH | -0.34 | 0.34 | 0.02 | 1.74 | 1.77 | ||
| H2C=NOH | Optimized | -0.32 | 0.34 | 0.02 | 0.66 | 0.69 | |
| From H2C=NH | -0.05 | 0.31 | 0.03 | 0.23 | 0.28 |
| Coupling | Molecule | KOD | KOP | KSD | KFC | K | J | Jexpt. |
| 15N-HX | methanimine | -0.24 | -1.14 | 0.12 | 8.78 | 7.52 | -9.16 | |
| (Z)-ethanimine | -0.20 | -1.01 | 0.10 | 10.04 | 8.93 | -10.88 | ||
| methanaloxime | -0.17 | -1.13 | 0.05 | 11.10 | 9.85 | -12.00 | -13.88 [67]a | |
| (Z)-ethanaloxime | -0.12 | -1.09 | 0.07 | 12.38 | 11.23 | -13.68 | -15.93 [67]b | |
| 15N-HY | methanimine | -0.29 | -0.85 | 0.19 | -2.80 | -3.75 | 4.56 | |
| (E)-ethanimine | -0.25 | -0.84 | 0.14 | -2.84 | -3.80 | 4.63 | ||
| methanaloxime | -0.23 | -0.99 | 0.06 | -1.74 | -2.90 | 3.53 | 2.68 [67]a | |
| (E)-ethanaloxime | -0.19 | -1.05 | 0.02 | -2.08 | -3.30 | 4.02 | 2.93 [67]b | |
| 15N-CX | (E)-ethanimine | -0.10 | -1.33 | 0.10 | 31.39 | 30.06 | -9.21 | |
| (E)-ethanaloxime | -0.05 | -0.44 | 0.13 | 31.91 | 31.55 | -9.67 | |9.0| [68]c | |
| 15N-CY | (Z)-ethanimine | -0.14 | -2.27 | 0.11 | -11.72 | -14.01 | 4.29 | |
| (Z)-ethanaloxime | -0.10 | -1.54 | -0.05 | -4.98 | -6.68 | 2.05 | |1.8| [68]c | |
| C-HZ | methanimine | -0.26 | -0.86 | -0.02 | -3.58 | -4.72 | -14.26 | -13.1 [65] |
| (Z)-ethanimine | -0.21 | -0.90 | -0.03 | -3.40 | -4.55 | -13.74 | ||
| (E)-ethanimine | -0.22 | -0.87 | -0.03 | -3.01 | -4.12 | -12.46 | ||
| CY-HX | (Z)-ethanimine | -0.12 | 0.06 | 0.01 | 5.00 | 4.94 | 14.94 | |
| (Z)-ethanaloxime | -0.13 | 0.08 | 0.01 | 2.58 | 2.54 | 7.68 | ||
| CX-HY | (E)-ethanimine | -0.12 | 0.05 | 0.01 | 4.47 | 4.42 | 13.34 | |
| (E)-ethanaloxime | -0.13 | 0.09 | 0.01 | 2.72 | 2.69 | 8.14 | ||
| HX-HY | Methanimine | -0.31 | 0.31 | 0.03 | 1.27 | 1.31 | 15.76 | 17.6 [65] |
| methanaloxime | -0.32 | 0.34 | 0.02 | 0.66 | 0.69 | 8.33 |
| Coupling | Molecule | KOD | KOP | KSD | KFC | K | J | Jexpt. |
| cis-CY-HZ | (Z)-ethanimine | -0.01 | -0.07 | -0.02 | 3.84 | 3.74 | 11.30 | |
| trans-CX-HZ | (E)-ethanimine | -0.23 | 0.19 | 0.02 | 5.55 | 5.52 | 16.69 | |
| cis-HY-HZ | Methanimine | -0.07 | 0.02 | 0.01 | 1.53 | 1.48 | 17.80 | 17.0 [65] |
| (E)-ethanimine | -0.04 | -0.01 | 0.01 | 1.33 | 1.30 | 15.66 | ||
| trans-HX-HZ | Methanimine | -0.37 | 0.31 | 0.03 | 2.03 | 2.00 | 24.06 | 25.2 [65] |
| (Z)-ethanimine | -0.36 | 0.30 | 0.03 | 1.95 | 1.92 | 23.08 |
One-bond coupling

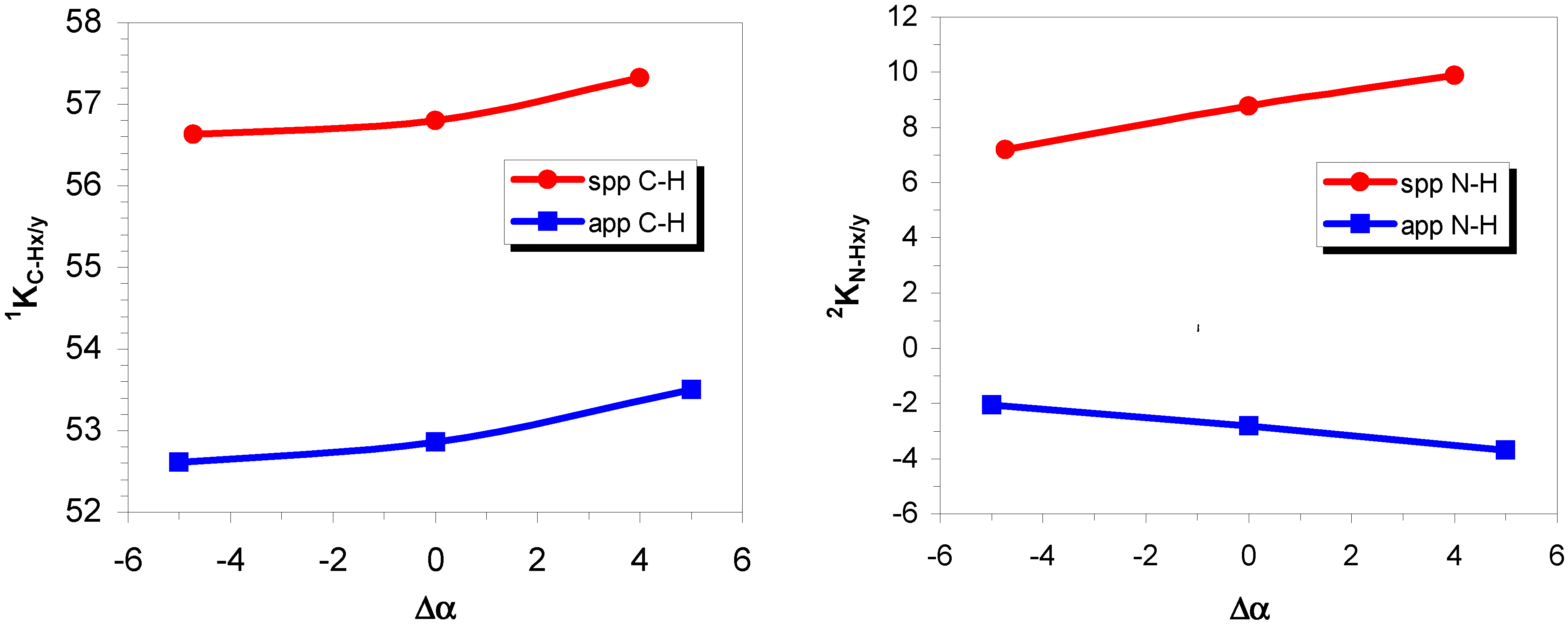
Two-bond coupling
Three-bond coupling
Conclusions
Acknowledgments
References and Notes
- See the Nobel Prize in Chemistry 2002. http://www.nobel.se/chemistry/laueates/2002.
- Alkorta, I.; Elguero, J. Int. J. Mol. Sci. 2003, 4, ?? –?? [CrossRef]
- Scheurer, C.; Brüschweiler, R. J. Am. Chem. Soc. 1999, 121, 8661–8662. [CrossRef]
- Del Bene, J. E.; Perera, S. A.; Bartlett, R. J. J. Am. Chem. Soc. 2000, 122, 3560–3561. [CrossRef]
- Pecul, M.; Leszczynski, J.; Sadlej, J. J. Phys. Chem. A. 2000, 104, 8105–8113. [CrossRef]
- Del Bene, J. E.; Bartlett, R. J. J. Am. Chem. Soc. 2000, 122, 10480–10481. [CrossRef]
- Bagno, A. Chem.-Eur. J. 2000, 6, 2925–2930. [CrossRef]
- Czernek, J.; Brüschweiler, R. J. Am. Chem. Soc. 2001, 123, 11079–11080. [CrossRef]
- Del Bene, J. E.; Perera, S. A.; Bartlett, R. J. Magn. Res. Chem. 2001, 39, S109–S114. [CrossRef]
- Barfield, M. J. Am. Chem. Soc. 2002, 124, 4158–4168. [CrossRef]
- Del Bene, J. E.; Perera, S. A.; Bartlett, R. J.; Elguero, J.; Alkorta, I.; López-Leonardo, C.; Alajarin, M. J. Am. Chem. Soc. 2002, 124, 6393–6397. [CrossRef]
- Provasi, P. F.; Aucar, G. A.; Sauer, S. P. A. J. Chem. Phys. 2000, 112, 6201–6208.
- Sauer, S. P. A.; Provasi, P. F.; Aucar, G. A. to be published.
- Helgaker, T.; Jaszuński, M.; Ruud, K.; Górska, A. Theor. Chem. Acc. 1998, 99, 175–182. [CrossRef]
- Enevoldsen, T.; Oddershede, J.; Sauer, S. P. A. Theor. Chem. Acc. 1998, 100, 275–284. [CrossRef]
- Provasi, P. F.; Aucar, G. A.; Sauer, S. P. A. J. Chem. Phys. 2001, 115, 1324–1334.
- Hansen, P. E. Prog. NMR Spectrosc. 1981, 14, 175–296. [CrossRef]
- Krivdin, L. B.; Kalabin, G. A. Prog. NMR Spectrosc. 1989, 21, 293–448. [CrossRef]
- Gil, V. M. S.; von Philipsborn, W. Magn. Res. Chem. 1989, 27, 409–430. [CrossRef]
- Kamieńska-Trela, K. Annual Reports on NMR Spectroscopy 1995, 30, 131–230.
- Contreras, R. H.; Peralta, J. E. Prog. NMR Spectrosc. 2000, 37, 321–425. [CrossRef]
- Kirby, A. J. The Anomeric Effect and Related Stereoelectronic Effects at Oxygen; Springer Verlag: Berlin, 1983. [Google Scholar]
- Juaristi, E.; Cuevas, G. The Anomeric Effect; CRC Press: Boca Raton, 1995. [Google Scholar]
- Reed, A.; Schleyer, P. v. R. J. Am. Chem. Soc. 1990, 112, 1434–1445.
- Sauer, S. P. A. J. Phys. B: At. Mol. Opt. Phys. 1997, 30, 3773–3780. [CrossRef]
- Wigglesworth, R. D.; Raynes, W. T.; Sauer, S. P. A.; Oddershede, J. Molec. Phys. 1997, 92, 77–88.
- Wigglesworth, R. D.; Raynes, W. T.; Sauer, S. P. A.; Oddershede, J. Molec. Phys. 1998, 94, 851–862.
- Sauer, S. P. A.; Møller, C. K.; Koch, H.; Paidarová, I.; Špirko, V. Chem. Phys. 1998, 238, 385–399.
- Kirpekar, S.; Sauer, S. P. A. Theor. Chem. Acc. 1999, 103, 146–153. [CrossRef]
- Wigglesworth, R. D.; Raynes, W. T.; Kirpekar, S.; Oddershede, J.; Sauer, S. P. A. J. Chem. Phys. 2000, 112, 3735–3746.
- Sauer, S. P. A.; Raynes, W. T. J. Chem. Phys. 2000, 113, 3121–3129.
- Grayson, M.; Sauer, S. P. A. Mol. Phys. 2000, 98, 1981–1990.
- Sauer, S. P. A.; Raynes, W. T.; Nicholls, R. A. J. Chem. Phys. 2001, 115, 5994–6006.
- Thouless, D. J. The Quantum Mechanics of Many-Body Systems; Academic Press: New York, 1961. [Google Scholar]
- Čížek, J.; Paldus, J. J. Chem. Phys. 1967, 47, 3976–3985.
- Chambaud, G.; Levy, B.; Millie, P. Theo. Chim. Acta. 1978, 48, 103–118. [CrossRef]
- Scuseria, G. E.; Contreras, R. H. Theo. Chim. Acta. 1981, 59, 437–450. [CrossRef]
- Scuseria, G. E.; Engelmann, a. R.; Contreras, R. H. Theo. Chim. Acta. 1982, 61, 49–57. [CrossRef]
- Scuseria, G. E.; Contreras, R. H. Chem. Phys. Lett. 1982, 93, 425–428.
- Righini, R.; Giribet, C. G.; Ruiz de Azúa, M. C.; Contreras, R. H. J. Mol. Struct. (Theochem). 1990, 210, 199–204. [CrossRef]
- Aucar, G. A.; Contreras, R. H. J. Magn. Reson. 1991, 93, 413–418.
- Contreras, R. H.; Ruiz de Azúa, M. C.; Giribet, C. G.; Aucar, G. A.; Loboyan de Bonczok, R. J. Mol. Struct. (Theochem). 1993, 284, 249–269. [CrossRef]
- Lobayan, R. M.; Aucar, G. A. J. Mol. Struct. (Theochem). 1998, 452, 1–11. [CrossRef]
- Lobayan, R. M.; Aucar, G. A. J. Mol. Struct. (Theochem). 1998, 452, 13–23. [CrossRef]
- Scuseria, G. E.; Geertsen, J.; Oddershede, J. J. Chem. Phys. 1989, 90, 2338–2343.
- Peng, H. W. Proc. Roy. Soc. London A. 1941, 178, 499–505. [CrossRef]
- McLachlan, A. D.; Ball, M. A. Rev. Mod. Phys. 1964, 36, 844–855. [CrossRef]
- Rowe, D. J. Rev. Mod. Phys. 1968, 40, 153–166. [CrossRef]
- Nielsen, E. S.; Jørgensen, P.; Oddershede, J. J. Chem. Phys. 1980, 73, 6238–6246.
- Ramsey, N. F. Phys. Rev. 1953, 91, 303–307. [CrossRef]
- Mills, I.; Cvitaš, T.; Homann, K.; Kallay, N.; Kuchitsu, K. Quantities, Units, Symbols in Physical Chemistry; Blackwell Scientific Publications: Oxford, 1993. [Google Scholar]
- Sauer, S. P. A. J. Chem. Phys. 1993, 98, 9220–9221.
- Oddershede, J. Adv. Quantum Chem. 1978, 2, 275–352.
- Sauer, S. P. A.; Packer, M. J. The ab initio calculation of molecular properties other than the potential energy surface. In Computational Molecular Spectroscopy; Bunker, P. R., Jensen, P., Eds.; John Wiley; Sons: London, 2000; chapter 7; pp. 221–252. [Google Scholar]
- Geertsen, J.; Oddershede, J. Chem. Phys. 1984, 90, 301–311.
- DALTON,an electronic structure program, Release 1.2: Helgaker, T.; Jensen, H. J. Aa.; Jørgensen, P.; Olsen, J.; Ruud, K.; Ågren, H.; Auer, A. A.; Bak, K. L.; Bakken, V.; Christiansen, O.; Coriani, S.; Dahle, P.; Dalskov, E. K.; Enevoldsen, T.; Fernandez, B.; Hättig, C.; Hald, K.; Halkier, A.; Heiberg, H.; Hettema, H.; Jonsson, D.; Kirpekar, S.; Kobayashi, R.; Koch, H.; Mikkelsen, K. V.; Norman, P.; Packer, M. J.; Pedersen, T. B.; Ruden, T. A.; Sanchez, A.; Saue, T.; Sauer, S. P. A.; Schimmelpfennig, B.; Sylvester-Hvid, K. O.; Taylor, P. R.; Vahtras, O. 2001. http://www.kjemi.uio.no/software/dalton/dalton.html.
- The aug-cc-pVTZ-J basis sets can be found at http://fyskem.ki.ku.dk/sauer/basissets
- Dunning, T. H., Jr. J. Chem. Phys. 1989, 90, 1007–1023.
- Kendall, R. A.; Dunning, T. H.; Harrison, R. J. J. Chem. Phys. 1992, 96, 6796–6806.
- Geertsen, J.; Oddershede, J.; Raynes, W. T.; Scuseria, G. E. J. Magn. Reson. 1991, 93, 458–471.
- Guilleme, J.; San Fabián, J. J. Chem. Phys. 1998, 109, 8168–8181.
- Gaussian 98, Revision A.7: Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Zakrzewski, V. G.; Montgomery, J. A.; Stratmann, R. E., Jr.; Burant, J. C.; Dapprich, S.; Millam, J. M.; Daniels, A. D.; Kudin, K. N.; Strain, M. C.; Farkas, O.; Tomasi, J.; Barone, V.; Cossi, M.; Cammi, R.; Mennucci, B.; Pomelli, C.; Adamo, C.; Clifford, S.; Ochterski, J.; Petersson, G. A.; Ayala, P. Y.; Cui, Q.; Morokuma, K.; Malick, D. K.; Rabuck, A. D.; Raghavachari, K.; Foresman, J. B.; Cioslowski, J.; Ortiz, J. V.; Baboul, A. G.; Stefanov, B. B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Gomperts, R.; Martin, R. L.; Fox, D. J.; Keith, T.; Al-Laham, M. A.; Peng, C. Y.; Nanayakkara, A.; Gonzalez, C.; Challacombe, M.; Gill, P. M. W.; Johnson, B.; Chen, W.; Wong, M. W.; res, J. L.; Gonzalez, C.; Head-Gordon, M.; Replogle, E. S.; Pople, J. A. Gaussian,Inc.: Pittsburgh PA, 1998.
- Lovas, F. J.; Suenram, R. D.; Johnson, D. R.; Clark, F. O.; Tiemann, E. J. Chem. Phys. 1980, 72, 4964–4972. [CrossRef]
- Mills, I.; Cvitaš, T.; Homann, K.; Kallay, N.; Kuchitsu, K. Quantities, Units, Symbols in Physical Chemistry; Blackwell Scientific Publications: Oxford, 1993. [Google Scholar]
- Braillon, B.; Lasne, M. C.; Ripoll, J. L.; Denis, J. M. Nouv. J. Chim. 1982, 6, 121–122.
- Yonezawa, T.; Morishima, I. J. Mol. Spectrosc. 1968, 27, 210–217. [CrossRef]
- Crépaux, D.; Lehn, J. M.; Dean, R. R. Mol. Phys. 1969, 16, 225–239.
- Lichter, R. L.; Dorman, D. E.; Wasylishen, R. J. Am. Chem. Soc. 1974, 96, 930–932. [CrossRef]
- Wray, V. Progress in NMR Spectroscopy 1979, 13, 177–256.
- Gomez, C. A.; Provasi, P. F.; Aucar, G. A. J. Mol. Struct. (THEOCHEM). submitted.
- Oddershede, J.; Jørgensen, P.; Beebe, N. H. F. Chem. Phys. 1977, 25, 451–458.
- Geertsen, J.; Oddershede, J.; Scuseria, G. E. J. Chem. Phys. 1987, 87, 2138–2142.
- Vahtras, O.; Ågren, H.; Jørgensen, P.; Helgaker, T.; Aa. Jensen, H. J. Chem. Phys. Lett. 1993, 209, 201–206.
- Malkin, V. G.; Malkina, O. L.; Salahub, D. R. Chem. Phys. Lett. 1994, 221, 91–99.
- Perera, S. A.; Sekino, H.; Bartlett, R. J. J. Chem. Phys. 1994, 101, 2186–2191.
- Auer, A. A.; Gauss, J. J. Chem. Phys. 2001, 115, 1619–1622.
- See e.g.March, J. Advanced Organic Chemistry: Reactions, Mechanisms, and Strcuture; John Wiley & Sons: New York, 1985. [Google Scholar]
- Zaccari, D. G.; Snyder, J. P.; Peralta, J. E.; Taurian, O. E.; Contreras, R. H.; Barone, V. Mol. Phys. 2002, 100, 705–715.
- Barone, V.; Peralta, J. E.; Contreras, R. H.; Sosnin, A. V.; Krivdin, L. B. Magn. Reson. Chem. 2001, 39, 600–606. [CrossRef]
- Contreras, R. H.; Giribet, C. G.; Ruiz de Azúa, M. C.; Cavasotto, C. N.; Aucar, G. A.; Krivdin, L. J. Mol. Struct. (Theochem). 1990, 210, 175–186. [CrossRef]
- Wolfe, S.; Pinto, B. M.; Varma, V.; Leung, R. Y. N. Can. J. Chem. 1990, 68, 1051–1062.
- Yonezawa, T.; Morishima, I.; Fukuta, K.; Ohmori, Y. J. Molec. Spectrosc. 1969, 31, 341–345. [CrossRef]
- Perlin, A. S.; Casu, B. Tetrahedron Lett. 1969, 2921–2924.
- Cuevas, G.; Juaristi, E. J. Am. Chem. Soc. 2002, 124, 13088–13096. [CrossRef]
- Zinchenko, S. V.; Kiselev, R. Yu.; Krivdin, L. B. Zh. Org. Khim.. 1991, 27, 1233–1239.
- Krivdin, L. B.; Zinchenko, S. V.; Kalabin, G. A.; Facelli, J. C.; Tufró, M. F.; Contreras, R. H.; Denisov, A. Yu.; Gavrilyuk, O. A.; Mamatyuk, V. I. J. Chem. Soc. Faraday Trans. 1992, 88, 2459–2463. [CrossRef]
- Krivdin, L. B.; Shcherbakov, V. V.; Kalabin, G. A. Zh. Org. Khim. 1986, 22, 342–348.
- Kintzinger, J. P.; Lehn, J. M. Chem. Commun. 1967, 660, 660–661.
© 2003 by MDPI (http://www.mdpi.org). Reproduction for noncommercial purposes permitted.
Share and Cite
Provasi, P.F.; Aucar, G.A.; Sauer, S.P.A. The Effect of Substituents on Indirect Nuclear Spin-Spin Coupling Constants: Methan- and Ethanimine, Methanal- and Ethanaloxime. Int. J. Mol. Sci. 2003, 4, 231-248. https://0-doi-org.brum.beds.ac.uk/10.3390/i4040231
Provasi PF, Aucar GA, Sauer SPA. The Effect of Substituents on Indirect Nuclear Spin-Spin Coupling Constants: Methan- and Ethanimine, Methanal- and Ethanaloxime. International Journal of Molecular Sciences. 2003; 4(4):231-248. https://0-doi-org.brum.beds.ac.uk/10.3390/i4040231
Chicago/Turabian StyleProvasi, Patricio F., Gustavo A. Aucar, and Stephan P. A. Sauer. 2003. "The Effect of Substituents on Indirect Nuclear Spin-Spin Coupling Constants: Methan- and Ethanimine, Methanal- and Ethanaloxime" International Journal of Molecular Sciences 4, no. 4: 231-248. https://0-doi-org.brum.beds.ac.uk/10.3390/i4040231




