Self-Triggered Formation Control of Nonholonomic Robots
Abstract
:1. Introduction
- Design and implementation of a novel self-triggered Lyapunov-based control for nonlinear systems, using a dual stability approach in order to guarantee practical stability. When the Lyapunov function is greater than a given threshold, asymptotic stability is guaranteed. After that, the system is bounded on the Lyapunov threshold level.
- Evaluation of centralized and decentralized triggering mechanisms for formation control of nonholonomic robots tracking nonlinear trajectories, comparing both with a periodic implementation. The experimental set-up includes three mobiles robot remotely controlled in a scenario with four wireless camera sensors.
- The design and implementation of a delay compensation strategy that leverages one of the main strengths of STC, namely that the next sampling instant is known in advance.
Notation
2. Problem Statement
2.1. Formation Control Problem
2.2. Lyapunov Formation Controller
3. Lyapunov Based Self-Triggering Control Proposal
- 1.
- The function , with .
- 2.
- The functions in Equation (13) are such that are Lipschitz continuous on the working compact set . The Lipschitz constants on of functions and are represented by and respectively.
4. Simulation Results
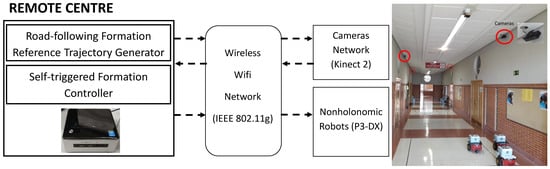
5. Remote Centre Task Scheduler
- A non-holonomic mobile robot formation. Each robot locally implements a periodic servosystem for linear and angular velocity tracking.
- A set of sensor nodes covers the entire experimental area and provides each robot with pose information using computer vision.
- An IEEE 802.11g standard wireless network that links the remote centre to the robots and the set of sensor nodes.
- A remote centre that performs the principal tasks: trajectory generation for the virtual leader considered the reference for the road-following formation, trajectory generation for each real robot with respect to the virtual leader, new measurement request to the camera network, pose estimation of each robot unit based on the UKF, and application of the self-triggered control strategy.
5.1. Delay Compensation
- is the maximum network delay, it is the maximum time to transmit a message via the wireless communication network.
- is the maximum sensor delay, i.e., the time between the start of a measurement acquisition in the sensor node and the instant it is ready to be sent to the remote centre. This time includes image acquisition and processing.
- is the control computing time of the remote centre.
- is the dominant constant time that characterizes the robot dynamics.
- At time instant , the cameras start the measurement process with image acquisition. This time is previously indicated to the cameras by the STC of the remote centre. Computation of this time is explained in Step 5.
- When the pose measurement () is ready, the cameras send it and the acquisition time () to the remote centre.
- At time instant , the UKF of the remote centre corrects the prediction of the states for time instant with the measurement sent by the camera (). Next, the UKF predicts the states at time instant and sends this information to the STC controller. With this information, the STC generates linear and angular speed commands for each robot () and computes the next update instant (). The control signal () and the application time are sent to the robot ()
- At time instant the control signal is applied to the robot; thus, the desired control signal is reached at time instant compensating the robot dynamics.
- After sending the control signal to the robots, the remote centre sends the next measurement acquisition time to the cameras (). This time is computed taking into account the next sampling instant and all the delays ().
5.2. Control Design Dependent on State Estimation
6. Experimental Tests
Results
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Oh, K.K.; Park, M.C.; Ahn, H.S. A survey of multi-agent formation control. Automatica 2015, 53, 424–440. [Google Scholar] [CrossRef]
- Guinaldo, M.; Fábregas, E.; Farias, G.; Dormido-Canto, S.; Chaos, D.; Sánchez, J.; Dormido, S. A Mobile Robots Experimental Environment with Event-Based Wireless Communication. Sensors 2013, 13, 9396–9413. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Santos, C.; Espinosa, F.; Santiso, E.; Martínez, M.; Mazo, M. Aperiodic Consensus Control for Tracking Nonlinear Trajectories of a Platoon of Vehicles. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems, Gran Canaria, Spain, 15–18 September 2015; pp. 1983–1988. [Google Scholar]
- Yan, Z.; Xu, D.; Chen, T.; Zhang, W.; Liu, Y. Leader–Follower Formation Control of UUVs with Model Uncertainties, Current Disturbances, and Unstable Communication. Sensors 2018, 18, 662. [Google Scholar] [CrossRef] [PubMed]
- Dong, X.; Yu, B.; Shi, Z.; Zhong, Y. Time-Varying Formation Control for Unmanned Aerial Vehicles: Theories and Applications. IEEE Trans. Control Syst. Technol. 2015, 23, 340–348. [Google Scholar] [CrossRef]
- Lee, W.; Kim, D. Autonomous Shepherding Behaviors of Multiple Target Steering Robots. Sensors 2017, 17, 2729. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.C.; Chiu, Y.H.; Wen, C.Y. Using Hybrid Angle/Distance Information for Distributed Topology Control in Vehicular Sensor Networks. Sensors 2014, 14, 20188–20216. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guzey, H.M.; Vignesh, N.; Jagannathan, S.; Dierks, T.; Acar, L. Distributed consensus-based event-triggered approximate control of nonholonomic mobile robot formations. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 3194–3199. [Google Scholar]
- Li, X.; Chen, H. An Interactive Control Algorithm Used for Equilateral Triangle Formation with Robotic Sensors. Sensors 2014, 14, 7229–7247. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pawlowski, A.; Guzmán, J.L.; Rodríguez, F.; Berenguel, M.; Sánchez, J.; Dormido, S. The influence of event-based sampling techniques on data transmission and control performance. In Proceedings of the 2009 IEEE Conference on Emerging Technologies Factory Automation, Mallorca, Spain, 22–25 September 2009; pp. 1–8. [Google Scholar]
- Cloosterman, M.B.G.; van de Wouw, N.; Heemels, W.P.M.H.; Nijmeijer, H. Stability of Networked Control Systems With Uncertain Time–Varying Delays. IEEE Trans. Autom. Control 2009, 54, 1575–1580. [Google Scholar] [CrossRef]
- Luan, X.; Shi, P.; Liu, F. Stabilization of Networked Control Systems With Random Delays. IEEE Trans. Ind. Electron. 2011, 58, 4323–4330. [Google Scholar] [CrossRef]
- Cuenca, A.; García, P.; Albertos, P.; Salt, J. A Non–Uniform Predictor-Observer for a Networked Control System. Int. J. Control Autom. Syst. 2011, 9, 1194–1202. [Google Scholar] [CrossRef]
- Li, H.; Shi, Y. Network-Based Predictive Control for Constrained Nonlinear Systems With Two–Channel Packet Dropouts. IEEE Trans. Ind. Electron. 2014, 61, 1574–1582. [Google Scholar] [CrossRef]
- Zhao, Y.B.; Liu, G.P.; Rees, D. Actively Compensating for Data Packet Disorder in Networked Control Systems. IEEE Trans. Circuits Syst. II Express Briefs 2010, 57, 913–917. [Google Scholar] [CrossRef]
- Casanova, V.; Salt, J.; Cuenca, A.; Piza, R. Networked Control Systems: Control structures with bandwidth limitations. Int. J. Syst. Control Commun. 2009, 1, 267–296. [Google Scholar] [CrossRef]
- Ojha, U.; Chow, M.Y. Realization and validation of Delay Tolerant Behavior Control based Adaptive Bandwidth Allocation for networked control system. In Proceedings of the 2010 IEEE International Symposium on Industrial Electronics, Bari, Italy, 4–7 July 2010; pp. 2853–2858. [Google Scholar]
- Postoyan, R.; Bragagnolo, M.; Galbrun, E.; Daafouz, J.; Nesic, D.; Castellan, E. Nonlinear event-triggered tracking control of a mobile robot: Design, analysis and experimental results. IFAC Proc. Vol. 2013, 46, 318–323. [Google Scholar] [CrossRef]
- Santos, C.; Martínez-Rey, M.; Espinosa, F.; Gardel, A.; Santiso, E. Event-Based Sensing and Control for Remote Robot Guidance: An Experimental Case. Sensors 2017, 17, 2034. [Google Scholar] [CrossRef] [PubMed]
- Borgers, D.P.; Heemels, W.P.M.H. Event-Separation Properties of Event-Triggered Control Systems. IEEE Trans. Autom. Control 2014, 59, 2644–2656. [Google Scholar] [CrossRef]
- Chen, X.; Hao, F.; Ma, B. Periodic event-triggered cooperative control of multiple non-holonomic wheeled mobile robots. IET Control Theory Appl. 2017, 11, 890–899. [Google Scholar] [CrossRef]
- Socas, R.; Dormido, S.; Dormido, R.; Fabregas, E. Event-Based Control Strategy for Mobile Robots in Wireless Environments. Sensors 2015, 15, 30076–30092. [Google Scholar] [CrossRef] [Green Version]
- Linsenmayer, S.; Dimarogonas, D.V.; Allgöwer, F. Event-based vehicle coordination using nonlinear unidirectional controllers. IEEE Trans. Control Netw. Syst. 2018, 5, 1575–1584. [Google Scholar] [CrossRef]
- Miskowicz, M. Event-Based Control and Signal Processing; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Hu, Y.; Lu, Q.; Hu, Y. Event-Based Communication and Finite–Time Consensus Control of Mobile Sensor Networks for Environmental Monitoring. Sensors 2018, 18, 2547. [Google Scholar] [CrossRef]
- Mazo, M.; Anta, A.; Tabuada, P. On self-triggered control for linear systems: Guarantees and complexity. In Proceedings of the 2009 European Control Conference (ECC), Budapest, Hungary, 23–26 August 2009; pp. 3767–3772. [Google Scholar]
- Eqtami, A.; Heshmati-alamdari, S.; Dimarogonas, D.V.; Kyriakopoulos, K.J. Self-triggered Model Predictive Control for nonholonomic systems. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 638–643. [Google Scholar]
- Santos, C.; Mazo, M., Jr.; Espinosa, F. Adaptive self-triggered control of a remotely operated P3DX robot: Simulation and experimentation. Robot. Auton. Syst. 2014, 62, 847–854. [Google Scholar] [CrossRef]
- Tiberi, U.; Johansson, K. A simple self-triggered sampler for perturbed nonlinear systems. Nonlinear Anal. Hybrid Syst. 2013, 10, 126–140. [Google Scholar] [CrossRef]
- Santos, C.; Espinosa, F.; Santiso, E.; Mazo, M. Aperiodic Linear Networked Control Considering Variable Channel Delays: Application to Robots Coordination. Sensors 2015, 15, 12454–12473. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Velasco, M.; Marti, P.; Fuertes, J.M. The self-triggered task model for real-time control systems. Proceedings of 24th IEEE Real–Time Systems Symposium RTSS 2003, Cancun, Mexico, 3–5 December 2003; pp. 1–4. [Google Scholar]
- Zhu, Z.; Sun, J.; Qi, G.; Chai, Y.; Chen, Y. Frequency Regulation of Power Systems with Self–Triggered Control under the Consideration of Communication Costs. Appl. Sci. 2017, 7, 688. [Google Scholar] [CrossRef]
- Heemels, W.P.M.H.; Johansson, K.H.; Tabuada, P. An introduction to event-triggered and self-triggered control. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 3270–3285. [Google Scholar]
- Santos, C.; Espinosa, F.; Santiso, E.; Martinez-Rey, M. A simplified event-triggering condition non-dependent on measurement error. In Proceedings of the 2017 3rd International Conference on Event-Based Control, Communication and Signal Processing (EBCCSP), Funchal, Portugal, 24–26 May 2017; pp. 1–6. [Google Scholar]
- Ono, M.; Droge, G.; Grip, H.; Toupet, O.; Scrapper, C.; Rahmani, A. Road-following formation control of autonomous ground vehicles. In Proceedings of the 2015 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 4714–4721. [Google Scholar]
- Wang, Z.; Liu, Y. Visual regulation of a nonholonomic wheeled mobile robot with two points using Lyapunov functions. In Proceedings of the 2010 International Conference on Mechatronics and Automation (ICMA), Xi’an, China, 4–7 August 2010; pp. 1603–1608. [Google Scholar]
- Amoozgar, M.; Zhang, Y. Trajectory tracking of Wheeled Mobile Robots: A kinematical approach. In Proceedings of the 2012 IEEE/ASME International Conference on Mechatronics and Embedded Systems and Applications (MESA), Suzhou, China, 8–10 July 2012; pp. 275–280. [Google Scholar]
- Brockett, R.W. Asymptotic stability and feedback stabilization. In Differential Geometric Control Theory; Birkhauser: Boston, MA, USA, 1983; pp. 181–191. [Google Scholar]
- Grines, V.; Medvedev, T.; Pochinka, O. Dynamical Systems on 2- and 3-Manifolds; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Khalil, H. Nonlinear Systems; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Kurzweil, J. On the inversion of Lypaunov’s second theorem on stability of motion. Czechoslov. Math. J. 1956, 6, 217–259. [Google Scholar]
- Lamnabhi-Lagarrigu, F.; Loria, A.; Panteley, E.; Laghrouche, S. Taming Heterogeneity and Complexity of Embedded Control; Wiley-ISTE: London, UK, 2007. [Google Scholar]
- Chaillet, A.; Loria, A. Necessary and sufficient conditions for uniform semiglobal practical asymptotic stability: Application to cascaded systems. Automatica 2006, 42, 1899–1906. [Google Scholar] [CrossRef]
- Espinosa, F.; Salazar, M.; Pizarro, D.; Valdes, F. Electronics Proposal for Telerobotics Operation of P3DX Units. In Remote and Telerobotics; Mollet, N., Ed.; InTech: London, UK, 2010; Chapter 1. [Google Scholar]
- Wang, J.; Olson, E. AprilTag 2: Efficient and robust fiducial detection. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016. [Google Scholar]












| Periodic [10 ms] | STC Centralized (26) | STC Decentralized (27) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R1 | R2 | R3 | Formation | R1 | R2 | R3 | Formation | R1 | R2 | R3 | Formation | |
| Updates | 6500 | 6500 | 6500 | 6500 | 29 | 29 | 29 | 29 | 29 | 30 | 28 | 87 |
| 1.31 | 1.39 | 1.04 | 3.74 | 1.12 | 1.58 | 0.92 | 3.62 | 1.19 | 1.39 | 1.37 | 3.95 | |
| Periodic [10 ms] | STC Centralized (26) | STC Decentralized (27) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R1 | R2 | R3 | Formation | R1 | R2 | R3 | Formation | R1 | R2 | R3 | Formation | |
| AVG Updates | 6200 | 6200 | 6200 | 6200 | 32.70 | 32.70 | 32.70 | 32.70 | 30.37 | 30.89 | 30.22 | 91.48 |
| STD Updates | 0 | 0 | 0 | 0 | 4.78 | 4.78 | 4.78 | 14.34 | 3.26 | 3.69 | 6.99 | 10.51 |
| AVG | 3.54 | 3.56 | 3.82 | 10.91 | 3.35 | 3.23 | 3.16 | 9.74 | 3.17 | 3.26 | 3.28 | 9.71 |
| STD | 1.68 | 1.71 | 1.84 | 4.96 | 1.25 | 1.23 | 1.27 | 3.64 | 1.25 | 1.23 | 1.28 | 3.69 |
| Periodic [10 ms] | STC Centralized (26) | STC Decentralized (27) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R1 | R2 | R3 | Formation | R1 | R2 | R3 | Formation | R1 | R2 | R3 | Formation | |
| Updates | 6500 | 6500 | 6500 | 6500 | 125 | 125 | 125 | 125 | 123 | 119 | 136 | 378 |
| 2.89 | 4.61 | 3.12 | 10.62 | 2.94 | 4.90 | 3.72 | 11.56 | 2.24 | 3.34 | 3.05 | 8.63 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, C.; Espinosa, F.; Martinez-Rey, M.; Gualda, D.; Losada, C. Self-Triggered Formation Control of Nonholonomic Robots. Sensors 2019, 19, 2689. https://0-doi-org.brum.beds.ac.uk/10.3390/s19122689
Santos C, Espinosa F, Martinez-Rey M, Gualda D, Losada C. Self-Triggered Formation Control of Nonholonomic Robots. Sensors. 2019; 19(12):2689. https://0-doi-org.brum.beds.ac.uk/10.3390/s19122689
Chicago/Turabian StyleSantos, Carlos, Felipe Espinosa, Miguel Martinez-Rey, David Gualda, and Cristina Losada. 2019. "Self-Triggered Formation Control of Nonholonomic Robots" Sensors 19, no. 12: 2689. https://0-doi-org.brum.beds.ac.uk/10.3390/s19122689