Interactive Errors Analysis and Scale Factor Nonlinearity Reduction Methods for Lissajous Frequency Modulated MEMS Gyroscope
Abstract
:1. Introduction
2. Working Principle and Scheme Design
2.1. Dynamical Model of Gyroscope
2.2. Basic Working Principle of LFM
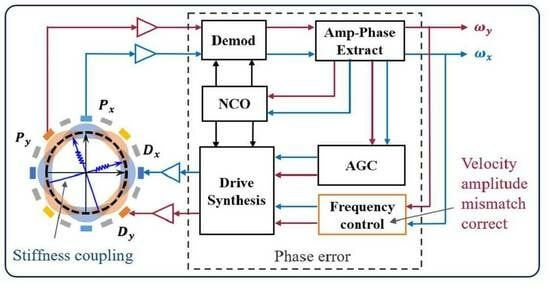
2.3. Control Scheme of the LFM
2.4. Readout Characteristics of the LFM
3. Interactive Error Analysis and Correction
3.1. Analysis of Interaction Effect
3.2. Suppression of Stiffness Coupling by Quadrature Voltage
3.3. Identification and Compensation for the System Phase Error
4. Validations and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MEMS | Micro-Electro-Mechanical System |
| SF | Scale Factor |
| ZRO | Zero Rate Output |
| AM | Amplitude Modulated |
| FM | Frequency Modulated |
| QFM | Quadrature Frequency Modulated |
| IFM | Indexed Frequency Modulated |
| LFM | Lissajous Frequency Modulated |
| ASIC | Application-Specific Integrated Circuit |
| PLL | Phase-Locked Loop |
| AGC | Automatic Gain Control |
| CSWaP | Cost, Size, Weight, and Power |
| NCO | Numerically Controlled Oscillator |
| FIR | Finite Impulse Response |
| ADC | Analog-to-Digital Converter |
| DAC | Digital-to-Analog Converter |
| PI | Proportional Integral |
Appendix A. Glossary
| Symbol | Description | Symbol | Description |
|---|---|---|---|
| vibration displacements of the X and Y modes | angular gain | ||
| control forces of the X and Y modes | input angular rate | ||
| amplitudes of the vibration displacements | damping of the X and Y modes | ||
| change rates of the amplitudes | damping coupling between the X and Y modes | ||
| phases of the vibration displacements | stiffness of the X and Y modes | ||
| phases of the control forces | stiffness coupling between the X and Y modes | ||
| in-phase control forces of the X and Y modes | average damping between the X and Y modes | ||
| quadrature control forces of the X and Y modes | anisodamping between the X and Y modes | ||
| amplitude control forces of the X and Y modes | the average stiffness between the X and Y modes | ||
| the instantaneous frequencies of the X and Y modes | real-time phase difference in the displacements | ||
| amplitudes of the vibration velocity | the reciprocal sum of the velocity ratio | ||
| change rates of the vibration velocity amplitudes | the reciprocal difference of the velocity ratio | ||
| difference between the displacement phase and the force phase of the X and Y modes | summation of the instantaneous frequencies | ||
| amplified amplitudes of the displacements | difference in the instantaneous frequencies | ||
| phase lags generated by blocks in the loop | phase lag generated by the resonator |
References
- Endean, D.; Christ, K.; Duffy, P.; Freeman, E.; Glenn, M.; Gnerlich, M.; Johnson, B.; Weinmann, J. Near-navigation grade tuning fork MEMS gyroscope. In Proceedings of the IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Naples, FL, USA, 1–5 April 2019; pp. 1–4. [Google Scholar]
- Zhang, H.; Zhang, C.; Chen, J.; Li, A. A review of symmetric silicon MEMS gyroscope mode-matching technologies. Micromachines 2022, 13, 1255. [Google Scholar] [CrossRef] [PubMed]
- Passaro, V.M.; Cuccovillo, A.; Vaiani, L.; De Carlo, M.; Campanella, C.E. Gyroscope technology and applications: A review in the industrial perspective. Sensors 2017, 17, 2284. [Google Scholar] [CrossRef] [PubMed]
- Sonmezoglu, S.; Alper, S.E.; Akin, T. An automatically mode-matched MEMS gyroscope with wide and tunable bandwidth. J. Microelectromech. Syst. 2014, 23, 284–297. [Google Scholar] [CrossRef]
- Aktakka, E.E.; Woo, J.K.; Egert, D.; Gordenker, R.J.; Najafi, K. A microactuation and sensing platform with active lockdown for in situ calibration of scale factor drifts in dual-axis gyroscopes. IEEE-ASME Trans. Mechatron. 2014, 20, 934–943. [Google Scholar] [CrossRef]
- Cui, M.; Huang, Y.; Wang, W.; Cao, H. MEMS gyroscope temperature compensation based on drive mode vibration characteristic control. Micromachines 2019, 10, 248. [Google Scholar] [CrossRef]
- Zotov, S.A. High-Range Angular Rate Sensor Based on Mechanical Frequency Modulation. J. Microelectromech. Syst. 2012, 21, 398–405. [Google Scholar] [CrossRef]
- Kline, M.H.; Yeh, Y.C.; Eminoglu, B.; Najar, H.; Boser, B.E. Quadrature FM gyroscope. In Proceedings of the IEEE Symposium on Mass Storage Systems and Technologies, Long Beach, CA, USA, 6–10 May 2013; pp. 604–608. [Google Scholar]
- Eminoglu, B.; Yeh, Y.C.; Izyumin, I.I.; Nacita, I.; Boser, B.E. Comparison of long-term stability of AM versus FM gyroscopes. In Proceedings of the IEEE International Conference on Micro Electro Mechanical Systems (MEMS), Shanghai, China, 24–28 January 2016. [Google Scholar]
- Tsukamoto, T.; Tanaka, S. Fully Differential Single Resonator FM Gyroscope Using CW/CCW Mode Separator. J. Microelectromech. Syst. 2018, 27, 1–10. [Google Scholar] [CrossRef]
- Ren, X.; Zhou, X.; Yu, S.; Wu, X.; Xiao, D. Frequency-modulated mems gyroscopes: A review. IEEE Sens. J. 2021, 21, 26426–26446. [Google Scholar] [CrossRef]
- Izyumin, I.I.; Kline, M.H.; Yeh, Y.C.; Eminoglu, B.; Ahn, C.H.; Hong, V.A.; Yang, Y.; Ng, E.J.; Kenny, T.W.; Boser, B.E. A 7ppm, 6/hr frequency-output MEMS gyroscope. In Proceedings of the IEEE Symposium on Mass Storage Systems and Technologies, Santa Clara, CA, USA, 30 May–5 June 2015; pp. 33–36. [Google Scholar]
- Kline, M.; Yeh, Y.C.; Eminoglu, B.; Izyumin, I.; Daneman, M.; Horsley, D.; Boser, B. MEMS gyroscope bias drift cancellation using continuous-time mode reversal. In Proceedings of the 17th International Conference on Solid-State Sensors, Actuators and Microsystems (Transducers Eurosensors), Barcelona, Spain, 16–20 June 2013; pp. 1855–1858. [Google Scholar]
- Taheri-Tehrani, P.; Challoner, A.D.; Horsley, D.A. Micromechanical rate integrating gyroscope with angle-dependent bias compensation using a self-precession method. IEEE Sens. J. 2018, 18, 3533–3543. [Google Scholar] [CrossRef]
- Bernstein, J.J.; Bancu, M.G.; Bauer, J.M.; Cook, E.H.; Kumar, P.; Newton, E.; Nyinjee, T.; Perlin, G.E.; Ricker, J.A.; Teynor, W.A.; et al. High Q diamond hemispherical resonators: Fabrication and energy loss mechanisms. J. Micromech. Microeng. 2015, 25, 085006. [Google Scholar] [CrossRef]
- Ren, X.; Zhou, X.; Tao, Y.; Li, Q.; Wu, X.; Xiao, D. Radially pleated disk resonator for gyroscopic application. J. Microelectromech. Syst. 2021, 30, 825–835. [Google Scholar] [CrossRef]
- Zega, V.; Comi, C.; Fedeli, P.; Frangi, A.; Corigliano, A.; Minotti, P.; Langfelder, G.; Falorni, L.; Tocchio, A. A dual-mass frequency-modulated (FM) pitch gyroscope: Mechanical design and modelling. In Proceedings of the IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Lake Como, Italy, 26–29 March 2018; pp. 1–4. [Google Scholar]
- Zega, V.; Comi, C.; Minotti, P.; Langfelder, G.; Falorni, L.; Corigliano, A. A new MEMS three-axial frequency-modulated (FM) gyroscope: A mechanical perspective. Eur. J. Mech.-A/Solids 2018, 70, 203–212. [Google Scholar] [CrossRef]
- Izyumin, I.; Kline, M.; Yeh, Y.C.; Eminoglu, B.; Boser, B. A 50 μW, 2.1 mdeg/s/ frequency-to-digital converter for frequency-output MEMS gyroscopes. In Proceedings of the 2014–40th European Solid-State Circuits Conference (ESSCIRC), Venice, Italy, 22–26 September 2014; pp. 399–402. [Google Scholar]
- Leoncini, M.; Bestetti, M.; Bonfanti, A.; Facchinetti, S.; Minotti, P.; Langfelder, G. Fully Integrated, 406 μA, 5 °/h, Full Digital Output Lissajous Frequency-Modulated Gyroscope. IEEE Trans. Ind. Electron. 2018, 66, 7386–7396. [Google Scholar] [CrossRef]
- Wang, X.; Zheng, X.; Shen, Y.; Xia, C.; Liu, G.; Jin, Z.; Ma, Z. A Digital Control Structure for Lissajous Frequency-Modulated Mode MEMS Gyroscope. IEEE Sens. J. 2022, 22, 19207–19219. [Google Scholar] [CrossRef]
- Bestetti, M.; Bonfanti, A.G.; Falorni, L.; Gianollo, M.; Padovani, C.; Langfelder, G. Full-digital output ASIC for Lissajous Frequency Modulated MEMS Gyroscopes. In Proceedings of the IEEE International Conference on Electronics, Circuits and Systems (ICECS), Glasgow, UK, 24–26 October 2022; pp. 1–4. [Google Scholar]
- Wang, P.; Li, Q.; Xu, Y.; Zhang, Y.; Xi, X.; Wu, Y.; Wu, X.; Xiao, D. Calibration of coupling errors for scale factor nonlinearity improvement in navigation-grade honeycomb disk resonator gyroscope. IEEE Trans. Ind. Electron. 2022, 70, 5347–5355. [Google Scholar] [CrossRef]
- Zotov, S.; Prikhodko, I.; Simon, B.; Trusov, A.; Shkel, A. Self-calibrated MEMS gyroscope with AM/FM operational modes, dynamic range of 180 dB and in-run bias stability of 0.1 deg/hr. In Proceedings of the DGON Inertial Sensors and Systems (ISS), Karlsruhe, Germany, 16–17 September 2014; pp. 1–17. [Google Scholar]
- Sabater, A.B.; Moran, K.M. Angle random walk minimization for frequency modulated gyroscopes. In Proceedings of the IEEE International Symposium on Inertial Sensors and Systems, Naples, FL, USA, 1–5 April 2019; pp. 1–4. [Google Scholar]
- Bordiga, E.; Bestetti, M.; Langfelder, G. AGC-less operation of high-stability Lissajous frequency-modulated MEMS gyroscopes. In Proceedings of the 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors (Transducers Eurosensors), Berlin, Germany, 23–27 June 2019; pp. 594–597. [Google Scholar]
- Bestetti, M.; Mussi, G.; Padovani, C.; Donadel, A.; Valzasina, C.; Langfelder, G.; Bonfanti, A.G. On amplitude-gain-control optimization for Lissajous frequency modulated MEMS gyroscopes. In Proceedings of the IEEE Sensors, Sydney, Australia, 31 October–3 November 2021; pp. 1–4. [Google Scholar]
- Alattas, K.A.; Mohammadzadeh, A.; Mobayen, S.; Aly, A.A.; Felemban, B.F.; Vu, M.T. A new data-driven control system for MEMSs gyroscopes: Dynamics estimation by type-3 fuzzy systems. Micromachines 2021, 12, 1390. [Google Scholar] [CrossRef]
- Jafari, M.; Mobayen, S.; Roth, H.; Bayat, F. Nonsingular terminal sliding mode control for micro-electro-mechanical gyroscope based on disturbance observer: Linear matrix inequality approach. J. Vib. Control 2022, 28, 1126–1134. [Google Scholar] [CrossRef]
- Fei, J.; Wang, Z.; Liang, X.; Feng, Z.; Xue, Y. Fractional sliding-mode control for microgyroscope based on multilayer recurrent fuzzy neural network. IEEE Trans. Fuzzy Syst. 2021, 30, 1712–1721. [Google Scholar] [CrossRef]
- Ruan, Z.; Ding, X.; Pu, Y.; Gao, Y.; Li, H. In-Run Automatic Mode-Matching of Whole-Angle Micro-Hemispherical Resonator Gyroscope Based on Standing Wave Self-Precession. IEEE Sens. J. 2022, 22, 13945–13957. [Google Scholar] [CrossRef]
- Liu, X.; Qin, Z.; Li, H. Online Compensation of Phase Delay Error Based on PF Characteristic for MEMS Vibratory Gyroscopes. Micromachines 2022, 13, 647. [Google Scholar] [CrossRef]
- Sun, J.; Liu, K.; Yu, S.; Zhang, Y.; Xi, X.; Lu, K.; Shi, Y.; Wu, X.; Xiao, D. Identification and Correction of Phase Error for Whole-angle Micro-shell Resonator Gyroscope. IEEE Sens. J. 2022, 22, 19228–19236. [Google Scholar] [CrossRef]
- Zheng, X.; Wang, X.; Shen, Y.; Xia, C.; Tong, W.; Jin, Z.; Ma, Z. Identification and suppression of driving force misalignment angle for a MEMS gyroscope using parametric excitation. J. Micromech. Microeng. 2023, 33, 055002. [Google Scholar] [CrossRef]
- Lynch, D.D. Vibratory gyro analysis by the method of averaging. In Proceedings of the 2nd St. Petersburg Conference on Gyroscopic Technology and Navigation, St. Petersburg, Russia, 24–25 May 1995; pp. 26–34. [Google Scholar]
- Saukoski, M.; Aaltonen, L.; Halonen, K.A. Zero-rate output and quadrature compensation in vibratory MEMS gyroscopes. IEEE Sens. J. 2007, 7, 1639–1652. [Google Scholar] [CrossRef]














| Signal Flow Point | Signal Flow Phase |
|---|---|
| O | |
| A | |
| B | |
| C | |
| D | |
| E 1 |
| Symbol | Description | Value | Unit |
|---|---|---|---|
| primary modal frequency | 4955.5 × 2 | rad | |
| secondary modal frequency | 4975.5 × 2 | rad | |
| initial frequency split | 20 × 2 | rad | |
| primary modal quality factor | 50,000 | ||
| secondary modal quality factor | 48,000 | ||
| azimuth of principal stiffness axis | 1.5 | deg | |
| azimuth of principal damping axis | 5 | deg | |
| system phase error | 5 | deg | |
| initial demodulation phase shift | /3 | rad |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Wang, X.; Yan, K.; Chen, Z.; Ma, Z.; Wang, X.; Zhang, A.; Lu, Q. Interactive Errors Analysis and Scale Factor Nonlinearity Reduction Methods for Lissajous Frequency Modulated MEMS Gyroscope. Sensors 2023, 23, 9701. https://0-doi-org.brum.beds.ac.uk/10.3390/s23249701
Li R, Wang X, Yan K, Chen Z, Ma Z, Wang X, Zhang A, Lu Q. Interactive Errors Analysis and Scale Factor Nonlinearity Reduction Methods for Lissajous Frequency Modulated MEMS Gyroscope. Sensors. 2023; 23(24):9701. https://0-doi-org.brum.beds.ac.uk/10.3390/s23249701
Chicago/Turabian StyleLi, Rui, Xiaoxu Wang, Kaichen Yan, Zhennan Chen, Zhengya Ma, Xiquan Wang, Ao Zhang, and Qianbo Lu. 2023. "Interactive Errors Analysis and Scale Factor Nonlinearity Reduction Methods for Lissajous Frequency Modulated MEMS Gyroscope" Sensors 23, no. 24: 9701. https://0-doi-org.brum.beds.ac.uk/10.3390/s23249701