City-Specific Spatiotemporal Infant and Neonatal Mortality Clusters: Links with Socioeconomic and Air Pollution Spatial Patterns in France
Abstract
:1. Introduction
2. Methods
2.1. Study Setting and Population
2.1.1. MAs
2.1.2. Study Population
2.2. Potential Risk Factors
2.2.1. Deprivation Index
2.2.2. Traffic Exposure Assessment
2.3. Statistical Methods
2.3.1. Spatial Analysis
2.3.2. Global and Local Spatial Analysis
3. Results
3.1. Social Heath Inequality Trends
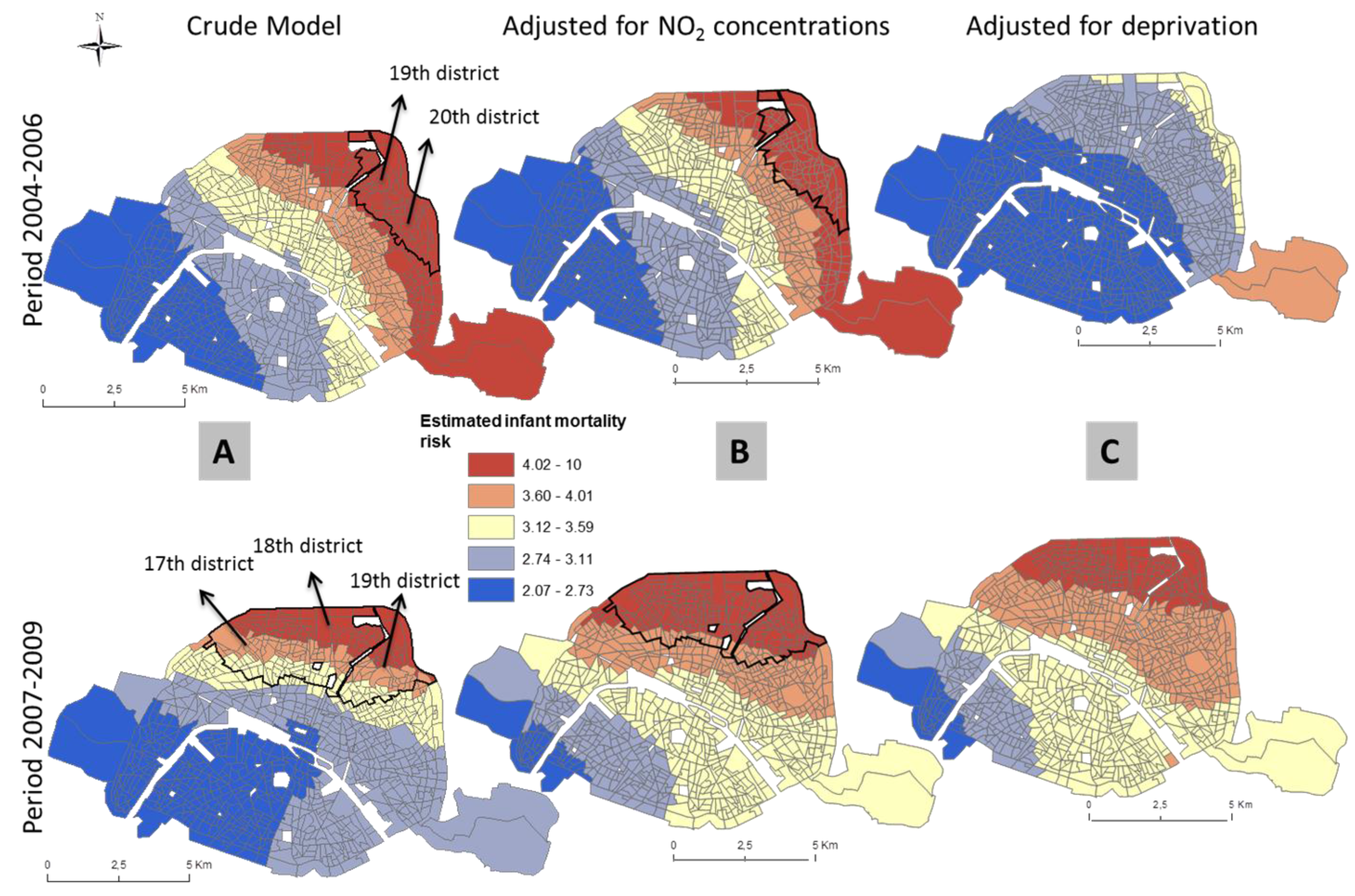
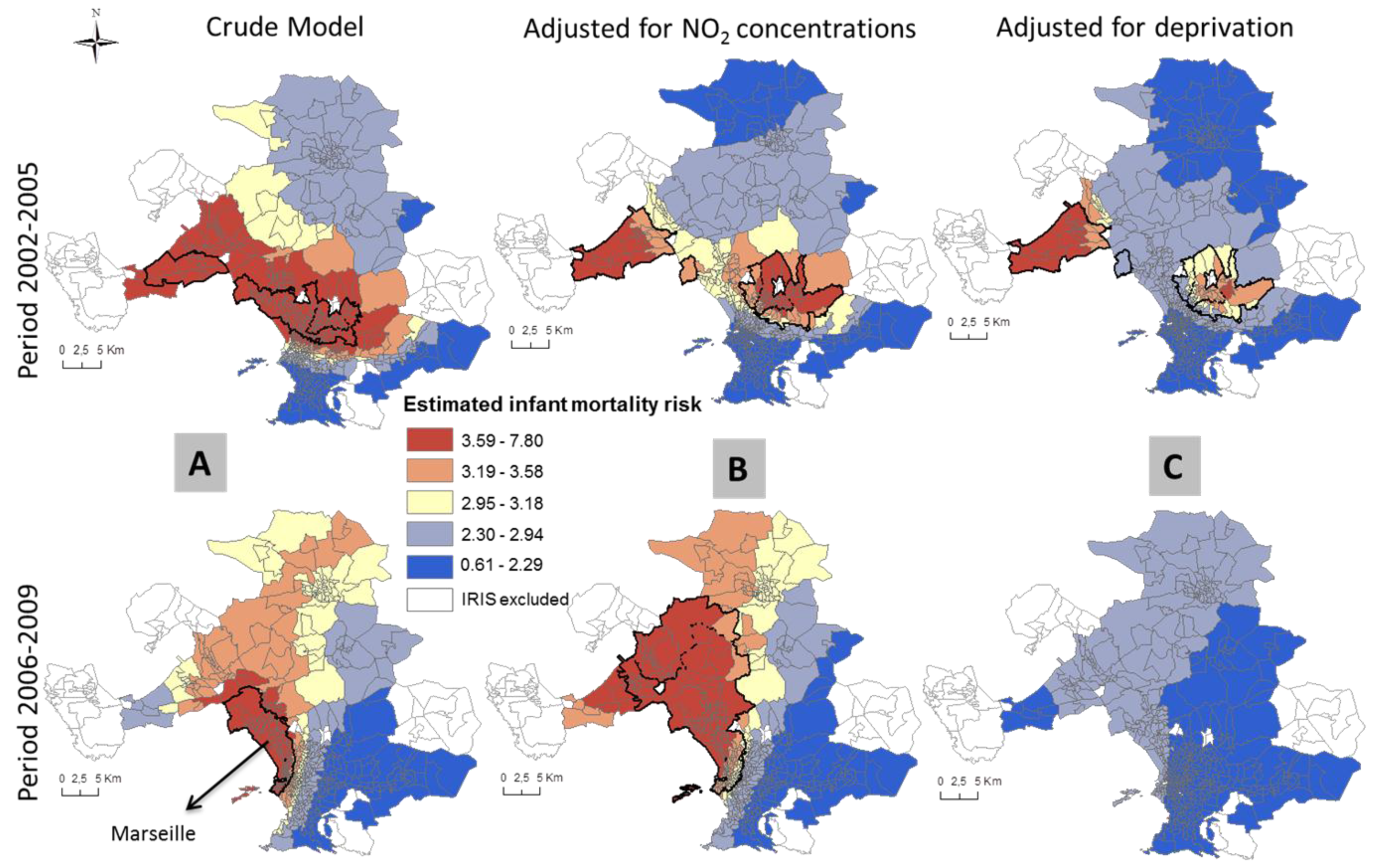
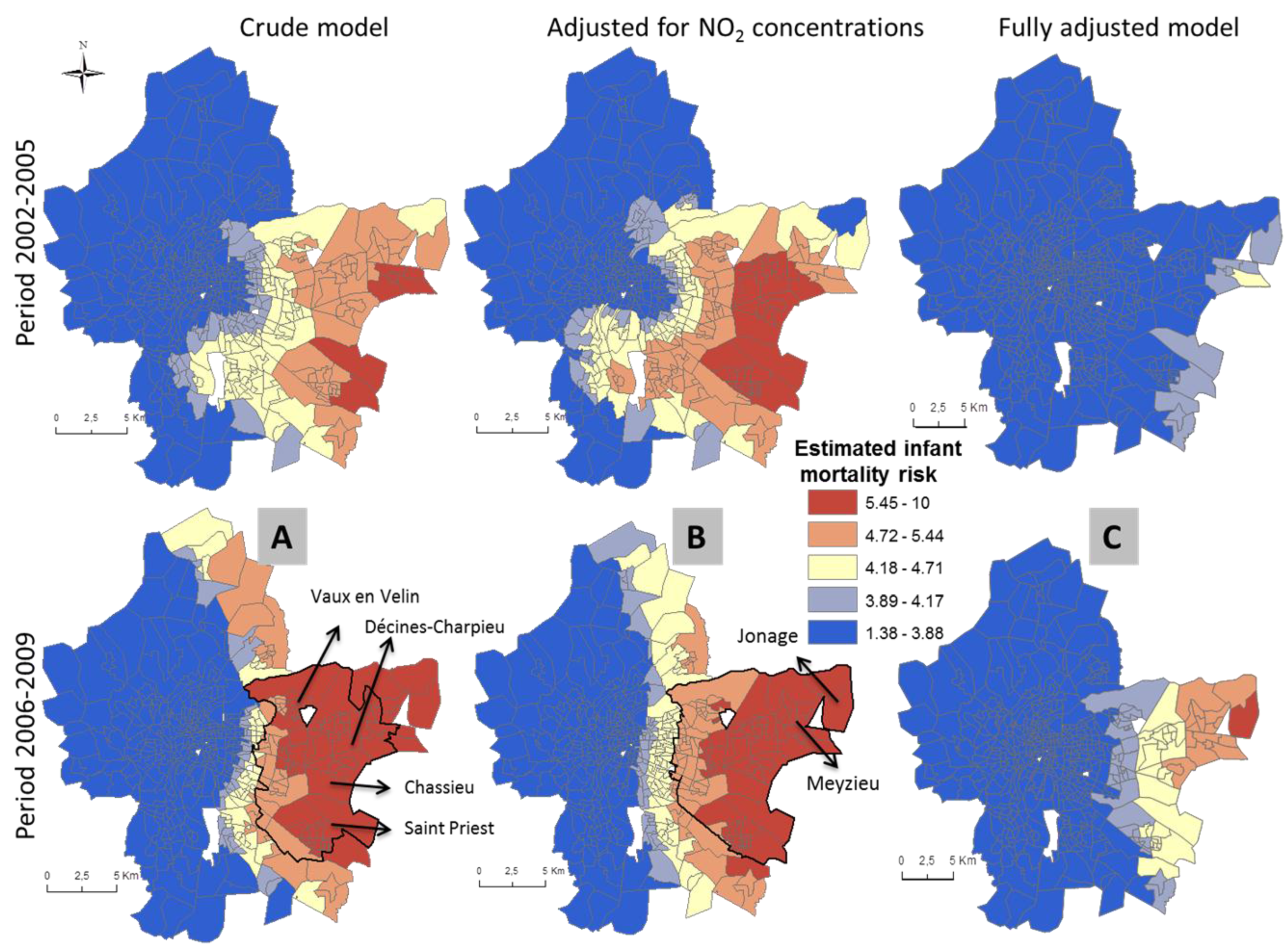
3.2. Patterns of Spatial Variation in Health Risk
4. Discussion
4.1. Trends in Inequalities
4.2. Spatial Inequalities
4.3. Usefulness of Spatial Analysis in Public Health
4.4. Relevance of Infectious Disease to Spatial Analysis
4.5. Strengths and Limitations
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- OECD Data, Health Status, Infant Mortality Rates. Available online: https://data.oecd.org/healthstat/infant-mortality-rates.htm (accessed on 20 June 2016).
- Institute of Medicine (US) Committee on Understanding Premature Birth and Assuring Healthy Outcomes. Preterm Birth: Causes, Consequences, and Prevention; Behrman, R.E., Butler, A.S., Eds.; The National Academies Collection: Reports Funded by National Institutes of Health; National Academies Press (US): Washington, DC, USA, 2007. [Google Scholar]
- National Vital Statistics Reports; Volume 55, Number 14 (Revisied 13 June 2007). Available online: http://www.cdc.gov/nchs/data/nvsr/nvsr55/nvsr55_14.pdf (accessed on 20 June 2016).
- National Vital Statistics Reports; Volume 57, Number 2 (30 July 2008). Available online: https://www.cdc.gov/nchs/data/nvsr/nvsr57/nvsr57_02.pdf (accessed on 20 June 2016).
- Lawn, J.E.; Gravett, M.G.; Nunes, T.M.; Rubens, C.E.; Stanton, C.; GAPPS Review Group. GAPPS Review Group Global report on preterm birth and stillbirth (1 of 7): Definitions, description of the burden and opportunities to improve data. BMC Pregnancy Childbirth 2010, 10. [Google Scholar] [CrossRef] [PubMed]
- Prioux, F.; Barbieri, M. Recent Demographic developments in France: Relatively low mortality at advanced ages. Population 2012, 67. [Google Scholar] [CrossRef] [PubMed]
- Euro-Peristat Project. European Perinatal Health Report 2010. Available online: http://www.europeristat.com (accessed on 20 June 2016).
- Borrell, C.; Cirera, E.; Ricart, M.; Pasarín, M.I.; Salvador, J. Social inequalities in perinatal mortality in a Southern European city. Eur. J. Epidemiol. 2003, 18, 5–13. [Google Scholar] [CrossRef] [PubMed]
- Agyemang, C.; Vrijkotte, T.G.M.; Droomers, M.; van der Wal, M.F.; Bonsel, G.J.; Stronks, K. The effect of neighbourhood income and deprivation on pregnancy outcomes in Amsterdam, The Netherlands. J. Epidemiol. Community Health 2009, 63, 755–760. [Google Scholar] [CrossRef] [PubMed]
- Calling, S.; Li, X.; Sundquist, J.; Sundquist, K. Socioeconomic inequalities and infant mortality of 46,470 preterm infants born in Sweden between 1992 and 2006. Paediatr. Perinat. Epidemiol. 2011, 25, 357–365. [Google Scholar] [CrossRef] [PubMed]
- Grady, S.C. Racial disparities in low birthweight and the contribution of residential segregation: A multilevel analysis. Soc. Sci. Med. 2006, 63, 3013–3029. [Google Scholar] [CrossRef] [PubMed]
- Grady, S.C.; Enander, H. Geographic analysis of low birthweight and infant mortality in Michigan using automated zoning methodology. Int. J. Health Geogr. 2009, 8, 10. [Google Scholar] [CrossRef] [PubMed]
- Tsai, S.-S.; Chen, C.-C.; Hsieh, H.-J.; Chang, C.-C.; Yang, C.-Y. Air pollution and postneonatal mortality in a tropical city: Kaohsiung, Taiwan. Inhal. Toxicol. 2006, 18, 185–189. [Google Scholar] [CrossRef] [PubMed]
- Ritz, B.; Wilhelm, M.; Zhao, Y. Air pollution and infant death in southern California, 1989–2000. Pediatrics 2006, 118, 493–502. [Google Scholar] [CrossRef] [PubMed]
- Hajat, S.; Armstrong, B.; Wilkinson, P.; Busby, A.; Dolk, H. Outdoor air pollution and infant mortality: Analysis of daily time-series data in 10 English cities. J. Epidemiol. Community Health 2007, 61, 719–722. [Google Scholar] [CrossRef] [PubMed]
- Woodruff, T.J.; Darrow, L.A.; Parker, J.D. Air pollution and postneonatal infant mortality in the United States, 1999–2002. Environ. Health Perspect. 2008, 116, 110–115. [Google Scholar] [CrossRef] [PubMed]
- Vrijheid, M.; Casas, M.; Bergstrom, A.; Carmichael, A.; Cordier, S.; Eggesbø, M.; Eller, E.; Fantini, M.P.; Fernández, M.F.; Fernández-Somoano, A.; et al. European birth cohorts for environmental health research. Environ. Health Perspect. 2012, 120, 29–37. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Root, E.D.; Meyer, R.E.; Emch, M.E. Evidence of localized clustering of gastroschisis births in North Carolina, 1999–2004. Soc. Sci. Med. 2009, 68, 1361–1367. [Google Scholar] [CrossRef] [PubMed]
- Padilla, C.M.; Deguen, S.; Lalloue, B.; Blanchard, O.; Beaugard, C.; Troude, F.; Navier, D.Z.; Vieira, V.M. Cluster analysis of social and environment inequalities of infant mortality. A spatial study in small areas revealed by local disease mapping in France. Sci. Total Environ. 2013, 454–455, 433–441. [Google Scholar] [CrossRef] [PubMed]
- Kihal-Talantikite, W.; Padilla, C.M.; Lalloue, B.; Rougier, C.; Defrance, J.; Zmirou-Navier, D.; Deguen, S. An exploratory spatial analysis to assess the relationship between deprivation, noise and infant mortality: An ecological study. Environ. Health Glob. Access Sci. Source 2013, 12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meng, G.; Hall, G.B.; Thompson, M.E.; Seliske, P. Spatial and environmental impacts on adverse birth outcomes in Ontario. Can. Geogr. 2013, 57, 154–172. [Google Scholar] [CrossRef]
- Congdon, P.; Southall, H. Small area variations in infant mortality in England and Wales in the inter-war period and their link with socio-economic factors. Health Place 2004, 10, 363–382. [Google Scholar] [CrossRef] [PubMed]
- Arntzen, A.; Samuelsen, S.O.; Bakketeig, L.S.; Stoltenberg, C. Socioeconomic status and risk of infant death. A population-based study of trends in Norway, 1967–1998. Int. J. Epidemiol. 2004, 33, 279–288. [Google Scholar] [CrossRef] [PubMed]
- Arntzen, A.; Mortensen, L.; Schnor, O.; Cnattingius, S.; Gissler, M.; Andersen, A.-M.N. Neonatal and postneonatal mortality by maternal education—A population-based study of trends in the Nordic countries, 1981–2000. Eur. J. Public Health 2008, 18, 245–251. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Singh, G.K.; Kogan, M.D. Persistent socioeconomic disparities in infant, neonatal, and postneonatal mortality rates in the United States, 1969–2001. Pediatrics 2007, 119, e928–e939. [Google Scholar] [CrossRef] [PubMed]
- Sovio, U.; Dibden, A.; Koupil, I. Social determinants of infant mortality in a historical Swedish cohort. Paediatr. Perinat. Epidemiol. 2012, 26, 408–420. [Google Scholar] [CrossRef] [PubMed]
- Padilla, C.M.; Kihal-Talantikite, W.; Vieira, V.M.; Rossello, P.; Le Nir, G.; Zmirou-Navier, D.; Deguen, S. Air quality and social deprivation in four French metropolitan areas—A localized spatio-temporal environmental inequality analysis. Environ. Res. 2014, 134, 315–324. [Google Scholar] [CrossRef] [PubMed]
- INSEE Découpage infracommunal en IRIS. Available online: http://www.insee.fr/fr/methodes/default.asp?page=zonages/iris.htm (accessed on 20 June 2016).
- Geographic Terms and Concepts—Block Groups. Available online: https://www.census.gov/geo/reference/gtc/gtc_bg.html (accessed on 20 June 2016).
- Lalloué, B.; Monnez, J.-M.; Padilla, C.; Kihal, W.; Le Meur, N.; Zmirou-Navier, D.; Deguen, S. A statistical procedure to create a neighborhood socioeconomic index for health inequalities analysis. Int. J. Equity Health 2013, 12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McHugh, C.; Carruthers, D.; Edmunds, H. ADMS-Urban: An air quality management system for traffic, domestic and industrial pollution. Int. J. Environ. Pollut. 1997, 8, 437–440. [Google Scholar]
- Carruthers, D.J.; Edmunds, H.A.; Lester, A.E.; McHugh, C.A.; Singles, R.J. Use and validation of ADMS-Urban in contrasting urban and industrial locations. Int. J. Environ. Pollut. 2000, 14, 364–374. [Google Scholar] [CrossRef]
- Soulhac, L.; Salizzoni, P.; Cierco, F.-X.; Perkins, R. The model SIRANE for atmospheric urban pollutant dispersion; part I, presentation of the model. Atmos. Environ. 2011, 45, 7379–7395. [Google Scholar] [CrossRef]
- Soulhac, L.; Salizzoni, P.; Mejean, P.; Didier, D.; Rios, I. The model SIRANE for atmospheric urban pollutant dispersion; PART II, validation of the model on a real case study. Atmos. Environ. 2012, 49, 320–337. [Google Scholar] [CrossRef]
- Chaix, B.; Gustafsson, S.; Jerrett, M.; Kristersson, H.; Lithman, T.; Boalt, A.; Merlo, J. Children’s exposure to nitrogen dioxide in Sweden: Investigating environmental injustice in an egalitarian country. J. Epidemiol. Community Health 2006, 60, 234–241. [Google Scholar] [CrossRef] [PubMed]
- Yanosky, J.D.; Schwartz, J.; Suh, H.H. Associations between measures of socioeconomic position and chronic nitrogen dioxide exposure in Worcester, Massachusetts. J. Toxicol. Environ. Health A 2008, 71, 1593–1602. [Google Scholar] [CrossRef] [PubMed]
- Crouse, D.L.; Ross, N.A.; Goldberg, M.S. Double burden of deprivation and high concentrations of ambient air pollution at the neighbourhood scale in Montreal, Canada. Soc. Sci. Med. 2009, 69, 971–981. [Google Scholar] [CrossRef] [PubMed]
- Ritz, B.; Wilhelm, M. Ambient air pollution and adverse birth outcomes: Methodologic issues in an emerging field. Basic Clin. Pharmacol. Toxicol. 2008, 102, 182–190. [Google Scholar] [CrossRef] [PubMed]
- Brauer, M.; Lencar, C.; Tamburic, L.; Koehoorn, M.; Demers, P.; Karr, C. A cohort study of traffic-related air pollution impacts on birth outcomes. Environ. Health Perspect. 2008, 116, 680–686. [Google Scholar] [CrossRef] [PubMed]
- Darrow, L.A.; Klein, M.; Flanders, W.D.; Waller, L.A.; Correa, A.; Marcus, M.; Mulholland, J.A.; Russell, A.G.; Tolbert, P.E. Ambient air pollution and preterm birth: A time-series analysis. Epidemiology 2009, 20, 689–698. [Google Scholar] [CrossRef] [PubMed]
- Shah, P.S.; Balkhair, T. Knowledge synthesis group on determinants of preterm/LBW births air pollution and birth outcomes: A systematic review. Environ. Int. 2011, 37, 498–516. [Google Scholar] [CrossRef] [PubMed]
- Stieb, D.M.; Chen, L.; Eshoul, M.; Judek, S. Ambient air pollution, birth weight and preterm birth: A systematic review and meta-analysis. Environ. Res. 2012, 117, 100–111. [Google Scholar] [CrossRef] [PubMed]
- Maroziene, L.; Grazuleviciene, R. Maternal exposure to low-level air pollution and pregnancy outcomes: A population-based study. Environ. Health Glob. Access Sci. Source 2002, 1, 6. [Google Scholar]
- Vieira, V.; Webster, T.; Weinberg, J.; Aschengrau, A. Spatial-temporal analysis of breast cancer in upper Cape Cod, Massachusetts. Int. J. Health Geogr. 2008, 7, 46. [Google Scholar] [CrossRef] [PubMed]
- Webster, T.; Hoffman, K.; Weinberg, J.; Vieira, V.; Aschengrau, A. Community- and Individual-level socioeconomic status and breast cancer risk: Multilevel modeling on Cape Cod, Massachusetts. Environ. Health Perspect. 2008, 116, 1125–1129. [Google Scholar] [CrossRef] [PubMed]
- Vieira, V.; Webster, T.; Weinberg, J.; Aschengrau, A. Spatial analysis of bladder, kidney, and pancreatic cancer on upper Cape Cod: An application of generalized additive models to case-control data. Environ. Health 2009, 8, 3. [Google Scholar] [CrossRef] [PubMed]
- Kiffer, C.R.V.; Camargo, E.C.G.; Shimakura, S.E.; Ribeiro, P.J., Jr.; Bailey, T.C.; Pignatari, A.C.; Monteiro, A.M. A spatial approach for the epidemiology of antibiotic use and resistance in community-based studies: The emergence of urban clusters of Escherichia coli quinolone resistance in Sao Paulo, Brasil. Int. J. Health Geogr. 2011, 10, 17. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wood, S.N. Generalized Additive Models: An Introduction with R; Chapman and Hall/CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Wood, S.N. Stable and efficient multiple smoothing parameter estimation for generalized additive models. J. Am. Stat. Assoc. 2004, 99, 673–686. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R. Generalized Additive Models; Chapman and Hall: London, UK, 1990. [Google Scholar]
- Kelsall, J.; Wakefield, J. Modeling spatial variation in risk: A geostatistical approach. Am. Stat. Assoc. 2002, 97, 692–701. [Google Scholar] [CrossRef]
- Vieira, V.; Webster, T.; Weinberg, J.; Aschengrau, A.; Ozonoff, D. Spatial analysis of lung, colorectal, and breast cancer on Cape Cod: An application of generalized additive models to case-control data. Environ. Health Glob. Access Sci. Source 2005, 4, 11. [Google Scholar]
- Webster, T.; Vieira, V.; Weinberg, J.; Aschengrau, A. Method for mapping population-based case-control studies: An application using generalized additive models. Int. J. Health Geogr. 2006, 5, 26. [Google Scholar] [CrossRef] [PubMed]
- Vieira, V.; Webster, T.; Aschengrau, A.; Ozonoff, D. A method for spatial analysis of risk in a population-based case-control study. Int. J. Hyg. Environ. Health 2002, 205, 115–120. [Google Scholar] [CrossRef] [PubMed]
- Young, R.; Weinberg, J.; Vieira, V.; Aschengrau, A.; Webster, T. A multilevel non-hierarchical study of birth weight and socioeconomic status. Int. J. Health Geogr. 2010, 9, 36. [Google Scholar] [CrossRef] [PubMed]
- Glinianaia, S.V.; Ghosh, R.; Rankin, J.; Pearce, M.S.; Parker, L.; Pless-Mulloli, T. No improvement in socioeconomic inequalities in birthweight and preterm birth over four decades: A population-based cohort study. BMC Public Health 2013, 13, 345. [Google Scholar] [CrossRef] [PubMed]
- Smith, L.K.; Manktelow, B.N.; Draper, E.S.; Springett, A.; Field, D.J. Nature of socioeconomic inequalities in neonatal mortality: Population based study. BMJ 2010, 341, c6654. [Google Scholar] [CrossRef] [PubMed]
- O’Neill, M.S.; Jerrett, M.; Kawachi, I.; Levy, J.I.; Cohen, A.J.; Gouveia, N.; Wilkinson, P.; Fletcher, T.; Cifuentes, L.; Schwartz, J. Health, wealth, and air pollution: Advancing theory and methods. Environ. Health Perspect. 2003, 111, 1861–1870. [Google Scholar] [CrossRef] [PubMed]
- Ponce, N.A.; Hoggatt, K.J.; Wilhelm, M.; Ritz, B. Preterm birth: The interaction of traffic-related air pollution with economic hardship in Los Angeles neighborhoods. Am. J. Epidemiol. 2005, 162, 140–148. [Google Scholar] [CrossRef] [PubMed]
- Carbajal-Arroyo, L.; Miranda-Soberanis, V.; Medina-Ramón, M.; Rojas-Bracho, L.; Tzintzun, G.; Solís-Gutiérrez, P.; Méndez-Ramírez, I.; Hurtado-Díaz, M.; Schwartz, J.; Romieu, I. Effect of PM(10) and O(3) on infant mortality among residents in the Mexico city Metropolitan area: A case-crossover analysis, 1997–2005. J. Epidemiol. Community Health 2011, 65, 715–721. [Google Scholar] [CrossRef] [PubMed]
- Jørgensen, T.; Mortensen, L.H.; Andersen, A.-M.N. Social inequality in fetal and perinatal mortality in the Nordic countries. Scand. J. Public Health 2008, 36, 635–649. [Google Scholar] [CrossRef] [PubMed]
- Bell, M.L.; Ebisu, K.; Belanger, K. Ambient air pollution and low birth weight in Connecticut and Massachusetts. Environ. Health Perspect. 2007, 115, 1118–1124. [Google Scholar] [CrossRef] [PubMed]
- Miranda, M.L.; Maxson, P.; Edwards, S. Environmental contributions to disparities in pregnancy outcomes. Epidemiol. Rev. 2009, 31, 67–83. [Google Scholar] [CrossRef] [PubMed]
- Slama, R.; Thiebaugeorges, O.; Goua, V.; Aussel, L.; Sacco, P.; Bohet, A.; Forhan, A.; Ducot, B.; Annesi-Maesano, I.; Heinrich, J.; et al. Maternal personal exposure to airborne benzene and intrauterine growth. Environ. Health Perspect. 2009, 117, 1313–1321. [Google Scholar] [CrossRef] [PubMed]
- Weck, R.L.; Paulose, T.; Flaws, J.A. Impact of environmental factors and poverty on pregnancy outcomes. Clin. Obstet. Gynecol. 2008, 51, 349–359. [Google Scholar] [CrossRef] [PubMed]
- Slama, R.; Darrow, L.; Parker, J.; Woodruff, T.J.; Strickland, M.; Nieuwenhuijsen, M.; Glinianaia, S.; Hoggatt, K.J.; Kannan, S.; Hurley, F.; et al. Meeting report: Atmospheric pollution and human reproduction. Environ. Health Perspect. 2008, 116, 791–798. [Google Scholar] [CrossRef] [PubMed]
- Breeze, A.C. Infectious diseases of the fetus and newborn infant, 6th edn. Arch. Dis. Child. Fetal Neonatal Ed. 2007, 92, F156. [Google Scholar] [CrossRef]
- Rapport D’information sur les Nouvelles Menaces des Maladies Infectieuses Émergentes. Available online: http://www.senat.fr/rap/r11-638/r11-6381.pdf (accessed on 20 June 2016).
- Nkoghe, D.; Padilla, C.; Becquart, P.; Wauquier, N.; Moussavou, G.; Akué, J.P.; Ollomo, B.; Pourrut, X.; Souris, M.; Kazanji, M.; et al. Risk factors for Zaire ebolavirus—Specific IgG in rural Gabonese populations. J. Infect. Dis. 2011, 204, S768–S775. [Google Scholar] [CrossRef] [PubMed]
- Green, C.G.; Krause, D.O.; Wylie, J.L. Spatial analysis of campylobacter infection in the Canadian province of Manitoba. Int. J. Health Geogr. 2006, 5, 2. [Google Scholar] [CrossRef] [PubMed]
- Louis, V.R.; Phalkey, R.; Horstick, O.; Ratanawong, P. Modeling tools for dengue risk mapping—A systematic review. Int. J. Health Geogr. 2014, 13, 50. [Google Scholar] [CrossRef] [PubMed]
- Weisent, J.; Rohrbach, B.; Dunn, J.R.; Odoi, A. Socioeconomic determinants of geographic disparities in campylobacteriosis risk: A comparison of global and local modeling approaches. Int. J. Health Geogr. 2012, 11, 45. [Google Scholar] [CrossRef] [PubMed]
- Almeida, A.S.; Werneck, G.L. Prediction of high-risk areas for visceral leishmaniasis using socioeconomic indicators and remote sensing data. Int. J. Health Geogr. 2014, 13, 13. [Google Scholar] [CrossRef] [PubMed]
- Carter, R.; Mendis, K.N.; Roberts, D. Spatial targeting of interventions against malaria. Bull. World Health Organ. 2000, 78, 1401–1411. [Google Scholar] [PubMed]
- Kuehl, K.S.; Loffredo, C.A. A cluster of hypoplastic left heart malformation in Baltimore, Maryland. Pediatr. Cardiol. 2006, 27, 25–31. [Google Scholar] [CrossRef] [PubMed]
- Vieira, V.M.; Weinberg, J.M.; Webster, T.F. Individual-level space-time analyses of emergency department data using generalized additive modeling. BMC Public Health 2012, 12, 687. [Google Scholar] [CrossRef] [PubMed]
- Cockings, S.; Martin, D. Zone design for environment and health studies using pre-aggregated data. Soc. Sci. Med. 2005, 60, 2729–2742. [Google Scholar] [CrossRef] [PubMed]
- Haynes, R.; Daras, K.; Reading, R.; Jones, A. Modifiable neighbourhood units, zone design and residents’ perceptions. Health Place 2007, 13, 812–825. [Google Scholar] [CrossRef] [PubMed]
- Flowerdew, R.; Manley, D.J.; Sabel, C.E. Neighbourhood effects on health: Does it matter where you draw the boundaries? Soc. Sci. Med. 2008, 66, 1241–1255. [Google Scholar] [CrossRef] [PubMed]
- Jerrett, M.; Gale, S.; Kontgis, C. Spatial modeling in environmental and public health research. Int. J. Environ. Res. Public Health 2010, 7, 1302–1329. [Google Scholar] [CrossRef] [PubMed]
- Nkansah-Amankra, S.; Luchok, K.J.; Hussey, J.R.; Watkins, K.; Liu, X. Effects of maternal stress on low birth weight and preterm birth outcomes across neighborhoods of South Carolina, 2000–2003. Matern. Health J. 2010, 14, 215–226. [Google Scholar] [CrossRef] [PubMed]
- De Graaf, J.P.; Steegers, E.A.P.; Bonsel, G.J. Inequalities in perinatal and maternal health. Curr. Opin. Obstet. Gynecol. 2013, 25, 98–108. [Google Scholar] [CrossRef] [PubMed]
- Patra, J.; Bakker, R.; Irving, H.; Jaddoe, V.W.V.; Malini, S.; Rehm, J. Dose-response relationship between alcohol consumption before and during pregnancy and the risks of low birthweight, preterm birth and small for gestational age (SGA)-a systematic review and meta-analyses. BJOG Int. J. Obstet. Gynaecol. 2011, 118, 1411–1421. [Google Scholar] [CrossRef] [PubMed]
- O’Leary, C.M.; Nassar, N.; Kurinczuk, J.J.; Bower, C. The effect of maternal alcohol consumption on fetal growth and preterm birth. BJOG Int. J. Obstet. Gynaecol. 2009, 116, 390–400. [Google Scholar] [CrossRef] [PubMed]
- Northstone, K.; Emmett, P.; Rogers, I. Dietary patterns in pregnancy and associations with socio-demographic and lifestyle factors. Eur. J. Clin. Nutr. 2008, 62, 471–479. [Google Scholar] [CrossRef] [PubMed]
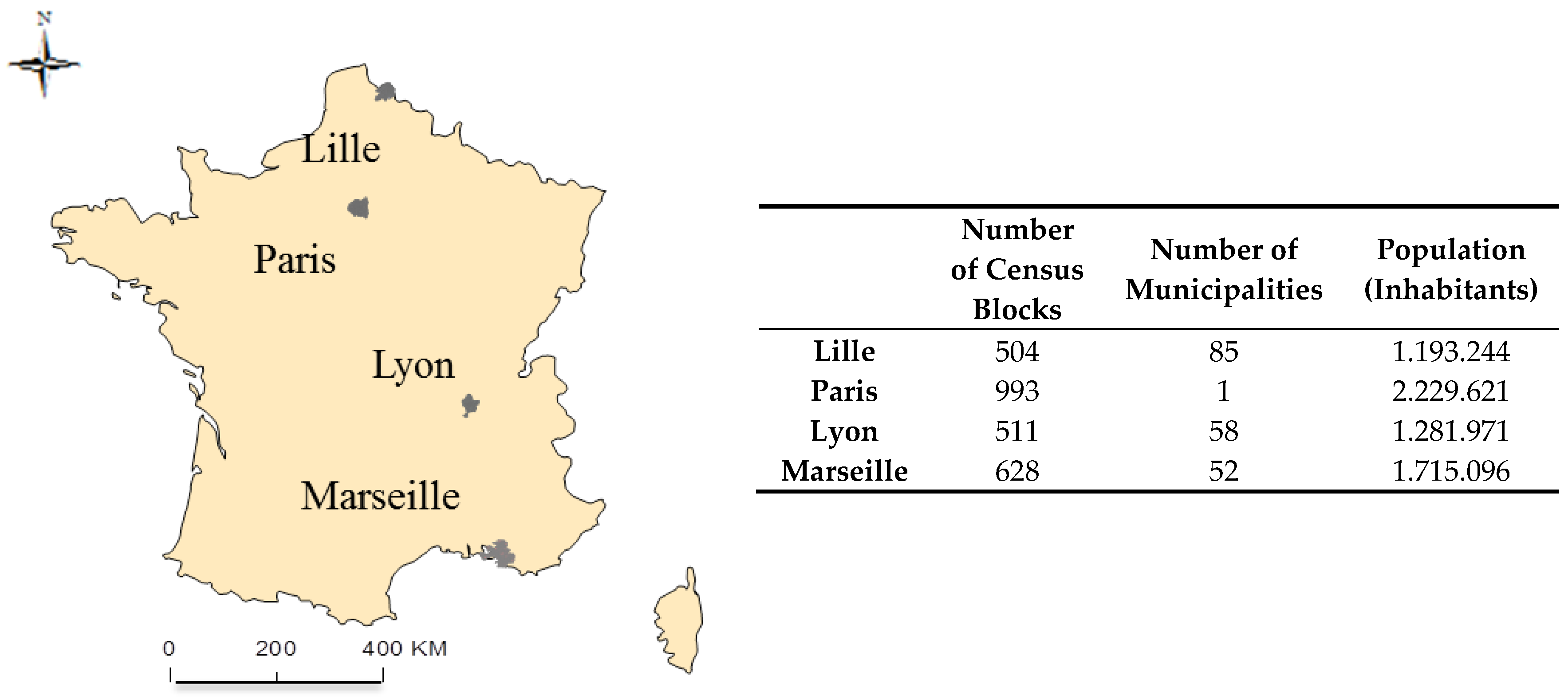

| Study Areas | Infant Mortality Rates (‰) | Neonatal Mortality Rates (‰) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | Most Deprived Census Blocks † | Least Deprived Census Blocks ‡ | Most Deprived Census Blocks | Least Deprived Census Blocks | |||||||||
| P1 * | P2 * | Percent Change (%) ** | P1 | P2 | Percent Change (%) | P1 | P2 | Percent Change (%) | P1 | P2 | Percent Change (%) | ||
| Lille | 472 | 5.85 | 5.26 | −10.10 | 2.65 | 2.93 | +10.36 | 4.20 | 3.51 | −16.53 | 1.75 | 2.30 | +31.93 |
| Lyon | 492 | 4.54 | 5.38 | +18.62 | 2.60 | 2.98 | +14.15 | 3.04 | 3.72 | +22.64 | 1.68 | 1.86 | +10.47 |
| Marseille | 565 | 4.32 | 3.81 | −11.72 | 2.29 | 1.98 | −13.60 | 2.37 | 2.58 | +9.01 | 1.57 | 1.05 | −33.15 |
| Paris city | 935 | 4.12 | 3.99 | −3.03 | 2.46 | 3.13 | +27.45 | 2.96 | 2.76 | −6.56 | 1.77 | 2.50 | +41.36 |
| (A) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Highest NO2 Census Blocks ‡ | Infant Mortality Rate (‰) | Neonatal Mortality Rate (‰) | |||||||||||
| Most Deprived Census Blocks † | Least Deprived Census Blocks † | Most Deprived Census Blocks | Least Deprived Census Blocks | ||||||||||
| N | P1 * | P2 * | Percent Change (%) ** | P1 | P2 | Percent Change (%) | P1 | P2 | Percent Change (%) | P1 | P2 | Percent Change (%) | |
| Lille | 472 | 5.91 | 5.49 | −7.09 | 3.78 | 4.48 | +18.34 | 4.58 | 3.82 | −16.52 | 2.91 | 3.28 | +12.82 |
| Lyon | 492 | 4.33 | 3.97 | −8.36 | 2.36 | 3.71 | +57.27 | 2.71 | 2.95 | +9.03 | 1.35 | 3.09 | +129.3 |
| Marseille | 565 | 3.72 | 4.54 | +21.97 | 0.0 | 4.84 | --- | 1.98 | 2.86 | +44.11 | 0.0 | 3.87 | --- |
| Paris city | 935 | 5.56 | 4.70 | −15.54 | 2.52 | 2.91 | +15.13 | 4.24 | 3.30 | −22.22 | 1.56 | 2.30 | +47.24 |
| (B) | |||||||||||||
| Lowest NO2 Census Blocks ‡ | Infant Mortality Rate (‰) | Neonatal Mortality Rate (‰) | |||||||||||
| Most Deprived Census Blocks | Least Deprived Census Blocks † | Most Deprived Census Blocks | Least Deprived Census Blocks | ||||||||||
| N | P1 * | P2 * | Percent Change (%) ** | P1 | P2 | Percent Change (%) | P1 | P2 | Percent Change (%) | P1 | P2 | Percent Change (%) | |
| Lille | 472 | 5.67 | 4.79 | −15.50 | 2.19 | 2.46 | +12.17 | 3.51 | 2.54 | −27.73 | 1.27 | 1.92 | +51.63 |
| Lyon | 492 | 6.16 | 6.96 | +12.8 | 3.10 | 3.40 | +9.90 | 4.75 | 4.92 | +3.37 | 2.18 | 1.80 | −17.32 |
| Marseille | 565 | 3.94 | 3.72 | −5.73 | 2.00 | 2.17 | +8.19 | 2.63 | 3.10 | +17.83 | 1.24 | 0.9 | −27.18 |
| Paris city | 935 | 3.81 | 4.10 | +7.68 | 2.37 | 3.01 | +27.21 | 2.61 | 2.71 | +4.03 | 1.86 | 2.41 | +29.52 |
| Infant Mortality | Lille | Lyon | Paris City | Marseille | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 * | P2 | P1 | P2 | P1 | P2 | P1 | P2 | ||||||||||
| Unadjusted models | Test homogeneity global p-value ** | 0.001 | 0.003 | 0.155 | 0.001 | 0.018 | 0.019 | 0.001 | 0.013 | ||||||||
| Number of Significant Areas | 2 | 1 | 0 | 1 | 1 | 1 | 2 | 1 | |||||||||
| Adjusted models | Span | p-value | Span | p-value | Span | p-value | Span | p-value | Span | p-value | Span | p-value | Span | p-value | Span | p-value | |
| Deprivation index | 0.95 | 0.519 † | 0.85 | 0.173 | 0.95 | 0.368 | 0.95 | 0.024 | 0.95 | 0.394 | 0.95 | 0.163 | 0.75 | 0.004 | 0.85 | 0.103 | |
| NO2 concentrations | 0.45 | 0.001 | 0.80 | 0.036 | 0.55 | 0.128 | 0.90 | 0.004 | 0.95 | 0.027 | 0.95 | 0.004 | 0.75 | 0.006 | 0.85 | 0.045 | |
| Deprivation index & NO2 concentrations | 0.95 | 0.522 | 0.85 | 0.223 | 0.95 | 0.545 | 0.95 | 0.109 | 0.95 | 0.329 | 0.95 | 0.079 | 0.75 | 0.032 | 0.95 | 0.073 | |
| Neonatal Mortality | Lille | Lyon | Paris City | Marseille | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 * | P2 | P1 | P2 | P1 | P2 | P1 | P2 | ||||||||||
| Unadjusted models | Test homogeneity global p-value ** | 0.035 | 0.357 | 0.357 | 0.028 | 0.062 | 0.747 | 0.001 | 0.093 | ||||||||
| Number of Significant Areas | 1 | 0 | 0 | 1 | 0 | 0 | 3 | 0 | |||||||||
| Adjusted models | Span | p-value | Span | p-value | Span | p-value | Span | p-value | Span | p-value | Span | p-value | Span | p-value | Span | p-value | |
| Deprivation index | 0.95 | 0.864 † | 0.95 | 0.679 | 0.95 | 0.494 | 0.95 | 0.126 | 0.95 | 0.466 | 0.95 | 0.948 | 0.75 | 0.002 | 0.95 | 0.422 | |
| NO2 concentrations | 0.40 | 0.173 | 0.95 | 0.738 | 0.95 | 0.348 | 0.95 | 0.059 | 0.95 | 0.077 | 0.95 | 0.777 | 0.75 | 0.001 | 0.95 | 0.314 | |
| Deprivation index & NO2 concentrations | 0.95 | 0.911 | 0.95 | 0.788 | 0.95 | 0.831 | 0.95 | 0.304 | 0.95 | 0.622 | 0.95 | 0.953 | 0.75 | 0.006 | 0.95 | 0.353 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Padilla, C.M.; Kihal-Talantikit, W.; Vieira, V.M.; Deguen, S. City-Specific Spatiotemporal Infant and Neonatal Mortality Clusters: Links with Socioeconomic and Air Pollution Spatial Patterns in France. Int. J. Environ. Res. Public Health 2016, 13, 624. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph13060624
Padilla CM, Kihal-Talantikit W, Vieira VM, Deguen S. City-Specific Spatiotemporal Infant and Neonatal Mortality Clusters: Links with Socioeconomic and Air Pollution Spatial Patterns in France. International Journal of Environmental Research and Public Health. 2016; 13(6):624. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph13060624
Chicago/Turabian StylePadilla, Cindy M., Wahida Kihal-Talantikit, Verónica M. Vieira, and Séverine Deguen. 2016. "City-Specific Spatiotemporal Infant and Neonatal Mortality Clusters: Links with Socioeconomic and Air Pollution Spatial Patterns in France" International Journal of Environmental Research and Public Health 13, no. 6: 624. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph13060624






