A Novel Ensemble Algorithm for Solar Power Forecasting Based on Kernel Density Estimation

Abstract

A novel ensemble algorithm based on kernel density estimation (KDE) is proposed to forecast distributed generation (DG) from renewable energy sources (RES). The proposed method relies solely on publicly available historical input variables (e.g., meteorological forecasts) and the corresponding local output (e.g., recorded power generation). Given a new case (with forecasted meteorological variables), the resulting power generation is forecasted. This is performed by calculating a KDE-based similarity index to determine a set of most similar cases from the historical dataset. Then, the outputs of the most similar cases are used to calculate an ensemble prediction. The method is tested using historical weather forecasts and recorded generation of a PV installation in Portugal. Despite only being given averaged data as input, the algorithm is shown to be capable of predicting uncertainties associated with high frequency weather variations, outperforming deterministic predictions based on solar irradiance forecasts. Moreover, the algorithm is shown to outperform a neural network (NN) in most test cases while being exceptionally faster (32 times). Given that the proposed model only relies on public locally-metered data, it is a convenient tool for DG owners/operators to effectively forecast their expected generation without depending on private/proprietary data or divulging their own.

1. Introduction

Accurate prediction of power generation from renewable energy sources (RES) is a challenging task, posing problems for short-term operation of modern power systems [1]. This difficulty is due to the high uncertainties and complexity of both the associated variables and the equipment used for generation and grid connection. On the one hand, generation from RES is a function of multiple meteorological factors (temperature, humidity, wind flow, etc.) which are in and of themselves highly chaotic in nature and difficult to quantify [2,3]. On the other hand, the equipment used is also a source of significant uncertainty with reliability issues and failures commonly occurring in installed power electronics, inverter-side, grid-side, and even the metering apparatus [4]. The combined effect of chaotic input variables and complex energy conversion models render deterministic approaches infeasible for the prediction of distributed generation (DG) from RES. As such, statistical and/or probabilistic models are commonly employed not only to forecast DG but also to predict market behavior in the case of high RES deployment [5,6] which allows for a computationally efficient way of accounting for uncertainties in inputs.

In recent years, there has been increased interest in the use of ensemble methods for power system applications. Ensemble techniques have a decades-long track record in meteorological prediction, proving their potential to effectively predict highly chaotic processes [7].

The main premise of ensemble methods is to overcome both input and model uncertainties by compiling a set (ensemble) of separate predictions into a forecast of most likely outcomes. Each separate prediction is a result of varying input variables within their uncertainty range in addition to the model uncertainty. Therefore, a combination of these separate predictions yields a range of possible outputs representing a confidence/uncertainty region surrounding a most likely scenario.

In Figure 1, the concept of an ensemble forecast is visualized considering the case of DG production from RESs. Various meteorological factors are independent input variables and are associated with a significant level of uncertainty. In addition, the physical energy conversion models of DG units are also associated with a high uncertainty, leading to a significant change in energy generation as a result of small perturbances in the meteorological variables. Ensemble methods combine different scenarios based on both input and model uncertainties and establish a confidence interval around a most likely outcome. One can see that the employment of an ensemble technique involves the (continuously improving) prediction of some variable based on historical data, without knowledge of the physical model relating the inputs with the outputs. This is, in fact, the definition of machine learning (ML), and, as such, ensemble methods are often classified accordingly [8].

Paper Organization

This manuscript is organized as follows: Section 1 provides the motivation behind this study and an introduction to ensemble forecasting. Section 2 provides a comprehensive state-of-the-art review of recent literature on the topic. Section 3 describes the mathematical formulation of the proposed model. Section 4 presents the case study based on a solar photovoltaic (PV) installation in the center region of Portugal. Section 5 provides the simulation results and a comparison between the proposed method, a deterministic irradiance-based prediction, and a neural network (NN) approach. A discussion of the obtained results is then presented followed by prospects for future work following up on the current study. The conclusions are finally summarized in Section 6. More detailed supplementary data regarding the case study used are provided in Appendix A.

2. State-of-the-Art and Novel Contributions

As mentioned, the use of ensemble methods is gaining popularity with the increased complexity and uncertainty of distributed energy resources (DERs). Before presenting the proposed method, a review of recent works is presented to highlight the state-of-the-art scientific literature on ensemble methods applications to power systems in recent years.

2.1. State-of-the-Art

In Reference [9], different strategies for combining forecasts of solar photovoltaic (PV) generation were presented. In this study, the ensemble prediction was obtained by combining different probabilistic models rather than an ensemble of results of the same model. It used three models (i.e., QKNN, QRF, and QR) and the inputs were historical PV power and weather data.

By testing using the GEFCOM 2014 data, the results showed that the use of an ensemble of various probabilistic forecasts resulted in a significant increase in forecasting accuracy for solar photovoltaic (PV) systems as opposed to the use of individual ones, regardless of the ensemble strategy and/or scenarios considered. In Reference [10], the advantages and disadvantages of applying an ensemble to improve empirical mode decomposition (EMD) techniques were reported, which are mentioned as being commonly applied to wind forecasting. While the ensemble improved EMD models are associated with additional computational burden, they are reported to outperform other techniques, specifically in tackling the challenge of mode mixing. In addition, the authors reported it was significantly more beneficial to apply ensemble decomposition to artificial neural network (ANN) models as compared to using optimization methods to tune the ANN parameters. The previous statements were shown to hold for all time resolutions in wind power forecasting. In Reference [8], a comparison of numerous commonly used ensemble, ANN, and other ML techniques was performed for solar power forecasting. Random Forest (RF), an ensemble method, was found to exhibit the best performance. Two main conclusions were made by the study: (1) a seasonal bias was shown with spring and winter being more challenging to forecast than summer and autumn (keeping in mind that the data were from Norwich, UK) and, more importantly, that (2) a combination of simple algorithms yielded better and more reliable results than any individual algorithm on its own, regardless of its complexity.

In Reference [11], a short-term probabilistic forecasting method was proposed based on a competitive ensemble of different base predictors of PV power. The method was implemented using different probabilistic approaches which were trained as base predictors in order to obtain an ensemble of the predictive distribution with optimal characteristics of accuracy and reliability. In Reference [12], the reliability, robustness, and computational burden of a proposed PV power forecasting model based on the RF method was combined with the extra trees technique on an hourly basis and compared against supervised support vector regression. For a fair and comparative analysis, the models used comparable forecasting data, applicable for forecasting hourly PV power.

A probabilistic PV power forecasting model was proposed in Reference [13] and applied to several French PV plants considering six days of lead time with a resolution of thirty minutes. The proposed model was derived from multiple forecasts considering the national numerical weather predictions and including ensemble forecasts. Then, a free online parameter learning technique generated a weighted combination of the individual PV outputs, and the resulting weights were later sequentially computed before each forecast, using only historical data, with the goal of minimizing the continuous ranked probability score criterion.

An analog ensemble forecasting method for day-ahead regional with hourly resolution was presented in Reference [14]. The proposed model considered publicly available weather forecasts and power measurement data, considering some historical sets of temperature, irradiance, and terrain slopes as well, among others. To process the input data, clustering and blending strategies were used to improve the PV forecasting results which were compared and validated against several numerical models based on weather forecasts.

Photovoltaic power variability was studied in Reference [15], proposing a data-driven ensemble modeling technique to improve the forecasting of PV output. Also, three different models were analyzed within a recursive arithmetic average technique, considering stand-alone forecasting results. To prove the superiority of the proposed model, the comparison was carried out considering a considerable number of different training and testing samples, showing that the ensemble model generally outperforms different stand-alone forecasting models.

A PV forecasting model in Reference [16] used an ANN ensemble scheme based on particle swarm optimization with trained feed-forward neural network. The proposed model was constructed considering five different structures with varying network complexities, in order to improve the forecasting results. Then, the model was combined using trim aggregation after removing the error boundaries. Exogenous data, such as physical specification and environmental, were used as model inputs. Moreover, a clearness index was used to classify days accordingly with their features, considering a yearly basis analysis with a real case study. It was shown that ensemble schemes improve the forecast results in comparison with benchmark models.

In Reference [17], an hourly PV power forecasting model was presented based on clustering and ensemble prediction using the RF method. First, clustering was used to improve the computational burden by selecting the necessary weather variables. Then, the RF method with different parameters was implemented as a component model to find weather regimes making up the ensemble prediction. Finally, weighted computation was carried to analyze the different forecasting weather regimes in order to obtain the final results. Ridge regression was used to determine the weight of each weather variable automatically.

In Reference [18], a hybrid PV forecasting model combined the ML method with the Theta statistical method. Multiple ML components were used: long short-term memory, gate recurrent unit, and unsupervised learning. Structural and data diversity were key to improving the accuracy of the model. Four different approaches were implemented for validation, considering two real case studies. The proposed hybrid model was shown to be superior to traditional ML without statistical components.

In Reference [5], a new ensemble technique was employed to improve probabilistic forecasting of day-ahead price forecasting of the Iberian market. An approach based on kernel density estimation (KDE) was used to “activate” the best set of input variables which minimize the forecasting error. This study is an example of numerous others applying probabilistic and ML techniques for electricity price forecasting which has been increasing exponentially in the past decade as shown by Reference [6]. The latter shows that, while non-existent before 2003, probabilistic methods (or hybrid ones) have quickly gained ground as one of the main approaches used contemporarily for price forecasting [19,20,21]. The analysis in Reference [22] has shown that, for the case of price forecasting, while combining different forecasts in an ensemble framework does not necessarily always bring about improved accuracy, it does contribute to more reliable forecasting by decreasing the risk associated with an individual method.

Based on the conducted literature review, the following points were noted and were carried forth in the formulation, analysis, and discussion made throughout this paper:

• The use of combinatorial ensemble techniques is shown to significantly improve the accuracy of RES-based DG forecasting in addition to guaranteeing a more reliable and/or robust prediction;
• An ensemble of simple probabilistic/statistical techniques is shown to produce better and more robust DG forecasting than individual complex models;
• KDE has been recently employed to “activate” input sets for probabilistic price forecasting models, showing great success in improving the accuracy. This was only found to be tested on price forecasting, and no studies were found using this methodology for DG forecasting [5].

2.2. Novel Contributions

In this study, we proposed an ensemble algorithm based on the following key points:

• The objective was to develop an algorithm suitable for predicting DG from RESs. The specific focus of this study was on solar PV; however, the proposed approach is generalizable;
• Only historical, publicly available data (e.g., meteorological forecasts) and the corresponding local output (i.e., recorded power generation) were given as inputs (i.e., no knowledge of any physical model was known and no dependence on private/proprietary data were needed);
• The algorithm can run despite inconsistency or loss of data points. Using KDE, the most suitable inputs are “activated” from the historical dataset.

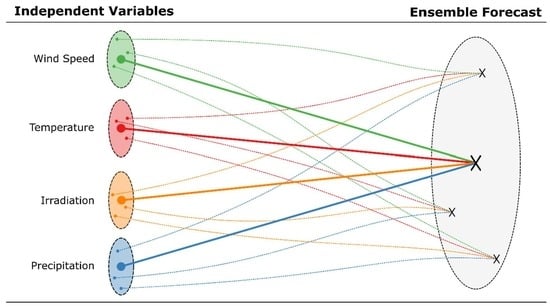
3. Proposed Methodology

Consider an output variable P that has a value which depends on a set of inputs $\mathrm{V}:=\left\{v_1,v_2,\dots N_V\right\}$ through some unknown model f:

$$P=f\left(\mathrm{V}\right)=f\left(v_1,v_2,\dots N_V\right)$$

(1)

where $N_V$ is the number of independent variables which affect output P. For the purpose of generalization, the inputs V are considered multidimensional, such that:

$$v_1=\left\{v_{1,1}, v_{1,2}, \dots v_{1,H_1}\right\}$$

(2)

In this case, $H_1$ is the number of dimensions of $v_1$. Now, consider scenario “new” for which we are trying to predict the output $P^{new}$, given a set of conditions ${\mathrm{V}}^{new}$:

$$P^{new}=f\left({\mathrm{V}}^{new}\right)=f\left(v_1^{new},v_2^{new},\dots N_V^{new}\right)$$

(3)

The goal is to predict the value of $P^{new}$ given only the new conditions ${\mathrm{V}}^{new}$ and a historical set of $N_o$ cases (with no knowledge of f):

$$P^{old,o}=f\left({\mathrm{V}}^{old,o}\right)=f\left(v_1^{old,o},v_2^{old,o},\dots N_V^{old,o}\right); \forall o=1,2,\dots , N_o$$

(4)

While the model function f is assumed to be chaotic, in this model we assume that the number of independent input variables and their dimensions remain constant and, therefore, the following equations hold:

$$N_V^{new}=N_V^{old,o}=N_V; H_i^{new}=H_i^{old,o}=N_H; \forall o=1,2,\dots , N_o; i=1,2,\dots , N_V$$

(5)

At this stage, the objective was to select a subset of Ns cases which were most suitable to form an ensemble prediction of $P^{new}$. To do this, the KDE function similar to Reference [5] was used to calculate a similarity index $s_{old,new}$ between the new case and each of the old cases in the historical dataset. In this case, the most similar Ns cases (with the highest similarity index) can be activated by means of the product of kernel functions of each variable. This is visualized in Figure 2.

The Gaussian kernel functions were used to construct the similarity index KDE, as they are most suitable for cases when little or no knowledge of the model is known.

$$s_{old,new}={\left({\displaystyle \prod }_i^{N_V}{\displaystyle \prod }_j^{N_H}{e}^{-\frac{1}{2}{\left(\frac{v_{i,h}^{old}-v_{i,h}^{new}}{b_i}\right)}^2}\right)}^{\frac{1}{N_V{N}_H}}$$

(6)

The bandwidth value b_i can be used to increase or decrease the sampling window (relative to the full range of the historical samples) for each variable in the same manner that KDE works, i.e., the narrower the bandwidth, the higher assumed correlation between variable v and the output P. Therefore, the value of b_i for each variable i can be expressed by means of a tuning coefficient ${\alpha }_i$:

$$b_i={\alpha }_i\left(\underset{\mathrm{o}}{\max }\left(v_i^{old,o}\right)-\underset{\mathrm{o}}{\min }\left(v_i^{old,o}\right)\right); \forall o=1,2,\dots , N_o ; i=1,2,\dots , N_V$$

(7)

In this way, this normalized tuning coefficient is varied from 0 (exclusive) to 1 (inclusive), corresponding to a bandwidth value between zero (exclusive) and the maximum range of the historical value of the variable (inclusive):

$$0<{\alpha }_i\le 1 \forall i=1,2,\dots , N_V$$

(8)

The similarity index in Equation (6) can be simplified in case all input independent variables are scalars. In this case, $N_H$ is equal to one, and the equation is reduced accordingly:

$$s_{old,new}={\left({\displaystyle \prod }_i^{N_V}{e}^{-\frac{1}{2}{\left(\frac{v_i^{old}-v_i^{new}}{b_i}\right)}^2}\right)}^{\frac{1}{N_V}}$$

(9)

Given a new case, the similarity index is calculated for all old cases in the historical dataset. We can now construct a sorted array S which has elements that correspond to the index of the old case; this array thus contains the indices of the historical dataset, sorted from most to least similar to the current case based on their calculated similarity index for Equation (9):

$$\mathrm{S}=\left[k_1,k_2\dots k_{N_o}\right]$$

(10)

In this case, $k_1$ is the index o of the historical case with the highest, $k_2$ to the second highest, etc. Now, the top Ns samples can be selected to perform the ensemble prediction. The simplest prediction is to calculate the mean value of the top Ns $P^{old}$ values:

$${\widehat{P}}^{new}\approx \frac{{\sum }_{i=1}^{N_s}{P}_{k_i}^{old}}{Ns}$$

(11)

To obtain a confidence/uncertainty interval around this expected output, percentile ranks can be used by constructing a cumulative distribution function of the top Ns values. By doing so, a confidence interval can be determined as follows:

$${\widehat{P}}_{lb,x\%}^{new}\le {\widehat{P}}_{ }^{new}\le {\widehat{P}}_{ub,x\%}^{new}$$

(12)

$${\widehat{P}}_{lb,x\%}^{new}={\rho }_{\frac{1}{2}\left(100-x\right)\%}\left(\left\{P_{k_1}^{old},P_{k_2}^{old},\dots ,P_{k_{Ns}}^{old}\right\}\right)$$

(13)

$${\widehat{P}}_{ub,x\%}^{new}={\rho }_{\frac{1}{2}\left(100+x\right)\%}\left(\left\{P_{k_1}^{old},P_{k_2}^{old},\dots ,P_{k_{Ns}}^{old}\right\}\right)$$

(14)

What Equation (12) means is that for a confidence of x%, ${\widehat{P}}_{ }^{new}$ lies between the lower and upper bounds equal to ${\widehat{P}}_{lb,x\%}^{new}$ and ${\widehat{P}}_{ub,x\%}^{new}$, respectively; which are calculated, as per Equations (13) and (14), by means of the percentile ${\rho }_{\frac{1}{2}\left(100-x\right)\%}$ and ${\rho }_{\frac{1}{2}\left(100+x\right)\%}$ of the top Ns values $\left(\left\{P_{k_1}^{old},P_{k_2}^{old},\dots ,P_{k_{Ns}}^{old}\right\}\right)$, respectively.

It must be noted that there are clearly more complex means of calculating ${\widehat{P}}^{new}$ and the confidence bounds. However, the main focus of this study was to highlight the use of the similarity index to extract the set S, and the choice of the simplest ensemble prediction afterwards was intentional to demonstrate the power of such a selection algorithm even with the most basic ensemble applied.

4. Case Study and Validation

4.1. PV Installation in Portugal

In order to test and validate the proposed algorithm, a real case study was used based on solar PV installations located in the vicinity of the city of Coimbra in the center region (“Região do Centro”) of Portugal as shown in Figure 3. The technical specifications of the plant are listed in

Table 1. Technical specifications of the solar photovoltaic (PV) plant used as a case study.

Parameter	Value	Units
Number of Panels (300 kWp each)	53	-
Panel Area (each)	1.713	m2
Total Installed Capacity	18	kWp
Inverter Capacity	20	kW
Nominal DC Voltage	600	V
Overall Efficiency	20	%

. Historical forecasts and measurements are available for the same installation for a full year from 15 March 2015 to 15 March 2016 as detailed in

Table 2. Details of variables in the historical dataset provided (from 15 March 2015 to 15 March 2016).

Historical Variable	Data Source	Spatial Resolution	Temporal Resolution	Units
Wind Speed	Meteorological Forecast	22 km	3 h	m/s
Temperature	Meteorological Forecast	22 km	3 h	°C
Solar Irradiance	Meteorological Forecast	22 km	3 h	W/m2
Precipitation	Meteorological Forecast	22 km	3 h	mm
Humidity	Meteorological Forecast	22 km	3 h	%
Inverter AC Power (Output)	Real Measurement	-	~5 min	kW

. Annual plots of all variables are provided in Appendix A1.

In this case, the historical weather forecasts were the input variables (V) and are publicly provided by the Global Forecasting System (GFS) model with a 22 km resolution. The GFS’s data are available for any region of the world and is publicly available online [23]. The forecasts are made at 18:00 (UTC time) of each day for the day-ahead with a 3 h resolution (average of each 3 h interval of the day: 0:00, 3:00, 6:00, ..., 21:00). The provided forecasts are for wind speed, temperature, solar irradiance, precipitation, and humidity.

The output AC power of the inverter was recorded for the same year. A 20 kW SMA Sunny Tripower inverter was installed with 2 maximum power point trackers (MPPTs) installed (4 strings per inverter). The logging frequency of the AC power output was approximately 5 min. For this study, the recorded AC power was synchronized with the forecasts by applying a 3 h average (averaging can be seen in Figure A6). It is important to stress that the proposed prediction method was only given the averaged output power as input. However, high-resolution data were used for validation to test if uncertainties associated with high frequencies were captured.

4.2. Numerical Irradiance-Based Forecast

Given that the GFS data and the output power were synchronized, and since MPPTs were installed with the inverters, one can use the following equation to predict the maximum possible power output from the current installation for each data point.

$$P_t\approx P_t^{irr}={\eta }_{avg}{N}_p{A}_p{R}_t^{wf}$$

(15)

where $P_t^{irr}$ is the predicted power output at time t calculated numerically from the irradiance forecast,${\eta }_{avg}$ is the overall average energy conversion efficiency of the PV plant (accounting for the PV conversion and inverter efficiency), $N_p$ and $A_p$ are the number of panels and the area of each panel (in m²), respectively, and $R_t^{wf}$ is the direct incident solar irradiance (W/m²) obtained from the weather forecast for time t.

4.3. Seasonal Test Weeks

Also, in order to check for seasonal effects and/or bias, four test weeks were extracted from the annual data corresponding to all four seasons. The annual measured output power, annual predicted maximum output (based on irradiance estimation in Equation (15)), and detailed plots thereof for all four representative weeks are shown in Figure 4.

By inspecting the plots shown in Figure 4, particularly comparing the maximum theoretical output based on irradiance and recorded power, two important observations are worthy of noting:

• During the summer, the maximum power output prediction based on Equation (15) was greater than the recorded value. This is what one would expect, and the operating efficiency and/or reliability of the installation would seldom reach the maximum theoretical power output;
• During the winter, the prediction based only on solar irradiation failed to predict any value of output power (one can see that the predicted values were zeros throughout the winter and also by looking at the plot of the winter week). This is due to the fact that the meteorological forecasts provided by GFS are averaged over large temporal and spatial resolutions. As such, the forecasted irradiance would dissipate during winter weather conditions.

As such, it is clear that relying solely on the irradiance models, is insufficient to make any prediction of the expected power output of the solar PV installations.

Therefore, the objective of this case study was to check if the proposed method, taking into consideration GFS data as input variables and the recorded (and synchronized) AC power output of the plant, would be capable of accurately forecasting the power output under different meteorological conditions.

The GFS meteorological data are plotted for the entire year in Figure A1, Figure A2, Figure A3, Figure A4, Figure A5 and Figure A6 in the Appendix A. Zoomed-in plots are also provided for each test week in order to show the seasonal differences and highlight some visible correlation between the weather conditions and the recorded AC power output. The plots of spring, summer, autumn, and winter are shown in Figure 5, Figure 6, Figure 7 and Figure 8, respectively.

4.4. Implementation and Validation

To test the proposed algorithm in Section 2, the power output for each of the four test weeks was forecasted, only taking as input variables the meteorological forecasts provided by GFS. The hour of the day and day of the year were appended to the array of input variables in order to give the potential of favoring closer times/dates. The input variable array for this case was as follows:

$$\mathrm{V}=\left\{{\mathrm{v}}_1,{\mathrm{v}}_2,{\mathrm{v}}_3,{\mathrm{v}}_4,{\mathrm{v}}_5,{\mathrm{v}}_6,{\mathrm{v}}_7\right\}$$

(16)

The description of each variable and the choice of the bandwidth tuning coefficients (Equations (7) and (8)) are provided in

Table 3. Description of input variables for the historical dataset and value chosen for bandwidth coefficient for the KDE-based similarity index calculator.

Bandwidth Coefficient	Value
${\mathit{\alpha }}_{\mathit{v}\mathbf{1}}$ (hour of the day)	0.4
${\mathit{\alpha }}_{\mathit{v}\mathbf{2}}$ (day of the year)	1.0
${\mathit{\alpha }}_{\mathit{v}\mathbf{3}}$ (wind speed forecast)	0.8
${\mathit{\alpha }}_{\mathbf{v}4}$ (temperature forecast)	0.5
${\mathit{\alpha }}_{\mathit{v}\mathbf{5}}$ (solar irradiance forecast)	0.1
${\mathit{\alpha }}_{\mathit{v}\mathbf{6}}$ (precipitation forecast)	0.8
${\mathit{\alpha }}_{\mathit{v}\mathbf{7}}$ (humidity forecast)	0.5

. As explained in Section 2, the smaller the value of $\alpha$, the higher the assumed correlation between the output variable and its corresponding input variable. The values used in this study were assumed based on the well-established physical relationships between each meteorological variable and the target one (PV output power). For instance, solar irradiance was associated with the most dependence and thus a value of 0.1 was chosen, etc. This can heuristically be set based on visual inspection of Figure 5, Figure 6, Figure 7 and Figure 8.

In order to investigate the performance of the proposed algorithm, the results obtained for the four test weeks are against the numerical irradiance-based forecast based on Equation (15), and an ANN (trained using the same data). A feed-forward ANN was used with 1 hidden layer and 10 neurons. The performance of all three methods was compared in terms of computational time and accuracy. Since the ANN was trained using the Levenberg–Marquardt algorithm [24], its results and computational time both varied in every run due to the random data division and training process employed. Therefore, to evaluate the results in a fair manner, the ANN was run a sufficiently large number of times (10,000 runs), and the average runtime and forecast results were used for comparison.

To quantify the forecast error, three criteria were used: the mean absolute error (MAE), root mean square deviation (RMSD), and the normalized root mean square deviation (NRMSD). The MAE provides a simple overall measurement of the mean error between forecasted ($\widehat{P}$) and real ($P$) values:

$$MAE=\frac{{\sum }_{t=1}^{N_t}\left|{\widehat{P}}_t-P_t\right| }{N_T}$$

(17)

where the subscript t corresponds to the value at time step t and N_t is the total number of time steps. The RMSD is based on the on the quadratic mean:

$$RMSD=\sqrt{\frac{{\sum }_{t=1}^{N_t}{\left({\widehat{P}}_t-P_t\right)}^2 }{N_T}}$$

(18)

Both the MAE and RMSD provide a scale-dependent measure of the deviation between the forecasted and real values. The NRMSD provides a normalized measure as a percentage which is sometimes more favorable when comparing different models.

$$NRMSD=\frac{RMSD}{\left(P_{max}-P_{min}\right)}\cdot 100\%$$

(19)

$P_{max}$ and $P_{min}$ are the maximum and minimum values of the real data, respectively. As such, the NRMSD provides a scale-independent measure. The MAE, RMSD, NRMSD, and computational time are all used to assess the performance of the different approaches for all four test weeks.

The proposed algorithm was developed as original code by the authors using the MATLAB R2019b environment on a standard laptop computer with the following specifications: Intel Core i7-8550U CPU @ 1.80 GHz, 16.0 GB RAM, Windows 10 64 bit operating system. The neural network used for validation was based on the MATLAB 2019b Statistics and Machine Learning Toolbox [24].

5. Results and Discussion

5.1. Results of the Proposed Ensemble Algorithm

The results of the proposed ensemble algorithm are shown in Figure 9. The predicted value was plotted, along with confidence intervals of 68%, 95%, and 99.7%. The following points are noted:

• The proposed ensemble algorithm successfully managed to forecast the wind power output, relying only on the historical GFS meteorological data, for all four tests weeks of all seasons;
• The power production in cases when the deterministic model based on irradiance was inadequate (i.e., winter season) was successfully predicted;
• Despite only being provided averaged data, the confidence intervals successfully managed to cover high-frequency fluctuations during most days;
• The confidence interval grows and shrinks in response to such fluctuations even within the same day (e.g., Summer week, day 5);
• The forecasted mostly underestimated the power output than. This is favorable to overestimation particularly from the point of view of operators of DG installations.

5.2. Comparison and Validation

A comparison between the forecast obtained and that of an irradiance-based numerical model (Equation (15)) and an ANN was used to validate the proposed method. As elaborated in the previous section, the same data were used to train the ANN. Since a random data division and training method was employed (which aimed to minimize the computational time of the ANN), the average of a sufficiently large number of runs of the ANN (i.e., 10,000 runs) was used for a fair comparison.

The comparison was made considering the MAE, RMSD, and NRMSD error criteria for each of the test weeks and is shown in

Table 4. Comparison of the MAE, RMSD, and NRMSD error criteria for the results obtained for each of the test weeks from the irradiance forecast, ANN, and the proposed method.

Criterion	Method	Winter	Spring	Summer	Autumn
MAE (kW)	Irradiance Forecast	34.6	15.7	17.4	15.3
	Neural Network	10.7	15.5	8.4	7.9
	Proposed Method	12.6	14.0	3.6	7.7
RMSD (kW)	Irradiance Forecast	3.062	2.138	2.508	1.857
	Neural Network	0.949	2.114	1.203	0.951
	Proposed Method	1.115	1.914	0.523	0.928
NRMSD (%)	Irradiance Forecast	34.6	15.7	17.4	15.3
	Neural Network	10.7	15.5	8.4	7.9
	Proposed Method	12.6	14.0	3.6	7.7

. The different forecasts are visualized in the plots shown in Figure 10. The computational time to forecast all four weeks by the proposed method and the ANN (average of 10,000 runs in each case) is shown in

Table 5. Comparison of the computational time between the proposed method and the ANN.

	Computational Time to Forecast all Four Weeks (Average of 10,000 runs)
Neural Network	1.46 s
Proposed Method	0.045 s

.

By comparing the results of the different models, the following points can be verified:

• According to all error criteria used, the proposed method outperformed the irradiance-based prediction for all seasons. It outperformed the ANN in all seasons except winter;
• Both the ANN and the proposed method managed to provide a reasonably accurate prediction of the output power in the winter, where a numerical irradiance-based model completely fails;
• Despite the ANN being capable of providing a better average error for the winter, the capability of the proposed method to capture high-frequency fluctuations in its confidence intervals provides an advantage over the ANN;
• The proposed method was extraordinarily fast in terms of computational time, being 32 times faster than the ANN while outperforming the ANN in the majority of situations.

5.3. Prospects for Future Work

After testing the proposed method, confirming its validity, and taking note of its superior performance particularly in terms of providing a highly computationally efficient forecast, the following recommendations are provided for future work following on this study:

• The effect of using additional meteorological variables (e.g., absolute and relative atmospheric pressure) should be investigated in terms of the forecast accuracy and computational burden;
• Optimal tuning of the bandwidth coefficients should be studied. This can be performed in a pre-processing stage (e.g., with correlation analysis) or using a reinforcement learning-based design in which the values are self-tuned every time the code is run. In the latter, using an optimization method to determine the optimal values may be an option for a hybrid structure;
• Due to the fact of its high computational efficiency and its reliance only on publicly available historical weather forecasts, the proposed method seems to have great potential to be applied to forecast RES-based DG. As such, follow-up work should test the proposed method on other RES technologies such as wind power.

6. Conclusions

In this study, a novel ensemble algorithm based on kernel density estimation (KDE) was proposed to forecast RES-based DG, particularly PV power. The proposed method relies solely on publicly available historical series of independent input variables (i.e., historical meteorological forecasts) and the corresponding local output (i.e., recorded power generation). Given a new case (with forecasted meteorological variables), the resulting power generation was forecasted. For the new case to be forecasted, a KDE-based similarity index was used to determine a set of most similar cases from the historical dataset. Then, the corresponding outputs of the most similar cases were used to calculate an ensemble prediction for the forecasted power generation. The proposed method was tested by considering meteorological and recorded power generation from a PV installation around the city of Coimbra, in the center region of Portugal. Despite only being given averaged data as inputs, the developed algorithm was capable of predicting uncertainties associated with high frequency variations in weather conditions, outperforming deterministic prediction based on solar irradiance forecasts. The proposed method outperformed an ANN in most cases while being exceptionally faster (32 times more than the computational time). Given its exceptional computational efficiency and its reliance solely on public data (weather forecasts) and local metered data (power generation), it is a convenient tool for use by owners or operators of solar power installations to effectively forecast their expected generation without depending on private/proprietary data or divulging their own.