Multi-Scale Analyses and Modeling of Metallic Nano-Layers
Abstract
:1. Introduction
2. Materials and Methods
2.1. Plastic Deformation Kinematics
2.2. Entropic Kinetics and Constitutive Model at Nano-Scale
2.3. Deep-Learning Single Layer Calibration (SLC) Method
Training and Learning Techniques in The SLC Approach
2.4. Statistical Mechanics and Homogenized Crystal Plasticity Constitutive Model
3. Results and Discussion
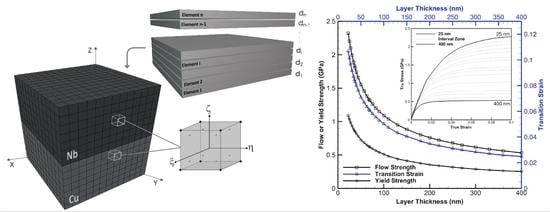
3.1. Nano-Scale Constitutive Parameters and Predictions
3.2. Homogenized Level Effective Functionals and Constants
3.3. Homogenized Level Temperature Effects
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. General Steps of Solving Equilibrium Equation—FE
- Equilibrium Equation
- Finite Element Discretization
- Residual Force
- Newton-Raphson Solver
- Residual Derivative
- Material Stiffness
- Geometrical Stiffness
- Calculation of and in Appendix B.
Appendix B. General Steps of Acquiring System Stiffness—CP
- Kinematics
- Plastic Deformation Rate Dependence
- Second Piola–Kirchhoff Stress
- Elastoplastic Parts
- Nonlinear Solution–Defined Residual Function
- Nonlinear Iteration Obtaining 2nd Piola–Kirchhoff Stress
- Updated Constitutive Model and Evolving Parameters
- Elastic Deformation Gradient
- Cauchy Stress
- Elastoplastic Material Tensor
References
- Gleiter, H.; Hansen, N.; Horsewell, A.; Leffers, T.; Lilholt, H. Deformation of Polycrystals: Mechanisms and microstructures. In Proceedings of the 2nd RISO Symposium on Metallurgy and Materials Science, Roskilde, Denmark, 14–18 September 1981; pp. 15–21. [Google Scholar]
- Gleiter, H. Nanostructured materials: Basic concepts and microstructure. Acta Mater. 2000, 48, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Misra, A. An overview of interface-dominated deformation mechanisms in metallic multilayers. Curr. Opin. Solid State Mater. Sci. 2011, 15, 20–28. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Gleiter, H.; Wu, C.; OY, Z.C. Non-equilibrium properties of nano structured materials. In Materials Science Forum; Trans Tech Publications Ltd.: Zurich-Uetikon, Switzerland, 2003; Volume 426, pp. 2363–2368. [Google Scholar]
- Hirth, J.P. The influence of grain boundaries on mechanical properties. Metall. Trans. 1972, 3, 3047–3067. [Google Scholar] [CrossRef]
- Ashby, M. The deformation of plastically non-homogeneous materials. Philos. Mag. 1970, 21, 399–424. [Google Scholar] [CrossRef]
- Demkowicz, M.; Hoagland, R.; Hirth, J. Interface structure and radiation damage resistance in Cu-Nb multilayer nanocomposites. Phys. Rev. Lett. 2008, 100, 136102. [Google Scholar] [CrossRef] [PubMed]
- Birringer, R. Nanocrystalline materials. Mater. Sci. Eng. A 1989, 117, 33–43. [Google Scholar] [CrossRef]
- Gleiter, H.; Hahn, H.; Schimmel, T. Advances in nanomaterials. Beilstein J. Nanotechnol. 2013, 4, 805–806. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koehler, J. Attempt to design a strong solid. Phys. Rev. B 1970, 2, 547. [Google Scholar] [CrossRef]
- Dao, M.; Lu, L.; Asaro, R.; De Hosson, J.T.M.; Ma, E. Toward a quantitative understanding of mechanical behavior of nanocrystalline metals. Acta Mater. 2007, 55, 4041–4065. [Google Scholar] [CrossRef] [Green Version]
- Hall, E. The deformation and ageing of mild steel: III discussion of results. Proc. Phys. Soc. Ser. B 1951, 64, 747. [Google Scholar] [CrossRef]
- Petch, N.J. The Cleavage Strength of Polycrystals. J. Iron Steel Inst. 1953, 174, 25–28. [Google Scholar]
- Misra, A.; Hirth, J.; Hoagland, R. Length-scale-dependent deformation mechanisms in incoherent metallic multilayered composites. Acta Mater. 2005, 53, 4817–4824. [Google Scholar] [CrossRef]
- Misra, A.; Demkowicz, M.; Zhang, X.; Hoagland, R. The radiation damage tolerance of ultra-high strength nanolayered composites. JOM 2007, 59, 62–65. [Google Scholar] [CrossRef]
- Carpenter, J.; Vogel, S.; LeDonne, J.; Hammon, D.; Beyerlein, I.; Mara, N.A. Bulk texture evolution of Cu–Nb nanolamellar composites during accumulative roll bonding. Acta Mater. 2012, 60, 1576–1586. [Google Scholar] [CrossRef]
- Schiøtz, J.; Jacobsen, K.W. A maximum in the strength of nanocrystalline copper. Science 2003, 301, 1357–1359. [Google Scholar] [CrossRef] [Green Version]
- Ashby, M. Results and consequences of a recalculation of the frank-read and the orowan stress. Acta Metall. 1966, 14, 679–681. [Google Scholar] [CrossRef]
- Geers, M.G.; Kouznetsova, V.G.; Matouš, K.; Yvonnet, J. Homogenization methods and multiscale modeling: Nonlinear problems. In Encyclopedia of Computational Mechanics Second Edition; Wiley: Hoboken, NJ, USA, 2017; pp. 1–34. [Google Scholar]
- Dehm, G.; Jaya, B.N.; Raghavan, R.; Kirchlechner, C. Overview on micro-and nanomechanical testing: New insights in interface plasticity and fracture at small length scales. Acta Mater. 2018, 142, 248–282. [Google Scholar] [CrossRef]
- Raghavan, R.; Wheeler, J.M.; Harzer, T.P.; Chawla, V.; Djaziri, S.; Thomas, K.; Philippi, B.; Kirchlechner, C.; Jaya, B.N.; Wehrs, J.; et al. Transition from shear to stress-assisted diffusion of copper–chromium nanolayered thin films at elevated temperatures. Acta Mater. 2015, 100, 73–80. [Google Scholar] [CrossRef]
- Kroner, E. On the plastic deformation of polycrystals. Acta Metall. 1961, 9, 155–161. [Google Scholar]
- Peirce, D.; Asaro, R.; Needleman, A. An analysis of nonuniform and localized deformation in ductile single crystals. Acta Metall. 1982, 30, 1087–1119. [Google Scholar] [CrossRef]
- Asaro, R.J.; Rice, J. Strain localization in ductile single crystals. J. Mech. Phys. Solids 1977, 25, 309–338. [Google Scholar] [CrossRef] [Green Version]
- Rice, J.R. Inelastic constitutive relations for solids: An internal-variable theory and its application to metal plasticity. J. Mech. Phys. Solids 1971, 19, 433–455. [Google Scholar] [CrossRef]
- Orowan, E. Zur kristallplastizität. iii. Zeitschrift für Physik 1934, 89, 634–659. [Google Scholar] [CrossRef]
- Cottrell, A.H. Dislocations and Plastic Flow in Crystals; Clarendon Press: Oxford, UK, 1953. [Google Scholar]
- Langer, J.; Bouchbinder, E.; Lookman, T. Thermodynamic theory of dislocation-mediated plasticity. Acta Mater. 2010, 58, 3718–3732. [Google Scholar] [CrossRef] [Green Version]
- Truesdell, C.; Toupin, R. The classical field theories. In Principles of Classical Mechanics and Field Theory/Prinzipien der Klassischen Mechanik und Feldtheorie; Springer: Berlin/Heidelberg, Germany, 1960; pp. 226–858. [Google Scholar]
- Coleman, B.D.; Noll, W. The thermodynamics of elastic materials with heat conduction and viscosity. In The Foundations of Mechanics and Thermodynamics; Springer: Berlin/Heidelberg, Germany, 1974; pp. 145–156. [Google Scholar]
- Holzapfel, A.G. Nonlinear Solid Mechanics II. 2000. Available online: elibrary.matf.bg.ac.rs/bitstream/handle/123456789/2762/NonlinearSolidMechHOLZAPFELP2.pdf?sequence=1 (accessed on 17 January 2021).
- Frost, H.J.; Ashby, M.F. Deformation Mechanism Maps: The Plasticity and Creep of Metals and Ceramics; Pergamon Press: Oxford, UK, 1982. [Google Scholar]
- Kocks, W. Thermodynamics and kinetics of slip. Progr. Mater. Sci. 1975, 19, 291. [Google Scholar]
- Van Swygenhoven, H.; Derlet, P.; Frøseth, A. Nucleation and propagation of dislocations in nanocrystalline fcc metals. Acta Mater. 2006, 54, 1975–1983. [Google Scholar] [CrossRef]
- Keshavarz, S.; Molaeinia, Z.; Reid, A.; Langer, S. Morphology Dependent Flow Stress in Nickel-Based Superalloys in the Multi-Scale Crystal Plasticity Framework. Crystals 2017, 7, 334. [Google Scholar] [CrossRef] [Green Version]
- Freund, Y.; Schapire, R.E. Experiments with a new boosting algorithm. In icml; Citeseer: Princeton, NJ, USA, 1996; Volume 96, pp. 148–156. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting (with discussion and a rejoinder by the authors). Ann. Stat. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- Berdichevsky, V.L. Variational principles. In Variational Principles of Continuum Mechanics; Springer: Berlin/Heidelberg, Germany, 2009; pp. 3–44. [Google Scholar]
- Berdichevsky, V. Thermodynamics of Chaos and Order; CRC Press: Boca Raton, FL, USA, 1997; Volume 90. [Google Scholar]
- Kröner, E. Continuum theory of defects. Phys. Defects 1981, 35, 217–315. [Google Scholar]
- Berdichevsky, V.L. Homogenization in micro-plasticity. J. Mech. Phys. Solids 2005, 53, 2457–2469. [Google Scholar] [CrossRef]
- Taylor, G.I. Plastic strain in metals. J. Inst. Metals 1938, 62, 307–324. [Google Scholar]
- Kocks, U. The relation between polycrystal deformation and single-crystal deformation. Metall. Mater. Trans. B 1970, 1, 1121–1143. [Google Scholar] [CrossRef]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Hill, R. On constitutive macro-variables for heterogeneous solids at finite strain. Proc. R. Soc. Lond. A Math. Phys. Sci. 1972, 326, 131–147. [Google Scholar]
- Jennings, A.T.; Burek, M.J.; Greer, J.R. Microstructure versus size: Mechanical properties of electroplated single crystalline Cu nanopillars. Phys. Rev. Lett. 2010, 104, 135503. [Google Scholar] [CrossRef]
- Kim, J.Y.; Jang, D.; Greer, J.R. Insight into the deformation behavior of niobium single crystals under uniaxial compression and tension at the nanoscale. Scr. Mater. 2009, 61, 300–303. [Google Scholar] [CrossRef]
- Snel, J.; Monclús, M.; Castillo-Rodriguez, M.; Mara, N.; Beyerlein, I.; Llorca, J.; Molina-Aldareguia, J.M. Deformation mechanism map of Cu/Nb nanoscale metallic multilayers as a function of temperature and layer thickness. JOM 2017, 69, 2214–2226. [Google Scholar] [CrossRef] [Green Version]
- Mara, N.; Bhattacharyya, D.; Hirth, J.; Dickerson, P.; Misra, A. Mechanism for shear banding in nanolayered composites. Appl. Phys. Lett. 2010, 97, 021909. [Google Scholar] [CrossRef]
- Chokshi, A.; Rosen, A.; Karch, J.; Gleiter, H. On the validity of the Hall-Petch relationship in nanocrystalline materials. Scr. Metall. 1989, 23, 1679–1683. [Google Scholar] [CrossRef] [Green Version]
- Argon, A.; Yip, S. The strongest size. Philos. Mag. Lett. 2006, 86, 713–720. [Google Scholar] [CrossRef]
- Herring, C. Diffusional viscosity of a polycrystalline solid. J. Appl. Phys. 1950, 21, 437–445. [Google Scholar] [CrossRef]
- Coble, R. A model for boundary diffusion controlled creep in polycrystalline materials. J. Appl. Phys. 1963, 34, 1679–1682. [Google Scholar] [CrossRef]
- Mara, N.; Misra, A.; Hoagland, R.; Sergueeva, A.; Tamayo, T.; Dickerson, P.; Mukherjee, A. High-temperature mechanical behavior/microstructure correlation of Cu/Nb nanoscale multilayers. Mater. Sci. Eng. A 2008, 493, 274–282. [Google Scholar] [CrossRef]
- Misra, A.; Hoagland, R.; Kung, H. Thermal stability of self-supported nanolayered Cu/Nb films. Philos. Mag. 2004, 84, 1021–1028. [Google Scholar] [CrossRef]
- Lieou, C.K.; Bronkhorst, C.A. Thermodynamic theory of crystal plasticity: Formulation and application to polycrystal fcc copper. J. Mech. Phys. Solids 2020, 138, 103905. [Google Scholar] [CrossRef] [Green Version]









| Constitutive Model Parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| p | q | r | m | ||||||
| Material Elastic Constants | Cu | Nb |
|---|---|---|
| (GPa) | ||
| (GPa) | ||
| (GPa) | ||
| (GPa) | ||
| (J) | ||
| b(m) |
| Material Parameters | Cu | Nb |
|---|---|---|
| 5.0 × 106 | 6.0 × 106 | |
| p | 0.98 | 1.01 |
| q | 1.12 | 1.14 |
| r | 1.115 | 1.121 |
| 0.2 | 0.002 | |
| 70,000.0 | 76,741.0 | |
| m | −0.50 | −0.50 |
| (MPa) | 4.80 | 6.30 |
| (MPa) | 5.20 | 7.10 |
| (MPa) | 3000.0 | 20,000.0 |
| Cu | Nb | ||||||
|---|---|---|---|---|---|---|---|
| (GPa) | (GPa/K) | (GPa) | (GPa/K) | ||||
| (GPa) | (GPa/K) | (GPa) | (GPa/K) | ||||
| (GPa) | (GPa/K) | (GPa) | (GPa/K) | ||||
| (GPa) | (GPa/K) | (GPa) | (GPa/K) | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moleinia, Z.; Bahr, D.F. Multi-Scale Analyses and Modeling of Metallic Nano-Layers. Materials 2021, 14, 450. https://0-doi-org.brum.beds.ac.uk/10.3390/ma14020450
Moleinia Z, Bahr DF. Multi-Scale Analyses and Modeling of Metallic Nano-Layers. Materials. 2021; 14(2):450. https://0-doi-org.brum.beds.ac.uk/10.3390/ma14020450
Chicago/Turabian StyleMoleinia, Zara, and David F. Bahr. 2021. "Multi-Scale Analyses and Modeling of Metallic Nano-Layers" Materials 14, no. 2: 450. https://0-doi-org.brum.beds.ac.uk/10.3390/ma14020450