Impacts of Different Tillage Practices on Soil Water Infiltration for Sustainable Agriculture
Abstract
:1. Introduction
2. Materials and Methods
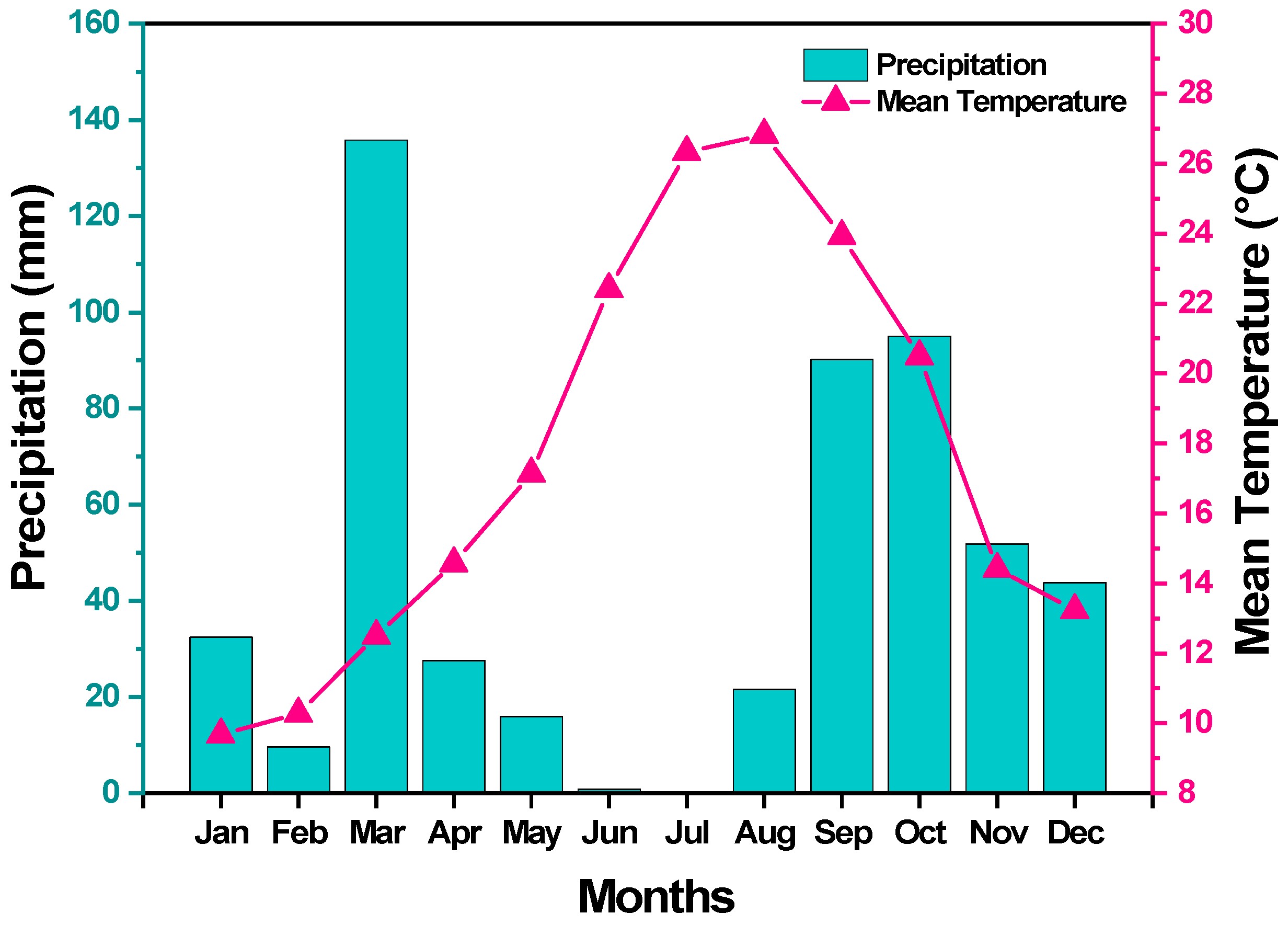
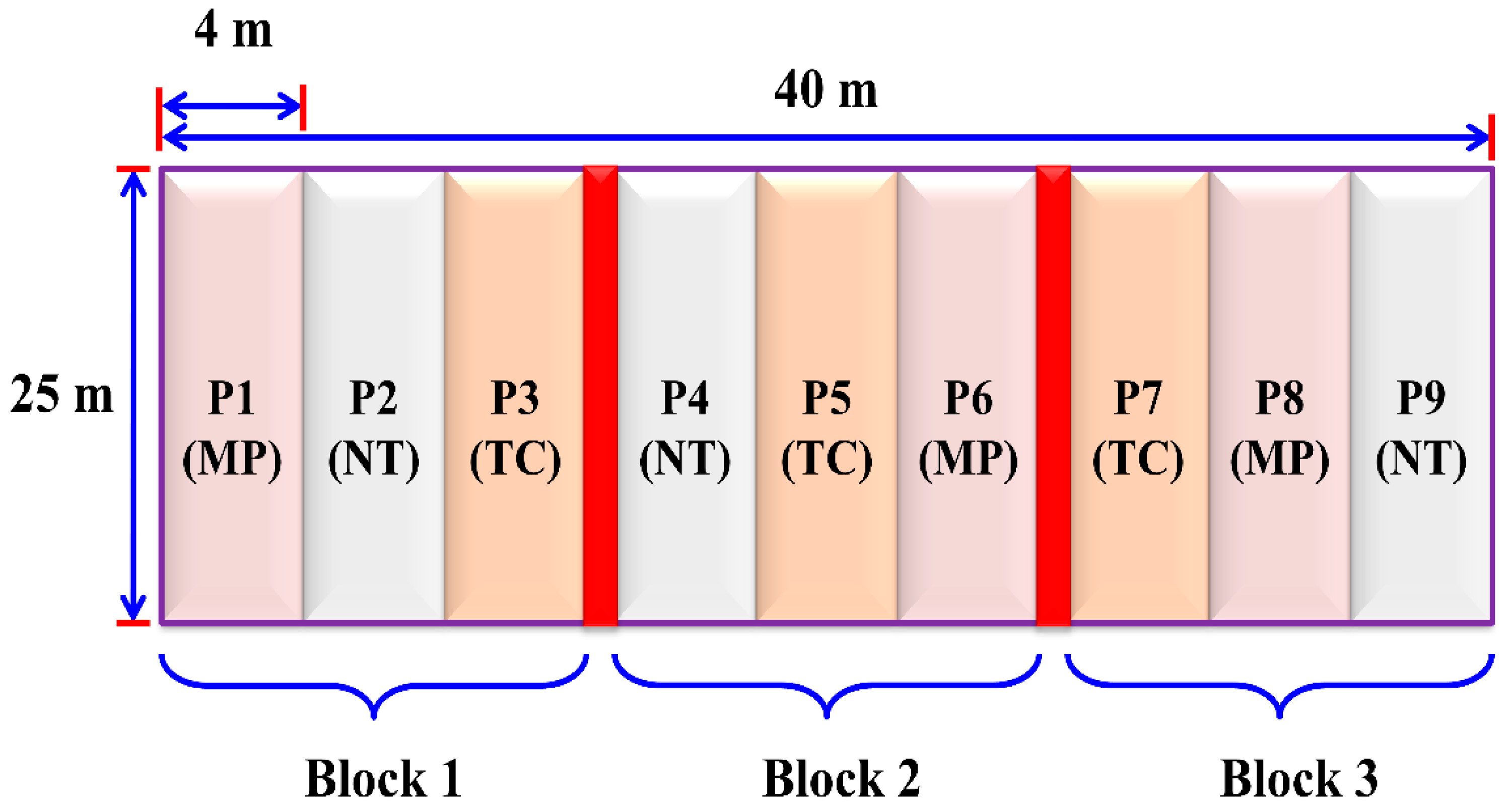
2.1. Characterizations of the Study Area, Soil Properties and Experimental Layout
2.2. Soil Water Infiltration Measurement
2.3. Infiltration Rate Estimation Models
2.3.1. Philip Model
2.3.2. Kostiakov Model
2.3.3. Horton Model
2.4. Model Performance Evaluation Criteria
3. Results and Discussion
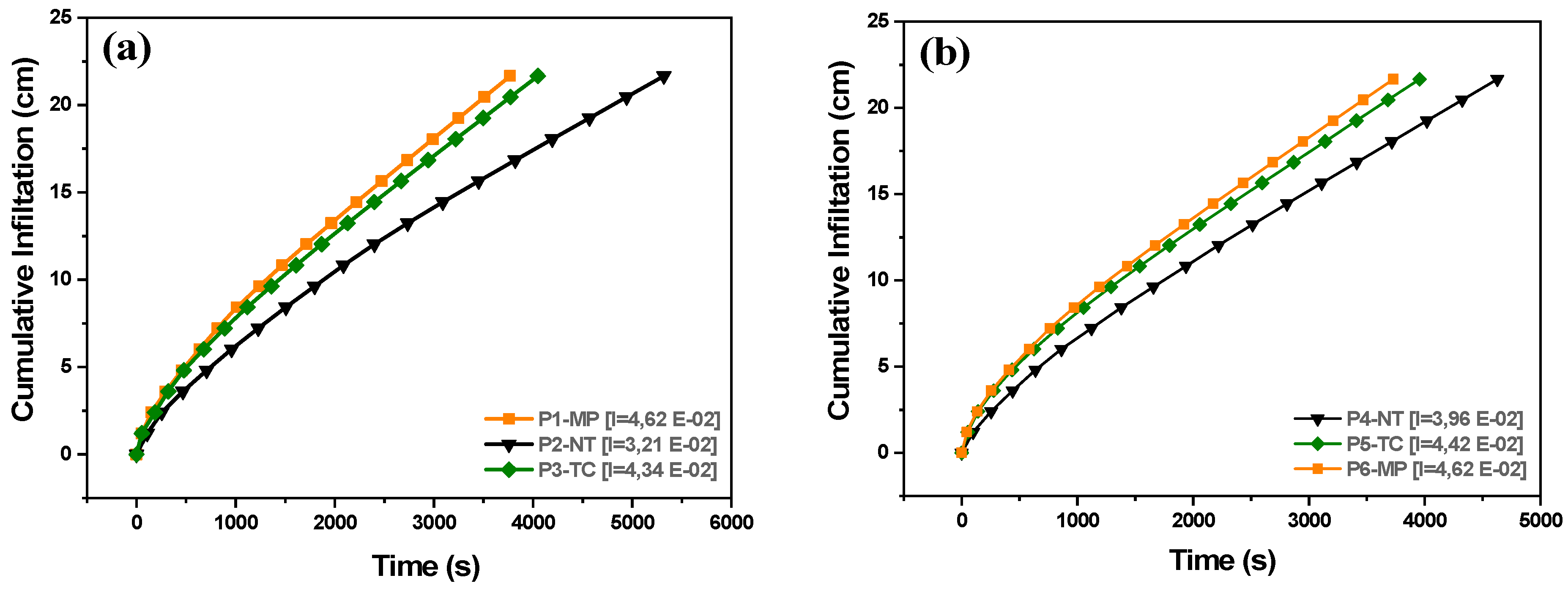
3.1. Effect of Tillage Practices on Measured Soil Water Infiltration
3.2. Parameter Estimation for the Infiltration Models
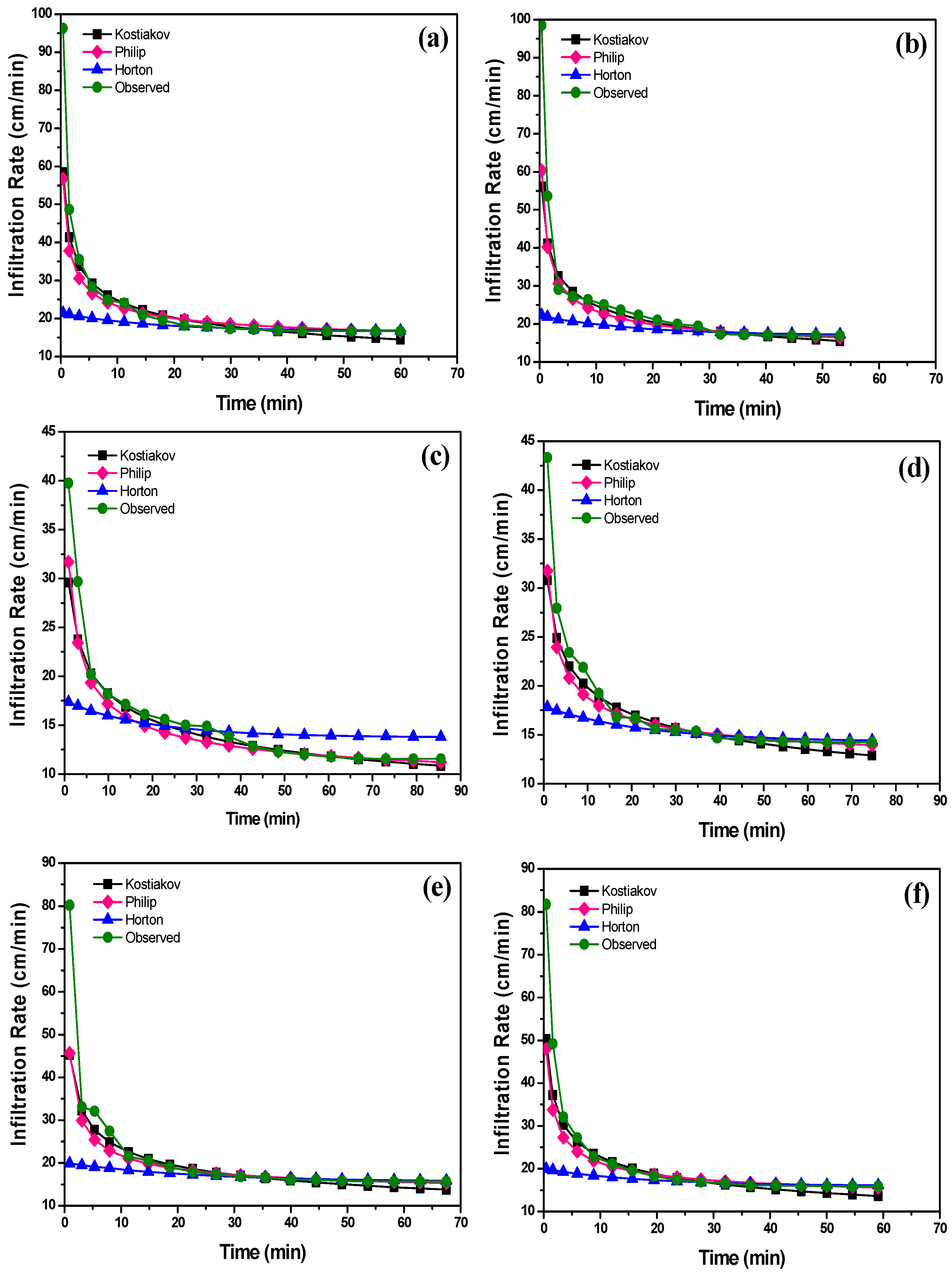
3.3. Performance of the Infiltration Models for Predicting Cumulative Infiltration
4. Effect of Tillage on Soil Water Infiltration Characteristics by Model Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| EC | Electrical conductivity |
| Ksat | Saturated hydraulic conductivity |
| S | soil sorptivity |
| A | stable infiltration rate |
| a | Kostiakov’s time Coefficient |
| b | Kostiakov’s time exponent |
| fp | Infiltration rates at time t (min) |
| fc | Final infiltration rate |
| f0 | Infiltration rate at t = 0 |
| pi | Mean observed cumulative infiltration |
| p | Observed cumulative infiltration |
| mi | Mean simulated cumulative infiltration |
| m | Simulated cumulative infiltration |
| n | Total numbers of samples |
| I (t) | Cumulative infiltration rate |
| i (t) | Infiltration rate |
| t | Time |
| NT | No-tillage |
| MP | Moldboard plow |
| TC | Tine cultivation |
| R2 | Coefficient of determination |
| RMSE | Root mean square error |
References
- Klik, A.; Rosner, J. Long-term experience with conservation tillage practices in Austria: Impacts on soil erosion processes. Soil Tillage Res. 2020, 203, 104669. [Google Scholar] [CrossRef]
- Dokić, D.; Gavran, M.; Gregić, M.; Gantner, V. The Impact of Trade Balance of Agri-Food Products on the State’s Ability to Withstand the Crisis. HighTech Innov. J. 2020, 1, 107–111. [Google Scholar] [CrossRef]
- Ghazouani, H.; Capodici, F.; Ciraolo, G.; Maltese, A.; Rallo, G.; Provenzano, G. Potential of thermal images and simulation models to assess water and salt stress: Application to potato crop in central Tunisia. Chem. Eng. Trans. 2017, 58, 709–714. [Google Scholar]
- Williams, J.; Reardon, C.; Wuest, S.; Long, D. Soil water infiltration after oilseed crop introduction into a Pacific Northwest winter wheat–fallow rotation. J. Soil Water Conserv. 2020, 75, 739–745. [Google Scholar] [CrossRef]
- Chari, M.M.; Poozan, M.T.; Afrasiab, P. Modelling soil water infiltration variability using scaling. Biosyst. Eng. 2020, 196, 56–66. [Google Scholar] [CrossRef]
- Singh, B.; Sihag, P.; Deswal, S. Modelling of the impact of water quality on the infiltration rate of the soil. Appl. Water Sci. 2019, 9, 15. [Google Scholar] [CrossRef] [Green Version]
- Ekwueme, B.N.; Agunwamba, J.C. Modeling the Influence of Meteorological Variables on Runoff in a Tropical Watershed. Civ. Eng. J. 2020, 6, 2344–2351. [Google Scholar] [CrossRef]
- Carvalho, D.F.; Eduardo, E.N.; Almeida, W.S.D.; Santos, L.A.; Alves Sobrinho, T. Water erosion and soil water infiltration in different stages of corn development and tillage systems. Rev. Bras. Eng. Agríc. Ambient. 2015, 19, 1072–1078. [Google Scholar] [CrossRef] [Green Version]
- Sihag, P.; Tiwari, N.; Ranjan, S. Estimation and inter-comparison of infiltration models. Water Sci. 2017, 31, 34–43. [Google Scholar] [CrossRef] [Green Version]
- Mishra, S.K.; Tyagi, J.V.; Singh, P.V.P. Comparison of infiltration models. Hydrol. Process. 2003, 17, 2629–2652. [Google Scholar] [CrossRef]
- Philip, J. The theory of infiltration: 1. The infiltration equation and its solution. Soil Sci. 1957, 83, 345–358. [Google Scholar] [CrossRef]
- Singh, V.P.; Yu, F.X. Derivation of Infiltration Equation Using Systems Approach. J. Irrig. Drain. Eng. 1990, 116, 837–858. [Google Scholar] [CrossRef]
- Kostiakov, A.N. On the dynamics of the coefficient of water percolation in soils and the necessity of studying it from the dynamic point of view for the purposes of amelioration. Trans. Sixth Comm. Int. Soc. Soil Sci. 1932, 1, 7–21. [Google Scholar]
- Horton, R.E. An Approach Toward a Physical Interpretation of Infiltration-Capacity. Soil Sci. Soc. Am. J. 1941, 5, 399–417. [Google Scholar] [CrossRef]
- Machiwal, D.; Jha, M.K.; Mal, B. Modelling Infiltration and quantifying Spatial Soil Variability in a Wasteland of Kharagpur, India. Biosyst. Eng. 2006, 95, 569–582. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, P.; Zhao, X.; Li, P. Evaluation and modelling of furrow infiltration for uncropped ridge - furrow tillage in Loess Plateau soils. Soil Res. 2012, 50, 360–370. [Google Scholar] [CrossRef]
- Mahapatra, S.; Jha, M.K.; Biswal, S.; Senapati, D. Assessing Variability of Infiltration Characteristics and Reliability of Infiltration Models in a Tropical Sub-humid Region of India. Sci. Rep. 2020, 10, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Fenu, G.; Malloci, F.M. DSS LANDS: A Decision Support System for Agriculture in Sardinia. HighTech Innov. J. 2020, 1, 129–135. [Google Scholar] [CrossRef]
- Schjønning, P.; Lamandé, M.; Crétin, V.; Nielsen, J.A. Upper subsoil pore characteristics and functions as affected by field traffic and freeze–thaw and dry–wet treatments. Soil Res. 2017, 55, 234–244. [Google Scholar] [CrossRef]
- Blanco-Canqui, H.; Ruis, S.J. No-tillage and soil physical environment. Geoderma 2018, 326, 164–200. [Google Scholar] [CrossRef]
- Salem, H.M.; Valero, C.; Muñoz, M.Á; Gil Rodríguez, M.; Silva, L.L. Short-term effects of four tillage practices on soil physical properties, soil water potential, and maize yield. Geoderma 2015, 237–238, 60–70. [Google Scholar] [CrossRef] [Green Version]
- Ahuchaogu, I.; Etim, I.; Etuk, A. Research Paper Effects of Tillage Methods on Soil Infliltration Rate in Uyo, Nigeria. Cont. J. Eng. Sci. 2015, 10, 10–20. [Google Scholar]
- Li, Y.; Li, Z.; Cui, S.; Jagadamma, S.; Zhang, Q. Residue retention and minimum tillage improve physical environment of the soil in croplands: A global meta-analysis. Soil Tillage Res. 2019, 194, 104292. [Google Scholar] [CrossRef]
- Cullum, R. Macropore flow estimations under no-till and till systems. Catena 2009, 78, 87–91. [Google Scholar] [CrossRef]
- Truman, C.; Potter, T.; Nuti, R.; Franklin, D.; Bosch, D. Antecedent water content effects on runoff and sediment yields from two Coastal Plain Ultisols. Agric. Water Manag. 2011, 98, 1189–1196. [Google Scholar] [CrossRef]
- Głąb, T.; Kulig, B. Effect of mulch and tillage system on soil porosity under wheat (Triticum Aestivum). Soil Tillage Res. 2008, 99, 169–178. [Google Scholar] [CrossRef]
- de Almeida, W.S.; Panachuki, E.; de Oliveira, P.T.S.; da Silva Menezes, R.; Sobrinho, T.A.; de Carvalho, D.F. Effect of soil tillage and vegetal cover on soil water infiltration. Soil Tillage Res. 2018, 175, 130–138. [Google Scholar] [CrossRef]
- Mizuba, M.; Hammel, J. Infiltration rates in fall-seeded winter wheat fields following preplant subsoil tillage. J. Soil Water Conserv. 2001, 56, 133–137. [Google Scholar]
- Govindasamy, P.; Mowrer, J.; Rajan, N.; Provin, T.; Hons, F.; Bagavathiannan, M. Influence of long-term (36 years) tillage practices on soil physical properties in a grain sorghum experiment in Southeast Texas. Arch. Agron. Soil Sci. 2021, 67, 234–244. [Google Scholar] [CrossRef]
- Robinson, G.W. A new method for the mechanical analysis of soils and other dispersions. J. Agric. Sci. 1922, 12, 306–321. [Google Scholar] [CrossRef] [Green Version]
- Brady, N.; Weil, R. The Nature and Properties of Soils, 12th ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Yoro, G.; Godo, G. Les méthodes de mesure de la densité apparente: Analyse de la dispersion des résultats dans un horizon donné. Cah. ORSTOM. Pédol. 1990, 25, 423–429. [Google Scholar]
- Campbell, D.; Henshall, J. Bulk density. In Soil Analysis: Physical Methods; Smith, K.A., Mullins, C.E., Eds.; Marcel Dekker: New York, NY, USA, 1991. [Google Scholar]
- Okalebo, J.R.; Gathua, K.W.; Woomer, P.L. Laboratory Methods of Soil and Plant Analysis: A Working Manual, 2nd ed.; Sacred Africa: Nairobi, Kenya, 2002. [Google Scholar]
- Ibitoye, A. Laboratory Manual on Basic Soil Analysis, 2nd ed.; Foladaye Publishing Company: Akure, Nigeria, 2006. [Google Scholar]
- Reynolds, W. Ring or cylinder infiltrometers. Methods Soil Anal. 2002, 4, 818–843. [Google Scholar]
- Qiaosheng, S.; Zuoxin, L.; Zhenying, W.; Haijun, L. Simulation of the soil wetting shape under porous pipe sub-irrigation using dimensional analysis. Irrig. Drain. 2007, 56, 389–398. [Google Scholar] [CrossRef]
- Duan, R.; Fedler, C.B.; Borrelli, J. Field evaluation of infiltration models in lawn soils. Irrig. Sci. 2011, 29, 379–389. [Google Scholar] [CrossRef]
- Fan, R.; Zhang, X.; Yang, X.; Liang, A.; Jia, S.; Chen, X. Effects of tillage management on infiltration and preferential flow in a black soil, Northeast China. Chin. Geogr. Sci. 2013, 23, 312–320. [Google Scholar] [CrossRef] [Green Version]
- Stone, L.R.; Schlegel, A.J. Tillage and Crop Rotation Phase Effects on Soil Physical Properties in the West-Central Great Plains. Agron. J. 2010, 102, 483–491. [Google Scholar] [CrossRef]
- Wienhold, B.J.; Tanaka, D.L. Haying, tillage, and nitrogen fertilization influences on infiltration rates at a conservation reserve program site. Soil Sci. Soc. Am. J. 2000, 64, 379–381. [Google Scholar] [CrossRef] [Green Version]
- Osanyinpeju, K.L.; Dada, P.O. Soil Porosity and Water Infiltration as Influenced by Tillage Practices on Federal University of Agriculture Abeokuta, Ogun State, Nigeria Soil. Int. J. Latest Technol. Eng. Manag. Appl. Sci. 2018, 7, 2278–2540. [Google Scholar]
- Schwartz, R.; Baumhardt, R.; Evett, S. Tillage effects on soil water redistribution and bare soil evaporation throughout a season. Soil Tillage Res. 2010, 110, 221–229. [Google Scholar] [CrossRef]
- Celik, I.; Ersahin, S. Evaluation of tillage influence on infiltration characteristics in a clay soil. J. Food Agric. Environ. 2011, 9, 653–658. [Google Scholar]
- Presley, D.R.; Sindelar, A.J.; Buckley, M.E.; Mengel, D.B. Long-Term Nitrogen and Tillage Effects on Soil Physical Properties under Continuous Grain Sorghum. Agron. J. 2012, 104, 749–755. [Google Scholar] [CrossRef] [Green Version]
- Kahlon, M.S.; Lal, R.; Ann-Varughese, M. Twenty two years of tillage and mulching impacts on soil physical characteristics and carbon sequestration in Central Ohio. Soil Tillage Res. 2013, 126, 151–158. [Google Scholar] [CrossRef]
- Alvarez, R.; Steinbach, H. A review of the effects of tillage systems on some soil physical properties, water content, nitrate availability and crops yield in the Argentine Pampas. Soil Tillage Res. 2009, 104, 1–15. [Google Scholar] [CrossRef]
- Ordoñez-Morales, K.D.; Cadena-Zapata, M.; Zermeño-González, A.; Campos-Magaña, S. Effect of Tillage Systems on Physical Properties of a Clay Loam Soil under Oats. Agriculture 2019, 9, 62. [Google Scholar] [CrossRef] [Green Version]
- Capowiez, Y.; Cadoux, S.; Bouchant, P.; Ruy, S.; Roger-Estrade, J.; Richard, G.; Boizard, H. The effect of tillage type and cropping system on earthworm communities, macroporosity and water infiltration. Soil Tillage Res. 2009, 105, 209–216. [Google Scholar] [CrossRef]
- Shukla, M.K.; Lal, R.; Unkefer, P. Experimental Evaluation of Infiltration Models for Different Land Use and Soil Management Systems. Soil Sci. 2003, 168, 178–191. [Google Scholar] [CrossRef]
- Saito, T.; Yasuda, H.; Suganuma, H.; Inosako, K.; Abe, Y.; Kojima, T. Predicting Soil Infiltration and Horizon Thickness for a Large-Scale Water Balance Model in an Arid Environment. Water 2016, 8, 96. [Google Scholar] [CrossRef] [Green Version]
- Mbagwu, J. Testing the goodness of fit of selected infiltration models on soils with different land use histories. Int. Centr. Theor. Phys. 1993. Available online: https://inis.iaea.org/search/search.aspx?orig_q=RN:25043561 (accessed on 9 March 2021).
- Ogbe, V.; Jayeoba, O.; Ode, S. Comparison of four soil infiltration models on a sandy soil in Lafia, Southern Guinea Savanna Zone of Nigeria. Prod. Agric. Technol. 2011, 7, 116–126. [Google Scholar]
- Hangen, E.; Buczko, U.; Bens, O.; Brunotte, J.; Hüttl, R. Infiltration patterns into two soils under conventional and conservation tillage: Influence of the spatial distribution of plant root structures and soil animal activity. Soil Tillage Res. 2002, 63, 181–186. [Google Scholar] [CrossRef]
- Adindu, R.U.; Igbokwe, K.; Dike, I. Philip Model. Capability to Estimate Infiltration for Solis of Aba, Abia State. J. Earth Sci. Geotech. Eng. 2015, 5, 63–68. [Google Scholar]
- Nnoli, N.O.; Balogun, A.A.; Omotosho, J.A.; Agele, S.O. Empirical analysis of dry spells during growing season with respect to maize crop in Nigeria. Theor. Appl. Clim. 2020, 142, 525–542. [Google Scholar] [CrossRef]
- Al-Janabi, A.M.S.; Ghazali, A.H.; Yusuf, B. Modified models for better prediction of infiltration rates in trapezoidal permeable stormwater channels. Hydrol. Sci. J. 2019, 64, 1918–1931. [Google Scholar] [CrossRef]
- Ghorbani Dashtaki, S.; Homaee, M.; Mahdian, M. Estimating soil water infiltration parameters using Artificial Neural Networks. J. Water Soil 2009, 23, 185–198. [Google Scholar]
- Shao, Q.; Baumgartl, T. Field evaluation of three modified infiltration models for the simulation of rainfall sequences. Soil Sci. 2016, 181, 45–56. [Google Scholar] [CrossRef]
- Puigdefábregas, J. The role of vegetation patterns in structuring runoff and sediment fluxes in drylands. Earth Surf. Process. Landf. 2005, 30, 133–147. [Google Scholar] [CrossRef]
- Jha, M.K.; Mahapatra, S.; Mohan, C.; Pohshna, C. Infiltration characteristics of lateritic vadose zones: Field experiments and modeling. Soil Tillage Res. 2019, 187, 219–234. [Google Scholar] [CrossRef]
- Dashtaki, S.G.; Homaee, M.; Mahdian, M.H.; Kouchakzadeh, M. Site-Dependence Performance of Infiltration Models. Water Resour. Manag. 2009, 23, 2777–2790. [Google Scholar] [CrossRef]
- Silva, L.L. Fitting infiltration equations to centre-pivot irrigation data in a Mediterranean soil. Agric. Water Manag. 2007, 94, 83–92. [Google Scholar] [CrossRef]
- Basahi, J.; Kenimer, A.L.; Fipps, G.; Sabbagh, G.J. The effect of droplet impact energy produced by sprinkler system on soil erosion, runoff and infiltration rate. ASAE Pap. 1998, 98, 2060. [Google Scholar]
- Silva, L.L. The effect of spray head sprinklers with different deflector plates on irrigation uniformity, runoff and sediment yield in a Mediterranean soil. Agric. Water Manag. 2006, 85, 243–252. [Google Scholar] [CrossRef]

| Soil Property | Value | Analysis Method | Reference |
|---|---|---|---|
| Clay (%) | 25.60 | Pipette method | [30] |
| Sand (%) | 67.15 | - | - |
| Silt (%) | 6.90 | - | - |
| Texture | Sandy clay loam | Textural triangle | [31] |
| Bulk density (g/cm3) | 1.69 | Core method | [32] |
| Penetration resistance (daN/cm2) | 2.04 | Electronic penetrometer | [33] |
| Water content (cm3/cm3) | 13.27 | Gravimetric method | [33] |
| Water field porosity (%) | 67.58 | Core method | [32] |
| Total porosity (%) | 32.78 | Core method | [32] |
| EC (dS/m) | 0.98 | Saturated paste extract | [34] |
| pH | 7.54 | pH meter | [35] |
| Soil organic matter (%) | 2.01 | Colorimetric method | [34] |
| Treatments | Field/Plot Number | Infiltration Models | ||||||
|---|---|---|---|---|---|---|---|---|
| Philip | Kostiakov | Horton | ||||||
| S (cm/min1/2) | A (cm/min) | a | b | fc (cm/min) | f0 (cm/min) | k | ||
| MP | 1 | 0.159 | 0.0031 | 0.059 | 0.714 | 16.663 | 21.370 | 3.136 |
| 6 | 0.168 | 0.0032 | 0.079 | 0.684 | 16.663 | 21.705 | 3.483 | |
| 8 | 0.183 | 0.0029 | 0.068 | 0.702 | 16.989 | 22.490 | 3.555 | |
| Mean | 0.170 | 0.0031 | 0.069 | 0.700 | 16.772 | 21.855 | 3.391 | |
| TC | 3 | 0.140 | 0.0031 | 0.052 | 0.724 | 15.640 | 20.063 | 2.808 |
| 5 | 0.149 | 0.0031 | 0.069 | 0.691 | 15.920 | 20.890 | 3.493 | |
| 7 | 0.151 | 0.0034 | 0.067 | 0.702 | 17.469 | 22.284 | 3.424 | |
| Mean | 0.147 | 0.0032 | 0.062 | 0.706 | 16.343 | 21.079 | 3.242 | |
| NT | 2 | 0.139 | 0.0021 | 0.037 | 0.741 | 13.750 | 17.728 | 2.961 |
| 4 | 0.116 | 0.0030 | 0.063 | 0.772 | 14.251 | 18.080 | 2.453 | |
| 9 | 0.094 | 0.0015 | 0.031 | 0.722 | 7.708 | 11.205 | 1.635 | |
| Mean | 0.116 | 0.002 | 0.043 | 0.745 | 11.903 | 14.467 | 2.298 | |
| Treatments | Field/Plot Number | Infiltration Models | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Philip | Kostiakov | Horton | ||||||||
| R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | ||
| MP | 1 | 0.975 | 7.78 | 3.04 | 0.919 | 7.95 | 2.98 | 0.628 | 15.71 | 6.55 |
| 6 | 0.976 | 9.76 | 3.78 | 0.927 | 9.15 | 3.42 | 0.622 | 19.30 | 7.87 | |
| 8 | 0.968 | 9.58 | 3.77 | 0.916 | 10.46 | 3.89 | 0.593 | 19.75 | 8.32 | |
| Mean | 0.973 | 9.04 | 3.53 | 0.92 | 9.19 | 3.43 | 0.61 | 18.25 | 7.58 | |
| TC | 3 | 0.959 | 8.40 | 2.93 | 0.892 | 8.37 | 2.98 | 0.564 | 15.07 | 5.88 |
| 5 | 0.982 | 9.12 | 3.69 | 0.94 | 8.25 | 3.40 | 0.676 | 16.84 | 7.19 | |
| 7 | 0.962 | 10.12 | 4.53 | 0.927 | 8.66 | 4.08 | 0.671 | 18.09 | 7.82 | |
| Mean | 0.967 | 9.21 | 3.72 | 0.92 | 8.43 | 3.49 | 0.64 | 16.67 | 6.96 | |
| NT | 2 | 0.988 | 2.54 | 1.39 | 0.961 | 2.80 | 1.19 | 0.833 | 6.32 | 3.43 |
| 4 | 0.987 | 3.04 | 1.37 | 0.935 | 3.14 | 1.48 | 0.740 | 6.82 | 3.03 | |
| 9 | 0.968 | 4.50 | 1.62 | 0.906 | 4.34 | 1.64 | 0.626 | 7.34 | 2.76 | |
| Mean | 0.981 | 3.36 | 1.46 | 0.934 | 3.57 | 1.44 | 0.733 | 6.83 | 3.07 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amami, R.; Ibrahimi, K.; Sher, F.; Milham, P.; Ghazouani, H.; Chehaibi, S.; Hussain, Z.; Iqbal, H.M.N. Impacts of Different Tillage Practices on Soil Water Infiltration for Sustainable Agriculture. Sustainability 2021, 13, 3155. https://0-doi-org.brum.beds.ac.uk/10.3390/su13063155
Amami R, Ibrahimi K, Sher F, Milham P, Ghazouani H, Chehaibi S, Hussain Z, Iqbal HMN. Impacts of Different Tillage Practices on Soil Water Infiltration for Sustainable Agriculture. Sustainability. 2021; 13(6):3155. https://0-doi-org.brum.beds.ac.uk/10.3390/su13063155
Chicago/Turabian StyleAmami, Roua, Khaled Ibrahimi, Farooq Sher, Paul Milham, Hiba Ghazouani, Sayed Chehaibi, Zahra Hussain, and Hafiz M. N. Iqbal. 2021. "Impacts of Different Tillage Practices on Soil Water Infiltration for Sustainable Agriculture" Sustainability 13, no. 6: 3155. https://0-doi-org.brum.beds.ac.uk/10.3390/su13063155







