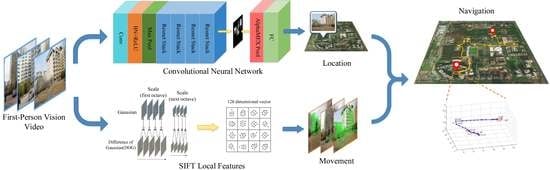
A CNN-SIFT Hybrid Pedestrian Navigation Method Based on First-Person Vision
Abstract
:1. Introduction
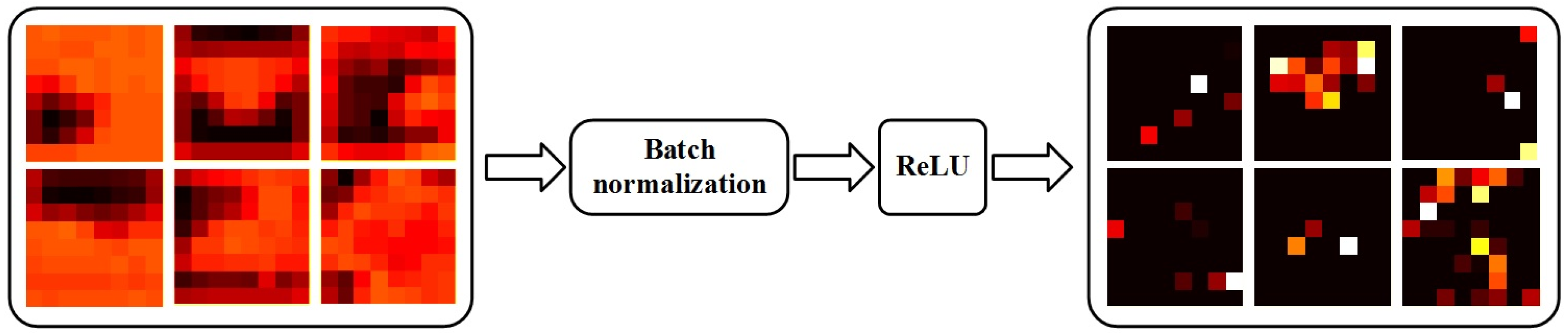
- Based on the proposed AlphaMEX function, an end-to-end trainable global pooling layer is designed, named AlphaMEX Global Pool. This novel global pooling layer has three advantages: First, it improves the performance of state-of-the-art CNN structures without inserting any redundant layers or parameters; second, it is smarter than any traditional global pooling method that could be well trained end-to-end; and, finally, it is more appropriate in modern CNN structures, as the feature-maps become sparse after batch normalization (BN) [20] and rectified linear unit (ReLU) [21] combined layers, which are commonly used in state-of-the-art “non-plain” CNNs.
- A novel iterative structure is designed for pedestrian navigation, which combines the AlphaMEX CNN-based localization and the SIFT-based movement estimation. As the SIFT-based movement estimation requires continuous frames, the iterative structure is appropriate for the hybrid method. Also, an iterative function is indispensable in the road detection algorithm (see Section 4.3). The proposed iterative structure concisely combines both of the characteristics.
- Experimental results on CIFAR [22], Street View House Numbers (SVHN) [23] and ImageNet [24] datasets demonstrate the effectiveness of the AlphaMEX Global Pool. Movement can be well estimated with an adequate accuracy based on the proposed projective geometry algorithm in the model test. In addition, an FPV database named “BuaaFPV” is designed for further validation.
2. Related Work
3. Materials and Methods
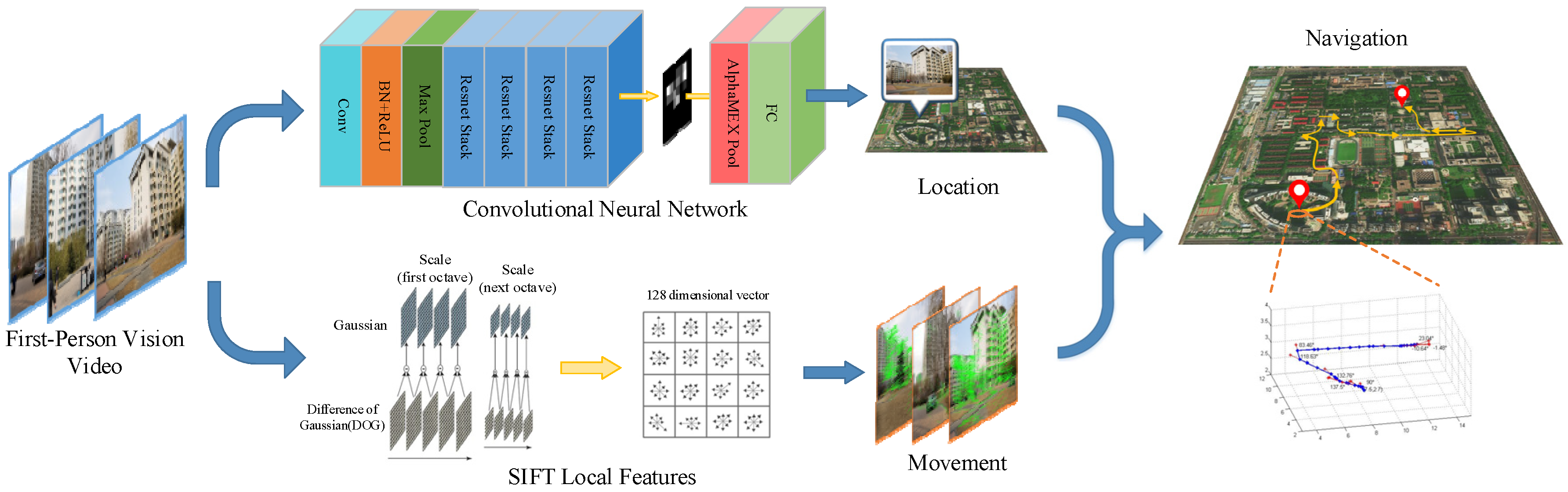
3.1. AlphaMEX CNN-Based Localization
3.1.1. Sparsity Analysis
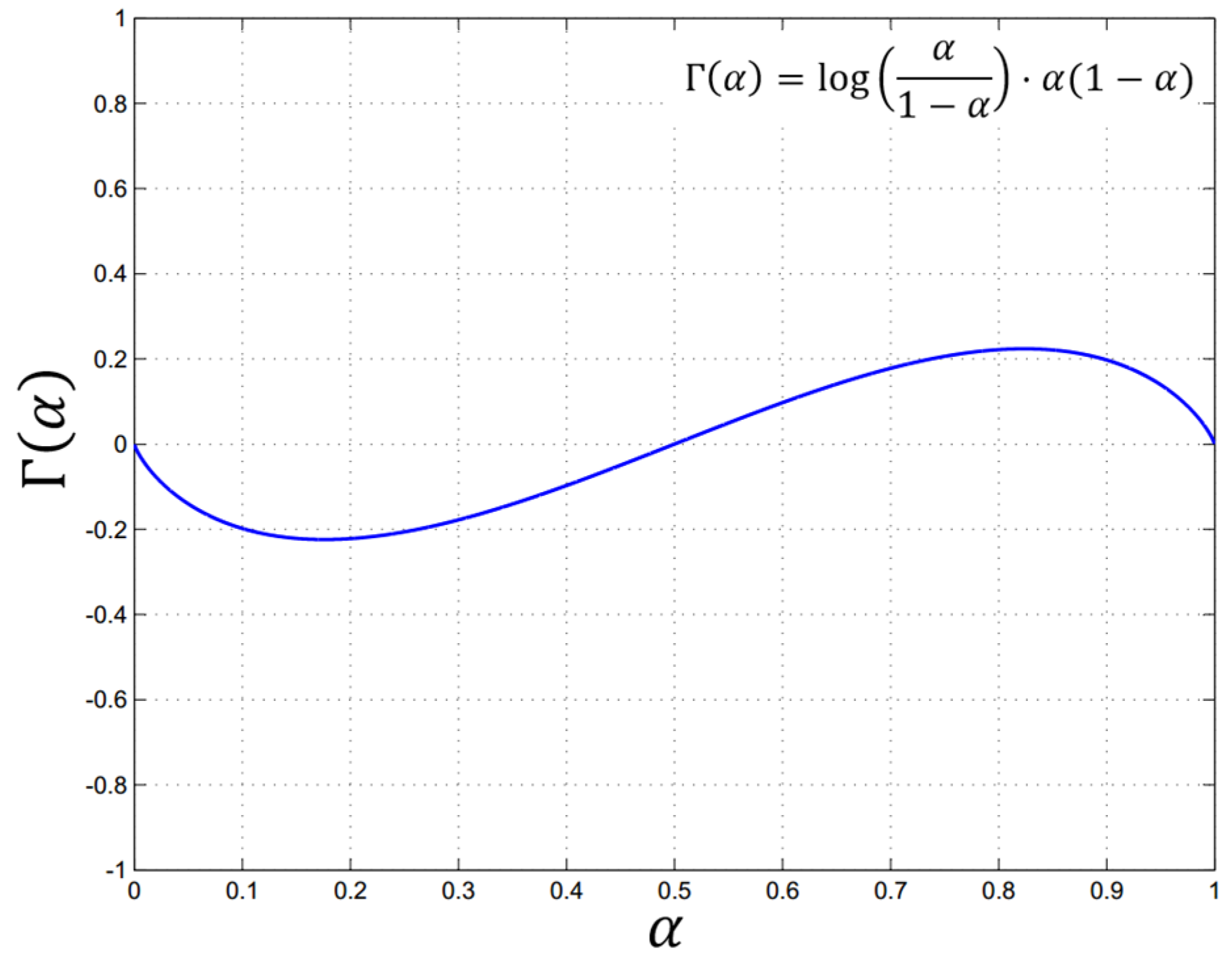
3.1.2. AlphaMEX
- Function outputs the minimum value, when right-sided limits to 0:
- Function outputs the average value, when limits to :
- Function outputs the maximum value, when left-sided limits to 1:
- The “collapsing” property:
3.2. SIFT-Based Movement Calculation
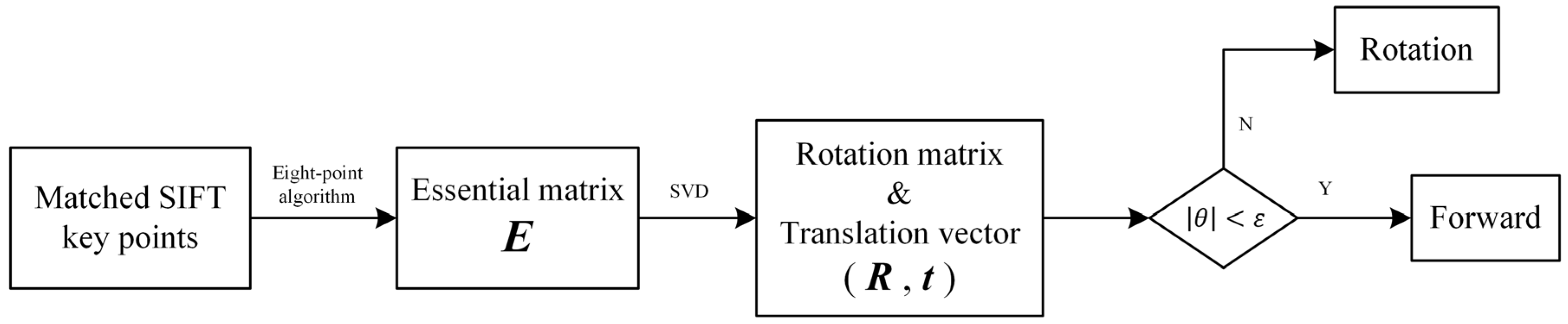
3.2.1. Essential Matrix
- Estimate the essential matrix, , by the eight-point algorithm [53], which sets up a least-squares problem with the set of matched SIFT key points.
- Extract and from . Supposing that the Singular-Value Decomposition (SVD) of is , where and are unitary matrices, there are four possible choices for and :where . is defined as:
- Find the correct . Testing with a single point to determine if it is in front of both cameras is sufficient to decide between the four different solutions.
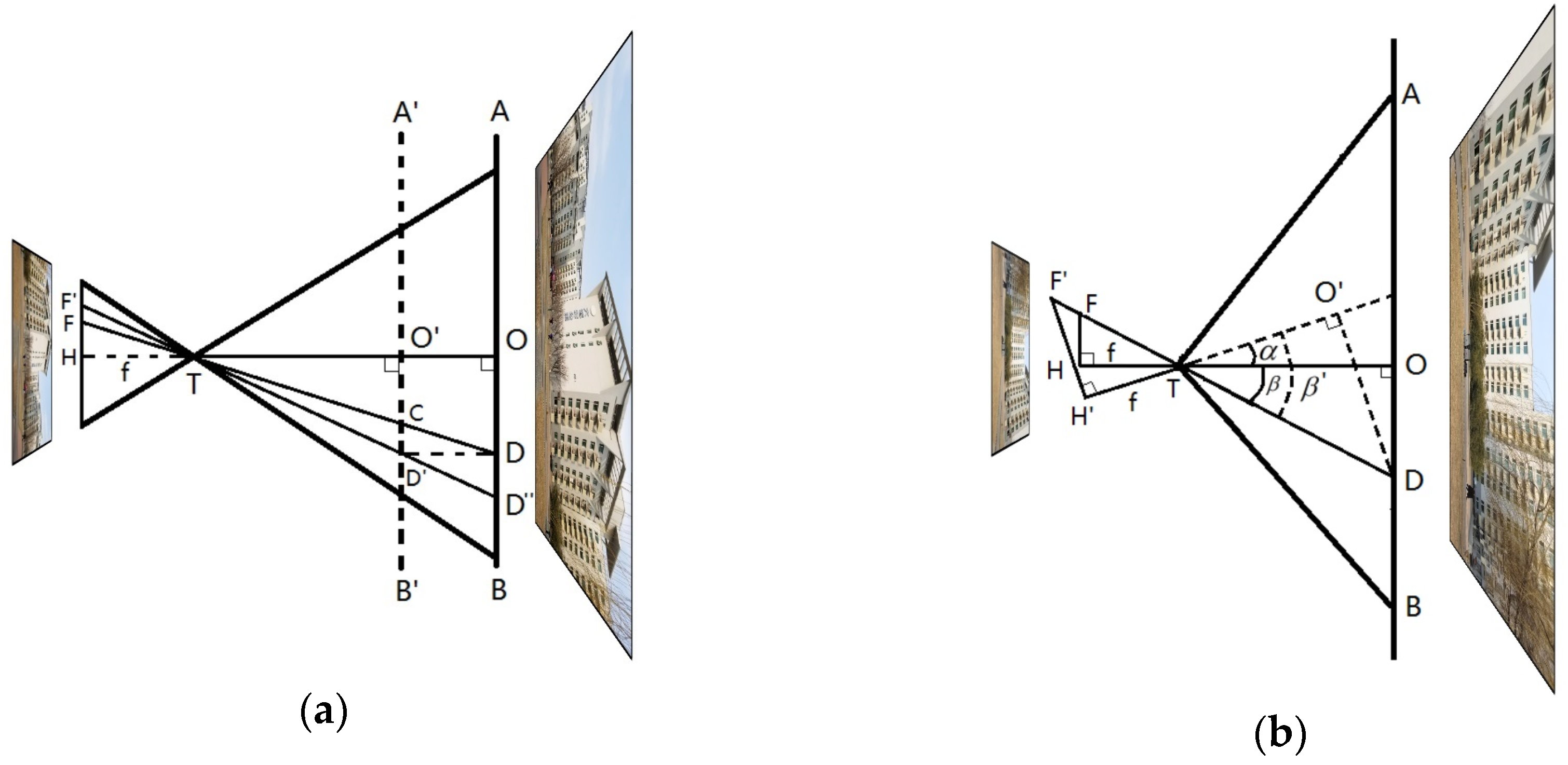
3.2.2. Forward Movement and Rotation of the Camera
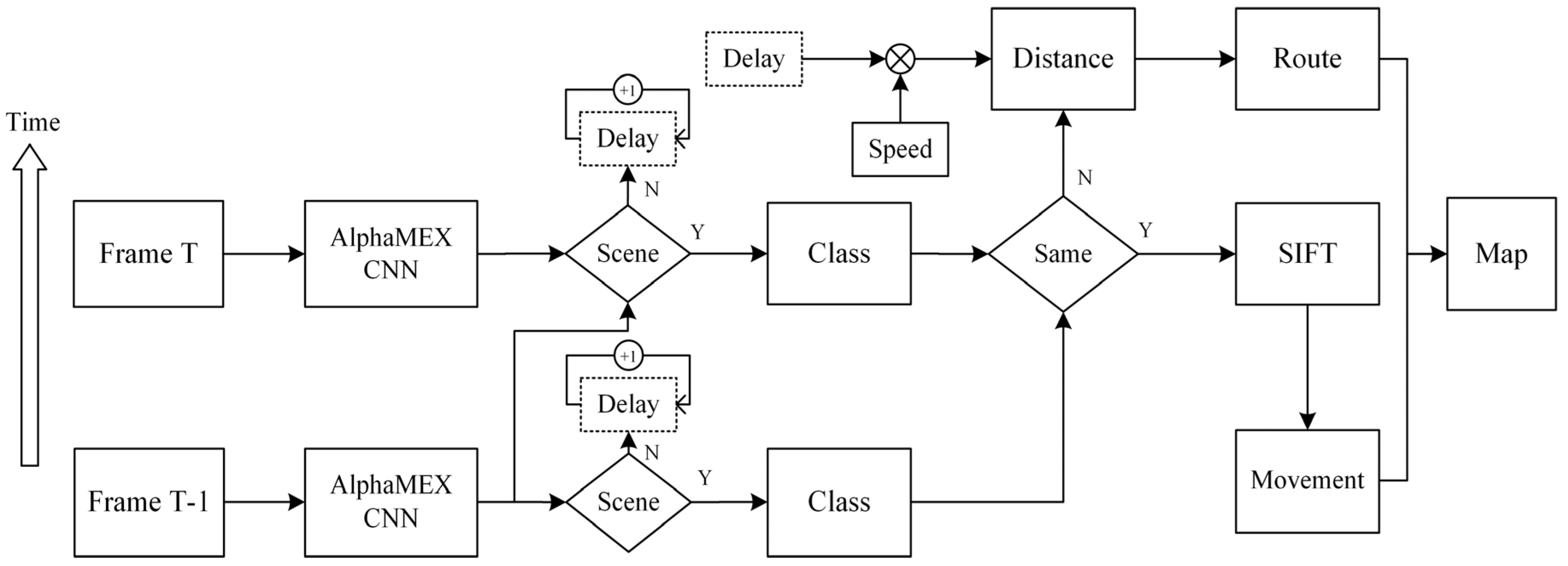
3.3. CNN-SIFT Hybrid Pedestrian Navigation
- If it is the first frame, feed it into AlphaMEX CNN and output a Road/Scene decision with scene class (if the decision is Scene). If not, name it Frame T, feed it into AlphaMEX CNN and output a Road/Scene decision which is made by both the current frame and the previous frame (see Section 4.3). If the decision is Scene, go to step 2. If not, go to step 3.
- Compare the scene class of the current frame with the scene class of the previous frame. If it is the same, feed these two frames into the SIFT-based movement estimation algorithm and go to step 5. If not, go to step 4.
- Make the global parameter Delay increase one and go to step 1 with next frame. Parameter Delay is used for counting the frames of Road, which is initialized zero and will be initialized after a route is calculated.
- Calculate the distance between the two typical scenes with the product of Delay and the walking speed. The distance helps in drawing routes on the map. Repeat step 1 on next frame.
- Calculate the wearer’s movements and plot the trajectory on the map. Repeat step 1 on next frame.
4. Results
4.1. AlphaMEX CNN Image Classification Results
4.2. SIFT-Based Movement Estimation Results
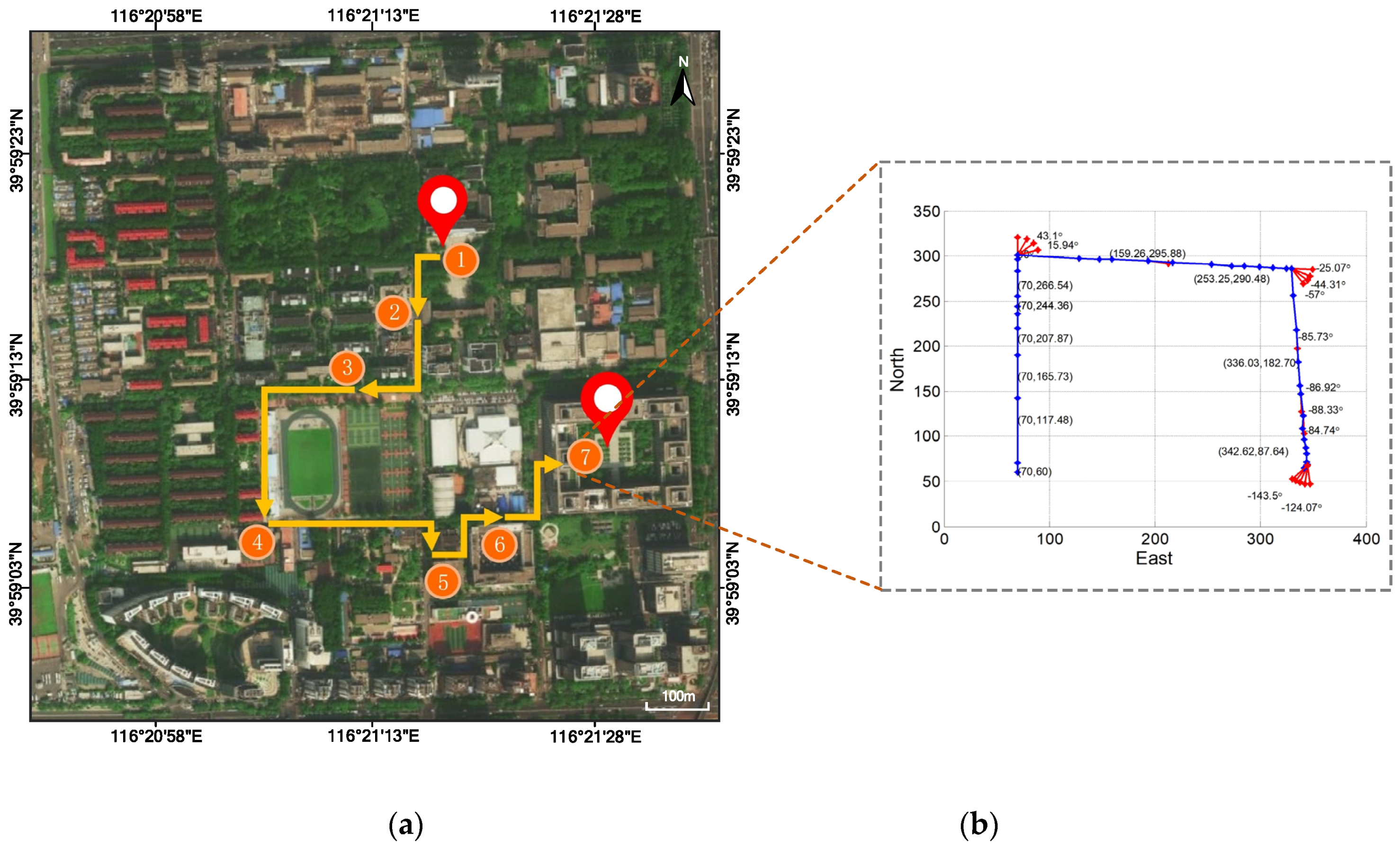
4.3. Pedestrian Navigation Results
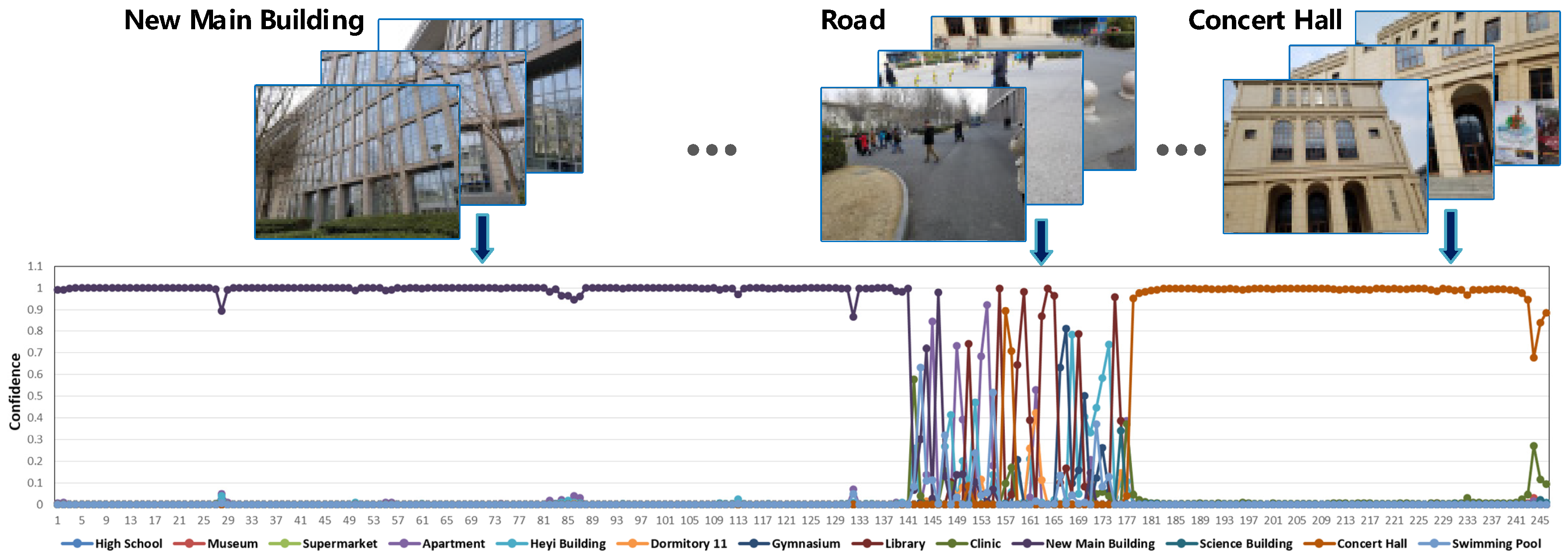
- Frames with continuous absolute confidence are accepted as a typical scene.
- If the maximum confidence of a frame or its previous frame is lower than 0.85, it will be identified as “Road”.
- As the wearer walks with constant speed (1.4m/s), the period represents the walking distance.
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Betancourt, A.; Morerio, P.; Regazzoni, C.S.; Rauterberg, M. The evolution of First-Person Vision methods: A survey. IEEE Trans. Circuits Syst. Video Technol. 2015, 25, 744–760. [Google Scholar] [CrossRef]
- Kanade, T.; Hebert, M. First-person vision. Proc. IEEE 2012, 100, 2442–2453. [Google Scholar] [CrossRef]
- Li, C.; Kitani, K.M. Model recommendation with virtual probes for egocentric hand detection. In Proceedings of the 2013 IEEE International Conference on Computer Vision (ICCV), Sydney, Australia, 1–8 December 2013; pp. 2624–2631. [Google Scholar]
- Li, C.; Kitani, K.M. Pixel-level hand detection in ego-centric videos. In Proceedings of the IEEE Computer Vision and Pattern Recognition (CVPR), Orlando, FL, USA, 23–28 June 2013; pp. 3570–3577. [Google Scholar]
- Wang, H.; Choudhury, R.R.; Nelakuditi, S.; Bao, X. InSight: Recognizing humans without face recognition. In Proceedings of the 14th Workshop on Mobile Computing Systems and Applications, Jekyll Island, GA, USA, 26–27 February 2013; p. 7. [Google Scholar]
- Zariffa, J.; Popovic, M.R. Hand contour detection in wearable camera video using an adaptive histogram region of interest. J. Neuroeng. Rehabilit. 2013, 10, 114. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Narayan, S.; Kankanhalli, M.S.; Ramakrishnan, K.R. Action and interaction recognition in first-person videos. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Columbus, OH, USA, 23–28 June 2014; pp. 526–532. [Google Scholar]
- Matsuo, K.; Yamada, K.; Ueno, S.; Naito, S. An attention-based activity recognition for egocentric video. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Columbus, OH, USA, 23–28 June 2014; pp. 565–570. [Google Scholar]
- Damen, D.; Leelasawassuk, T.; Haines, O.; Calway, A.; Mayol-Cuevas, W. Multi-user egocentric online system for unsupervised assistance on object usage. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–7 September 2014; pp. 481–492. [Google Scholar]
- Poleg, Y.; Arora, C.; Peleg, S. Temporal segmentation of egocentric videos. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 2537–2544. [Google Scholar]
- Zheng, K.; Lin, Y.; Zhou, Y.; Salvi, D.; Fan, X.; Guo, D.; Wang, S. Video-based action detection using multiple wearable cameras. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–7 September 2014; pp. 727–741. [Google Scholar]
- Castle, R.O.; Gawley, D.J.; Klein, G.; Murray, D.W. Video-rate recognition and localization for wearable cameras. In Proceedings of the British Machine Vision Conference, Coventry, UK, 10–13 September 2007; pp. 1–10. [Google Scholar]
- Castle, R.O.; Gawley, D.J.; Klein, G.; Murray, D.W. Towards simultaneous recognition, localization and mapping for hand-held and wearable cameras. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 4102–4107. [Google Scholar]
- Davison, A.J.; Reid, I.D.; Molton, N.D.; Stasse, O. MonoSLAM: Real-time single camera SLAM. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1052–1067. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Castle, R.; Klein, G.; Murray, D.W. Video-rate localization in multiple maps for wearable augmented reality. In Proceedings of the 12th IEEE International Symposium on Wearable Computers (ISWC), Pittsburgh, PA, USA, 28 September–1 October 2008; pp. 15–22. [Google Scholar]
- Kameda, Y.; Ohta, Y. Image retrieval of First-Person Vision for pedestrian navigation in urban area. In Proceedings of the 2010 20th International Conference on Pattern Recognition (ICPR), Istanbul, Turkey, 23–26 August 2010; pp. 364–367. [Google Scholar]
- Li, T.; Zhang, H.; Gao, Z.; Chen, Q.; Niu, X. High-Accuracy Positioning in Urban Environments Using Single-Frequency Multi-GNSS RTK/MEMS-IMU Integration. Remote Sens. 2018, 10, 205. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; pp. 1150–1157. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Ft. Lauderdale, FL, USA, 11–13 April 2011; pp. 315–323. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images. Tech Report. 2009. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.222.9220&rep=rep1&type=pdf (accessed on 8 April 2009).
- Netzer, Y.; Wang, T.; Coates, A.; Bissacco, A.; Wu, B.; Ng, A.Y. Reading digits in natural images with unsupervised feature learning. In Proceedings of the Advances in Neural Information Processing Systems Workshop on Deep Learning and Unsupervised Feature Learning, Granada, Spain, 12–17 December 2011; p. 5. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the IEEE Conference on Computer Visual Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Fathi, A.; Hodgins, J.K.; Rehg, J.M. Social interactions: A first-person perspective. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 1226–1233. [Google Scholar]
- Yarbus, A.L. Eye movements during perception of complex objects. In Eye Movements and Vision; Springer: Boston, MA, USA, 1967; pp. 171–211. [Google Scholar]
- Bisio, I.; Delfino, A.; Lavagetto, F.; Marchese, M. Opportunistic detection methods for emotion-aware smartphone applications. In Psychology and Mental Health: Concepts, Methodologies, Tools, and Applications; IGI Global: Hershey, PA, USA, 2016; pp. 670–704. [Google Scholar]
- Philipose, M.; Ren, X. Egocentric recognition of handled objects: Benchmark and analysis. In Proceedings of the 2009 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Miami, FL, USA, 20–25 June 2009; pp. 1–8. [Google Scholar]
- Betancourt, A.; López, M.M.; Regazzoni, C.S.; Rauterberg, M. A sequential classifier for hand detection in the framework of egocentric vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Columbus, OH, USA, 23–28 June 2014; pp. 600–605. [Google Scholar]
- Lu, Z.; Grauman, K. Story-driven summarization for egocentric video. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2714–2721. [Google Scholar]
- Hodges, S.; Williams, L.; Berry, E.; Izadi, S.; Srinivasan, J.; Butler, A.; Wood, K. SenseCam: A retrospective memory aid. In Proceedings of the International Conference on Ubiquitous Computing, Orange County, CA, USA, 17–21 September 2006; pp. 177–193. [Google Scholar]
- Sundaram, S.; Cuevas, W.W.M. High level activity recognition using low resolution wearable vision. In Proceedings of the 2009 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Miami, FL, USA, 20–25 June 2009; pp. 25–32. [Google Scholar]
- Ogaki, K.; Kitani, K.M.; Sugano, Y.; Sato, Y. Coupling eye-motion and ego-motion features for first-person activity recognition. In Proceedings of the 2012 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Providence, RI, USA, 16–21 June 2012; pp. 1–7. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Takizawa, H.; Orita, K.; Aoyagi, M.; Ezaki, N.; Mizuno, S. A Spot Navigation System for the Visually Impaired by Use of SIFT-Based Image Matching. In Proceedings of the International Conference on Universal Access in Human-Computer Interaction, Los Angeles, CA, USA, 2–7 August 2015; pp. 160–167. [Google Scholar]
- Hu, M.; Chen, J.; Shi, C. Three-dimensional mapping based on SIFT and RANSAC for mobile robot. In Proceedings of the 2015 IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems (CYBER), Shenyang, China, 8–12 June 2015; pp. 139–144. [Google Scholar]
- Pang, Y.; Sun, M.; Jiang, X.; Li, X. Convolution in convolution for network in network. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 1587–1597. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Han, J.; Han, J.; Shao, L. Cosaliency detection based on intrasaliency prior transfer and deep intersaliency mining. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1163–1176. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y. Convolutional neural networks for sentence classification. arXiv, 2014; arXiv:1408.5882. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Lin, M.; Chen, Q.; Yan, S. Network in network. arXiv, 2013; arXiv:1312.4400. [Google Scholar]
- Srivastava, R.K.; Greff, K.; Schmidhuber, J. Training very deep networks. In Proceedings of the Twenty-ninth Annual Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 2377–2385. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Visual Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; Weinberger, K.Q.; Maaten, L. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; p. 3. [Google Scholar]
- Khoshkbarforoushha, A.; Khosravian, A.; Ranjan, R. Elasticity management of streaming data analytics flows on clouds. J. Comput. Syst. Sci. 2017, 89, 24–40. [Google Scholar] [CrossRef]
- Khoshkbarforoushha, A.; Ranjan, R.; Gaire, R.; Abbasnejad, E.; Wang, L. Distribution based workload modelling of continuous queries in clouds. IEEE Trans. Emerg. Top. Comput. 2017, 5, 120–133. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, L.; Zomaya, A.Y.; Chen, D.; Ranjan, R. Task-tree based large-scale mosaicking for massive remote sensed imageries with dynamic dag scheduling. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 2126–2137. [Google Scholar] [CrossRef]
- Wang, L.; Ma, Y.; Zomaya, A.Y.; Ranjan, R.; Chen, D. A parallel file system with application-aware data layout policies for massive remote sensing image processing in digital earth. IEEE Trans. Parallel Distrib. Syst. 2015, 26, 1497–1508. [Google Scholar] [CrossRef]
- Menzel, M.; Ranjan, R.; Wang, L.; Khan, S.U.; Chen, J. CloudGenius: A hybrid decision support method for automating the migration of web application clusters to public clouds. IEEE Trans. Comput. 2015, 64, 1336–1348. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Fergus, R. Stochastic pooling for regularization of deep convolutional neural networks. arXiv, 2013; arXiv:1301.3557. [Google Scholar]
- Lee, C.Y.; Gallagher, P.W.; Tu, Z. Generalizing pooling functions in convolutional neural networks: Mixed, gated, and tree. In Proceedings of the 19th International Conference on Artificial Intelligence and Statistics (AISTATS), Cadiz, Spain, 7–11 May 2016; pp. 464–472. [Google Scholar]
- Cohen, N.; Sharir, O.; Shashua, A. Deep simnets. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4782–4791. [Google Scholar]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003; pp. 237–360. [Google Scholar]
- Torr, P.H.; Zisserman, A. MLESAC: A new robust estimator with application to estimating image geometry. Comput. Vis. Image Underst. 2000, 78, 138–156. [Google Scholar] [CrossRef]
- Sutskever, I.; Martens, J.; Dahl, G.; Hinton, G. On the importance of initialization and momentum in deep learning. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 1139–1147. [Google Scholar]
- Springenberg, J.T.; Dosovitskiy, A.; Brox, T.; Riedmiller, M. Striving for simplicity: The all convolutional net. arXiv, 2014; arXiv:1412.6806. [Google Scholar]
- Lee, C.Y.; Xie, S.; Gallagher, P.; Zhang, Z.; Tu, Z. Deeply-supervised nets. In Proceedings of the Eighteenth International Conference on Artificial Intelligence and Statistics, San Diego, CA, USA, 10–12 May 2015; pp. 562–570. [Google Scholar]
- Huang, G.; Sun, Y.; Liu, Z.; Sedra, D.; Weinberger, K.Q. Deep networks with stochastic depth. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 646–661. [Google Scholar]
- Matsushita, Y.; Ofek, E.; Ge, W.; Tang, X.; Shum, H.Y. Full-frame video stabilization with motion inpainting. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1150–1163. [Google Scholar] [CrossRef] [PubMed]
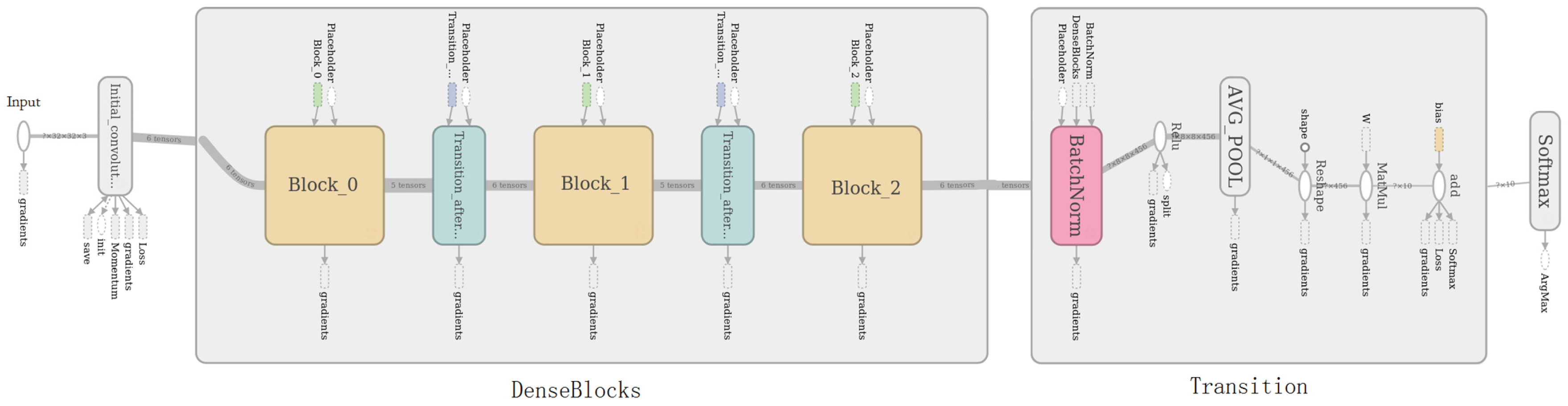



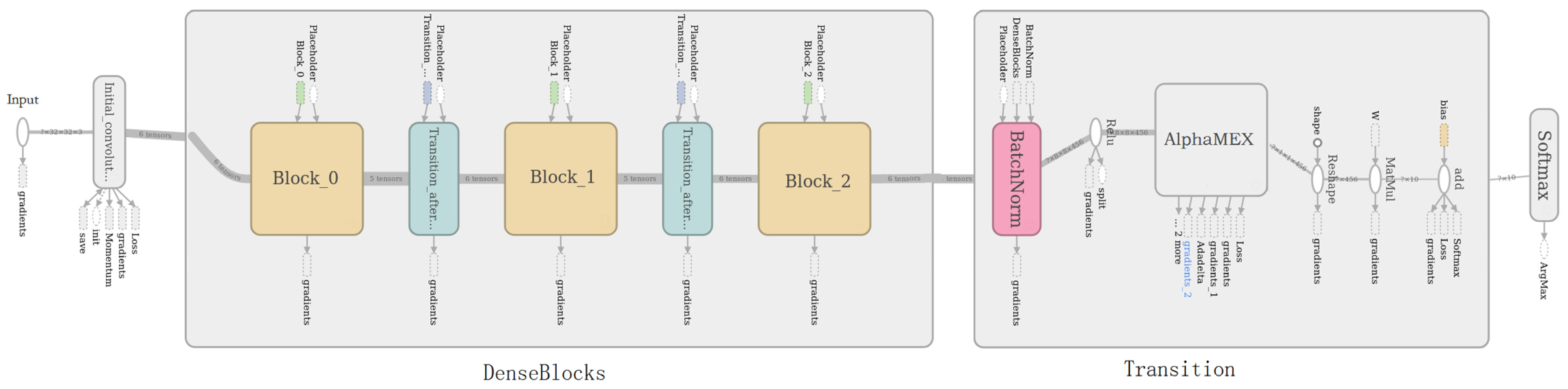



| Layers | Output Size | Feature-Maps | DenseNet-40 (k = 12) | AlphaMEX-DenseNet-40 (k = 12) |
|---|---|---|---|---|
| Convolution | 24 | conv, stride 1 | ||
| Dense Block (1) | 268 | |||
| Transition Layer (1) | 268 | conv | ||
| 268 | average pool, stride 2 | |||
| Dense Block (2) | 312 | |||
| Transition Layer (2) | 312 | conv | ||
| 312 | average pool, stride 2 | |||
| Dense Block (3) | 456 | |||
| Classification Layer | 456 | global average pool | AlphaMEX global pool | |
| - | - | fully-connected, softmax | ||
| Error rate/F1 score | - | - | 5.24%/95.31% | 5.03%/95.63% |
| Method | Depth | Params (M) | C10 | C10+ | C100 | C100+ | SVHN |
|---|---|---|---|---|---|---|---|
| Network in Network [41] | - | 0.97 | 10.41 | 8.81 | 35.68 | - | 2.35 |
| SimNet [52] | - | - | - | 7.82 | - | - | - |
| Deeply Supervised Net [57] | - | 0.97 | 9.69 | 7.97 | - | 34.57 | 1.92 |
| Highway Network [42] | - | - | - | 7.72 | - | 32.39 | - |
| All-CNN [56] | - | 1.3 | 9.08 | 7.25 | - | 33.71 | - |
| AlphaMEX-All-CNN | - | 1.3 | 8.99 | 7.07 | - | 29.10 | - |
| ResNet [43] | 110 | 1.7 | - | 6.61 | - | - | - |
| ResNet (reported by [58]) | 110 | 1.7 | 13.63 | 6.41 | 44.74 | 27.22 | 2.01 |
| AlphaMEX-ResNet | 110 | 1.7 | 8.41 | 5.84 | 32.87 | 27.71 | 1.97 |
| DenseNet (k = 12) [44] | 40 | 1.0 | 7.00 | 5.24 | 27.55 | 24.42 | 1.79 |
| AlphaMEX-DenseNet (k = 12) | 40 | 1.0 | 6.54 | 5.03 | 27.24 | 23.71 | 1.73 |
| Method | Top-1 | Top-5 |
|---|---|---|
| AlphaMEX Global Pool | 28.1 | 9.1 |
| Global Average Pool | 29.8 | 10.5 |
| Δ | 1.7 | 1.4 |
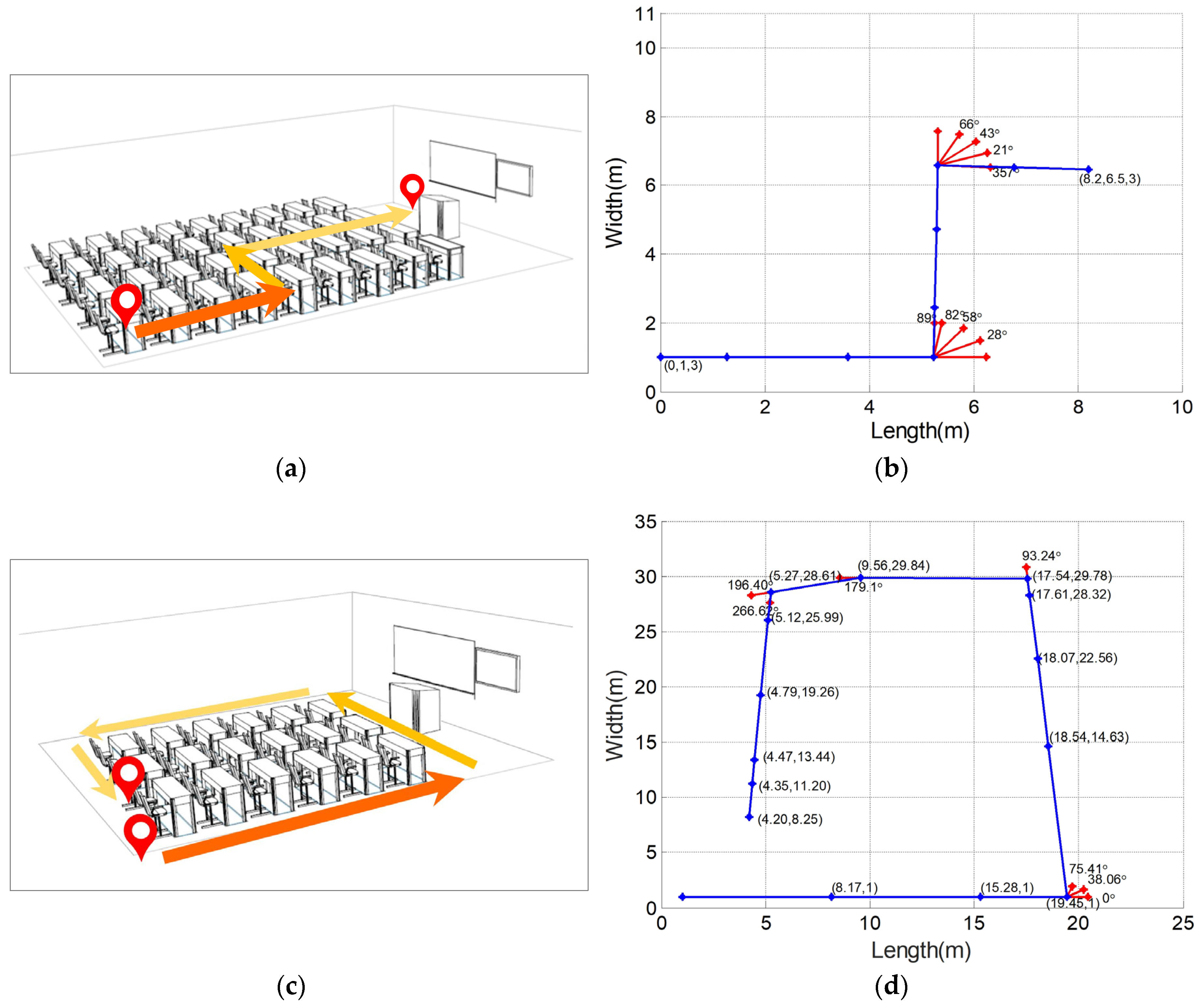
| Moving Forward | Calculated Distance (m) | Actual Distance (m) | Absolute Error (m) | Relative Error (%) |
| part1 | 5.2372 | 5.00 | 0.2372 | 4.74 |
| part3 | 5.5839 | 6.00 | −0.4161 | −6.94 |
| part5 | 2.8602 | 3.00 | −0.1398 | −4.66 |
| Rotation | Calculated Angle (°) | Actual Angle (°) | Absolute Error (°) | Relative Error (%) |
| part2 | 89.2533 | 90.00 | −0.7467 | −0.83 |
| part4 | 92.6742 | 90.00 | 2.6742 | 2.97 |
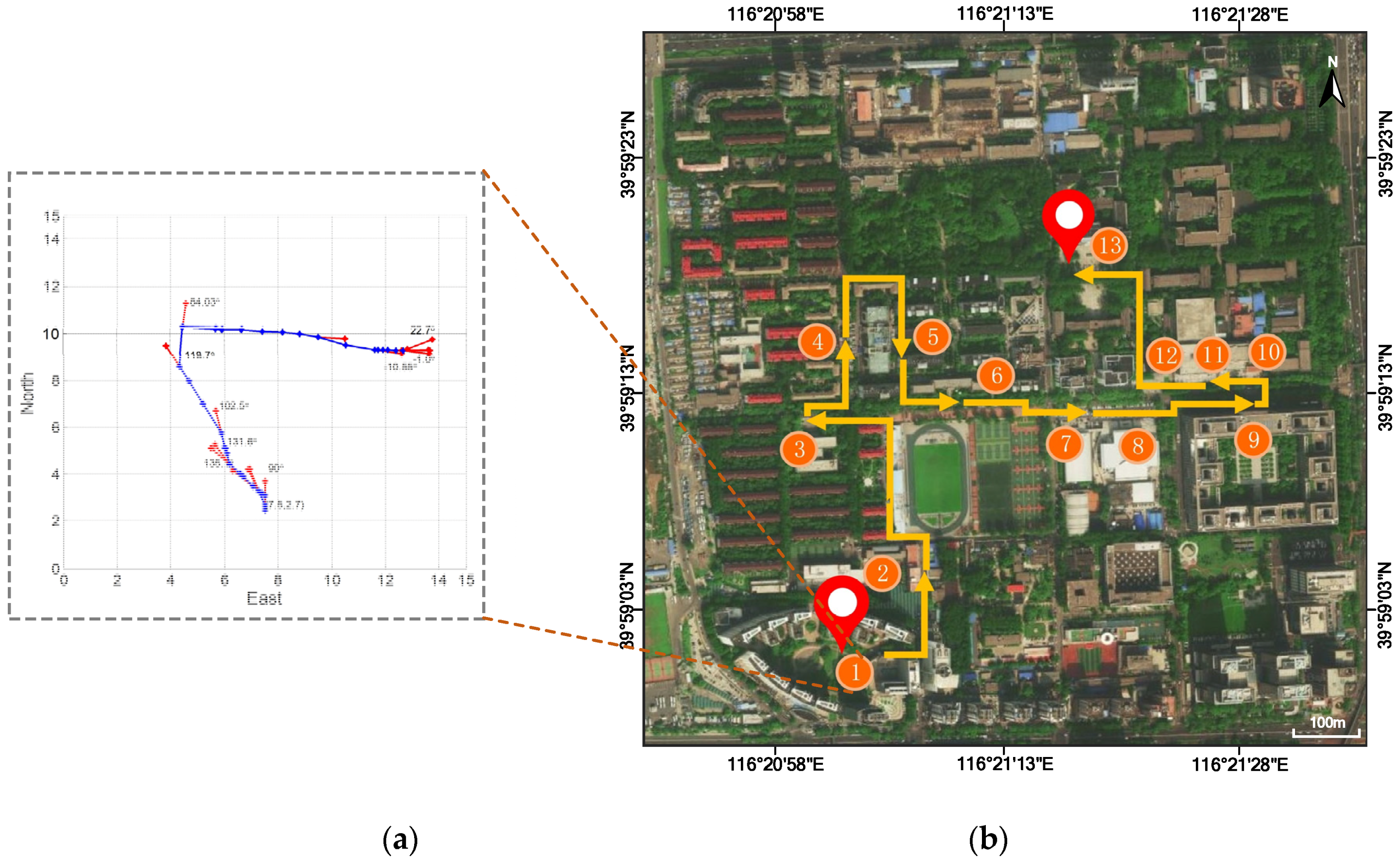
| Moving Forward | Calculated Distance (m) | Actual Distance (m) | Absolute Error (m) | Relative Error (%) |
| part1 | 18.501 | 19.00 | −0.499 | −2.63 |
| part3 | 28.644 | 30.00 | −1.356 | −4.52 |
| part5 | 12.713 | 13.00 | −0.287 | −2.20 |
| part7 | 20.685 | 20.00 | 0.685 | 3.43 |
| Rotation | Calculated Angle (°) | Actual Angle (°) | Absolute Error (°) | Relative Error (%) |
| 93.2403 | 90.00 | 3.2403 | 3.60 | |
| part4 | 85.8142 | 90.00 | −4.1858 | −4.65 |
| part6 | 87.5610 | 90.00 | −2.4390 | −2.71 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Q.; Zhang, B.; Lyu, S.; Zhang, H.; Sun, D.; Li, G.; Feng, W. A CNN-SIFT Hybrid Pedestrian Navigation Method Based on First-Person Vision. Remote Sens. 2018, 10, 1229. https://0-doi-org.brum.beds.ac.uk/10.3390/rs10081229
Zhao Q, Zhang B, Lyu S, Zhang H, Sun D, Li G, Feng W. A CNN-SIFT Hybrid Pedestrian Navigation Method Based on First-Person Vision. Remote Sensing. 2018; 10(8):1229. https://0-doi-org.brum.beds.ac.uk/10.3390/rs10081229
Chicago/Turabian StyleZhao, Qi, Boxue Zhang, Shuchang Lyu, Hong Zhang, Daniel Sun, Guoqiang Li, and Wenquan Feng. 2018. "A CNN-SIFT Hybrid Pedestrian Navigation Method Based on First-Person Vision" Remote Sensing 10, no. 8: 1229. https://0-doi-org.brum.beds.ac.uk/10.3390/rs10081229