Depth from Satellite Images: Depth Retrieval Using a Stereo and Radiative Transfer-Based Hybrid Method
Abstract
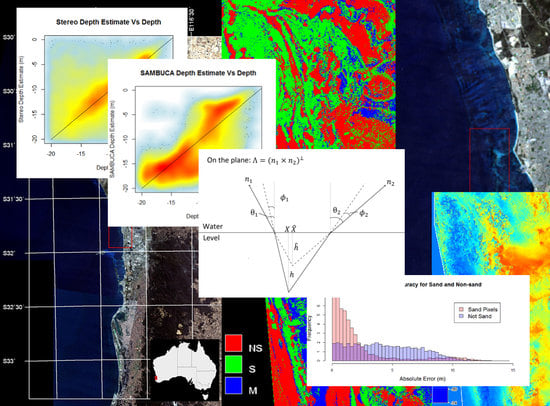
:1. Introduction
2. Materials and Methods
2.1. Satellite Images
2.2. LiDAR Bathymetry
2.3. Towed Video
2.4. Creating a Sand/Non-Sand Mask
2.5. SAMBUCA Method
- the subsurface remote-sensing reflectance (just below the waterline);
- the subsurface remote-sensing reflectance of the infinitely deep water column;
- the vertical attenuation coefficient for diffuse down-welling light;
- the vertical attenuation coefficient for diffuse up-welling light originating from the bottom;
- the vertical attenuation coefficient for diffuse upwelling light originating from each layer in the water column;
- for the bottom reflectance for two different substrates;
- is the proportion of substrate 1 (so is the proportion of substrate 2); and
- is the length of the water column through which the light is passing.
2.6. Stereo Method
2.6.1. Rational Polynomial Coefficients
- x is the latitude,
- y is the longitude,
- h is the position of the scene point relative to the WGS84 geoid,
- r is the row number in the image, and
- c is the column number in the image.
2.6.2. Accounting for Refraction
2.6.3. Determining Corresponding Pixels
3. Results
3.1. Effect of Depth
3.2. Image Texture as a Measure of Confidence
3.3. The Effect of Seabed Substrate
3.4. Hybrid of Satellite-Based Bathymetry Approaches
3.4.1. Potential Best Achievable Results Using the Most Accurate Pixels
3.4.2. Decision Based on Local Texture
3.4.3. Decision Based on Cover Type
4. Discussion
4.1. On the Overall Accuracy of the Methods
4.2. Combining Satellite-Based Bathymetry Approaches
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Collings, S.; Campbell, N.A.; Keesing, J. Quantifying the discriminatory power of remote sensing technologies for benthic habitat mapping. Int. J. Remote Sens. 2018. accepted. [Google Scholar]
- Symonds, G.; Black, K.P.; Young, I.R. Wave-driven flow over shallow reefs. J. Geophys. Res. 1995, 100, 2639–2648. [Google Scholar] [CrossRef]
- Brando, V.; Decker, A. Satellite hyperspectral remote sensing for estimating estuarine and coastal water quality. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1378–1387. [Google Scholar] [CrossRef]
- Pacheco, A.; Horta, J.; Loureiro, C.; Ferreira, O. Retrieval of nearshore bathymetry from Landsat 8 images: A tool for coastal monitoring in shallow waters. Remote Sens. Environ. 2015, 159, 102–116. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Passive remote sensing techniques for mapping water depth and bottom features. Appl. Opt. 1978, 17, 379–383. [Google Scholar] [CrossRef] [PubMed]
- Martin-Lauzer, F.-R. Imagery-Derived Bathymetry Validated. Available online: http://www.hydro-international.com/issues/articles/id1454-imageryderived__Bathymetry_Validated.html (accessed on 1 June 2013).
- McConchie, R.F. Great Barrier Reef in 3D. ABC. Available online: http://www.abc.net.au/news/rural/2013-11-21/great-barrier-reef-map/5108374 (accessed on 9 May 2016).
- International Hydrography Organisation. Satellite Derived Bathymetry (Paper for Consideration by CSPCWG). Available online: http://www.iho.int/mtg_docs/com_wg/CSPCWG/CSPCWG11-NCWG1/CSPCWG11-08.7A-Satellite%20Bathymetry.pdf (accessed on 15 July 2015).
- DigitalGlobe. Worldview-2 Data Sheet. 2009. Available online: https://dg-cms-uploads-production.s3.amazonaws.com/uploads/document/file/98/WorldView2-DS-WV2-rev2.pdf (accessed on 7 August 2018).
- Markham, B.; Storey, J.; Morfitt, R. Landsat-8 sensor characterization and calibration. Remote Sens. Environ. 2015, 7, 2279–2282. [Google Scholar] [CrossRef]
- European Space Agency. The Operational Copernicus Optical High Resolution Land Mission. Available online: http://esamultimedia.esa.int/docs/S2-Data_Sheet.pdf (accessed on 13 February 2015).
- Tewinkel, G.C. Water depths from aerial photographs. Photogramm. Eng. 1963, 29, 1037–1042. [Google Scholar]
- Westaway, R.M.; Lane, S.N.; Hicks, M. Remote sensing of clear-water, shallow, gravel-bed rivers using digital photogrammetry. Photogramm. Eng. Remote Sens. 2001, 67, 1271–1281. [Google Scholar]
- Feurer, D.; Bailly, J.S.; Puech, C.; Le Coarer, Y.; Viau, A. Very-high-resolution mapping of river-immersed topography by remote sensing. Prog. Phys. Geogr. 2008, 32, 403–419. [Google Scholar] [CrossRef]
- Javernicka, L.; Brasingtonb, J.; Carusoa, B. Modeling the topography of shallow braided rivers using Structure-from-Motion photogrammetry. Geomorphology 2014, 213, 166–182. [Google Scholar] [CrossRef]
- Salomonson, V.; Abrams, M.J.; Kahle, A.; Barnes, W.; Xiong, X.; Yamaguchi, Y. Evolution of NASA’s Earth observation system and development of the Moderate-Resolution Imaging Spectroradiometer and the Advanced Spaceborne Thermal Emission and Reflectance Radiometer instruments. In Land Remote Sensing and Global Environmental Change; Ramachandran, B., Justice, C.O., Abrams, M.J., Eds.; NASA’s Earth Observing System and the Science of ASTER and MODIS; Springer: New York, NY, USA, 2010; pp. 3–34. [Google Scholar]
- Zhang, H.-G.; Yang, K.; Lou, X.; Li, D.; Shi, A.; Fu, B. Bathymetric mapping of submarine sand waves using multiangle sun glitter imagery: A case of the Taiwan Banks with ASTER stereo imagery. J. Appl. Remote Sens. 2015, 9, 9–13. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Holderied, K.; Sinclair, M. Determination of water depth with high-resolution satellite imagery over variable bottom types. Limnol. Oceanogr. 2003, 48, 547–556. [Google Scholar] [CrossRef] [Green Version]
- Hobi, M.L.; Ginzler, C. Accuracy assessment of digital surface models based on WorldView-2 and ADS80 stereo remote sensing data. Sensors 2012, 2, 6347–6368. [Google Scholar] [CrossRef] [PubMed]
- Davis, C.H.; Jiang, H.; Wang, X. Modeling and estimation of the spatial variation of elevation error in high resolution DEMs from stereo-image processing. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2483–2489. [Google Scholar] [CrossRef]
- Carl, S.; Miller, D. GAF’s Innovative Stereo Approach. 2014. Available online: https://www.gaf.de/sites/default/files/PR_GAF_RWE_Bathymetry.pdf (accessed on 7 August 2018).
- Botha, E.J.; Brando, V.; Dekker, A.J. Effects of per-pixel variability on uncertainties in bathymetric retrievals from high-resolution satellite images. Remote Sens. 2016, 8, 459. [Google Scholar] [CrossRef]
- Aguilar, M.A.; Saldaña, M.; Aguilar, F.J. Generation and quality assessment of stereo-extracted DSM from GeoEye-1 and WorldView-2 imagery. IEEE Trans. Geosci. Remote Sens. 2013, 52, 1259–1271. [Google Scholar] [CrossRef]
- Murase, T.; Tanaka, M.; Tani, T.; Miyashita, Y.; Ohkawa, N.; Ishiguro, S.; Suzuki, Y.; Kayanne, H.; Yamano, H. A photogrammetric correction procedure for light refraction effects at a two-medium boundary. Photogramm. Eng. Remote Sens. 2008, 9, 1129–1136. [Google Scholar] [CrossRef]
- Fryer, J.G. Photogrammetry through shallow water. Aust. J. Geod. 1983, 38, 25–38. [Google Scholar]
- Hedley, J.D.; Harborne, A.R.; Mumby, P.J. Simple and robust removal of sun glint for mapping shallow-water benthos. Int. J. Remote Sens. 2005, 26, 2107–2112. [Google Scholar] [CrossRef]
- Miecznik, G.; Grabowksa, D. WorldView-2 bathymetric capabilities. Int. Soc. Opt. Photonics 2012. [Google Scholar] [CrossRef]
- Parker, H.; Sinclair, M. The successful application of airborne LiDAR bathymetry surveys using latest technology. In Proceedings of the 2012 Oceans—Yeosu, Yeosu, Korea, 21–24 May 2012. [Google Scholar]
- International Hydrographic Organsiation (IHO). IHO Standards for Hydrographic Surveys; IHO: La Condamine, Monaco, 2008. [Google Scholar]
- Campbell, N.A.; Atchley, W.R. The geometry of canonical variate analysis. Syst. Zool. 1981, 30, 268–280. [Google Scholar] [CrossRef]
- Chia, J.; Caccetta, P.A.; Furby, S.L.; Wallace, J.F. Derivation of plantation type maps. In Proceedings of the 13th Australasian Remote Sensing and Photogrammetry Conference, Canberra, Australia, 21–24 November 2006. [Google Scholar]
- O’Neill, N.T.; Gauthier, Y.; Lambert, E.; Hubert, L.; Dubois, J.M.M.; Dubois, H.R.E. Imaging spectrometry applied to the remote sensing of submerged seaweed. Spectr. Signat. Objects Remote Sens. 1988, 287, 315. [Google Scholar]
- Lyzenga, D.R. Remote sensing of bottom reflectance and water attenuation parameters in shallow water using aircraft and Landsat data. Int. J. Remote Sens. 1981, 2, 71–82. [Google Scholar] [CrossRef]
- Deidda, M.; Sanna, G. Bathymetric extraction using Worldview-2 high resolution images. Int. Soc. Photogramm. Remote Sens. 2012, XXXIX-B8, 153–157. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters: 2. Deriving bottom depths and water properties by optimization. Appl. Opt. 1999, 38, 3831–3843. [Google Scholar] [CrossRef] [PubMed]
- Wettle, M.; Brando, V.E. SAMBUCA: Semi-Analytical Model for Bathymetry, Un-Mixing, and Concentration Assessment; CSIRO Land and Water Science Report. 2006. Available online: www.clw.csiro.au/publications/science/2006/sr22-06.pdf (accessed on 7 August 2018).
- Brando, V.; Anstee, J.M.; Wettle, M.; Dekker, A.G.; Phinn, S.R.; Roelfsema, C. A physics based retrieval and quality assessment of bathymetry from suboptimal hyperspectral data. Remote Sens. Environ. 2009, 113, 755–770. [Google Scholar] [CrossRef]
- Hedley, J.D.; Mumby, P.J. A remote sensing method for resolving depth and subpixel composition of aquatic benthos. Limnol. Oceanogr. 2003, 48, 480–488. [Google Scholar] [CrossRef] [Green Version]
- Lee, Z.; Kendall, L.C.; Chen, R.F.; Peacock, T.G. Properties of the water column and bottom derived from Airborne Visible Imaging Spectrometer (AVIRIS) data. J. Geophys. Res. Oceans 2001, 106, 11639–11651. [Google Scholar] [CrossRef]
- Maritorena, S.; Morel, A.; Gentili, B. Diffuse reflectance of oceanic shallow waters: Influence of water depth and bottom albedo. Limnol. Oceanogr. 1994, 39, 1689–1703. [Google Scholar] [CrossRef] [Green Version]
- Lee, Z.; Weidemann, A.; Arnone, R. Combined effect of reduced band number and increased bandwidth on shallow water remote sensing: The case of WorldView 2. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2577–2586. [Google Scholar] [CrossRef]
- Dowman, I.; Dolloff, J.T. An evaluation of rational functions for photogrammetric restitution. Int. Arch. Photogramm. Remote Sens. 2000, 33, 254–266. [Google Scholar]
- Lee, Z.P. Applying narrowbands remote-sensing reflectance models to wideband data. Appl. Opt. 2009, 48, 3177–3183. [Google Scholar] [CrossRef] [PubMed]
- Di, K.; Ma, R.; Li, R. Deriving 3D shorelines from high resolution IKONOS satellite images with rational functions. In Proceedings of the 2001 ASPRS Annual Convention, St. Louis, MO, USA, 23–27 April 2001. [Google Scholar]
- Scharstein, D.; Szeliski, R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms. Int. J. Comput. Vis. 2002, 47, 7–42. [Google Scholar] [CrossRef]
- Yang, Q. Stereo matching using tree filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 834–846. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Mordohai, P. A quantitative evaluation of confidence measures for stereo vision. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2121–2133. [Google Scholar] [PubMed]
- Engal, G.; Mintz, M.; Wildes, R.P. A stereo confidence metric using single view imagery with comparison to five alternative approaches. Image Vis. Comput. 2004, 22, 943–957. [Google Scholar]
- Burns, B.A.; Taylor, J.R.; Sidhu, H. Uncertainties in bathymetric retrievals. In Proceedings of the 17th National Conference of the Australian Meteorological and Oceanographic Society (IOP Publishing), Canberra, Australia, 27–29 January 2010. [Google Scholar]
- Anstee, J.M.; Botha, E.J.; Williams, R.J.; Dekker, A.G.; Brando, V.E. Optimizing classification accuracy of estuarine macrophytes: By combining spatial and physics-based image analysis. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010; pp. 1367–1370. [Google Scholar]
- Botha, E.J.; Brando, V.E.; Dekker, A.G.; Anstee, J.M.; Sagar, S. Increased spectral resolution enhances coral detection under varying water conditions. Remote Sens. Environ. 2013, 131, 247–261. [Google Scholar] [CrossRef]
- Lyzenga, D.R.; Malinas, N.P.; Tanis, F.J. Multispectral bathymetry using a simple physically based algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2251–2259. [Google Scholar] [CrossRef]
- Jalobeanu, A. Predicting spatial uncertainties in stereo photogrammetry: Achievements and intrinsic limitations. In Proceedings of the 7th International Symposium on Spatial Data Quality, Coimbra, Portugal, 12–14 October 2011. [Google Scholar]
- Lee, Z.; Arnone, R.; Hu, C.; Werdell, J.; Lubac, B. Uncertainties of optical parameters and their propagations in an analytical ocean color inversion algorithm. Appl. Opt. 2010, 49, 369–381. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Boss, E.S.; Roeslar, C. Uncertainties of inherent optical properties obtained from semianalytical inversions of ocean color. Appl. Opt. 2005, 44, 4047–4085. [Google Scholar] [CrossRef]
- Sagar, S.; Brando, V.E.; Sambridge, M. Noise estimation of remote sensing reflectance using a segmentation approach suitable for optically shallow waters. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7504–7512. [Google Scholar] [CrossRef]
- Jalobeanu, A.; Goncalves, G. The unknown spatial quality of dense point clouds derived from stereo images. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1013–1017. [Google Scholar] [CrossRef]
- Alharthy, A. A consistency test between predicted and actual accuracy of photogrammetry measurements. In Proceedings of the American Society for Photogrammetry and Remote Sensing Annual Conference, Baltimore, MD, USA, 7–11 March 2005. [Google Scholar]












| Parameter | Specification |
|---|---|
| LiDAR System | Fugro LADS Mark II |
| IMU | GEC-Marconi FIN3110 |
| Platform | DeHavilland Dash-8 |
| Height | 365–670 m |
| Laser | Nd:Yag |
| Operating Frequency | 900 Hz |
| Nominal Point Spacing | 4.5 m |
| Estimates with <1 m of Error | % of Total Pixels |
|---|---|
| SAMBUCA | 25.3% |
| Stereo | 38.4% |
| Both | 8.96% |
| Sand | Non-Sand | Mixed | All | |
|---|---|---|---|---|
| Stereo | 3.05 | 2.85 | 2.95 | 2.94 |
| SAMBUCA | 2.19 | 3.44 | 2.71 | 2.84 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Collings, S.; Botha, E.J.; Anstee, J.; Campbell, N. Depth from Satellite Images: Depth Retrieval Using a Stereo and Radiative Transfer-Based Hybrid Method. Remote Sens. 2018, 10, 1247. https://0-doi-org.brum.beds.ac.uk/10.3390/rs10081247
Collings S, Botha EJ, Anstee J, Campbell N. Depth from Satellite Images: Depth Retrieval Using a Stereo and Radiative Transfer-Based Hybrid Method. Remote Sensing. 2018; 10(8):1247. https://0-doi-org.brum.beds.ac.uk/10.3390/rs10081247
Chicago/Turabian StyleCollings, Simon, Elizabeth J. Botha, Janet Anstee, and Norm Campbell. 2018. "Depth from Satellite Images: Depth Retrieval Using a Stereo and Radiative Transfer-Based Hybrid Method" Remote Sensing 10, no. 8: 1247. https://0-doi-org.brum.beds.ac.uk/10.3390/rs10081247