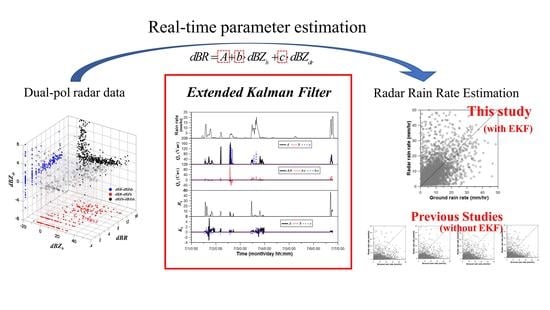
Real-Time Parameter Estimation of a Dual-Pol Radar Rain Rate Estimator Using the Extended Kalman Filter
Abstract
:1. Introduction
2. Methodology
2.1. Rain Rate Estimator of the Dual-Pol Radar
2.2. Kalman Filter
2.3. Extended Kalman Filter
3. Derivation of the Model
3.1. State-Space Model for Dual-Pol Radar Rain Rate Estimator
3.2. Error Covariance and Initial Condition of the Extended Kalman Filter
4. Application, Results, and Discussion
4.1. Study Area and Data
4.1.1. Radar and Rain Gauges Located at Study Area
4.1.2. Rain Gauge and the Corresponding Radar Data for the Storm Events Used in This Study
4.2. Case of Shinpo Rain Gauge (No. 936) and the Corresponding Radar Data for the Event Occurred in 2016
4.2.1. Initial Condition and Result
4.2.2. Comparison with the Least Squares Method
4.2.3. Radar Rain Rate vs. Ground Rain Rate
4.3. Case of Considering All Rain Gauges and the Corresponding Radar Data
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Habib, E.; Malakpet, C.G.; Tokay, A.; Kucera, P.A. Sensitivity of streamflow simulation to temporal variability and estimation of Z-R relationships. J. Hydrol. Eng. 2008, 13, 1177–1186. [Google Scholar] [CrossRef]
- Legates, D.R. Real-time calibration of radar precipitation estimates. Prof. Geogr. 2000, 52, 235–246. [Google Scholar] [CrossRef]
- Michelson, D.B.; Koistinen, J. Gauge-radar network adjustment for the baltic sea experiment. Phys. Chem. Earth (B) 2000, 25, 915–920. [Google Scholar] [CrossRef]
- Brown, P.E.; Diggle, P.J.; Lord, M.E.; Young, P.C. Space-time calibration of radar rainfall data. J. Royal Stat. Soc. Appl. Stat. 2001, 50, 221–242. [Google Scholar] [CrossRef]
- Costa, M.; Alpuim, T. Adjustment of state space models in view of area rainfall estimation. Environmetrics 2010, 22, 530–540. [Google Scholar] [CrossRef] [Green Version]
- Yoo, C.; Ha, E.; Kim, B.; Kim, K.; Choi, J. Sampling error of areal average rainfall due to radar partial coverage. J. Korea Water Resour. Assoc. 2008, 41, 545–558. [Google Scholar] [CrossRef] [Green Version]
- Alfieri, L.; Claps, P.; Laio, F. Time-dependent Z-R relationship for estimating rainfall fields from radar measurements. Nat. Hazard. Earth Sys. Sci. 2010, 10, 149–158. [Google Scholar] [CrossRef] [Green Version]
- Marshall, J.S.; Palmer, W.M.K. The distribution of raindrop with size. J. Atmos. Sci. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Krajewski, W.F.; Smith, J.A. Radar hydrology: Rainfall estimation. Adv. Water Resour. 2002, 25, 1387–1394. [Google Scholar] [CrossRef]
- Twomey, S. On the measurement of precipitation intensity by radar. J. Meteorol. 1952, 10, 66–67. [Google Scholar] [CrossRef] [Green Version]
- Blanchard, D.C. Raindrop size distribution in Hawaiian rains. J. Meteorol. 1953, 10, 457–473. [Google Scholar] [CrossRef] [Green Version]
- Jones, D.M.A. Rainfall Drop-Size Distribution and Radar Reflectivity; Illinois State Water Survey: Champaign, IL, USA, 1956. [Google Scholar]
- Battan, L.J. Radar Observation of the Atmosphere; The University of Chicago Press: Chicago, IL, USA, 1973. [Google Scholar]
- Harter, R.M. An Estimation of Rainfall Amounts Using Radar-Derived Z-R Relationships. Master’s Thesis, Purdue University, West Lafayette, IN, USA, 1990. [Google Scholar]
- Rosenfeld, D.; Wolff, D.B.; Amitai, E. The window probability matching method for rainfall measurements with radar. J. Appl. Meteorol. 1994, 33, 682–693. [Google Scholar] [CrossRef] [Green Version]
- Steiner, M.; Smith, J.A. Reflectivity, rain rate, and kinetic energy flux relationships based on raindrop spectra. J. Appl. Meteorol. 2000, 39, 1923–1940. [Google Scholar] [CrossRef]
- Uijlenhoet, R.; Steiner, M.; Smith, J.A. Variability of raindrop size distributions in a squall line and implications for radar rainfall estimation. J. Hydrol. 2003, 4, 43–61. [Google Scholar] [CrossRef]
- Kim, J.; Yoo, C. Use of a dual Kalman filter for real-time correction of mean field bias of radar rain rate. J. Hydrol. 2014, 519, 2785–2796. [Google Scholar] [CrossRef]
- Kim, J.; Yoo, C.; Lim, S.; Choi, J. Usefulness of relay-information-transfer for radar QPE. J. Hydrol. 2015, 531, 308–319. [Google Scholar] [CrossRef]
- Rendon, S.H.; Vieux, B.E.; Pathak, C.S. Deriving radar specific Z-R relationships for hydrologic operations. In Proceedings of the World Environmental and Water Resources Congress 2011: Bearing Knowledge for Sustainability, Palm Springs, CA, USA, 22–26 May 2011; pp. 4682–4687. [Google Scholar]
- Rendon, S.H.; Vieux, B.E.; Pathak, C.S. Continuous forecasting and evaluation of derived Z-R relationships in a sparse rain gauge network using NEXRAD. J. Hydrol. Eng. 2013, 18, 175–182. [Google Scholar] [CrossRef]
- Jung, S.H.; Kim, K.E.; Ha, K.J. Real-time estimation of improved radar rainfall intensity using rainfall intensity measured by rain gauges. Asia-Pac. J. Atmos. Sci. 2005, 41, 751–762. [Google Scholar]
- Hudlow, M.D. Technological developments in real-time operational hydrologic forecasting in the United States. J. Hydrol. 1988, 102, 69–92. [Google Scholar] [CrossRef]
- Borga, M.; Anagnostou, E.N.; Frank, E. On the use of real-time radar rainfall estimates for flood prediction in mountainous basins. J. Geophys. Res. Atmos. 2000, 105, 2269–2280. [Google Scholar] [CrossRef]
- Young, C.B.; Bradley, A.A.; Krajewski, W.F.; Kruger, A.; Morrissey, M.L. Evaluating NEXRAD multisensor precipitation estimates for operational hydrologic forecasting. J. Hydrometeorol. 2000, 1, 241–254. [Google Scholar] [CrossRef] [Green Version]
- Krajewski, W.F.; Kruger, A.; Singh, S.; Seo, B.C.; Smith, J.A. Hydro-NEXRAD-2: Real-time access to customized radar-rainfall for hydrologic applications. J. Hydroinform. 2013, 15, 580–590. [Google Scholar] [CrossRef]
- Chen, H.; Chandrasekar, V. The quantitative precipitation estimation system for Dallas–Fort Worth (DFW) urban remote sensing network. J. Hydrol. 2015, 531, 259–271. [Google Scholar] [CrossRef] [Green Version]
- Krajewski, W.F.; Ceynar, D.; Demir, I.; Goska, R.; Kruger, A.; Langel, C.; Mantilla, R.; Niemeier, J.; Quintero, F.; Seo, B.; et al. Real-time flood forecasting and information system for the state of Iowa. Bull. Am. Meteorol. Soc. 2017, 98, 539–554. [Google Scholar] [CrossRef]
- Anagnostou, E.N.; Krajewski, W.F. Real-time radar rainfall estimation. Part I: Algorithm formulation. J. Atmos. Oceanic Technol. 1999, 16, 189–197. [Google Scholar] [CrossRef]
- Anagnostou, E.N.; Krajewski, W.F. Real-time radar rainfall estimation. Part II: Case study. J. Atmos. Oceanic Technol. 1999, 16, 198–205. [Google Scholar] [CrossRef]
- Kotarou, T.; Takumi, N.; Takaaki, Y. Operational calibration of raingauge radar by 10-minute telemeter rainfall. In Proceedings of the 3rd International Symposium on Hydrological Applications of Weather Radars, Sao Paulo, Brazil, 20–23 August 1995; pp. 75–81. [Google Scholar]
- Seo, B.C.; Krajewski, W.F.; Kruger, A.; Domaszczynski, P.; Smith, J.A.; Steiner, M. Radar-rainfall estimation algorithms of Hydro-NEXRAD. J. Hydroinform. 2011, 13, 277–291. [Google Scholar] [CrossRef]
- Schneebeli, M.; Berne, A. An extended Kalman filter framework for polarimetric X-band weather radar data processing. J. Atmos. Ocean. Technol. 2012, 29, 711–730. [Google Scholar] [CrossRef]
- Ahnert, P.R.; Krajewski, W.F.; Jonson, E.R. Kalman filter estimation of radar-rainfall field bias. In Proceedings of the 23rd Conference on Radar Meteorology, AMS, Boston, MA, USA, 22–26 September 1986; pp. JP33–JP37. [Google Scholar]
- Lin, D.S.; Krajewski, W.F. Recursive methods of estimating radar-rainfall field bias. In Proceedings of the 24th Radar Meteorology conference, Tallahassee, FL, USA, 27–31 March 1989; pp. 648–651. [Google Scholar]
- Smith, J.A.; Krajewski, W.F. Estimation of the mean field bias of radar rainfall estimates. J. Appl. Meteorol. 1991, 30, 397–412. [Google Scholar] [CrossRef] [Green Version]
- Lee, Y.H.; Singh, V.P. Application of the Kalman filter to the Nash model. Hydrol. Process. 1998, 12, 755–767. [Google Scholar] [CrossRef]
- Seo, D.J.; Breidenbach, J.P.; Johnson, E.R. Real-time estimation of mean field bias in radar rainfall data. J. Hydrol. 1999, 223, 131–147. [Google Scholar] [CrossRef]
- Yoo, C.; Kim, J.; Chung, J.H.; Yang, D.M. Mean field bias correction of the very short range forecast rainfall using the Kalman filter. J. Korean Soc. Hazard Mitig. 2011, 11, 17–28. [Google Scholar] [CrossRef] [Green Version]
- Chumchean, S.; Seed, A.; Sharma, A. Correcting of real-time radar rainfall bias using a Kalman filtering approach. J. Hydrol. 2006, 317, 123–137. [Google Scholar] [CrossRef]
- Chandrasekar, V.; Bringi, V.N. Error structure of multiparameter radar and surface measurements of rainfall. Part I: Differential reflectivity. J. Atmos. Oceanic Technol. 1988, 5, 783–795. [Google Scholar] [CrossRef] [Green Version]
- Aydin, K.; Zhao, Y.; Seliga, T.A. Rain-induced attenuation effects on C-band dual-polarization meteorological radars. Geosci. Remote Sens. Lett. 1989, 27, 57–66. [Google Scholar] [CrossRef]
- Chandrasekar, V.; Bring, V.N.; Balakrishana, N.; Zrnic, D.S. Error structure of multiparameter radar and surface measurements of rainfall. Part III: Specific differential phase. J. Atmos. Oceanic Technol. 1990, 7, 621–629. [Google Scholar] [CrossRef] [Green Version]
- Aydin, K.; Giridhar, V. C-band dual-polarization radar observables in rain. J. Atmos. Sci. 1992, 9, 383–390. [Google Scholar] [CrossRef] [Green Version]
- Gorgucci, E.; Chandrasekar, V.; Scarchilli, G. Radar and surface measurement of rainfall during CaPE: 26 July 1991 case study. J. Appl. Meteor. 1995, 34, 1570–1577. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V. Polarimetric Doppler Weather Radar, Principles and Applications; Cambridge University Press: New York, NY, USA, 2001. [Google Scholar]
- Ryzhkov, A.V.; Giangrade, S.E.; Schuur, T.J. Rainfall estimation with a polarimetric prototype of WSR-88D. J. Appl. Meteor. 2005, 44, 502–515. [Google Scholar] [CrossRef] [Green Version]
- Lee, G.W. Sources of errors in rainfall measurements by polarimetric radar: Variability of drop size distributions, observational noise, and variation of relationships between R and polarimetric parameters. J. Atmos. Oceanic Technol. 2006, 23, 1005–1028. [Google Scholar] [CrossRef]
- Cifelli, R.; Chandrasekar, V.; Lim, S.; Kennedy, P.C.; Wang, Y.; Rutledge, S.A. A new dual-polarization radar rainfall algorithm: Application in Colorado precipitation events. J. Atmos. Oceanic Technol. 2011, 28, 352–364. [Google Scholar] [CrossRef] [Green Version]
- WRC. Development and Application of Cross Governmental Dual-pol. Radar Harmonization; Weather Radar Center: Seoul, Korea, 2014. [Google Scholar]
- Kwon, S.; Lee, G.; Kim, G. Rainfall estimation from an operational S-band dual-polarization radar: Effect of radar calibration. J. Meteor. Soc. Japan. 2015, 93, 65–79. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Liu, L.; Wen, H.; Wu, C.; Zhang, Y. Evaluation of the polarimetric-radar quantitative precipitation estimates of an extremely heavy rainfall event and nine common rainfall events in Guangzhou. Atmosphere 2018, 9, 330. [Google Scholar] [CrossRef] [Green Version]
- Kalman, R.E. A new approach to linear filtering and prediction problems. Trans. ASME J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Park, S.W. Real-Time Flood Forecasting by Transfer Function Types Model and Filtering Algorithm. Ph.D. Thesis, Dongguk University, Seoul, Korea, 1993. [Google Scholar]
- Jang, S.G. Combining Forecast Methods of Chungju Dam Streamflow using Kalman Filter. Master’s Thesis, Seoul National University, Seoul, Korea, 2002. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Gelb, A. Applied Optimal Estimation; The MIT Press: Cambridge, MA, USA, 1974. [Google Scholar]
- Schmidt, S.F. Computational Techniques in Kalman filtering, in Theory and Applications of Kalman Filtering; NATO Advisory Group for Aerospace Research and Development: London, UK, 1970; Volume 139, pp. 219–292. [Google Scholar]
- Simon, D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Adamowski, K.; Muir, J. A Kalman filter modelling of space-time rainfall using radar and raingauge observations. Can. J. Civil Eng. 1989, 16, 767–773. [Google Scholar] [CrossRef]
- O’Connell, P.E.; Clarke, R.T. Adaptive hydrological forecasting—A review. Hydrolog. Sci. J. 1981, 26, 179–205. [Google Scholar]
- Hebson, C.; Wood, E.F. Partitioned state and parameter estimation for real-time flood forecasting. Appl. Math. Comput. 1985, 17, 357–374. [Google Scholar] [CrossRef]
- Seo, B.H.; Gang, G.W. A hydrologic prediction of streamflows for flood forecasting and warning system. J. Korea Water Resour. Assoc. 1985, 18, 153–161. [Google Scholar]
- Chou, C.M.; Wang, R.Y. Application of wavelet-based multi-model Kalman filters to real-time flood forecasting. Hydrol. Process. 2004, 18, 987–1008. [Google Scholar] [CrossRef]
- Eigbe, U.; Beck, M.B.; Hirano, W.F. Kalman filtering in groundwater flow modelling: Problems and prospects. Stoch. Hydrol. Hydraul. 1998, 12, 15–32. [Google Scholar] [CrossRef]
- Wang, G.T.; Yu, Y.S.; Wu, K. Improved flood routing by ARMA modelling and the Kalman filter technique. J. Hydrol. 1987, 93, 175–190. [Google Scholar]
- Wang, C.H.; Bai, Y.L. Algorithm for real time correction of stream flow concentration based on Kalman filter. J. Hydrol. Eng. 2008, 13, 290–296. [Google Scholar] [CrossRef]
- Sage, A.; Husa, G.W. Adaptive filtering with unknown prior statistics. In Proceedings of the Joint Automatic Control Conference, Washington, DC, USA, 7–9 May 1969; Volume 7, pp. 760–769. [Google Scholar]
- Francois, C.; Quesney, A.; Ottle, C. Sequential assimilation of ERS-1 SAR data into a coupled land surface-hydrological model using an extended Kalman filter. J. Hydrometeorol. 2003, 4, 473–487. [Google Scholar] [CrossRef]
- Korea Meteorological Administration KMA. 2019. Available online: http://www.data.kma.go.kr (accessed on 27 June 2019).
- Chen, H.; Lim, S.; Chandrasekar, V.; Jang, B.J. Urban hydrological applications of dual-polarization X-band radar: Case study in Korea. J. Hydrol. Eng. 2017, 22, E5016001. [Google Scholar] [CrossRef]
- Gou, Y.; Ma, Y.; Chen, H.; Yin, J. Utilization of a C-band polarimetric radar for severe rainfall event analysis in complex terrain over eastern China. Remote Sens. 2019, 11, 22. [Google Scholar] [CrossRef] [Green Version]
- Murty, Y.V.V.S.; Smolinski, W.J. Design and implementation of a digital differential relay for a 3-phase power transformer based on Kalman filtering theory. IEEE Trans. Power Del. 1988, 3, 525–533. [Google Scholar] [CrossRef]
- Leung, H.; Zhu, Z.; Ding, Z. An aperiodic phenomenon of the extended Kalman filter in filtering noisy chaotic signals. IEEE Trans. Signal Process. 2000, 48, 1807–1810. [Google Scholar] [CrossRef]
- Macias, J.A.; Gomez, A. Self-tuning of Kalman filters for harmonic computation. IEEE Trans. Power Del. 2006, 21, 501–503. [Google Scholar] [CrossRef]
- Sachidananda, M.; Zrnic, D.S. Rain rate estimates from differential polarization measurements. J. Atmos. Oceanic Technol. 1987, 4, 588–598. [Google Scholar] [CrossRef] [Green Version]
- Brandes, E.A.; Zhang, G.; Vivekanandan, J. Experiments in rainfall estimation with a polarimetric radar in a subtropical environment. J. Appl. Meteor. 2002, 41, 674–685. [Google Scholar] [CrossRef] [Green Version]
- Gorgucci, E.; Scarchilli, G.; Chandrasekar, V.; Bringi, V.N. Rainfall estimation from polarimetric radar measurements: Composite algorithms immune to variability in raindrop shape–size relation. J. Atmos. Oceanic Technol. 2001, 18, 1773–1786. [Google Scholar] [CrossRef]















| References | Parameters | ||
|---|---|---|---|
| A | b | c | |
| Chandrasekar and Bringi (1988) [41] | −26.20 | 0.94 | −1.08 |
| Aydin et al. (1989) [42] | −26.78 | 0.96 | −1.17 |
| Chandrasekar et al. (1990) [43] | −27.03 | 0.97 | −1.08 |
| Aydin and Giridhar (1992) [44] | −26.25 | 0.95 | −1.17 |
| Gorgucci et al. (1995) [45] | −20.00 | 0.92 | −0.37 |
| Bringi and Chandrasekar (2001) [46] | −21.74 | 0.71 | −3.43 |
| Ryzhkov et al. (2005) [47] | −17.99 | 0.74 | −1.03 |
| Lee (2006) [48] | −24.79 | 0.94 | −1.13 |
| Cifelli et al. (2011) [49] | −21.74 | 0.93 | −3.43 |
| WRC (2014) [50] | −20.91 | 0.91 | −4.25 |
| Kwon et al. (2015) [51] | −22.10 | 0.95 | −5.55 |
| Zhang et al. (2018) [52] | −20.76 | 0.93 | −0.41 |
| Steps | Kalman Filter | Extended Kalman Filter |
|---|---|---|
| Initial values | , , , | , , , |
| State estimate prediction | ||
| State estimate error covariance prediction | ||
| Kalman gain | ||
| State estimate update | ||
| State estimate error covariance update | ||
| No. | Duration | Type | Total Rainfall (mm) | Maximum Rainfall Intensity (mm/h) |
|---|---|---|---|---|
| 1 | 1–6 July 2016 | Frontal | 177.8 | 10.4 |
| 2 | 25–28 August 2018 | Typhoon | 190.1 | 13.1 |
| 3 | 1–3 October 2019 | Typhoon | 203.9 | 22.8 |
| 4 | 22–25 July 2020 | Frontal | 167.8 | 12.8 |
| No. | Year | EKF | Chandrasekar and Bringi (1988) [41] | Chandrasekar et al. (1990) [43] | Lee (2006) [48] | Kwon et al. (2015) [51] | LSM |
|---|---|---|---|---|---|---|---|
| 1 | 2016 | 1.02 | 5.06 | 4.70 | 5.00 | 3.96 | 1.07 |
| 2 | 2018 | 1.04 | 3.08 | 2.91 | 2.34 | 1.23 | 0.95 |
| 3 | 2019 | 1.00 | 5.99 | 5.62 | 4.96 | 9.45 | 1.04 |
| 4 | 2020 | 0.97 | 3.77 | 3.67 | 2.75 | 1.85 | 1.04 |
| Mean | 1.01 | 4.27 | 4.02 | 3.48 | 2.48 | 1.02 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Na, W.; Yoo, C. Real-Time Parameter Estimation of a Dual-Pol Radar Rain Rate Estimator Using the Extended Kalman Filter. Remote Sens. 2021, 13, 2365. https://0-doi-org.brum.beds.ac.uk/10.3390/rs13122365
Na W, Yoo C. Real-Time Parameter Estimation of a Dual-Pol Radar Rain Rate Estimator Using the Extended Kalman Filter. Remote Sensing. 2021; 13(12):2365. https://0-doi-org.brum.beds.ac.uk/10.3390/rs13122365
Chicago/Turabian StyleNa, Wooyoung, and Chulsang Yoo. 2021. "Real-Time Parameter Estimation of a Dual-Pol Radar Rain Rate Estimator Using the Extended Kalman Filter" Remote Sensing 13, no. 12: 2365. https://0-doi-org.brum.beds.ac.uk/10.3390/rs13122365