1. Introduction
This work handles a specific family of phenotyping problems: visual object’s part counting, done by first detecting the objects in the image, and then counting their constituting parts. Such problems repeatedly arise in field phenotyping contexts. Examples include counting the number of bananas in banana bunches [
1], spikelets in wheat spikes [
2,
3], berries per grape cluster [
4], flowers on apple trees [
5,
6], leaves in potted plants [
7,
8], or mangoes per-tree [
9]. Specifically, in this work we address the first three above-mentioned problems. Image examples with annotations for each task are shown in
Figure 1.
Agricultural applications often incorporate robotic systems to reduce labor tensions, especially in developing countries [
10,
11]. Such systems, as well as systematic yield estimation, require reliable computer vision methods operating in field conditions [
11,
12,
13]. This environment is highly challenging: crops vary significantly in shape, size, and color, and there are significant illumination variance and occlusion problems [
11]. The part counting task addressed here has to be solved robustly in this complex environment.
In many cases, part count is an important yield indicator, and measuring it automatically is important for yield prediction and breed selection [
4,
9,
14,
15]. Specifically, spikelets counting provides yield quantification for wheat crop and thus can assist in crop management [
3]. The number of bananas in a bunch is related to bunch weight and thus productivity [
16]. For grapes, yield estimation of a vineyard can be performed using berry detection [
4,
17] and counting [
15]. These three very different problems are handled here with the same algorithm, thus demonstrating that the proposed method is fairly general and can handle different part-counting problems with minor adjustments. While such problems usually involve (object) detection and (part) counting, they should not be confused with single-stage counting or detection problems, and require a non-trivial combination of them, as presented in this work.
Object detection is a first step in several types of agricultural applications including robotic harvesting and spraying [
15,
18,
19], measurement of object properties [
20,
21,
22,
23], or object (not parts) counting [
24]. Object count is a common phenotype needed for tasks as yield estimation [
4,
24,
25,
26], blossom level estimation for fruit thinning decisions [
5,
6,
27], or plant’s leaf counting for growth stage and health estimation [
7,
8,
28,
29].
The two tasks of detection and counting were approached with both traditional computer vision techniques and deep Convolutional Neural Networks (CNNs). Specifically, fruit detection systems using traditional techniques were presented in [
10,
13], and CNN-based works can be found in [
30,
31]. One line of influential detection networks includes two-stage networks like Faster R-CNN [
32] or Mask R-CNN [
33]. Another line of work includes fully differentiable one-stage architectures. Early one-stage networks as YOLO [
34] and SSD [
35] presented faster detectors, but with accuracy lower by 10–40% relative to two-stage methods [
36]. Later, one-stage networks like RetinaNet [
36] and more recently EfficientDet [
37] were able to close the accuracy gap. An advanced version of YOLO, the YOLOv3 model [
38], was successfully augmented and applied recently for tomato [
30] and kiwi fruit [
31] detection.
For counting, a successful work based on traditional techniques can be found in [
39,
40,
41], but CNNs designed for the task currently provide the state-of-the-art accuracy [
42,
43].
In general, deep learning methods can produce higher accuracy, but often require a large annotated image sample and a long training schedule [
11]. On the other hand, CNNs avoid the tedious feature engineering process and are often able to provide general solutions applicable to a family of different but related tasks.
The approach suggested in this work handles the object part counting with a two-stage approach of (a) detecting the objects and (b) counting the parts in their detected regions. However, the combination of these two stages into a single system raises several questions. First, parts are much smaller than their containing objects, so scale difference should be accounted for. A second set of considerations arises w.r.t the combination of object detection and part counting into a single network. Should the two modules share components (like a shared backbone subnetwork)? Should they be trained together, end-to-end, or independently? How should the detection confidence threshold, above which objects are sent for counting, be determined? In this work, we explore the design space of possible solutions for part-counting networks and find a good solution based on a single network combining stages for a detector, scaling, and counting.
One may wonder why the “parts counting” task (which is essentially a “detect-then-count” procedure) cannot be reduced into plain counting, by simply taking pictures containing a single object in each image. Indeed, in principal this is possible. In some agricultural contexts, the two-stage part-object nature was bypassed by using images of a single centralized object [
6,
28,
29]. However, solving a part counting problem by taking images of single objects has significant disadvantages. The counting procedure needs to be automated, rather than being done by a tedious manual approach. If a human has to detect the objects and take single-object images, the process is partially manual. Therefore, it is slower, costs more, and is less scalable than a fully automated system. Another option is to have a robotic system first detecting the objects, than moving to a close position to each object for taking a second image, isolating it from a wider scene. While this does not involve human intervention, such a system is much more complex to develop, and it also is likely to be slower than a system based on high resolution images containing multiple objects. Therefore, for automatic and flexible field phenotyping, the solution of keeping one object per image is significantly less scalable.
As we are interested in designing a unified network for the part counting task, we rely on a one-stage architecture as a baseline detector in this work. Specifically, we chose RetinaNet that introduced the use of a Feature Pyramid Network (FPN) [
44] for handling larger scale variability of objects and a “focal loss” variant which balances between positive examples (which are few in a detection task) and negative examples.
As for the counting section, one influential approach for CNN-based counting is based on explicit object localization: objects are first detected, then counted. The detection task can be defined as detection of the object’s centers, and so the output is a density map showing where objecthood probability is high [
8,
45]. In [
2], spike and spikelets were counted independently with a density estimation approach, providing very good results of relative error <1% for spikelets and <5% for spikes. However, data were obtained in glassdoor conditions. In [
46], it was shown that density map estimation can stay reliable through significant input domain shift when proper techniques of domain-adversarial learning are used. Alternatively, localization can be based on bounding box detection [
14,
24,
47] or segmentation [
48,
49,
50]. These methods require object location annotations like center point annotations (for density estimation), bounding boxes (for detection), or surrounding polygons (for segmentation). The second successful approach is via a global [
7,
8,
51] or local direct regression model [
26,
52]. In global regression, the model implements a function mapping the entire image (or region) to a single number, which is the predicted count. In local regression the image (or region) is divided into local regions and each of them is mapped to a local predicted count. The local counts are then summed to get the global count.
The literature contains contrasting evidence regarding the relative accuracy of localization-based versus direct regression methods, and the better choice seems to depend on data distribution and quantity, and on availability of annotation. In [
47], a detection based method was found superior to direct regression and it is claimed to be more robust to train–test domain changes. By contrast, in [
52] direct regression provides higher accuracy than density estimation. In [
8], the two approaches show similar performance. An advantage of detection based methods is in being more “explainable”, as it allows to visually inspect where in the image the network finds objects. However, more computation effort is required at test time, and an additional annotating effort at train time. In this work, we experiment with both localization-based and direct regression approaches in the counting section of the network.
While the network proposed is counting the number of visible object parts, the real quantity of interest is the actual part count, which includes also occluded parts. This gap is more pronounced for round objects like a banana bunch, and less for flatter objects like spikes. Following the work in [
53], this problem can be overcome by assuming that on average there is a constant ratio of visible to occluded fruits, and training a linear regressor for inferring the actual count from the visible count. We show in our banana experiments that this technique is indeed applicable to part counting, with minor loss in accuracy.
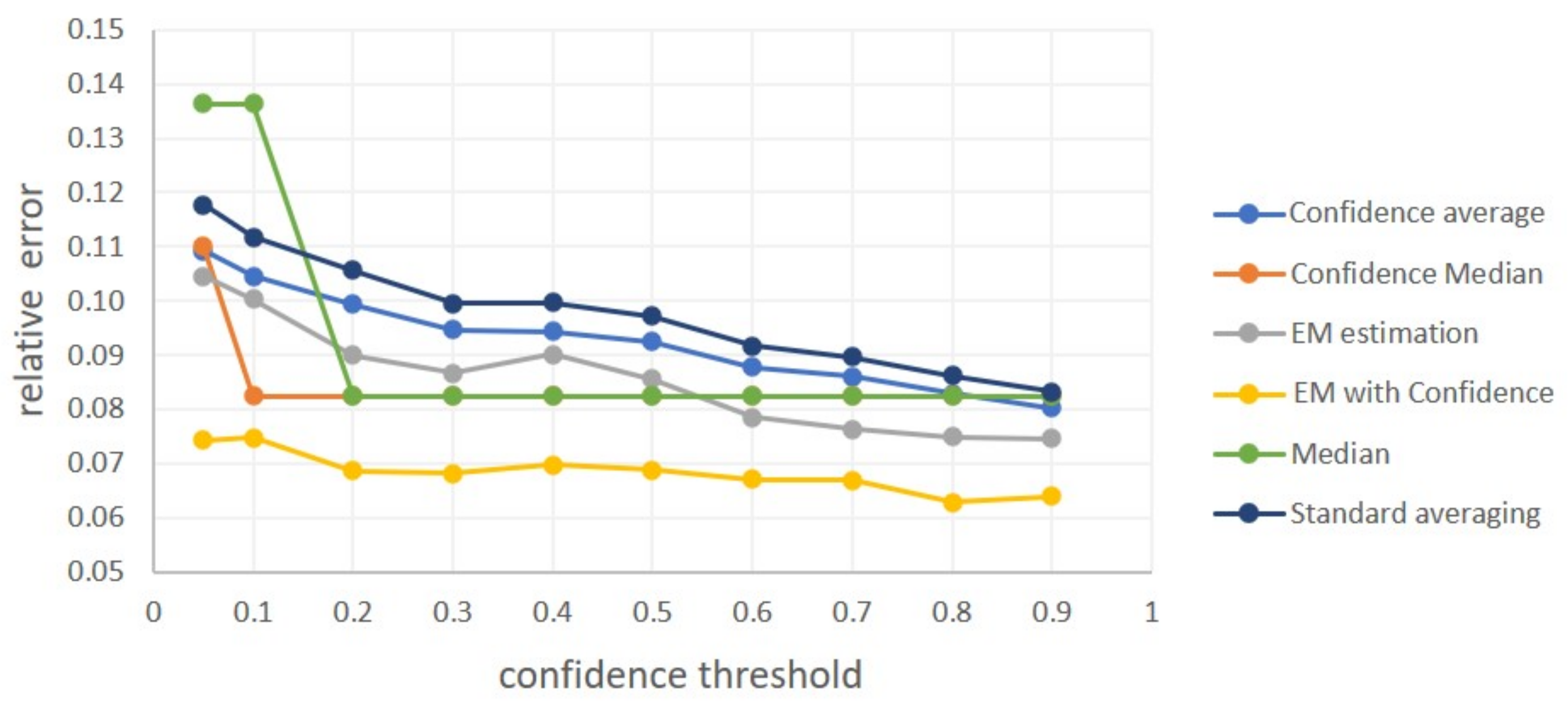
Beyond part counting for a specific object, in yield estimation we are often interested in the average count across an object population. This is the case for example with spikelet count, where the average count over an entire plot or field are of interest. While the solution can be obtained trivially by plain averaging, other options are possible. First, a solution can be obtained by independent plain counting of objects and parts, then dividing the numbers. Second, when a two-stage approach is used, plain averaging includes in the average “false counts” generated by false detections of non-objects. To reduce the impact of false counts, robust estimation methods can be used. We experiment in the space of possible solutions and find that a combination of lower detection thresholds and robust estimation, based on Gaussian assumptions, provides the best alternative.
Our contribution is therefore as follows:
Exploring the design space possible for part counting networks with respect to architecture, training methodology and component reuse, and finding a successful general part counting algorithm.
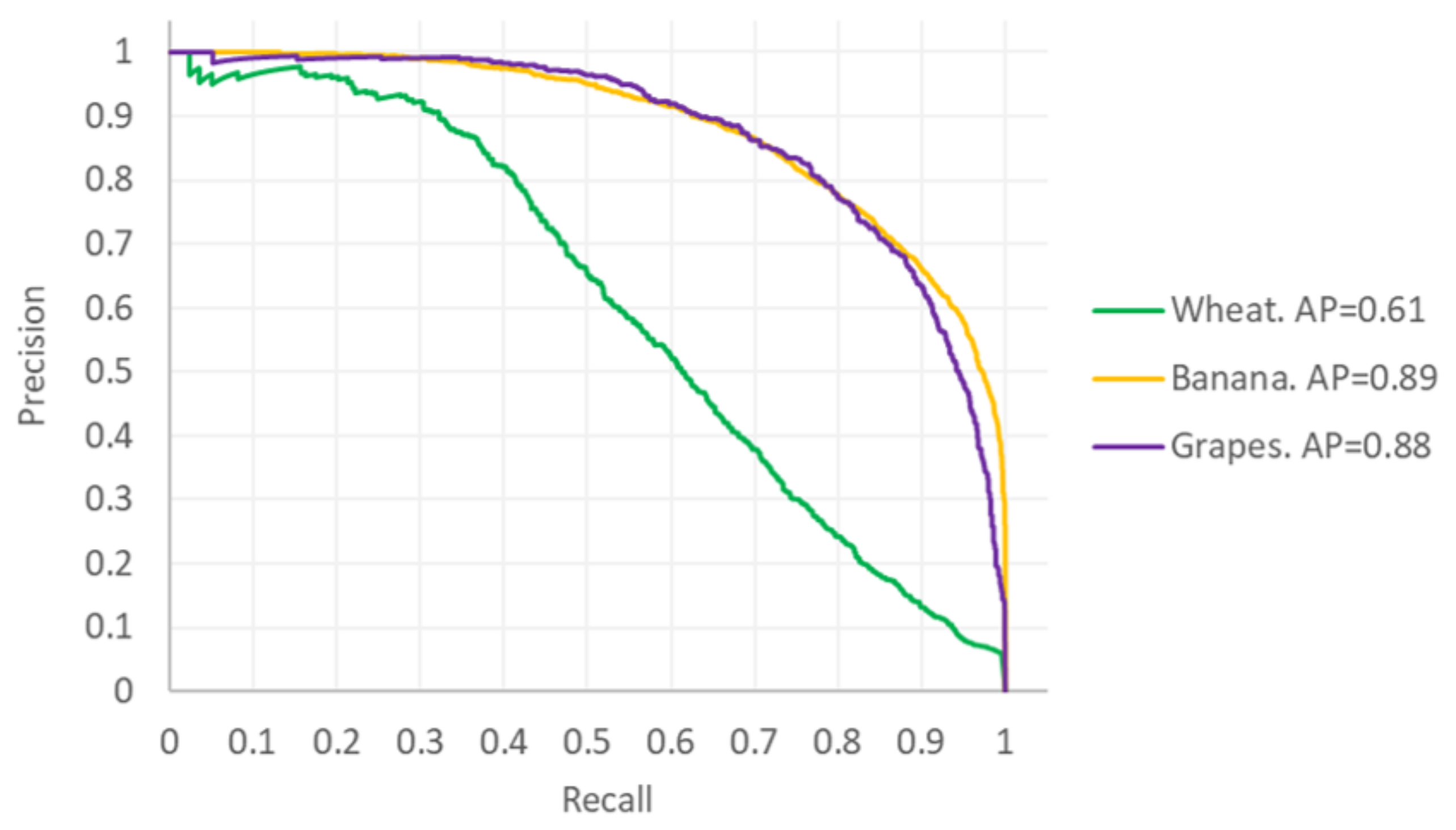
Showing the applicability of the developed method to three important phenotyping problems, with low count deviation of 9.2–11.5%.
Developing a robust estimation module enabling better estimation of population average part count (compared to plain averaging) and showing its utility for wheat spikelet count.
An earlier version of this paper was published as a conference paper [
54]. The current paper, however, contains significant added content. First, we experiment with the architecture of the suggested network in [
54]. It includes two independent sections for detection and counting, where each has its own copy of ResNet-50-based [
55] backbone module. Two alternative architectures reducing this redundancy were considered. One is based on using a single backbone module with shared weights in both sections of the network. In the other, the backbone module is dropped from the counting section and replaced by a cropped and resized representation of the detected object, obtained by the detector’s backbone. A set of systematic experiments were carried in order to check component reuse opportunities and training methodology, revealing a possible trade-off between accuracy, model size, and computational complexity. Second, the method was tested on a new dataset not included in the conference version, the grapes dataset, which is based on the publicly available Embrapa WGISD212 dataset [
15,
56]. Third, the new task of average spikelet-per-spike count per field, is considered here. As plain averaging of the sample would produce a biased estimator of this value, due to false alarms, an alternative approach is presented. It is based on applying the robust mean estimation methods on top of the network’s estimates of the spikelets-per-spike values. These methods, presented here for the first time, were tested using new images, obtained from six different field plots.
The rest of the paper is organized as follows: we describe the data and the algorithm in
Section 2, present results in
Section 3, discussion in
Section 4 and conclusions in
Section 5.