Estimating the Fractional Cycle Biases for GPS Triple-Frequency Precise Point Positioning with Ambiguity Resolution Based on IGS Ultra-Rapid Predicted Orbits
Abstract
:1. Introduction
2. GPS Triple-Frequency PPP AR
2.1. Basic Observation Equations
2.2. FCBs Estimation and PPP AR
2.3. Test Data Description
3. Results and Analysis
3.1. FCB Results and Analysis
3.2. PPP Results and Analysis
3.2.1. Static PPP
3.2.2. Kinematic PPP
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, T.; Wang, J.; Laurichesse, D. Modeling and quality control for reliable precise point positioning integer ambiguity resolution with GNSS modernization. GPS Solut. 2014, 18, 429–442. [Google Scholar] [CrossRef]
- Geng, J.; Guo, J.; Chang, H.; Li, X. Toward global instantaneous decimeter-level positioning using tightly coupled multi-constellation and multi-frequency GNSS. J. Geod. 2018, 93, 977–991. [Google Scholar] [CrossRef] [Green Version]
- Geng, J.; Guo, J.; Meng, X.; Gao, K. Speeding up PPP ambiguity resolution using triple-frequency GPS/BeiDou/Galileo/QZSS data. J. Geod. 2020, 94, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Ge, M.; Chen, J.; Douša, J.; Gendt, G.; Wickert, J. A computationally efficient approach for estimating high-rate satellite clock corrections in realtime. GPS Solut. 2012, 16, 9–17. [Google Scholar] [CrossRef]
- Li, P.; Zhang, X.; Ren, X.; Zuo, X.; Pan, Y. Generating GPS satellite fractional cycle bias for ambiguity-fixed precise point positioning. GPS Solut. 2016, 20, 771–782. [Google Scholar] [CrossRef]
- Geng, J.; Guo, J. Beyond three frequencies: An extendable model for single-epoch decimeter-level point positioning by exploiting Galileo and BeiDou-3 signals. J. Geod. 2020, 94, 1–15. [Google Scholar] [CrossRef]
- Laurichesse, D.; Banville, S.; Innovation: Instantaneous Centimeter-level Multi-frequency Precise Point Positioning. GPS World 4 July 2018. Available online: https://www.gpsworld.com/innovation-instantaneous-centimeter-level-multi-frequency-precise-point-positioning/ (accessed on 1 June 2021).
- El-Mowafy, A.; Deo, M.; Kubo, N. Maintaining real-time precise point positioning during outages of orbit and clock corrections. GPS Solut. 2017, 21, 937–947. [Google Scholar] [CrossRef]
- Douša, J. The impact of errors in predicted GPS orbits on zenith troposphere delay estimation. GPS Solut. 2010, 14, 229–239. [Google Scholar] [CrossRef]
- Li, Y.; Gao, Y.; Li, B. An impact analysis of arc length on orbit prediction and clock estimation for PPP ambiguity resolution. GPS Solut. 2015, 19, 201–213. [Google Scholar] [CrossRef]
- Li, Y.; Gao, Y.; Shi, J. Improved PPP ambiguity resolution by COES FCB estimation. J. Geod. 2016, 90, 437–450. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hugentobler, U.; Dach, R.; Steigenberger, P.; Hauschild, A. Apparent clock variations of the Block IIF-1 (SVN62) GPS satellite. GPS Solut. 2011, 16, 303–313. [Google Scholar] [CrossRef]
- Xie, X.; Fang, R.; Geng, T.; Wang, G.; Zhao, Q.; Liu, J. Characterization of GNSS signals tracked by the iGMAS network considering recent BDS-3 satellites. Remote Sens. 2018, 10, 1736. [Google Scholar] [CrossRef] [Green Version]
- Pan, L.; Zhang, X.; Guo, F.; Liu, J. GPS inter-frequency clock bias estimation for both uncombined and ionospheric-free combined triple-frequency precise point positioning. J. Geod. 2019, 93, 473–487. [Google Scholar] [CrossRef]
- Odijk, D.; Zhang, B.; Khodabandeh, A.; Odolinski, R.; Teunissen, P.J.G. On the estimability of parameters in undifferenced, uncombined GNSS network and PPP-RTK user models by means of S-system theory. J. Geod. 2015, 90, 15–44. [Google Scholar] [CrossRef]
- Qu, L.; Du, M.; Wang, J.; Gao, Y.; Zhao, Q.; Zhang, Q.; Guo, X. Precise point positioning ambiguity resolution by integrating BDS-3e into BDS-2 and GPS. GPS Solut. 2019, 23, 63. [Google Scholar] [CrossRef]
- Guo, J.; Geng, J. GPS satellite clock determination in case of inter-frequency clock biases for triple-frequency precise point positioning. J. Geod. 2018, 92, 1133–1142. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hauschild, A.; Steigenberger, P.; Langley, R.B. Three’s the challenge: A close look at GPS SVN62 triple-frequency signal combinations finds carrier-phase variations on the new L5. GPS World 2010, 21, 8–19. [Google Scholar]
- Li, X.; Ge, M.; Zhang, H.; Wickert, J. A method for improving uncalibrated phase delay estimation and ambiguity-fixing in real-time precise point positioning. J. Geod. 2013, 87, 405–416. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. Success probability of integer GPS ambiguity rounding and bootstrapping. J. Geod. 1998, 72, 606–612. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Zhang, X.; Ge, M.; Schuh, H. Three-frequency BDS precise point positioning ambiguity resolution based on raw observables. J. Geod. 2018, 92, 1357–1369. [Google Scholar] [CrossRef] [Green Version]
- Gao, W.; Gao, C.; Pan, S.; Wang, D.; Deng, J. Improving ambiguity resolution for medium baselines using combined GPS and BDS dual/triple-frequency observations. Sensors 2015, 15, 27525–27542. [Google Scholar] [CrossRef]
- Johnston, G.; Riddell, A.; Hausler, G. The International GNSS Service. Teunissen, In Handbook of Global Navigation Satellite Systems, 1st ed.; Peter, J.G., Montenbruck, O., Eds.; Springer: Cham, Switzerland, 2017; pp. 967–982. [Google Scholar] [CrossRef]
- Li, H.; Zhou, X.; Wu, B. Fast estimation and analysis of the inter-frequency clock bias for Block IIF satellites. GPS Solut. 2013, 17, 347–355. [Google Scholar] [CrossRef]
- Gu, S.; Shi, C.; Lou, Y.; Liu, J. Ionospheric effects in uncalibrated phase delay estimation and ambiguity-fixed PPP based on raw observable model. J. Geod. 2015, 89, 447–457. [Google Scholar] [CrossRef]
- Nandarajah, N.; Khodabandeh, A.; Wang, K.; Choudhury, M.; Teunissen, P.J.G. Multi-GNSS PPP-RTK: From Large- to Small-Scale Networks. Sensors 2018, 18, 1078. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Zhang, X.; Li, P.; Ma, F.; Pan, L. Multi-GNSS fractional cycle bias products generation for GNSS ambiguity-fixed PPP at Wuhan University. GPS. Solut. 2020, 24, 1–13. [Google Scholar] [CrossRef]
- Liu, G.; Guo, F.; Wang, J.; Du, M.; Qu, L. Triple-frequency GPS un-differenced and uncombined PPP ambiguity resolution using observable-specific satellite signal biases. Remote Sens. 2020, 12, 2310. [Google Scholar] [CrossRef]




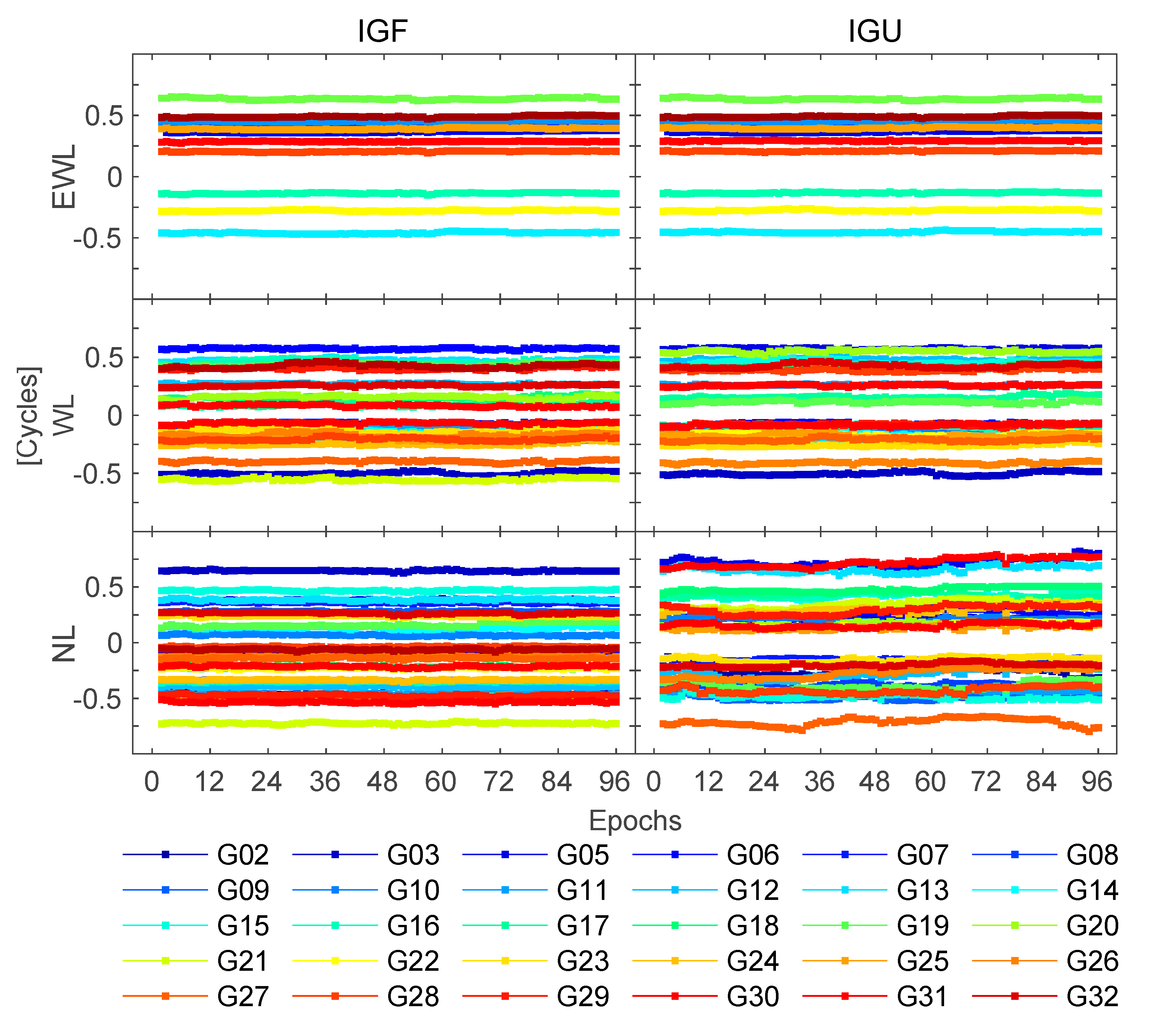

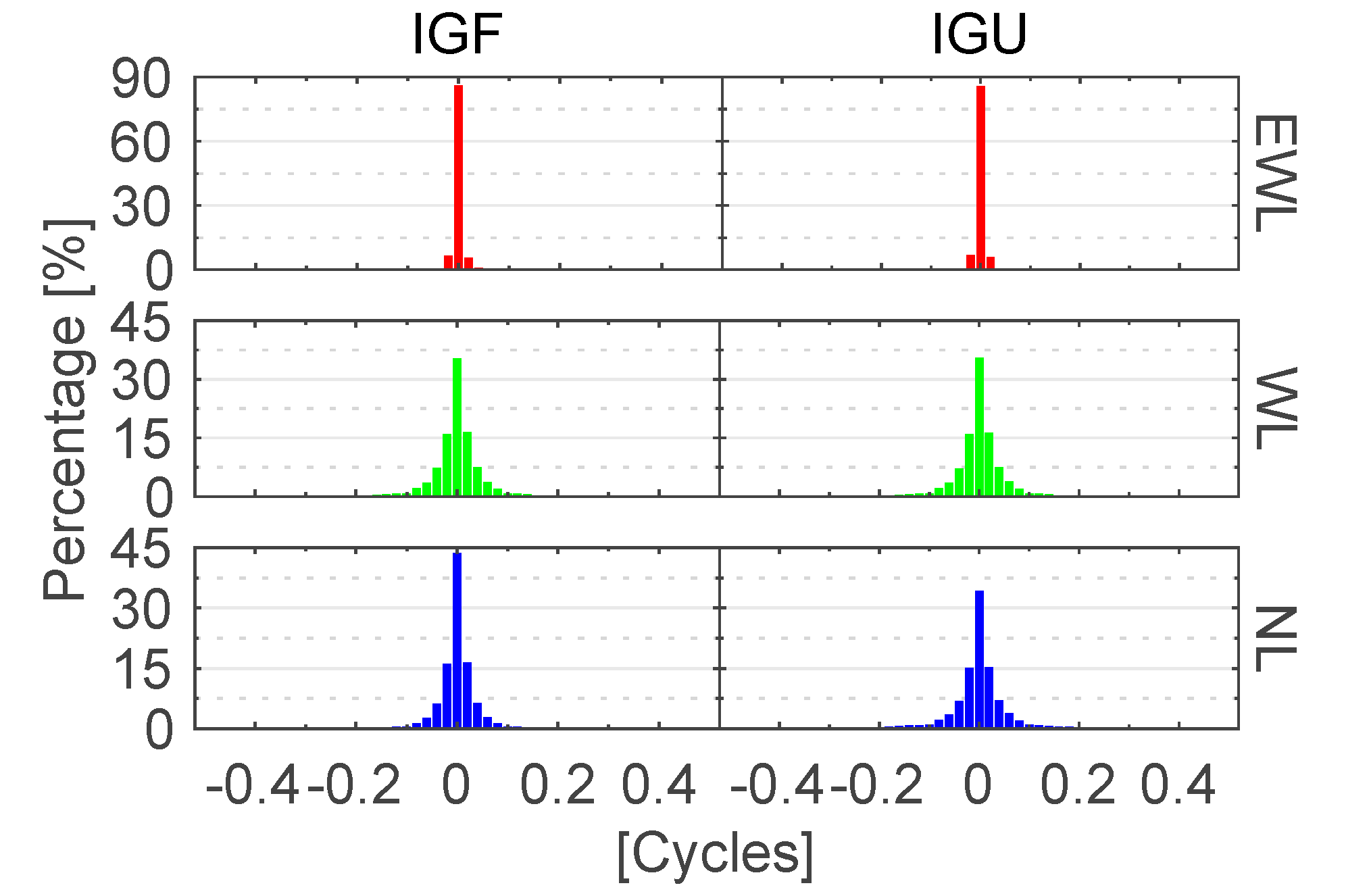

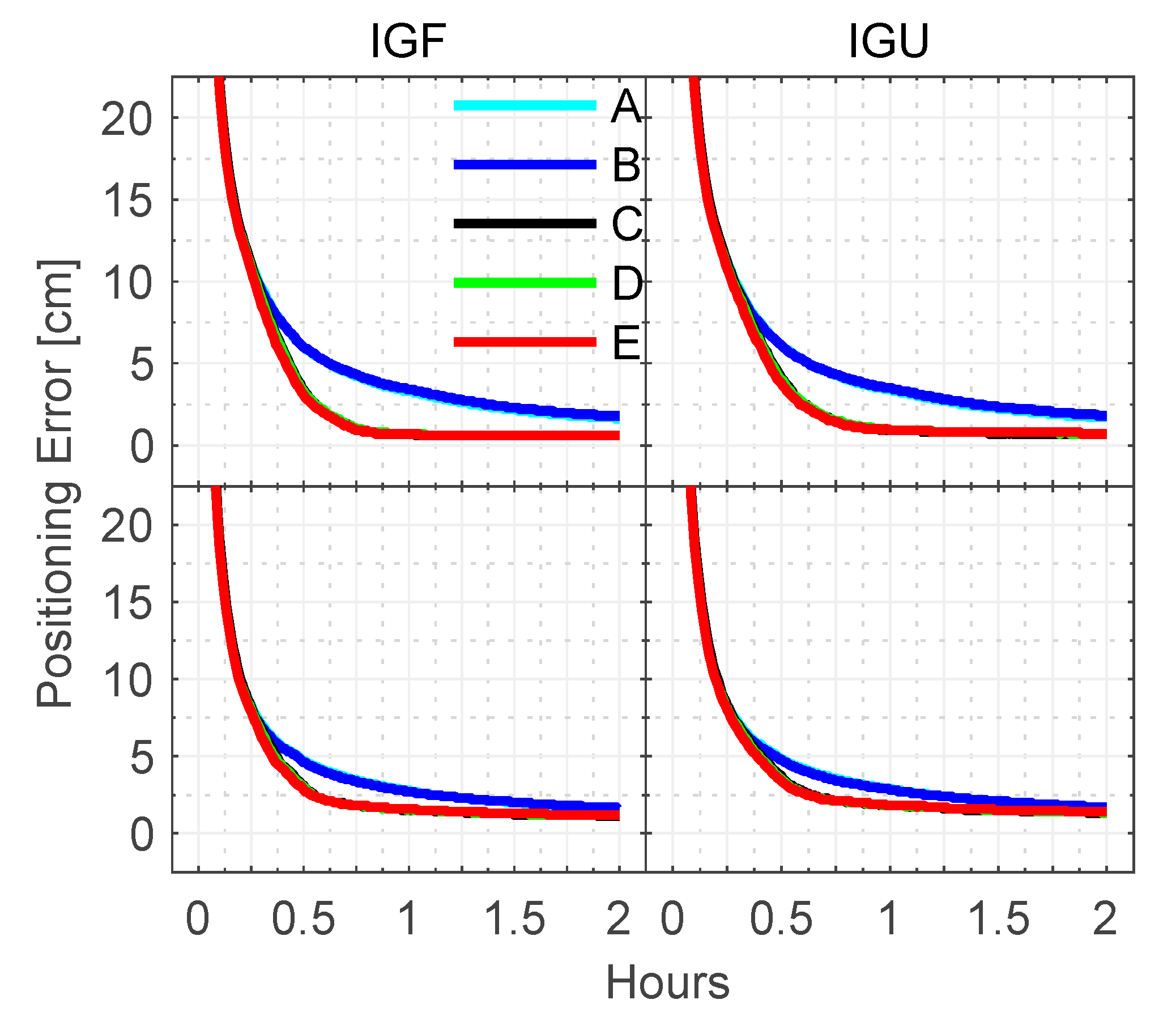

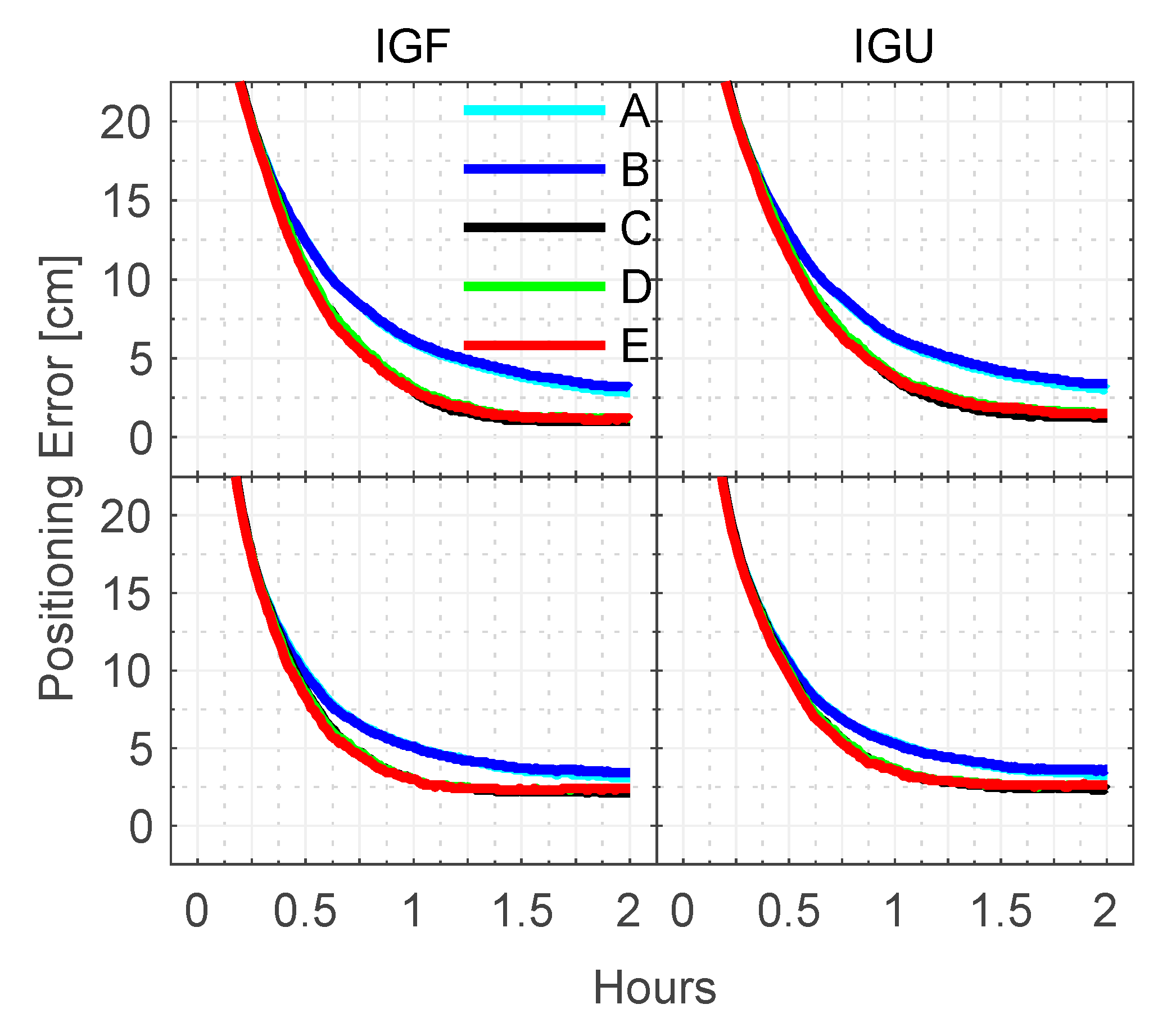
| Item | TTFF (min) | Fixing Rate (%) | Convergence Time (min) | RMS (cm) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IGF | IGU | IGF | IGU | IGF | IGU | IGF | IGU | |||||||
| H | V | H | V | E | N | U | E | N | U | |||||
| A | - | - | - | - | 38 | 29 | 38 | 30 | 3.0 | 1.0 | 2.8 | 3.1 | 1.0 | 2.9 |
| B | - | - | - | - | 38 | 29 | 38 | 29 | 3.2 | 1.0 | 2.7 | 3.2 | 1.0 | 2.8 |
| C | 26.1 | 30.6 | 97.9 | 96.5 | 26 | 23 | 28 | 25 | 0.4 | 0.4 | 1.5 | 0.6 | 0.6 | 1.8 |
| D | 24.7 | 29.3 | 98.0 | 96.6 | 26 | 22 | 28 | 24 | 0.5 | 0.5 | 1.6 | 0.7 | 0.6 | 1.8 |
| E | 23.3 | 27.0 | 98.1 | 97.0 | 25 | 22 | 27 | 24 | 0.5 | 0.5 | 1.6 | 0.7 | 0.6 | 1.8 |
| Item | TTFF (min) | Fixing Rate (%) | Convergence Time (min) | RMS (cm) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IGF | IGU | IGF | IGU | IGF | IGU | IGF | IGU | |||||||
| H | V | H | V | E | N | U | E | N | U | |||||
| A | - | - | - | - | 38 | 30 | 40 | 32 | 1.3 | 1.1 | 2.8 | 1.4 | 1.2 | 3.1 |
| B | - | - | - | - | 38 | 30 | 40 | 32 | 1.3 | 1.1 | 2.8 | 1.4 | 1.2 | 3.0 |
| C | 36.0 | 43.9 | 97.0 | 95.6 | 32 | 28 | 35 | 30 | 0.7 | 0.8 | 2.4 | 0.9 | 1.1 | 2.6 |
| D | 34.6 | 42.2 | 97.1 | 95.8 | 32 | 27 | 35 | 30 | 0.7 | 0.9 | 2.4 | 0.9 | 1.0 | 2.6 |
| E | 31.1 | 37.9 | 97.4 | 96.3 | 31 | 27 | 34 | 30 | 0.7 | 0.9 | 2.4 | 0.9 | 1.0 | 2.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, L.; Zhang, P.; Jing, C.; Du, M.; Wang, J.; Zhao, Q.; Li, J. Estimating the Fractional Cycle Biases for GPS Triple-Frequency Precise Point Positioning with Ambiguity Resolution Based on IGS Ultra-Rapid Predicted Orbits. Remote Sens. 2021, 13, 3164. https://0-doi-org.brum.beds.ac.uk/10.3390/rs13163164
Qu L, Zhang P, Jing C, Du M, Wang J, Zhao Q, Li J. Estimating the Fractional Cycle Biases for GPS Triple-Frequency Precise Point Positioning with Ambiguity Resolution Based on IGS Ultra-Rapid Predicted Orbits. Remote Sensing. 2021; 13(16):3164. https://0-doi-org.brum.beds.ac.uk/10.3390/rs13163164
Chicago/Turabian StyleQu, Lizhong, Pu Zhang, Changfeng Jing, Mingyi Du, Jian Wang, Qile Zhao, and Juanjuan Li. 2021. "Estimating the Fractional Cycle Biases for GPS Triple-Frequency Precise Point Positioning with Ambiguity Resolution Based on IGS Ultra-Rapid Predicted Orbits" Remote Sensing 13, no. 16: 3164. https://0-doi-org.brum.beds.ac.uk/10.3390/rs13163164






