1. Introduction
Snow performs a prominent role in estimating the earth’s energy balance and hydrological cycle [
1,
2,
3]. Heavy snowfalls and rapid snowmelt can result in economic damage and loss of life [
4]. To effectively monitor these events, daily and accurate quantifications of snow-covered areas (SCA) are essential for tracking trends and changes in the spatial extent and duration of snow-covered land surfaces [
1,
5]. Additionally, snow depth (SD) measurements serve as auxiliary data for SCA estimation and could be obtained through remote sensing [
6].
Various optical sensors have been developed for automated snow cover detection, including the Moderate Resolution Imaging Spectroradiometer (MODIS) on the Terra and Aqua satellites launched by NASA [
7,
8,
9,
10]. While MODIS provides daily snow cover maps at a moderate resolution of 500 m, it faces challenges, such as data gaps caused by cloud obscuration [
1], degradation in accuracy over dense forest areas and shallow snow areas [
7,
11], and limited to daytime conditions [
12,
13].
The estimated accuracy of MODIS snow cover products is generally over 90% at locations worldwide [
14]. However, these results were achieved mainly by overestimating cloud-contaminated pixels [
5], which leaves a limited set of comparable data available for validation purposes and is more likely to achieve higher accuracy. Given that the mean cloud coverage of daily MODIS snow cover products is around 50% in Northern Xinjiang, China [
9], cloud contamination is a severe impairment in applications of SCA mapping in Xinjiang solely based on MODIS snow products [
15]. In contrast, passive microwave remote sensing can penetrate clouds and operate during the day and nighttime but offers a much lower spatial resolution [
1,
13]. As a result, microwave-based snow products are well suited for global snow mapping but are unable to resolve detailed landscape features of regional snow at a local scale of ≤1 km [
1].
Nighttime light (NTL) data offers another approach to mapping SCA. Foster, in 1983, first implemented NTL for SCA detection using observations from the Defense Meteorological Satellite Program’s Operational Line-Scan System (DMSP-OLS) [
16]. However, the use of DMSP-OLS data for SCA retrieval was limited due to its saturation effect and coarse spatial resolution [
17]. The Visible Infrared Imaging Radiometer Suite (VIIRS) Day/Night Band (DNB) onboard the Suomi National Polar-orbiting Partnership (SNPP) launched in October 2011 overcomes these limitations [
18,
19]. The DNB is a panchromatic band that measures night lights and reflected solar (or lunar) lights at a spatial resolution of 750 m and captures an image twice a day, around 1:30 pm and 1:30 am local time. Within undeveloped and uninhabited regions with low or no artificial light source at the local crossing time of 1:30 am, VIIRS DNB data directly embodies the reflected lunar illuminance by the observed surface and indicates the presence of snow covers. Compared with conventional optical-based satellite observations, the advantages of mapping snow using NTL data include (1) the capability of retrieving SCA information under low-light conditions, particularly useful in areas with limited daytime hours due to high latitudes, or even perpetual nighttime conditions in the winters of the North and South Pole [
20,
21]; and (2) better data consistency (less cloud obscuration) because continental cloud coverage occurs less during nighttime compared to daytime [
16,
22]. In the current study focused on Xinjiang, the cloud coverage across the 14 consecutive scenes of VIIRS DNB during nighttime (~1:30 am) ranges from 3.07% to 49.04%, while the cloud coverage of MODIS (~10:30 am) ranges from 23.86% to 57.27%.
Following the launch of SNPP-VIIRS in 2011, Miller et al. [
23] qualitatively demonstrated that the snow cover distribution details of a single VIIRS DNB imagery and a daytime VIIRS pass (true color) are consistent. Although this study provided evidence for the potential viability of VIIRS DNB for snow cover detection, the identification was based solely on visual interpretation and limited to a single pair of images.
Quantitative demonstrations of utilizing NTL on the retrieval of SCA were recently brought out by Huang et al. [
21], in which a Minimum Error Thresholding algorithm was implemented for deriving SCA from VIIRS DNB data, with the accuracy of 80.3% and 76.7% for two case study areas, respectively. Additionally, this study highlighted the possibility of deriving accurate SCA maps with fewer data gaps by combining MODIS and VIIRS DNB imagery. So far, to the best of our knowledge, only this study has provided empirical evidence that combining MODIS and VIIRS DNB can map SCA accurately and thus require further affirmations. It is unclear if this approach can also achieve high-accuracy results for large areas and across a wider range of topographic characteristics.
In addition, Stopic and Dias [
20] tested seven automated algorithms (i.e., Otsu, Li, Yen, triangle, minimum, mean, and Isodata) on four different case study areas (i.e., Colorado, USA; Ontario, Canada; Alaska, USA; Saskatchewan, Canada). To ensure the variety of multiple characteristics among the study areas, this study selected four regions with different traits in terms of latitudes, elevations, land cover types, and topographies. The results indicate that the higher overall accuracies achieved by the mean thresholding algorithm in Colorado and Alaska are attributed to their mountainous terrain features. Moreover, this study found that compared to MODIS, the VIIRS DNB snow extent tends to underestimate snow cover, which was explained by the presence of forest land covers. Although the effects of forests on the accuracy of snow detection are not surprising, it is important to note that the SCA estimations of MODIS substantially decrease over forested areas and shallow or patchy snow-covered surfaces. In other words, MODIS-derived SCA maps might not be the best dataset to take as “ground truth” reference maps. Lastly, the four study areas elected for examinations are all located in North America; hence they are insufficient to represent the spatial characteristics worldwide. This raises the question of whether these conclusions could transfer to Asia, particularly in Xinjiang, where an extensive variety of elevations, land cover types, and landforms are present.
Compared to the abovementioned snow maps generated from satellite observations through automated algorithms, the snow cover maps produced interactively with manual inputs by NOAA’S Interactive Multisensor Snow and Ice Mapping System (IMS) are a costly though highly reliable data source [
5,
24]. The production of IMS maps is dependent on visual interpretations by human analysts. Analysts are assigned to examine various available satellite imagery, automated snow mapping algorithms, and other ancillary data to map the snow distribution over clouds [
25]. For a given pixel, when analysts do not have enough information to change the analysis, the IMS product for the present day is not updated, and the analysis from the previous day remains in effect [
25]. This allows the IMS maps free of clouded pixels but makes the production of IMS maps time-consuming and expensive. However, these efforts have been proven to be valuable and worthwhile. Recent studies have shown that IMS maps of snow and ice are highly accurate and therefore are used as the reference data source for validations [
26]. The consistency between the IMS product and in situ data has been evaluated by Chen et al. [
26], who concluded a daily rate agreement of about 80–90% over the United States and southern Canada. Other validation results based on in situ measurements have shown an accuracy of over 90% in the Tibetan Plateau [
27,
28]. As all IMS SCA maps are obtained using the same procedure based on the same data source, it is within reason to postulate that the IMS SCA mapping is a reliable reference data for areas located in the northern hemisphere. Thus, in this study, we regarded IMS as the ground-truth reference data for accuracy assessment.
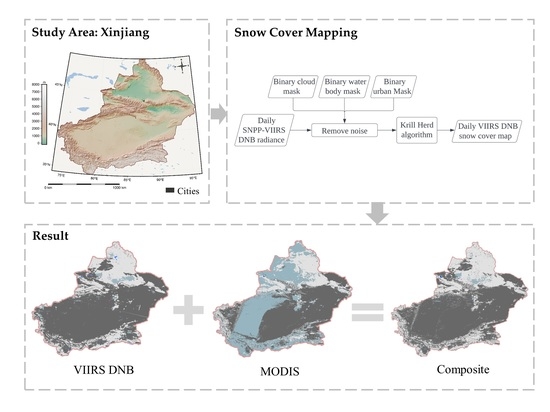
Accordingly, our study is placed in the context of the need for affirmations of automated snow cover mapping with VIIRS DNB data for large and topographically complicated areas in arid central Asia, particularly in Xinjiang, where the distribution of snow is of great importance. The main objectives of this study are to: (1) attempt a novel approach for the daily mappings of snow cover distribution utilizing VIIRS DNB data; (2) alleviate the data gaps of optical-based snow maps by providing snow cover information with the support of VIIRS DNB data, particularly in regions with frequent cloud obscurations and higher latitudes; and (3) reveal the strengths and short-comings of various snow mapping methods at a local scale.
5. Conclusions
This paper presented an approach for obtaining nighttime SCA maps over large areas with diverse topography conditions in Xinjiang, based on VIIRS DNB nighttime light data. We demonstrated the utility of snow cover detection, and of combining daily VIIRS DNB measures with MODIS snow maps to map SCA across ~1,664,900 km2 of Xinjiang Province. Our method yielded reliable SCA estimations that outperformed AMSR2 snow cover products.
The overall accuracy of our SCA predictions was satisfactory though not outstanding when compared to MODIS. However, the ability to provide more snow distribution information is invaluable, and therefore, VIIRS DNB serves well as a complementary dataset for MODIS snow maps.
The results of this work motivate future research focused on improving SCA mapping based on VIIRS DNB and MODIS to introduce certain temporal corrections before combining the observations from these two datasets. Additionally, in situ observations of SCA from meteorological stations are indispensable for higher credibility in data validation. Furthermore, a long-term case study is essential to confirm the feasibility of improving MODIS snow cover mapping by integrating VIIRS DNB data. We also propose using this method to produce snow maps during polar nights, when daytime observations by MODIS are ineffective.