Surface Daytime Net Radiation Estimation Using Artificial Neural Networks
Abstract
:1. Introduction
2. Data and Methodology
2.1. Data
2.1.1. In-Situ Data
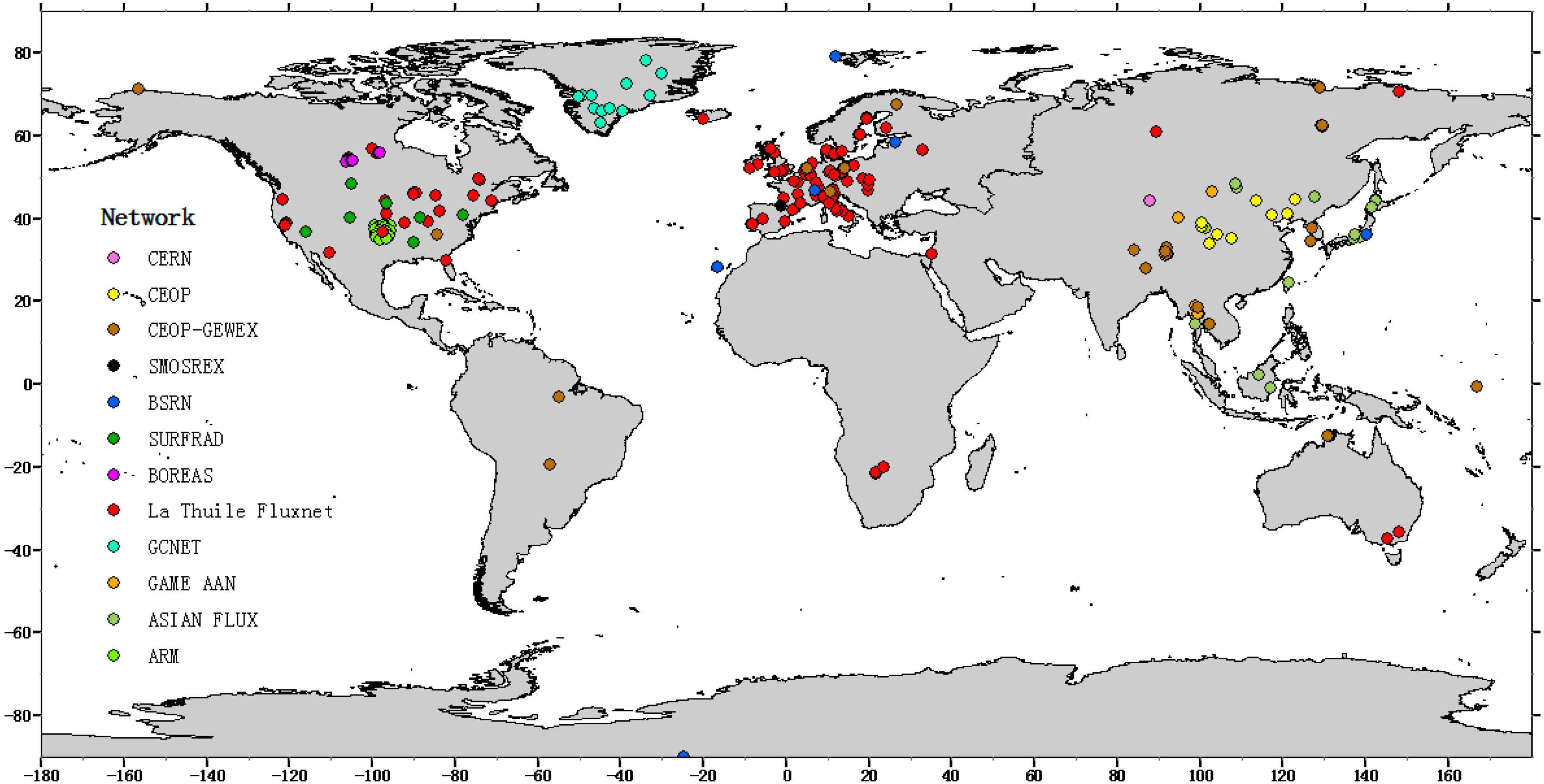
| Abbreviation | Full Name | URL | Temporal Resolution |
|---|---|---|---|
| La Thuile Fluxnet | Global Fluxnet (La Thuile dataset) | [31] | 30 minute |
| ARM | Atmospheric Radiation Measurement | [32] | 10 minute |
| Asia Flux | [33] | \ | 30 minute |
| BSRN [34] | Baseline Surface Radiation Network | [35] | 1 minute |
| SURFRAD [36,37] | Surface Radiation Network | [38] | 3 hourly |
| BOREAS | Boreal Ecosystem-Atmosphere Study | [39] | 30 minute |
| GAME AAN | GEWEX Asian Monsoon Experiment | [40] | 30 minute |
| GC-Net [41] | Greenland Climate Network | [42] | 1 hourly |
| CEOP-GEWEX | Coordinated Enhanced Observing Period | [43] | 30 minute |
| CEOP [44,45,46,47] | Coordinated Enhanced Observation Network of China | \ | 30 minute |
| SMOSREX [48] | Surface Monitoring Of Soil Reservoir Experiment | [49] | 30 minute |
| CERN | Chinese Ecosystem Research Network | [50] | 30 minute |
| IGBP Land Cover Types | No. of Sites |
|---|---|
| Barren& Sparse vegetation | 6 |
| Cropland | 43 |
| Deciduous Broadleaf Forest (DBF) | 28 |
| Deciduous Needleleaf Forest (DNF) | 7 |
| Evergreen Broadleaf Forest (EBF) | 10 |
| Evergreen Needleleaf Forest (ENF) | 47 |
| Grassland | 57 |
| Ice | 18 |
| Mixed Forest (MF) | 8 |
| Savanna | 6 |
| Shrubland | 10 |
| Wetland | 11 |
| Total | 251 |
| Class | Classification Criteria | No. of Observations |
|---|---|---|
| S1 | NDVI < 0.2 and albedo ≤ 0.25 | 9790 |
| S2 | NDVI < 0.2 and 0.25 < albedo < 0.7 | 9974 |
| S3 | NDVI < 0.2 and albedo ≥ 0.7 | 8930 |
| S4 | NDVI ≥ 0.2 | 173,396 |
2.1.2. Remotely Sensed Data
2.1.3. Model Reanalysis Data


2.1.4. Other Parameters

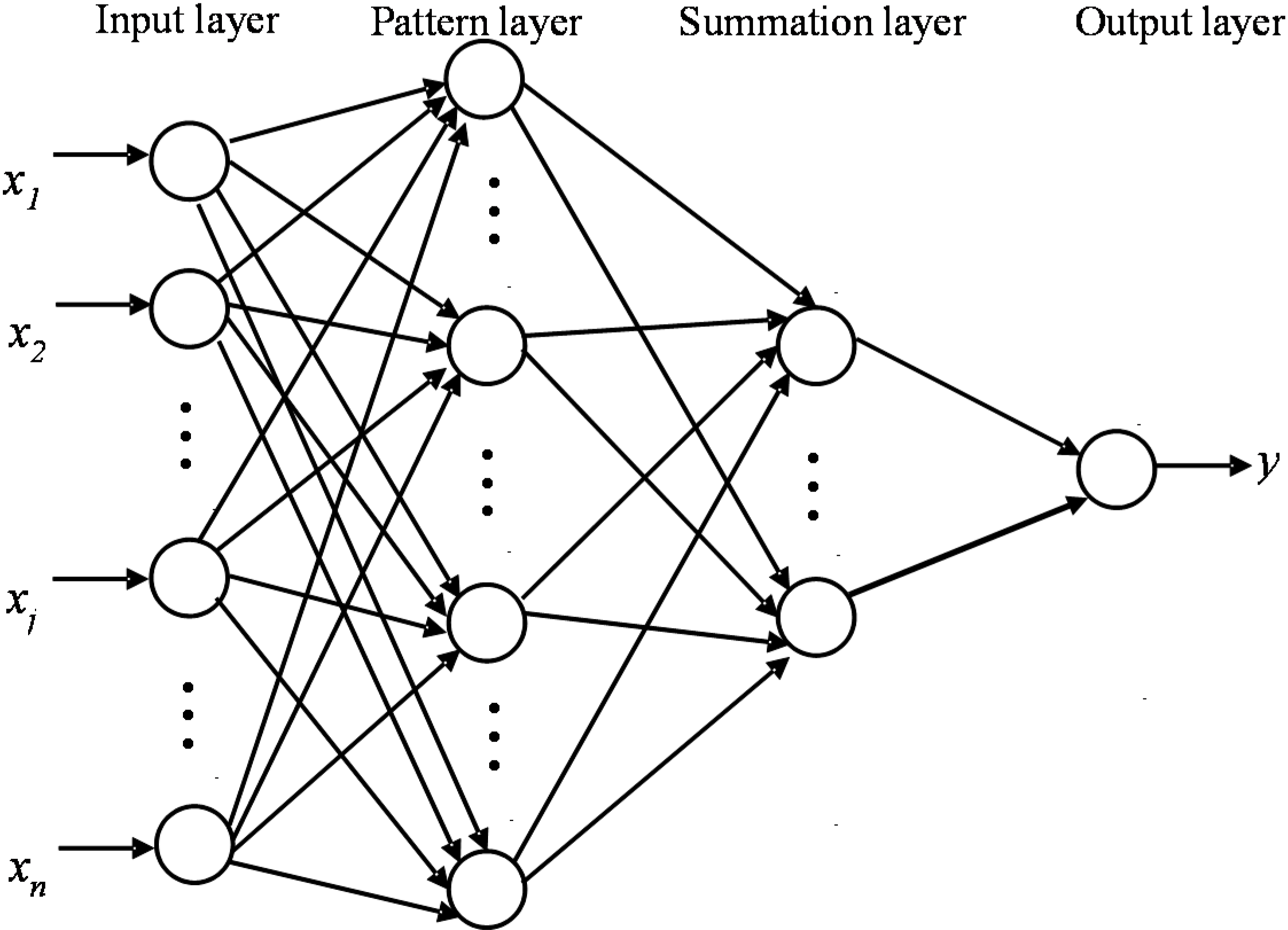
2.2. Methodology


| Abbreviation | Name | Unit | Data Type | |
|---|---|---|---|---|
| Response Variable | Rn | Surface net radiation | W∙m−2 | In-situ |
| Independent Variables | Rsi | Surface incoming solar radiation | W∙m−2 | |
| ABD | Surface albedo | Remotely Sensed Product | ||
| NDVI | Normalized Difference Vegetation Index | |||
| T | Daily air mean temperature | °C | Re-Analysis Product | |
| Tmin | Daily air minimum temperature | °C | ||
| Tmax | Daily air maximum temperature | °C | ||
| RH | Daily mean relative humidity | % | ||
| PS | Surface air pressure | Pa | ||
| W | Wind speed | m∙s−1 | ||
| ea | Water vapor pressure | KPa | ||
| dr | Inverse relative Earth-Sun distance | |||
| CI | Clearness Index | |||
| BI | Brightness Index |
3. Results and Discussion
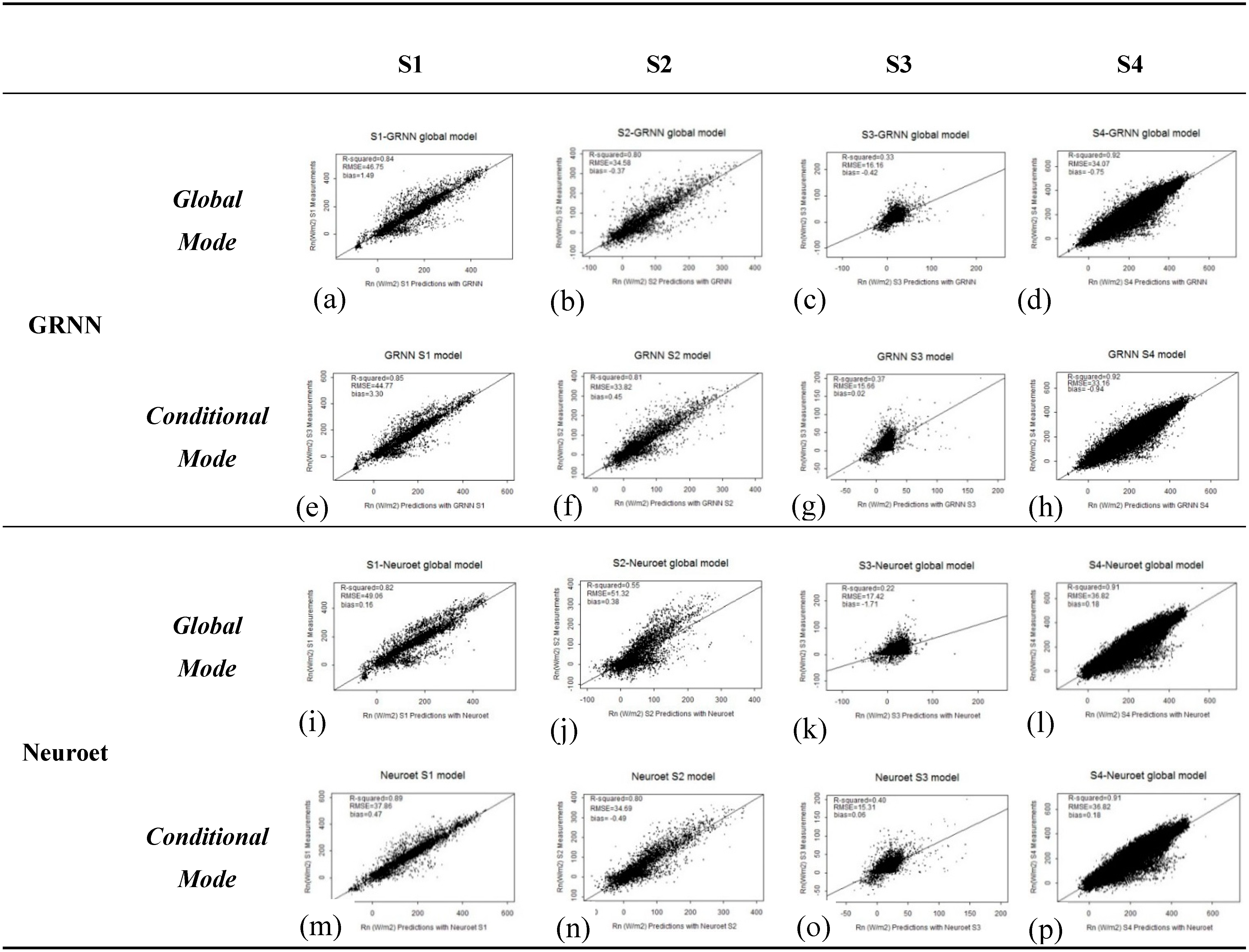
3.1. Comparison of the Two ANN Models
| Global Model | |||
|---|---|---|---|
| R2 | RMSE (W∙m−2) | bias (W∙m−2) | |
| GRNN | 0.92 | 34.27 | −0.61 |
| Neuroet | 0.91 | 37.79 | 0.10 |

| Global Model | ||||||||
| S1 | S2 | S3 | S4 | |||||
| GRNN | Neuroet | GRNN | Neuroet | GRNN | Neuroet | GRNN | Neuroet | |
| R2 | 0.84 | 0.82 | 0.80 | 0.55 | 0.33 | 0.22 | 0.92 | 0.91 |
| RMSE (W∙m−2) | 46.75 | 49.06 | 34.58 | 51.32 | 16.16 | 17.42 | 34.07 | 36.82 |
| bias (W∙m−2) | 1.49 | 0.16 | −0.37 | 0.38 | −0.42 | −1.71 | -0.75 | 0.18 |
| Conditional Models | ||||||||
| S1 | S2 | S3 | S4 | |||||
| GRNN | Neuroet | GRNN | Neuroet | GRNN | Neuroet | GRNN | Neuroet | |
| R2 | 0.85 | 0.89 | 0.81 | 0.80 | 0.37 | 0.40 | 0.92 | 0.91 |
| RMSE (W∙m−2) | 44.77 | 37.86 | 33.82 | 34.69 | 15.66 | 15.31 | 33.16 | 36.57 |
| bias (W∙m−2) | 3.30 | 0.47 | 0.45 | −0.49 | 0.02 | 0.06 | −0.94 | 0.52 |
| Model Type | Optimal Number of Hidden Neurons | ||
|---|---|---|---|
| Global | 14 | 0.91 | 0.91 |
| S1 | 13 | 0.93 | 0.89 |
| S2 | 12 | 0.75 | 0.76 |
| S3 | 10 | 0.44 | 0.44 |
| S4 | 14 | 0.90 | 0.91 |
3.2. Influences of Data Scaling
| Model Type | GRNN | Neuroet | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Z-Score Normalized | Linear Scaling | Z-Score Normalized | Linear Scaling | |||||||||
| R2 | RMSE (W∙m−2) | bias (W∙m−2) | R2 | RMSE (W∙m−2) | bias (W∙m−2) | R2 | RMSE (W∙m−2) | bias (W∙m−2) | R2 | RMSE (W∙m−2) | bias (W∙m−2) | |
| Global | 0.92 | 34.27 | −0.61 | 0.93 | 33.05 | −0.29 | 0.91 | 37.79 | 0.10 | 0.91 | 37.67 | 0.61 |
| S1 | 0.85 | 44.77 | 3.30 | 0.85 | 43.43 | 18.58 | 0.89 | 37.86 | 0.47 | 0.88 | 39.86 | 0.93 |
| S2 | 0.81 | 33.82 | 0.45 | 0.83 | 31.53 | 30.87 | 0.80 | 34.69 | −0.49 | 0.77 | 36.83 | 0.11 |
| S3 | 0.37 | 15.66 | 0.02 | 0.44 | 14.72 | 7.85 | 0.40 | 15.31 | 0.06 | 0.36 | 15.71 | −0.05 |
| S4 | 0.92 | 33.16 | −0.94 | 0.92 | 33.08 | 0.92 | 0.91 | 36.57 | 0.52 | 0.91 | 36.67 | −0.49 |
3.3. Sensitivity Analysis
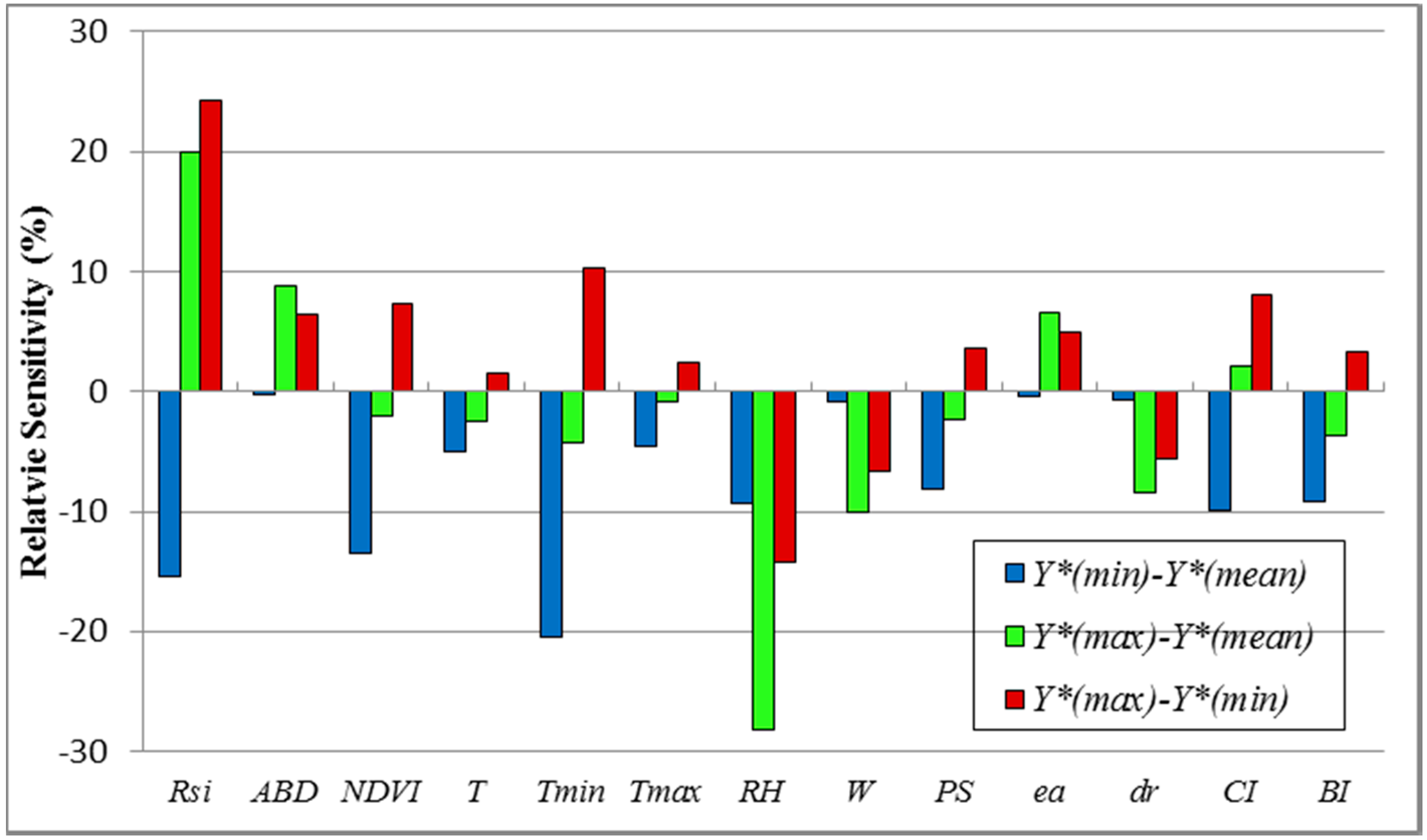
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rosenberg, N.J.; Blad, B.L.; Verma, S.B. Microclimate—The Biological Environment; Wiley: New York, NY, USA, 1983; pp. 44–45. [Google Scholar]
- Hurtado, E.; Sobrino, J.A. Daily net radiation estimated from air temperature and NOAA-AVHRR data: A case study for the Iberian Peninsula. Int. J. Remote Sens. 2001, 22, 1521–1533. [Google Scholar] [CrossRef]
- Kalthoff, N.; Fiebig-Wittmaack, M.; MeiBner, C.; Kohler, M.; Uriarte, M.; Bischoff-Gauß, I.; Gonzales, E. The energy balance, evapotranspiration and nocturnal dew deposition of an arid valley in the andes. J. Arid Environ. 2006, 65, 420–443. [Google Scholar] [CrossRef]
- Allen, R.; Tasumi, M.; Trezza, R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (metric)—Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Monteith, J.L.; Unsworth, M.H. Principles of Environmental Physics; Edward Arnold: London, UK, 1990; p. 291. [Google Scholar]
- Liang, S.L.; Wang, K.C.; Zhang, X.T.; Wild, M. Review on estimation of land surface radiation and energy budgets from ground measurement, remote sensing and model simulations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 225–240. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The era-interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.K.; et al. Merra: Nasa’s modern-era retrospective analysis for research and applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Uppala, S.M.; KÅllberg, P.W.; Simmons, A.J.; Andrae, U.; Bechtold, V.D.C.; Fiorino, M.; Gibson, J.K.; Haseler, J.; Hernandez, A.; Kelly, G.A.; et al. The era-40 re-analysis. Q. J. R. Meteorol. Soc. 2005, 131, 2961–3012. [Google Scholar] [CrossRef]
- Liang, S.L.; Zhang, X.T.; He, T.; Cheng, J.; Wang, D.D. Remote sensing of Earth surface radiation budge. In Remote Sensing of Land Surface Turbulent Fluxes and Soil Surface Moisture Content: State of the Art; Petropoulos, G.P., Ed.; CRC Press: Boca Raton, FL, USA, 2013; pp. 125–165. [Google Scholar]
- Zhang, X.T.; Liang, S.L.; Q., Z.G.; Wu, H.R.; Zhao, X. Generating Global Land Surface Satellite (GLASS) incident shortwave radiation and photosynthetically active radiation products from multiple satellite data. Remote Sens. Environ. 2014, 152, 318–332. [Google Scholar] [CrossRef]
- Davies, J.A. A note on relationship between net radiation and solar radiation. Q. J. R. Meteorol. Soc. 1967, 93, 109–115. [Google Scholar] [CrossRef]
- Gay, L. The regression of net radiation upon solar radiation. Theor. Appl. Climatol. 1971, 19, 1–14. [Google Scholar]
- Kaminsky, K.Z.; Dubayah, R. Estimation of surface net radiation in the boreal forest and northern prairie from shortwave flux measurements. J. Geophys. Res. Atmos. 1997, 102, 29707–29716. [Google Scholar] [CrossRef]
- Alados, I.; Foyo-Moreno, I.; Olmo, F.J.; Alados-Arboledas, L. Relationship between net radiation and solar radiation for semi-arid shrub-land. Agric. For. Meteorol. 2003, 116, 221–227. [Google Scholar] [CrossRef]
- Al-Riahi, M.; Al-Jumaily, K.; Kamies, I. Measurements of net radiation and its components in semi-arid climate of baghdad. Energy Convers. Manag. 2003, 44, 509–525. [Google Scholar] [CrossRef]
- Iziomon, M.G.; Mayer, H.; Matzarakis, A. Empirical models for estimating net radiative flux: A case study for three mid-latitude sites with orographic variability. Astrophys. Space Sci. 2000, 273, 313–330. [Google Scholar] [CrossRef]
- Kjaersgaard, J.; Cuenca, R.; Plauborg, F.; Hansen, S. Long-term comparisons of net radiation calculation schemes. Bound. Layer Meteorol. 2007, 123, 417–431. [Google Scholar] [CrossRef]
- Wang, K.; Liang, S. Estimation of daytime net radiation from shortwave radiation measurements and meteorological observations. J. Appl. Meteorol. Climatol. 2009, 48, 634–643. [Google Scholar] [CrossRef]
- Kjaersgaard, J.H.; Cuenca, R.H.; Martinez-Cob, A.; Gavilan, P.; Plauborg, F.; Mollerup, M.; Hansen, S. Comparison of the performance of net radiation calculation models. Theor. Appl. Climatol. 2009, 98, 57–66. [Google Scholar] [CrossRef]
- Sentelhas, P.C.; Gillespie, T.J. Estimating hourly net radiation for leaf wetness duration using the penman-monteith equation. Theor. Appl. Climatol. 2008, 91, 205–215. [Google Scholar] [CrossRef]
- Bisht, G.; Bras, R.L. Estimation of net radiation from the MODIS data under all sky conditions: Southern great plains case study. Remote Sens. Environ. 2010, 114, 1522–1534. [Google Scholar] [CrossRef]
- Bisht, G.; Venturini, V.; Islam, S.; Jiang, L. Estimation of the net radiation using modis (moderate resolution imaging spectroradiometer) data for clear sky days. Remote Sens. Environ. 2005, 97, 52–67. [Google Scholar] [CrossRef]
- Long, D.; Gao, Y.; Singh, V.P. Estimation of daily average net radiation from modis data and dem over the Baiyangdian watershed in north China for clear sky days. J. Hydrol. 2010, 388, 217–233. [Google Scholar] [CrossRef]
- Ma, Y.; Su, Z.; Li, Z.; Koike, T.; Menenti, M. Determination of regional net radiation and soil heat flux over a heterogeneous landscape of the Tibetan plateau. Hydrol. Process. 2002, 16, 2963–2971. [Google Scholar] [CrossRef]
- Jiang, B.; Zhang, Y.; Liang, S.L.; Yao, Y.J.; Jia, K.; Zhao, D. Empirical estimation of daytime net radiation from shortwave radiation and the other ancillary information. Agric. For. Meteorol. 2014. under review. [Google Scholar]
- Ferreira, A.; Soria-Olivas, E.; López, A.; Lopez-Baeza, E. Estimating net radiation at surface using artificial neural networks: A new approach. Theor. Appl. Climatol. 2011, 106, 263–279. [Google Scholar] [CrossRef]
- Geraldo-Ferreira, A.; Soria-Olivas, E.; Gomez-Sanchis, J.; Serrano-Lopez, A.J.; Velazquez-Blazquez, A.; Lopez-Baeza, E. Modelling net radiation at surface using “in situ” netpyrradiometer measurements with artificial neural networks. Expert Syst. Appl. 2011, 38, 14190–14195. [Google Scholar]
- Specht, D.F. A general regression network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef] [PubMed]
- Noble, P.A.; Tribou, E.H. Neuroet: An easy-to-use artificial neural network for ecological and biological modeling. Ecol. Model. 2007, 203, 87–98. [Google Scholar] [CrossRef]
- Fluxnet. Available online: http://www.fluxdata.org/ (accessed on 7 November 2014).
- U.S. Department of Energy. ARM-Data. Available online: http://www.archive.arm.gov/ (accessed on 7 November 2014).
- AsiaFlux. Available online: http://www.asiaflux.net/ (accessed on 7 November 2014).
- Ohmura, A.; Gilgen, H.; Hegner, H.; Müller, G.; Wild, M.; Dutton, E.G.; Forgan, B.; Fröhlich, C.; Philipona, R.; Heimo, A.; et al. Baseline Surface Radiation Network (BSRN/WCRP): New precision radiometry for climate research. Bull. Am. Meteorol. Soc. 1998, 79, 2115–2136. [Google Scholar]
- BSRN-World Radiation Monitoring Center Baseline Surface Radiation Network. Available online: http://www.bsrn.awi.de/ (accessed on 7 November 2014).
- Augustine, J.A.; DeLuisi, J.J.; Long, C.N. Surfrad—A national surface radiation budget network for atmospheric research. Bull. Am. Meteorol. Soc. 2000, 81, 2341–2357. [Google Scholar] [CrossRef]
- Augustine, J.A.; Hodges, G.B.; Cornwall, C.R.; Michalsky, J.J.; Medina, C.I. An update on SURFRAD—The GCOS surface radiation budget network for the continental United States. J. Atmos. Ocean. Technol. 2005, 22, 1460–1472. [Google Scholar] [CrossRef]
- ESRL Global Mnotoring Division. Available online: http://www.esrl.noaa.gov/gmd/grad/surfrad/ (accessed on 7 November 2014).
- BOREAS Project. Available online: http://daac.ornl.gov/BOREAS/bhs/BOREAS_Home.html (accessed on 7 November 2014).
- GAME-AAN. Available online: http://www.hyarc.nagoya-u.ac.jp/game/phase-1/game-aan.html (accessed on 7 November 2014).
- Steffen, K.; Box, J.; Abdalati, W. Greenland climate network: GC-Net. In US Army Cold Regions Reattach and Engineering (CRREL); CRREL Special Report; University of Colorado at Boulder: Boulder, CO, USA, 1996; pp. 98–103. [Google Scholar]
- Greenland Climate Network (GC-Net). Available online: http://cires.colorado.edu/science/groups/steffen/gcnet/ (accessed on 7 November 2014).
- Earth Observing Laboratory. Available online: http://www.eol.ucar.edu/projects/ceop/ (accessed on 7 November 2014).
- Jia, Z.Z.; Liu, S.M.; Xu, Z.W.; Chen, Y.J.; Zhu, M.J. Validation of remotely sensed evapotranspiration over the Hai River Basin, China. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Liu, S.M.; Xu, Z.W.; Wang, W.Z.; Jia, Z.Z.; Zhu, M.J.; Bai, J.; Wang, J.M. A comparison of eddy-covariance and large aperture scintillometer measurements with respect to the energy balance closure problem. Hydrol. Earth Syst. Sci. 2011, 15, 1291–1306. [Google Scholar] [CrossRef]
- Liu, S.M.; Xu, Z.W.; Zhu, Z.L.; Jia, Z.Z.; Zhu, M.J. Measurements of evapotranspiration from eddy-covariance systems and large aperture scintillometers in the Hai River Basin, China. J. Hydrol. 2013, 487, 24–38. [Google Scholar] [CrossRef]
- Xu, Z.W.; Liu, S.M.; Li, X.; Shi, S.J.; Wang, J.M.; Zhu, Z.L.; Xu, T.R.; Wang, W.Z.; Ma, M.G. Intercomparison of surface energy flux measurement systems used during the hiwater-musoexe. J. Geophys. Res. Atmos. 2013, 118, 13140–13157. [Google Scholar] [CrossRef]
- De Rosnay, P.; Calvet, J.C.; Kerr, Y.; Wigneron, J.P.; Lemaître, F.; Escorihuela, M.J.; Sabater, J.M.; Saleh, K.; Barrié, J.; Bouhours, G. Smosrex: A long term field campaign experiment for soil moisture and land surface processes remote sensing. Remote Sens. Environ. 2006, 102, 377–389. [Google Scholar] [CrossRef]
- Centre d’Etudes Spatiales de la BIOsphère. Available online: http://www.cesbio.ups-tlse.fr/ (accessed on 7 November 2014).
- CERN. Available online: http://www.cerndata.ac.cn/ (accessed on 7 November 2014).
- Tucker, C.J.; Pinzon, J.E.; Brown, M.E.; Slayback, D.A.; Pak, E.W.; Mahoney, R.; Vermote, E.F.; El Saleous, N. An extended AVHRR 8-km NDVI dataset compatible with MODIS and SPOT vegetation NDVI data. Int. J. Remote Sens. 2005, 26, 4485–4498. [Google Scholar] [CrossRef]
- Liang, S.; Zhao, X.; Liu, S.; Yuan, W.; Cheng, X.; Xiao, Z.; Zhang, X.; Liu, Q.; Cheng, J.; Tang, H.; et al. A long-term global land surface satellite (glass) data-set for environmental studies. Int. J. Digit. Earth 2013, 6, 5–33. [Google Scholar] [CrossRef]
- Liang, S.L.; Zhang, X.T.; Xiao, Z.Q.; Cheng, J.; Liu, Q.; Zhao, X. Global Land Surface Satellite (Glass) Products: Algorithms, Validation and Analysis; Springer: New York, NY, USA, 2013. [Google Scholar]
- Liu, Q.; Wang, L.Z.; Qu, Y.; Liu, N.F.; Liu, S.H.; Tang, H.R.; Liang, S.L. Preliminary evaluation of the long-term glass albedo product. Int. J. Digit. Earth 2013, 6, 69–95. [Google Scholar] [CrossRef]
- Qu, Y.; Liu, Q.; Liang, S.; Wang, L.; Liu, N.; Liu, S. Improved mapping daily land-surface broadband albedo from MODIS data. IEEE Geosci. Remote Sens. Lett. 2014, 52, 907–919. [Google Scholar] [CrossRef]
- Air Humidity Converter. Available online: http://www.cactus2000.de/uk/unit/masshum.shtml (accessed on 7 November 2014).
- Lowe, P.R.; Ficke, J.M. The Computation of Saturation Vapor Pressure; Environmental Prediction Research Facility, Naval Postgraduate School: Monterey, CA, USA, 1974. [Google Scholar]
- Irmak, S.; Irmak, A.; Jones, J.; Howell, T.; Jacobs, J.; Allen, R.; Hoogenboom, G. Predicting daily net radiation using minimum climatological data. J. Irrig. Drain. Eng. 2003, 129, 256–269. [Google Scholar] [CrossRef]
- Duan, Q.Y.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Xiao, Z.Q.; Liang, S.L.; Wang, J.D.; Chen, P.; Yin, X.J.; Zhang, Z.Q.; Song, J.L. Use of general regression neural networks for generating the glass leaf area index product from time-series MODIS surface reflectance. IEEE Trans. Geosci. Remote Sens. 2014, 52, 209–223. [Google Scholar] [CrossRef]
- Kang, H.Y.; Rule, R.A.; Noble, P.A. Artificial neural network modeling of phytoplankton blooms and its application to sampling sites within the same estuary. In Treatise on Coastal snd Estuarine Science; Wolanski, M., Ed.; Elsevier: Amsterdam, The Netherlands, 2012; Volume 9, pp. 161–171. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, B.; Zhang, Y.; Liang, S.; Zhang, X.; Xiao, Z. Surface Daytime Net Radiation Estimation Using Artificial Neural Networks. Remote Sens. 2014, 6, 11031-11050. https://0-doi-org.brum.beds.ac.uk/10.3390/rs61111031
Jiang B, Zhang Y, Liang S, Zhang X, Xiao Z. Surface Daytime Net Radiation Estimation Using Artificial Neural Networks. Remote Sensing. 2014; 6(11):11031-11050. https://0-doi-org.brum.beds.ac.uk/10.3390/rs61111031
Chicago/Turabian StyleJiang, Bo, Yi Zhang, Shunlin Liang, Xiaotong Zhang, and Zhiqiang Xiao. 2014. "Surface Daytime Net Radiation Estimation Using Artificial Neural Networks" Remote Sensing 6, no. 11: 11031-11050. https://0-doi-org.brum.beds.ac.uk/10.3390/rs61111031






