1. Introduction
In the present days, the spreading usage of Unmanned Aerial Vehicles (UAVs) spans a broad area of applications, both civil and military. This results in the need for their proper operation within different environments. Apart from the command and control link, remote collection of data from various user devices placed on UAVs, such as cameras or radar, is of great interest as well. As corresponding data rates are quite high, links operating in the L-band and above are required.
However, apart from the distance-dependent free-space path loss generally affecting the received signal power, radio wave propagation conditions are, in these bands, strongly influenced by the scenario between the UAV and its ground terminal as the line-of-sight (LoS) propagation conditions may not be always held. This may include, for example, signal attenuation by nearby objects causing slow signal fading or multipath effects due to scattering and reflections resulting in fast fading. If such signal attenuation results in an insufficient link’s signal-to-noise ratio (SNR), one may utilize beyond-LoS (BLoS) relayed data links, e.g., by satellites or other UAVs.
It is also highly probable that the link of interest will be influenced by the presence of vegetation, such as trees in the form of forests in rural areas or alleys in urban areas. This may generally happen in the close vicinity of both the UAV and its ground terminal, thus directly affecting the BLoS relays as well. This can be, e.g., the case of the scenarios from [
1]. To ensure proper link operation under such conditions, it is first necessary to thoroughly characterize such influence. Only after that, the corresponding link can be dimensioned properly.
From a very simplified point of view, radio wave propagation through trees can be addressed by using a so-called specific attenuation in dB per distance through the canopy in meters, as given for short paths through woodland in Rec. ITU-R P.833 for frequencies from 30 MHz up to 30 GHz [
2]. On the other hand, for an isolated tree and terrestrial paths with low elevation angles, [
2] suggests to use the radiative transfer theory, applied in [
3], and also account for ground reflections and diffraction around the canopy. For slant paths, generally applicable for UAV scenarios, [
2] recommends applying multiple scattering theory (MST) described in detail in
Section 2.2.
Unfortunately, the use of MST introduces enormous requirements in terms of computation time and the software implementation complexity [
4,
5,
6]. Recently, the authors have developed in [
7] a new model addressing scattering from tree canopies which significantly lowers the corresponding requirements by replacing MST coherent field calculations by utilizing the physical optics (PO) approach based on [
8]. In this way, near-field effects close to the canopy are modeled properly and smooth transitions between LoS and shadowed areas behind the canopy are achieved [
7].
In this paper, we follow the model developed in [
7] and, by adding the incoherent scattered field obtained by MST, we build a new propagation channel synthesizer for UAVs operating in close vicinities of tree canopies, which enables the generation of site-specific time series of received signal levels. This means that the output of this synthesizer can directly be utilized to obtain first- and second-order characteristics of the received signal for a particular scenario, i.e., respecting the positions of UAV, the terminal and trees, including the physical parameters of the canopies, such as dimensions and types of branches and leaves. It should be noted that the synthesizer’s output is multiplicative to other propagation effects. Thus, the resulting attenuation in dB can be summed with the attenuation obtained for any other propagation effect. In this way, the synthesizer relates to the SNR graphs of the link by directly influencing the corresponding signal levels.
The paper is organized as follows. In
Section 2, we present the theoretical background for PO and MST and we introduce the mixed PO/MST model developed by the authors in [
7]. In
Section 3, we build the new channel synthesizer based on the models presented in
Section 2. After that, in
Section 4, we validate the developed synthesizer by using an artificial scenario. In
Section 5, we validate the synthesizer against an actual experimental dataset obtained at 2 GHz.
Section 6 then concludes this paper.
3. The Proposed Channel Synthesizer
Now we have enough information to build the new channel synthesizer for UAVs in the presence of tree canopies. The purpose of this synthesizer is to generate a time series of received signal levels for the scenario of interest in the site-specific way, i.e., respecting the mutual positions of the UAV, its ground terminal, and trees, while accounting for physical parameters of the trees in terms of their dimensions, shapes, and types of branches and leaves.
3.1. Inputs
In general, we assume that the position of both the UAV and the corresponding ground terminal may change in time and we design the synthesizer so that these positions are required as an input. The conversion from position to time is then straightforward by accounting for the particular velocities of the UAV or the terminal.
Another input is formed by the fixed position of tree canopies where their center, geometrical shape and dimensions (e.g., radius and height for a cylindrical shape) need to be provided. After that, their surface is sampled for the purposes of PO with samples of dimension below half the wavelength. Further, the volume of the canopies needs to be spatially sampled (voxelized) to enable MST incoherent field calculations. The voxels may be, for example, cubes with sides exceeding half the wavelength as the incoherent field calculations are not very sensitive to this parameter [
6]. Regarding the MST calculations, the branches and leaves parameters such as length, radius, complex permittivity, number density, and spatial orientation probability need to be provided as well [
4,
5,
6].
The synthesizer is proposed for an incident plane wave, so the corresponding frequency, amplitude and polarization must be given as an input, as well.
3.2. Coherent Scattered Field
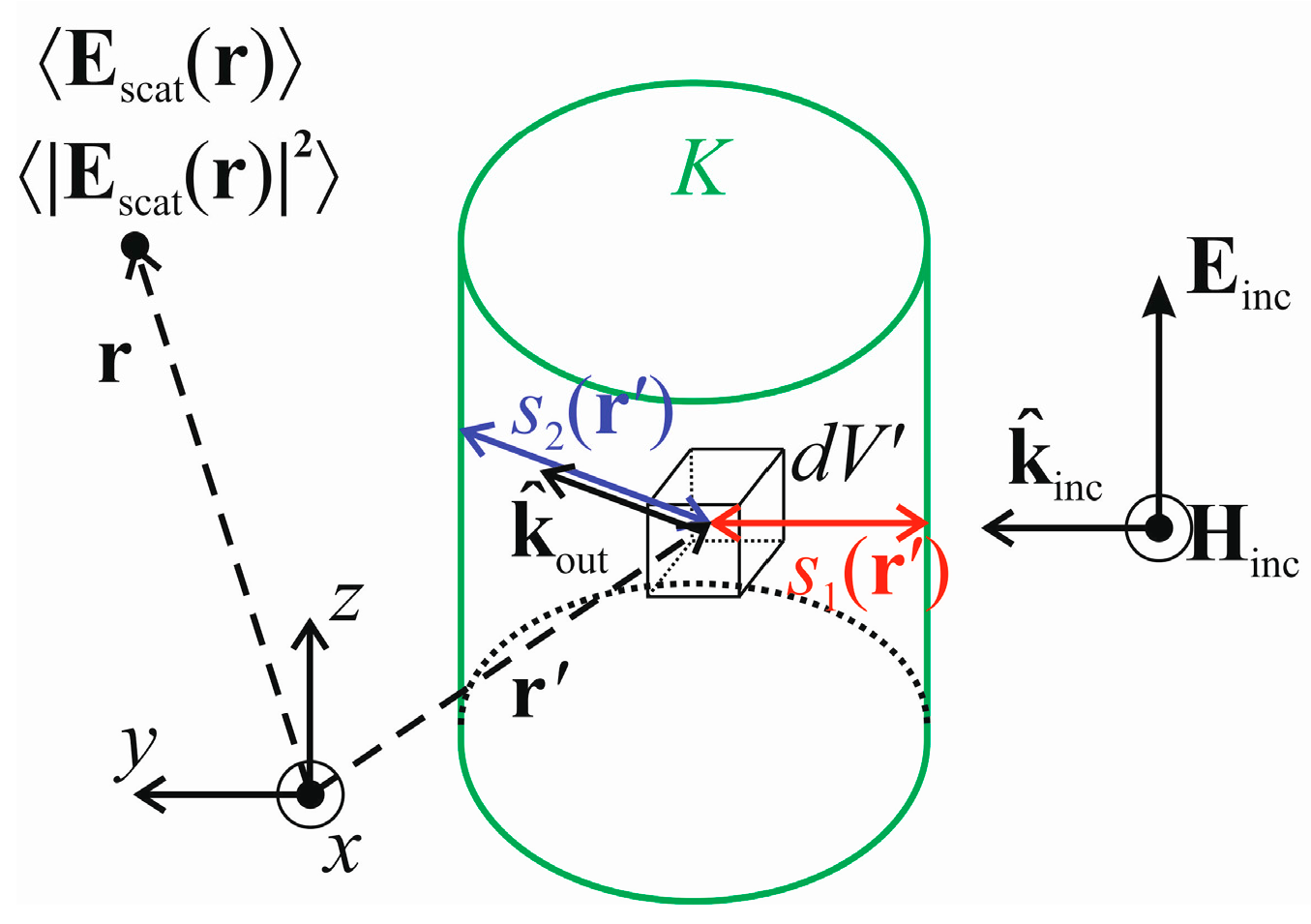
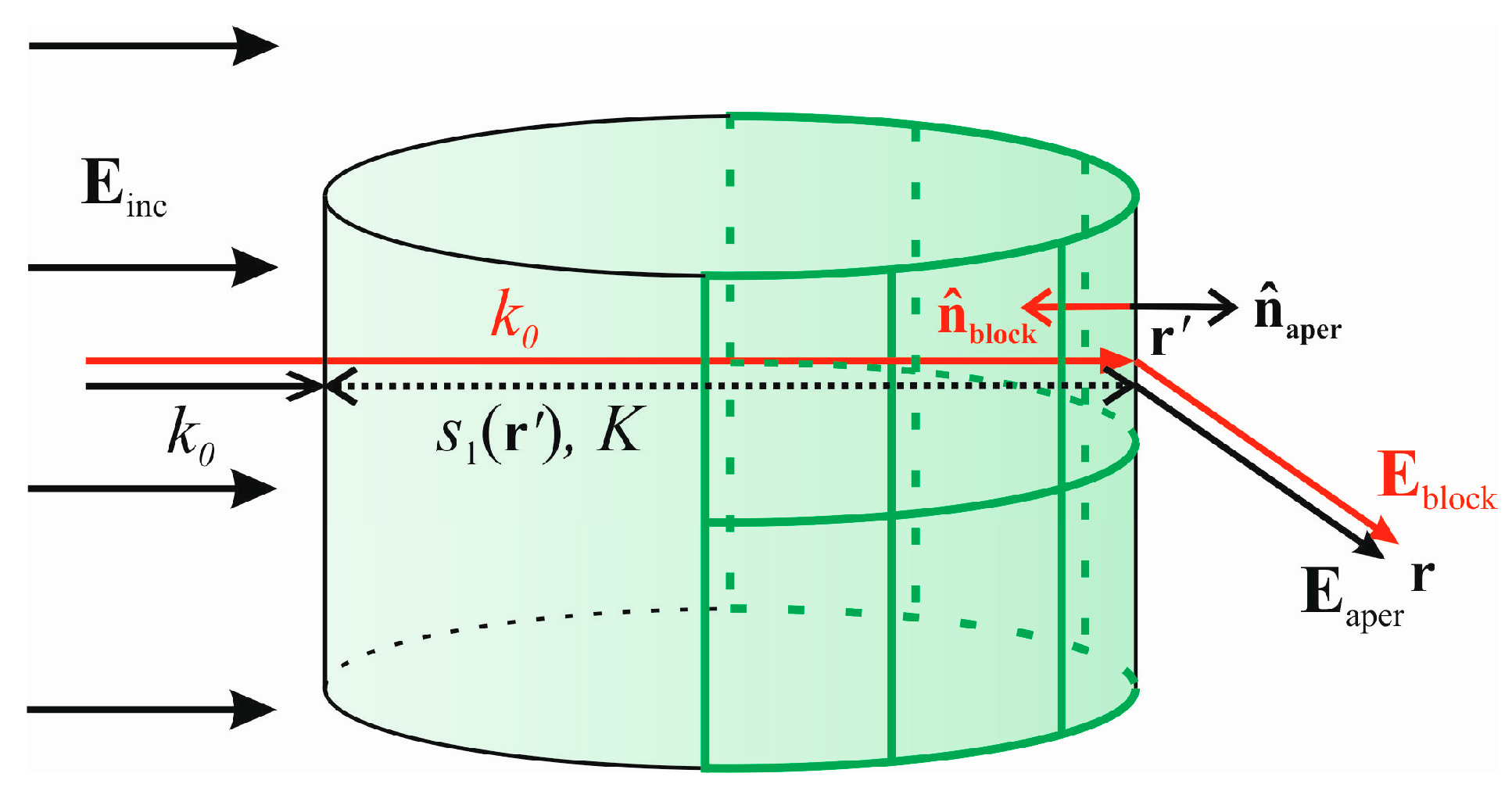
The coherent scattered field calculations follow the new combined PO/MST model described in
Section 2.3. First of all, the canopies’ surface samples visible from the UAV need to be identified. This can be done, for example, by determining the dot product between each surface sample normal vector and the incident plane wave direction; if the dot product is negative, the corresponding surface sample is illuminated. Another option may be using the algorithm provided in [
17] which may be suitable when the tree canopies are intersecting.
Following
Section 2.3, the blockage fields
and
are calculated first; see Equations (1) and (2). Then, the distances through the canopy towards individual illuminated surface samples are determined and the aperture fields
and
are obtained.
Summing the blockage and aperture coherent contributions with the direct fields and then results in the coherent scattered fields.
3.3. Incoherent Scattered Field
As the MST incoherent scattered field is obtained for the whole canopy as a power only, we need to adapt it for the purposes of the synthesizer. Thus, we break down the integration in Equation (7) into a summation of the fractional incoherent power scattered by individual voxels. For each voxel we, thus, need to use the distance through the canopy to and from it, as Equation (7) includes the term in and the term in . We should note here that changes due to the UAV movement and changes when the terminal reaches a different position.
Having the individual contributions to the total scattered power, we may turn them into the corresponding field intensities by applying the square root and adding phase information. As the incoherent scattered field is supposed to show a random nature, we assign a random phase to each of the voxels following the uniformly-distributed values between and . Further, based on the distances between the UAV and the individual voxels, we add another phase term: . Similarly, following the distances between the individual voxels and the ground terminal, we add another phase term as . In this way, the overall incoherent scattered power of a particular tree canopy is preserved and its randomness is expressed properly.
Following [
5], Equation (7) can be rearranged as:
and the phase information can be added as:
which can then be summed over all voxels
.
As the individual incoherent scattered field contributions contain the phase information, they can be directly summed with the coherent scattered field obtained by the combined PO/MST model. It should be noted that to reconstruct the
xyz field components from Equation (13), the projection following
and the field polarization must be applied, as in [
11].
3.4. Discussion and Workflow
Following
Section 3.2 and
Section 3.3, summing the coherent and incoherent scattered fields enables to obtain the resulting time series of received signal levels at the position of interest, i.e., at the ground terminal.
Assuming only the plane wave illuminating the tree canopies enables to save some computation time as the incident direction is the same throughout the scenario for one particular UAV position.
As the UAV moves,
changes and, as a consequence, the canopy’s equivalent scattering amplitude per unit volume in the forward scatter direction
and the complex propagation constant
inside the canopies should be updated, see (6). However, obtaining
is, as explained above in
Section 2.2, computationally very demanding. Following the analysis in [
4,
5,
6], we may, however, update these values only when the UAV’s position is changed significantly, e.g., when the elevation or azimuth w.r.t. the ground terminal changes by more than 5°. This enables us to provide a time series with a very small sampling step while keeping the calculations within reasonable computation times.
Similar situation is with the equivalent scattering cross section per unit volume
, which, moreover, depends also on the terminal position due to the scattering direction
. Fortunately,
applies only in the incoherent field calculations and, following the analysis in [
4,
5,
6], it dominates only in other than the forward scatter direction and its dependence on
is quite weak. A significant decrease in the resulting computation time can, thus, be achieved when
is for a particular tree calculated only for one selected backscatter direction,
, and this value is used for all the
and
directions. In this way, the reduction of the synthesizer’s computation time is very significant while the overall resulting accuracy is well preserved.
Another reduction of the computation time is also apparent from [
4,
5,
6]. The coherent scattered field obtained by the new modified PO/MST model dominates over the incoherent field only in a narrow area around the forward scatter direction. This means only selected trees located around the forward scatter direction need to be taken into account. However, such selection must be performed very carefully and based on the particular scenario of interest, otherwise discontinuities in the resulting time series may appear.
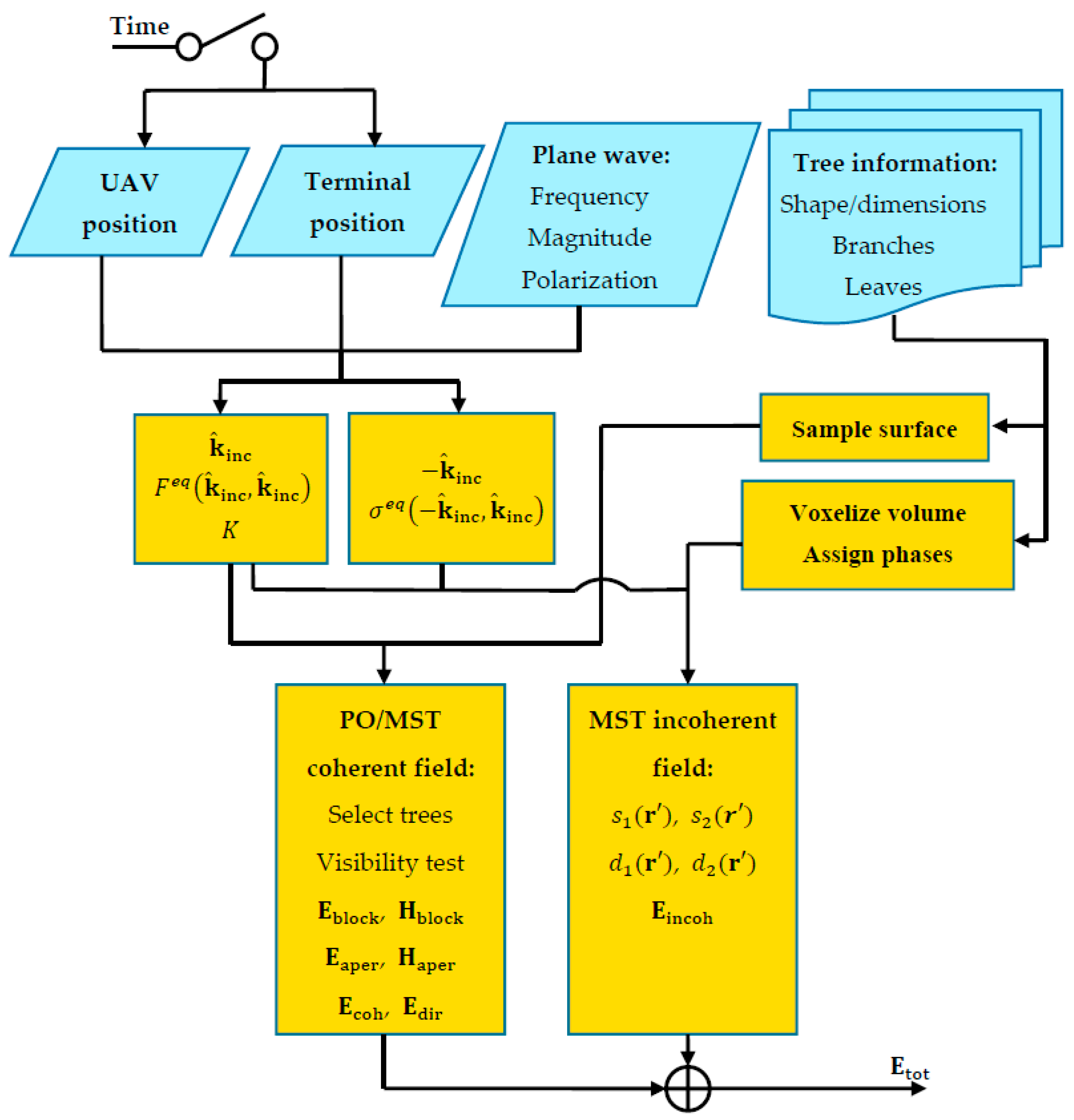
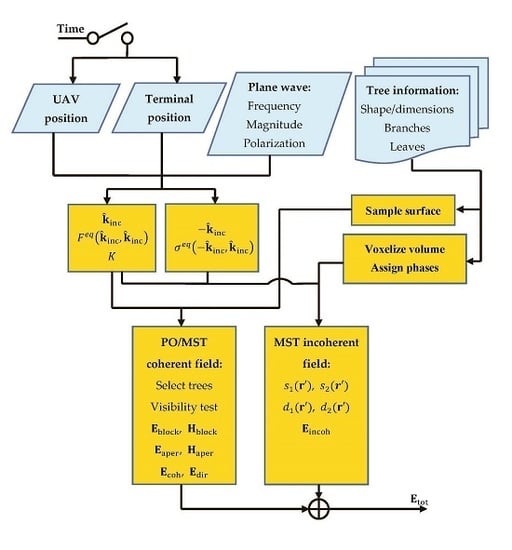
Now, in
Figure 4, we can summarize the whole workflow of the new proposed propagation channel synthesizer where each block clarifies its functionality. Following this diagram, the synthesizer has been implemented in the MATLAB environment for the validation purposes described below in
Section 4 and
Section 5.
4. Artificial Scenario Validation
Having the new proposed synthesizer implemented in software, it is convenient to first test its proper functionality using an artificially-defined scenario with a very simple geometry. This allows us to predict the expected results up to a certain level prior to using the synthesizer.
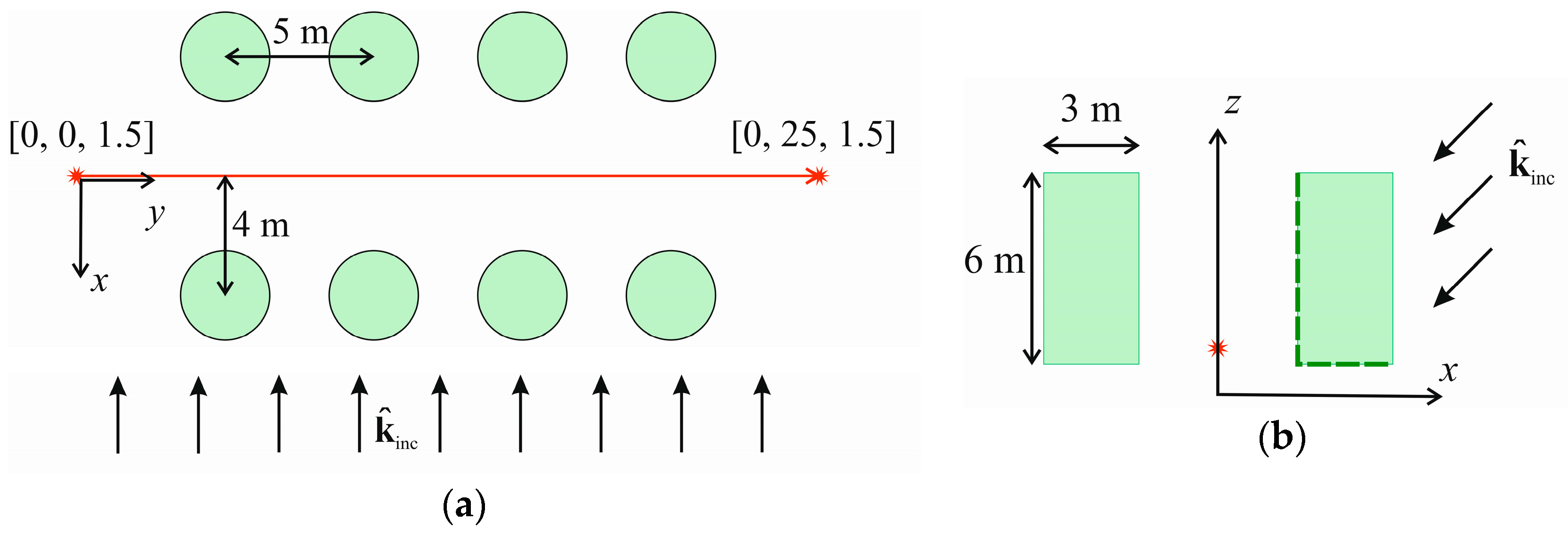
For these purposes, we have defined a simple alley of roadside trees, all of which have a cylindrical canopy of 1.5 m radius and 6 m height. In the
xyz Cartesian coordinate system, each canopy has the
z component of its center point at 4 m, i.e., the canopies span in the
z axis direction from 1 m to 7 m above ground level. The UAV is fixed under the elevation angle of 45° from the point of view of its ground terminal and, in azimuth, the incident plane wave is perpendicular to the alley. The terminal at a height of 1.5 m is supposed to be moving in the
y direction inside the alley from 0 m to 25 m with a sampling step of
, where
represents the wavelength of the incident plane wave which has the frequency set to 2 GHz and its polarization is vertical. The alley surrounds the terminal on its left and right side by four trees at a 4 m distance; the tree spacing is set to be 5 m. The branches and leaves parameters are the same as in [
2,
4,
5,
6]. Please see
Figure 5 below for more details.
As the trees are quite separated from each other and the distance from their center points towards the terminal is long, we may expect LoS propagation conditions towards the UAV within some parts of the terminal route. On the other hand, diffraction effects caused by the coherent scattered field should be clearly identified when the propagation path towards the UAV is blocked by a particular canopy. In addition, the resulting time series should follow the symmetry of the scenario where the terminal starts to move 5 m before the beginning of the alley and stops 5 m behind the alley.
As explained above in
Section 3.3, to save the computation time, only the trees on the right side of the terminal are utilized within the coherent scattered field calculations. Further, the value of
for the very first
direction is utilized throughout the calculations.
Figure 6 presents the results obtained by the proposed synthesizer. It should be noted that, on a PC with a 3.5 GHz quad-core processor and 16 GB RAM, the total computation time for the 834 terminal positions (distance of 25 m with a step of
) was only about 50 s, including the surface and volume sampling of the canopies. Again, it should be stressed that this synthesizer provides a site-specific time series respecting the geometry of the scenario, as well as the physical parameters of the tree canopies. For the considered tree dimensions and their number, full‑wave solutions using the multilevel fast multipole method (MLFMM) method in electromagnetic simulators would be impossible due to unrealistic memory requirements.
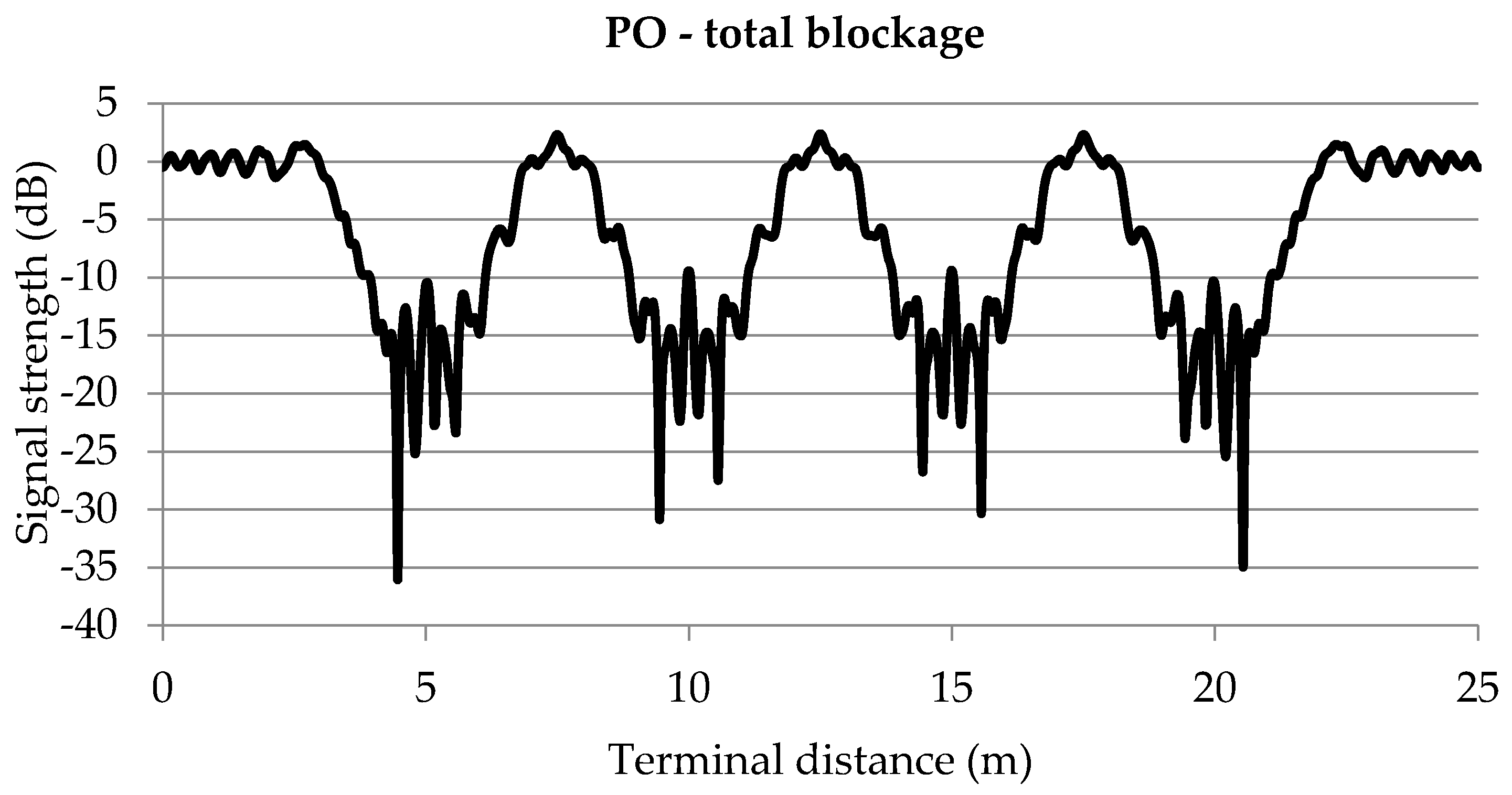
To support the obtained results, the same scenario was simulated in FEKO [
18] using the common PO for the case of completely absorbing canopies, i.e., not accounting for any field passing through dielectric objects. The resulting total coherent field is shown in
Figure 7. We should note that the corresponding computation time (excluding the surface sampling) was, in this case, about 70 s longer compared to the time required by the synthesizer, which may be caused by the denser surface sampling in FEKO.
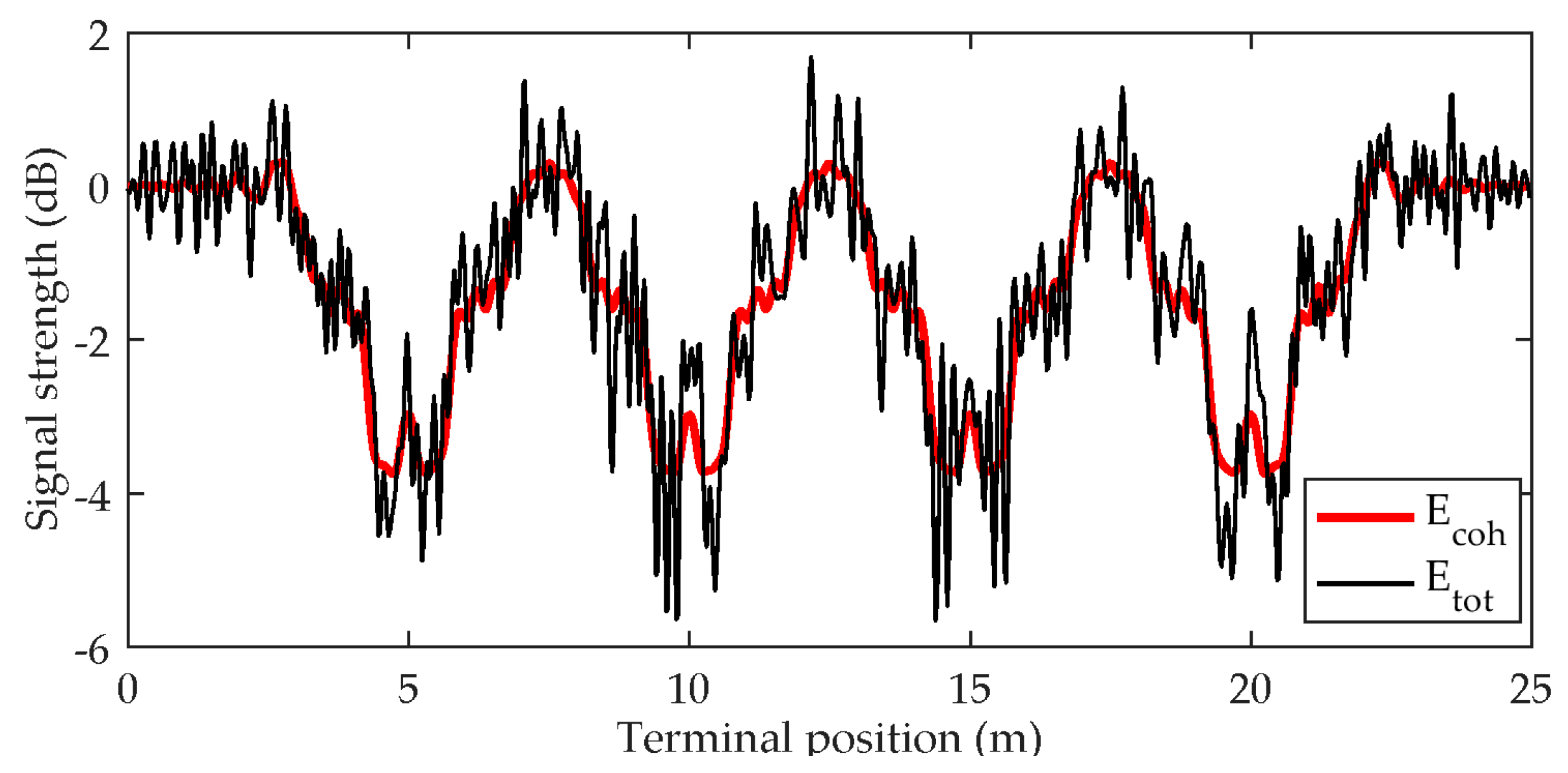
Now we can clearly see that the proposed simulator correctly provides the diffraction pattern around the tree canopies and also correctly identifies the LoS areas where the signal is close to its free space value of 0 dB, as shown by the red curve in
Figure 6 representing the coherent scattered field. The excess attenuation in the shadowed areas about is 4 dB, which nicely corresponds to the path through a canopy (about 4 m for the plane wave incident under the elevation of 45°) multiplied by the specific attenuation (about 1 dB/m at 2 GHz as in [
7]). We should note that, for the case of the totally absorbing tree canopies, the resulting attenuation is much stronger in
Figure 7; over 15 dB.
Concentrating on the black curve in
Figure 6 representing the total field (coherent and incoherent), we notice that under LoS conditions, the resulting signal variations are weaker (about 1 dB) than within the shadowed areas (about 2 dB) which is to be expected. Within LoS, the strong direct signal dominates and the resulting signal characteristics can be approximated by the Rice distribution, whereas in the shadowed areas, the direct component gets attenuated and the characteristics are closer to the Rayleigh distribution where the variations are more pronounced.
Based on the above provided analysis, the synthesizer may be claimed to be validated. However, a further validation against actual experimental data set is of interest as well and is, thus, presented in
Section 5.
5. Experimental Data Validation
Now, we may present the validation against an experimental dataset obtained during measurement trials with the use of a blimp as a UAV. The trials were taken in July 2015 at Fleming Square in Prague, Czech Republic, and the same measurement setup as in [
19] was utilized. This means that a 3D positioner attached to the UAV enabled instant pointing of the transmit (Tx) antennas towards the receiver (Rx) based on the corresponding GPS coordinates which, for Rx were 50°6′16.97′′N and 14°23′31.62′′E in the WGS84 coordinates.
The two Tx antennas, one left-handed (LHCP) and the other right-handed (RHCP) circularly polarized, enabled to transmit two unmodulated continuous wave signals with a stable output power of 27 dBm. These signals were distinguished by a frequency offset of 200 kHz and, thus, were transmitted at 2.00106 GHz and 2.00086 GHz.
The Rx utilized a dual-polarized patch antenna placed on a tripod at a height of 1.5 m above ground level with its main lobe oriented towards the zenith. Its four parallel channels enabled to simultaneously record both the co‑polarized and cross‑polarized components of the transmitted signals with a sampling rate of 10 kHz, i.e., four samples were obtained every 0.1 ms.
The whole measurement setup provided a sufficient dynamic range covering the fast fading observed during the measurements. For the maximum distance between the UAV and Rx of about 500 m and Rx noise floor of −126 dBm, the resulting dynamic range was about 65 dB, which was not exceeded during the measurements. The selected scenario is shown in
Figure 8, together with the UAV during the flight.
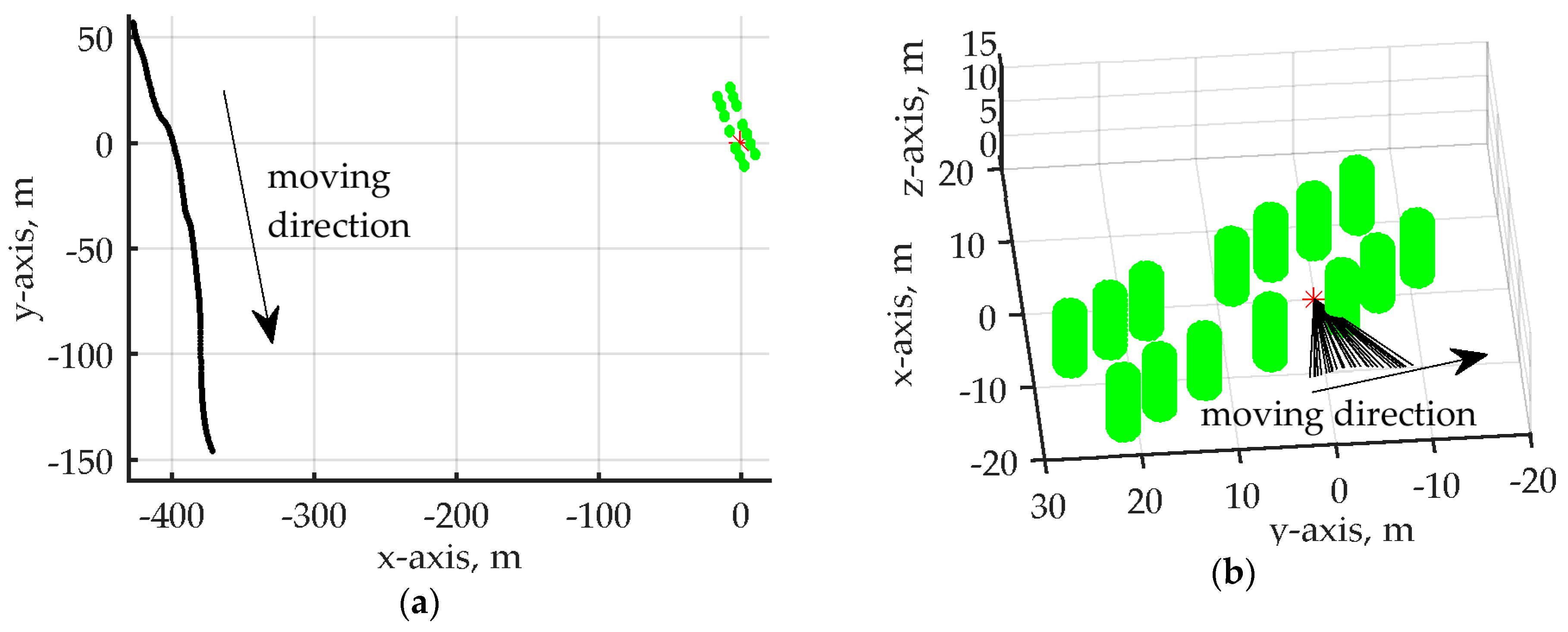
The position of trees were obtained from Google Maps [
20] and are shown from the top view together with the selected flyover of the UAV in
Figure 9a and also in
Figure 9b in more detail, including the incident plane wave directions and Rx position. We clearly see that, due to the spacing between the trees, LoS propagation conditions are achieved for more than half of the UAV flyover, whereas a blockage by one tree canopy occurs for the rest of the route.
As the deciduous trees in the alley are dense, higher specific attenuation than about 1 dB/m can be expected at 2 GHz. This was reflected in the synthesizer by using the physical parameters of the trees shown in
Table 1, which differ from [
2,
4,
5,
6] in the number density values. As a consequence, the resulting specific attenuation was obtained as 2.9 dB/m, which corresponds to the experimentally-obtained attenuation values as identified further in this section.
Before we can start analyzing the synthesizer’s output, we can summarize the simplifications applied during the simulations:
As the change of the UAV position in elevation and azimuth w.r.t. the Rx was less than 30°, thus, not very significant from the scattering characteristics point of view, only one value of and was calculated.
Only two trees influencing the coherent field calculations the most were considered within the combined PO/MST part of the simulator, namely the third and fourth tree from the right in the bottom row of trees in
Figure 9b.
the UAV speed was kept below 10 m/s, respecting the data sampling rate of 10 kHz, the spatial distance between two adjacent samples is below 1 mm, which is too dense. To characterize the fast fading thoroughly, a sufficient step may be longer, e.g., about . Following this, we provide an output for every 10th experimental data sample, which translates into a step in the UAV distance below .
Tree canopies are modeled simply as cylinders with radius of 1.8 m and height of 8 m with the bottom cap at the height of 1.5 m, i.e., the same as the Rx height.
Ground reflections are not included.
The simulation is carried out for a vertically polarized incident field, although the experimental data were obtained for the circularly polarized field.
Tree trunks were not considered.
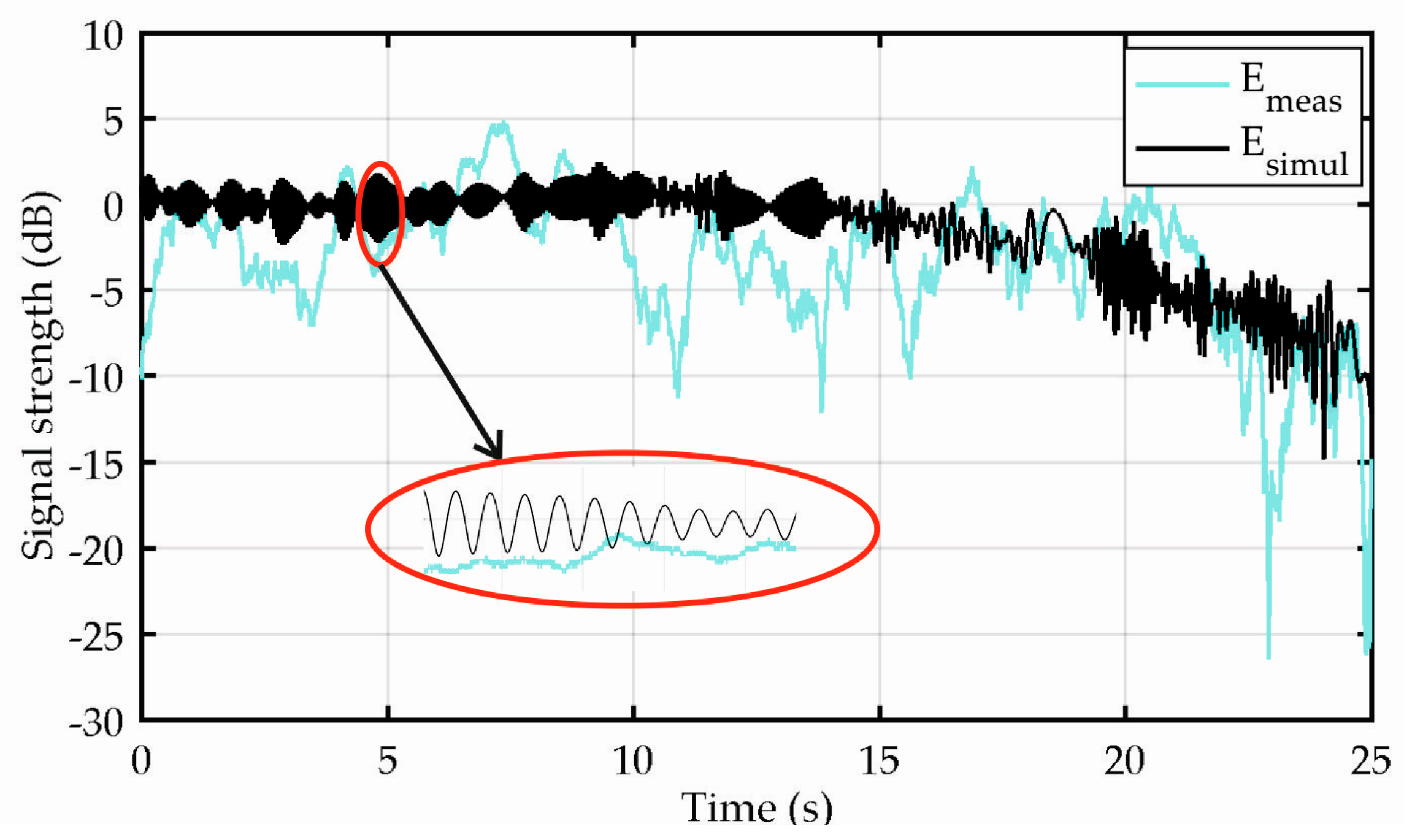
Now we may analyze the total field time series generated by the synthesizer, i.e., the sum of the coherent and incoherent scattered fields, shown in
Figure 10 by the black line alongside the cyan line representing the experimentally-obtained data. All of the signal levels are normalized with respect to the corresponding signal level in free space, thus showing signal enhancement by positive values and signal attenuation by the negative values. As the UAV was changing its position in all the three
x,
y and
z axes, the signal levels are shown simply against a time axis representing time of time flight in seconds. It should be noted that the total computation time on a PC with a 3.5 GHz quad-core processor and 16 GB RAM was about 15.3 h within which the results were provided for 26,000 UAV position samples. This corresponds to about 2 s required per one calculated value, which is quite feasible respecting the size of the scenario and site-specific character of the synthesizer.
At the beginning, the UAV was at the top left position in
Figure 9a and it was moving in the south‑southeast direction where the blockage by the tree started to occur, as indicated in
Figure 9b. In
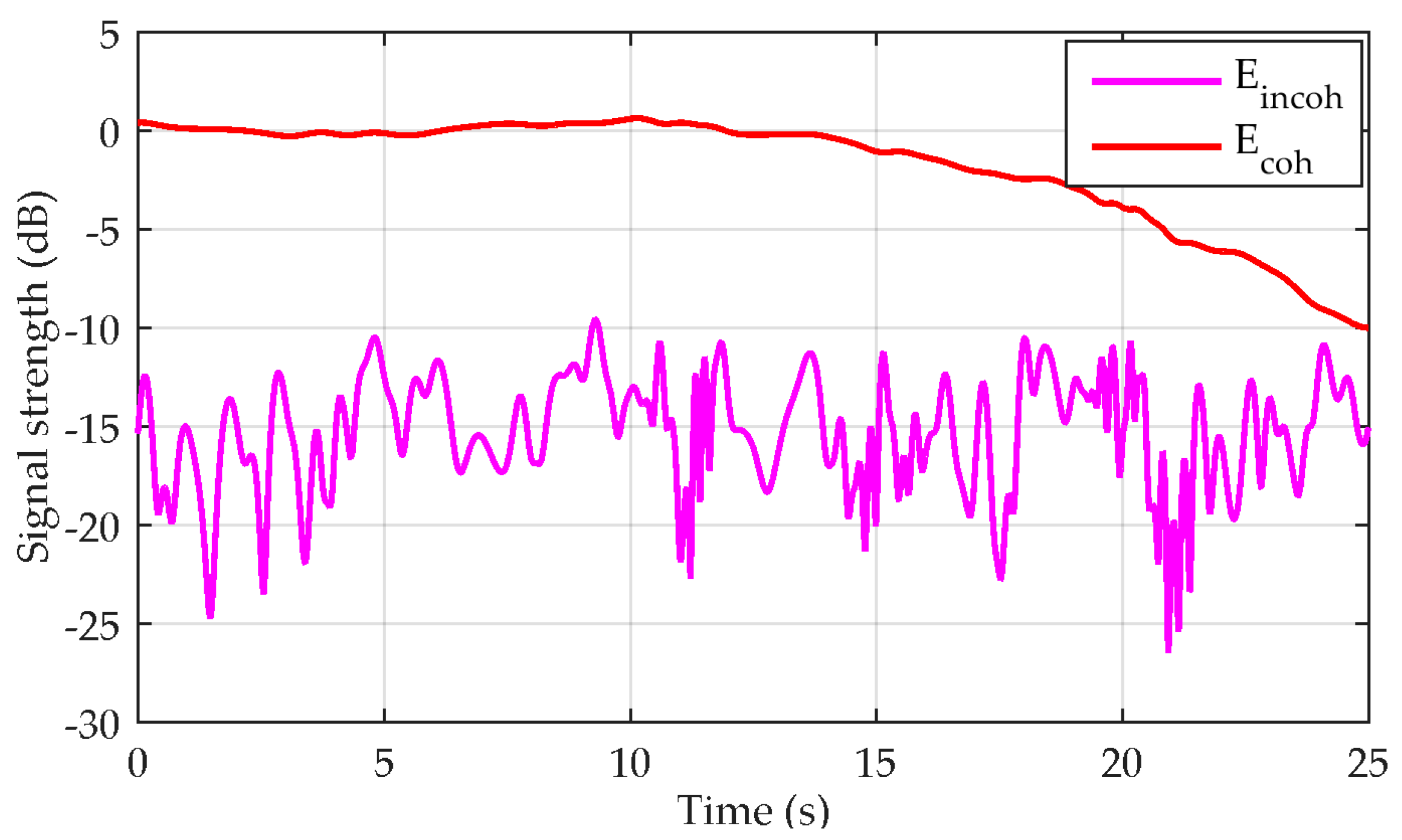
Figure 10, we can identify that the attenuation by the tree starts to be pronounced after the time of 15 s. Before this time, we can identify both the slow and fast fading present in the experimental data and, mainly, the fast fading in the generated output. The fast fading due to the incoherent scattered field in the simulated output is in the order of about 3 dB in magnitude, corresponding to the experimental data set only very roughly, while the deep fades (e.g., around 11 s, 14 s, 16 s, 23 s, and 25 s) are missing.
This is a consequence of the following: In the simulation, the actual tree canopies are idealistically represented by cylinders of scatterers and, thus, the blockage by individual large branches of the actual canopies is disregarded. Further, tree positions and dimensions should be obtained more precisely. More importantly, ground reflections were not included in the simulations. In addition, only the vertical polarization was addressed. Additionally, only the tree canopies, not the trunks, are considered. Despite all of this, the generated time series fit the experimentally-obtained data very closely.
In the shadowed area behind the tree, the resulting attenuation obtained by the synthesizer matches the experimental data very well, respecting the diffraction pattern around the canopy. The total attenuation is about 10 dB, which approximately corresponds to the maximum path through the canopy (about twice the radius, i.e., 3.6 m) multiplied by the resulting specific attenuation of 2.9 dB/m. Here, however, the experimental data may contain deep fades (e.g., around 23 s), which can be generally assigned to individual branches in the canopies or ground reflections disregarded by the simulation.
In
Figure 10, fewer changes in the synthesizer’s output can be noticed, for example, between the time of 15 s and 20 s. This is, however, simply a consequence of plotting the synthesizer’s output against the time axis within which the incidence direction does not change constantly, but follows the change in the UAV position, i.e., it is dependent on its speed and direction, which are not constant during the flight. Then, slower changes in the incidence direction are responsible for sparser time series when plotted against the time axis.
The detail shown in
Figure 10 enables to observe a very important characteristic of the resulting time series, which is their continuity. There are no abrupt changes present in the synthesizer’s output, which is an important feature of site-specific simulations where the resulting outputs respect the electromagnetic field continuity within a particular scenario.
To provide more insight into the synthesizer’s output,
Figure 11 provides the coherent and incoherent scattered field time series as generated inside the synthesizer. Clearly, the coherent scattered field is responsible for the attenuation by the tree canopy. On the other hand, the mean value of the incoherent scattered field is independent on the Tx position as the overall scattered power is about the same for all the incident directions and its instant magnitude is changing following the phase differences between Tx and each voxel in a canopy. We may also note that the incoherent scattered power is about 15 dB below the coherent one, which is in agreement with [
4,
5,
6,
7], and, thus, it has a stronger impact on the resulting field time series in the shadowed areas, as can be seen in
Figure 10 by the increase of the signal levels deviation.
Apart from the above presented narrowband channel characteristics, the synthesizer is also capable of directly providing wideband characteristics in the form of the channel impulse response (CIR). This can be obtained by assuming that the coherent and incoherent scattered field contributions originate from the center point of each canopy. Based on the total distance between Tx, canopy center and Rx, the time delay is calculated. Normalization with respect to power and time delay of the unobstructed direct signal between Tx and Rx, which may (LoS) or may not (NLoS) be present, can be applied.
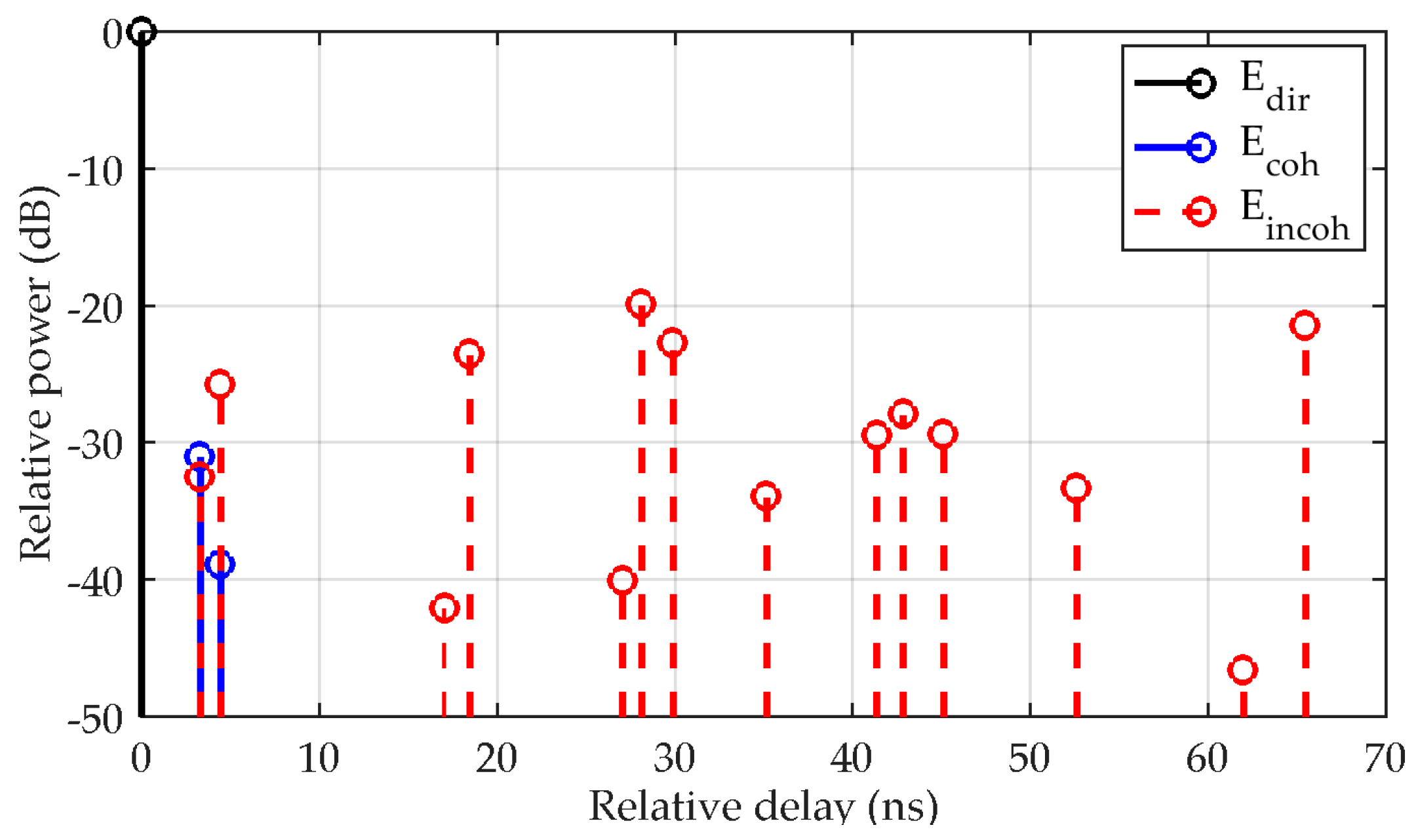
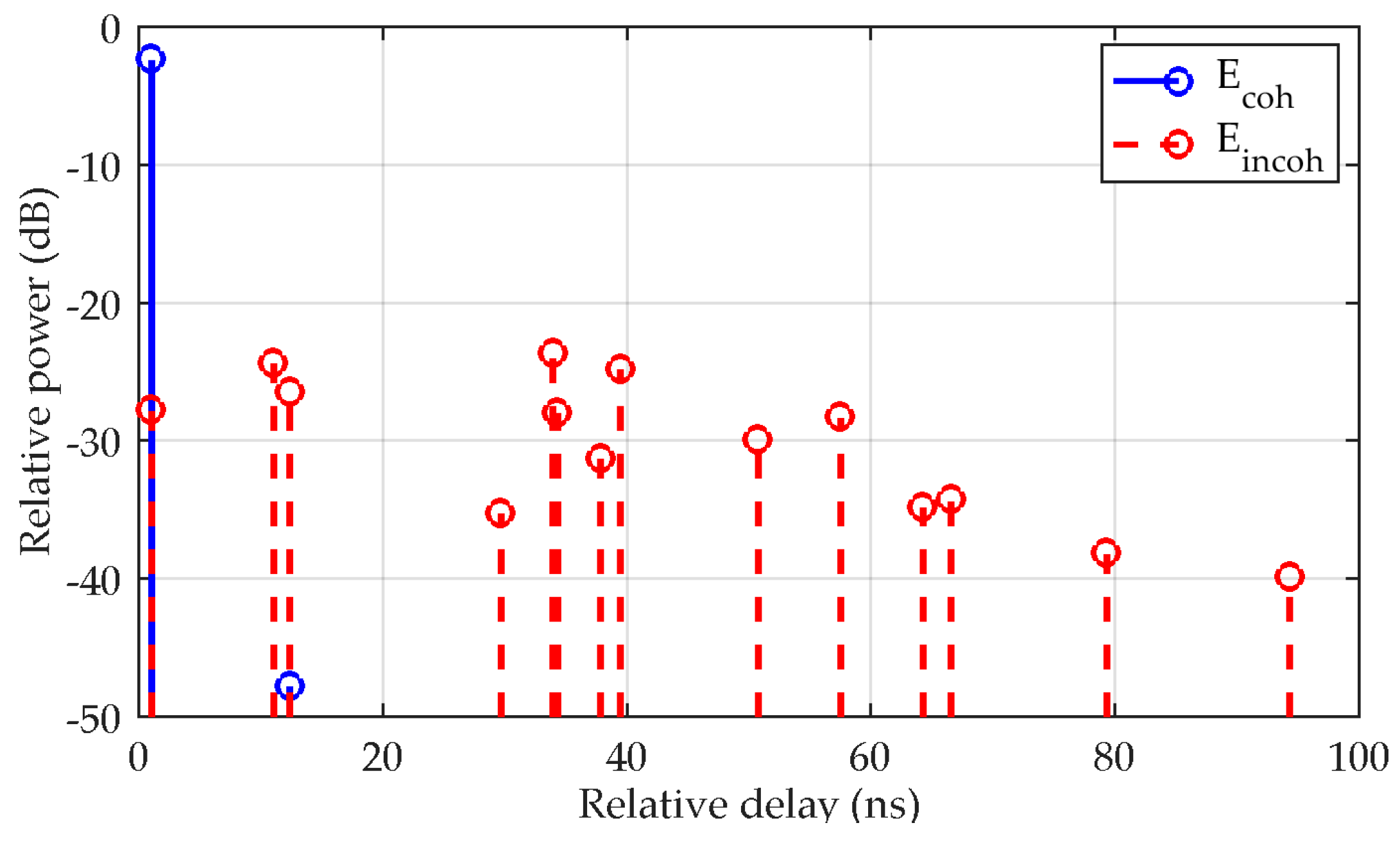
To demonstrate the differences between LoS and NLoS propagation conditions,
Figure 12 and
Figure 13 show the corresponding CIR characteristics for the experimental scenario from
Figure 8 and
Figure 9. Referring to
Figure 10 and
Figure 11, the CIR plots were generated for times of flight 5s (LoS) and 25 s (NLoS).
In
Figure 12, we clearly see that the direct signal (in black), actually present at Rx, is dominant. Its normalized power and time delay are 0 dB and 0 ns, respectively. The coherent scattered fields from the two closest tree canopies (in blue) have negligible effects on the resulting received signal as their level is at least 30 dB below the direct component. On the other hand, the level of incoherent scattered fields (in red) is generally higher. As already noted, this is the consequence of the fact that outside the forward scatter direction, the incoherent scattered field dominates. It should be noted that the resulting time delays of the incoherent scattered fields reflect the small separation of the tree canopies.
Figure 13 then shows the normalized CIR characteristics for the NLoS case achieved at the flight time 25 s. Now the direct signal between Tx and Rx is not shown, as it is actually blocked by a canopy. This is represented by the strong coherent scattered field with the lowest time delay which results in the attenuation behind the canopy. The other coherent scattered field from the second closest tree is negligible as it is outside the forward scatter direction. The incoherent scattered fields have about the same powers as in the LoS case, as these were not assumed to be blocked by other canopies. The longer maximum delay in the NLoS case is simply a consequence of the particular geometry.
In summary, the CIR characteristics can also be applied to the physical layer performance analyses where bit error rate (BER), word error rate (WER), etc., can be assessed for different modulation and coding schemes. The granularity of the CIR can be improved by further splitting the canopy contributions into those from each voxel, should this be required by the application. This resolution improvement does not affect the overall link’s SNR.
6. Discussion
The presented UAV channel synthesizer applicable in the presence of tree canopies relies on generating two types of scattered fields—coherent and incoherent. Their corresponding models have been presented in
Section 2. It should be noted that the validity of the PO/MST model for the coherent scattered field is limited by the fact that the path through a canopy should be below one or two skin depths, as noted in [
7]. This approximately restricts the model to frequencies from L to X band [
7] which are generally applicable for UAV communications.
It has also been demonstrated that a number of simplifications were made to generate the resulting time series within reasonable computation times. Mainly, the complex propagation constant within tree canopies was the same for all forward scatter directions. Similarly, as the worst case scenario, the incoherent scattered field calculations supposed the equivalent scattering cross section per unit volume to be independent of the scattering direction. Further, the coherent scattered fields were calculated only for the selected trees which were the closest to the forward scatter direction. Other simplifications then include neglecting ground reflections, presence of tree trunks, and blockage by main branches in the canopies. We have also restricted the analysis to the vertical polarization configuration, although the polarization information is present within the synthesizer.
It was demonstrated that the channel synthesizer matches the results that can be expected for an artificial scenario and, moreover, a very good match was identified for the case of the experimental data obtained for a typical UAV link in the presence of an alley of trees.
Due to the multiplicative nature of the synthesizer’s output, the generated time series can directly be converted into the resulting attenuation behind tree canopies and added, in the dB scale, to attenuation obtained for other propagation effects, e.g., diffraction by terrain features. In this way, the SNR graphs for a particular link can readily be obtained. It should be noted that the CIR characteristics generated by the synthesizer can also be used to simulate BER in the physical layer of UAV links.
7. Conclusions
We have presented a propagation channel synthesizer which enables the generation of a site-specific time series for the case of a signal propagating from a UAV towards its ground terminal, or vice versa, in the presence of tree canopies. This also includes any BLoS relay. Such scenarios can often be found in both urban and rural environments, for example, an alley of trees or a forest, respectively. Due to the size of the scenarios addressed, which may include several grown trees, full-wave solutions in electromagnetic simulators are not always possible.
However, we have introduced a new model which enables efficiently obtaining the coherent scattered fields based on PO, while accounting for the field passing through tree canopies. The incoherent scattered field is obtained by means of MST within the proposed synthesizer.
As a consequence, the generated time series are site-specific, correctly represent attenuation and diffraction effects caused by the presence of tree canopies, and follow the continuity of the electromagnetic field within the scenario of interest. Apart from the narrowband characteristics, the capability of the synthesizer to provide the wideband characteristics was demonstrated as well.
The synthesizer was validated using an artificial scenario, as well as an actual experimental dataset obtained with the use of a blimp as a UAV. An excellent agreement with the expected and actual results was found. With an average computation speed of one output value per 2 s for the case of a very large scenario including several grown trees, the proposed channel synthesizer proved to be a very efficient tool when the influence of vegetation on the UAV links is to be addressed.