Using UAS Hyperspatial RGB Imagery for Identifying Beach Zones along the South Texas Coast
Abstract
:1. Introduction
2. Background
2.1. Experiment Site
2.2. Color Features
2.3. Texture Features
2.4. Classification Techniques
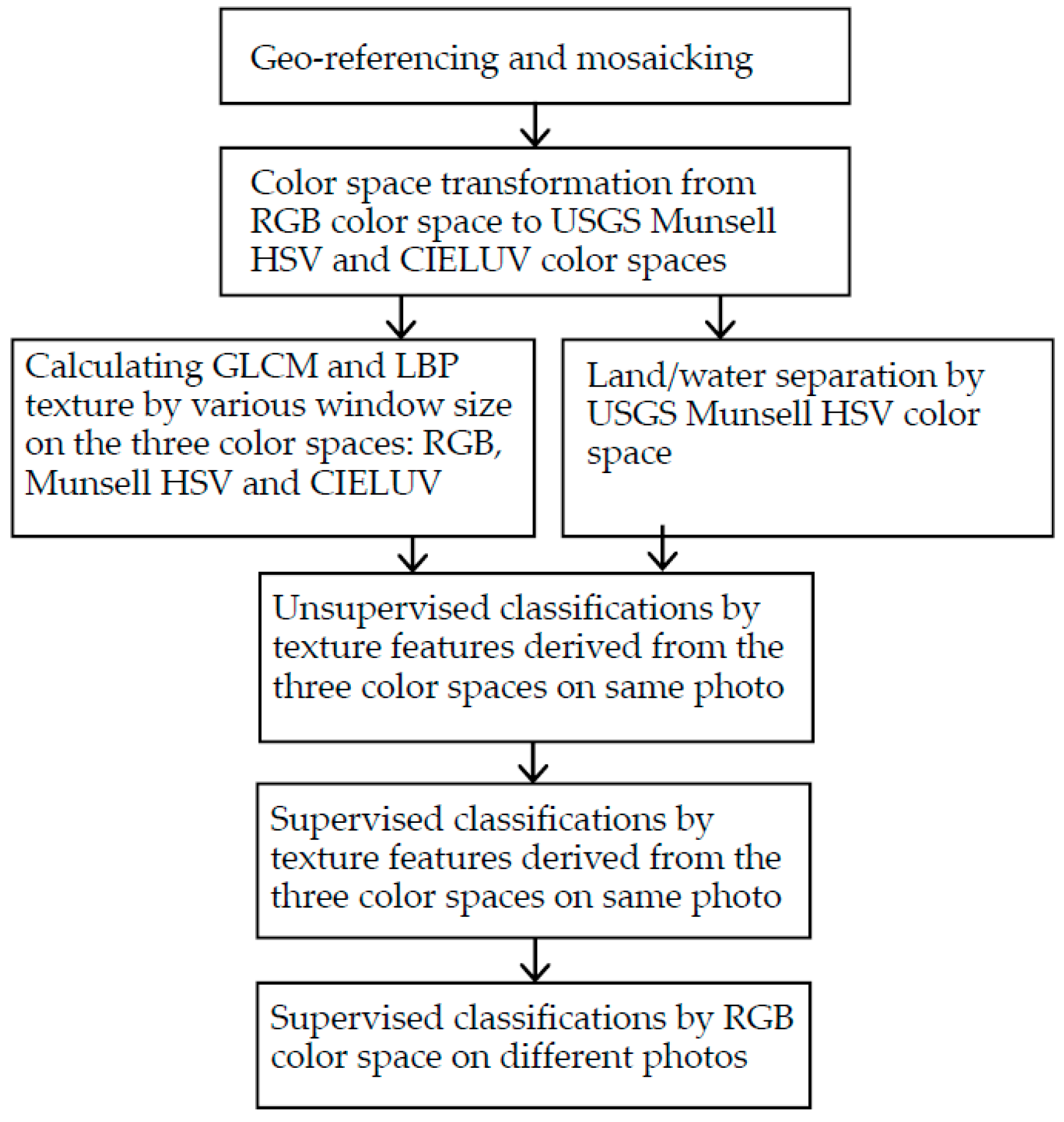
3. Materials and Methods
3.1. UAS Data
3.2. Sea and Land Separation by USGS Munsell Color System
3.2.1. Interaction of Light and Water and USGS Munsell Color Characteristics
3.2.2. Separation of Water and Land
3.3. ISODATA Identification of Beach Zones with Texture Features on the Same Photo
3.4. Supervised Classification for Beach Zones with Texture Features on the Same Photo
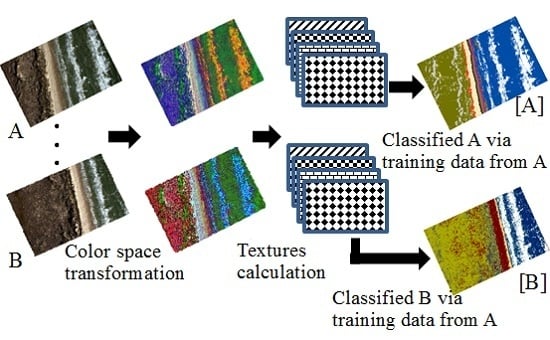
3.5. Beach Zone Classification in Different Photos Using a Training Set from Another Photo
4. Results and Discussions
4.1. Accuracies of Unsupervised Classification
4.2. Accuracies of Supervised Classification
4.3. Supervised Classification on Photos Using Training Sets from a Different Photo
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Woodroffe, C.D. Coasts: Form, Process and Evolution; Cambridge University Press: Cambridge, UK, 2002; pp. 248–320. [Google Scholar]
- Moore, L.J. Shoreline mapping techniques. J. Coast. Res. 2000, 16, 111–124. [Google Scholar]
- Addo, K.A.; Walkden, M.; Mills, J.P. Detection, measurement and prediction of shoreline recession in Accra, Ghana. ISPRS J. Photogram. Remote Sens. 2008, 63, 543–558. [Google Scholar] [CrossRef]
- Boak, E.H.; Turner, I.L. Shoreline definition and detection: A review. J. Coast. Res. 2005, 21, 688–703. [Google Scholar] [CrossRef]
- Texas General Land Office. Texas Coastal Construction Handbook; Texas General Land Office: Austin, TX, USA, 2001; pp. 4–9.
- Leatherman, S.P. Shoreline change mapping and management along the U.S. East Coast. J. Coast. Res. 2003, 38, 5–13. [Google Scholar]
- Crowell, M.; Leatherman, S.P.; Buckley, M.K. Historical shoreline change: Error analysis and mapping accuracy. J. Coast. Res., 1991, 7, 839–852. [Google Scholar]
- Turner, I.L.; Harley, M.D.; Drummond, C.D. UAVs for coastal surveying. Coast. Eng. 2016, 114, 19–24. [Google Scholar] [CrossRef]
- Mancini, F.; Dubbini, M.; Gattelli, M.; Stecchi, F.; Fabbri, S.; Gabbianelli, G. Using Unmanned Aerial Vehicles (UAV) for high-resolution reconstruction of topography: The Structure from motion approach on coastal environments. Remote Sens. 2013, 5, 6880–6898. [Google Scholar] [CrossRef] [Green Version]
- Long, N.; Millescamps, B.; Guillot, B.; Pouget, F.; Bertin, X. Monitoring the topography of a dynamic tidal inlet using UAV imagery. Remote Sens. 2016. [Google Scholar] [CrossRef] [Green Version]
- Gonçalves, J.A.; Henriques, R. UAV photogrammetry for topographic monitoring of coastal areas. ISPRS J. Photogram. Remote Sens. 2015, 104, 101–111. [Google Scholar] [CrossRef]
- Brunier, G.; Fleury, J.; Anthony, E.J.; Gardel, A.; Dussouillez, P. Close-range airborne Structure-from-Motion Photogrammetry for high-resolution beach morphometric surveys: Examples from an embayed rotating beach. Geomorphology 2016, 261, 76–88. [Google Scholar] [CrossRef]
- Papakonstantinou, A.; Topouzelis, K.; Pavlogeorgatos, G. Coastline zones identification and 3D coastal mapping using UAV spatial data. ISPRS Int. J. GeoInf. 2016. [Google Scholar] [CrossRef]
- Husson, E.; Ecke, F.; Reese, H. Comparison of manual mapping and automated object-based image analysis of non-submerged aquatic vegetation from very-high-resolution UAS images. Remote Sens. 2016, 8, 724. [Google Scholar] [CrossRef]
- Flynn, K.F.; Chapra, S.C. Remote sensing of submerged aquatic vegetation in a shallow non-turbid river using an unmanned aerial vehicle. Remote Sens. 2014, 6, 12815–12836. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, 6, 610–621. [Google Scholar] [CrossRef]
- Lillesand, T.; Kiefer, R.W.; Chipman, J. Remote Sensing and Image Interpretation, 6th ed.; John Wiley & Sons: Edison, NJ, USA, 2007. [Google Scholar]
- Laliberte, A.S.; Herrick, J.E.; Rango, A.; Winters, C. Acquisition, orthorectification, and object-based classification of Unmanned Aerial Vehicle (UAV) imagery for rangeland monitoring. Photogram. Eng. Remote Sens. 2010, 76, 661–672. [Google Scholar] [CrossRef]
- Feng, Q.; Liu, J.; Gong, J. UAV remote sensing for urban vegetation mapping using random forest and texture analysis. Remote Sens. 2015, 7, 1074–1094. [Google Scholar] [CrossRef]
- Ojala, T.; Pietikäinen, M.; Mäenpää, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Nanni, L.; Lumini, A.; Brahnam, S. Survey on LBP based texture descriptors for image classification. Expert Syst. Appl. 2012, 39, 3634–3641. [Google Scholar] [CrossRef]
- Tunnell, J.W., Jr. Geography, climate, and hydrology. In The Laguna Madre of Texas and Tamaulipas; Texas A&M University Press: College Station, TX, USA, 2001; pp. 7–27. [Google Scholar]
- Morton, R.A.; McGowen, J.H. Modern Depositional Environments of the Texas Coast; Bureau of Economic Geology, University of Texas: Austin, TX, USA, 1980. [Google Scholar]
- Weise, B.R.; White, W.A. Padre Island National Seashore: A Guide to the Geology, Natural Environments, and History of a Texas Barrier Island; Bureau of Economic Geology; University of Texas: Austin, TX, USA, 1980. [Google Scholar]
- Morton, R.A.; Speed, F.M. Evaluation of shorelines and legal boundaries controlled by water levels on sandy beaches. J. Coast. Res. 1998, 14, 1373–1384. [Google Scholar]
- Ilea, D.E.; Whelan, P.F. Image segmentation based on the integration of colour–texture descriptors—A review. Pattern Recognit. 2011, 44, 2479–2501. [Google Scholar] [CrossRef]
- Zhang, H.; Fritts, J.E.; Goldman, S.A. Image segmentation evaluation: A survey of unsupervised methods. Comput. Vis. Image Underst. 2008, 110, 260–280. [Google Scholar] [CrossRef]
- Kuehni, R.G. The early development of the Munsell system. Color Res. Appl. 2002, 27, 20–27. [Google Scholar] [CrossRef]
- Richards, J.A.; Jia, X. Remote Sensing Digital Image Analysis: An Introduction; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Ball, G.H.; Hall, D.J. ISODATA: A Method of Data Analysis and Pattern Classification; Stanford Research Institute: Menlo Park, CA, USA, 1965. [Google Scholar]
- Jensen, J.R. Introductory Digital Image Processing: A Remote Sensing Perspective; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with Support Vector Machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Su, L. Optimizing support vector machine learning for semi-arid vegetation mapping by using clustering analysis. ISPRS J. Photogram. Remote Sens. 2009, 64, 407–413. [Google Scholar] [CrossRef]
- Su, L.; Huang, Y. Support Vector Machine (SVM) classification: Comparison of linkage techniques using a clustering–based method for training data selection. GISci. Remote Sens. 2009, 46, 411–423. [Google Scholar] [CrossRef]
- Hsu, C.W.; Chang, C.C.; Lin, C.J. A Practical Guide to Support Vector Classification; Technical Report; Department of Computer Science and Information Engineering, National Taiwan University: Taipei, Taiwan, 2009. [Google Scholar]
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995.
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013; pp. 316–321. [Google Scholar]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007; pp. 840–898. [Google Scholar]



| Class | Munsell Hue | Munsell Value | Munsell Saturation |
|---|---|---|---|
| Vegetated land | high | middle | low |
| Sea | low | middle | middle |
| Shadows | very low | low | high |
| White foam | very low | high | high |
| Sand beach | high | high | high |
| Band | Red | Green | Blue | L of CIELUV | Munsell Value |
|---|---|---|---|---|---|
| Accuracy | 85.8 (0.81)* | 82.8 (0.77) | 81.3 (0.75) | 82.8 (0.77) | 83.6 (0.78) |
| Window Size | Contrast | Homogeneity | Variance | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Red | Green | Blue | Red | Green | Blue | Red | Green | Blue | |
| 3 × 3 | 85.1 (0.80) | 80.6 (0.74) | 81.3 (0.75) | 85.1 (0.80) | 82.8 (0.77) | 79.1 (0.72) | 85.8 (0.81) | 83.6 (0.78) | 81.3 (0.75) |
| 7 × 7 | 85.8 (0.81) | 79.9 (0.73) | 80.6 (0.74) | 85.8 (0.81) | 79.9 (0.73) | 77.6 (0.70) | 84.3 (0.79) | 79.1 (0.72) | 81.3 (0.75) |
| 15 × 15 | 86.6 (0.82) | 79.9 (0.73) | 82.8 (0.77) | 85.8 (0.81) | 82.1 (0.76) | 79.1 (0.72) | 65.7 (0.54) | 62.7 (0.50) | 63.4 (0.51) |
| 31 × 31 | 85.6 (0.82) | 76.1 (0.68) | 79.1 (0.72) | 85.1 (0.80) | 79.9 (0.73) | 77.6 (0.70) | 53.0 (0.38) | 57.5 (0.44) | 62.7 (0.51) |
| 63 × 63 | 76.1 (0.68) | 73.1 (0.64) | 69.4 (0.59) | 77.6 (0.70) | 72.4 (0.63) | 73.1 (0.64) | 56.0 (0.42) | 58.2 (0.45) | 61.2 (0.49) |
| Window Size | Contrast | Homogeneity | Variance | |||
|---|---|---|---|---|---|---|
| Munsell V | CIELUV L | Munsell V | CIELUV L | Munsell V | CIELUV L | |
| 3 × 3 | 82.8 (0.77) | 77.6 (0.70) | 82.8 (0.77) | 78.4 (0.71) | 82.8 (0.77) | 79.1 (0.72) |
| 7 × 7 | 81.3 (0.75) | 77.6 (0.70) | 83.6 (0.78) | 78.4 (0.71) | 83.6 (0.78) | 77.6 (0.70) |
| 15 × 15 | 79.9 (0.73) | 83.6 (0.78) | 83.6 (0.78) | 82.8 (0.77) | 67.9 (0.57) | 81.3 (0.75) |
| 31 × 31 | 76.9 (0.69) | 83.6 (0.78) | 81.3 (0.75) | 82.8 (0.77) | 63.4 (0.52) | 75.4 (0.67) |
| 63 × 63 | 71.6 (0.62) | 82.8 (0.77) | 74.6 (0.66) | 82.8 (0.77) | 61.9 (0.50) | 64.2 (0.52) |
| Scale 1 | Scale 2 | Scale 3a | Scale 3b | Scale 5 | |
|---|---|---|---|---|---|
| Red | 87.3 (0.83) | 85.8 (0.81) | 82.8 (0.77) | 82.1 (0.76) | 67.2 (0.56) |
| Green | 82.8 (0.77) | 81.3 (0.75) | 78.4 (0.71) | 78.4 (0.71) | 70.9 (0.61) |
| Blue | 82.1 (0.76) | 80.6 (0.74) | 79.1 (0.72) | 79.1 (0.72) | 73.1 (0.64) |
| L of CIELUV | 82.1 (0.76) | 83.6 (0.78) | 82.8 (0.77) | 82.8 (0.77) | 82.8 (0.77) |
| Munsell Value | 82.8 (0.77) | 82.1 (0.76) | 77.6 (0.70) | 79.1 (0.72) | 68.7 (0.58) |
| Red LBP | Green LBP | Blue LBP | |
|---|---|---|---|
| MLC | 92.1(0.89) | 92.1(0.89) | 92.1 (0.89) |
| RF | 88.6(0.84) | 88.6(0.84) | 93.0 (0.90) |
| SVM | 89.5(0.85) | 89.5(0.85) | 89.5 (0.85) |
| Window Size | MLC | RF | SVM | MLC | RF | SVM |
|---|---|---|---|---|---|---|
| Red GLCM Homogeneity by Red | RGB GLCM Homogeneity by Red | |||||
| 3 × 3 | 88.6 (0.83) | 87.7 (0.83) | 86.8 (0.81) | 94.7 (0.92) | 92.1 (0.89) | 93.9 (0.91) |
| 7 × 7 | 86.8 (0.81) | 88.6 (0.84) | 89.5 (0.85) | 93.9 (0.91) | 93.0 (0.90) | 94.7 (0.92) |
| 15 × 15 | 90.4 (0.86) | 90.4 (0.86) | 91.2 (0.87) | 92.1 (0.89) | 92.1 (0.89) | 93.9 (0.91) |
| 31 × 31 | 89.5 (0.85) | 89.5 (0.85) | 92.1 (0.89) | 93.0 (0.90) | 89.5 (0.85) | 94.7 (0.92) |
| 63 × 63 | 88.6 (0.84) | 89.4 (0.85) | 91.2 (0.87) | 92.1 (0.89) | 90.3 (0.86) | 92.0 (0.89) |
| DSC_7559 | DSC_7611 | DSC_7479 | |
|---|---|---|---|
| MLC | 92.1(0.89) | 94.4(0.92) | 91.3(0.88) |
| RF | 93.0(0.90) | 89.7(0.85) | 91.4(0.88) |
| SVM | 93.9(0.91) | 93.5(0.91) | 91.4(0.88) |
| Vegetated | Dry | Wet | Water | Row Total | User’s Accuracy (%) | |
|---|---|---|---|---|---|---|
| Vegetated | 15 | 3 | 0 | 0 | 18 | 83.3 |
| Dry | 0 | 33 | 0 | 0 | 33 | 100.0 |
| Wet | 0 | 0 | 15 | 4 | 19 | 78.9 |
| Water | 0 | 0 | 2 | 42 | 44 | 95.5 |
| Column Total | 15 | 36 | 17 | 46 | ||
| Producer’s Accuracy | 100.0 | 91.7 | 88.2 | 91.3 | 92.1 |
| Vegetated | Dry | Wet | Water | Row Total | User’s Accuracy (%) | |
|---|---|---|---|---|---|---|
| Vegetated | 35 | 3 | 0 | 0 | 38 | 92.1 |
| Dry | 3 | 24 | 0 | 1 | 28 | 85.7 |
| Wet | 0 | 0 | 7 | 3 | 10 | 70.0 |
| Water | 0 | 0 | 0 | 40 | 40 | 100.0 |
| Column Total | 38 | 27 | 7 | 44 | ||
| Producer’s Accuracy | 92.1% | 88.9% | 100.0% | 90.9% | 91.4 |
| Vegetated | Dry | Wet | Water | Row Total | User’s Accuracy (%) | |
|---|---|---|---|---|---|---|
| Vegetated | 28 | 0 | 0 | 0 | 28 | 100.0 |
| Dry | 0 | 25 | 3 | 0 | 28 | 89.3 |
| Wet | 0 | 0 | 7 | 2 | 9 | 77.8 |
| Water | 0 | 1 | 0 | 41 | 42 | 97.6 |
| Column Total | 28 | 26 | 10 | 43 | ||
| Producer’s Accuracy | 100.0 | 96.2 | 70.0 | 95.3 | 94.4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, L.; Gibeaut, J. Using UAS Hyperspatial RGB Imagery for Identifying Beach Zones along the South Texas Coast. Remote Sens. 2017, 9, 159. https://0-doi-org.brum.beds.ac.uk/10.3390/rs9020159
Su L, Gibeaut J. Using UAS Hyperspatial RGB Imagery for Identifying Beach Zones along the South Texas Coast. Remote Sensing. 2017; 9(2):159. https://0-doi-org.brum.beds.ac.uk/10.3390/rs9020159
Chicago/Turabian StyleSu, Lihong, and James Gibeaut. 2017. "Using UAS Hyperspatial RGB Imagery for Identifying Beach Zones along the South Texas Coast" Remote Sensing 9, no. 2: 159. https://0-doi-org.brum.beds.ac.uk/10.3390/rs9020159