Appendix A.1. Notation
The following notation and remarks will be used in several of the proofs below. We use P to denote the state-dependent stochastic choice of the DM, i.e., . The distribution over posteriors induced by P is denoted by . Recall that the support of is the collection , where , and is the probability assigned to posterior . Given and , the mixture of the induced distributions over posteriors is defined as usual: The support of the mixture is the union of the supports of and , and the probability of each in the support is the corresponding average of probabilities of in the two distributions.
Remark A1. Suppose that P solves either (*) or (**). If , then choosing a must be optimal given belief , that is . Indeed, if that was not the case then choosing the same distribution over posteriors but playing some action from the arg max would increase the utility of the DM without changing the cost of information. Furthermore, a must be the unique optimal action given belief . Indeed, if there are multiple optimal actions at some induced posterior, then this is inconsistent with optimality, as shown in the proof of Proposition 7.
Remark A2. Given P and , if and the posteriors induced by P and induced by are not equal, then the mixture has two different posteriors associated with the same action a. In particular, if P and are both optimal in (*), and if , then . Indeed, if P and are optimal, then so is any mixture of and .
Given a decision problem
, we write
for the expected utility that the DM obtains with choice
P. Notice that this can also be expressed using
as
Similarly, we write
for the cost of
P. Thus, problem (*) can be written as
, and problem (**) as
subject to
.
Appendix A.2. Proofs of Propositions
Proof of Proposition 1. Fix a decision problem
and
. We prove here that if
P is optimal for (**) then the budget constraint (
1) binds. As explained in the text, the rest of the argument is a standard application of the KKT theorem.
For each let . Denote , where . Then a choice P gives the DM expected utility of if and only if for every . Our assumption that different actions are optimal at different states means that whenever . It follows that if P achieves then P reveals the realized state with probability one, and therefore that .
Now, suppose that P is such that the constraint is slack, . Because it follows from the previous paragraph that . For define , where satisfies . Then , and since C is continuous in P we have that for small enough, so is feasible. This shows that P is not a solution for (**). □
Proof of Lemma 1. Fix
c and let
P be a solution to (**). By Proposition 1 the budget constraint binds, implying that
P must be informative. In particular, there must be two actions
such that
. Moreover, Proposition 1 implies that there is
, such that conditions (
4) and (
5) are satisfied. From (
4) we have that for every
or, after rearranging,
Because we assumed that actions are not duplicates, there exists some
at which
, which implies that the right-hand side of the last equation is strictly monotone in
. It follows that
is pinned down uniquely by
P. Denote this
by
.
Now, suppose that also solves (**) with the same c. By Proposition 1 solves (*) with some . We claim that it must be the case that . Indeed since they are both optimal in (**), and, since the budget constraint binds, . This implies that P is also optimal for (*) with , so by the previous paragraph .
Next, we prove that
is (weakly) decreasing. Let
and suppose per absurdum that
. Let
P be optimal for (**) with
c and
optimal for (**) with
. Then
where the first inequality follows from
P being optimal for (*) with
, the next equality holds since the budget constraint in (**) binds, the strict inequality is by the assumptions that
and
, and the last equality is again by the binding budget constraint. Rearranging gives
contradicting the optimality of
for (*) with
.
Finally, we show that the image of
contains the entire open interval
. Combining this with the monotonicity proved above implies both continuity and
. Suppose that
is in this interval. Let
P be optimal for (*) with
. Notice that
is impossible, since that would imply that any
also has an uninformative solution, contradicting the assumption that
. It also can not be that
since that would require the posteriors to be at the vertices of the simplex, contradicting (
4). Thus,
and it follows from Proposition 1 that
P is also optimal for (**) with
. Therefore,
, i.e.,
is in the image. This completes the proof. □
Proof of Proposition 2. Because there are only two states, we identify distributions over with the probability they assign to . Define to be the set of all , such that there exists a solution P to (*) satisfying . We break the proof into several claims.
Claim 1. The set is non-empty and bounded from above.
Proof. If
P is optimal and
then by (
4) we have
and also
. As
we either get
and
, or vice versa.
16 From Remark A1,
a and
b must be optimal given beliefs
and
, respectively. This is only possible if
when
is sufficiently small. It is also clear that choosing ′no information′ is not optimal for
small enough, since it is not optimal at
. Thus, every sufficiently small
is in
.
On the other hand, as the ratio converges to 1. Because must be in the convex-hull of the induced posteriors, all the induced posteriors necessarily converge to as (see the proof of Proposition 7 for details). Additionally, since we assumed that neither nor are optimal at , this implies that these actions are not considered for large enough . Thus, is bounded from above. □
Claim 2. Let . Then in problem (*) with there are two solutions, and , such that and .
Proof. First, consider a sequence converging to from below, such that for each n there is a solution to (*) with satisfying . Such a sequence exists by the definition of . By taking a subsequence if needed we may assume that converges. By the theorem of the maximum the limit is optimal at . In addition, we must have : For every we have for all n, implying . Additionally, it is impossible that or since these actions are not optimal at .
Second, let
be a sequence converging to
, but this time from above. Let
be a corresponding solution sequence such that
for each
n.
17 Subsequently, the limit
is optimal at
, and by the definition of
we have
for every
n, also implying that
. □
Claim 3. For and constructed in Claim 2, .
Proof. Because H is strictly concave over , it is sufficient to show that is a mean-preserving spread of . We consider two different cases. Suppose first that , i.e., neither of the two extreme actions is in the consideration set of . Subsequently, by Remark A1, every posterior induced by is in-between the two posteriors induced by . This implies that is a mean-preserving spread of as needed.
The other case is when . Since has at most two elements, the intersection contains exactly one element, say . Denote the support of by and the support by . Remark A1 implies that . In addition, since both and are optimal, Remark A2 implies that . Therefore, we again get that is a mean-preserving spread of and the claim is proved. If the argument is symmetric. □
So far, we have shown that , and that . By monotonicity proved in Lemma 1 this implies that for every . The next claim completes the proof of the proposition.
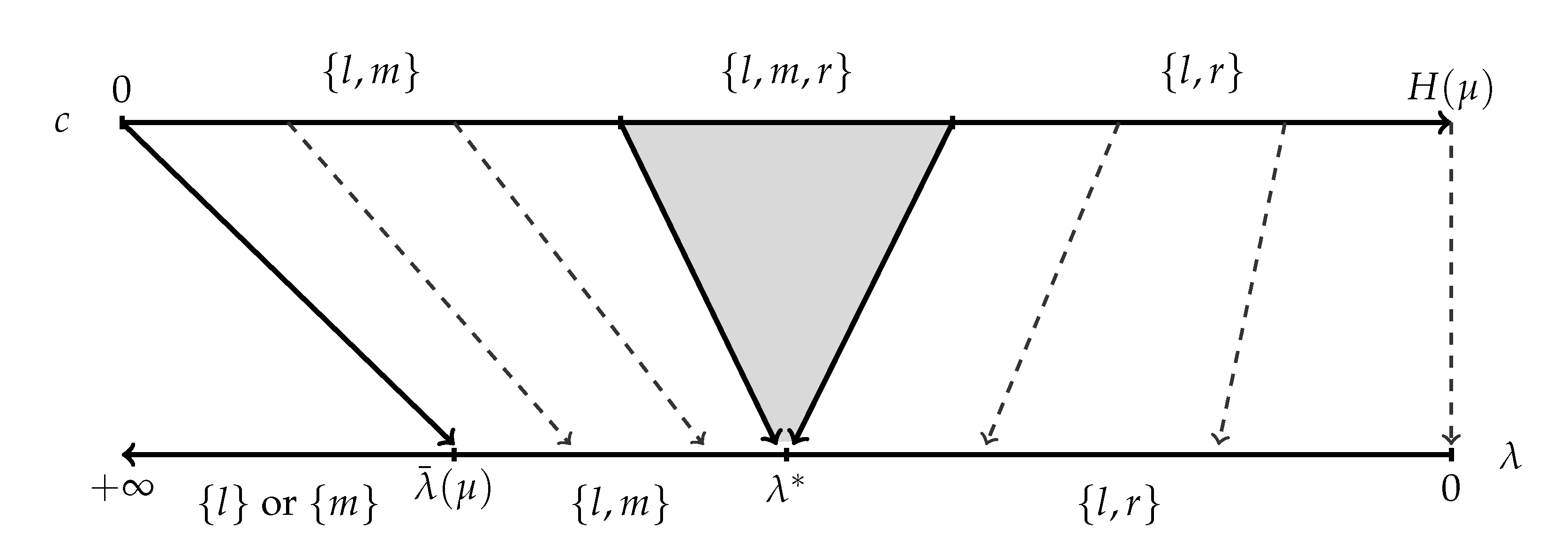
Claim 4. Denote . There is such that if P is optimal for (**) with then .
Proof. Assume, contrary to the claim, that there is a sequence converging to from below and a corresponding sequence , such that solves (**) with and for every n. Because of the budget constraint binds, we have for all n, so for n large enough also solves (*) with . Denote and the corresponding posteriors by (it can not be that since then ). Additionally, recall that are the posteriors induced by . There are three cases to consider:
First, it can not be that , since by Remark A2 this would imply and , contradicting the assumption that .
Second, suppose that for some action . Then again by Remark A2 this would imply . Additionally by Remark A1 the other posterior is smaller and bounded away from , contradicting the assumption that . The argument for is analogous.
Third, if , then both and are between and bounded away from , so can not converge to . □
Proof of Proposition 3. For the most part the proof follows the footsteps of the proof of Proposition 2. We only provide details when a different argument is needed.
Claim 5. For any , if P solves (*) then either or .
Proof. Suppose by contradiction that
P is optimal and
. From Remark A1, if
then the associated posterior
must satisfy
, implying that
for any
. Let
i be such that
. Then
contradicting the assumption in the proposition. □
Define to be the set of all , such that there exists a solution P to (*), satisfying .
Claim 6. The setis non-empty and bounded from above.
Proof. We first prove that, if is small enough and P solves (*), then . By Claim 5, this implies that , so .
For
o to be considered, Condition (
7) requires that for every
Summing up over all
i gives
Since this inequality clearly can not hold for small enough.
To show that is bounded, note that the assumption of the proposition implies that o is the unique optimal action at . By Proposition 7, this implies that obtaining no information is the unique optimal choice for all large enough. □
Claim 7. Let . Then in problem (*) with there are two solutions, and , such that and .
Proof. The proof is identical to that in Claim 2, except that to argue that we need to use Claim 5. □
Claim 8. For and constructed in the previous claim, .
Proof. We denote by the posterior corresponding to induced by and by the one induced by (if ).
Because
,
must coincide with the solution given in ([
9], Theorem 1) when all of the
’s are considered. In particular, the induced posteriors are symmetric in the sense that
is the same for all
i. It follows that
. On the other hand, by Remark A2 we must have
whenever
, implying that
where the strict inequality follows from
(recall Claim 5) and
. Therefore, we got that
, and since both are optimal for (*) with
it must be that
. □
Claim 9. Denote . There is such that if P is optimal for (**) with then .
Proof. Suppose by contradiction that , and that for each n solves (**) with but . Then , so for n large enough also solves (*) with . Since we can not have , so by Claim 5 . The exact same argument as in the previous claim gives . Moreover, is bounded away from zero, since is not in the convex-hull of any strict subset of . This implies that there is such that for every n. However, and are both optimal for (*) with , so . This contradicts the convergence of to . □
Proof of Proposition 4. Fix a collection as in the proposition. Define by . Because f is strictly convex, for each there is an affine function such that and for every . Let the set of actions be and the utility function be , where is the Dirac measure on state .
To complete the description of the decision problem we need to choose the prior . By assumption, one of the elements of , say , is in the convex hull of the others. Define for some .
Consider the set
We claim that this set contains a non-degenerate interval of
c values. Indeed, one element of this set is
. Additionally, we have
for some probability vector
, so
is also in this set. The strict concavity of
H implies that the former is strictly larger than the latter. By taking convex combinations of these two representations of
we can get any
c in between. Denote
and
. Note that
.
Finally, consider problem (**) with
. Subsequently, by the definition of
and
, there are strictly positive
satisfying
and
. We claim that this distribution over posteriors is optimal. Indeed, this gives an expected utility of
where the first equality is by the definition of
u and the affinity of
, the inequality is obvious, the next equality follows from
, and the last equality is by construction of
. On the other hand, for any feasible distribution over posteriors
we have
where the first equality is again by the definition of
u and the affinity of
, the inequality follows from
for all
j, and the last inequality follows from feasibility (the reduction of entropy must be at most
c). Moreover, if
for some
i, then
for every
j, so the first inequality is strict. This completes the proof. □
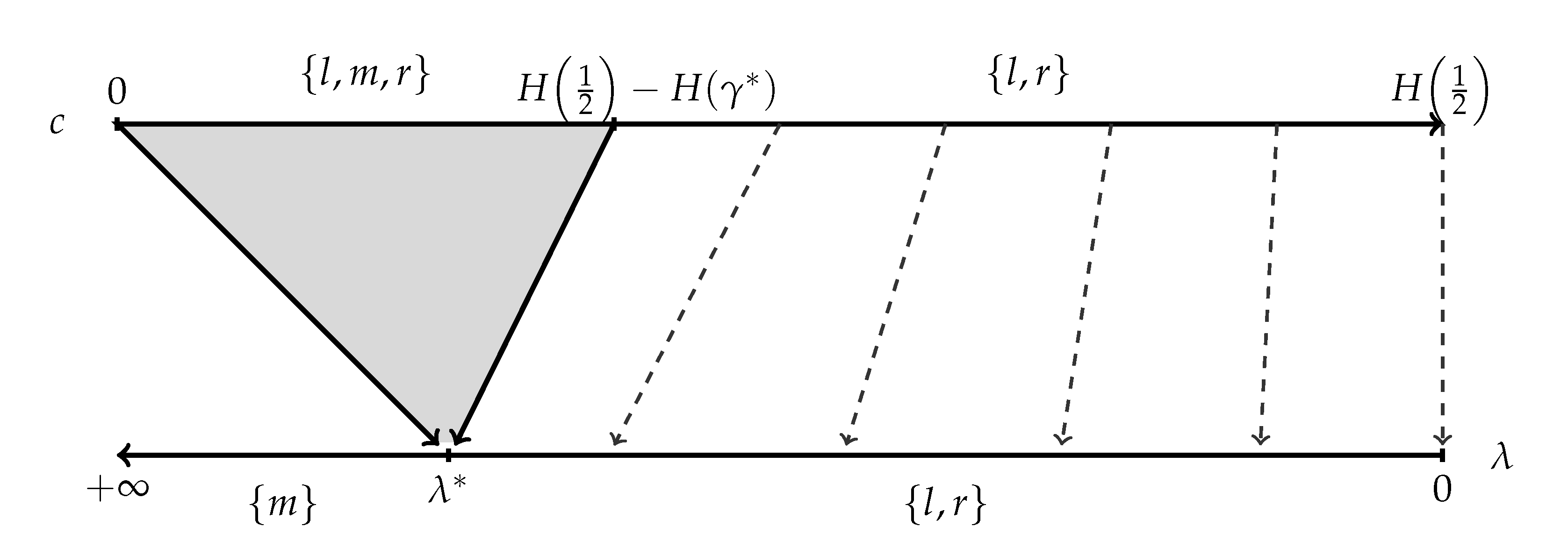
Proof of Proposition 7. From Proposition 1 and Lemma 1 it immediately follows that is equal to the infimum of the set of ’s for which an uninformative P is optimal in problem (*). Thus, to prove the proposition, it is enough to show that is an indifference point if and only if the set of such ’s is empty.
We start by showing that if
is not an indifference point then for
large enough the optimal solution to (*) is uninformative. For this proof, we view
as the unit simplex of
endowed with the metric
. Let
be the set of beliefs at which
is the unique optimal action. Because
K is relatively open in
and
, there is
such that
whenever
.
Let
. Suppose that
is large enough, so that
. If
P is optimal for (*) with
, the, n for every
and every
, we have
where the first equality is by (
4), and the next inequality is by the definition of
M. We thus get
where in the first equality we used the fact that optimal posteriors are never on the boundary of
(implied by condition (
4)), and the following inequality is by (
A1).
Now, since
, we also have for every
and every
Taking the maximum over
gives
where the last inequality is from (
A2). By the construction of
this implies that
for every
. Thus, by Remark A1,
P induces a unique posterior and is therefore uninformative.
In the other direction, we now claim that, if
is an indifference point, then an uninformative
P can not be a solution of (*) with any
. Indeed, let
be two optimal actions given belief
. Consider
, as given by
for every
. Note that
is optimal among the set of uninformative
P’s. However, we have
and
. Because
are not duplicates, condition (
4) can not hold for any
, implying that
is not optimal.
18 □
Appendix A.3. Proofs of Claims in the Example
We start with the following lemma.
Lemma A1. Fix a consideration set . The posteriors satisfy (
4)
with some if and only if: - (i)
For : .
- (ii)
For : and .
- (iii)
For : , and .
Proof - (i)
Condition (
4) with
and
requires
in state
and
in
. It is immediate to verify that these two equations are equivalent to
.
- (ii)
Similarly, condition (
4) with
and
requires
in
and
in
, and these two equations are satisfied if and only if the posteriors are as in the lemma.
- (iii)
When all three actions are considered condition (
4) is equivalent to the equations in both previous cases holding simultaneously. In particular, it implies that both
and
. This pins down
at
, and consequentially the posteriors
, as above.
□
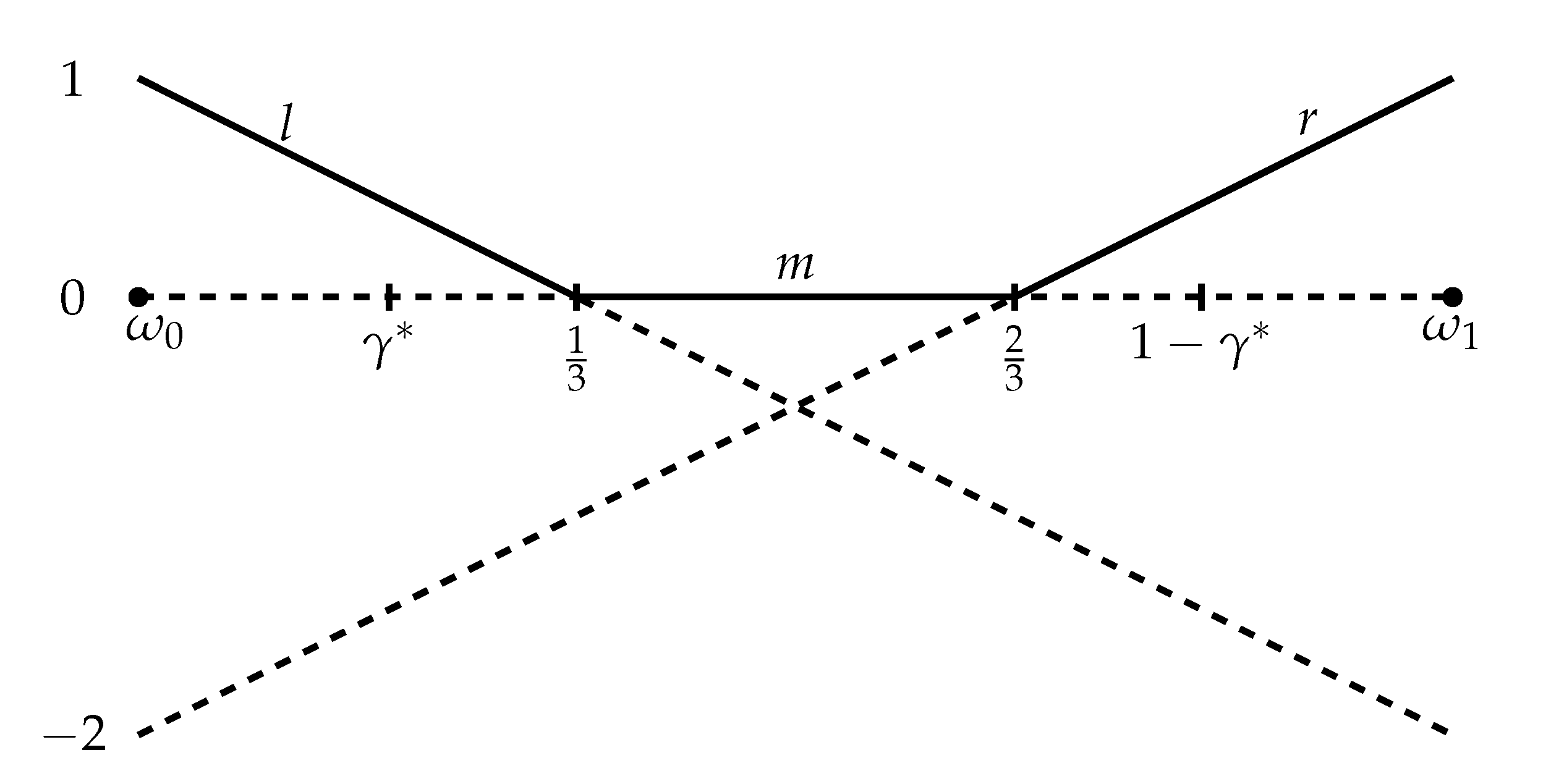
Case 1:
Claim 10. Solution of (*): If then and . If then and . If then any mixture (including degenerate) of the former two solutions is optimal.
Proof. Suppose
, and we will show that
is optimal. From Lemma A1 (i), condition (
4) is equivalent to
. Condition (
5) with
and
requires
Plugging in
and rearranging, this condition becomes
, which holds by assumption. Condition (
7), with
and
, is identical, given that
.
Suppose now that
. We need to show that obtaining no information is optimal. Condition (
4) is trivially satisfied, so we only need to check (
5) for
and
. For
, this gives
which is equivalent to
. For
, we get the exact same condition.
Finally, when it follows from the last two paragraphs that both and are still optimal. Because the set of optimal distributions over posteriors is convex, it follows that any mixture of these solutions is optimal as well. Note that at the posteriors of the risky actions in the solution are given by . □
Claim 11. Solution of (**): If then the solution is given by , , , and . If then and is determined by the equation .
Proof. Suppose
. We show that
is optimal. From Lemma A1 (iii) it must be that
,
, and that the value of the lagrange multiplier is
. Setting
and
, we get that
. In addition, the expected reduction of entropy from the prior to the posteriors is given by
so the budget constraint (
6) binds. By Proposition 1, we are done.
Once
it is no longer possible that all three actions are considered, since, given the location of the posteriors, the budget constraint can not bind. We show that
is optimal. Define
by the equation
, and set
. Let
. Subsequently,
and the budget constraint binds. Set
to solve
. Afterwards, condition (
4) is satisfied by Lemma A1 (i). Furthermore, since
we know that
, which implies that
. Thus, (
5) holds for
and
in the same way as in the case
of the previous claim. □
Case 2:
Claim 12. Solution of (*): When we have , , and the probabilities are set to satisfy . At the solution is not unique, with , , and all possible. When , , the posteriors are , , and the probabilities are adjusted, so that . Finally, for , it is optimal to obtain no information, and the consideration set is either or when is below or above , respectively.
Proof. The proof for
is identical to the
case. Suppose that
and we prove that
is optimal. By Lemma A1 (ii), condition (
4) is equivalent to
and
. We need to check condition (
5) with
and
. For
, this requires
which boils down to
. For
, the condition is
which, again, is equivalent to
. Finally, we need that
is in the interior of the convex hull of
and
. It is not hard to check that this is equivalent to
.
Note that at both solutions with and with are optimal, and therefore any mixture is optimal as well. This implies that is also optimal.
Suppose now that
. We consider the case where
, so obtaining no information implies that
and
(the case
in which
is similar). We need to check (
5) with
and
. These conditions are given by
and
respectively. For every
, the second inequality implies the first, and it is satisfied if and only if
. This completes the proof. □
Claim 13. Solution of (**): For the consideration set is , and the distribution over posteriors is determined by the equations , and . For the consideration set is , the posteriors are , and the probabilities adjust so that the expected posterior is equal to and the cost is equal to c. For , the consideration set is , the posteriors are determined by and , and their probabilities by .
Proof. Fix
c in the first range. The function
is strictly increasing on
, strictly decreasing on
, and is equal to
at both
and
. It follows that, for each
, there is a unique
, such that
, and that as
increases the corresponding
decreases. Therefore, given
, there is a unique way to choose the posteriors
and the probabilities
, such that (1)
; (2)
; and, (3)
.
19 Now, define
as the (unique) solution to
, and note that this implies
. By Lemma A1 (ii) condition (
4) holds. Finally,
implies that
, so condition (
4) holds in the same way as in the previous claim.
Moving on to , the distribution in the claim is optimal by Proposition 1 with . The lower end of the range of c is obtained by the distribution with support and only, while the upper end by the distribution with support and only.
When the proof is as in the previous claims. □
Case 3:
Claim 14. The solution of (*): for we have , , and determined by . For , the solution is , i.e., no information.
Proof. Fix
and set the posteriors as in the claim. Subsequently, (
4) holds by Lemma A1 (i). As in the previous cases above, condition (
5) with
and
is equivalent to
; for
in the current range it is easy to check that
, so the condition holds by assumption. Finally, we need that
, which is equivalent to
.
Assume now
. Set
and
. Condition (
5) with
and
requires
and
respectively. For any
in the range, the second inequality implies the first and it is satisfied if and only if
. □
Claim 15. The solution of (**): For any the consideration set is and . The posterior is determined by the equation , and the probability is then determined by the equation .
Proof. Fix c and define by . Let and set to solve . The fact that implies that , which in turn implies that as well as that . The optimality of these posteriors now follows in the same way as in the previous claim. □